| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Захват и эмиссия носителей заряда дефектами кристалла.
Здесь под дефектами подразумеваются любые локальные отступления от периодической структуры кристалла и в первую очередь мелкие и глубокие примесные центры. В § 3 уже отмечалось, что появление примесных центров в кристалле приводит к перераспределению электронов по уровням энергии. Один, два или даже три электрона, локализованных на донорном уровне, могут покинуть его и перейти в зону проводимости. С другой стороны, однократно или многократно ионизованный донорный центр захватывает электроны, перемещающиеся по кристаллу.
Акцепторные центры эмитируют в валентную зону дырки и захватывают их обратно (рис. 33).
Если один и тот же дефект может захватить электрон из зоны проводимости и дырку из валентной зоны, то носители

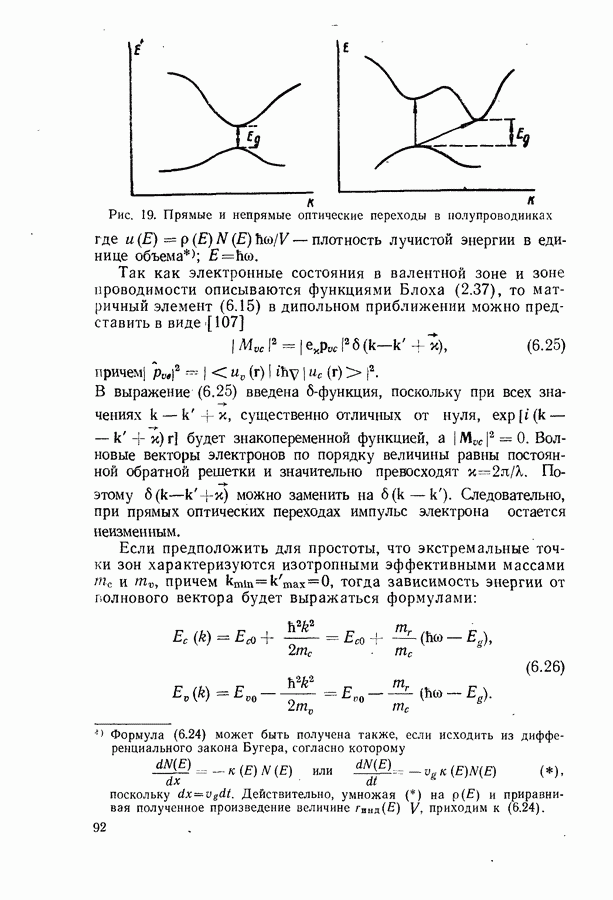
Рис. 33. Оптические и неоптическне переходы в слабо легированном полупроводнике: 1,2 — эмиссия и захват электрона донорным центром; 3,4 — эмиссия и захват дырки акцепторным дефектом; 5,6 — заброс электрона с акцепторного уровня в зону проводимости и его обратный переход; 7,8 — заброс электрона из валентной зоны на доиорный уровень и его обратный переход; 9—12 — переходы между глубокими уровнями дефекта и зонами;
13, 14 — переходы между примесными центрами
противоположных знаков рекомбинируют на нем и такой дефект называют центром рекомбинации. Если же носитель может эмитироваться дефектом только в ту дону, из которой он был захвачен, а переходы с другой зоной запрещены правилами отбора, то такой дефект называется центром прилипания, или ловушкой. Электрон, захваченный ловушкой из зоны проводимости, не может непосредственно перейти в валентную зону. Участие такого электрона в других переходах становится возможным только после обратного заброса его в зону проводимости. То же самое справедливо относительно дырок, захваченных ловушками из валентной зоны. Единственный переход, который они могут совершить, находясь на ловушке, это возвращение в валентную зону.
Переходы с участием примесных центров в кристалле бывают оптическими с поглощением или испусканием квантов света, неоптическими с поглощением или испусканием фононов, рекомбинацией Оже (§ 11) и т. д.
Ионизация примесных центров под действием квантов света, или фотоионизация, проявляется в спектрах поглощения. Очевидно, фотоионизация примесного центра будет возможна только в том случае, если энергия квантрв света не меньше глубины залегания дефекта  Для мелких водородоподобных примесных центров значение энергии ионизации
Для мелких водородоподобных примесных центров значение энергии ионизации  дается формулой (2.52) при значении квантового числа
дается формулой (2.52) при значении квантового числа  и имеет порядок
и имеет порядок  Следовательно, полосы поглощения, связанные с фотоионизацией мелких примесей, необходимо искать в спектре в области длин волн
Следовательно, полосы поглощения, связанные с фотоионизацией мелких примесей, необходимо искать в спектре в области длин волн

Обнаружение таких полос связано не только с техническими, но и с принципиальными трудностями. В этой области спектра больших значений достигает коэффициент поглощения света свободными носителями (§ 10).
Однако в некоторых соединениях энергия ионизации примесей значительно больше  и соответствующие спектры поглощения зафиксированы на опыте.
и соответствующие спектры поглощения зафиксированы на опыте.
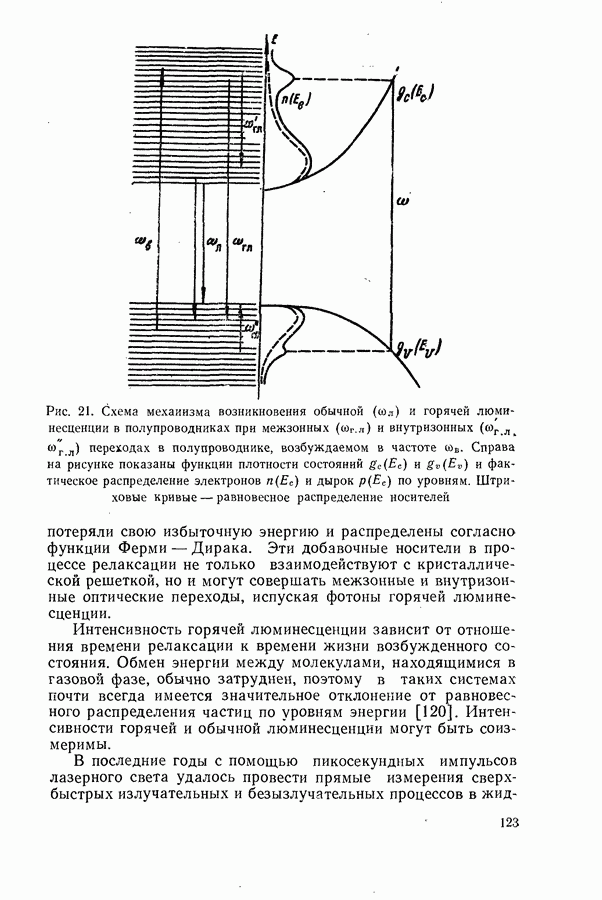
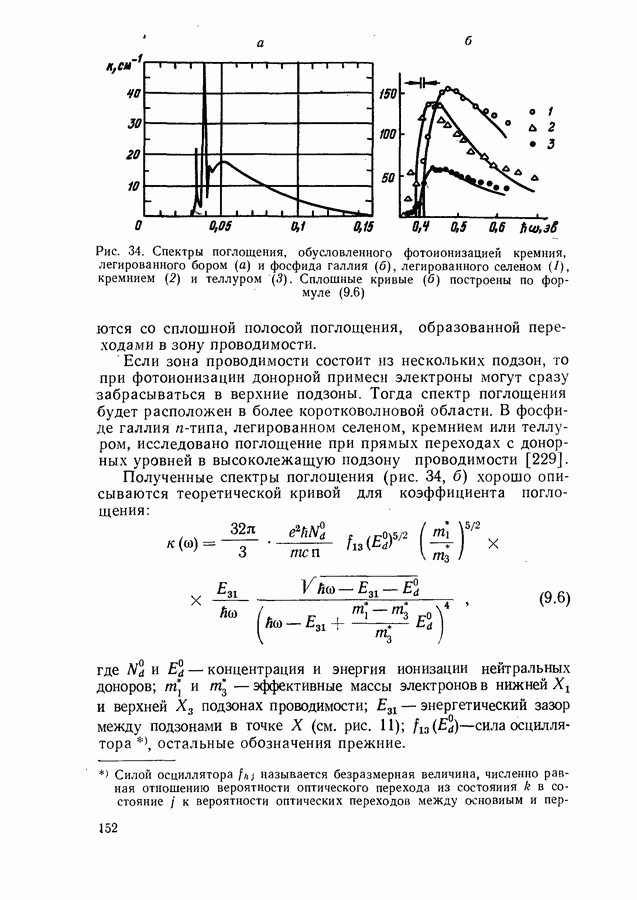
На рис. 34, а приведен спектр поглощения, связанный с фотоионизацией бора в монокристаллах кремния [111, 228]. Энергия пиков поглощения удовлетворяет формуле

где  — номера возбужденных состояний примеси. Пики поглощения, обусловленного переходами на более высокие энергетические уровни, неразличимы, так как они
— номера возбужденных состояний примеси. Пики поглощения, обусловленного переходами на более высокие энергетические уровни, неразличимы, так как они

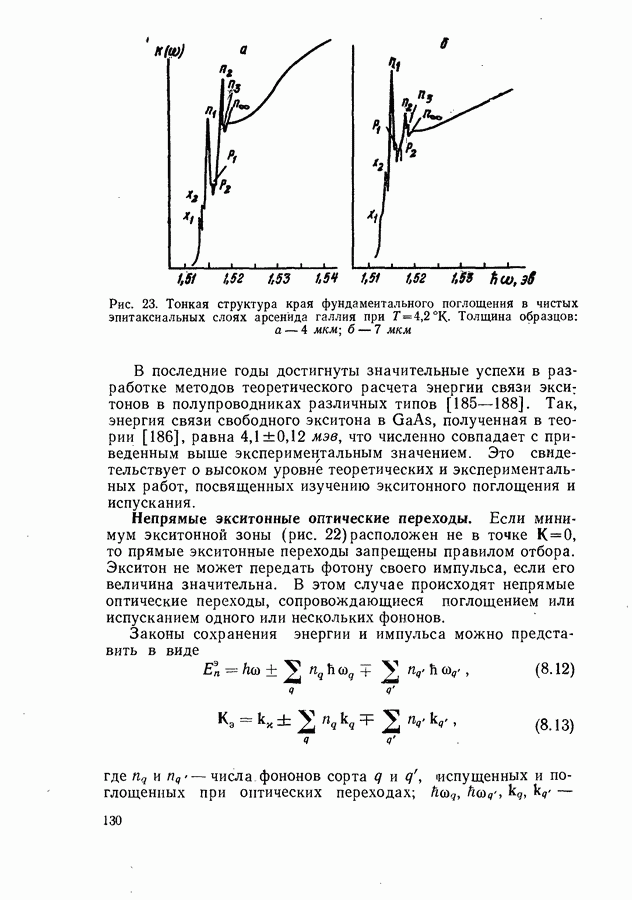
Рис. 34. Спектры поглощения, обусловленного фотоионизацией кремния, легированного бором (а) и фосфида галлия (б), легированного селеном (1), кремнием (2) и теллуром (3). Сплошные кривые (б) построены по формуле (9.6)
сливаются со сплошной полосой поглощения, образованной переходами в зону проводимости.
Если зона проводимости состоит из нескольких подзон, то при фотоионизации донорной примеси электроны могут сразу забрасываться в верхние подзоны. Тогда спектр поглощения будет расположен в более коротковолновой области. В фосфиде галлия  -типа, легированном селеном, кремнием или теллуром, исследовано поглощение при прямых переходах с донорных уровней в высоколежащую подзону проводимости [229].
-типа, легированном селеном, кремнием или теллуром, исследовано поглощение при прямых переходах с донорных уровней в высоколежащую подзону проводимости [229].
Полученные спектры поглощения (рис. 34, б) хорошо описываются теоретической кривой для коэффициента поглощения:

где  концентрация и энергия ионизации нейтральных доноров;
концентрация и энергия ионизации нейтральных доноров;  эффективные массы электронов в нижней
эффективные массы электронов в нижней  и верхней
и верхней  подзонах проводимости;
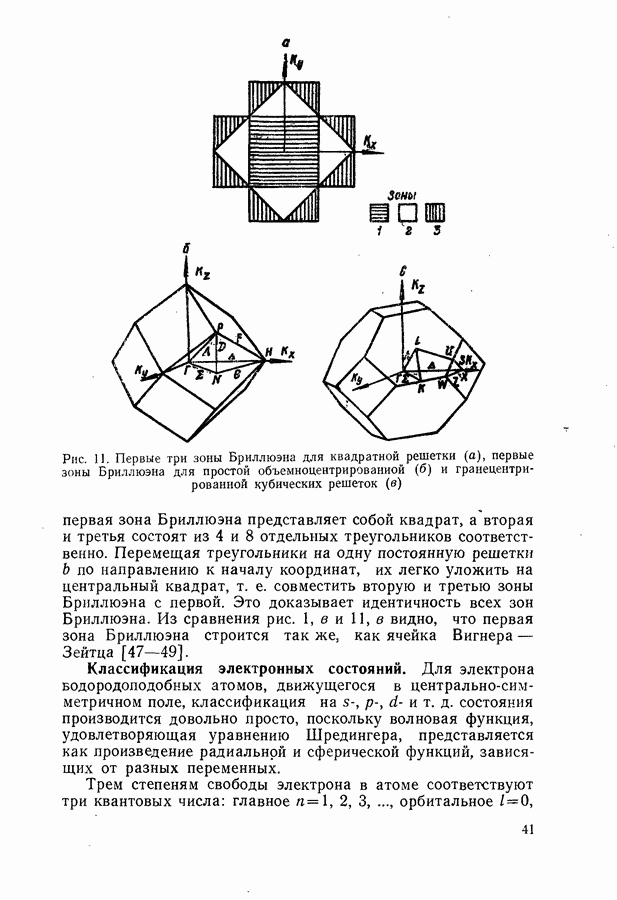
подзонах проводимости;  энергетический зазор между подзонами в точке X (см. рис. 11);
энергетический зазор между подзонами в точке X (см. рис. 11);  сила осциллятора, остальные обозначения прежние.
сила осциллятора, остальные обозначения прежние.
Вероятности переходов между уровнями примесных центров и зонами можно рассчитать в рамках теории возмущений по методу, изложенному в § 6. Основная трудность заключается в необходимости предварительного отыскания волновых функций  описывающих движение носителей, локализованных около примесных центров.
описывающих движение носителей, локализованных около примесных центров.
Обозначая эффективный периодический потенциал решетки через  уравнение Шредингера для таких функций можно представить в виде
уравнение Шредингера для таких функций можно представить в виде

где  потенциальная энергия электрона в поле локального дефекта.
потенциальная энергия электрона в поле локального дефекта.
Функция  в целом имеет сложный и в большинстве случаев малоизученный вид. Однако на больших по сравнению с размерами элементарной ячейки расстояниях дефект с зарядом
в целом имеет сложный и в большинстве случаев малоизученный вид. Однако на больших по сравнению с размерами элементарной ячейки расстояниях дефект с зарядом  создает электростатический потенциал, который можно аппроксимировать формулой для электростатического потенциала точечного заряда
создает электростатический потенциал, который можно аппроксимировать формулой для электростатического потенциала точечного заряда  где
где  диэлектрическая постоянная кристалла. В этой области
диэлектрическая постоянная кристалла. В этой области  равно потенциалу кулоновского взаимодействия точечных зарядов в среде
равно потенциалу кулоновского взаимодействия точечных зарядов в среде

Вблизи дефекта формула (9.8) неприменима. Поэтому принципиальное значение имеют размеры электронных орбит дефекта. В неглубоких примесных центрах энергия связи
электрона сравнительно невелика  Электрон внешней оболочки такого центра почти свободен. Размеры его орбиты составляют десятки ангстрем, т. е. орбита охватывает большое количество элементарных ячеек кристалла. Движение электронов мелких дефектов в первом приближении можно описывать с помощью уравнения Шредингера с кулоновским потенциалам (9.8).
Электрон внешней оболочки такого центра почти свободен. Размеры его орбиты составляют десятки ангстрем, т. е. орбита охватывает большое количество элементарных ячеек кристалла. Движение электронов мелких дефектов в первом приближении можно описывать с помощью уравнения Шредингера с кулоновским потенциалам (9.8).
В глубоких центрах энергия связи электрона значительно больше. Например, примеси атомов меди и золота в кремнии и германии связывают электроны с энергией порядка  Размеры орбит таких электронов составляют несколько ангстрем, т. е. сравнимы с величиной элементарной ячейки решетки. Отыскание волновых функций, описывающих движение электронов глубоких центров, представляет весьма сложную задачу, которая не получила удовлетворительного решения до настоящего времени.
Размеры орбит таких электронов составляют несколько ангстрем, т. е. сравнимы с величиной элементарной ячейки решетки. Отыскание волновых функций, описывающих движение электронов глубоких центров, представляет весьма сложную задачу, которая не получила удовлетворительного решения до настоящего времени.
Волновую функцию мелкого донорного состояния можно представить в виде [228]

где  число эквивалентных минимумов в зоне проводимости
число эквивалентных минимумов в зоне проводимости

— функции Блоха для  минимума;
минимума;  водородоподобная функция перекрытия; V — объем кристалла. Поскольку
водородоподобная функция перекрытия; V — объем кристалла. Поскольку  мало изменяется в пределах ячейки кристалла, то локально электрон движется, как будто он находится в состоянии с функцией Блоха
мало изменяется в пределах ячейки кристалла, то локально электрон движется, как будто он находится в состоянии с функцией Блоха 
Если имеется только один минимум, то

где

 эффективный радиус Бора (2.53), индекс
эффективный радиус Бора (2.53), индекс  указывает на то, что функции Блоха относятся к самой нижней зоне проводимости.
указывает на то, что функции Блоха относятся к самой нижней зоне проводимости.
Как видно из (9.14), удельный вес функций  в волновой функции донорного состояния с увеличением
в волновой функции донорного состояния с увеличением  быстро убывает. Поэтому вероятность прямых переходов донор — зона проводимости будет резко уменьшаться с увеличением
быстро убывает. Поэтому вероятность прямых переходов донор — зона проводимости будет резко уменьшаться с увеличением
значения  и энергии кванта света при
и энергии кванта света при  Этим объясняется падение поглощения на длинноволновом крае поглощения (рис. 34, а), связанного с фотоионизацией примеси, хотя плотность состояний в зоне проводимости растет с увеличением энергии
Этим объясняется падение поглощения на длинноволновом крае поглощения (рис. 34, а), связанного с фотоионизацией примеси, хотя плотность состояний в зоне проводимости растет с увеличением энергии  Ряд важных закономерностей, связанных с фотоионизацией мелких примесей, установлен в работах [230—237]. Квазиклассический расчет сечений многофононного захвата носителей на примесные центры в некондоновском приближении выполнен в работе [238].
Ряд важных закономерностей, связанных с фотоионизацией мелких примесей, установлен в работах [230—237]. Квазиклассический расчет сечений многофононного захвата носителей на примесные центры в некондоновском приближении выполнен в работе [238].
Теория оптических переходов с участием глубоких центров начала развиваться только в последние годы. Рассчитаны волновые функции и сечения ионизации для нескольких простых моделей глубокого дефекта.  Луковский [239] для расчета сечения ионизации глубокого центра, в частности индия в кремнии, в качестве
Луковский [239] для расчета сечения ионизации глубокого центра, в частности индия в кремнии, в качестве  использовал
использовал  -образный потенциал. В этой модели сечение ионизации
-образный потенциал. В этой модели сечение ионизации  при
при  равном энергии ионизации
равном энергии ионизации  С увеличением
С увеличением  быстро растет и достигает максимума, когда
быстро растет и достигает максимума, когда  а затем убывает как
а затем убывает как  при
при  Полученная закономерность согласуется с экспериментальными данными для примеси индия в кремнии с
Полученная закономерность согласуется с экспериментальными данными для примеси индия в кремнии с  Для более мелких примесей в кремнии, таких, как
Для более мелких примесей в кремнии, таких, как  теоретические результаты значительно расходятся с экспериментальными, поскольку в теории не учитывается дальнодействующая часть кулоновского потенциала.
теоретические результаты значительно расходятся с экспериментальными, поскольку в теории не учитывается дальнодействующая часть кулоновского потенциала.
При расчете коэффициента захвата носителей заряда глубокими ловушками в гомеополярных полупроводниках В. Л. Бонч-Бруевич [240] обобщил модель Луковского и потенциальную энергию электрона в поле ловушки аппроксимировал выражением

Вероятности захвата носителя дефектом и его эмиссии в зоны не являются независимыми параметрами. Так как при термодинамическом равновесии выполняется принцип детального равновесия, то отсюда следует, что указанные вероятности должны быть связаны достаточно общим соотношением.
Найдем эту связь для слабо легированного полупроводника  -типа. Статистика рекомбинации электронов и дырок в полупроводниках с небольшой концентрацией изолированных друг от друга дефектов наиболее полно исследована
-типа. Статистика рекомбинации электронов и дырок в полупроводниках с небольшой концентрацией изолированных друг от друга дефектов наиболее полно исследована
В. Шокли и В. Т. Ридом [71, 86, 241]. Поэтому рекомбинацию в такой модели полупроводника называют рекомбинацией Шокли — Рида. Обозначим вероятности переходов буквой  с соответствующими индексами, указывающими направление
с соответствующими индексами, указывающими направление
перехода электрона:  - вероятность перехода с уровня
- вероятность перехода с уровня  зоны проводимости на донор;
зоны проводимости на донор;  -вероятность обратного перехода.
-вероятность обратного перехода.
Обозначая концентрацию доноров через  а вероятности заполнения электронами уровней зоны проводимости и донорных уровней
а вероятности заполнения электронами уровней зоны проводимости и донорных уровней  через
через  скорости захвата и эмиссии электрона дефектом можно представить в виде:
скорости захвата и эмиссии электрона дефектом можно представить в виде:

Здесь по-прежнему  — плотность состояний в зоне проводимости. При термодинамическом равновесии
— плотность состояний в зоне проводимости. При термодинамическом равновесии  равны значениям функции Ферми — Дирака для энергий
равны значениям функции Ферми — Дирака для энергий  а вероятность того, что состояние с энергией
а вероятность того, что состояние с энергией  свободно, можно представить в виде
свободно, можно представить в виде

Согласно принципу детального равновесия, скорости любого прямого и обратного процесса равны. Поэтому из равенства  с учетом (9.18) находим
с учетом (9.18) находим

Легко убедиться, что вероятность эмиссии дырки с акцепторного уровня  на уровень
на уровень  зоны проводимости
зоны проводимости  связана с вероятностью захвата дырки акцептором
связана с вероятностью захвата дырки акцептором  аналогичным соотношением
аналогичным соотношением

Хотя формулы (9.19) и (9.20) строго доказаны для термодинамического равновесия, предполагается, что они справедливы и при отсутствии равновесия, когда скорости прямых и обратных переходов не равны.
Чтобы получить суммарные значения скоростей захвата или эмиссии электронов донорными центрами, необходимо проинтегрировать (9.16) и (9.17) по всем значениям энергии зоны проводимости. Если предположить при этом, что  не зависит от
не зависит от  то полные скорости
то полные скорости  будут выражаться простыми формулами:
будут выражаться простыми формулами:

где  число нейтральных (занятых электронами) доноров,
число нейтральных (занятых электронами) доноров,

— константа диссоциации доноров.
При термодинамическом равновесии

и полные скорости захвата и эмиссии равны. Хотя число свободных состояний в зоне проводимости, по которым производится интегрирование, может быть на много порядков больше  константа диссоциации не достигает слишком больших значений из-за наличия экспоненциального множителя под знаком интеграла (9.21). Величина
константа диссоциации не достигает слишком больших значений из-за наличия экспоненциального множителя под знаком интеграла (9.21). Величина  равна вероятности диссоциации донора с выбросом электрона на любой из уровней зоны проводимости. Аналогично вводится понятие диссоциации акцептора.
равна вероятности диссоциации донора с выбросом электрона на любой из уровней зоны проводимости. Аналогично вводится понятие диссоциации акцептора.
Как уже отмечалось, вероятности  зависят от волнового вектора, а следовательно, от энергии электрона. Поэтому формулы типа (9.16а), (9.17а) носят приближенный характер. При изменении концентрации примесей или интенсивности возбуждающего света в таких пределах, что сильно изменяется степень заполнения зон, параметры
зависят от волнового вектора, а следовательно, от энергии электрона. Поэтому формулы типа (9.16а), (9.17а) носят приближенный характер. При изменении концентрации примесей или интенсивности возбуждающего света в таких пределах, что сильно изменяется степень заполнения зон, параметры  нельзя считать постоянными. В частности, если
нельзя считать постоянными. В частности, если  уменьшается с увеличением
уменьшается с увеличением  то с увеличением накачки
то с увеличением накачки  как среднее значение
как среднее значение  также будет уменьшаться.
также будет уменьшаться.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
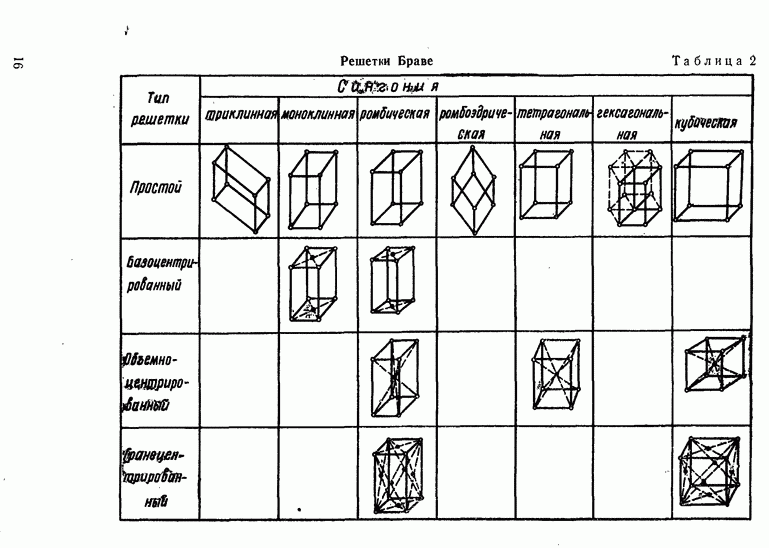
- Классификация кристаллических решеток.
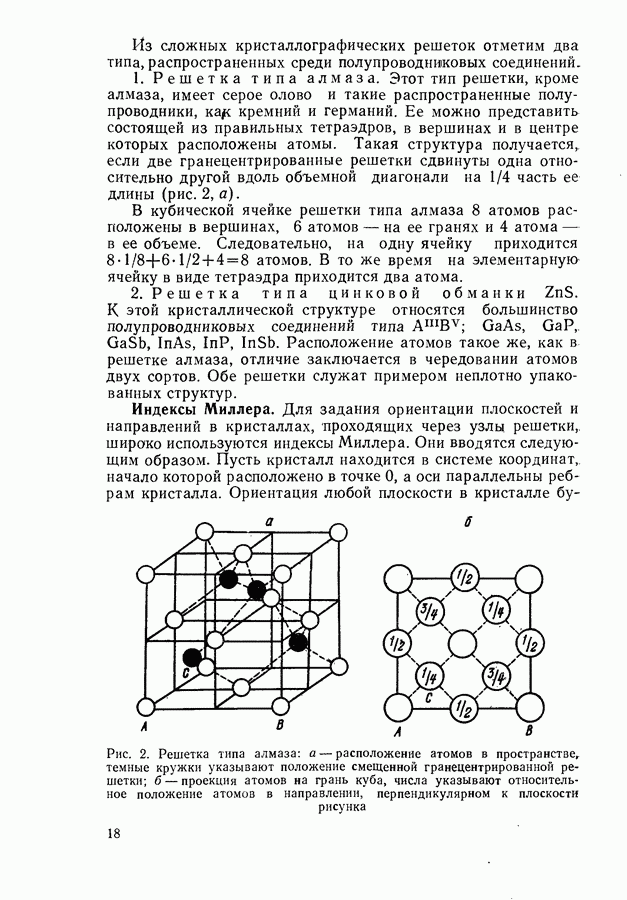
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
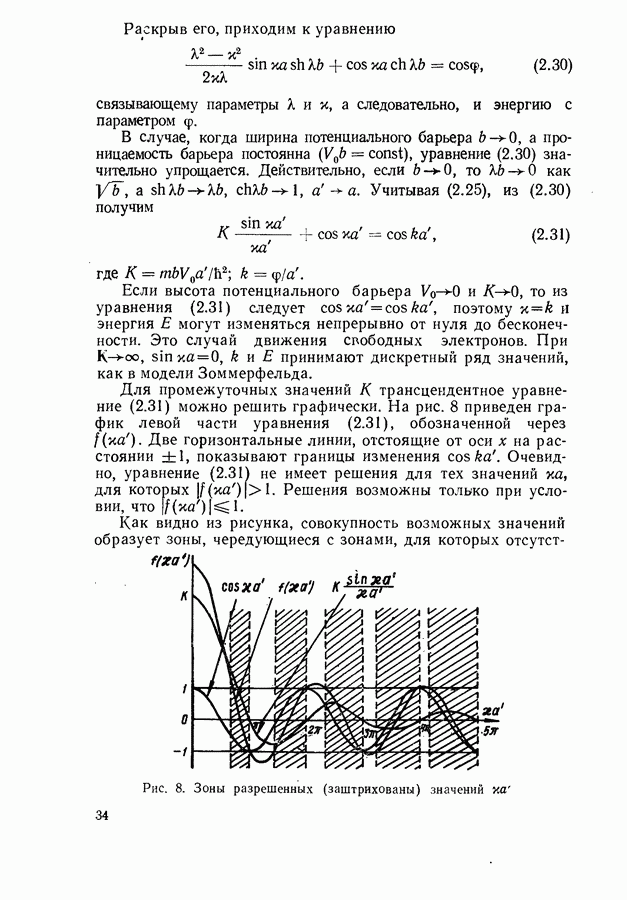
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
- Эффект Келдыша-Франца.
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
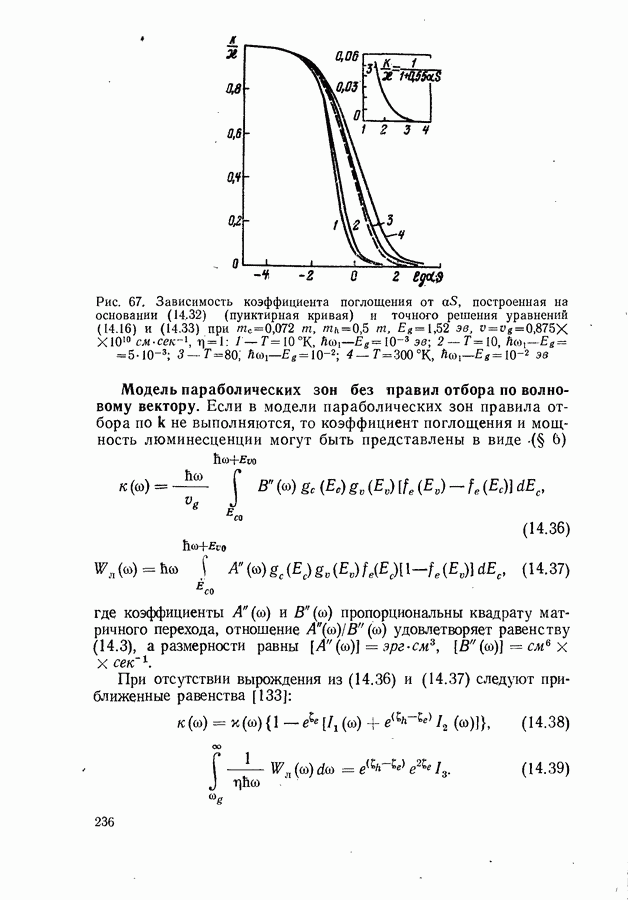
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
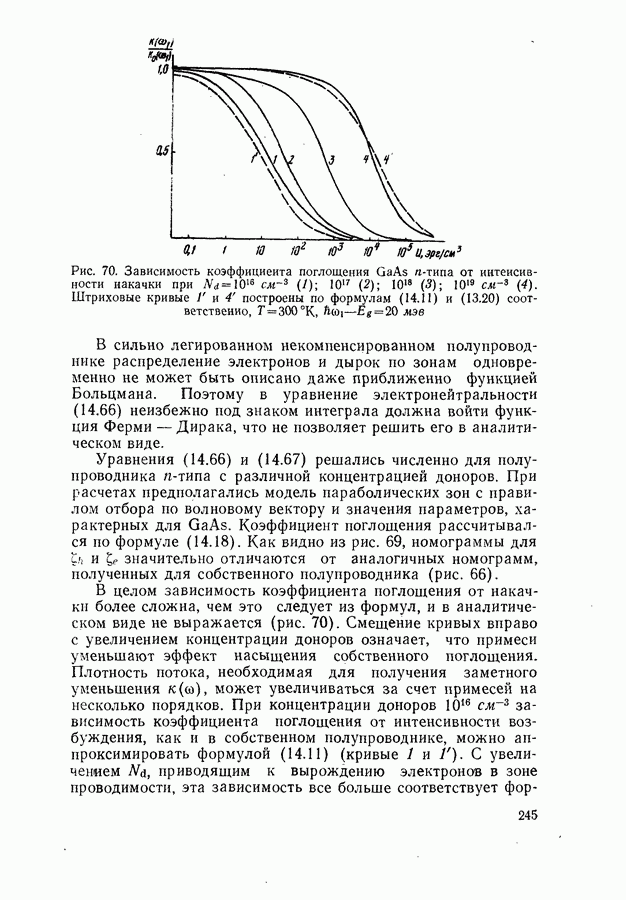
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
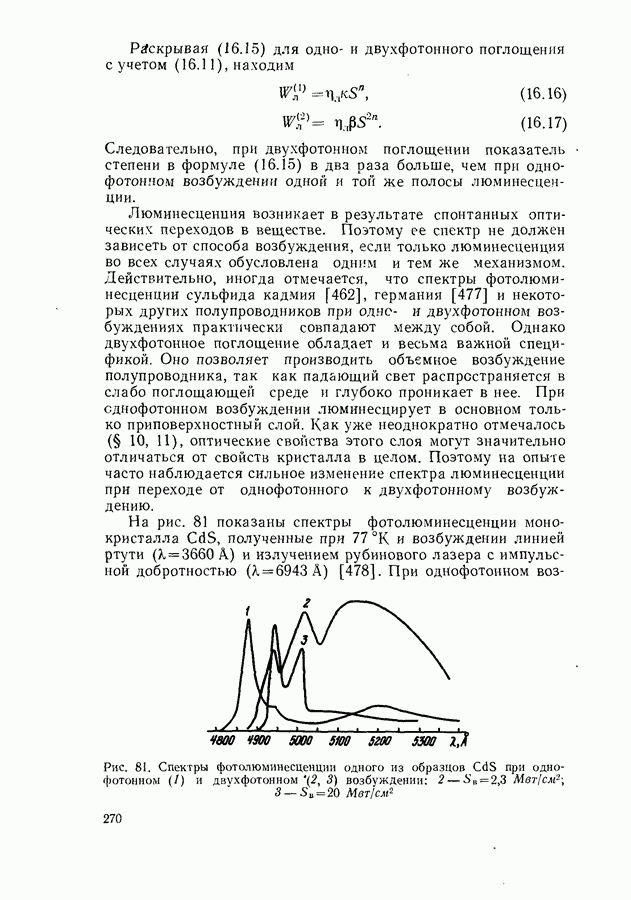
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
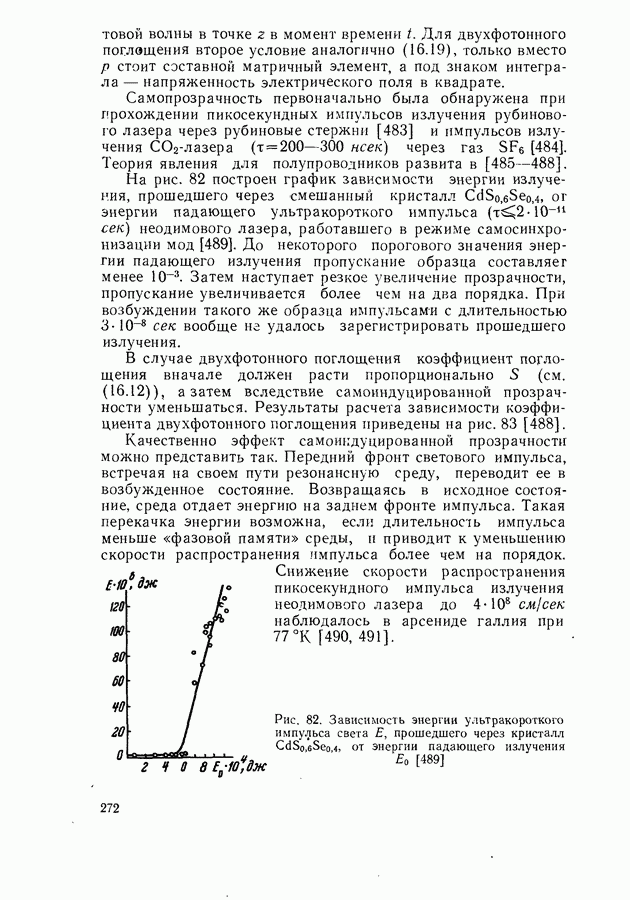
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
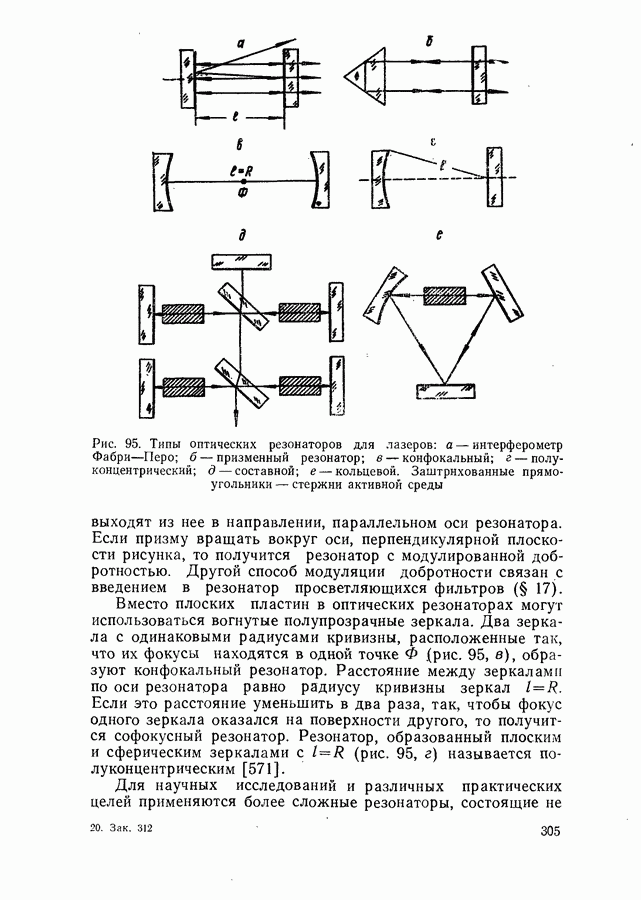
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
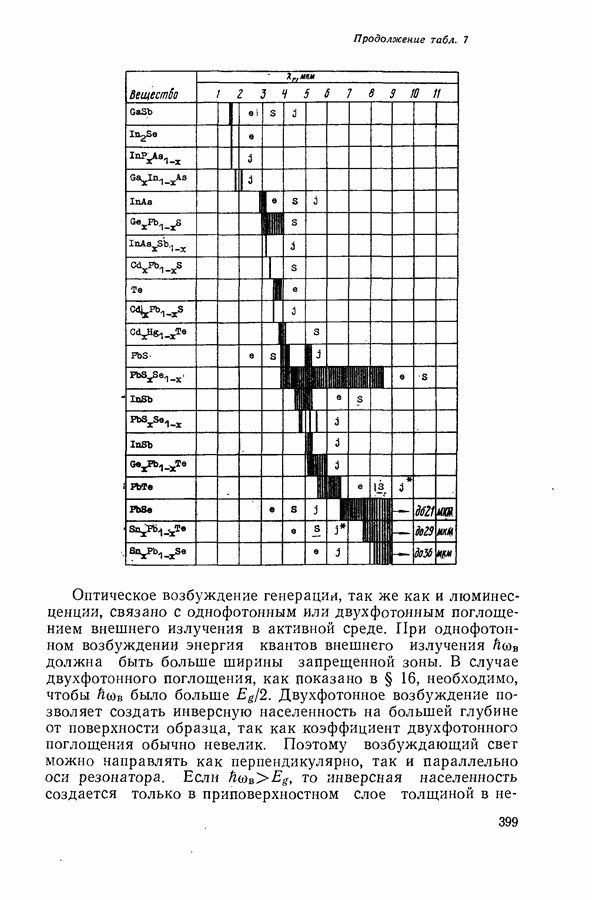
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
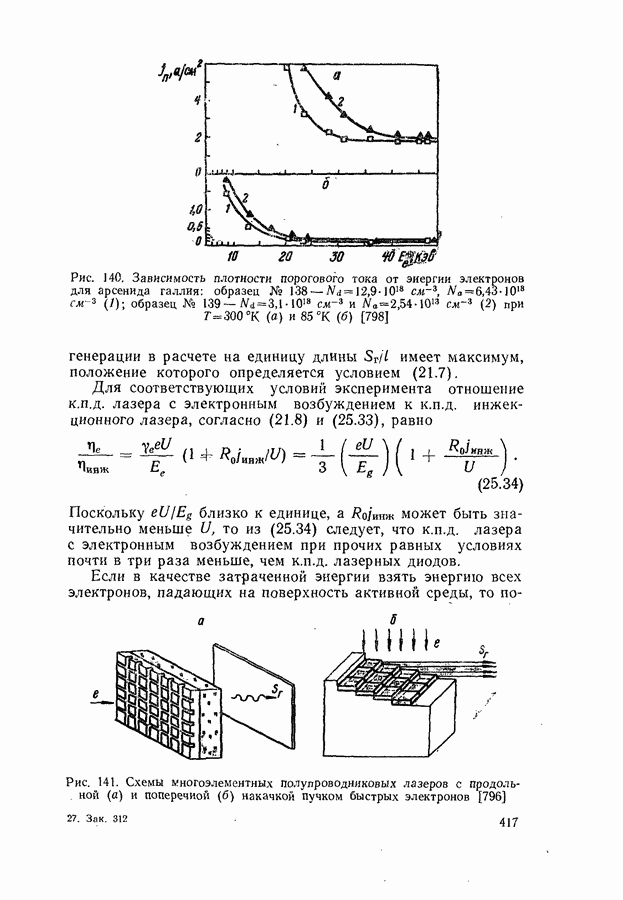
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
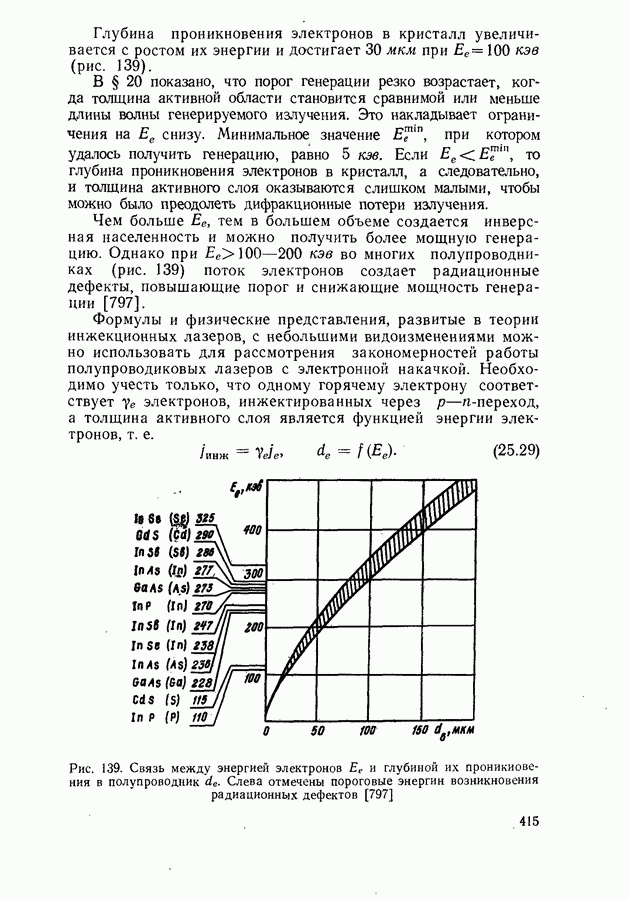
- Возбуждение генерации пучком быстрых электронов.