| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
Коэффициент двухфотонного поглощения.
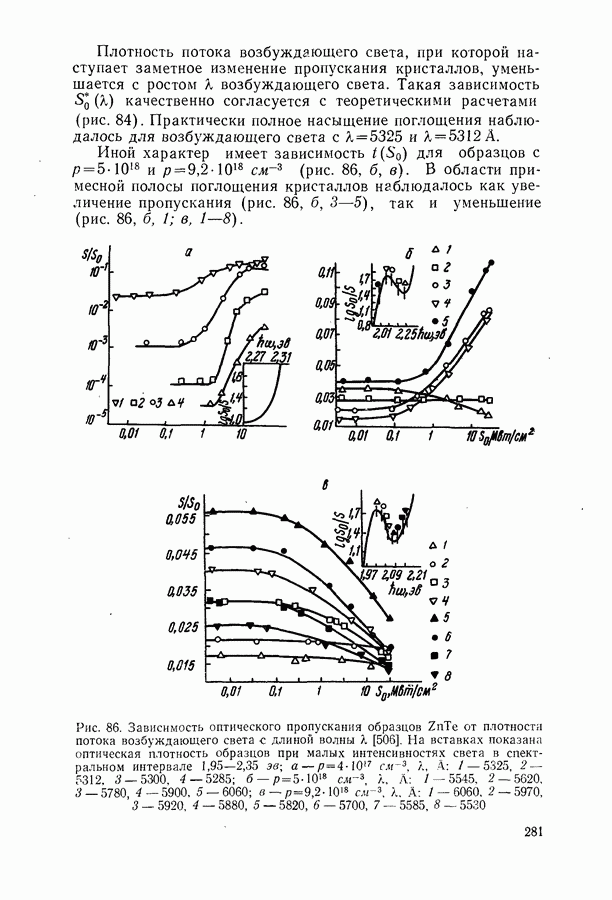
Создание в 1960 г. первого оптического квантового генератора на рубине не только положило начало бурному развитию квантовой электроники, но и послужило мощным стимулом для обнаружения и всестороннего исследования широкого круга явлений нелинейной оптики. Сейчас интенсивно исследуются: нелинейные

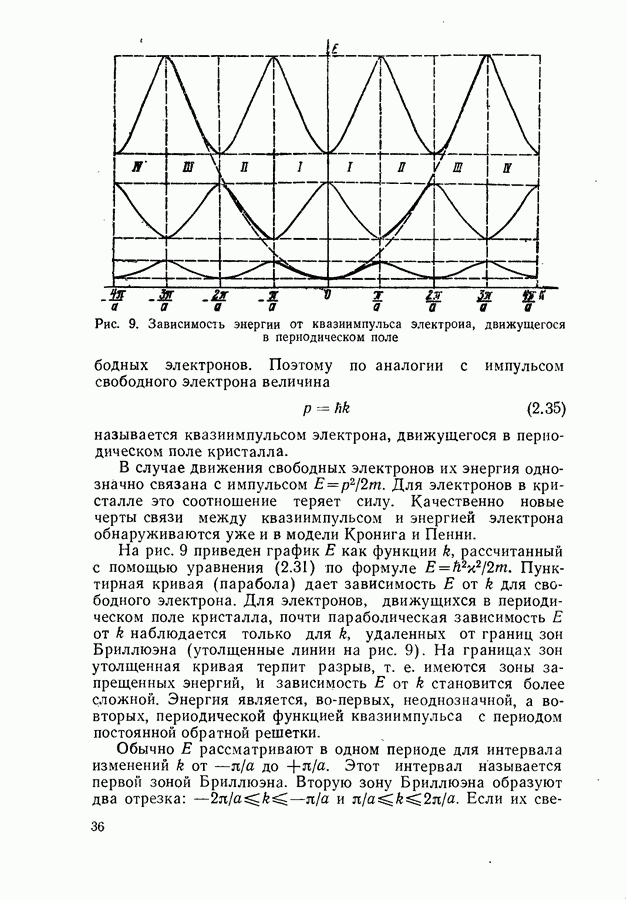
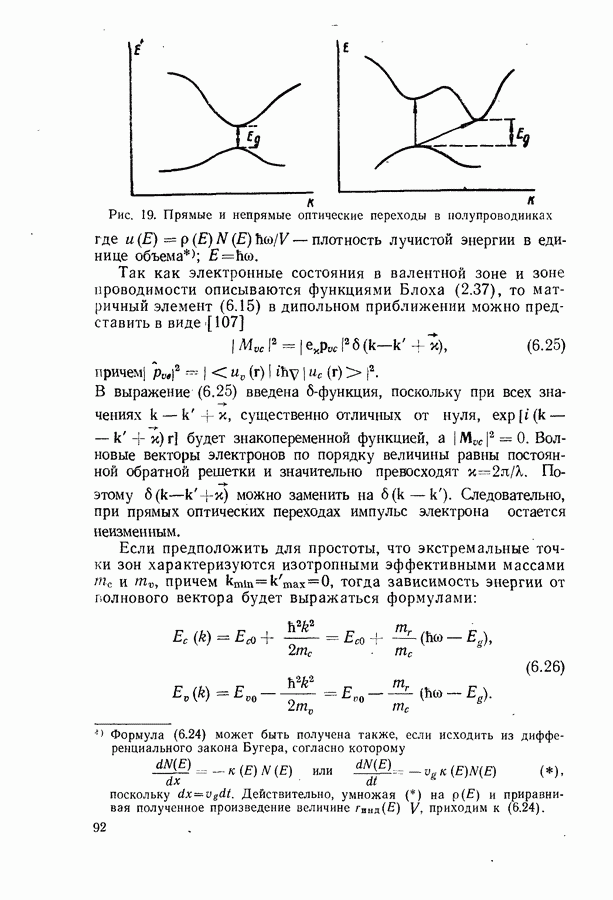
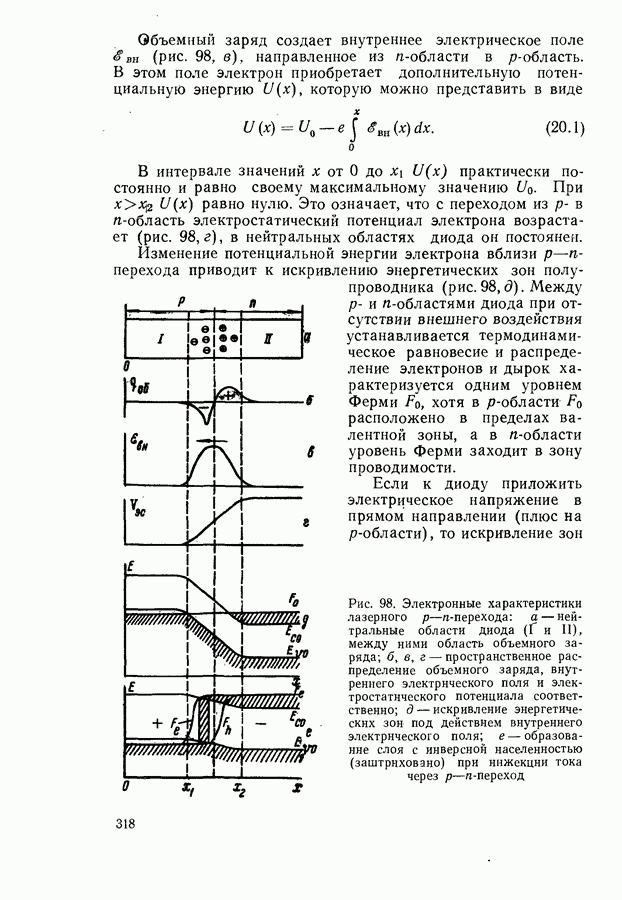
Рис. 78. Схема двухфотонных переходов: а — поглощение двух фотонов;  испускание двух фотонов; в — поглощение фотона
испускание двух фотонов; в — поглощение фотона  и испускание фотона
и испускание фотона  поглощение фотона
поглощение фотона  и испускание фотона
и испускание фотона  Штриховыми линиями показаны виртуальные (реально не существующие) уровни энергии
Штриховыми линиями показаны виртуальные (реально не существующие) уровни энергии
свойства сред (зависимость коэффициентов отражения, поглощения и показателя преломления от интенсивности света, обратный эффект Фарадея, эффект Штарка, многофотонное поглощение); взаимодействие полей в нелинейной среде (самофокусировка луча); вынужденное рассеяние света (комбинационное рассеяние, рассеяние Мандельштама-Бриллюэна и Фабелинского — Старикова); преобразование световых частот (параметрическая генерация, получение разностных и суммарных частот, удвоение частоты и т. д.). Нелинейная оптика выделилась в самостоятельный раздел физики. Ей посвящены тысячи оригинальных статей и большое количество монографий, обзоров и сборников [449—458].
Нелинейные оптические явления можно рассматривать как в классической теории с привлечением квантовомеханических представлений, так и в рамках чисто квантовой теории излучения. В классической электродинамике, в основе которой лежат уравнения Максвелла, предполагается, что при больших напряженностях электрического и магнитного  полей высокочастотные электрическая и магнитная проницаемости будут функциями
полей высокочастотные электрическая и магнитная проницаемости будут функциями  и
и  Уравнения Максвелла становятся нелинейными, принцип суперпозиции нарушается и возникает взаимодействие волн различных частот. Если, например, на вещество падает излучение двух частот
Уравнения Максвелла становятся нелинейными, принцип суперпозиции нарушается и возникает взаимодействие волн различных частот. Если, например, на вещество падает излучение двух частот  то возникают колебания обертонов
то возникают колебания обертонов  суммарные и разностные частоты
суммарные и разностные частоты 
При определенных, довольно общих предположениях вектор нелинейной поляризуемости среды можно разложить в ряд по степеням фурье-компонент электромагнитного поля. В линейной оптике учитывается только первый член разложения. Учет второго члена позволяет рассчитать двухфотонные процессы (рис. 78), третьего члена — трехфотонные процессы и 
В настоящем параграфе рассматриваются только двухфотонное поглощение и испускание в полупроводниках и явление самоиндуцированной прозрачности.
Вероятности двухфотонных переходов в системе частиц с дискретными уровнями энергии рассчитывались еще в 30-х  годах, сразу же после возникновения квантовой теории излучения. Эти вероятности получаются во втором приближении теории возмущения [43]. С помощью первого приближения, как показано в § 6, рассчитываются вероятности однофотонных переходов.
годах, сразу же после возникновения квантовой теории излучения. Эти вероятности получаются во втором приближении теории возмущения [43]. С помощью первого приближения, как показано в § 6, рассчитываются вероятности однофотонных переходов.
Предположим, что на образец падает два пучка света: один с частотой  волновым вектором
волновым вектором  вектором поляризации и плотностью фотонов в пучке
вектором поляризации и плотностью фотонов в пучке  а второй со значениями соответствующих величин, равными
а второй со значениями соответствующих величин, равными  Тогда в дипольном приближении вероятность перехода с поглощением квантов света и коэффициент поглощения
Тогда в дипольном приближении вероятность перехода с поглощением квантов света и коэффициент поглощения  будут выражаться формулами [459, 460]
будут выражаться формулами [459, 460]

где  диэлектрические проницаемости образца на частотах
диэлектрические проницаемости образца на частотах 
Входящий в (16.1) матричный элемент  называется составным, так как он составлен из комбинаций матричных элементов импульсов электрона
называется составным, так как он составлен из комбинаций матричных элементов импульсов электрона  для переходов между энергетическими зонами
для переходов между энергетическими зонами  в точке к зоны Бриллюэна:
в точке к зоны Бриллюэна:

Суммирование в (16.3) распространяется по всем промежуточным зонам, включая зоны сии. Следовательно, в двухфотонном переходе между двумя заданными состояниями участвуют все квантовомеханические состояния вещества, включая начальное и конечное. Если бы все промежуточные состояния давали равноценный вклад в составной матричный элемент, то задача теории многофотонных переходов была бы чрезвычайно сложной. Оказывается, что в зависимости от зонной структуры полупроводника, симметрии кристалла, величины матричных элементов отдельных переходов, поляризаций
и частот падающих квантов света основной вклад в составной матричный элемент для заданного двухквантового перехода вносит небольшое число промежуточных состояний. Поэтому задача приближенного расчета  значительно упрощается. Из сказанного очевидно, что расчеты, выполненные для одного конкретного случая, могут быть не применимы для рассмотрения других случаев.
значительно упрощается. Из сказанного очевидно, что расчеты, выполненные для одного конкретного случая, могут быть не применимы для рассмотрения других случаев.
Дельта-функция в формуле (16.1) означает что при двухфотонном поглощении сумма энергий двух поглощенных фотонов равна разности энергий  т. е. закон сохранения энергии имеет вид
т. е. закон сохранения энергии имеет вид

Наряду с двухфотонным поглощением происходят и другие двухфотонные переходы: одновременное испускание двух квантов света при переходе электрона с уровня  на уровень
на уровень  поглощение фотона с энергией
поглощение фотона с энергией  и испускание фотона с энергией
и испускание фотона с энергией  и наоборот. В зависимости от величины энергий фотонов вещество переходит либо на верхний, либо на нижний энергетический уровень (рис. 78). Во всех случаях должен выполняться закон сохранения энергии: энергия системы вещество
и наоборот. В зависимости от величины энергий фотонов вещество переходит либо на верхний, либо на нижний энергетический уровень (рис. 78). Во всех случаях должен выполняться закон сохранения энергии: энергия системы вещество  поле до и после двухфотонного перехода остается неизменной. Формула (16.4) справедлива для процессов, показанных на рис. 78, а, б. Для двух других случаез имеем
поле до и после двухфотонного перехода остается неизменной. Формула (16.4) справедлива для процессов, показанных на рис. 78, а, б. Для двух других случаез имеем

Если известна частота одного фотона, то закон сохранения энергии (16.5) позволяет рассчитать частоту другого фотона.
В дипольном приближении однофотонные переходы могут быть либо разрешенными, либо запрещенными (§ 6). Поскольку в составной матричный элемент (16.3) входят произведения матричных элементов, характеризующих однофотонные переходы между состояниями  то возможны три типа двухфотонных переходов: разрешенно-разрешенные (оба однофотонные переходы разрешены), разрешенно-запрещенные (один переход разрешен, второй запрещен) и запрещенно-запрещенные (оба перехода запрещены).
то возможны три типа двухфотонных переходов: разрешенно-разрешенные (оба однофотонные переходы разрешены), разрешенно-запрещенные (один переход разрешен, второй запрещен) и запрещенно-запрещенные (оба перехода запрещены).
Коэффициент двухфотонного поглощения в полупроводниках впервые рассчитан применительно к кристаллу CdS в работах [461, 462]. Модель вещества состояла из трех зон: одной валентной зоны и двух зон проводимости. Все зоны характеризуются изотропной массой и параболическим законом дисперсии. Более высокая зона проводимости рассматривалась как промежуточная, и из всей суммы (16.3) вычислялось только первое слагаемое в фигурных скобках.
Более последовательная теория двухфотонного поглощения поляризованного света в CdS с учетом всех зон проводимости и валентных зон развита в работах [459, 460]. Для составного матричного элемента получено выражение

справедливое при малых значениях  постоянная решетки). Суммирование по
постоянная решетки). Суммирование по  в (16.6) проводится по всем зонам проводимости и валентным зонам, кроме зон
в (16.6) проводится по всем зонам проводимости и валентным зонам, кроме зон  приведенная масса. Промежуточные зоны, для которых
приведенная масса. Промежуточные зоны, для которых  равны нулю, при расчетах не учитываются. Значения матричных элементов в точке
равны нулю, при расчетах не учитываются. Значения матричных элементов в точке  обозначены через
обозначены через 
Для разрешенно-разрешенных переходов расчеты по формулам

где  плотность первого потока излучения. Для запрещенно-разрешенных и запрещенно-запрещенных переходов получено соответственно
плотность первого потока излучения. Для запрещенно-разрешенных и запрещенно-запрещенных переходов получено соответственно

Коэффициенты  зависят от ориентации векторов поляризации обоих лучей и относительно слабо зависят от частоты
зависят от ориентации векторов поляризации обоих лучей и относительно слабо зависят от частоты 
Экспериментальное изучение частотной зависимости коэффициента поглощения позволяет определить тип оптических переходов при двухфотонном поглощении. В зависимости от зонной структуры кристалла и условий эксперимента может либо преобладать один тип переходов, либо наблюдаться их суперпозиция.
Расчеты коэффициента поглощения [459, 460] по формулам (16.2) и (16.6) для лазерного линейно поляризованного излучения  и естественного света
и естественного света  одновременно распространяющихся в кристалле
одновременно распространяющихся в кристалле  приводят к следующей общей формуле для
приводят к следующей общей формуле для 

Здесь зависимость  от
от  достаточно слабая и ею можно пренебречь. Если векторы
достаточно слабая и ею можно пренебречь. Если векторы  взаимно
взаимно
перпендикулярны и лежат в плоскости, перпендикулярной к оптической  и справедлива формула (16.8). При всех других ориентациях векторов поляризации выполняется обратное неравенство
и справедлива формула (16.8). При всех других ориентациях векторов поляризации выполняется обратное неравенство  и можно пользоваться выражением (16.7). Если непрерывно изменять угол между вектором поляризации первого лазерного луча и оптической осью кристалла, то можно плавно перейти от частотной зависимости коэффициента поглощения
и можно пользоваться выражением (16.7). Если непрерывно изменять угол между вектором поляризации первого лазерного луча и оптической осью кристалла, то можно плавно перейти от частотной зависимости коэффициента поглощения  даваемой формулой (16.7), к частотной зависимости (16.8) [459].
даваемой формулой (16.7), к частотной зависимости (16.8) [459].
Как видно из последних формул, межзонное двухфотонное поглощение так же, как и однофотонное поглощение, характеризуется пороговым значением энергий фотонов: поглощение отсутствует, если

Коэффициент двухфотонного поглощения прямо пропорционален интенсивности возбуждающего света. В общем случае, если в одном элементарном акте поглощается  одинаковых фотонов, то коэффициент поглощения можно представить в виде
одинаковых фотонов, то коэффициент поглощения можно представить в виде

где  параметр;
параметр;  плотность потока.
плотность потока.
В арсениде галлия и селениде кадмия валентная зона состоит из подзоны легких дырок, подзоны тяжелых дырок, соприкасающихся в точке  и отщепленной от них на величину
и отщепленной от них на величину  третьей подзоны. При возбуждении кристалла излучением неодимового лазера
третьей подзоны. При возбуждении кристалла излучением неодимового лазера  основной вклад в двухфотонное поглощение будут вносить состояния валентной зоны. Расчеты
основной вклад в двухфотонное поглощение будут вносить состояния валентной зоны. Расчеты  проведенные для этого случая, дают [463, 464]
проведенные для этого случая, дают [463, 464]

При  формула определяет коэффициент поглощения, связанного с переходами валентная подзона тяжелых дырок — зона проводимости; индекс
формула определяет коэффициент поглощения, связанного с переходами валентная подзона тяжелых дырок — зона проводимости; индекс  относится к подзоне легких дырок.
относится к подзоне легких дырок.
При выводе (16.13) предполагалось, что фотоны испускаются одним монохроматическим источником света, поэтому  Так же как и при однофотонном поглощении, графиком функции
Так же как и при однофотонном поглощении, графиком функции  для заданной ориентации, вектора поляризации служит одна плоская кривая. Если же происходит поглощение двух фотонов с различными энергиями, то функция
для заданной ориентации, вектора поляризации служит одна плоская кривая. Если же происходит поглощение двух фотонов с различными энергиями, то функция  может быть представлена двухмерной поверхностью.
может быть представлена двухмерной поверхностью.
Двухфотонное поглощение света при непосредственном возбуждении экситонов рассчитано в работах [465, 466], а для примесных полупроводников — в [467]. Общий метод расчета многофотонного поглощения света связанными электронами в твердых телах развит Л. В. Келдышем [468].
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
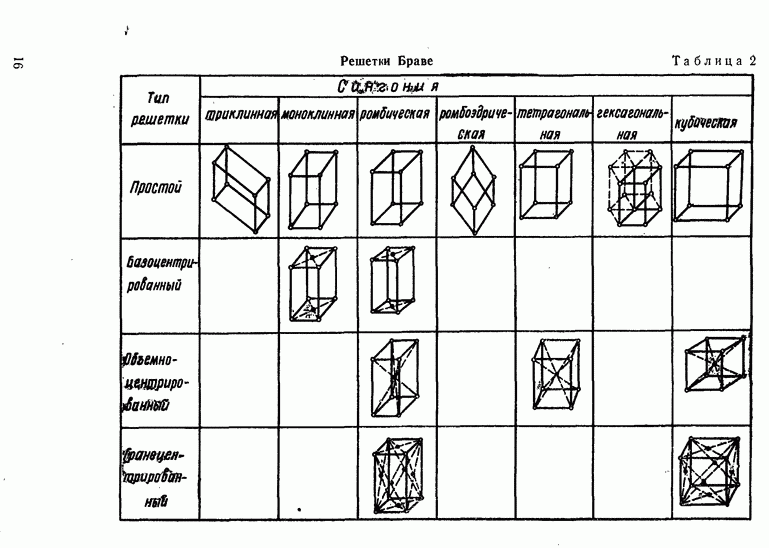
- Классификация кристаллических решеток.
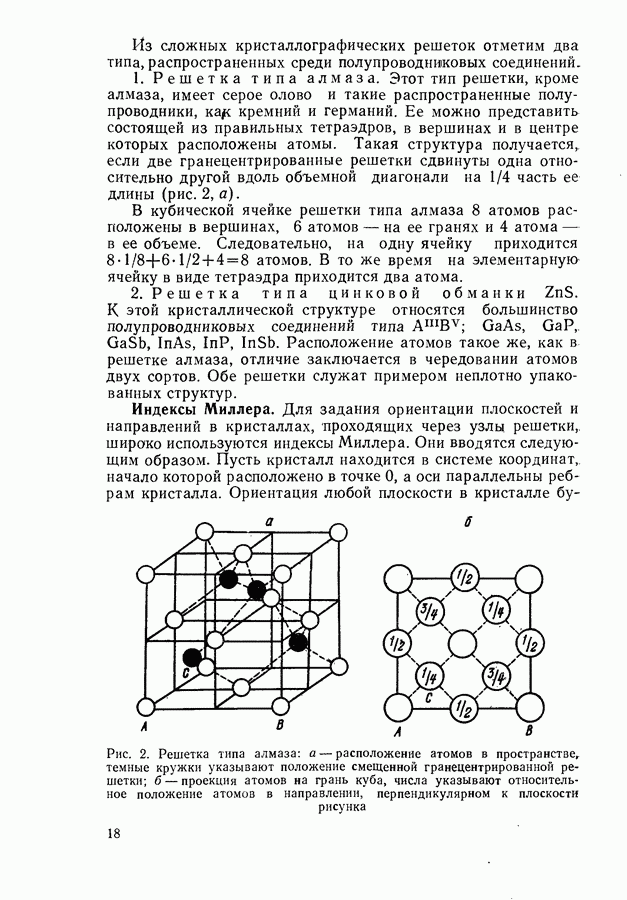
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
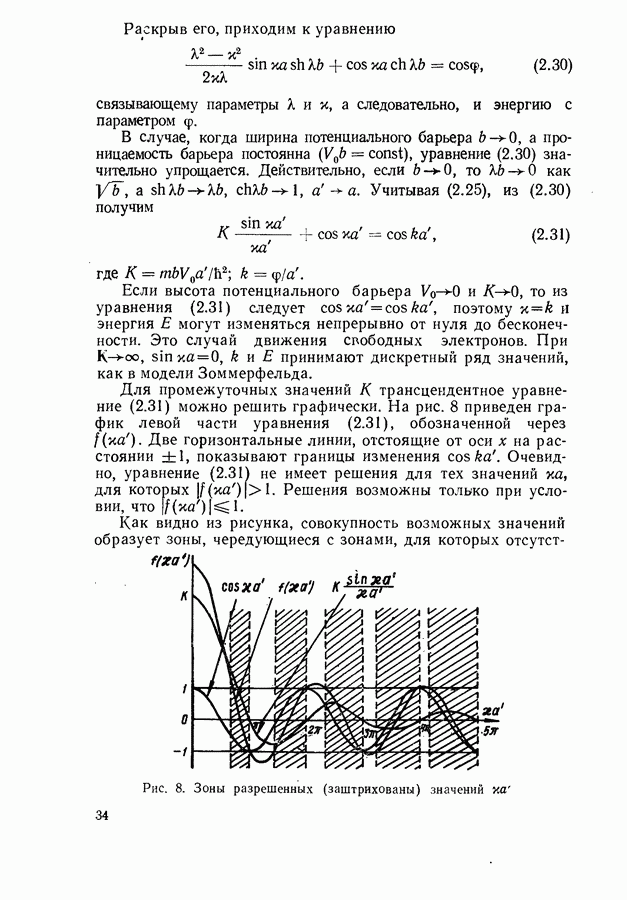
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
- Эффект Келдыша-Франца.
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
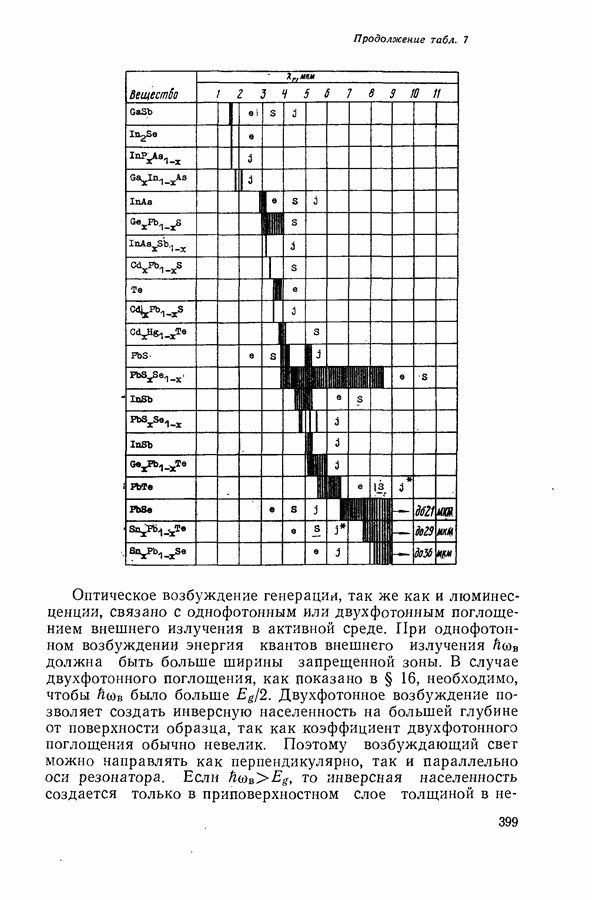
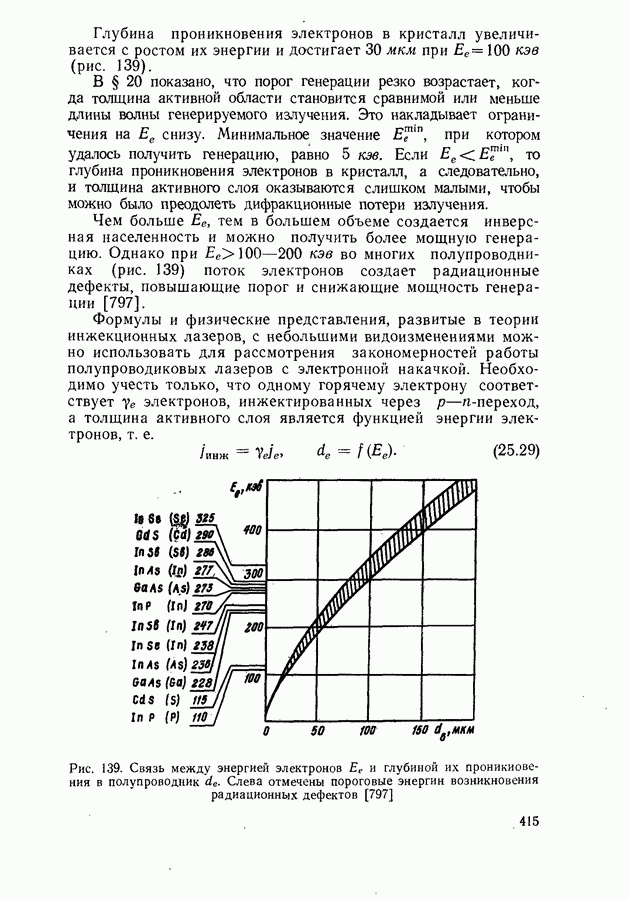
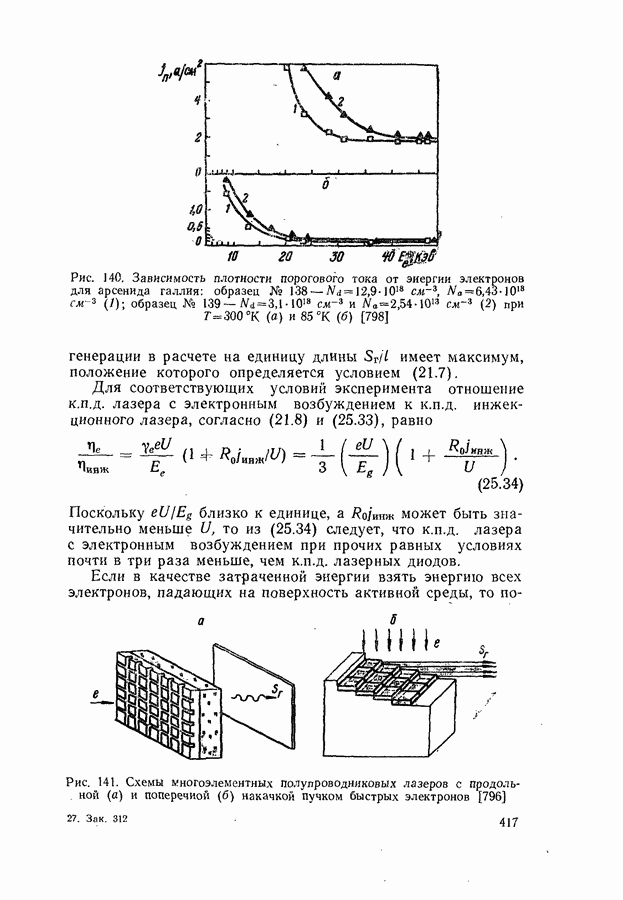
- Возбуждение генерации пучком быстрых электронов.