| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
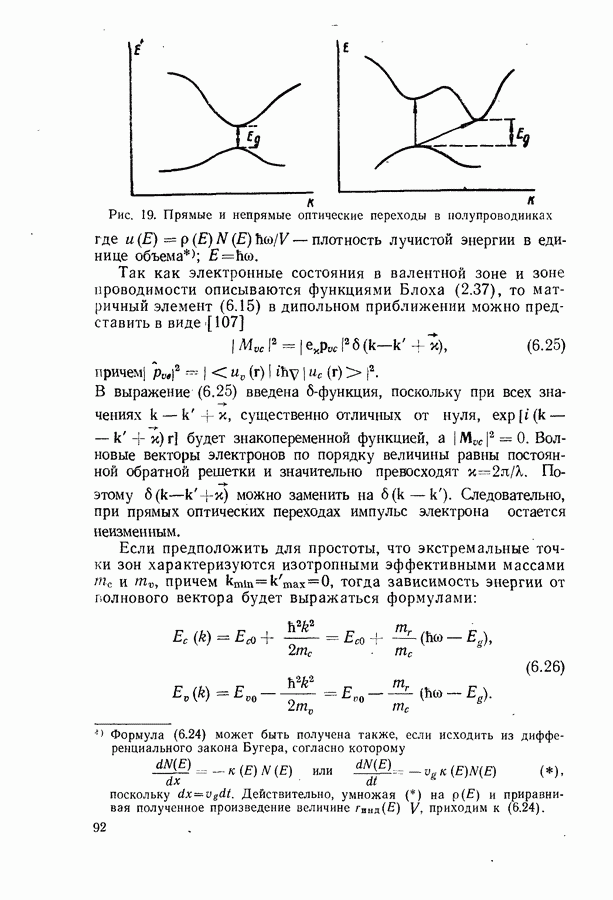
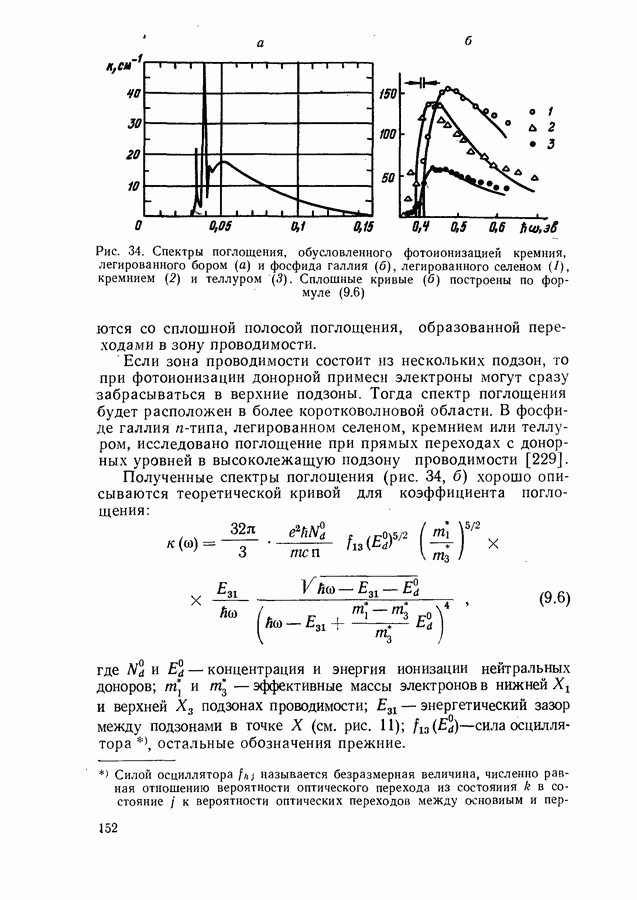
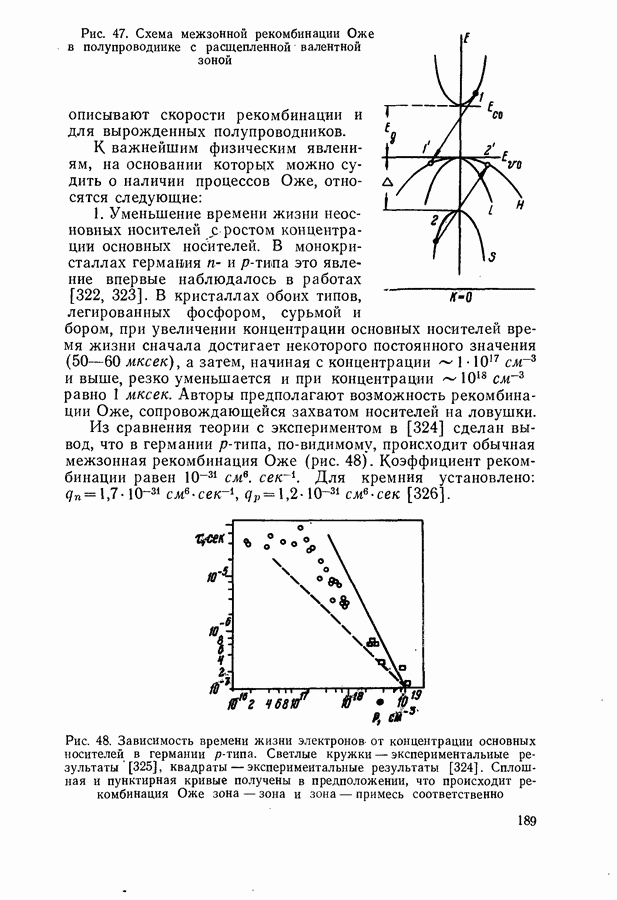
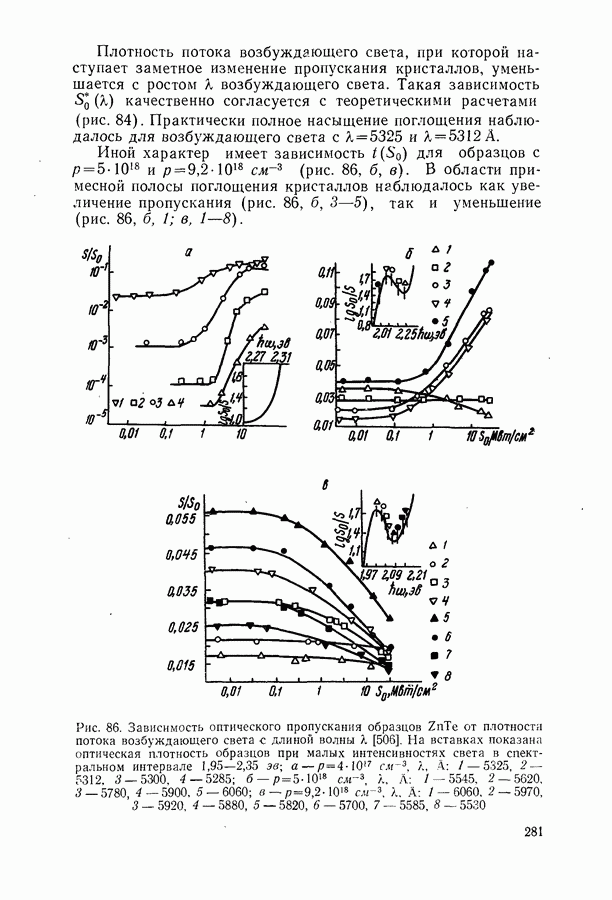
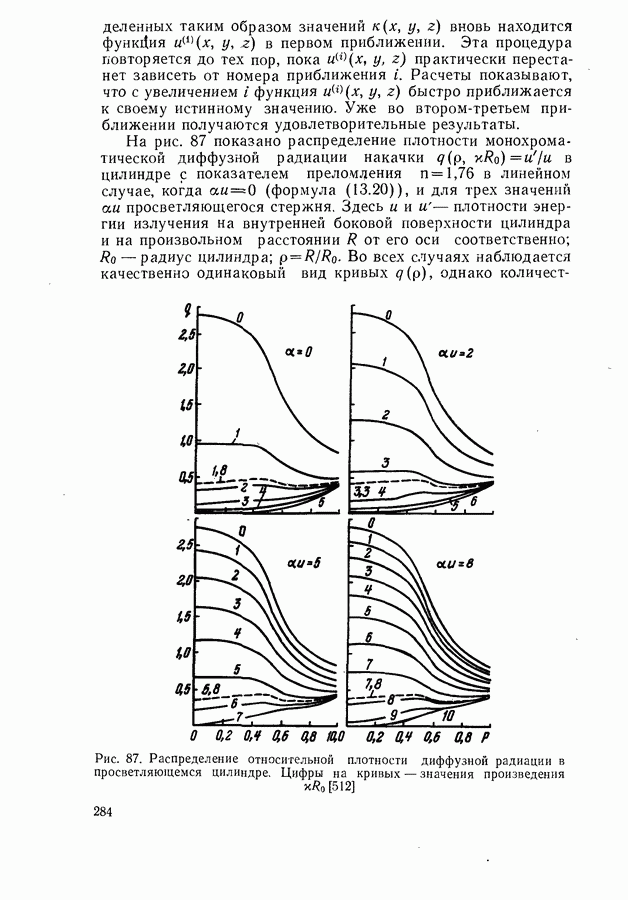
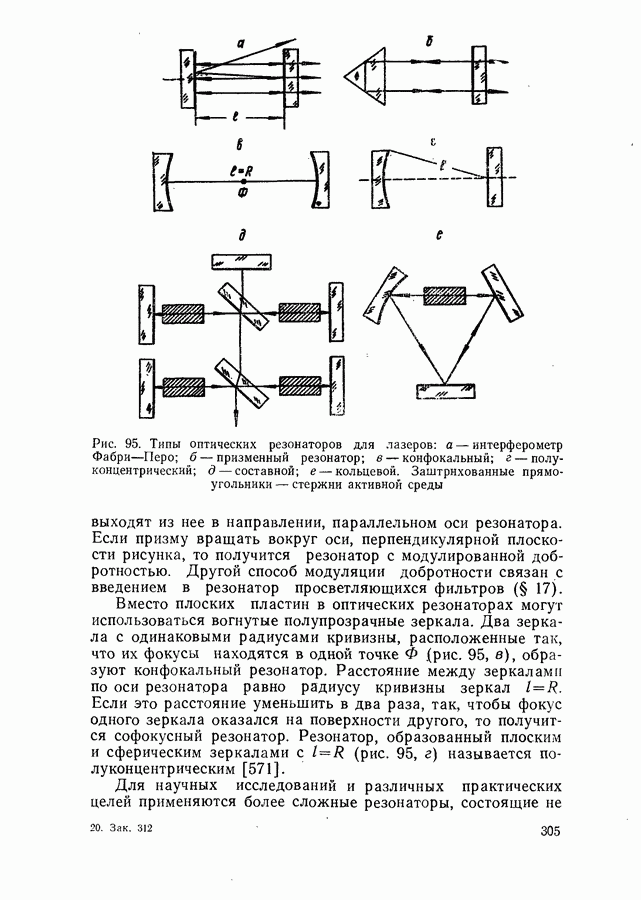
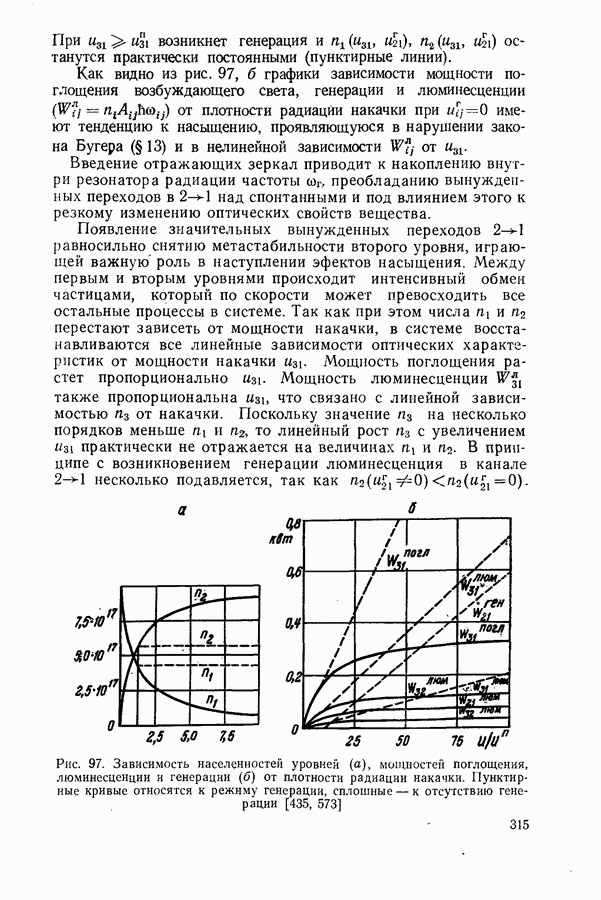
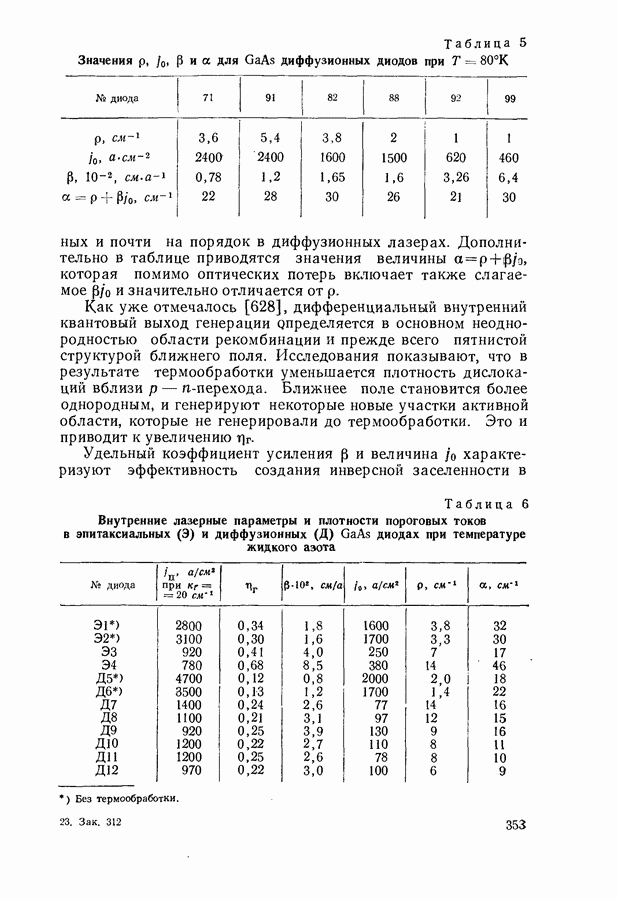
Зависимость порогового тока от коэффициента потерь в модели параболических зон.
Один из возможных механизмов рекомбинации в полупроводниковом лазере связан с межзонными переходами. При расчетах обычно используют модель параболических зон. Такое приближение оказывается, по-видимому, достаточно хорошим при высоких температурах и большой величине коэффициента потерь  когда роль хвостов плотности состояний, образующихся при сильном легировании, незначительна. Модель параболических зон использовалась для расчета порогового тока инжекционных лазеров неоднократно [106, 605]. Приводимое ниже изложение вопроса основано на работах [435, 600, 606—610].
когда роль хвостов плотности состояний, образующихся при сильном легировании, незначительна. Модель параболических зон использовалась для расчета порогового тока инжекционных лазеров неоднократно [106, 605]. Приводимое ниже изложение вопроса основано на работах [435, 600, 606—610].
Модель параболических зон рассмотрим в двух крайних случаях: прямых межзонных переходов и переходов без правила отбора. Число спонтанных переходов в единице объема за единицу времени, согласно (6.21), (6.23), равно в первом случае

во втором

Соотношение между коэффициентом усиления и  можно представить (§ 7) в виде
можно представить (§ 7) в виде

где  Величина
Величина  для прямых переходов и переходов без правил отбора равна соответственно
для прямых переходов и переходов без правил отбора равна соответственно


Частота излучения, коэффициент усиления на которой максимален, находится из условия равенства нулю производной от  по
по  и определяется расстоянием между квазиуровнями Ферми
и определяется расстоянием между квазиуровнями Ферми  В общем случае для прямых переходов получается довольно громоздкое выражение [607], принимающее, однако, простой вид, если
В общем случае для прямых переходов получается довольно громоздкое выражение [607], принимающее, однако, простой вид, если  В этом случае энергия фотона в максимуме спектра усиления равна
В этом случае энергия фотона в максимуме спектра усиления равна  (§ 15). В указанном приближении, которое справедливо при высоких температурах и несильном возбуждении, коэффициент усиления в случае прямых переходов равен
(§ 15). В указанном приближении, которое справедливо при высоких температурах и несильном возбуждении, коэффициент усиления в случае прямых переходов равен

где  определяется выражением (20.14). При заданных
определяется выражением (20.14). При заданных  наибольший коэффициент усиления получается, когда
наибольший коэффициент усиления получается, когда  , что соответствует промежуточно легированному полупроводнику
, что соответствует промежуточно легированному полупроводнику  -типа, если
-типа, если  Соотношение между величиной
Соотношение между величиной  и максимальным коэффициентом усиления, равным в пороге генерации
и максимальным коэффициентом усиления, равным в пороге генерации  имеет вид
имеет вид

В рассматриваемом приближении для модели параболических зон без правил отбора получено [606]

 задается (20.15). Соотношение между энергией
задается (20.15). Соотношение между энергией  и коэффициентом потерь
и коэффициентом потерь  имеет вид
имеет вид

Подставляя (20.12) в (20.9), проводя интегрирование под знаком интеграла  и используя (20.19), получаем выражение для плотности порогового тока [606]
и используя (20.19), получаем выражение для плотности порогового тока [606]

В области малых потерь  зависит от
зависит от  в степени 1/3. При некотором минимальном токе
в степени 1/3. При некотором минимальном токе

максимальный коэффициент усиления активного слоя равен нулю. Если  среда может только поглощать излучения, при
среда может только поглощать излучения, при  на некоторой частоте возникает усиление. Поэтому значение тока, при котором
на некоторой частоте возникает усиление. Поэтому значение тока, при котором  будем называть током инверсии. Параметр
будем называть током инверсии. Параметр  имеет наибольшее значение в промежуточно легированном полупроводнике
имеет наибольшее значение в промежуточно легированном полупроводнике  -типа и уменьшается с переходом к сильно легированному полупроводнику
-типа и уменьшается с переходом к сильно легированному полупроводнику  или
или  -типа. Для диода с компенсированной областью рекомбинации, когда концентрации ионизованных доноров и акцепторов равны,
-типа. Для диода с компенсированной областью рекомбинации, когда концентрации ионизованных доноров и акцепторов равны, 
В общем случае аналитическое выражение для зависимости порогового тока от коэффициента потерь получить не удается. Результаты численного расчета, проведенного при вариации параметров в широких пределах, изложены в работах [606, 607].
Как видно из рис. 101, при увеличении коэффициента потерь от  до 150 смгх порог генерации в компенсированном полупроводнике с параметрами арсенида галлия превышает
до 150 смгх порог генерации в компенсированном полупроводнике с параметрами арсенида галлия превышает  не более чем в два раза. Ток инверсии при высоких температурах достигает больших значений. Для d = 2 мкм и времени жизни носителей
не более чем в два раза. Ток инверсии при высоких температурах достигает больших значений. Для d = 2 мкм и времени жизни носителей  сек из графиков находим
сек из графиков находим  .
.
Начальные участки кривых на рис. 101 можно аппроксимировать формулой

где  - коэффициент пропорциональности,
- коэффициент пропорциональности,  В дальнейшем зависимость
В дальнейшем зависимость  от
от  становится линейной и удовлетворяет формуле
становится линейной и удовлетворяет формуле


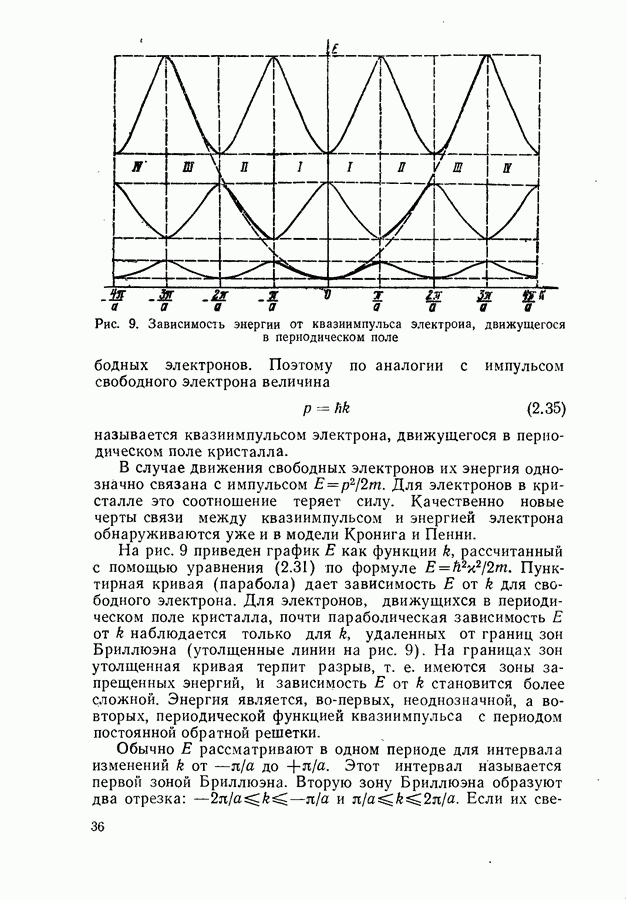
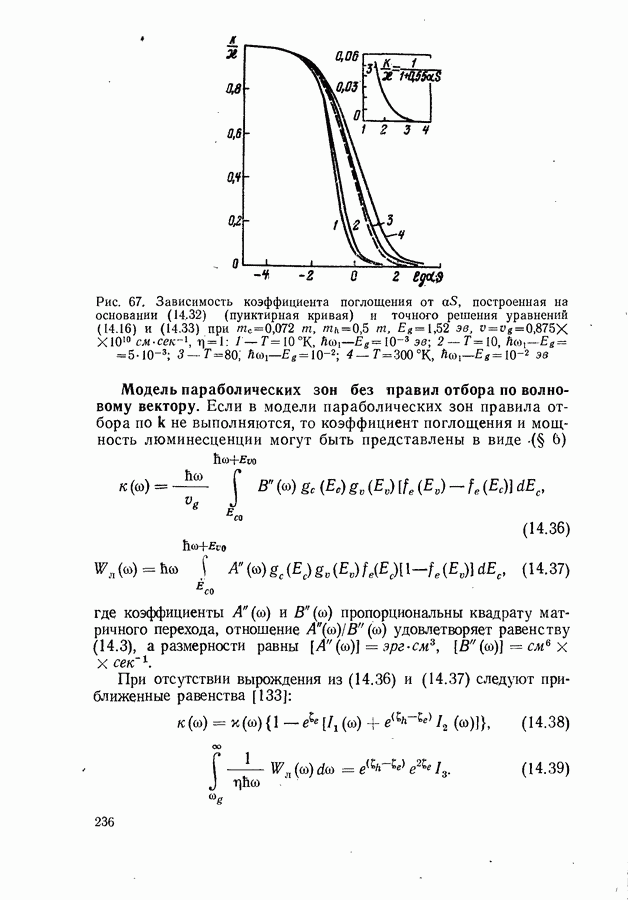
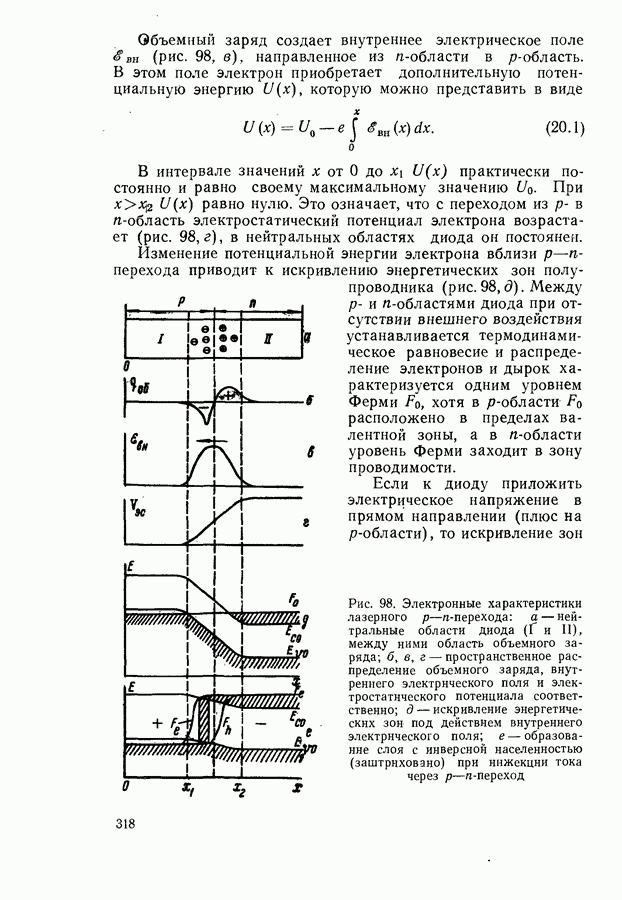
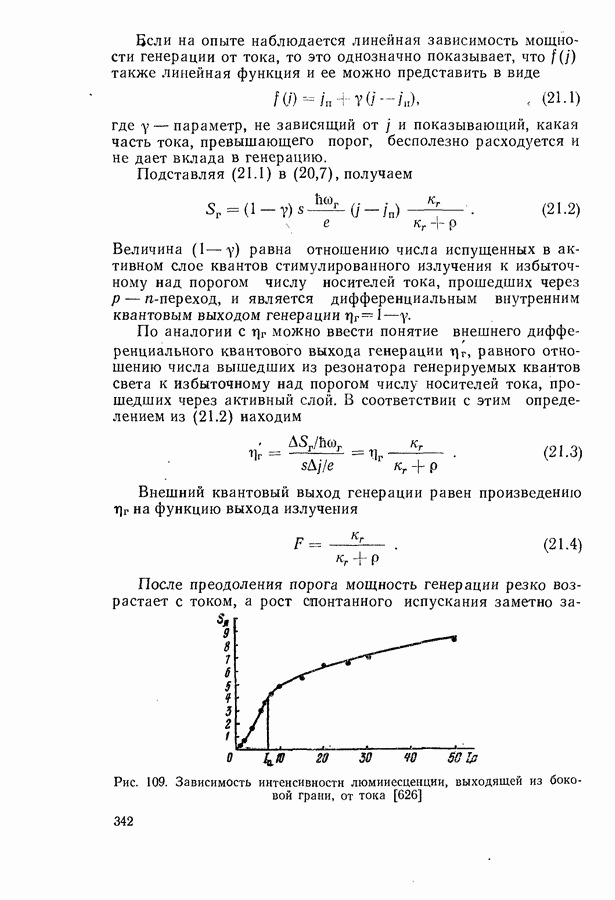
Рис. 101. Зависимость порога генерации от коэффициента потерь в модели параболических зон с правилом отбора по волновому вектору для компенсированного полупроводника с параметрами арсенида галлия при температурах, 
Параметр  равен отрезку, который отсекает прямая (20.23) на оси
равен отрезку, который отсекает прямая (20.23) на оси  Формула (20.23) дает правильное значение порога только на линейном участке кривой
Формула (20.23) дает правильное значение порога только на линейном участке кривой  поскольку при
поскольку при  стремится к
стремится к  а не к
а не к 
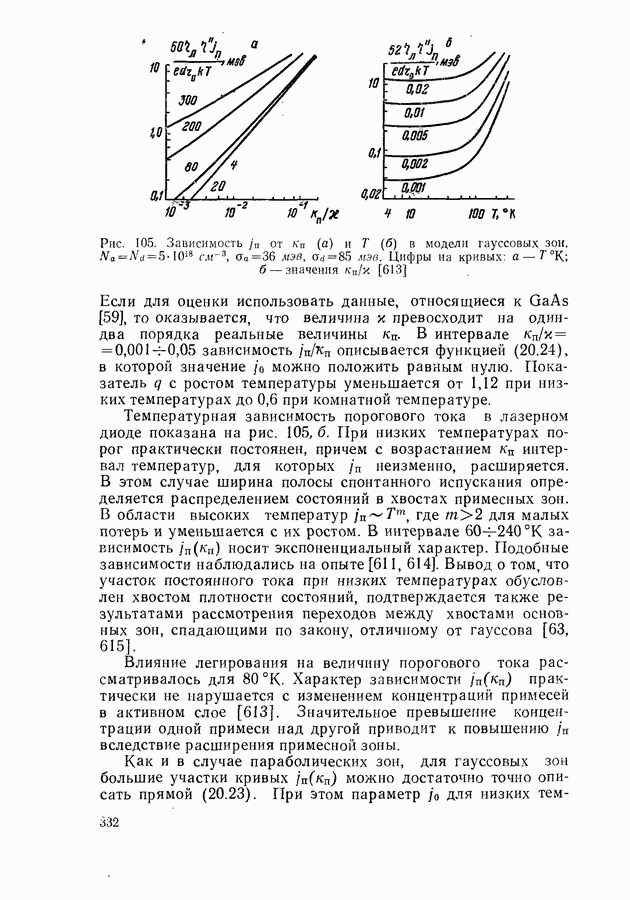
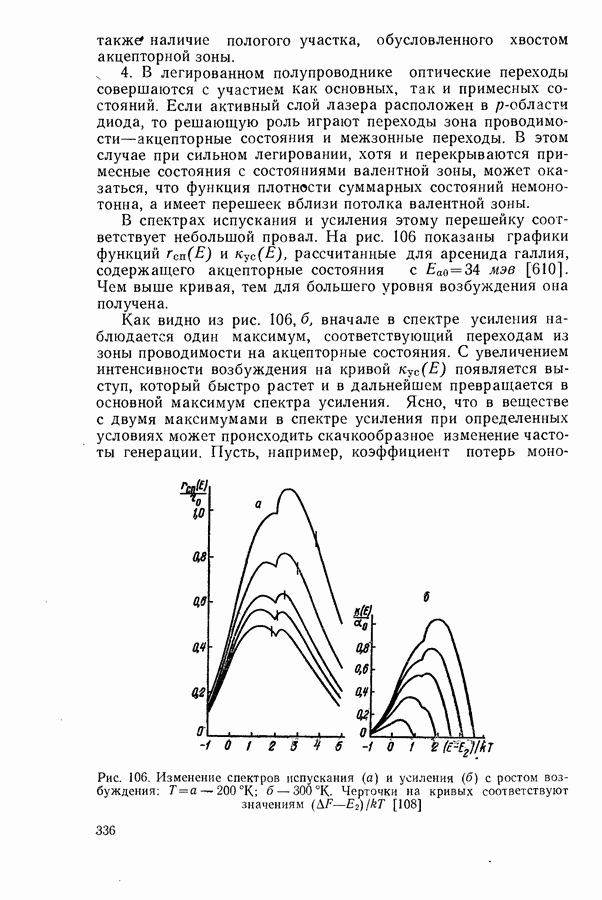
Из расчетов следует [606, 607], что в модели параболических зон как с правилом отбора по волновому вектору, так и без правила отбора при больших  зависимость
зависимость  от
от  вновь может стать нелинейной и аппроксимируется соотношением
вновь может стать нелинейной и аппроксимируется соотношением

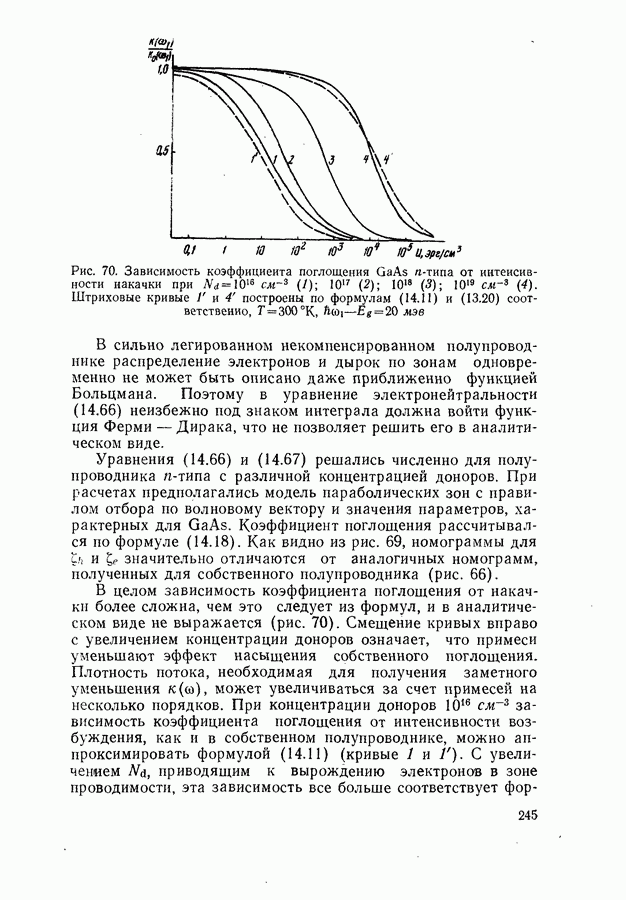
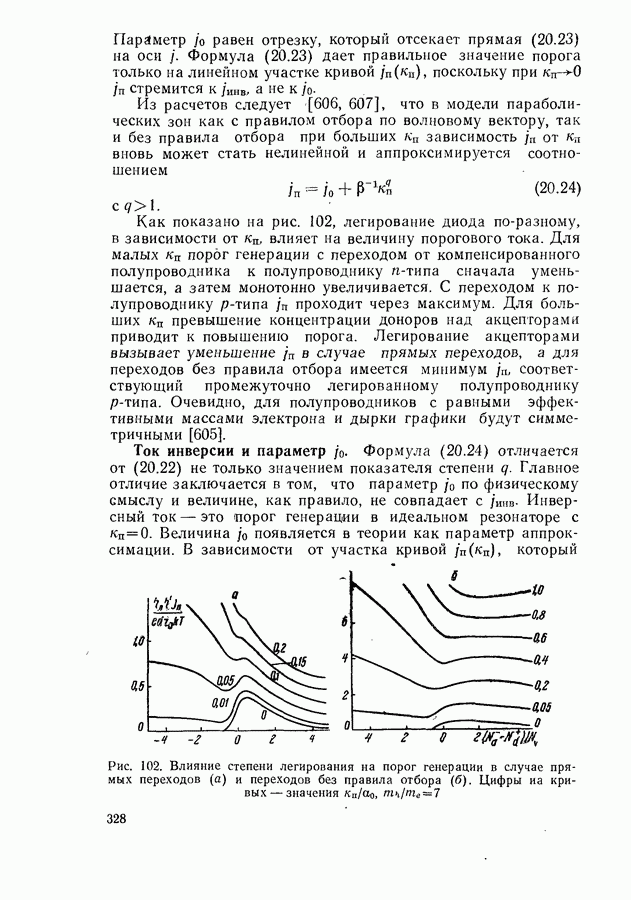
Как показано на рис. 102, легирование диода по-разному, в зависимости от  влияет на величину порогового тока. Для малых
влияет на величину порогового тока. Для малых  порог генерации с переходом от компенсированного полупроводника к полупроводнику
порог генерации с переходом от компенсированного полупроводника к полупроводнику  -типа сначала уменьшается, а затем монотонно увеличивается. С переходом к полупроводнику
-типа сначала уменьшается, а затем монотонно увеличивается. С переходом к полупроводнику  -типа
-типа  проходит через максимум. Для больших
проходит через максимум. Для больших  превышение концентрации доноров над акцепторами приводит к повышению порога. Легирование акцепторами вызывает уменьшение
превышение концентрации доноров над акцепторами приводит к повышению порога. Легирование акцепторами вызывает уменьшение  в случае прямых переходов, а для переходов без правила отбора имеется мииимум
в случае прямых переходов, а для переходов без правила отбора имеется мииимум  соответствующий промежуточно легированному полупроводнику
соответствующий промежуточно легированному полупроводнику  -типа. Очевидно, для полупроводников с равными эффективными массами электрона и дырки графики будут симметричными [605].
-типа. Очевидно, для полупроводников с равными эффективными массами электрона и дырки графики будут симметричными [605].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
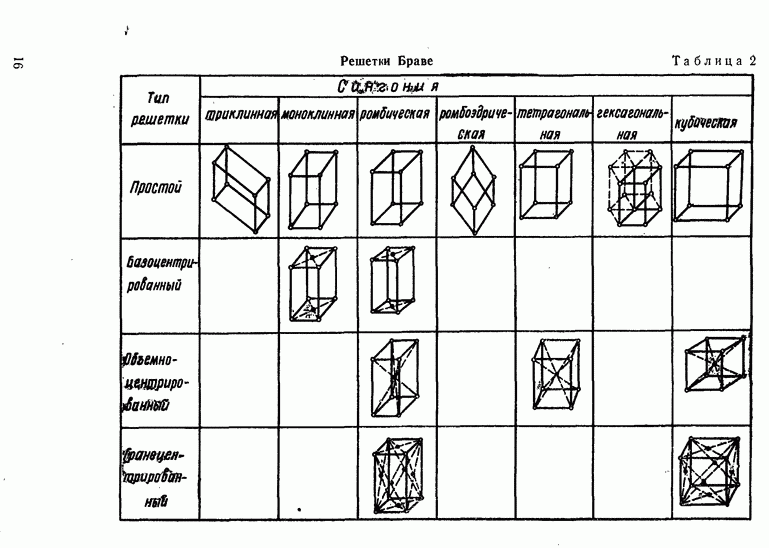
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
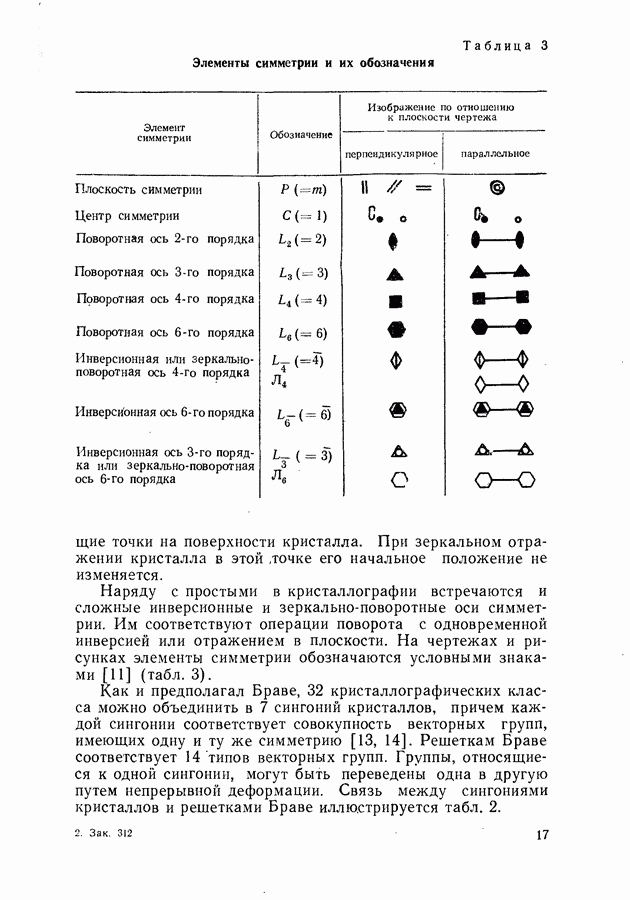
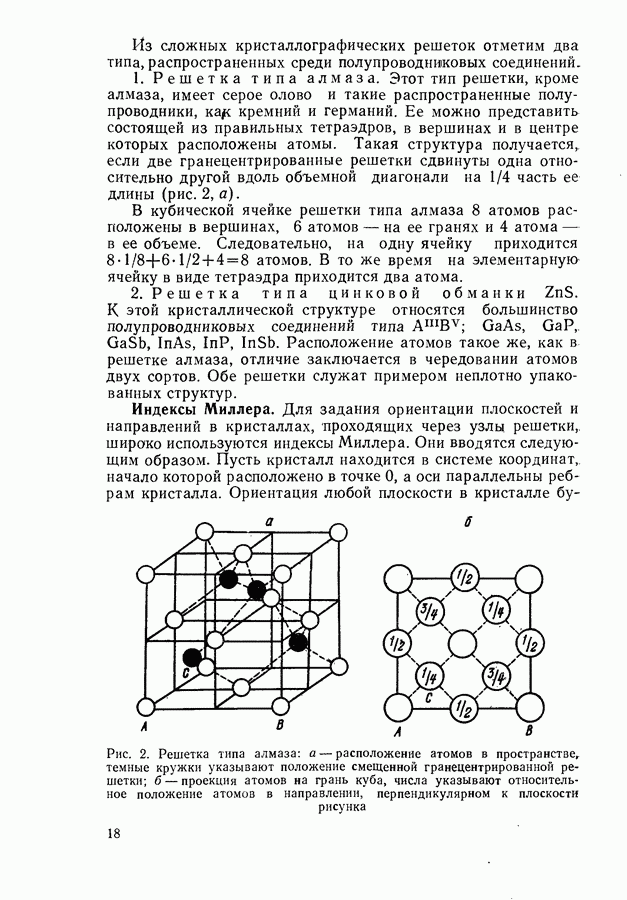
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
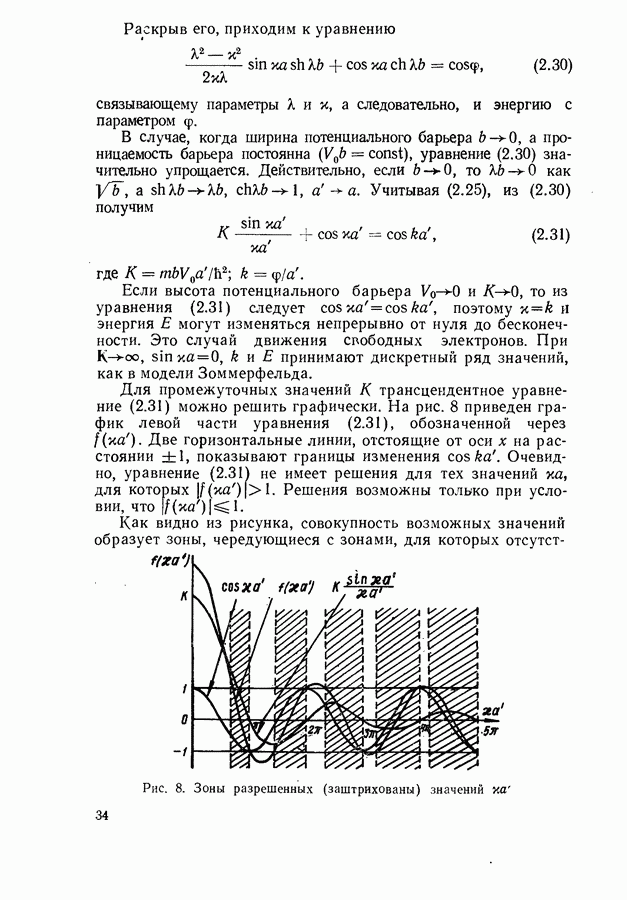
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
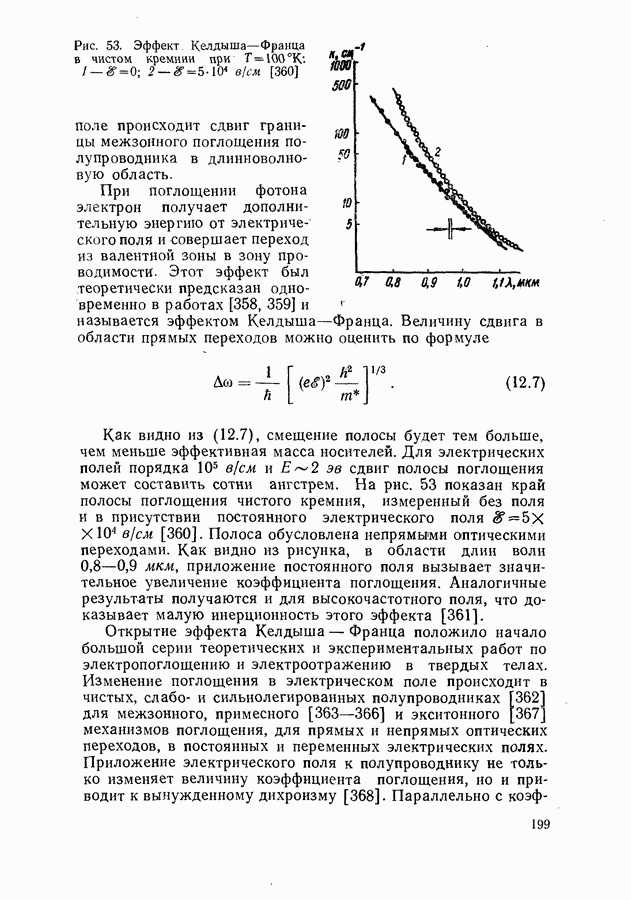
- Эффект Келдыша-Франца.
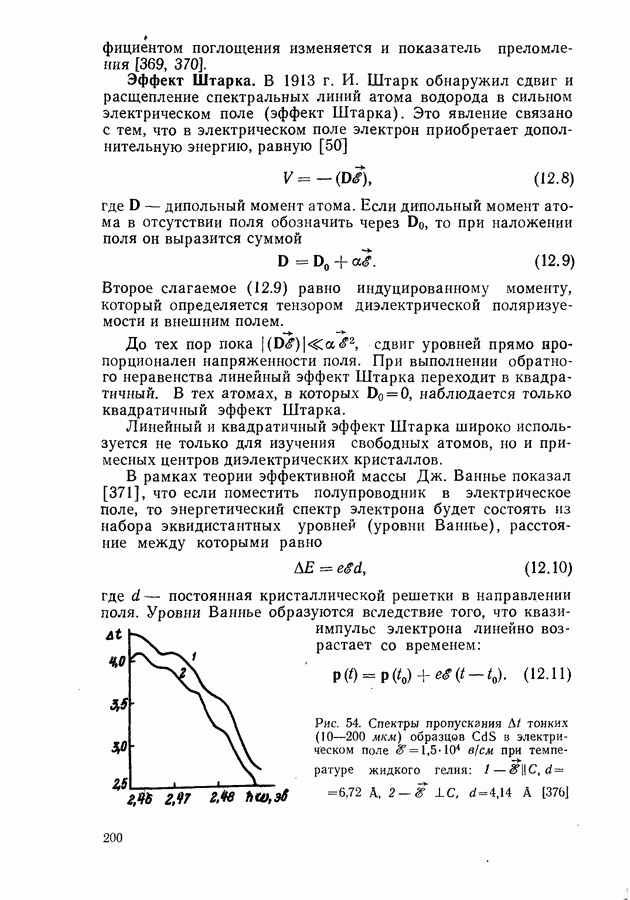
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
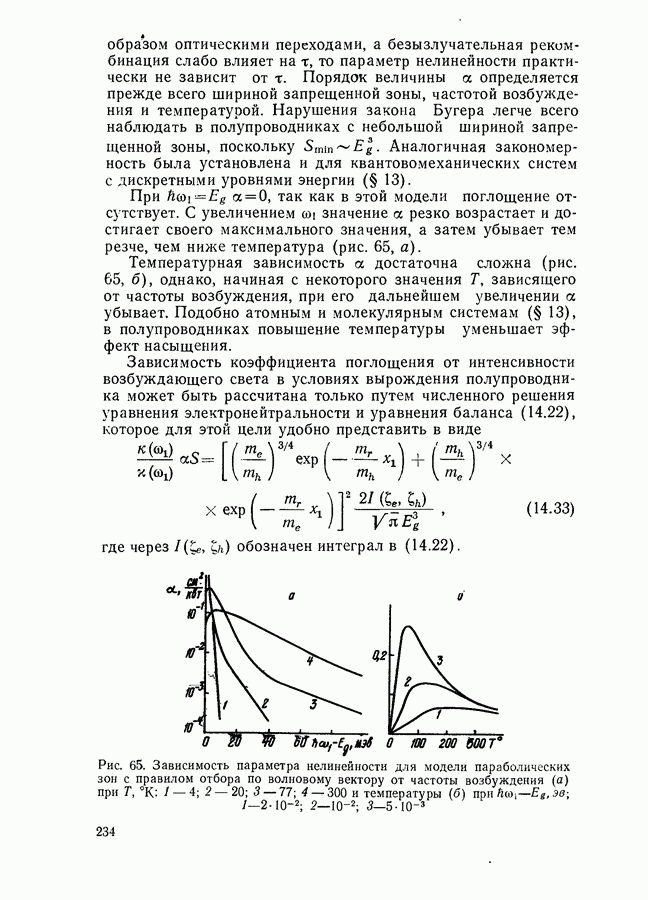
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
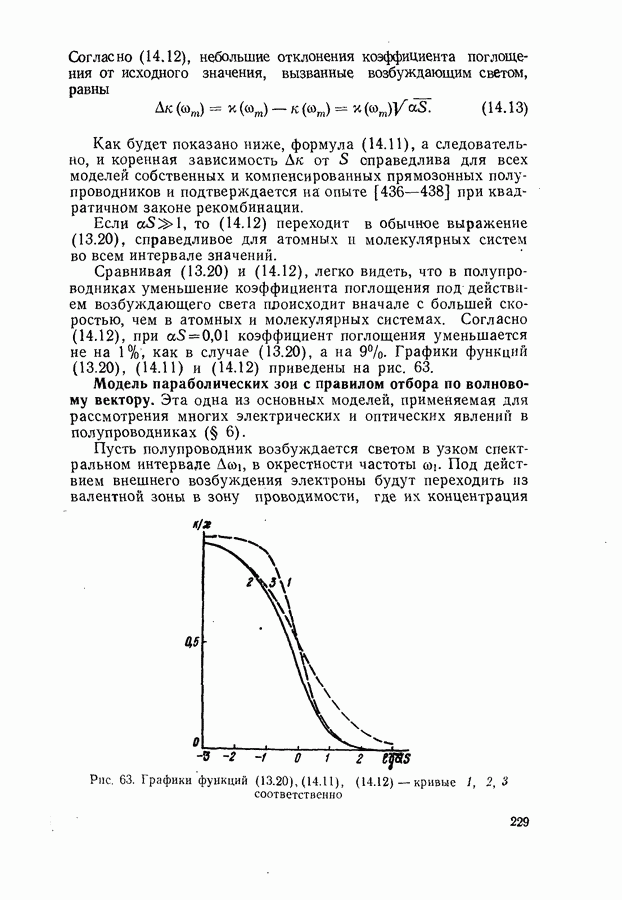
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
- Возбуждение генерации пучком быстрых электронов.