| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
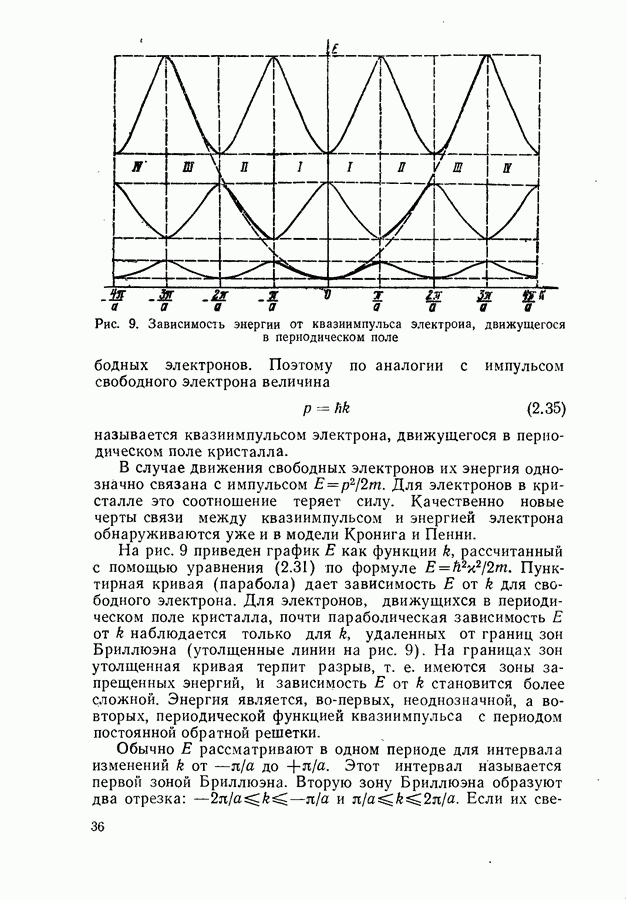
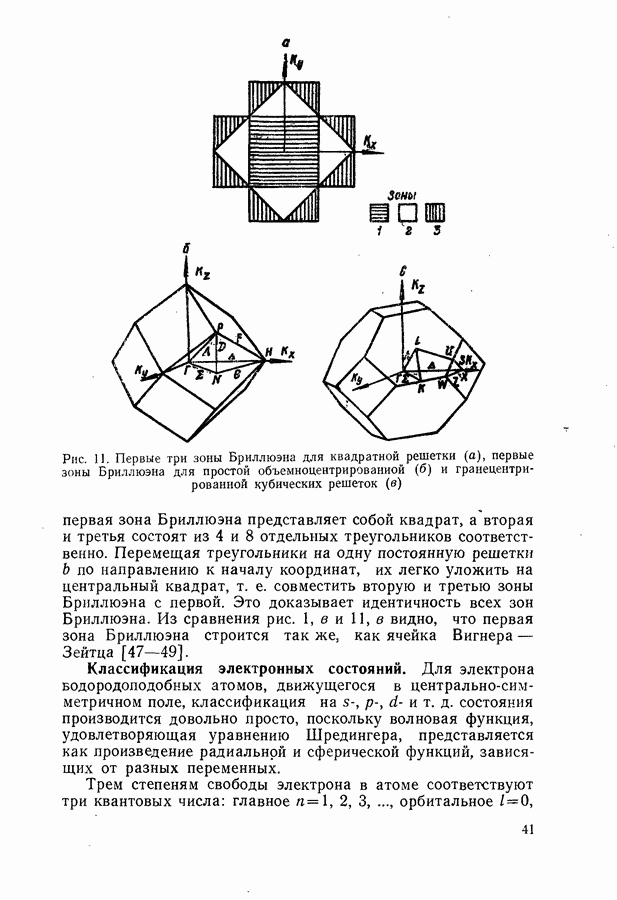
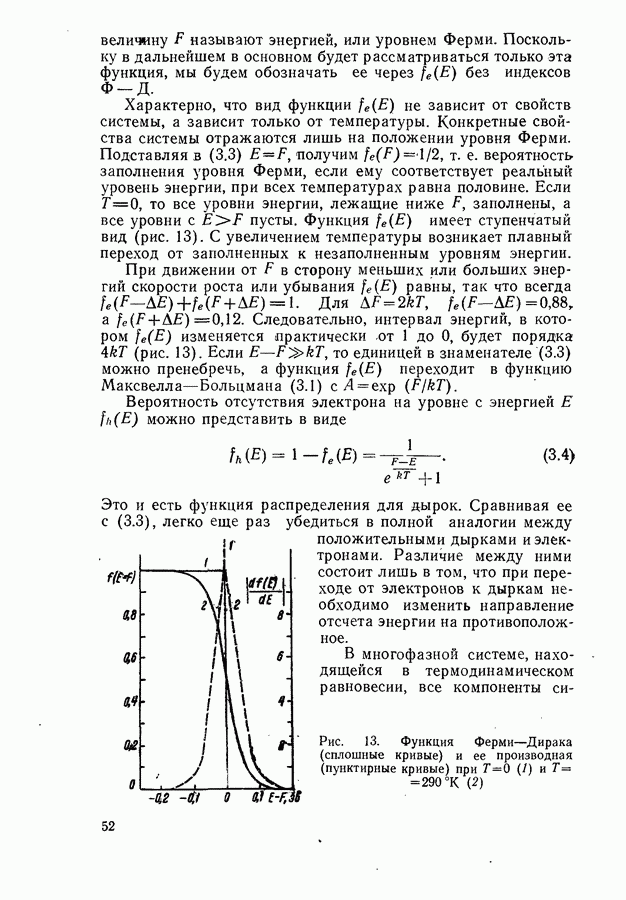
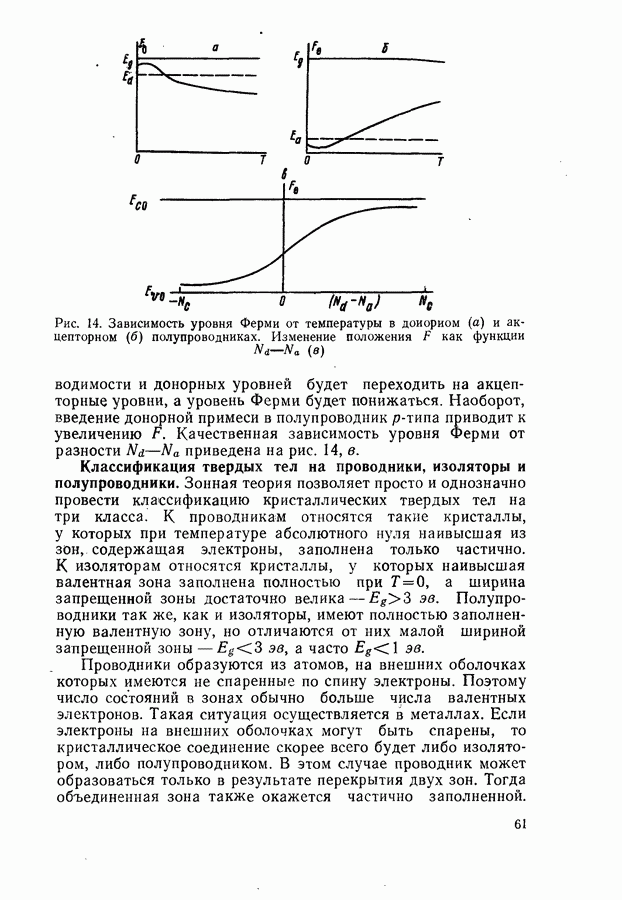
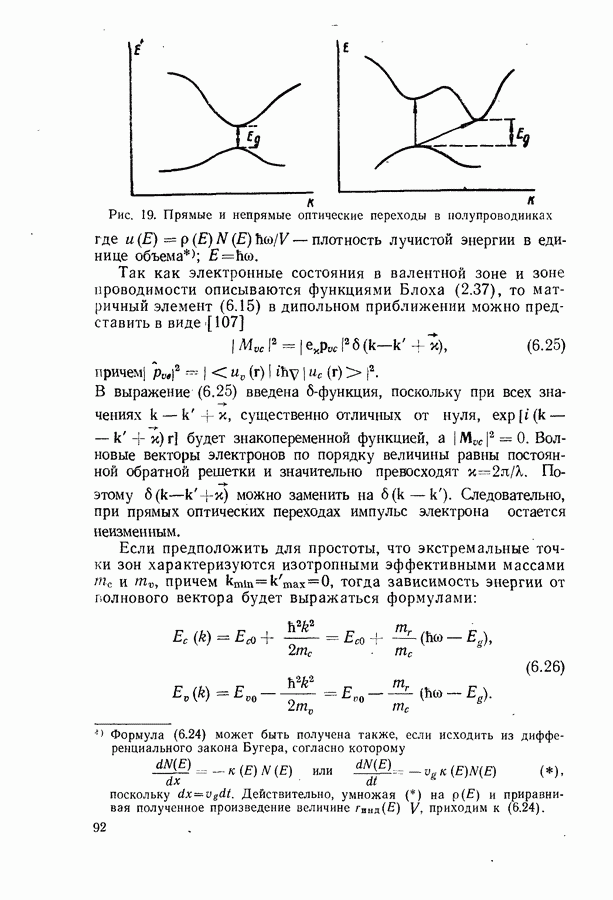
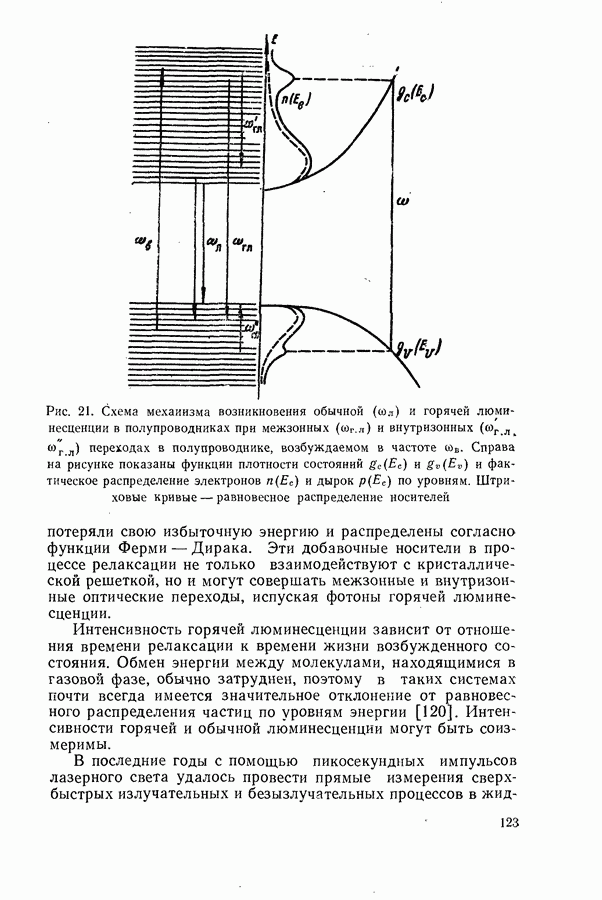
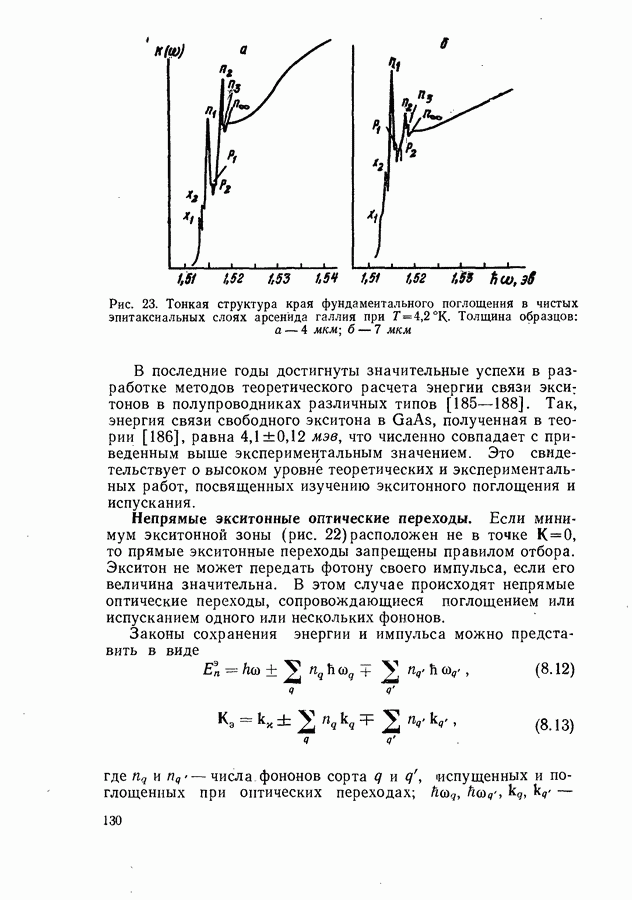
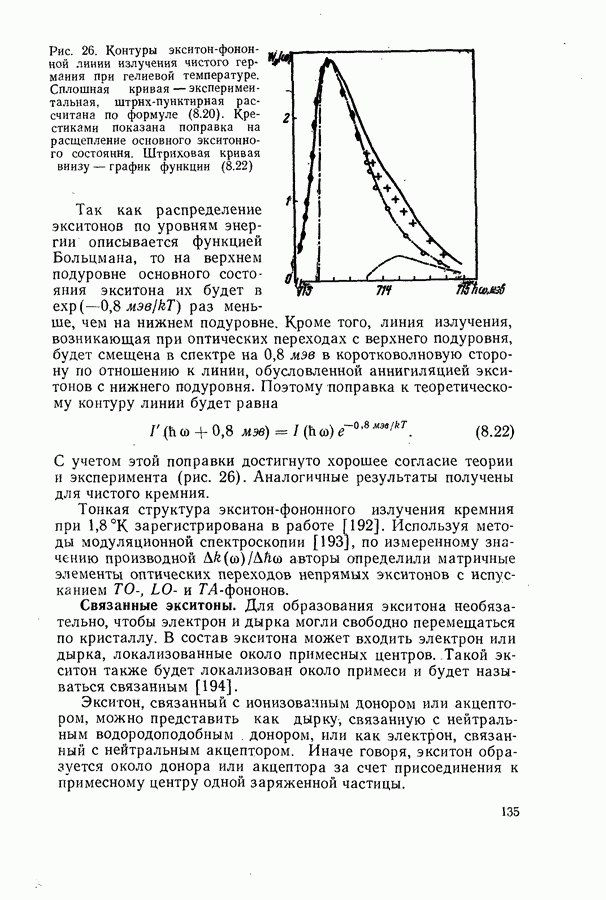
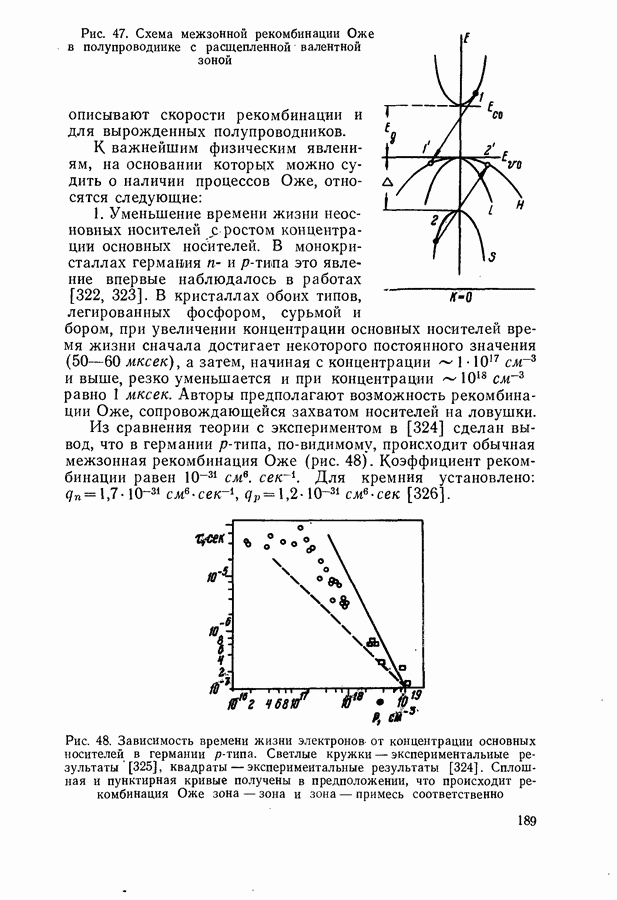
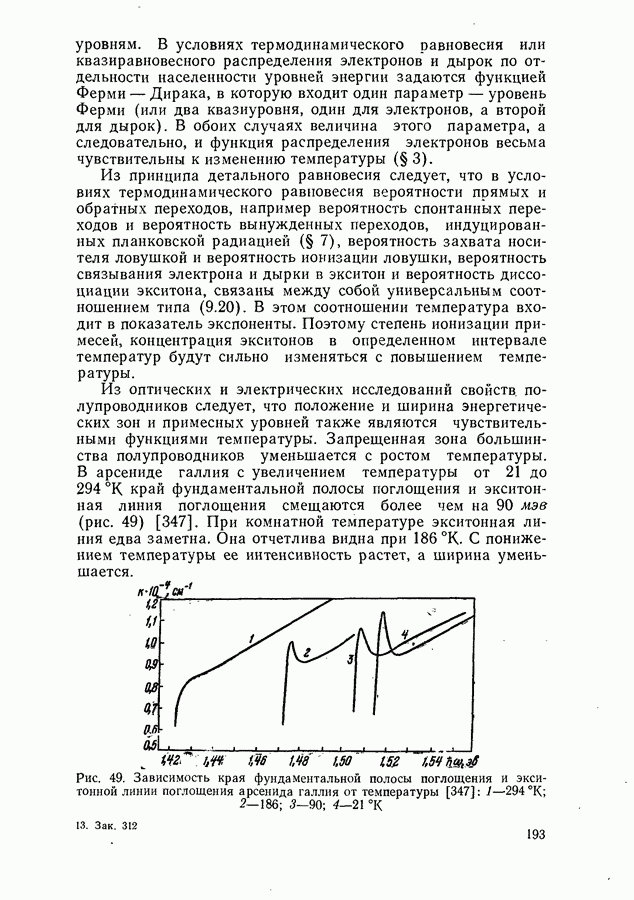
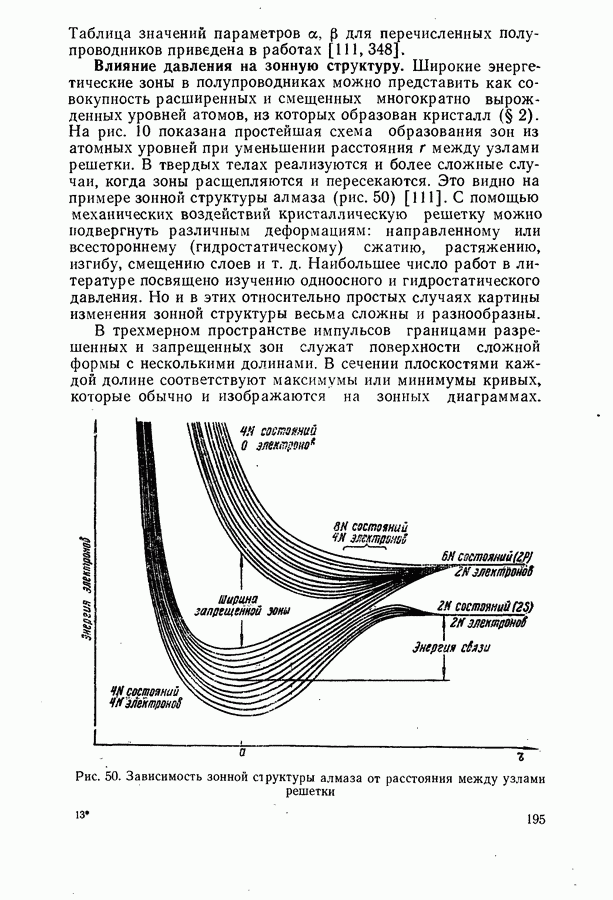
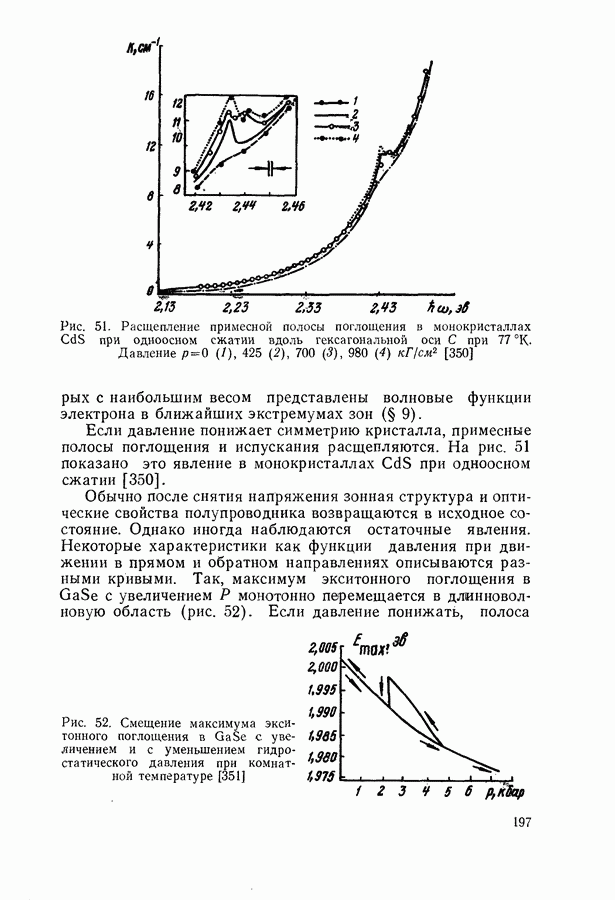
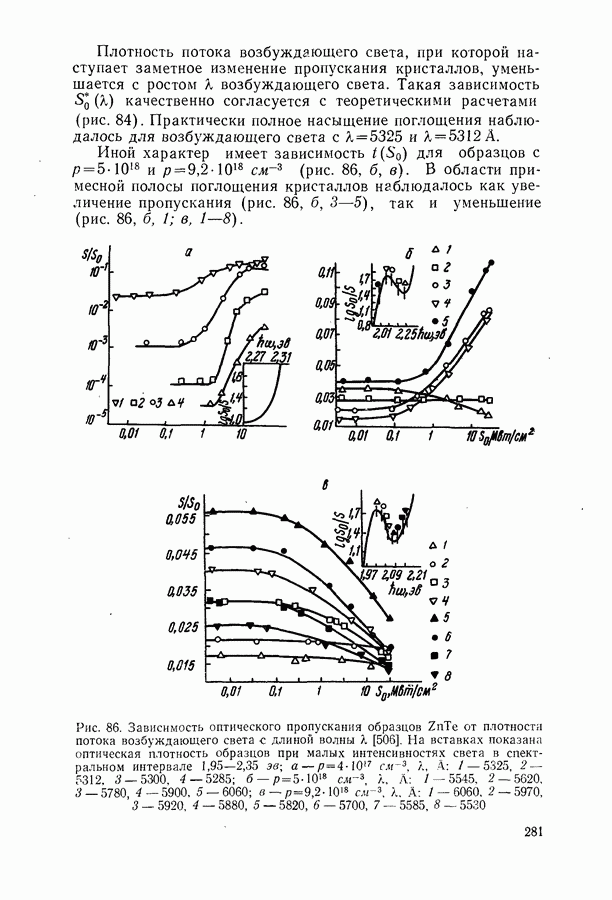
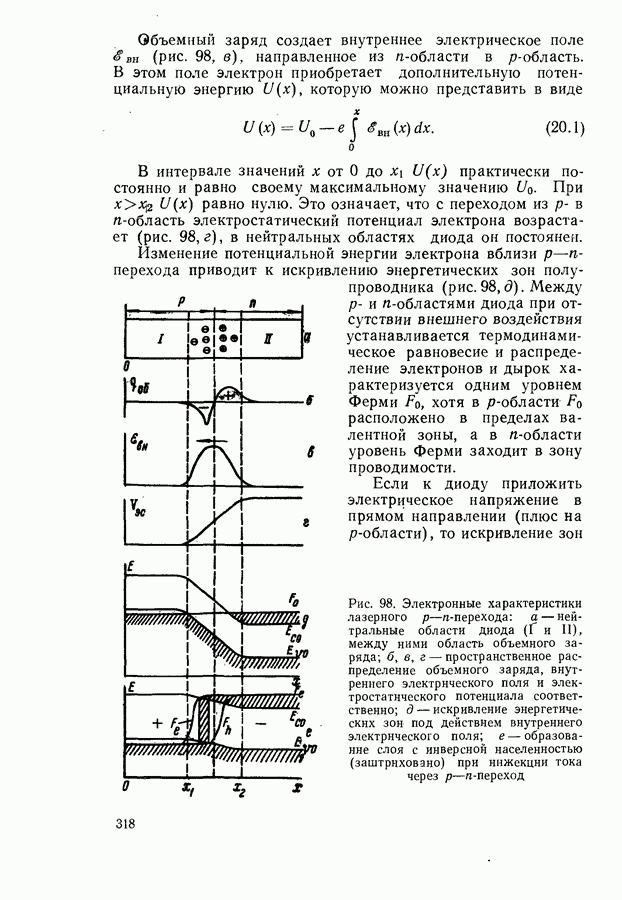
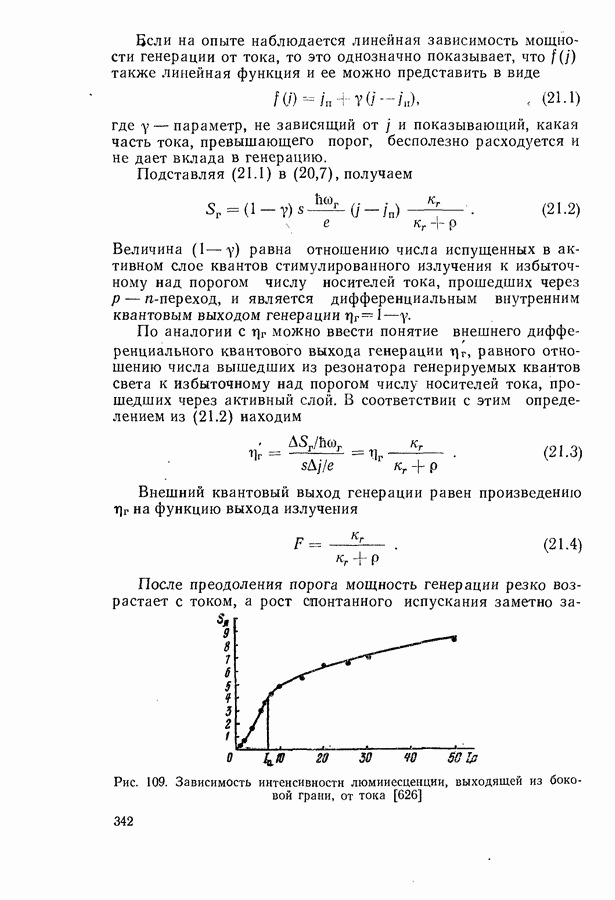
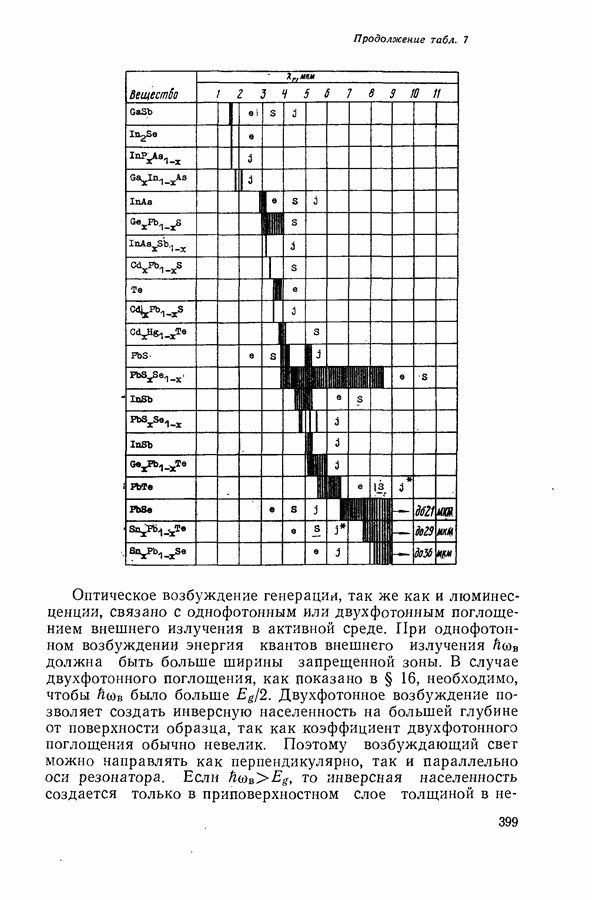
Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
Для стационарной генерации справедливо скоростное уравнение, вытекающее из уравнения непрерывности для тока [594, 600]:

где  полный ток через диод;
полный ток через диод;  скорости люминесценции, стимулированной, безызлучательной и индуцированной шумами рекомбинации в генерирующей части диода в расчете на единицу объема. Штрихами отмечены те же величины, но для негенерирующих частей области рекомбинации диода. Величина
скорости люминесценции, стимулированной, безызлучательной и индуцированной шумами рекомбинации в генерирующей части диода в расчете на единицу объема. Штрихами отмечены те же величины, но для негенерирующих частей области рекомбинации диода. Величина  равна отношению разности электронных токов в
равна отношению разности электронных токов в  и
и  -областях на значительном удалении от
-областях на значительном удалении от  -перехода к полному току через диод. Лазерные диоды имеют высокую концентрацию легирующих примесей
-перехода к полному току через диод. Лазерные диоды имеют высокую концентрацию легирующих примесей  поэтому
поэтому  и в дальнейшем значение
и в дальнейшем значение  полагается равным единице. Интегрирование (20.3) проводится по генерирующей и негенерирующей частям диода.
полагается равным единице. Интегрирование (20.3) проводится по генерирующей и негенерирующей частям диода.
Энергетическим условием стационарной генерации служит требование равенства максимального коэффициента усиления  коэффициенту потерь
коэффициенту потерь  Для резонаторов типа Фабри-Перо это равенство имеет вид (19.12).
Для резонаторов типа Фабри-Перо это равенство имеет вид (19.12).
Минимальный ток, при котором удовлетворяется условие  будет пороговым током. Поскольку в пороге нет смысла делить область рекомбинации на генерирующую и негенерирующую части, то, полагая в
будет пороговым током. Поскольку в пороге нет смысла делить область рекомбинации на генерирующую и негенерирующую части, то, полагая в  и
и
объединяя интегралы, получаем выражение для плотности порогового тока

где  — площадь
— площадь  -перехода;
-перехода;

— квантовый выход люминесценции. Если влияние шумов незначительно, то, согласно (20.4), можно считать, что  обратно пропорционально
обратно пропорционально 
Полное число квантов, генерируемых в диоде, на основании (20.3) можно представить в виде

где

С учетом (19.27) из (20.5) приходим к выражению для мощности генерации

Формула (20.7) получена из скоростного уравнения, равносильного закону сохранения энергии, и имеет широкие границы применимости. Она справедлива как при линейной, так и при нелинейной зависимости  от
от 
Существует ряд методов подавления шумов в инжекционном лазере (§ 24). Поэтому рассмотрим вначале порог генерации без учета радиационного шума. В инжекционных лазерах толщина активного слоя обычно меньше, чем толщина слоя, в котором происходит рекомбинация. В активном слое рекомбинирует только некоторая часть  носителей, пересекших
носителей, пересекших  -переход. Поэтому вводя
-переход. Поэтому вводя  и опуская в (20.4) второе слагаемое, получим
и опуская в (20.4) второе слагаемое, получим

где интегрирование проводится только в пределах объема активного слоя 
Предполагая, что испускание в Активном слое однородно, и вынося  в (20.8) за знак интеграла, получаем
в (20.8) за знак интеграла, получаем

Выражение для  при учете фона теплового испускания (см. § 21) имеет вид (7.17). Спектр люминесценции определяется энергетическим распределением инжектируемых в активный слой носителей. Это распределение задается квазиуровнями Ферми
при учете фона теплового испускания (см. § 21) имеет вид (7.17). Спектр люминесценции определяется энергетическим распределением инжектируемых в активный слой носителей. Это распределение задается квазиуровнями Ферми  для электронов и
для электронов и  для дырок и температурой диода
для дырок и температурой диода  Для лазерных полупроводников, таких, как например GaAs, обычно
Для лазерных полупроводников, таких, как например GaAs, обычно  кроме того, вблизи порога, когда выполняется условие
кроме того, вблизи порога, когда выполняется условие  скорость люминесценции практически совпадает со скоростью спонтанной рекомбинации, равной
скорость люминесценции практически совпадает со скоростью спонтанной рекомбинации, равной

Вычисление порога генерации основано на совместном решении уравнения баланса (20.3), уравнения электронейтральности типа (14.66) и энергетического условия генерации (19.12). При расчетах применяется следующий формальный прием. Задается значение уровня Ферми для электронов  и из уравнения нейтральности определяется уровень Ферми для дырок
и из уравнения нейтральности определяется уровень Ферми для дырок  По известным
По известным  рассчитываются коэффициент усиления и мощность люминесценции. Максимальное значение
рассчитываются коэффициент усиления и мощность люминесценции. Максимальное значение  по условию равно коэффициенту потерь, а
по условию равно коэффициенту потерь, а  связано с Яд соотношением (20.9). Таким образом, устанавливается связь между
связано с Яд соотношением (20.9). Таким образом, устанавливается связь между 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
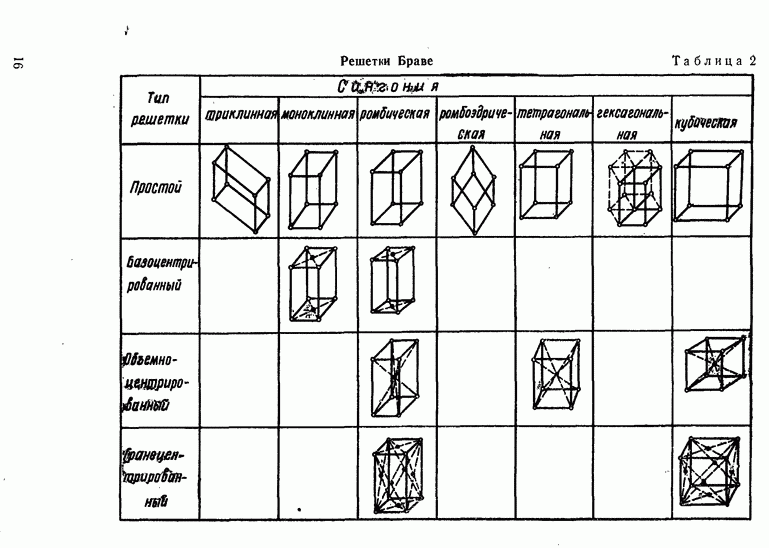
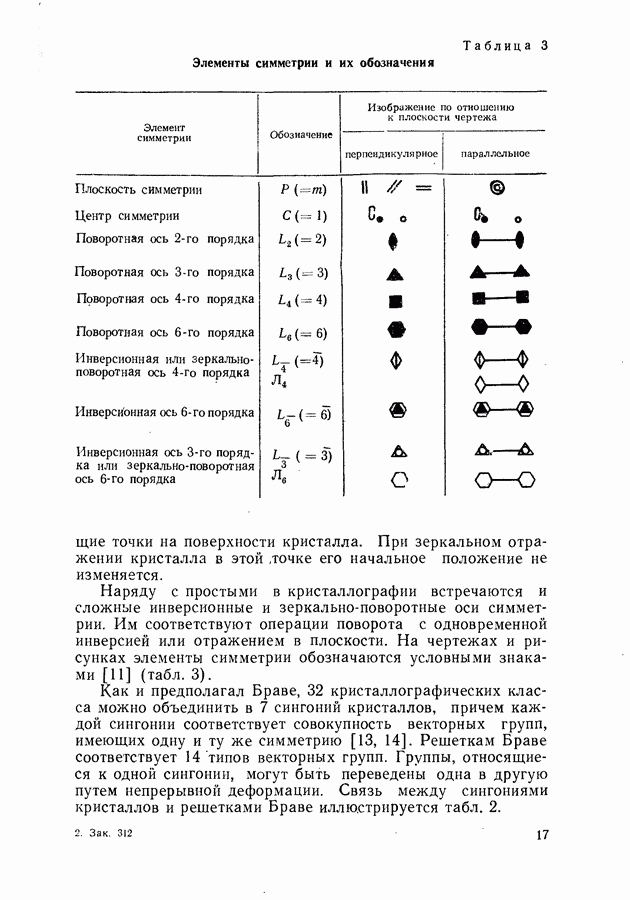
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
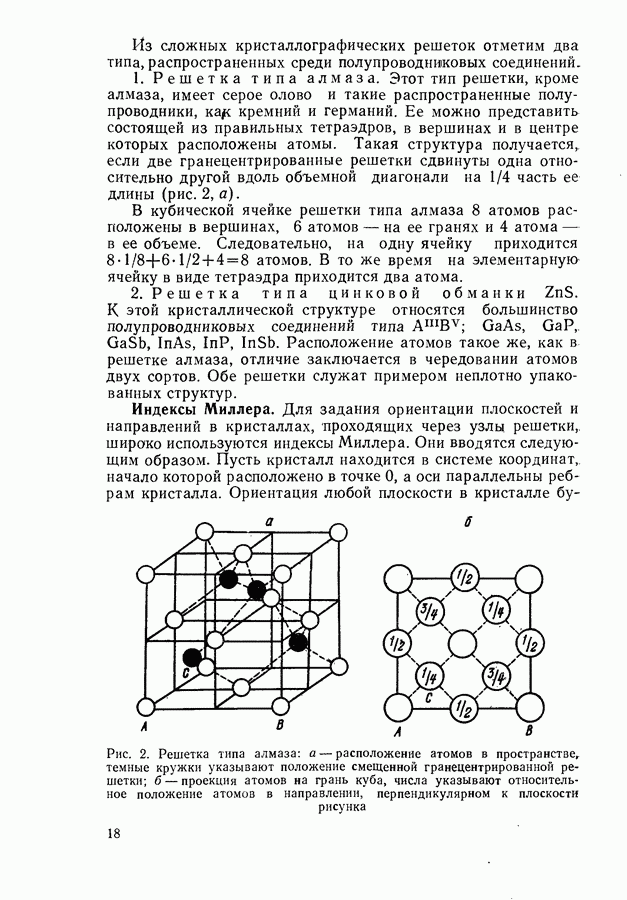
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
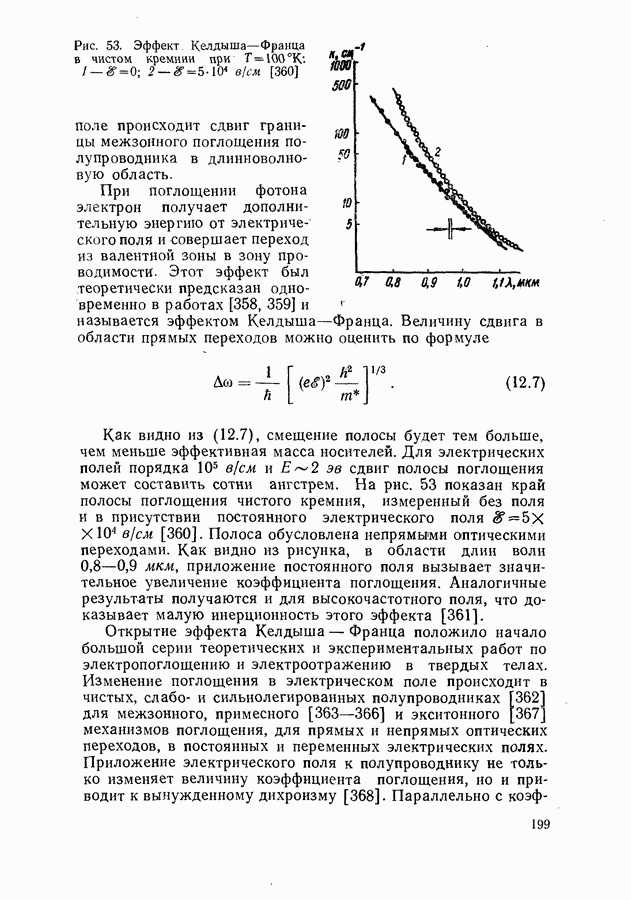
- Эффект Келдыша-Франца.
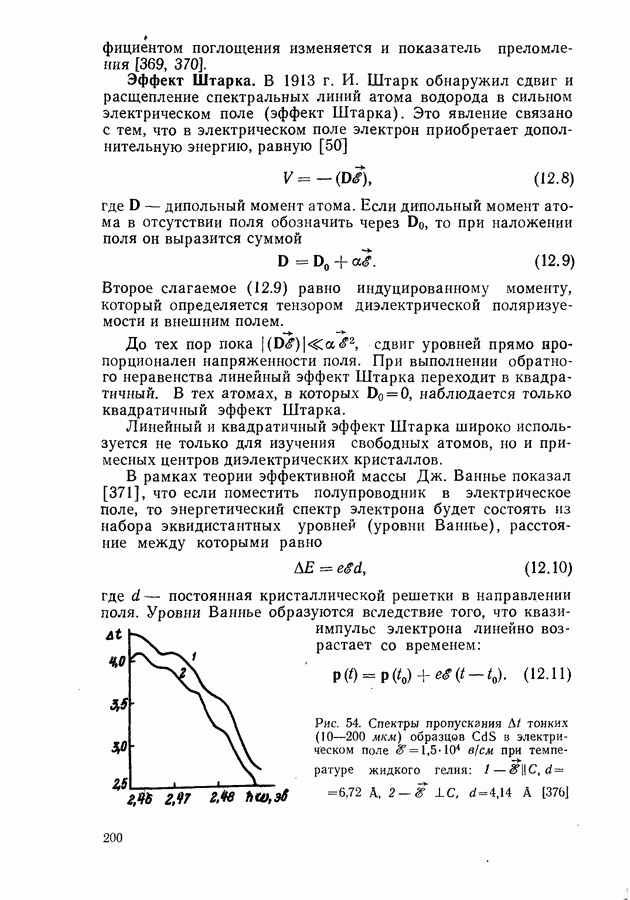
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
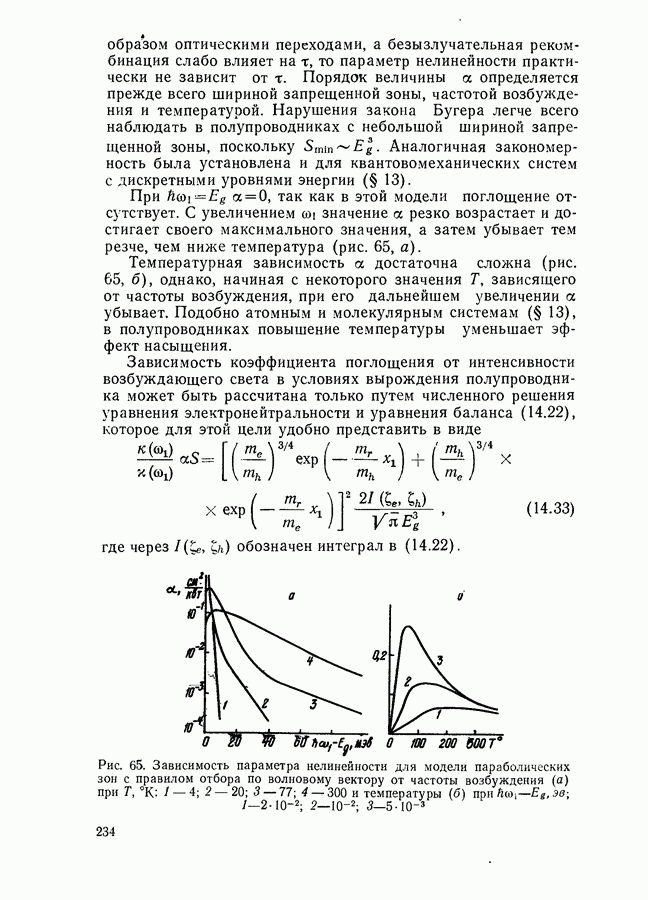
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
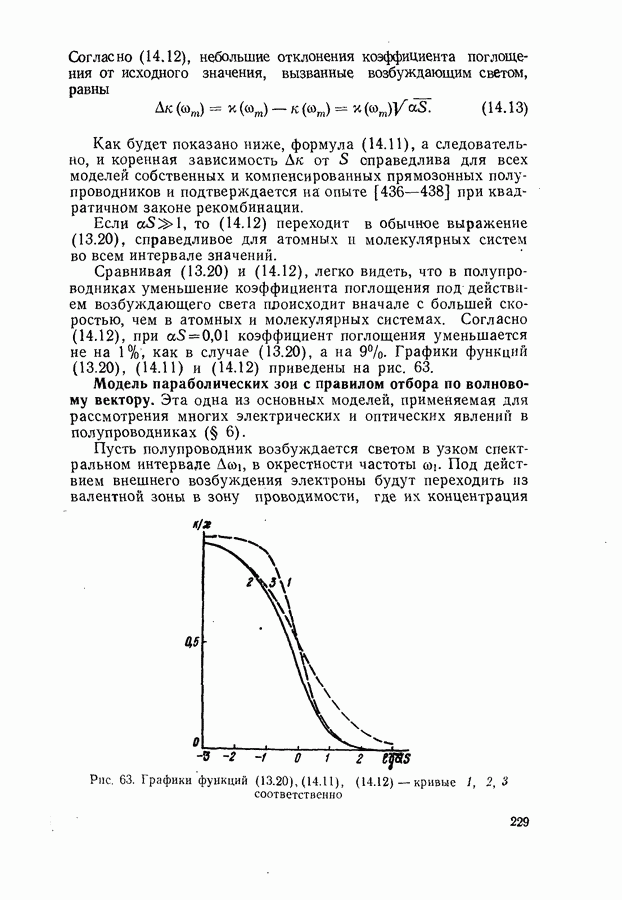
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
- Модель параболических зон с правилом отбора по волновому вектору.
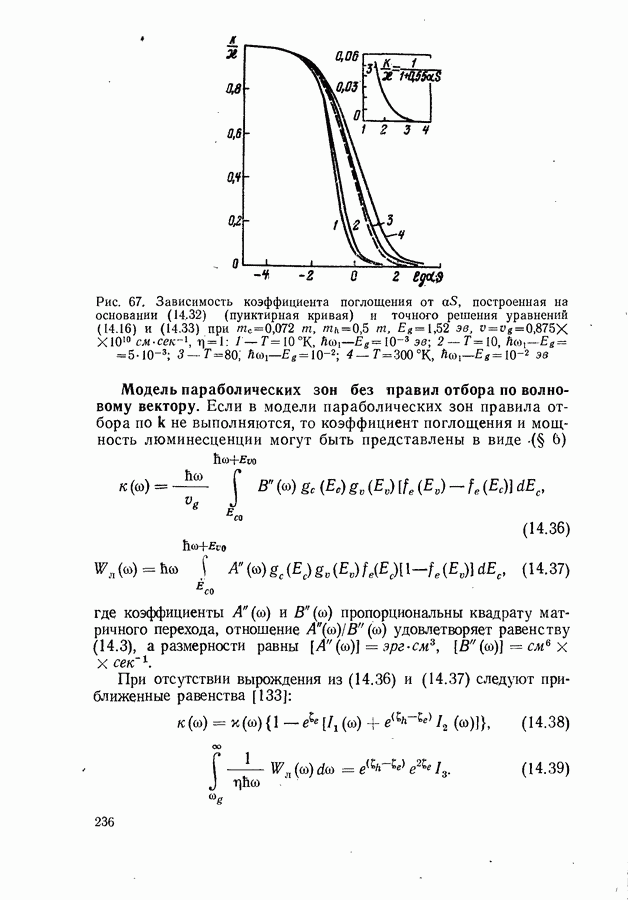
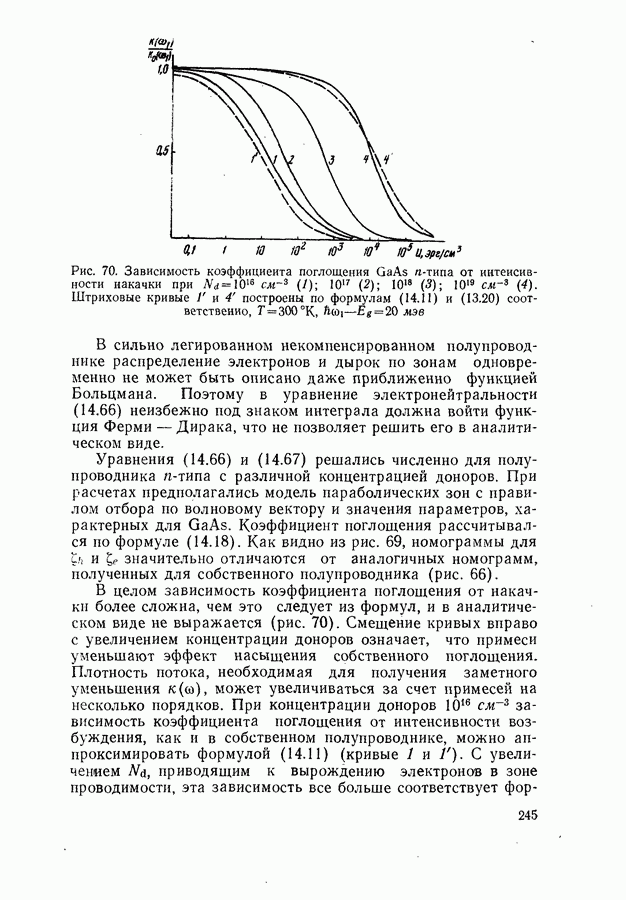
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
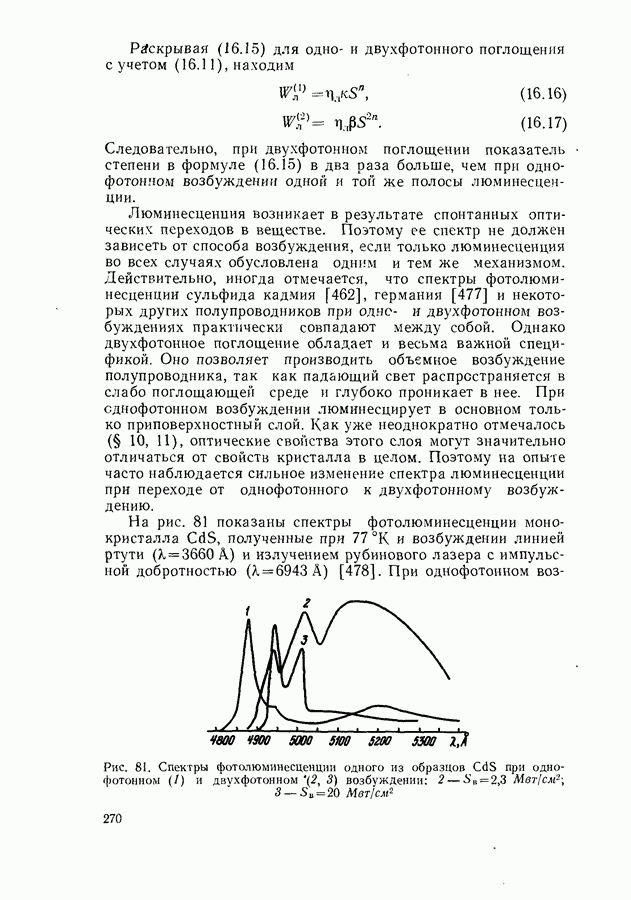
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
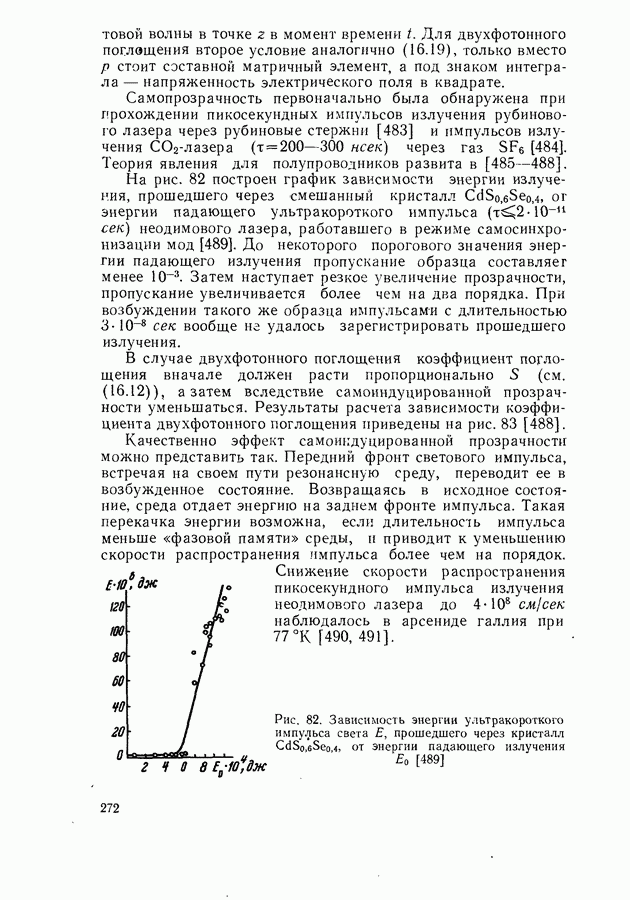
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
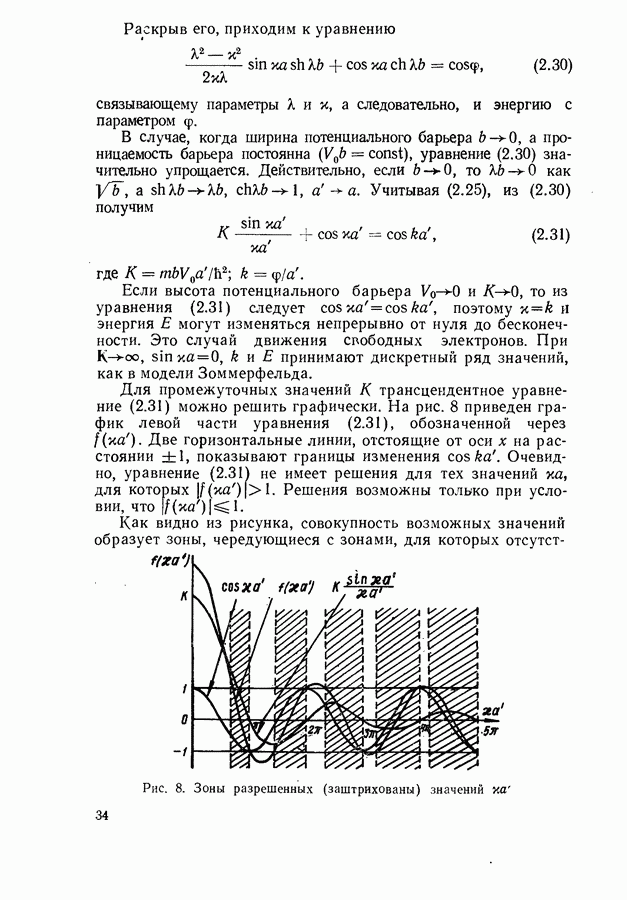
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
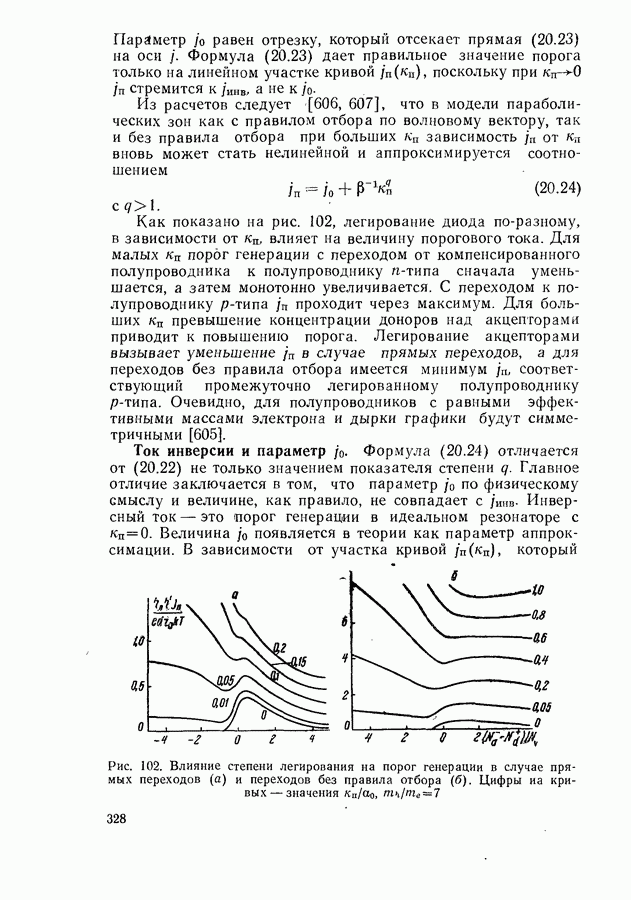
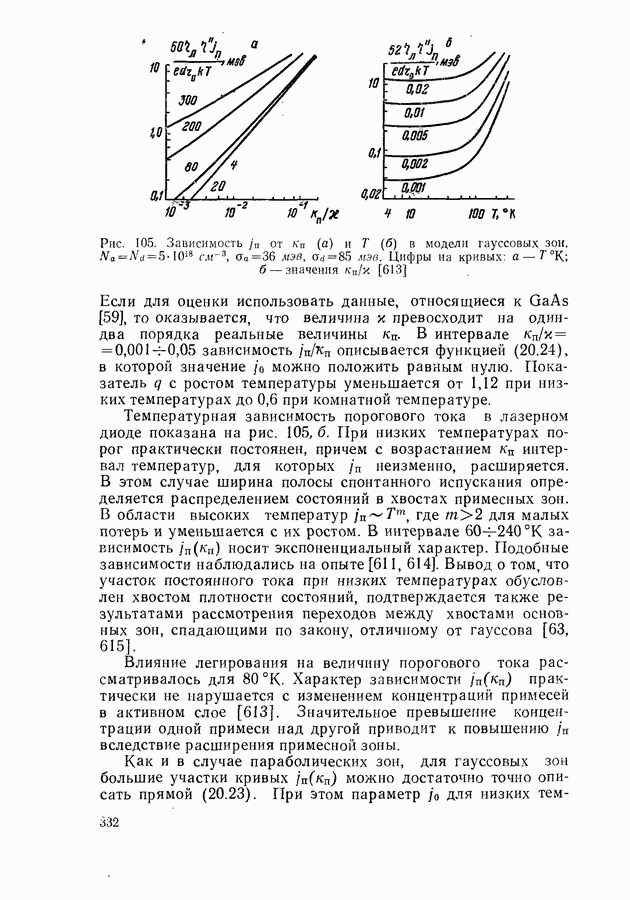
- Ток инверсии и параметр j0
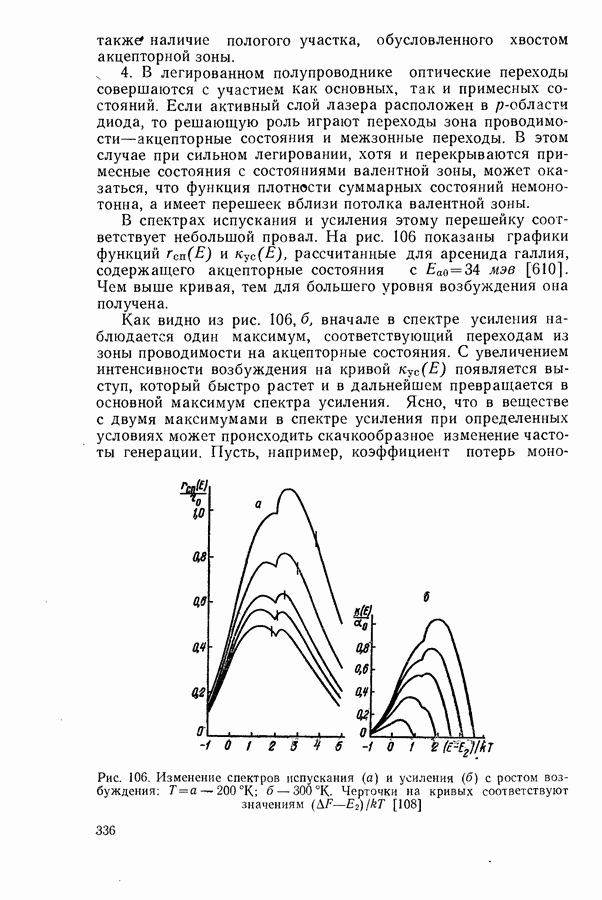
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
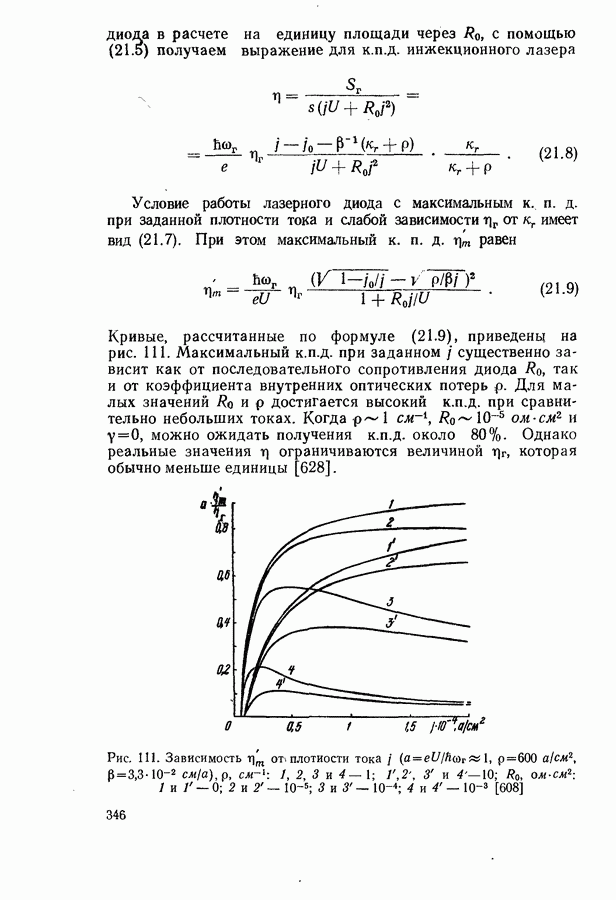
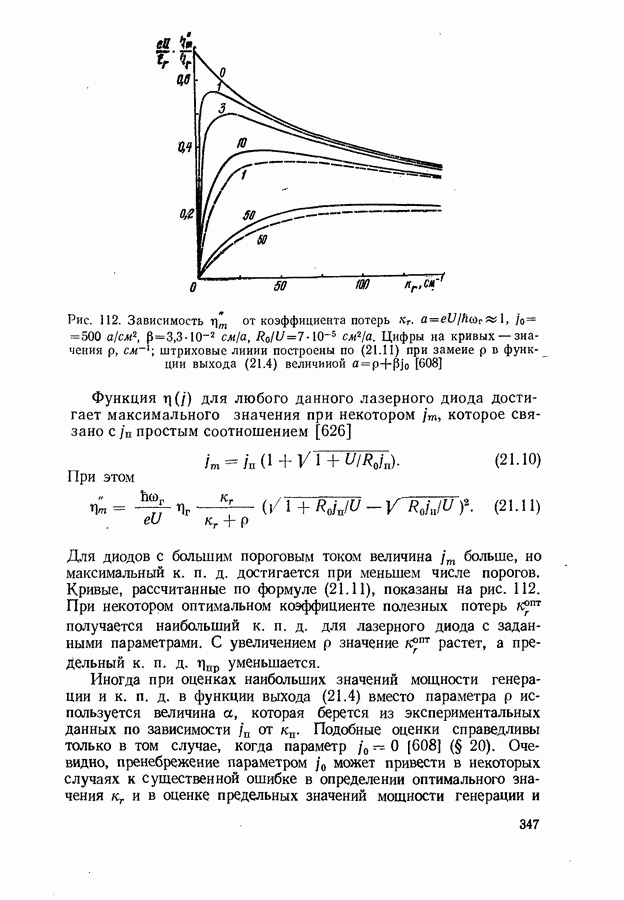
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
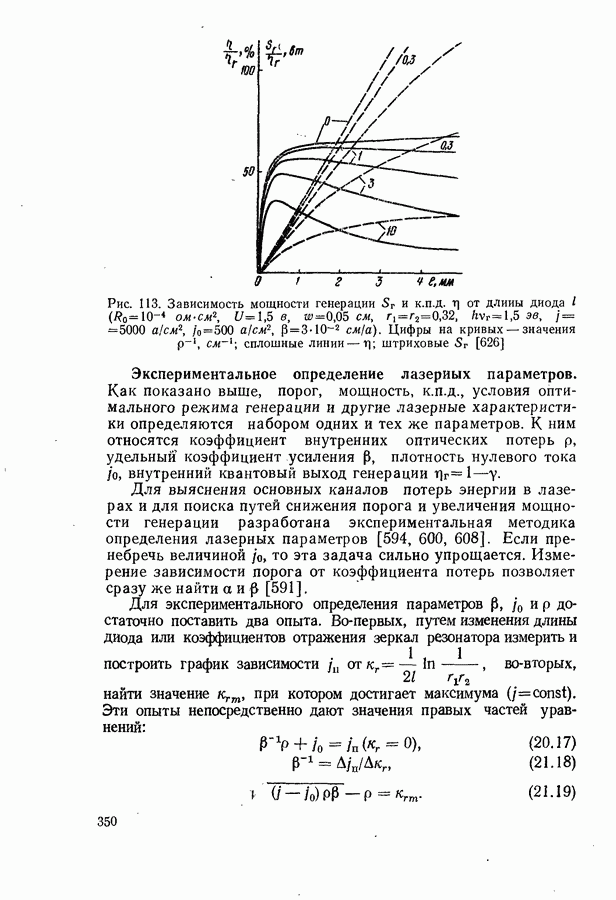
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
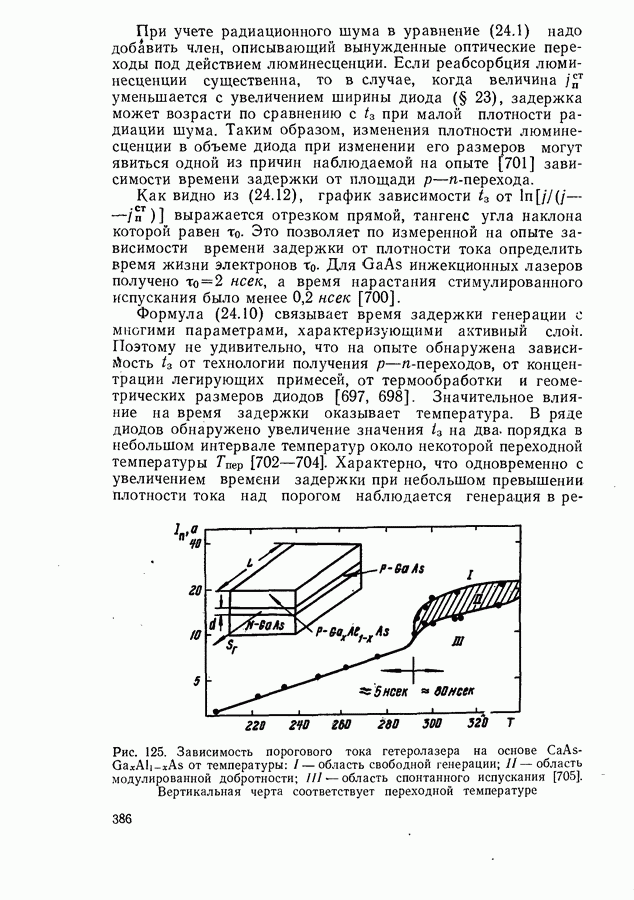
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
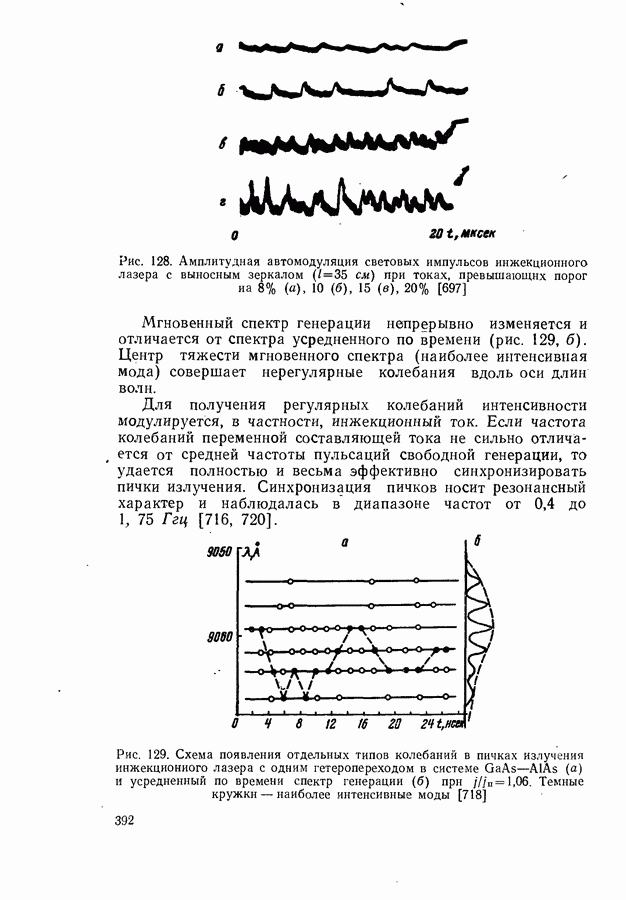
- Амплитудная и частотная автомодуляция излучения.
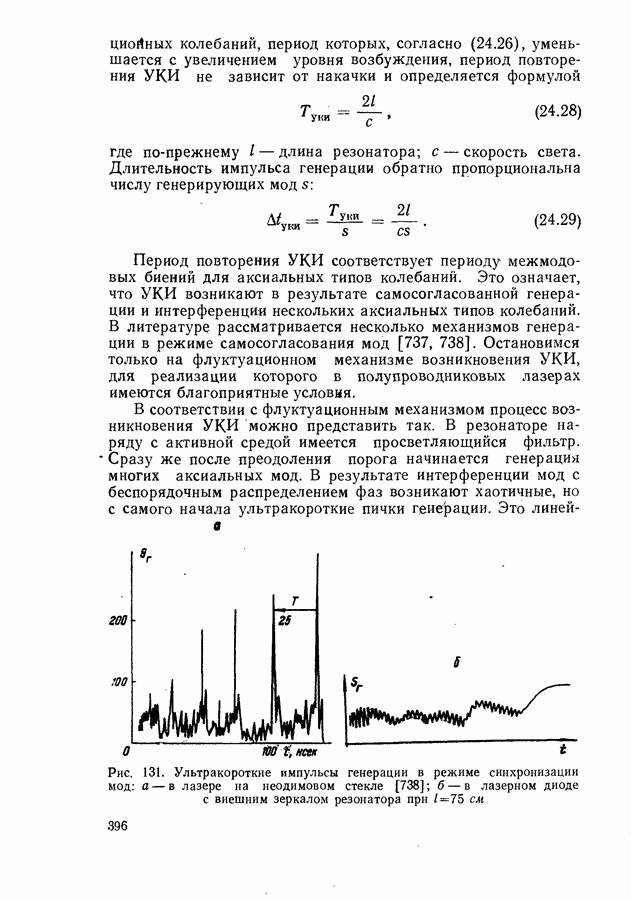
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
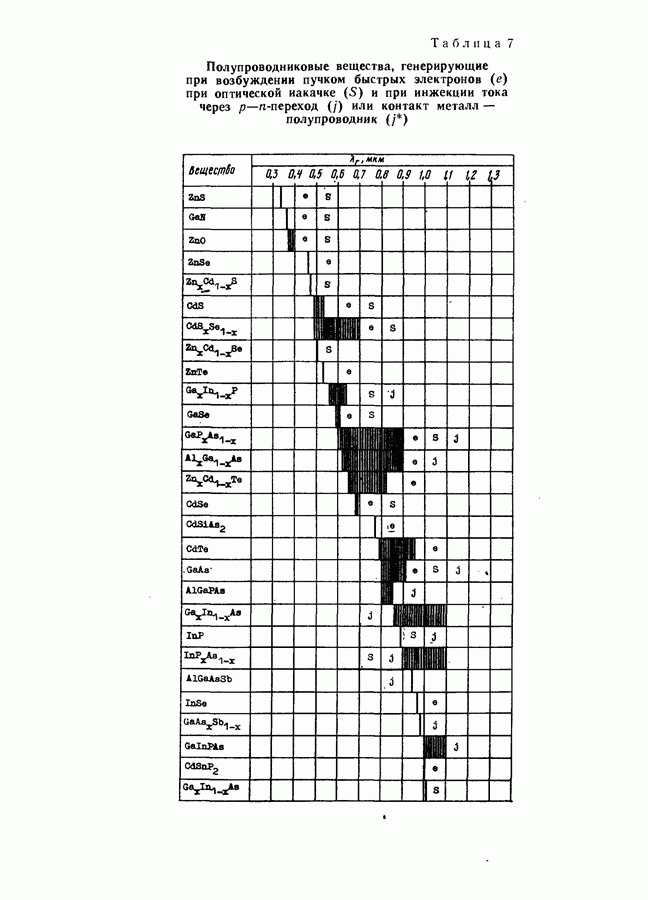
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
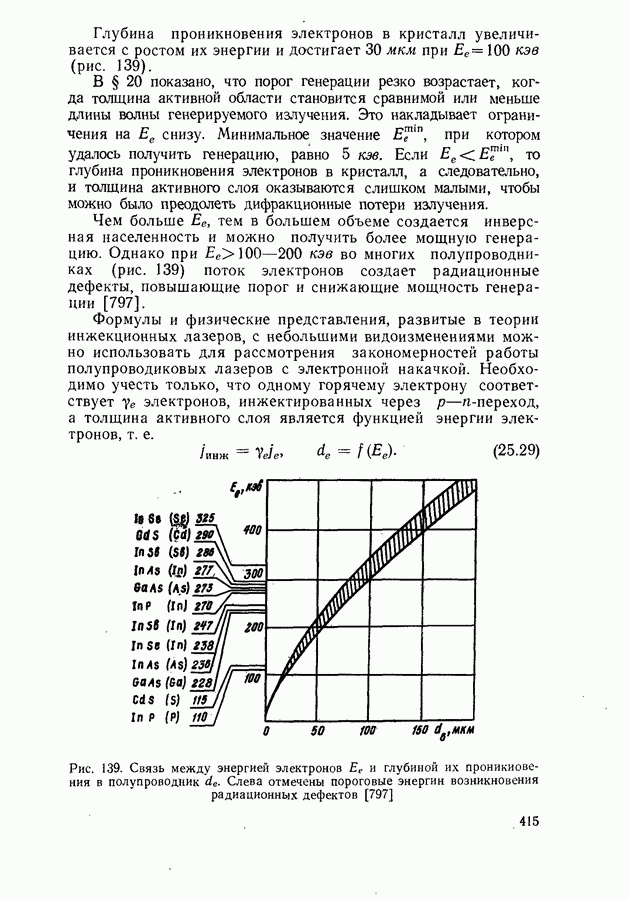
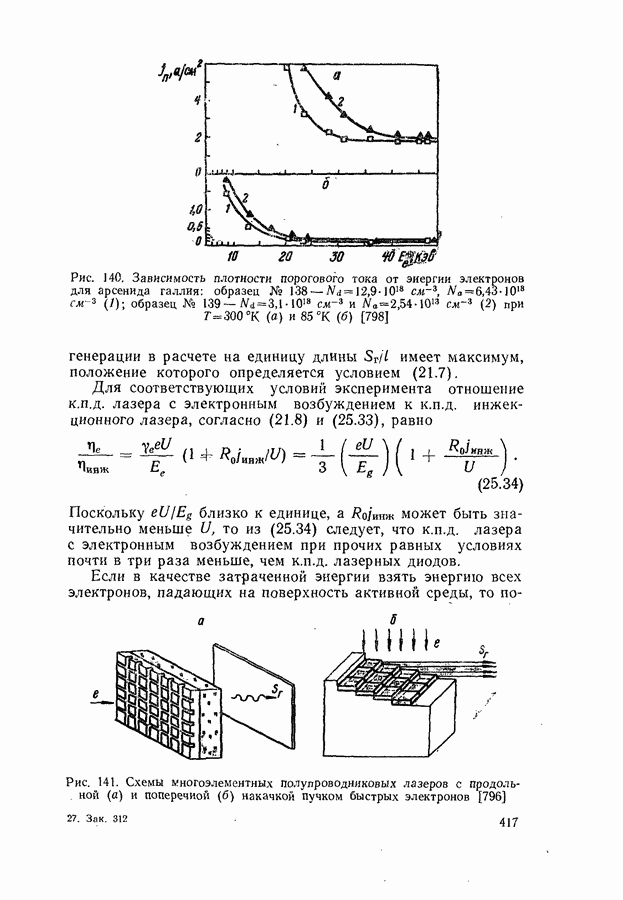
- Возбуждение генерации пучком быстрых электронов.