| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
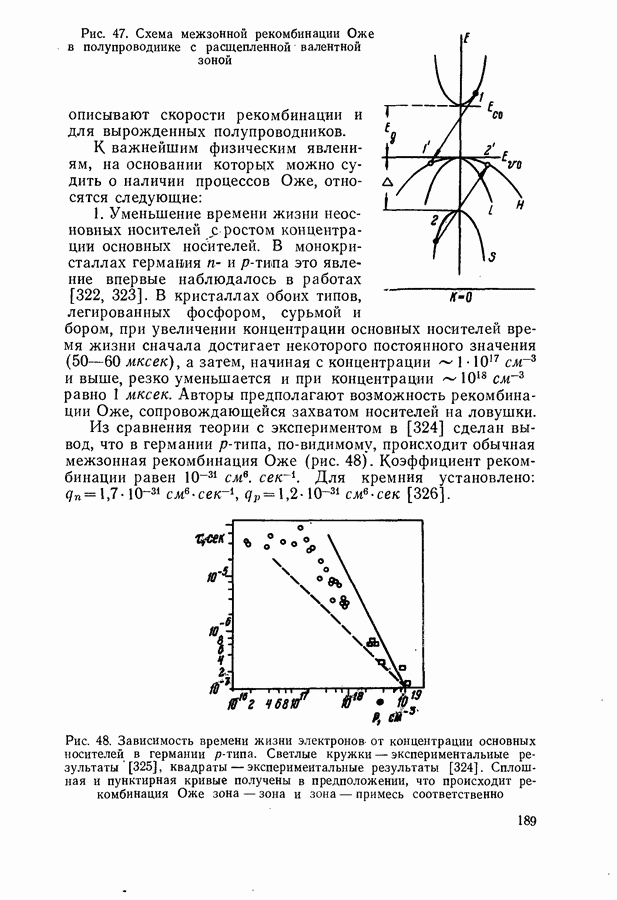
188
189
190
191
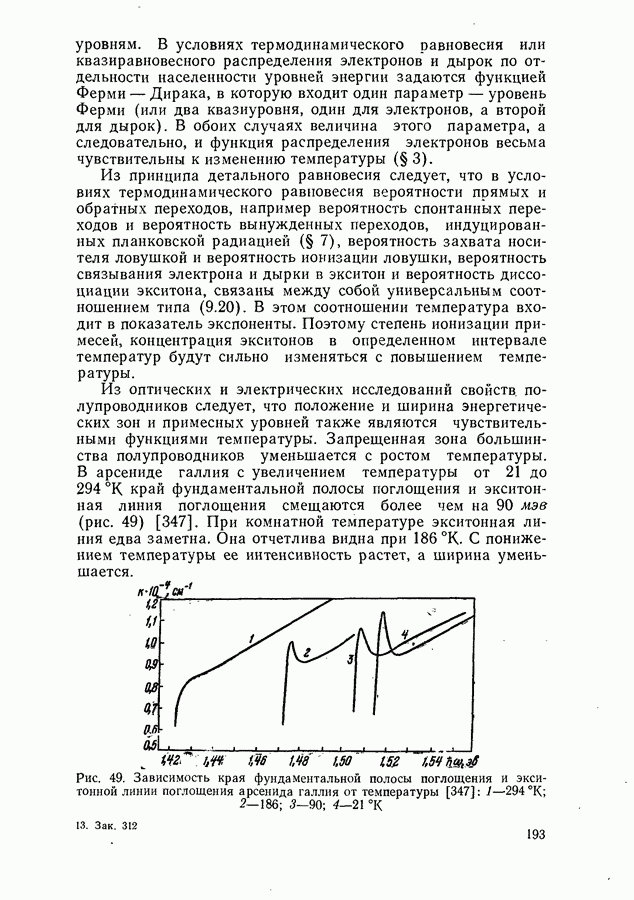
192
193
194
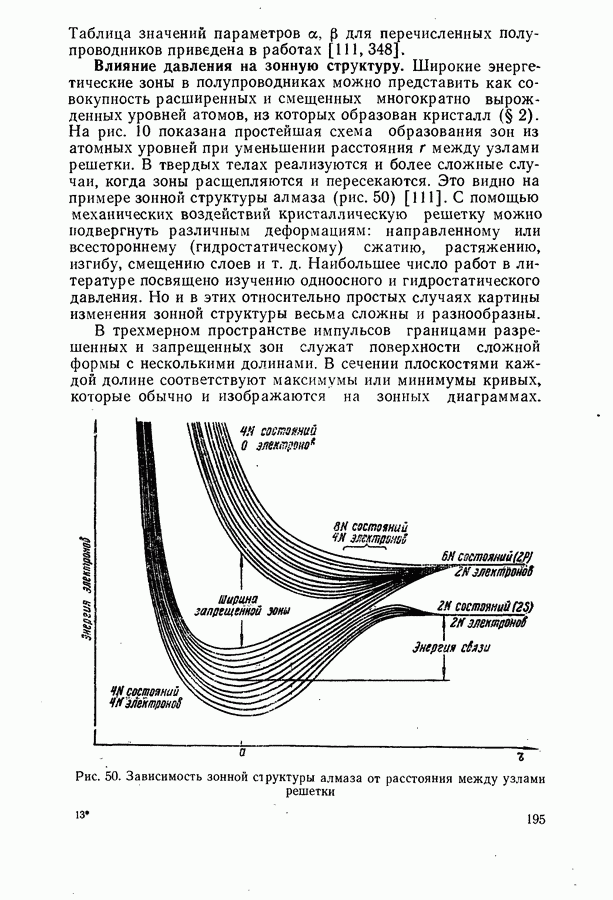
195
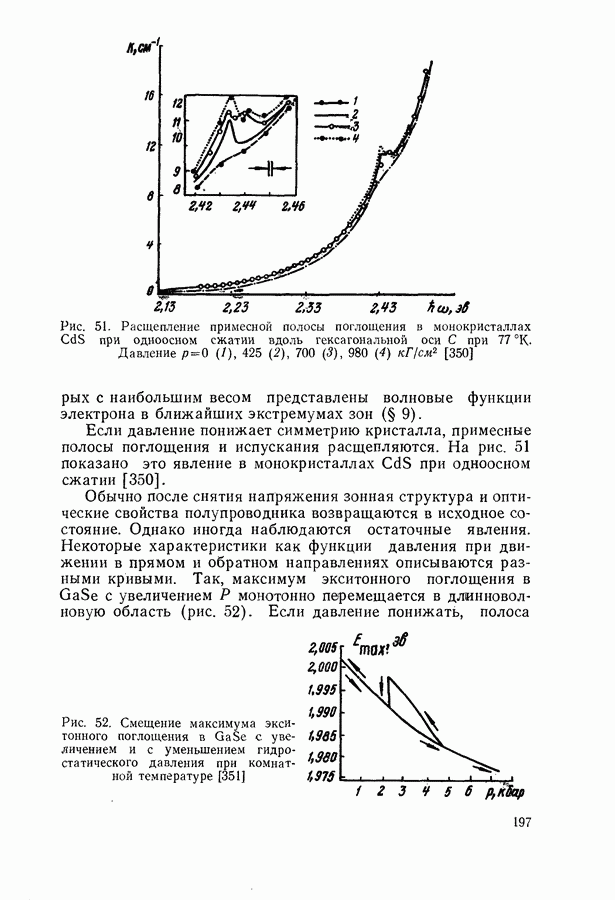
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
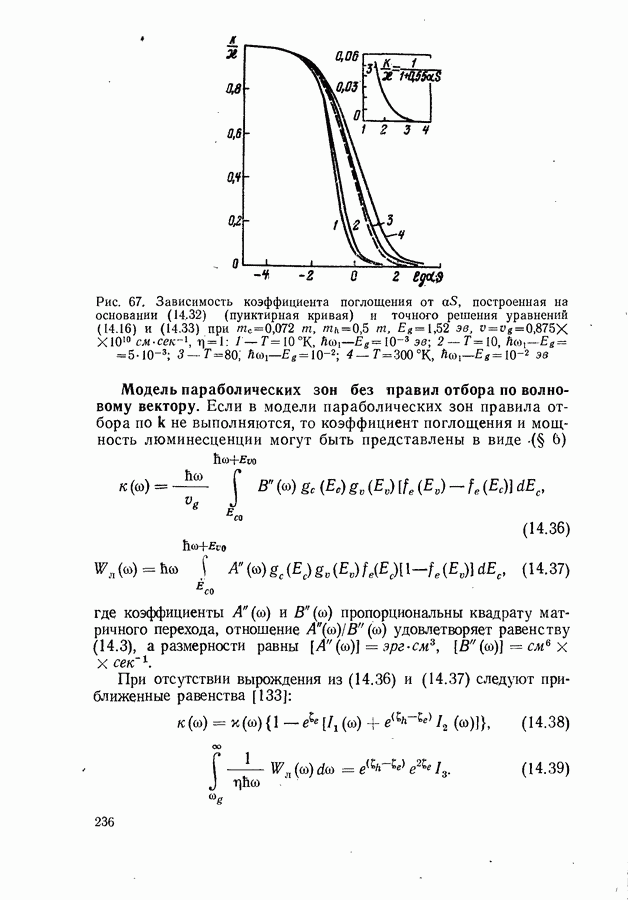
236
237
238
239
240
241
242
243
244
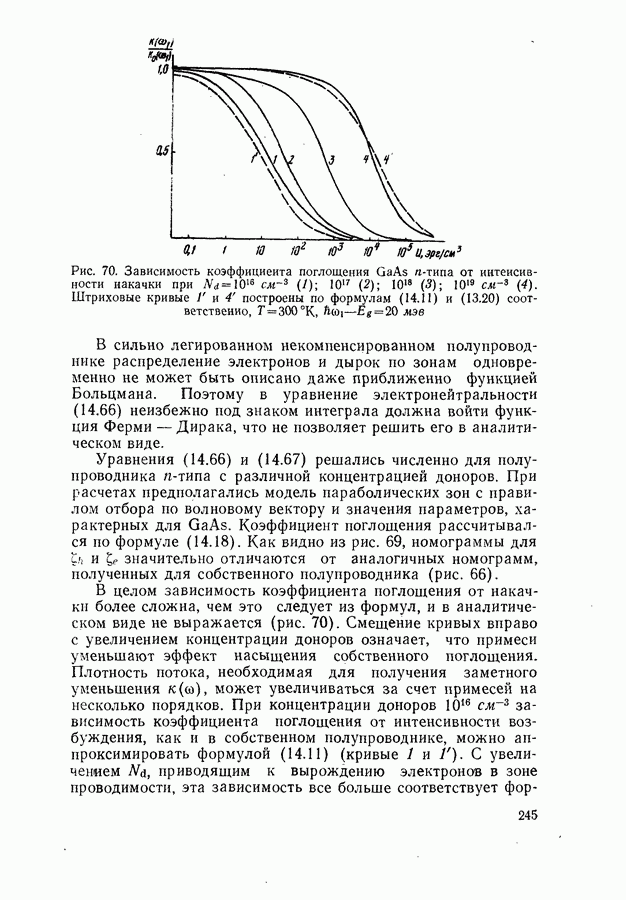
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
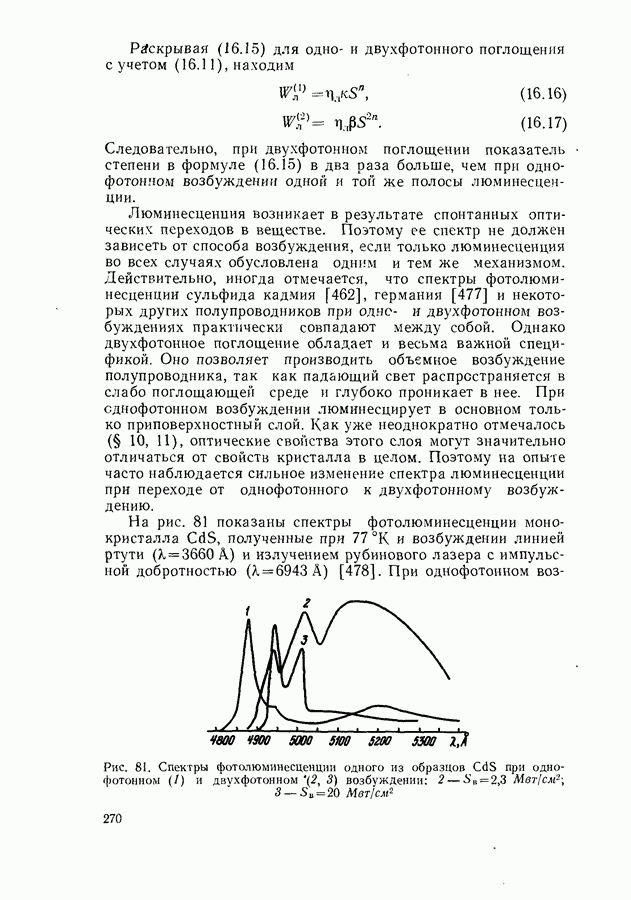
270
271
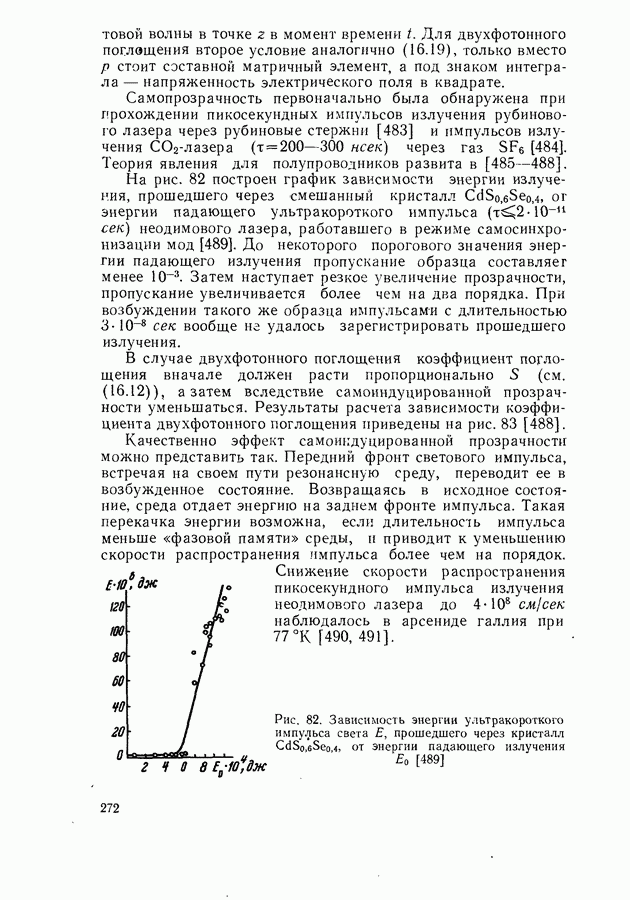
272
273
274
275
276
277
278
279
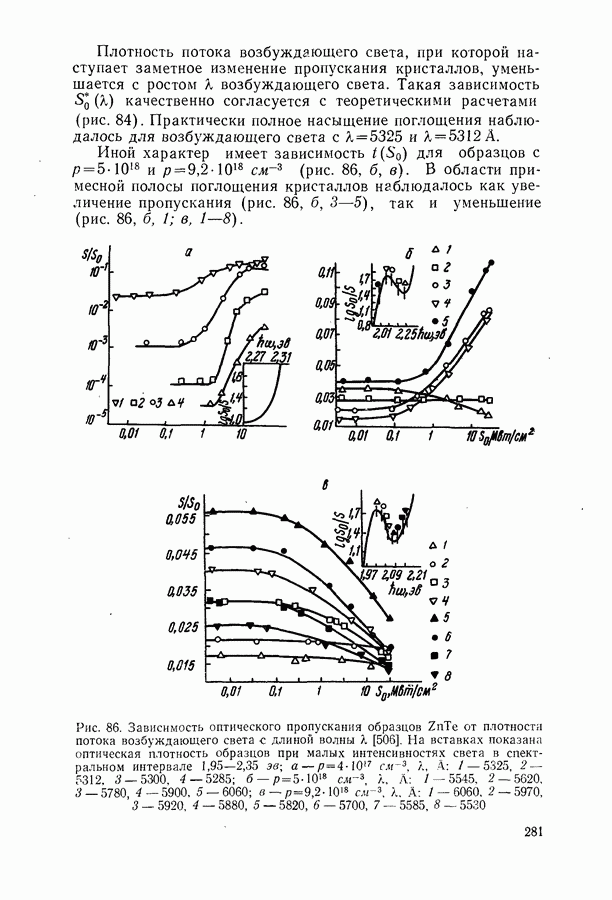
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
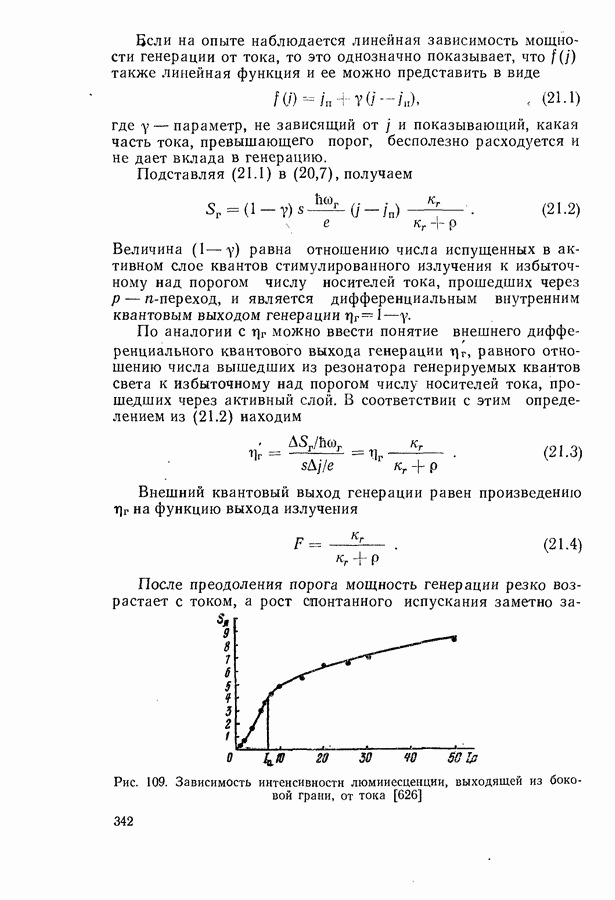
342
343
344
345
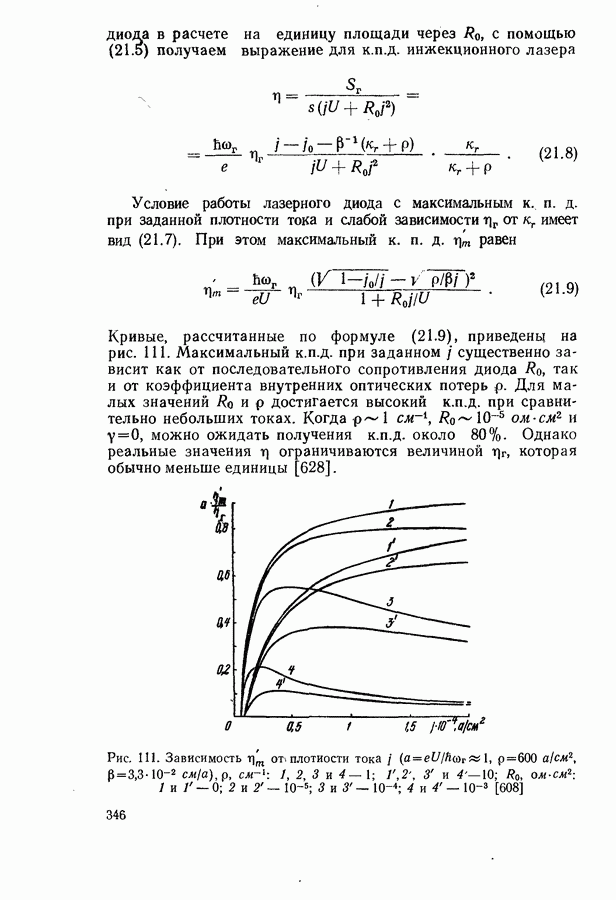
346
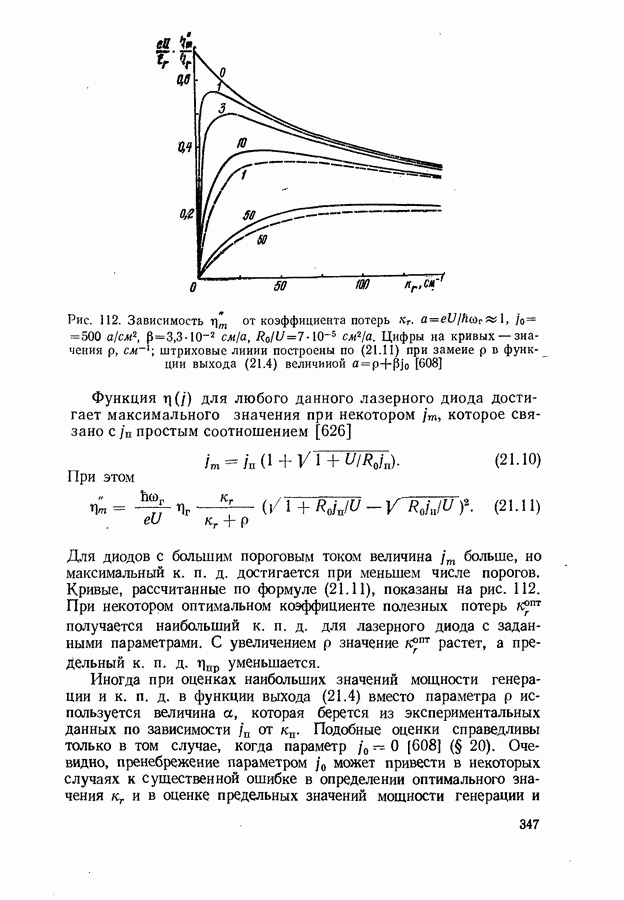
347
348
349
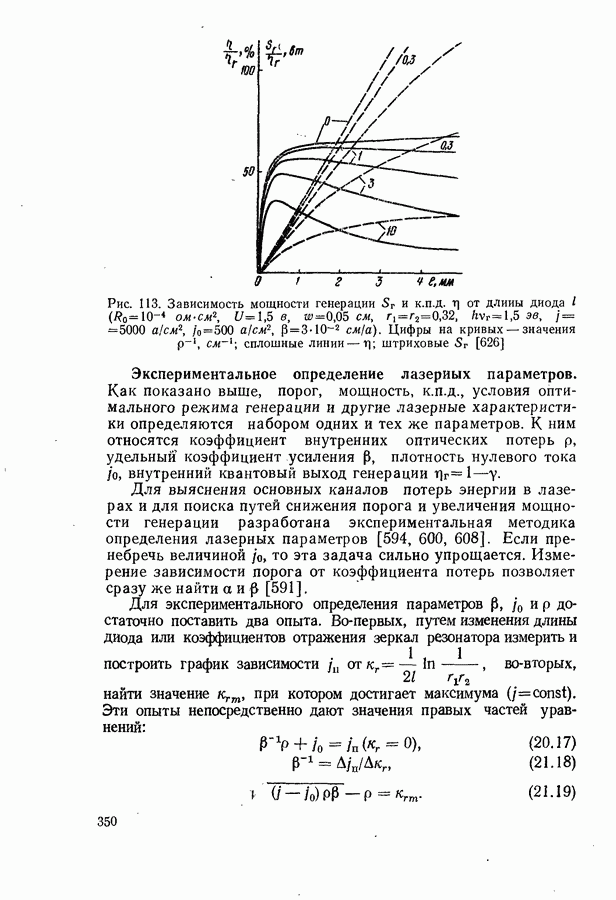
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
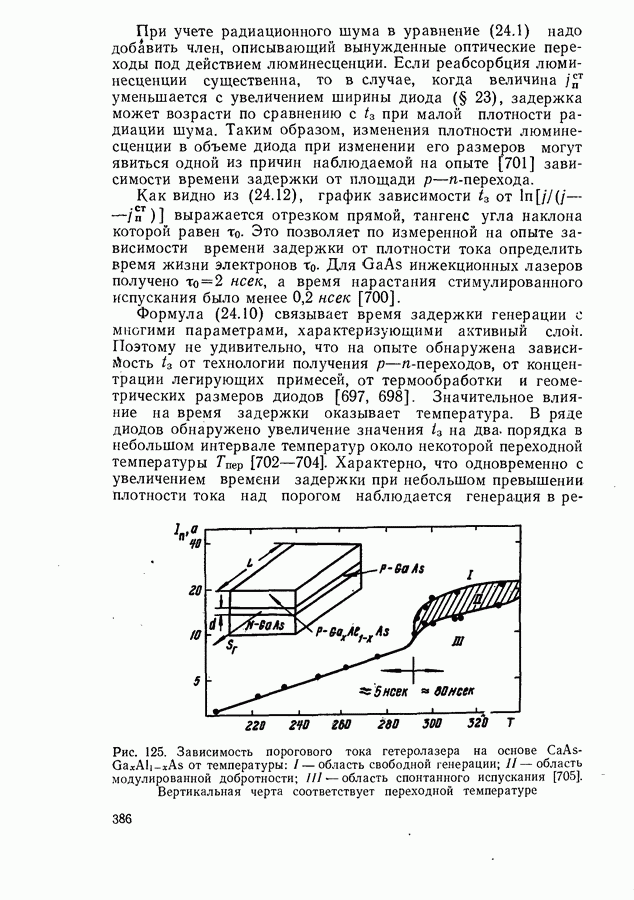
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
Скорости стимулированных и спонтанных переходов.
В рамках квантовой механики поглощение и испускание света характеризуется оператором взаимодействия [44, 87]

где

— оператор импульса;  - вектор-потенциал электромагнитной волны;
- вектор-потенциал электромагнитной волны;  заряд и мдсса электрона; с — скорость света;
заряд и мдсса электрона; с — скорость света;
 единичные векторы вдоль осей х, у, z; V — оператор набла. Второе слагаемое в (6.1) на несколько порядков меньше первого, и его необходимо учитывать только при рассмотрении многофотонных процессов. Поглощение света и рекомбинационное испускание можно описывать оператором
единичные векторы вдоль осей х, у, z; V — оператор набла. Второе слагаемое в (6.1) на несколько порядков меньше первого, и его необходимо учитывать только при рассмотрении многофотонных процессов. Поглощение света и рекомбинационное испускание можно описывать оператором

Пусть на кристалл падает плоская монохроматическая волна

с амплитудой  частотой
частотой  и волновым вектором
и волновым вектором  причем
причем  единичный вектор в направлении распространения волны,
единичный вектор в направлении распространения волны,  длина волны,
длина волны,  радиус-вектор. Учитывая связь между напряженностью электрического поля волны с? и А
радиус-вектор. Учитывая связь между напряженностью электрического поля волны с? и А

легко убедиться, что волне (6.3) соответствует вектор-потенциал

Подставляя (6.5) в (6.2), получаем

где

Если электрон в начальный момент времени  находится в состоянии, описываемом волновой функцией
находится в состоянии, описываемом волновой функцией  то вероятность обнаружить его в состоянии через промежуток времени
то вероятность обнаружить его в состоянии через промежуток времени  равна
равна

Здесь  матричный элемент оператора взаимодействия (6.7) и для определенности предполагается, что энергия
матричный элемент оператора взаимодействия (6.7) и для определенности предполагается, что энергия  состояния
состояния 
Так как, согласно определению,  -функция равна
-функция равна

то при достаточно больших  вместо (6.8) имеем
вместо (6.8) имеем

Вюдя единичный вектор поляризации  и учитывая, что плотность энергии волны
и учитывая, что плотность энергии волны

матричный элемент оператора взаимодействия можно представить в виде

где  показатель преломления;
показатель преломления;  общее число квантов света заданной плоской волны (моды); V — объем.
общее число квантов света заданной плоской волны (моды); V — объем.
Число переходов электрона из начального в конечное состояние за единицу времени равно производной от  по времени. Чтобы определить скорость всех переходов, индуцируемых электромагнитной волной, необходимо просуммировать
по времени. Чтобы определить скорость всех переходов, индуцируемых электромагнитной волной, необходимо просуммировать  по всем начальным и конечным состояниям, разность энергий которых равна
по всем начальным и конечным состояниям, разность энергий которых равна  Если, кроме того, возбуждающий свет состоит не из одной монохроматической волны, а содержит
Если, кроме того, возбуждающий свет состоит не из одной монохроматической волны, а содержит  мод
мод

то скорость индуцированных переходов гянд в единице объема кристалла за 1 сек будет равна

Здесь введено обозначение

При выводе (6.14) предполагалось, что все состояния с энергией  свободны. Если сделать обратное предположение, то для скорости переходов
свободны. Если сделать обратное предположение, то для скорости переходов  получится точно такое же выражение
получится точно такое же выражение
6.14), как и для переходов  В случае, когда верхние и нижние электронные состояния имеют конечные значения вероятностей заполнения
В случае, когда верхние и нижние электронные состояния имеют конечные значения вероятностей заполнения  скорость переходов между каждой парой состояний необходимо умножить на величину
скорость переходов между каждой парой состояний необходимо умножить на величину

Разность  равна вероятности того, что данное состояние к не занято электроном, или занято дыркой. Поскольку электроны в кристалле подчинятся статистике Ферми — Дирака, то возможны переходы электронов только в свободные состояния. Если состояние
равна вероятности того, что данное состояние к не занято электроном, или занято дыркой. Поскольку электроны в кристалле подчинятся статистике Ферми — Дирака, то возможны переходы электронов только в свободные состояния. Если состояние  занято, то
занято, то  и переход
и переход  невозможен. Поэтому первое слагаемое в последнем выражении относится к переходам
невозможен. Поэтому первое слагаемое в последнем выражении относится к переходам  а второе характеризует скорость обратных переходов
а второе характеризует скорость обратных переходов 
Таким образом, скорость переходов с поглощением света с учетом вынужденного испускания дается формулой [105, 106]

где опущена  -функция, выражающая закон сохранения энергии.
-функция, выражающая закон сохранения энергии.
В квантовой электродинамике [43, 87] скорость переходов с верхних в нижние состояния пропорциональна  причем первое слагаемое относится к индуцированным переходам, а единицей учитывается взаимодействие системы с нулевыми электромагнитными полями, приводящее к спонтанным переходам. Поэтому, если умножить (6.14) на произведение
причем первое слагаемое относится к индуцированным переходам, а единицей учитывается взаимодействие системы с нулевыми электромагнитными полями, приводящее к спонтанным переходам. Поэтому, если умножить (6.14) на произведение  и положить
и положить  то получится выражение для скорости спонтанных переходов
то получится выражение для скорости спонтанных переходов 
Однако величину  легко рассчитать с помощью принципа детального равновесия и не прибегая к квантовой теории излучения.
легко рассчитать с помощью принципа детального равновесия и не прибегая к квантовой теории излучения.
В условиях термодинамического равновесия скорость спонтанных переходов между всеми парами уровней равна скорости поглощения планковской радиации, для которой

Следовательно,

Здесь учтено, что  и
и

так как при термодинамическом равновесии вероятности заполнения уровней определяются функциями Ферми — Дирака 
Формулы (6.16) и (6.18) могут служить основой для решения широкого круга задач, связанных с взаимодействием света с кристаллами. В двух частных случаях легко провести суммирование  к и к и получить простые выражения для
к и к и получить простые выражения для 
Во-первых, если под действием света в системе возможны только такие оптические переходы, при которых сохраняется импульс, т. е. в приведенной зоне Бриллюэна  тогда матричный элемент будет содержать
тогда матричный элемент будет содержать  -функцию
-функцию  Суммирование по к исчезнет, а суммирование по к будет равносильно умножению на приведенную плотность состояний
Суммирование по к исчезнет, а суммирование по к будет равносильно умножению на приведенную плотность состояний  (см. (2.21)). Следовательно, скорости поглощения света и спонтанной рекомбинации будут равны:
(см. (2.21)). Следовательно, скорости поглощения света и спонтанной рекомбинации будут равны:

где  относится к верхним состояниям системы, а
относится к верхним состояниям системы, а  энергия нижних состояний
энергия нижних состояний 
Во-вторых, если правило отбора по волновому вектору не  выполняется и, кроме того, матричный элемент
выполняется и, кроме того, матричный элемент  одинаков для всех значений к и к, то из (6.16) и (6.18) получим [106]:
одинаков для всех значений к и к, то из (6.16) и (6.18) получим [106]:

Здесь  плотности состояний системы,
плотности состояний системы,  Все промежуточные случаи более сложны, и для их рассмотрения требуется задание конкретной модели вещества.
Все промежуточные случаи более сложны, и для их рассмотрения требуется задание конкретной модели вещества.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
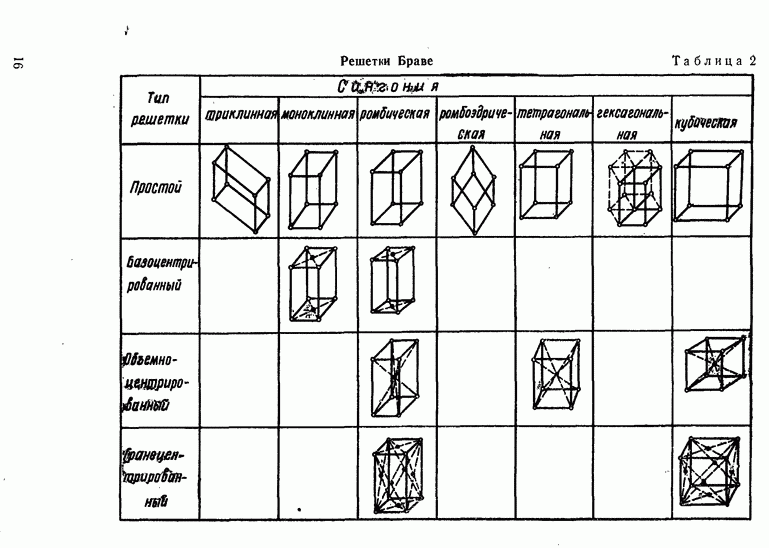
- Классификация кристаллических решеток.
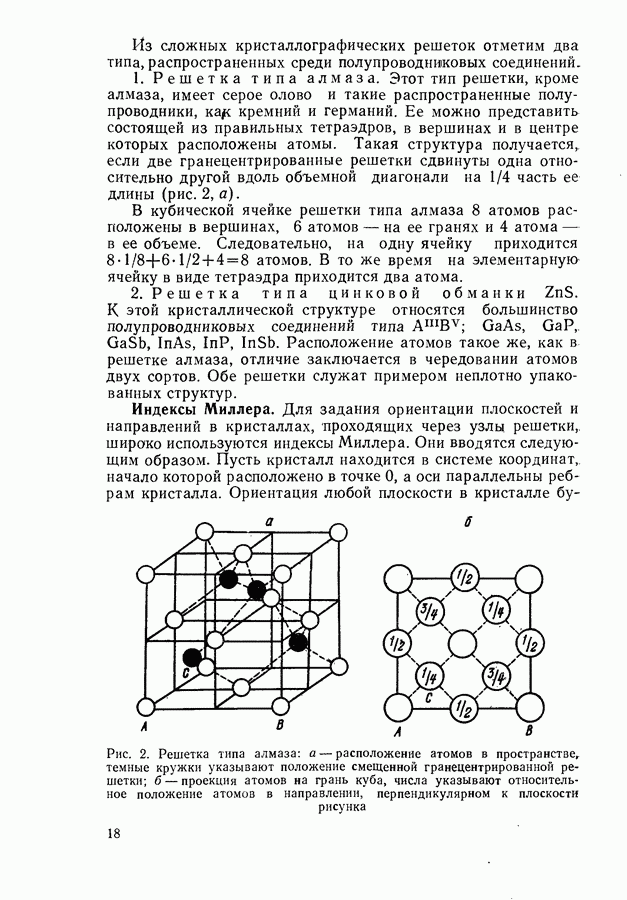
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
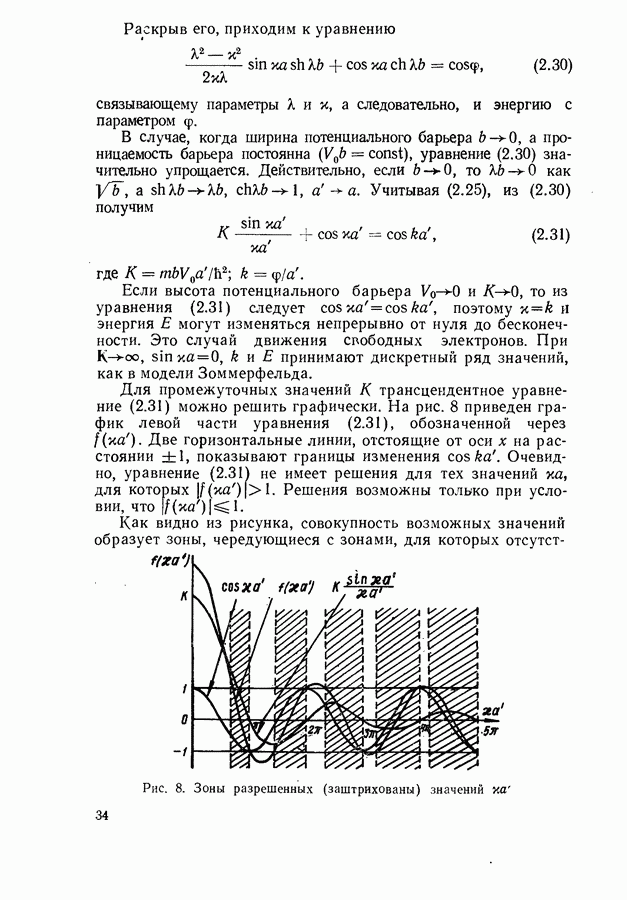
- Модель Зоммерфельда. Плотность состояний.
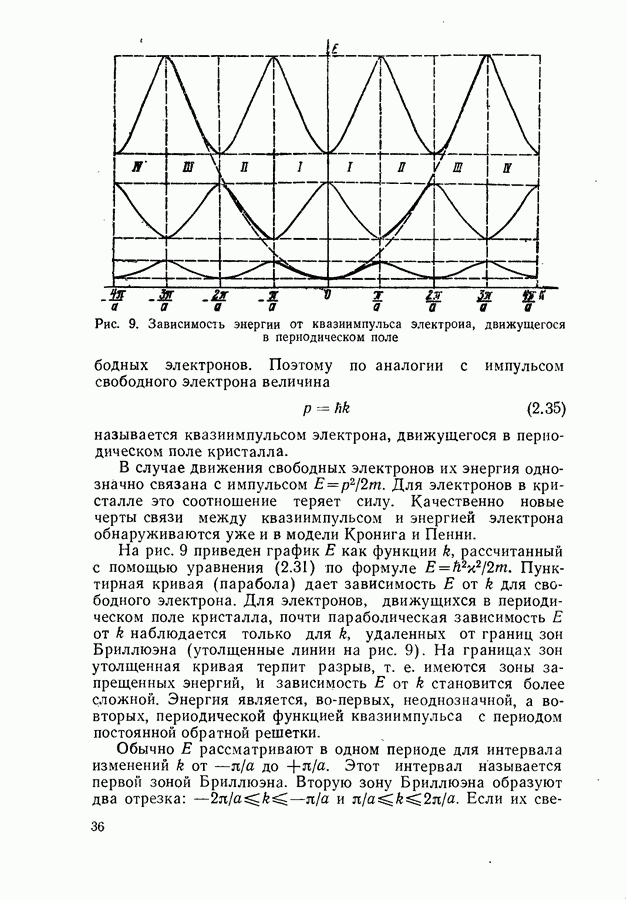
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
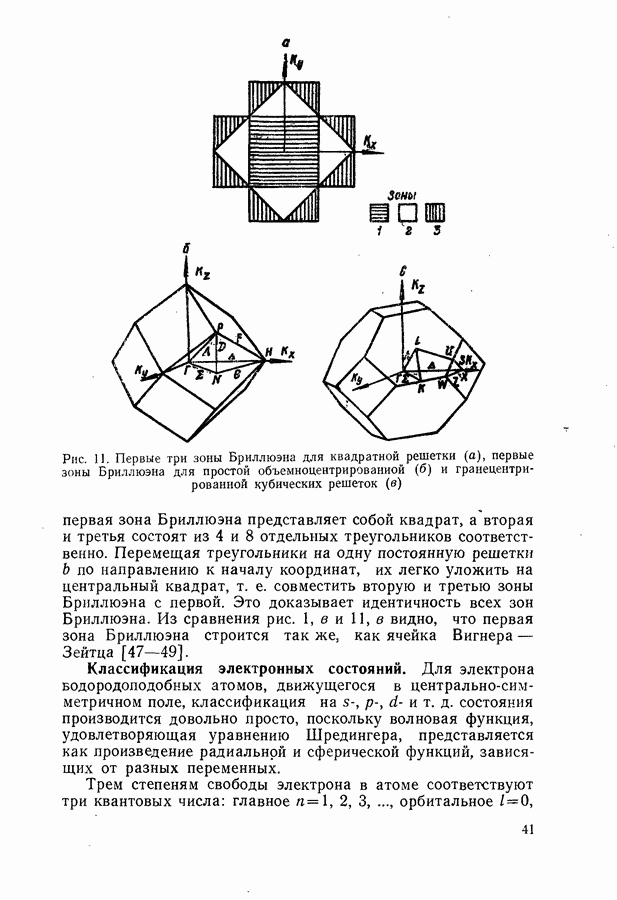
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
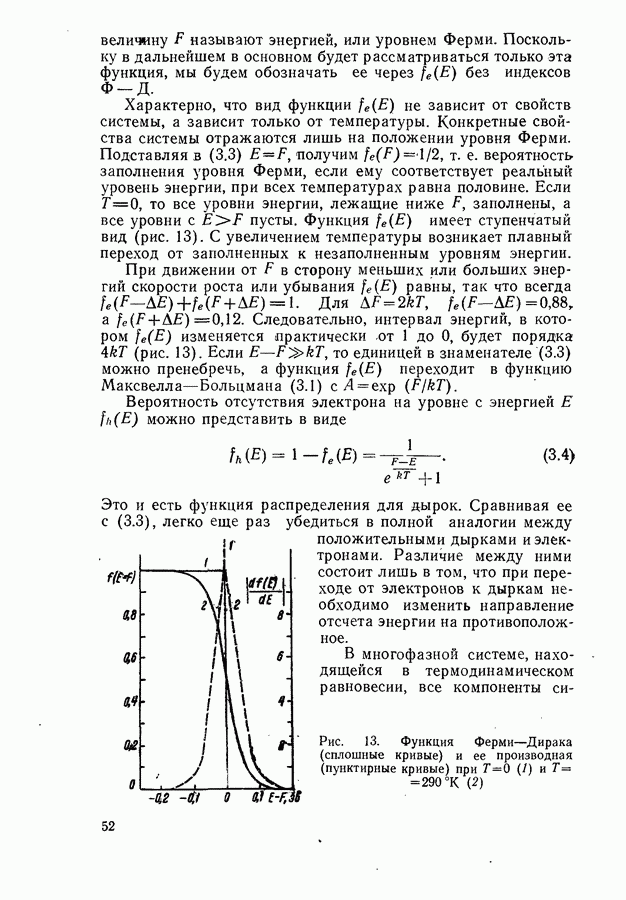
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
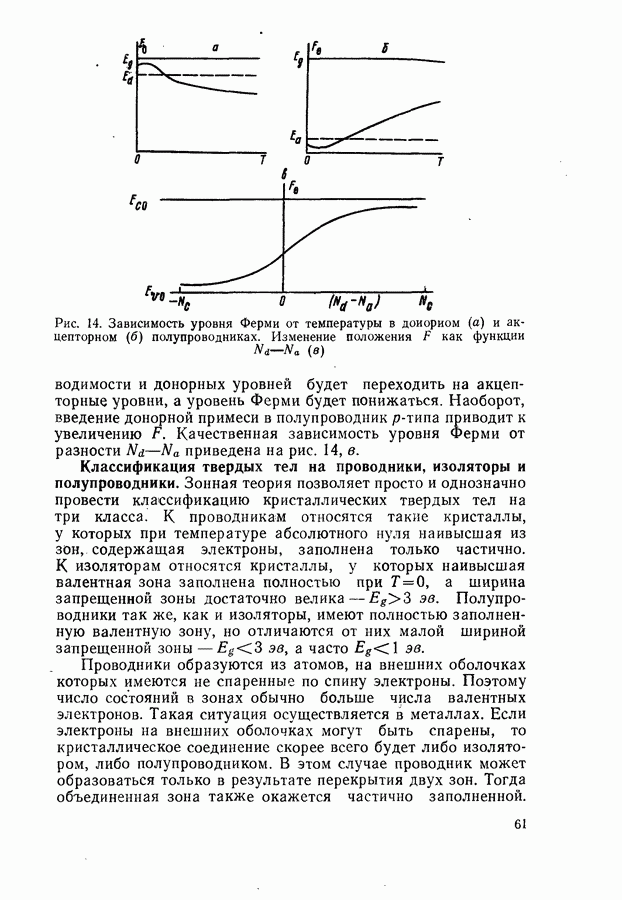
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
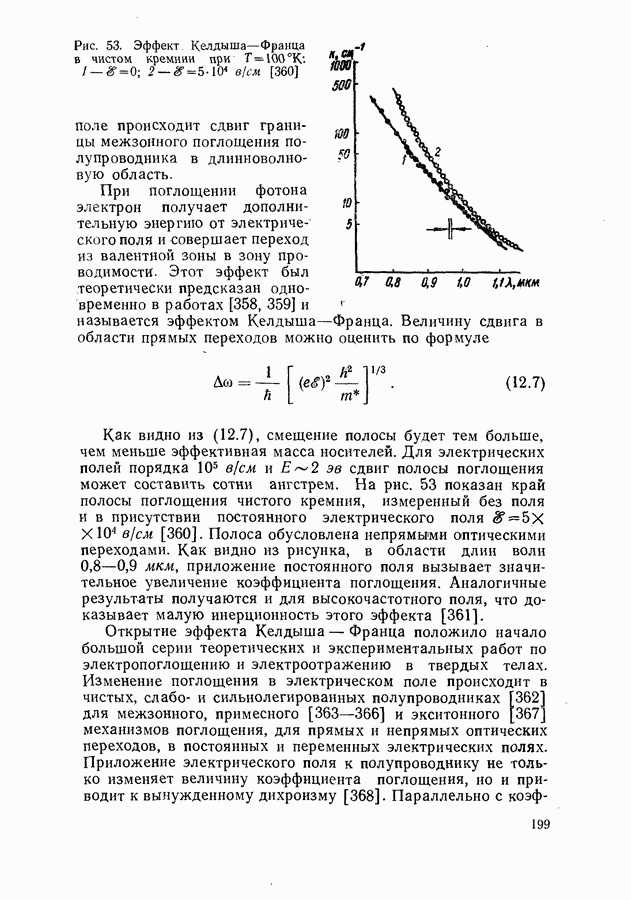
- Эффект Келдыша-Франца.
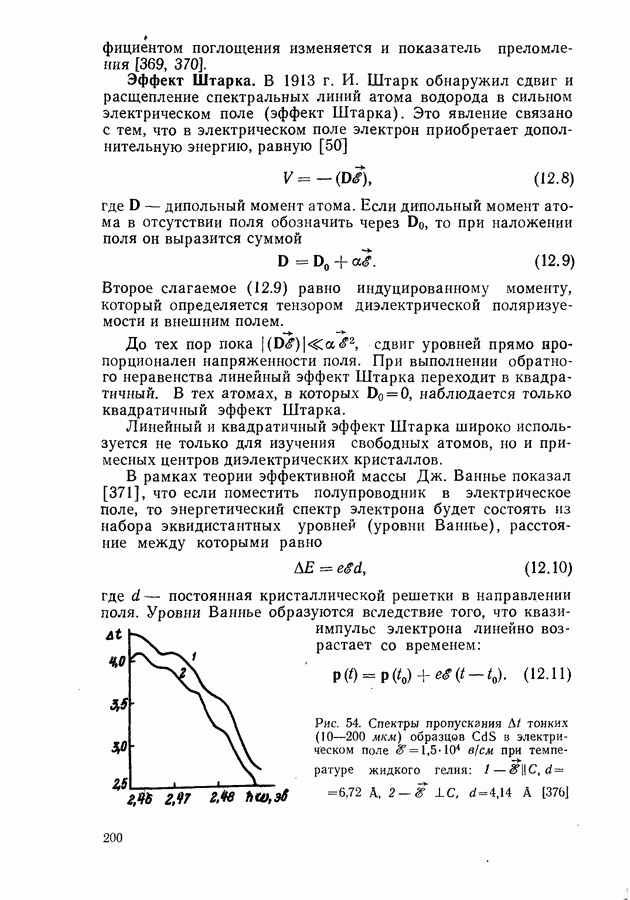
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
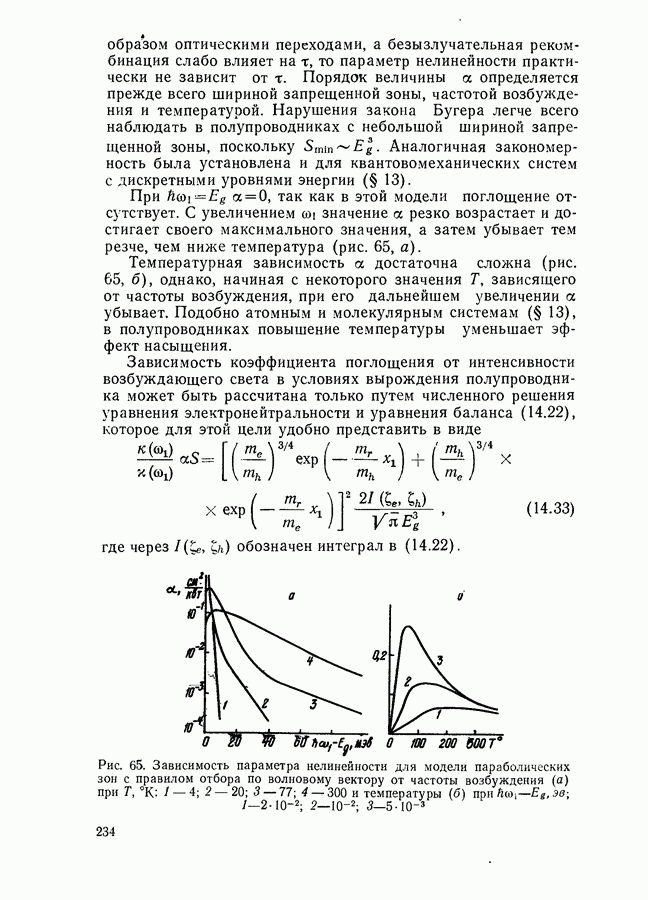
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
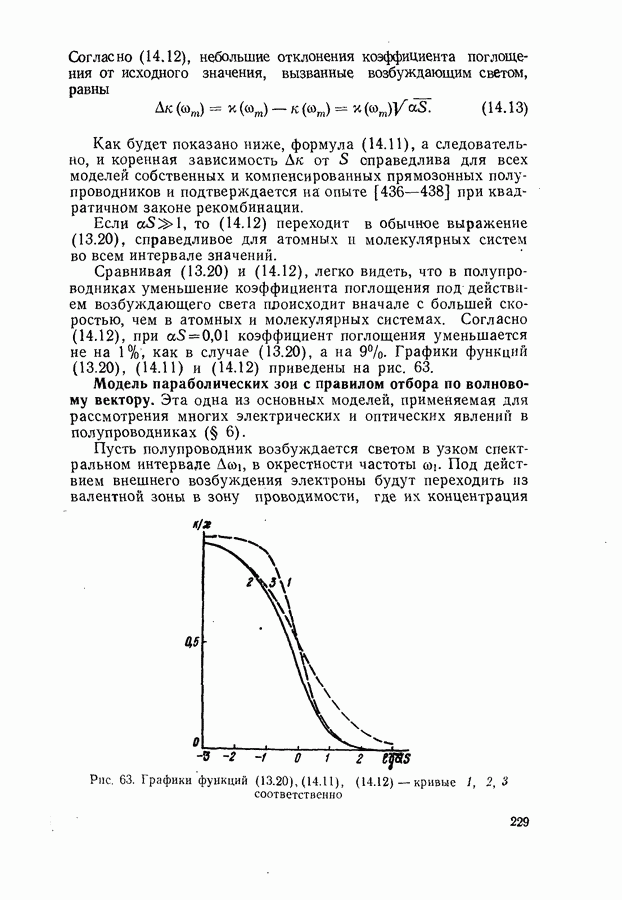
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
- Возбуждение генерации пучком быстрых электронов.