| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
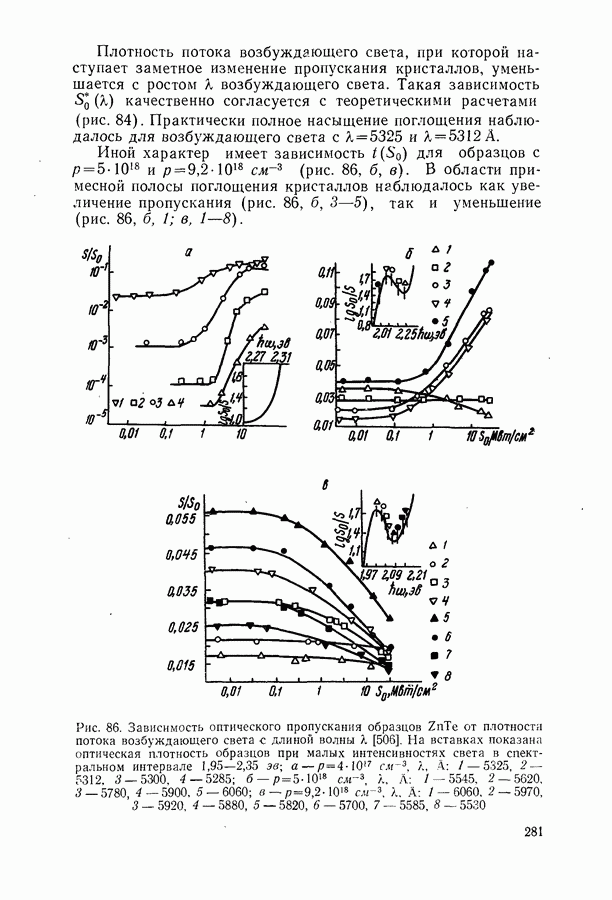
Энергетические уровни примесей.
Появление в кристаллической решетке чужеродных атомов приводит к точечным нарушениям периодичности потенциального поля. Если строго периодическую потенциальную энергию электрона в кристалле обозначить через  то при наличии дефектов в решетке потенциал будет равен
то при наличии дефектов в решетке потенциал будет равен  Величина
Величина  отлична от нуля в некотором объеме и определяет
отлична от нуля в некотором объеме и определяет
изменение потенциальной энергии электрона в окрестности дефекта.
Влияние примесей на энергетический спектр кристалла можно приближенно рассмотреть, если предположить, что  определяется чисто кулоновским взаимодействием электрона с точечным зарядом, т. е.
определяется чисто кулоновским взаимодействием электрона с точечным зарядом, т. е.  где
где  диэлектрическая проницаемость среды. Тогда уравнение
диэлектрическая проницаемость среды. Тогда уравнение
Шредингера (2.5) может быть сведено к уравнению для атома водорода с массой электрона  и зарядом
и зарядом  [38]. Энергия связанных состояний электрона такой модели равна
[38]. Энергия связанных состояний электрона такой модели равна

Здесь  главное квантовое число,
главное квантовое число,  масса электрона в вакууме. Так как при выводе этой формулы предполагалось, что дну зоны проводимости
масса электрона в вакууме. Так как при выводе этой формулы предполагалось, что дну зоны проводимости  соответствует энергия, равная кулю, то из (2.52) следует, что электрон вблизи примесных атомов обладает уровнями, лежащими в запрещенной зоне. Примеси, энергетический спектр которых соответствует (2.52), называют водородоподобными. В полупроводниках
соответствует энергия, равная кулю, то из (2.52) следует, что электрон вблизи примесных атомов обладает уровнями, лежащими в запрещенной зоне. Примеси, энергетический спектр которых соответствует (2.52), называют водородоподобными. В полупроводниках  обычно имеет большое значение, порядка 10 и более, а
обычно имеет большое значение, порядка 10 и более, а  поэтому невозбужденное примесное состояние отстоит от дна зоны проводимости на сотые или тысячные доли электрон-вольта. Например, для
поэтому невозбужденное примесное состояние отстоит от дна зоны проводимости на сотые или тысячные доли электрон-вольта. Например, для  Такие уровни называют еще мелкими примесными уровнями. Если температура
Такие уровни называют еще мелкими примесными уровнями. Если температура  то электроны сравнительно легко их покидают и переходят в зону проводимости.
то электроны сравнительно легко их покидают и переходят в зону проводимости.
Формула, аналогичная (2.52), получается и при рассмотрении движения дырок в кристалле, если энергию потолка валентной зоны  положить равной нулю и направить ось энергий сверху вниз. Тогда под
положить равной нулю и направить ось энергий сверху вниз. Тогда под  следует понимать эффективную массу дырки
следует понимать эффективную массу дырки  Обычно она больше эффективной массы электрона в зоне проводимости, и, следовательно, акцепторные уровни по сравнению с донорными уровнями расположены более глубоко в запрещенной зоне. Так, для GaAs
Обычно она больше эффективной массы электрона в зоне проводимости, и, следовательно, акцепторные уровни по сравнению с донорными уровнями расположены более глубоко в запрещенной зоне. Так, для GaAs  Однако и это значение
Однако и это значение  во много раз меньше ширины запрещенной зоны
во много раз меньше ширины запрещенной зоны  поэтому акцепторные уровни также относятся к мелким уровням.
поэтому акцепторные уровни также относятся к мелким уровням.
Таким образом, при сравнительно небольшой концентрации примесей лишь в изолированных точках кристалла появляются дополнительные энергетические уровни (рис. 12, а). В отличие от разрешенных состояний основных зон, принадлежащих всему кристаллу, примесные состояния

Рис. 12. Донорные и акцепторные локализованные уровни (а). Плотность состояний как функция энергии при слабом (б) и сильном  легировании
легировании
локализованы в микроскопических объемах, линейные размеры которых незначительно превышают боровский радиус

Электроны, находящиеся на примесных уровнях, связаны с дефектом и не могут перемещаться по кристаллу.
Если же в кристалл вводится большое количество примесей, то это приводит к более значительным изменениям его энергетического спектра. Во-первых, в результате взаимодействия примесных атомов между собой соответствующие им уровни расширяются, смещаются и образуют примесные зоны, подобно тому как из резких уровней атомов, образующих кристалл, получаются основные энергетические зоны твердого тела [57].
Однако в отличие от регулярного расположения основных атомов решетки, примеси распределены по кристаллу хаотически. В пределах макроскопических объемов могут быть заметные флуктуации концентрации иримеси, что приводит к флуктуации энергии электрона. Это служит дополнительным механизмом размытия уровней примесных атомов.
Во-вторых, введение примеси в полупроводник, как правило, сопровождается увеличением числа свободных носителей в кристалле. Атомы решетки оказываются как бы погруженными в электронный газ (плазму), который экранирует и ослабляет взаимодействие между электрическими зарядами кристалла. Поэтому основные зоны полупроводника смещаются, ширина запрещенной зоны обычно уменьшается. Кроме того, в результате флуктуаций концентрации примеси
исчезают резкие границы зон, образуются хвосты основных и примесных зон.
Образование примесной зоны можно установить экспериментально. Если в полупроводнике имеются не локальные примесные уровни, а сплошная зона, то при понижении температуры до нуля и «вымерзании» всех электронов из зоны проводимости его электропроводность стремится не к нулю, как в чистом полупроводнике, а к некоторому постоянному значению. Изменяется и температурная зависимость постоянной Холла [57, 58]. Эти опыты позволили установить, что, например, в германии, легированном донорами 5-й группы, примесная зона начинает образовываться уже при концентрации примеси 
Чем больше концентрация примеси, тем шире примесная зона. В частности, в арсениде галлия с увеличением концентрации доноров от  до
до  теоретически рассчитанная полуширина примесной зоны возрастает от 16 до
теоретически рассчитанная полуширина примесной зоны возрастает от 16 до  При изменении концентрации акцепторов в тех же пределах ширина акцепторной зоны увеличивается от 5 до
При изменении концентрации акцепторов в тех же пределах ширина акцепторной зоны увеличивается от 5 до  [59]. Ясно, что при некотором значении
[59]. Ясно, что при некотором значении  верхний край примесной зоны попадает в зону проводимости. Для того чтобы перекрылись акцепторная и валентная зоны, необходимо большое значение
верхний край примесной зоны попадает в зону проводимости. Для того чтобы перекрылись акцепторная и валентная зоны, необходимо большое значение  поскольку при одинаковых концентрациях доноров и акцепторов акцепторная зона имеет меньшую ширину и расположена более глубоко, чем донорная зона (рис. 12, б). В этом случае раздельное рассмотрение основных и примесных зон становится условным, поскольку имеются единые области непрерывного спектра, а энергия ионизации примесей обращается в нуль.
поскольку при одинаковых концентрациях доноров и акцепторов акцепторная зона имеет меньшую ширину и расположена более глубоко, чем донорная зона (рис. 12, б). В этом случае раздельное рассмотрение основных и примесных зон становится условным, поскольку имеются единые области непрерывного спектра, а энергия ионизации примесей обращается в нуль.
На основании исследования электропроводности и эффекта Холла установлено, что в  при концентрации доноров
при концентрации доноров  образуется хорошо проводящая примесная зона [60]. Если
образуется хорошо проводящая примесная зона [60]. Если  энергия ионизации
энергия ионизации  обращается в нуль. В арсениде галлия
обращается в нуль. В арсениде галлия  -типа
-типа  Стремится к нулю, если концентрация дырок больше
Стремится к нулю, если концентрация дырок больше 
Учитывая характер изменения физических свойств полупроводников в зависимости от концентрации примеси, все полупроводники можно разделить на слабо легированные, промежуточно легированные и сильно легированные. В слабо легированных кристаллах имеются локализованные в пространстве резкие примесные уровни. Волновые функции электронов различных примесных центров практически не перекрываются. В промежуточно легированных полупроводниках образуются примесные зоны, но они еще не перекрылись с основными зонами энергетического спектра. Если зона проводимости или валентная зона слились с примесными зонами, полупроводник будет относиться к сильно легированному [57].
"Пбсле создания инжекционных лазеров интерес к форме примесной зоны и хвостам плотности состояний основных зон значительно возрос. Без детального знания этих величин невозможно установить механизм генерации. Наличие хвостов и их форма определяют характер зависимости коэффициента усиления от накачки, зависимость порогового тока и мощности генерации от коэффициента потерь и температуры. Контур полосы люминесценции и край фундаментальной полосы поглощения также связаны с хвостами зон. В тунельных диодах они влияют на форму вольтамперной характеристики [61].
В работе [59] на основании сравнения контура полосы рекомбинационного излучения в  с расчетными данными сделан вывод, что плотность состояний в примесных зонах может быть хорошо описана гауссовой кривой
с расчетными данными сделан вывод, что плотность состояний в примесных зонах может быть хорошо описана гауссовой кривой

Величина  определяет полуширину зоны и может быть приближенно рассчитана по формуле [62]
определяет полуширину зоны и может быть приближенно рассчитана по формуле [62]

где  число примесных атомов в
число примесных атомов в  а
а

— обратная длина дебаевского экранирования. Интегрируя (2.54) по  от
от  до
до  находим
находим  Более последовательно вопросы экранирования рассмотрены в [63].
Более последовательно вопросы экранирования рассмотрены в [63].
С учетом «хвостов» плотность состояний в зоне будет выражаться вместо (2.21) более сложной функцией [62]:

Если  достаточно велико
достаточно велико  то, вынося из-под знака интеграла плавную функцию
то, вынося из-под знака интеграла плавную функцию  в точке
в точке  в окрестности которой острая функция
в окрестности которой острая функция  отлична от нуля, получим
отлична от нуля, получим  Следовательно, в зоне проводимости функция (2.57) переходит в (2.21).
Следовательно, в зоне проводимости функция (2.57) переходит в (2.21).
Для энергий, лежащих глубоко в запрещенной зоне  из (2.57) и (2.58) приближенно находим
из (2.57) и (2.58) приближенно находим

Согласно (2.59), в запрещенной зоне функция плотности состояний, возникших в результате сильного легирования полупроводника, переходит практически в крыло гауссовой кривой  (рис. 12, г). При вычислении интеграла (2.58) учитывалось, что для
(рис. 12, г). При вычислении интеграла (2.58) учитывалось, что для  подынтегральная функция существенно отлична от нуля только в окрестности точки
подынтегральная функция существенно отлична от нуля только в окрестности точки  и использовалось приближенное равенство:
и использовалось приближенное равенство: 
Несколько иные выражения для функции плотности состояний хвостов даны в работах [57, 64—69]. Результаты, полученные различными методами, сравниваются в работе [70].
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
- Эффект Келдыша-Франца.
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
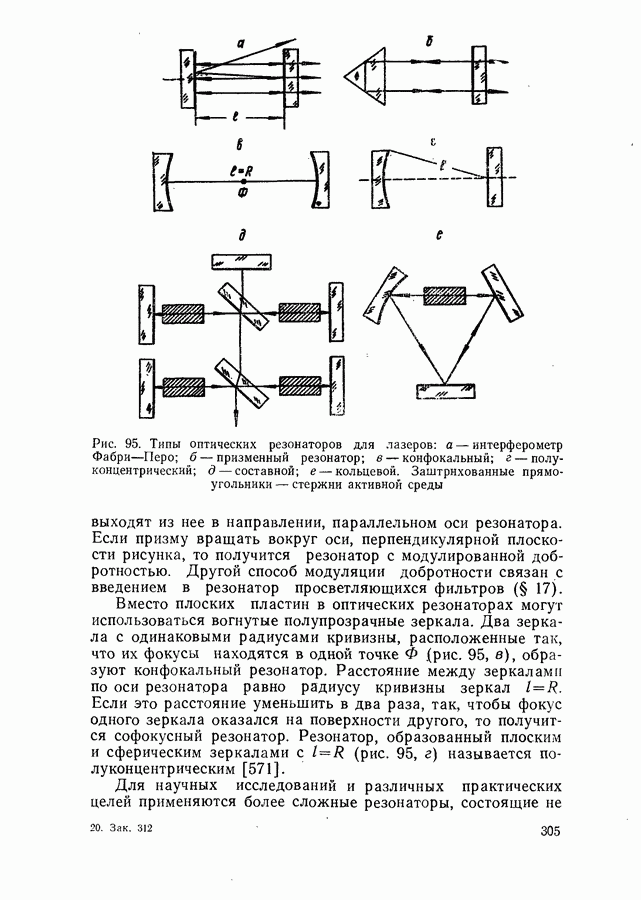
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
- Возбуждение генерации пучком быстрых электронов.