| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Универсальное соотношение между спектрами поглощения и люминесценции.
В 1957 г. Б. И. Степанов показал [119], что мощность люминесценции и коэффициент поглощения системы частиц с двумя электронно-колебательными состояниями связаны соотношением

где  населенности верхнего и нижнего электронноколебательных уровней;
населенности верхнего и нижнего электронноколебательных уровней;  частота чисто электронного перехода;
частота чисто электронного перехода;  фазовая скорость света. Формула (7.6) получила широкую известность как универсальное соотношение Степанова и многократно проверялась на опыте. Соотношение (7.6) справедливо в тех случаях, когда можно пренебречь стимулированным испусканием и когда перед актом испускания света успевает установиться равновесное распределение возбужденных центров по всем степеням свободы. В парах сложных молекул функция распределения по колебательным уровням молекулы зависит не только от температуры среды, но и от частоты возбуждающего света [120]. Поэтому для паров связь между
фазовая скорость света. Формула (7.6) получила широкую известность как универсальное соотношение Степанова и многократно проверялась на опыте. Соотношение (7.6) справедливо в тех случаях, когда можно пренебречь стимулированным испусканием и когда перед актом испускания света успевает установиться равновесное распределение возбужденных центров по всем степеням свободы. В парах сложных молекул функция распределения по колебательным уровням молекулы зависит не только от температуры среды, но и от частоты возбуждающего света [120]. Поэтому для паров связь между  несколько отличается от (7.6). Границы применимости универсального соотношения и его обобщения на некоторые более сложные системы рассмотрены в [121]. Механизмы поглощения и испускания света в сложных молекулах и полупроводниках существенно различны. В сложных молекулах распределение системы по уровням энергии описывается функцией Больцмана, а число актов поглощения или испускания света пропорционально населенности исходного колебательного уровня. В полупроводниках
несколько отличается от (7.6). Границы применимости универсального соотношения и его обобщения на некоторые более сложные системы рассмотрены в [121]. Механизмы поглощения и испускания света в сложных молекулах и полупроводниках существенно различны. В сложных молекулах распределение системы по уровням энергии описывается функцией Больцмана, а число актов поглощения или испускания света пропорционально населенности исходного колебательного уровня. В полупроводниках
равновесное распределение электронов по уровням разрешенных зон удовлетворяет функции Ферми — Дирака, а скорость оптических переходов пропорциональна произведению числа электронов в исходном состоянии на число дырок в конечном состоянии.
Несмотря на это, в оптических свойствах сложных молекул и полупроводников обнаруживается далеко идущая аналогия [122, 123]. Широким энергетическим зонам в полупроводниках соответствуют электронно-колебательные зоны в сложных молекулах. Сложные молекулы характеризуются обычно равновесным распределением по колебательным уровням энергии верхнего и нижнего электронных состояний. Такое частное равновесие устанавливается даже при интенсивном возбуждении и переводе значительной части молекул в возбужденное электронное состояние. Аналогичное явление наблюдается в полупроводниках. Нарушение полного термодинамического равновесия и перевод части электронов в зону проводимости сопровождается установлением равновесного распределения электронов отдельно по уровням валентной зоны и уровням зоны проводимости. Именно поэтому некоторые оптические свойства сложных молекул и собственных полупроводников весьма близки друг к другу.
Это проявляется особенно наглядно в универсальном соотношении между спектрами поглощения и люминесценции.
Рассмотрим собственный полупроводник, в общем случае не находящийся в состоянии термодинамического равновесия. Под действием внешнего возбуждения электроны будут переходить из валентной зоны в зону проводимости, где их концентрация станет больше, чем при термодинамическом равновесии. Одновременно происходит обратный процесс спонтанной, вынужденной и безызлучательной рекомбинации электронов и дырок.
Так как время установления равновесия между носителями в пределах одной зоны порядка  сек, а время рекомбинации, как правило, больше
сек, а время рекомбинации, как правило, больше  сек, то распределение электронов по уровням энергии зоны проводимости Ее и валентной зоны
сек, то распределение электронов по уровням энергии зоны проводимости Ее и валентной зоны  будет характеризоваться функцией Ферми — Дирака
будет характеризоваться функцией Ферми — Дирака

и двумя квазиуровнями Ферми  для электронов и дырок соответственно.
для электронов и дырок соответственно.
Легко убедиться, что для любой выделенной пары уровней выполняются равенства

где  разность квазиуровней Ферми.
разность квазиуровней Ферми.
Используя эти соотношения, с помощью (6.16) и (6.18) независимо от правил отбора находим [106]

Так как мощность спонтанного испускания  а коэффициент поглощения к
а коэффициент поглощения к  связан с
связан с  соотношением (6.24), то с помощью (7.10) приходим к универсальному соотношению между спектрами поглощения и спонтанного испускания [1241:
соотношением (6.24), то с помощью (7.10) приходим к универсальному соотношению между спектрами поглощения и спонтанного испускания [1241:

При термодинамическом равновесии распределение электронов и дырок характеризуется - одним уровнем Ферми, а  будет давать число фотонов в заданном типе электромагнитных колебаний планковского излучения:
будет давать число фотонов в заданном типе электромагнитных колебаний планковского излучения:

Подставляя (7.12) в (7.10) и учитывая, что  получим
получим  При термодинамическом равновесии скорость спонтанного испускания равна скорости поглощения планковской радиации, а из формулы (7.11) следует закон Кирхгофа
При термодинамическом равновесии скорость спонтанного испускания равна скорости поглощения планковской радиации, а из формулы (7.11) следует закон Кирхгофа

На основании (7.11) суммарную по частоте скорость спонтанной рекомбинации можно представить в виде интеграла

В частном случае, когда  этот интеграл переходит в форт мулу ван Русбрека и Шокли [125]
этот интеграл переходит в форт мулу ван Русбрека и Шокли [125]

Здесь

— коэффициент экстинкции, 
Соотношение (7.15) позволяет по измеренному значению коэффициента поглощения рассчитать скорость спонтанной рекомбинации при термодинамическом равновесии и оценить параметр В в выражении  Границы применимости этого выражения рассмотрены в предыдущем параграфе.
Границы применимости этого выражения рассмотрены в предыдущем параграфе.
Указанный метод определения  и В предложен ван Русбреком и Шокли [125]. Для германия при
и В предложен ван Русбреком и Шокли [125]. Для германия при  они получили
они получили 
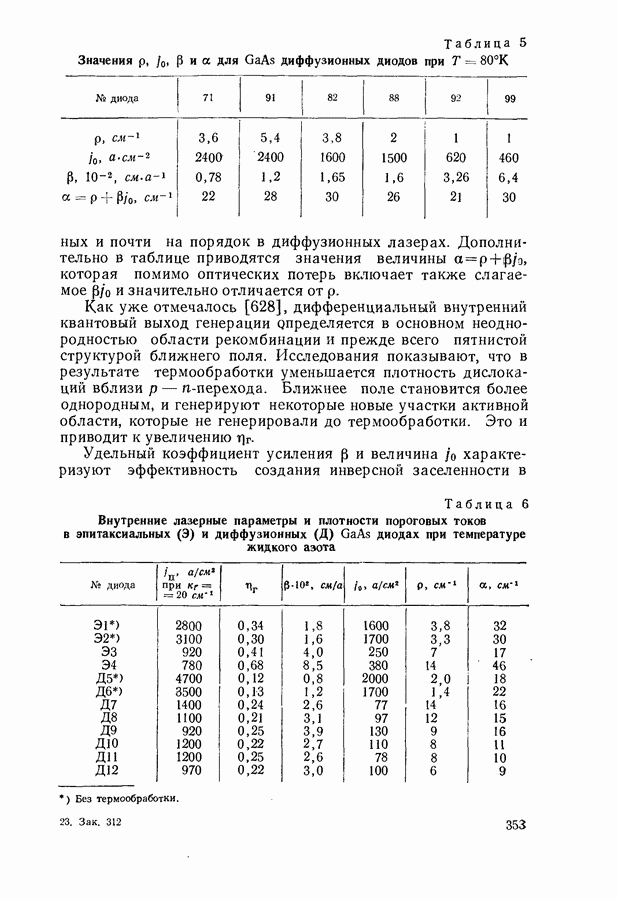
Значения константы рекомбинации и других параметров для ряда полупроводников при комнатной температуре приведены в табл. 4, взятой из работы [126], где имеются данные и для других температур.
Как видно из таблицы, для соединений  имеющих прямую зонную структуру, константа рекомбинации на несколько порядков больше, чем для непрямых полупроводников.
имеющих прямую зонную структуру, константа рекомбинации на несколько порядков больше, чем для непрямых полупроводников.
Во всех веществах, за исключением кремния, с уменьшением температуры значение В увеличивается [126]. Если в формулу (7.15) подставить аналитическое выражение для  то скорость и константу рекомбинации можно рассчитать теоретически [126].
то скорость и константу рекомбинации можно рассчитать теоретически [126].
Пользуясь определением люминесценции как превышением над фоном теплового испускания (7.5) и учитывая (7.11), находим [124]

Таблица 4 (см. скан) Значение скорости спонтанной рекомбинации  константы рекомбинации В, концентрации
константы рекомбинации В, концентрации  времени жизни
времени жизни  электронов и сечения рекомбинации
электронов и сечения рекомбинации  собственных полупроводников, где
собственных полупроводников, где  скорость теплового движения электронов
скорость теплового движения электронов
При термодинамическом равновесии, как и следовало ожидать, отношение (7.18) равно нулю, поскольку люминесценция отсутствует. Наоборот, если равновесие сильно нарушено, так что  то формула (7.18) переходит в (7.11). В этом случае практически все спонтанное испускание состоит из люминесценции. Расстояние между квазиуровнями Ферми равно энергии кванта
то формула (7.18) переходит в (7.11). В этом случае практически все спонтанное испускание состоит из люминесценции. Расстояние между квазиуровнями Ферми равно энергии кванта  при которой коэффициент поглощения меняет знак. Если
при которой коэффициент поглощения меняет знак. Если  то значение к
то значение к  положительно, если
положительно, если  оно отрицательно. Потому частоту
оно отрицательно. Потому частоту  называют частотой инверсии. Следовательно, формула (7.18) описывает не только поглощение, но и усиление, возникающее при достаточно больших накачках.
называют частотой инверсии. Следовательно, формула (7.18) описывает не только поглощение, но и усиление, возникающее при достаточно больших накачках.
Универсальное соотношение (7.18) значительно расширяет возможности для экспериментального исследования полупроводников. Оно связывает между собой величины  к
к  и позволяет по двум измеренным величинам находить третью. Это особенно важно для исследования активной области лазерных диодов, поскольку непосредственные измерения ее спектроскопических характеристик весьма сложны, а иногда вообще невозможны. Применение соотношения
и позволяет по двум измеренным величинам находить третью. Это особенно важно для исследования активной области лазерных диодов, поскольку непосредственные измерения ее спектроскопических характеристик весьма сложны, а иногда вообще невозможны. Применение соотношения
(7.18) в этом случае позволяет получить ряд новых результатов (см. § 21).
Если обобщить универсальное соотношение Б. И. Степанова (7.6) на случай больших интенсивностей и учесть фон теплового испускания [122], то получается формула, в точности совпадающая с (7.18). При этом по аналогии с квазиуровнями Ферми в полупроводниках для описания равновесного распределения электронов по электронно-колебательным уровням сложных молекул вводятся понятия химических потенциалов возбужденных  и невозбужденных
и невозбужденных  молекул. Тогда
молекул. Тогда  имеет смысл разности указанных химических потенциалов, а распределение частиц
имеет смысл разности указанных химических потенциалов, а распределение частиц  по колебательным уровням нижнего
по колебательным уровням нижнего  и верхнего
и верхнего  состояний представляется в виде
состояний представляется в виде

где  полное число частиц;
полное число частиц;  - статистические веса (функции плотности состояний).
- статистические веса (функции плотности состояний).
Введение химических потенциалов позволяет более наглядно выявить аналогию и специфику оптических свойств сложных молекул и полупроводников [124].
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
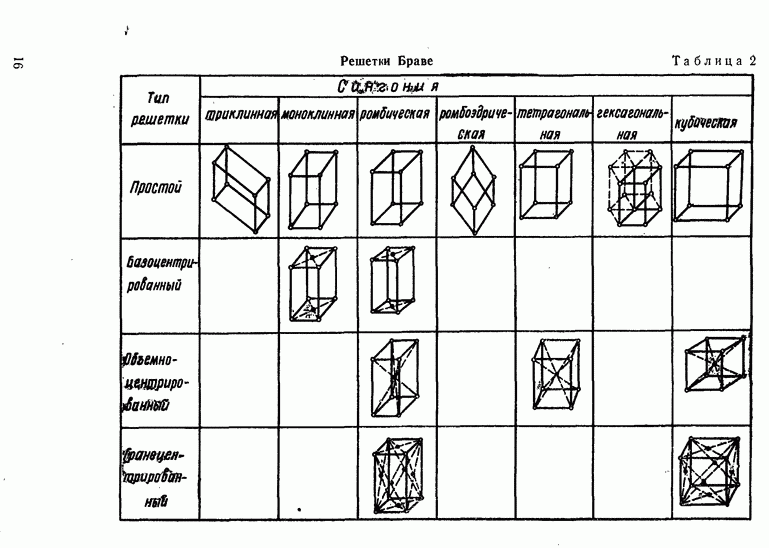
- Классификация кристаллических решеток.
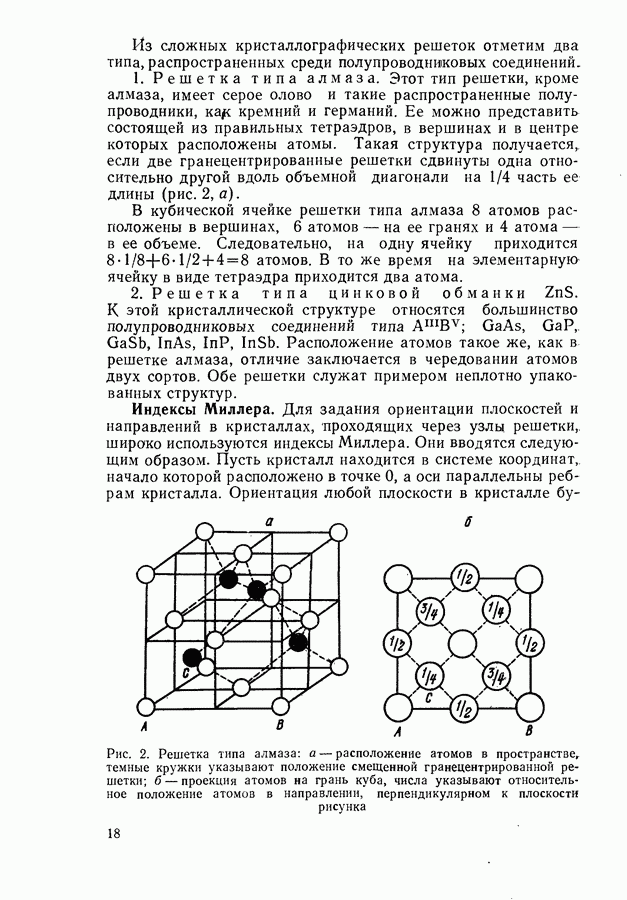
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
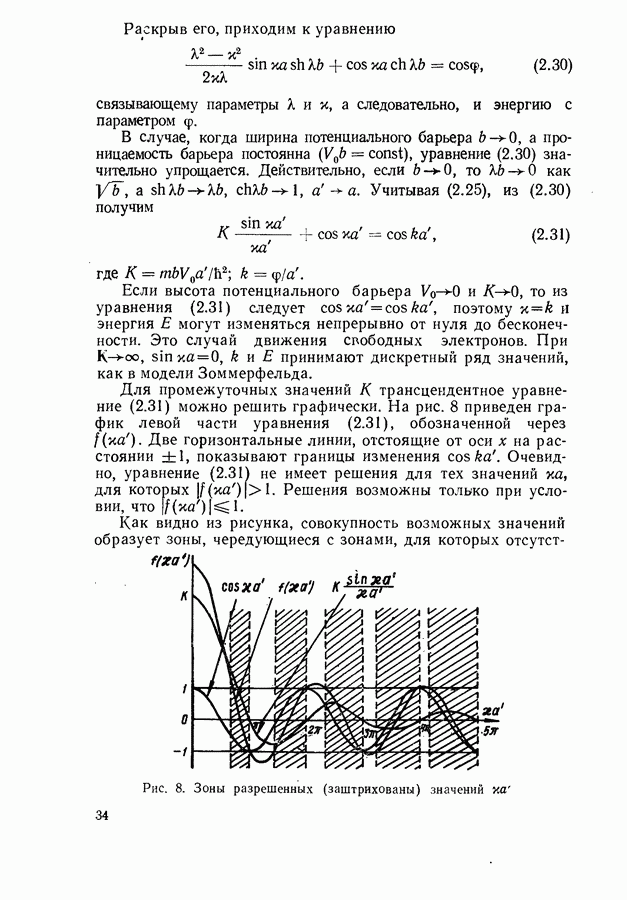
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
- Эффект Келдыша-Франца.
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
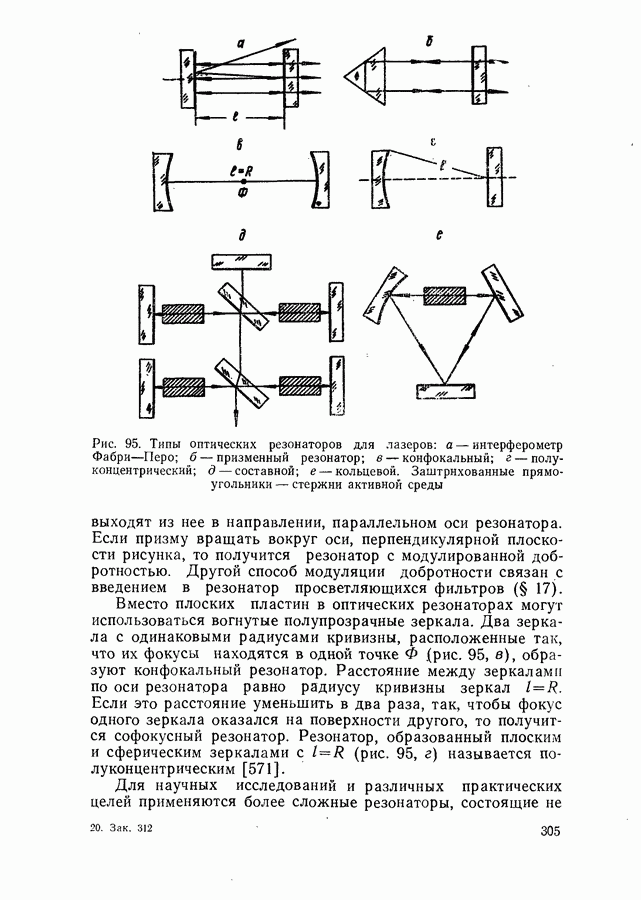
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
- Возбуждение генерации пучком быстрых электронов.