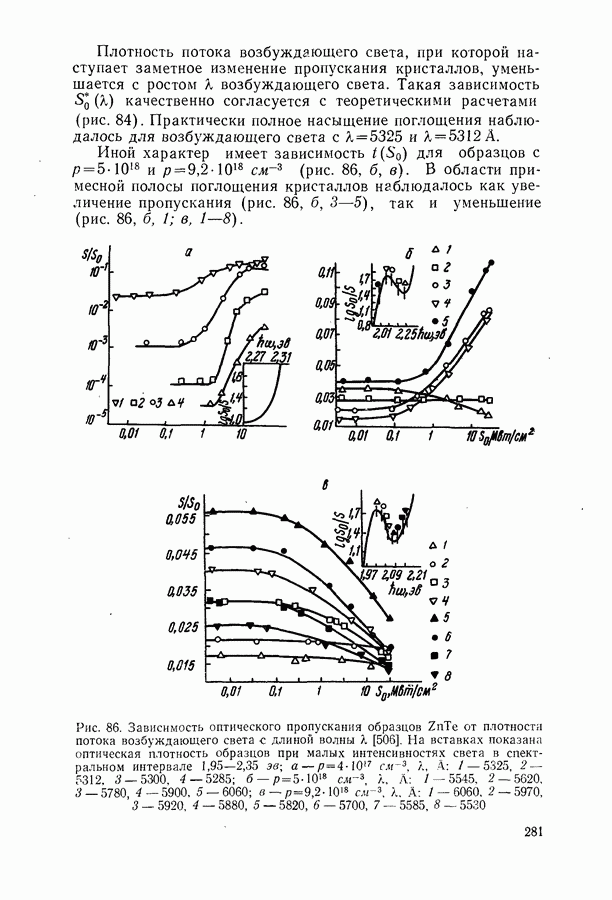
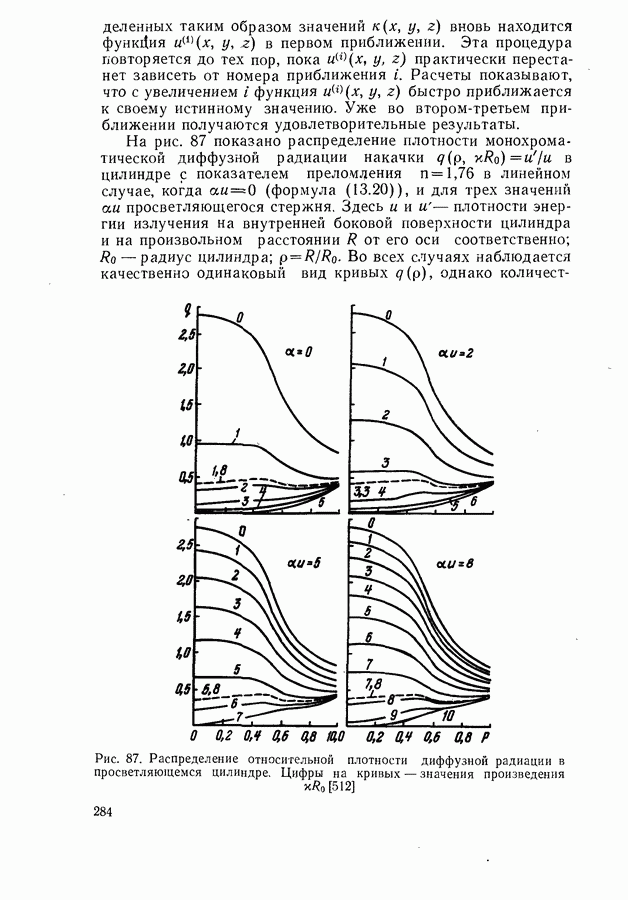
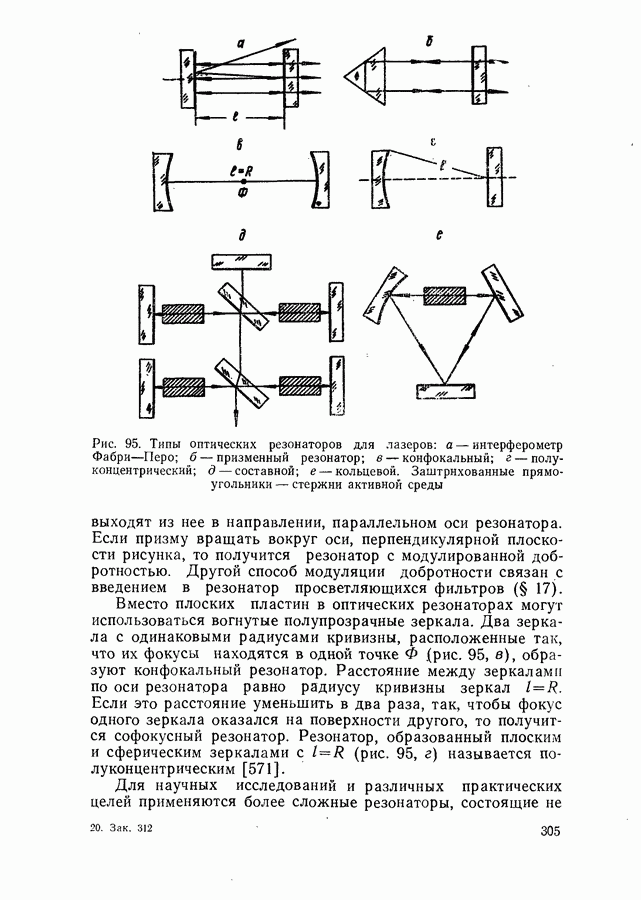
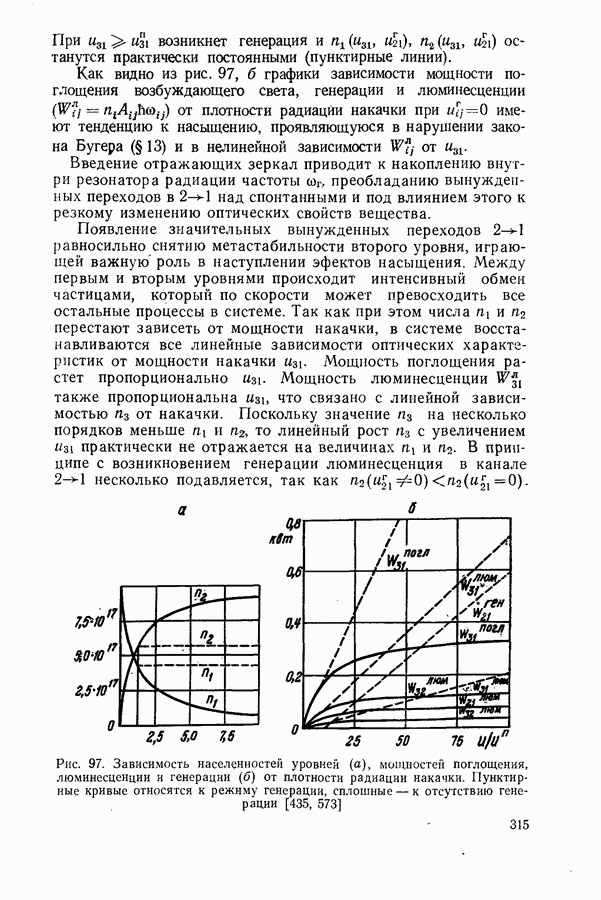
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
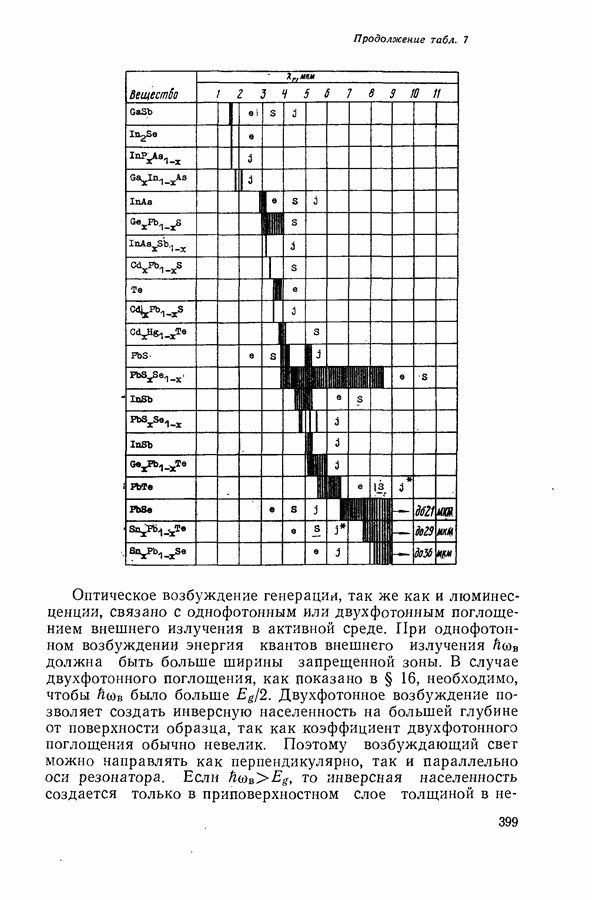
Модель Кронига и Пенни. Энергетические зоны.
Одномерная модель Кронига и Пенни — это бесконечная цепочка потенциальных ям прямоугольной формы (рис. 1). Движение электронов в такой системе характеризуется качественно новым и принципиально важным свойством: спектр разрешенных значений энергий электрона состоит не из отдельных уровней, как в изолированных атомах и в модели Зоммерфельда, а из широких зон. Поскольку зонная структура энергетического спектра является фундаментальным и неотъемлемым свойством твердого тела, модель Кронига и Пейни заслуживает детального рассмотрения. Уравнение Шредингера для этой модели решается точно, что позволяет выяснить физический смысл причин, приводящих к образованию зон.
Обозначим ширину потенциальной ямы (рис. 7) через а, а высоту и ширину барьера через  соответственно. Очевидно, рассматриваемая цепочка потенциальных ям будет периодической с периодом
соответственно. Очевидно, рассматриваемая цепочка потенциальных ям будет периодической с периодом  Уравнение (2.5), описывающее движение электрона в такой системе, принимает вид
Уравнение (2.5), описывающее движение электрона в такой системе, принимает вид

где введены обозначения

Уравнению (2.23) удовлетворяют функции  а
а  -функции
-функции  Поэтому волновые функции для трех областей цепочки (рис. 7) равны
Поэтому волновые функции для трех областей цепочки (рис. 7) равны

Функция  выражена через
выражена через  на том основании, что вследствие периодичности системы квадраты модулей функций для идентичных областей должны быть равны
на том основании, что вследствие периодичности системы квадраты модулей функций для идентичных областей должны быть равны  Это и означает, что сами функции могут отличаться лишь фазовым множителем
Это и означает, что сами функции могут отличаться лишь фазовым множителем 
Для нахождения постоянных коэффициентов в (2.26) воспользуемся непрерывностью волновой функции и ее производной во всем пространстве, т. е. наложим на функции условия

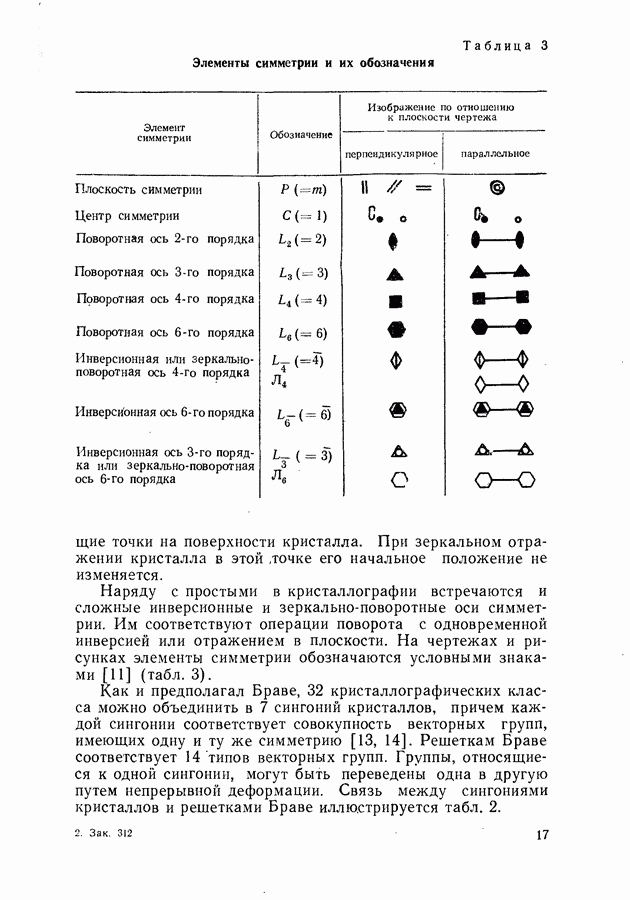
Непрерывность производной волновой функции следует из анализа уравнения Шредингера [44].
Подставляя (2.26) в (2.27), находим

Система однородных уравнений (2.28) имеет отличные от нуля решения только в том случае, если ее определитель равен нулю

Раскрыв его, приходим к уравнению

связывающему параметры  и
и  а следовательно, и энергию с параметром
а следовательно, и энергию с параметром 
В случае, когда ширина потенциального барьера  а проницаемость барьера постоянна
а проницаемость барьера постоянна  уравнение (2.30) значительно упрощается. Действительно, если
уравнение (2.30) значительно упрощается. Действительно, если  то
то  как
как  . Учитывая (2.25), из (2.30) получим
. Учитывая (2.25), из (2.30) получим

где 
Если высота потенциального барьера  то из уравнения (2.31) следует
то из уравнения (2.31) следует  поэтому
поэтому  и энергия
и энергия  могут изменяться непрерывно от нуля до бесконечности. Это случай движения свободных электронов. При
могут изменяться непрерывно от нуля до бесконечности. Это случай движения свободных электронов. При  и
и  принимают дискретный ряд значений, как в модели Зоммерфельда.
принимают дискретный ряд значений, как в модели Зоммерфельда.
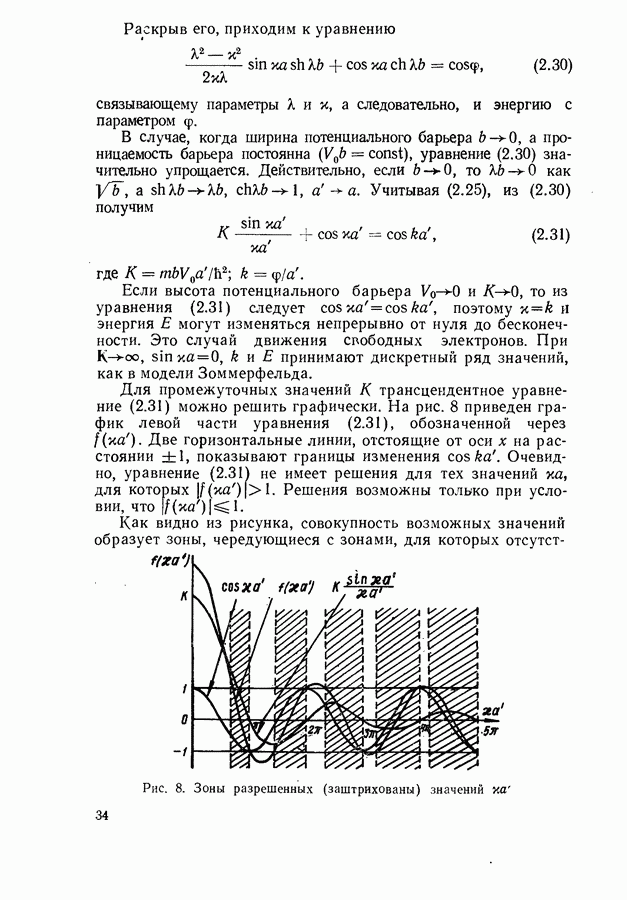
Для промежуточных значений К трансцендентное уравнение (2.31) можно решить графически. На рис. 8 приведен график левой части уравнения (2.31), обозначенной через  Две горизонтальные линии, отстоящие от оси х на расстоянии ±1, показывают границы изменения
Две горизонтальные линии, отстоящие от оси х на расстоянии ±1, показывают границы изменения  Очевидно, уравнение
Очевидно, уравнение  не имеет решения для тех значений
не имеет решения для тех значений  для которых
для которых  Решения возможны только при условии, что
Решения возможны только при условии, что 
Как видно из рисунка, совокупность возможных значений образует зоны, чередующиеся с зонами, для которых

Рис. 8. Зоны разрешенных (заштрихованы) значений 
отсутствуют решения уравнения Шредингера. Поскольку первое слагаемое в (2.31) содержит в знаменателе  ширина разрешенных зон растет с увеличением
ширина разрешенных зон растет с увеличением  а запрещенные зоны сужаются и в пределе вовсе исчезают. С ростом энергии вновь осуществляется переход к свободному движению электронов.
а запрещенные зоны сужаются и в пределе вовсе исчезают. С ростом энергии вновь осуществляется переход к свободному движению электронов.
В пределах разрешенных зон энергия электрона может изменяться непрерывно, поскольку  принимает любое значение от —1 до
принимает любое значение от —1 до  Однако это справедливо только для бесконечно протяженного кристалла. Реальные кристаллы всегда ограничены, поэтому волновые функции должны удовлетворять условию периодичности Борна — Кармана.
Однако это справедливо только для бесконечно протяженного кристалла. Реальные кристаллы всегда ограничены, поэтому волновые функции должны удовлетворять условию периодичности Борна — Кармана.
Как уже отмечалось, из требования периодичности квадрата модуля волновой функции следует

Умножив это равенство на  находим
находим

Это означает, что произведение

является периодической функцией от  с периодом а. Тогда волновую функцию удобно представить в виде
с периодом а. Тогда волновую функцию удобно представить в виде

Налагая на (2.33) условие периодичности и учитывая, что  получим
получим  а
а

где  целое число.
целое число.
Следовательно, параметр  принимает дискретный ряд значений, причем в каждой зоне имеется
принимает дискретный ряд значений, причем в каждой зоне имеется  состояний
состояний  соответствует одна волновая функция).
соответствует одна волновая функция).
Зависящую от времени волновую функцию  на основании (2.33) представим в виде
на основании (2.33) представим в виде

Условно ее можно рассматривать как волну, амплитуда которой не постоянна, а изменяется периодически от х с периодом а. Параметр  играет в ней такую же роль, как волновой вектор в уравнении плоской волны, описывающей движение
играет в ней такую же роль, как волновой вектор в уравнении плоской волны, описывающей движение

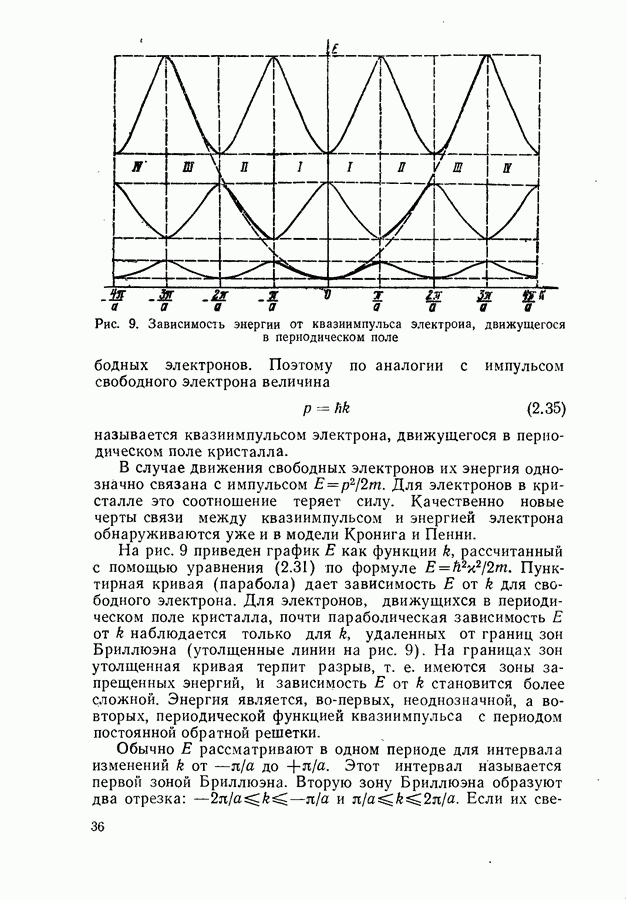
Рис. 9. Зависимость энергии от квазиимпульса электрона, движущегося в периодическом поле
свободных электронов. Поэтому по аналогии с импульсом свободного электрона величина

называется квазиимпульсом электрона, движущегося в периодическом поле кристалла.
В случае движения свободных электронов их энергия однозначно связана с импульсом  Для электронов в кристалле это соотношение теряет силу. Качественно новые черты связи между квазиимпульсом и энергией электрона обнаруживаются уже и в модели Кронига и Пенни.
Для электронов в кристалле это соотношение теряет силу. Качественно новые черты связи между квазиимпульсом и энергией электрона обнаруживаются уже и в модели Кронига и Пенни.
На рис. 9 приведен график  как функции
как функции  рассчитанный с помощью уравнения (2.31) по формуле
рассчитанный с помощью уравнения (2.31) по формуле  Пунктирная кривая (парабола) дает зависимость
Пунктирная кривая (парабола) дает зависимость  от
от  для свободного электрона. Для электронов, движущихся в периодическом поле кристалла, почти параболическая зависимость
для свободного электрона. Для электронов, движущихся в периодическом поле кристалла, почти параболическая зависимость  от
от  наблюдается только для
наблюдается только для  удаленных от границ зон Бриллюэна (утолщенные линии на рис. 9). На границах зон утолщенная кривая терпит разрыв, т. е. имеются зоны запрещенных энергий, И зависимость
удаленных от границ зон Бриллюэна (утолщенные линии на рис. 9). На границах зон утолщенная кривая терпит разрыв, т. е. имеются зоны запрещенных энергий, И зависимость  от
от  становится более сложной. Энергия является, во-первых, неоднозначной, а во-вторых, периодической функцией квазиимпульса с периодом постоянной обратной решетки.
становится более сложной. Энергия является, во-первых, неоднозначной, а во-вторых, периодической функцией квазиимпульса с периодом постоянной обратной решетки.
Обычно  рассматривают в одном периоде для интервала изменений
рассматривают в одном периоде для интервала изменений  от
от  до
до  Этот интервал называется первой зоной Бриллюэна. Вторую зону Бриллюэна образуют два отрезка:
Этот интервал называется первой зоной Бриллюэна. Вторую зону Бриллюэна образуют два отрезка:  Если их
Если их
свести вместе соответствующими концами, то график  будет таким же, как и в первой зоне. Третья зона состоит из отрезков
будет таким же, как и в первой зоне. Третья зона состоит из отрезков 
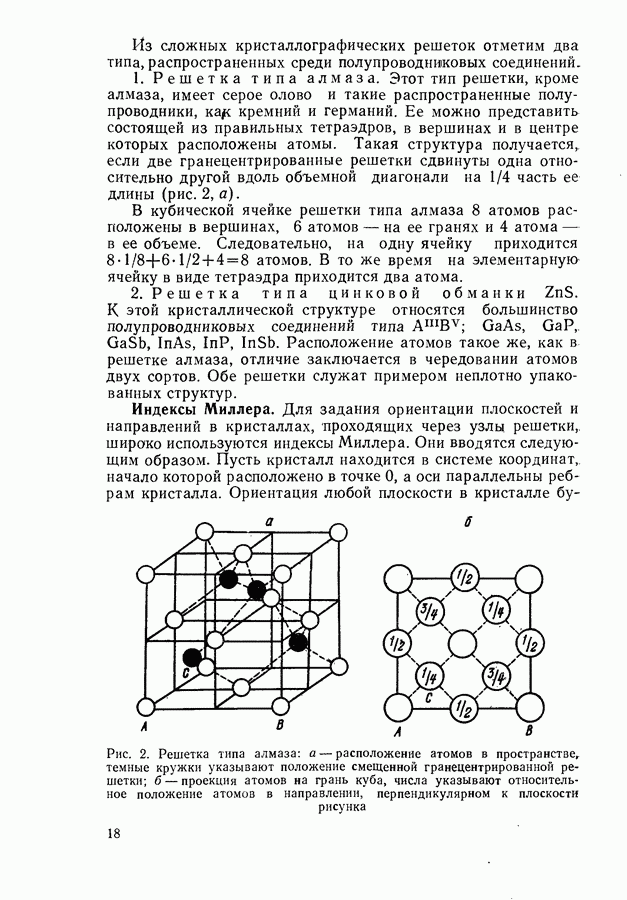
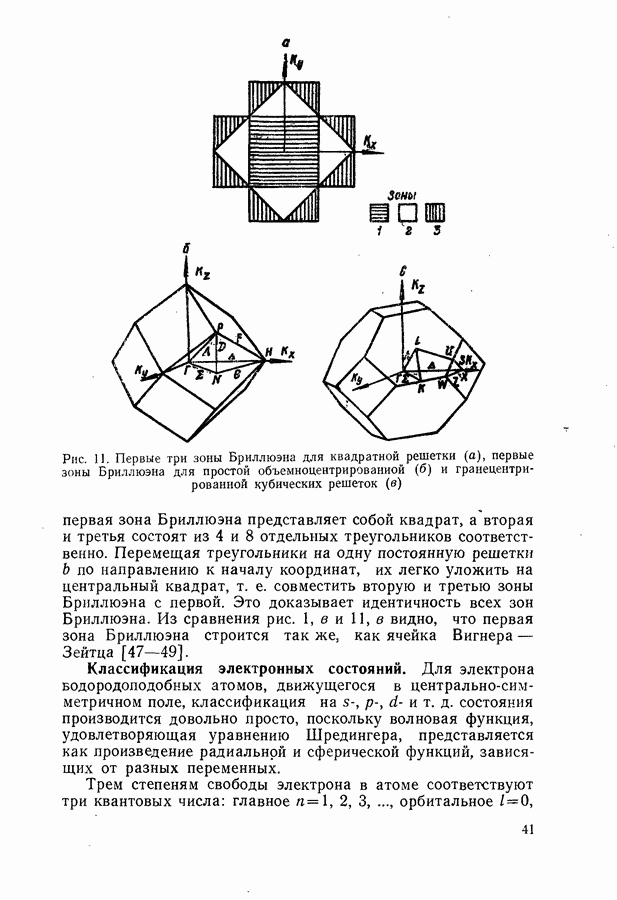
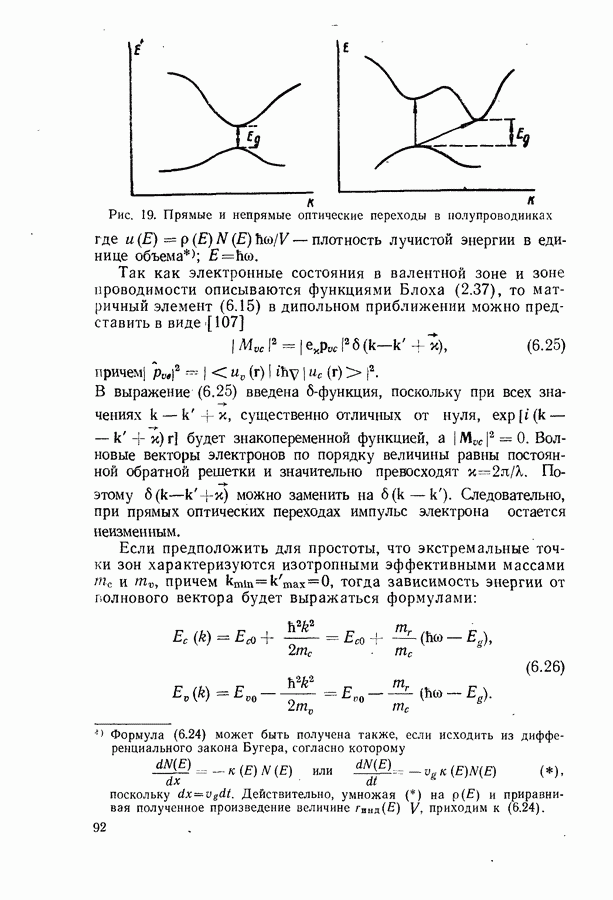
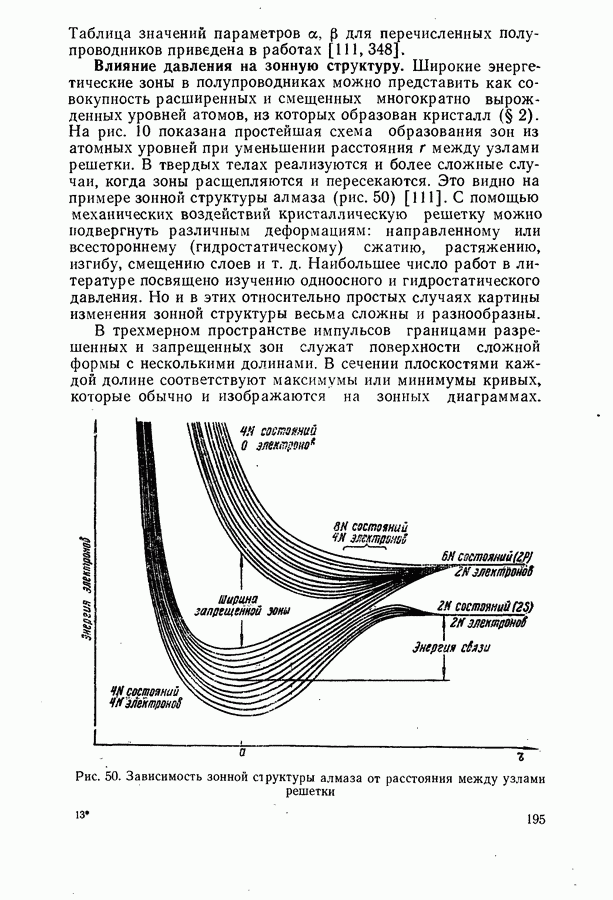
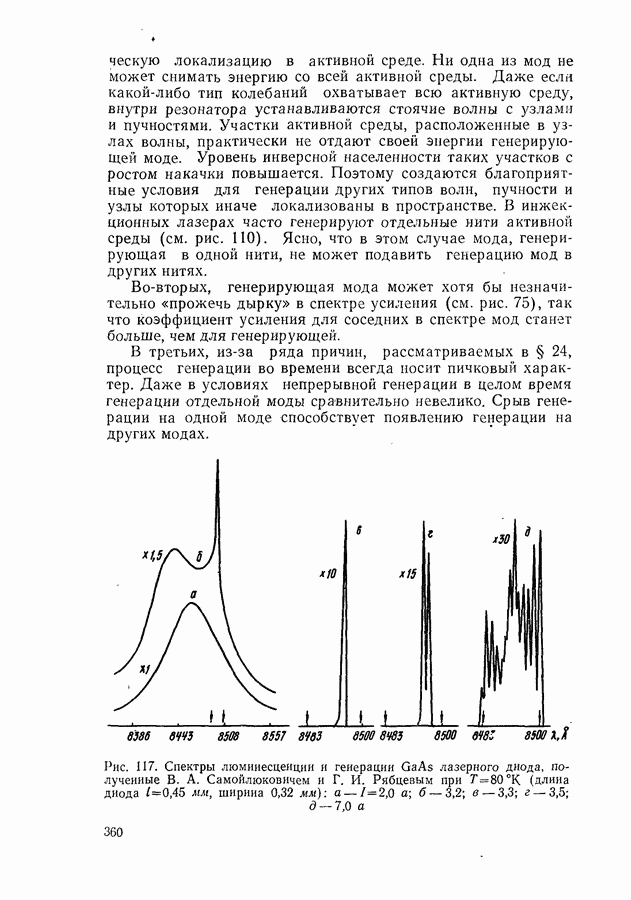
Таким образом, на основании исследования модели Кронига и Пенни можно построить качественно правильную картину энергетического спектра кристалла. Внутренние электроны атомов, мало подверженные действию внешних полей, занимают узкие атомные уровни, а валентные электроны располагаются в широких зонах (рис. 10), состоящих из  близко расположенных уровней. Зоны, полностью занятые валентными электронами в соответствии с принципом Паули, называются валентными, а пустые или частично заполненные — зонами проводимости. В теории часто ограничиваются рассмотрением только самой высокой валентной зоны и самой низкой зоны проводимости, поскольку многие физические процессы связаны с движением электронов исключительно в этих зонах.
близко расположенных уровней. Зоны, полностью занятые валентными электронами в соответствии с принципом Паули, называются валентными, а пустые или частично заполненные — зонами проводимости. В теории часто ограничиваются рассмотрением только самой высокой валентной зоны и самой низкой зоны проводимости, поскольку многие физические процессы связаны с движением электронов исключительно в этих зонах.
Процесс возникновения широких энергетических зон в кристаллах можно проследить из следующего мысленного эксперимента. Пусть имеется  атомов, которые расположены в пространстве так же, как в кристалле, но на значительно больших расстояниях друг от друга. Орбиты валентных электронов не возмущены. Тогда энергетический спектр системы
атомов, которые расположены в пространстве так же, как в кристалле, но на значительно больших расстояниях друг от друга. Орбиты валентных электронов не возмущены. Тогда энергетический спектр системы 

Рис. 10. Энергетический спектр кристалла (а) и его образование из дискретных уровней атомов при уменьшении расстояния между узлами решетки (б)
частйц как целого будет совпадать со спектром одного атома, только каждый простой уровень изолированного атома будет  -кратно вырожденным. Начнем теперь уменьшать расстояние между атомами. Валентные электроны соседних атомов станут взаимодействовать между собой. Из квантовой механики известно, что такое взаимодействие снимает вырождение уровней. Уровни будут расширяться и расщепляться все больше и больше по мере сокращения расстояния между атомами. Это и приводит к появлению зон (рис. 10).
-кратно вырожденным. Начнем теперь уменьшать расстояние между атомами. Валентные электроны соседних атомов станут взаимодействовать между собой. Из квантовой механики известно, что такое взаимодействие снимает вырождение уровней. Уровни будут расширяться и расщепляться все больше и больше по мере сокращения расстояния между атомами. Это и приводит к появлению зон (рис. 10).
Характерно, что из  состояний каждой зоны
состояний каждой зоны  состояниям соответствуют положительные значения к. Столько же состояний характеризуются отрицательным значением к. Если все состояния заполнены, то числа электронов, движущихся во взаимно противоположных состояниях, равны, а электрический ток отсутствует. Электроны полностью заполненных зон в переносе зарядов не участвуют.
состояниям соответствуют положительные значения к. Столько же состояний характеризуются отрицательным значением к. Если все состояния заполнены, то числа электронов, движущихся во взаимно противоположных состояниях, равны, а электрический ток отсутствует. Электроны полностью заполненных зон в переносе зарядов не участвуют.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
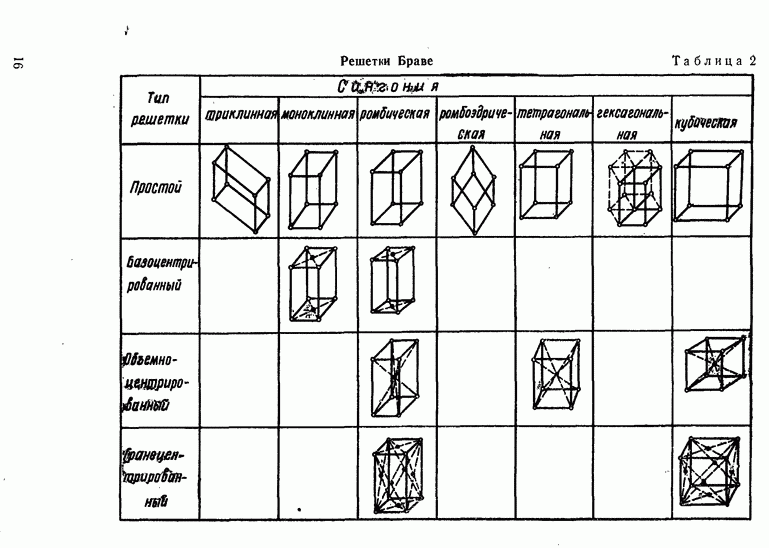
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
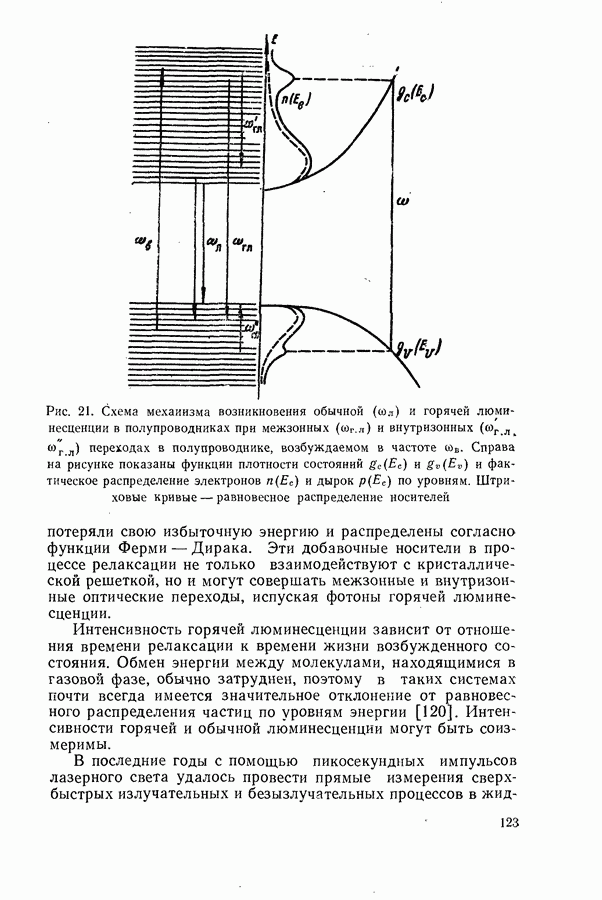
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
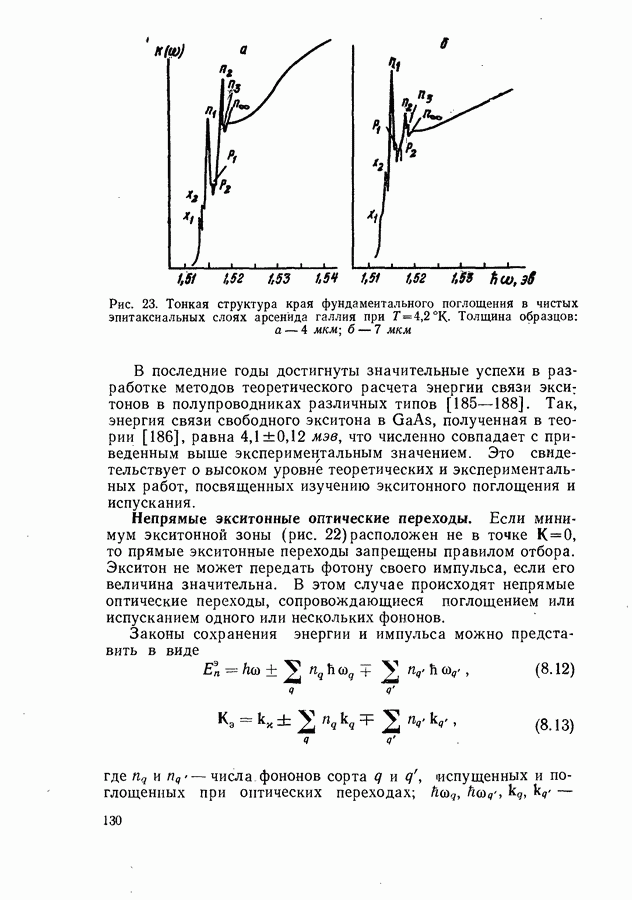
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
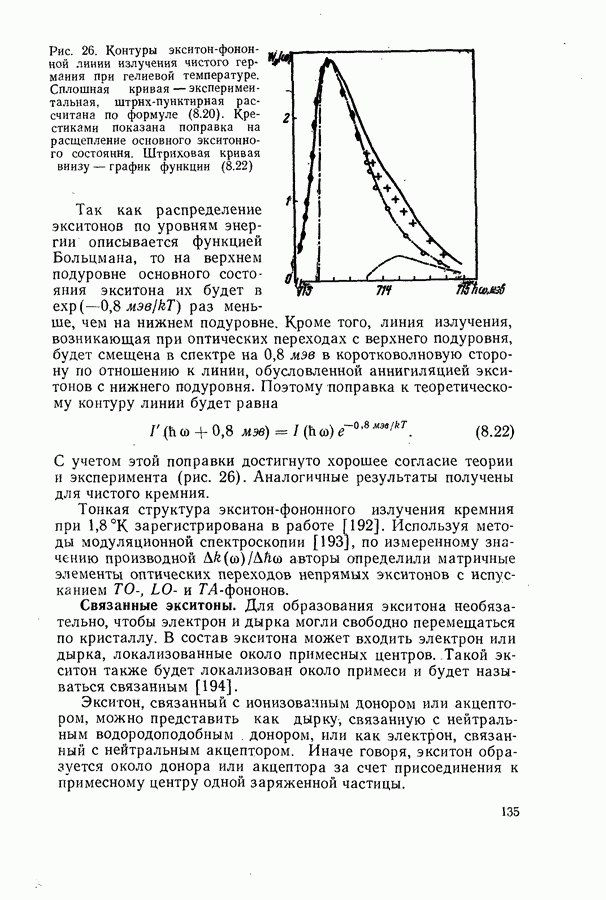
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
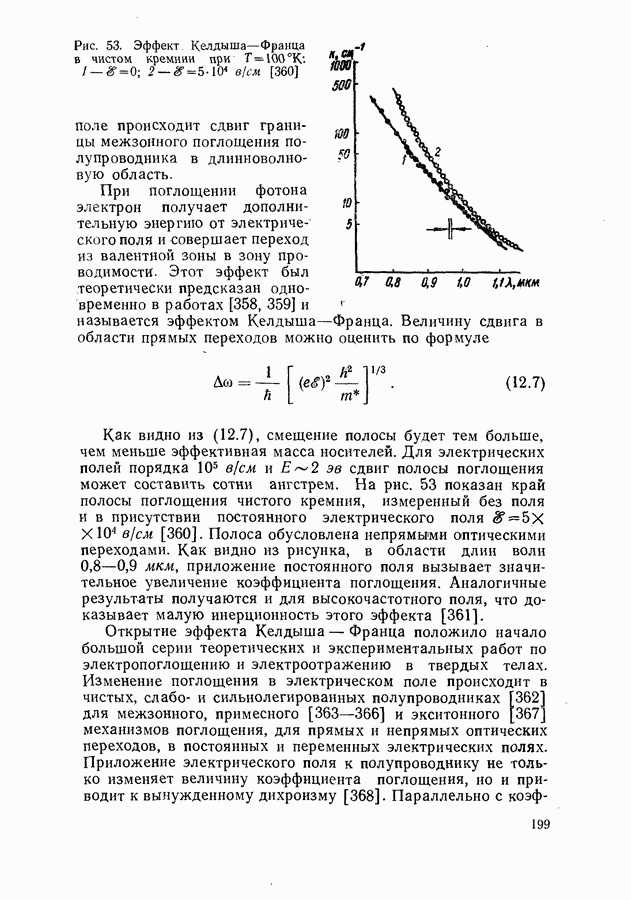
- Эффект Келдыша-Франца.
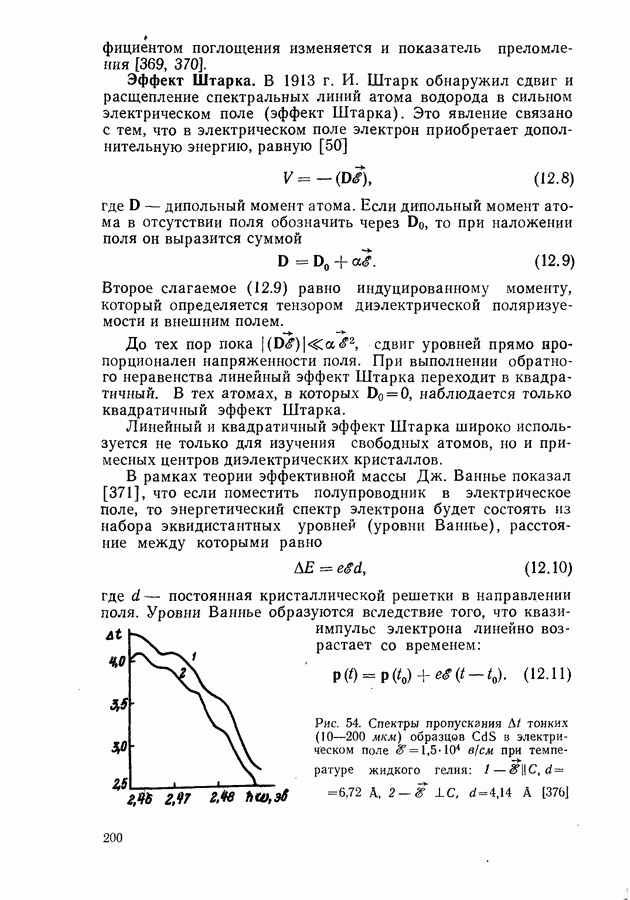
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
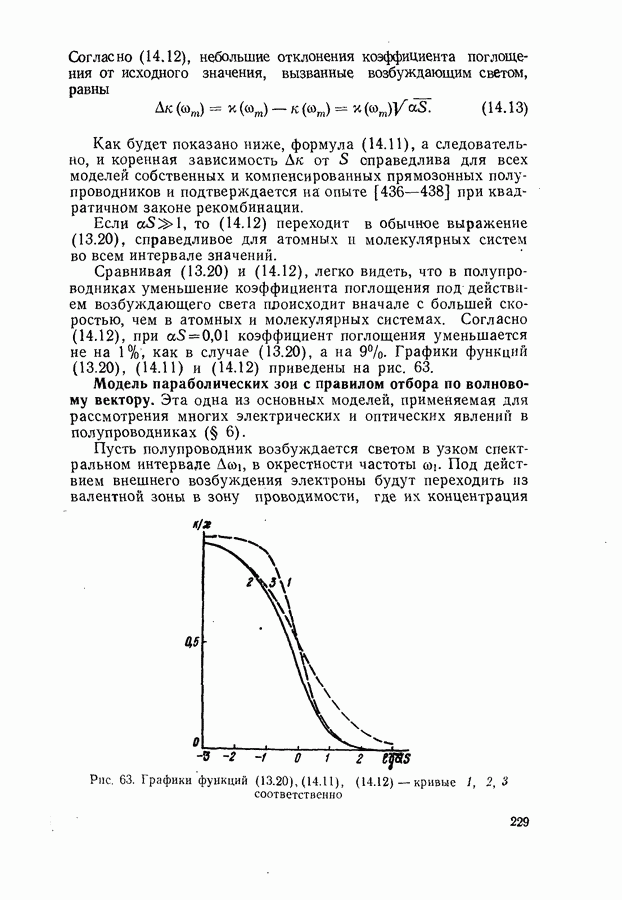
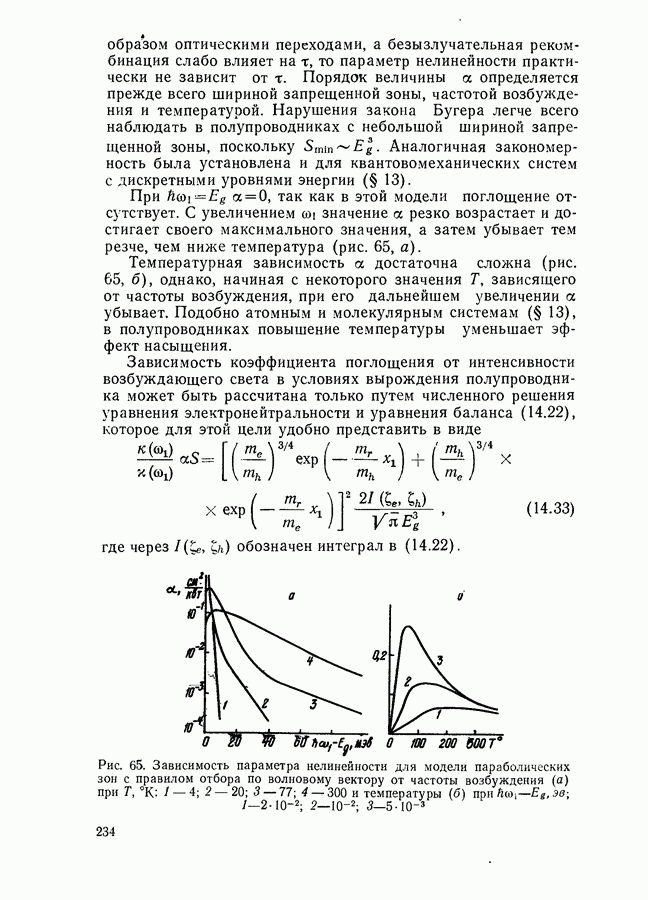
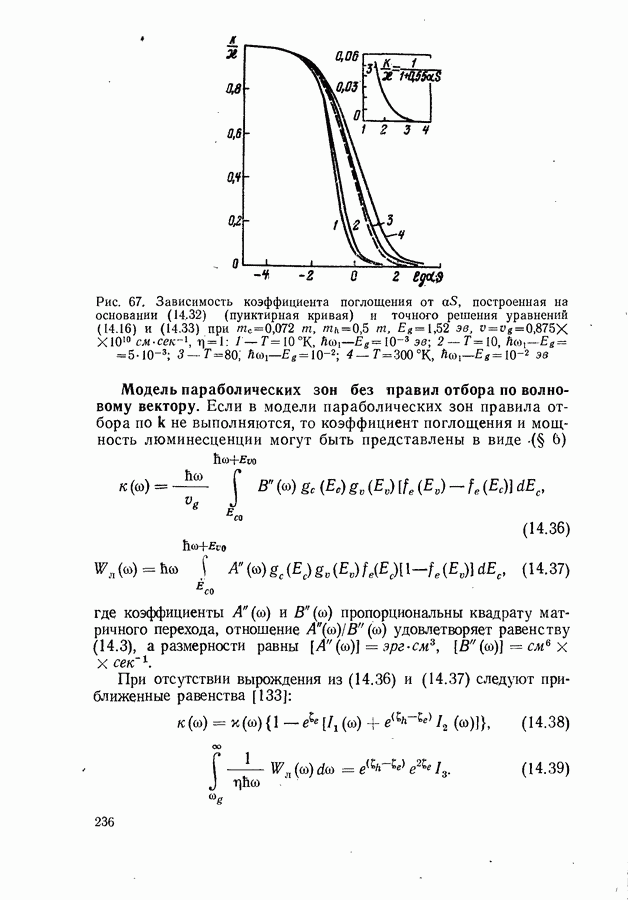
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
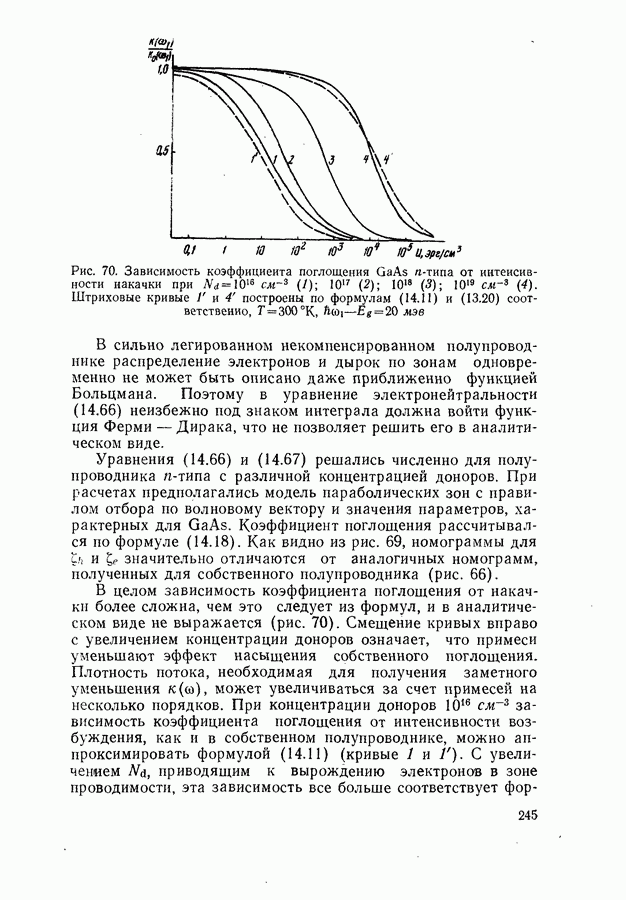
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
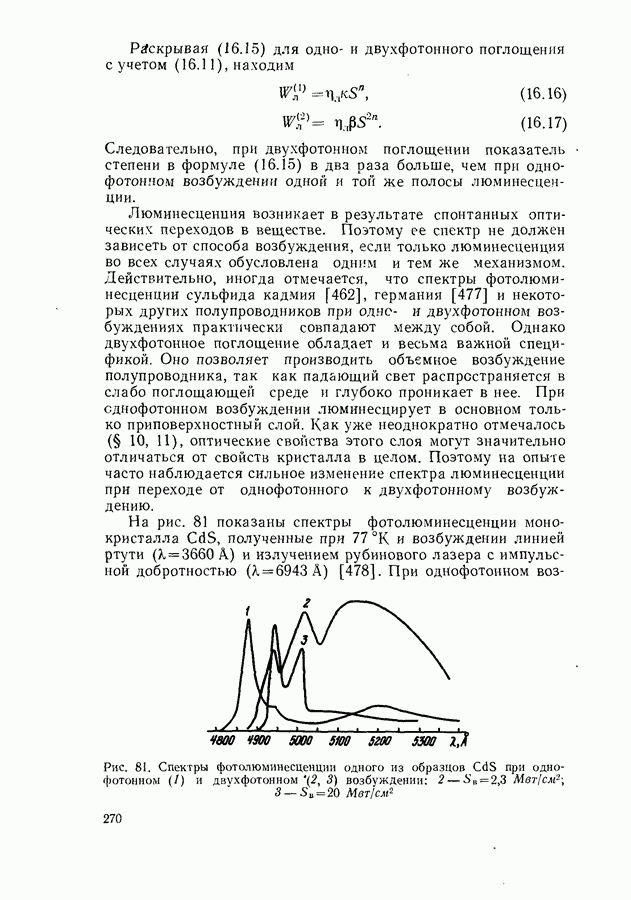
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
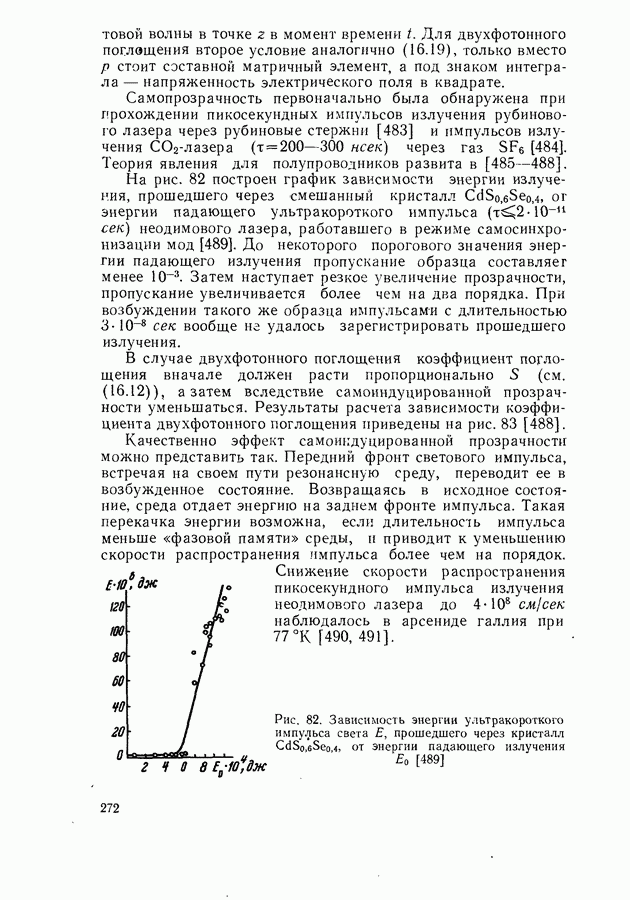
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
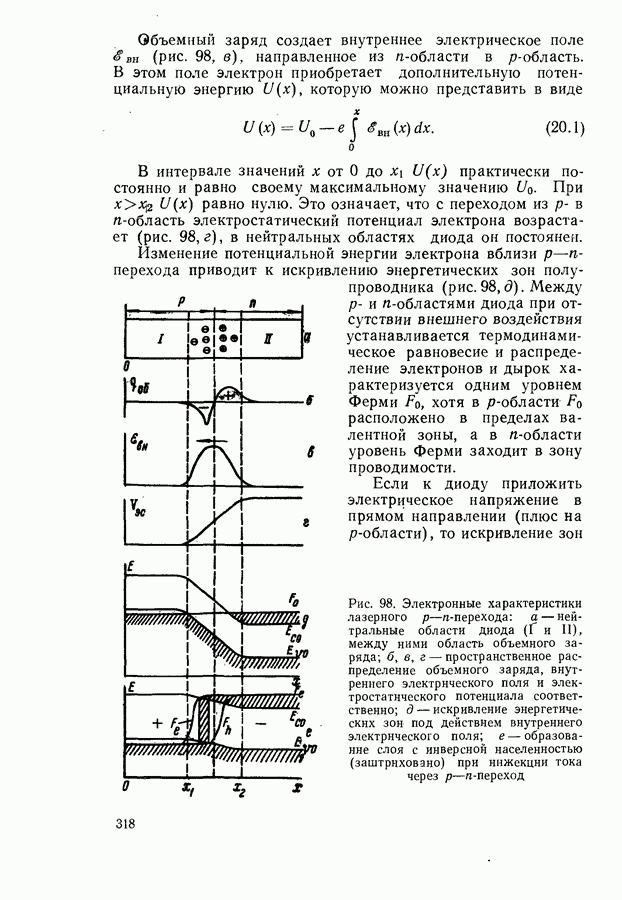
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
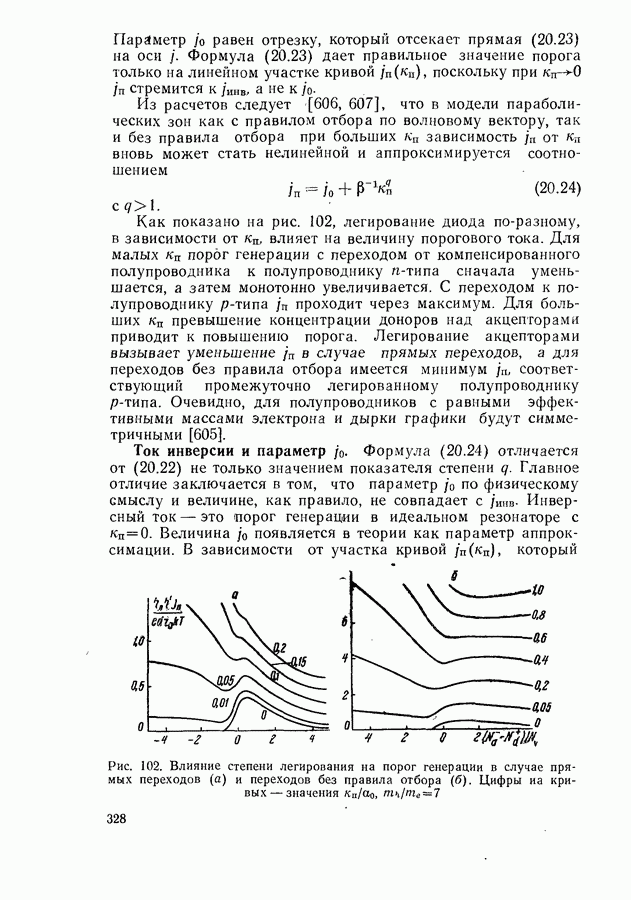
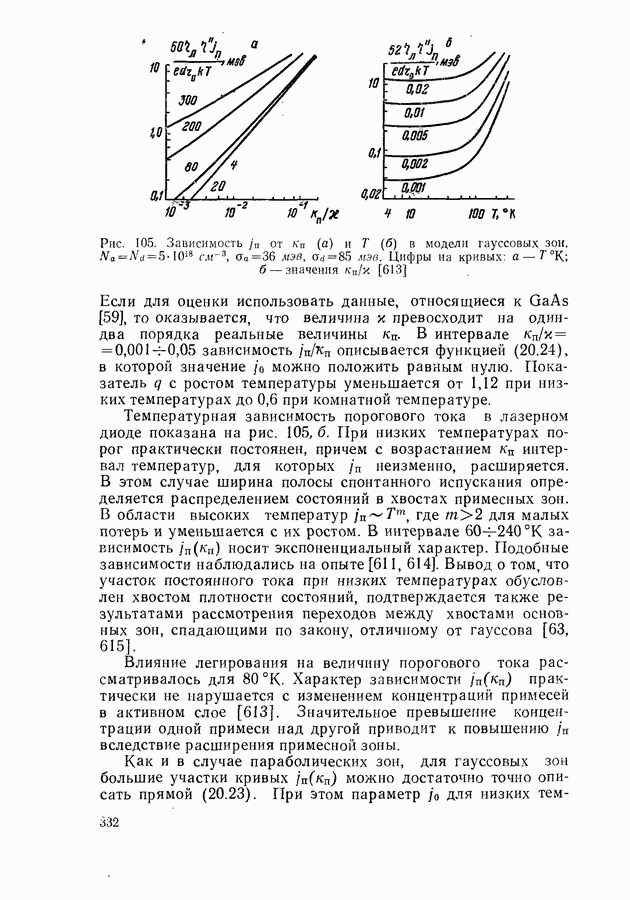
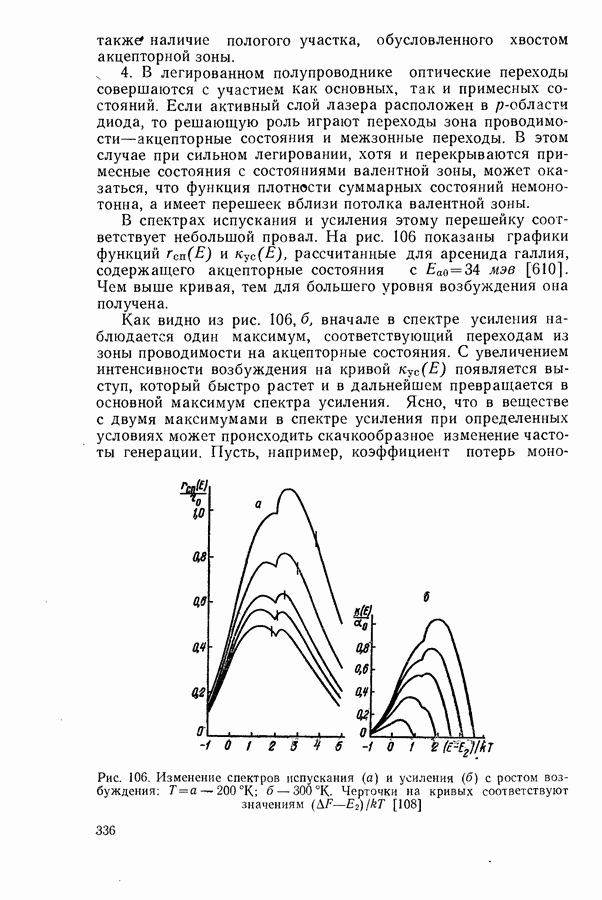
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
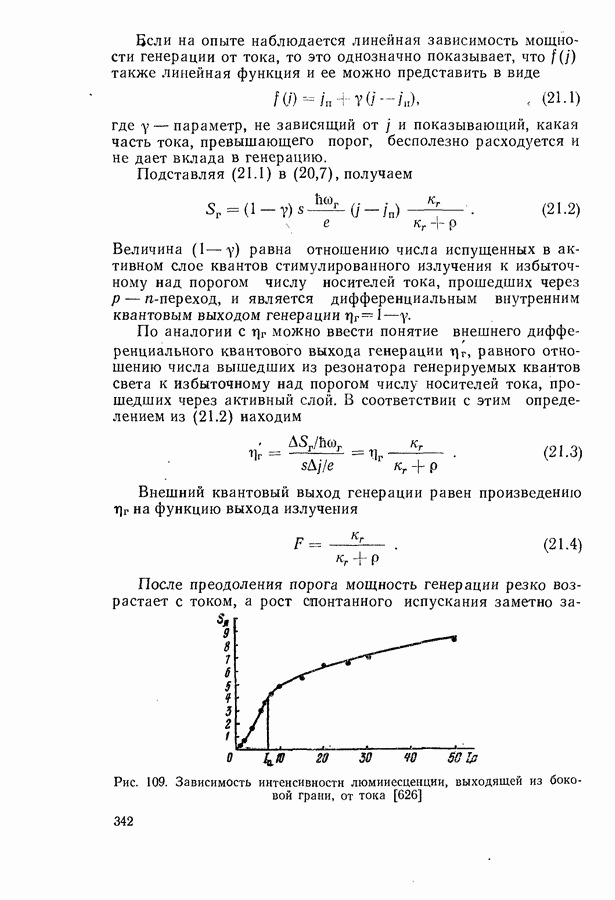
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
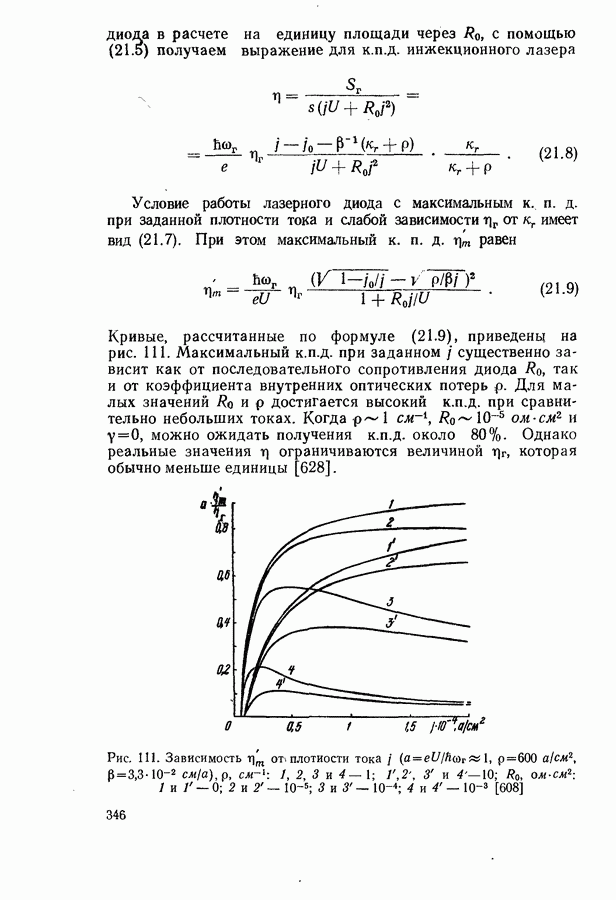
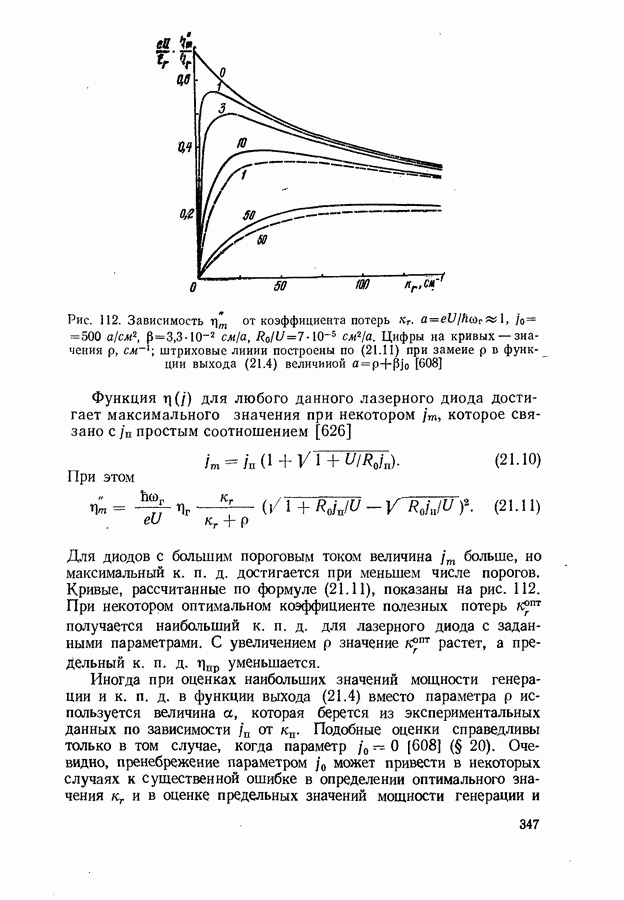
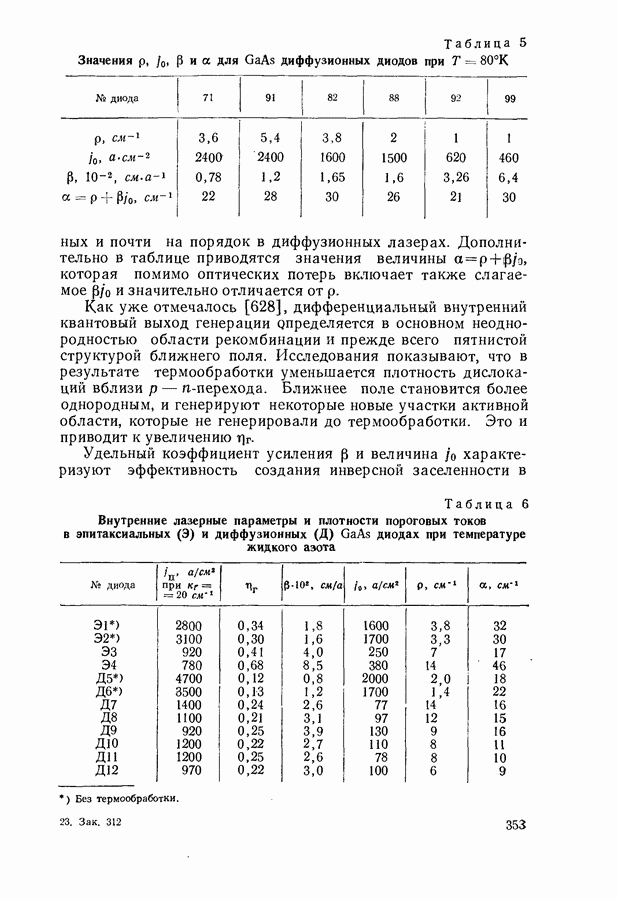
- Оптимальный режим генерации.
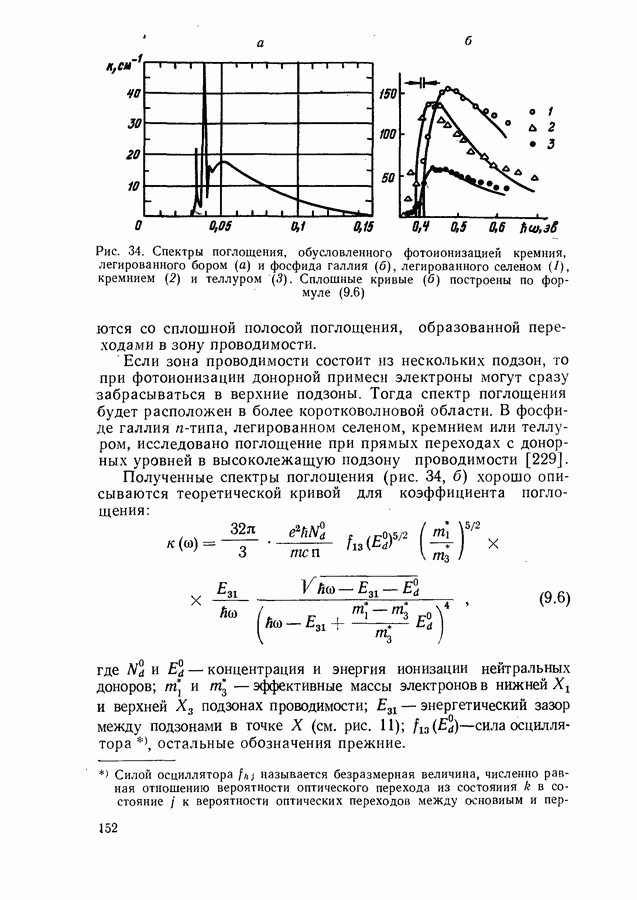
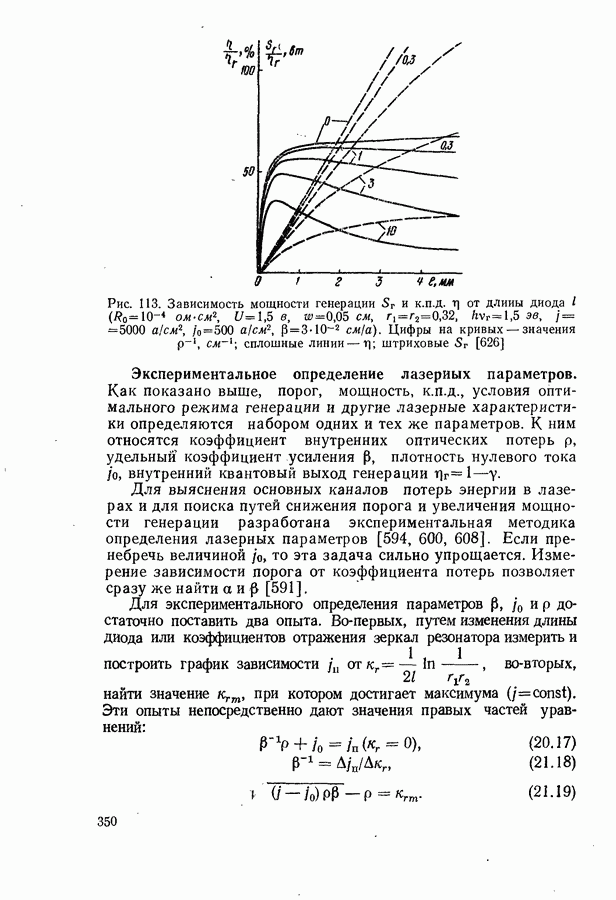
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
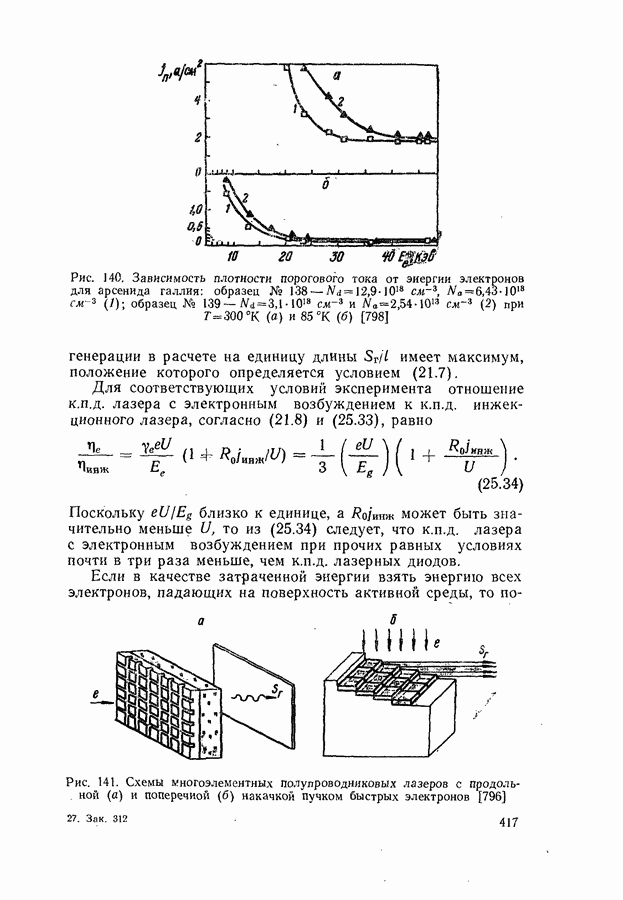
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
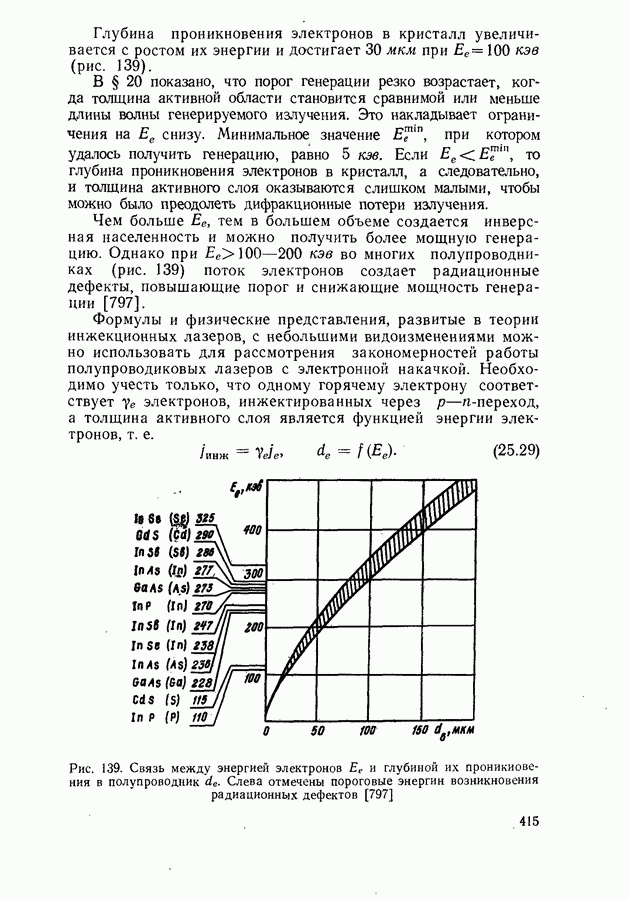
- Возбуждение генерации пучком быстрых электронов.