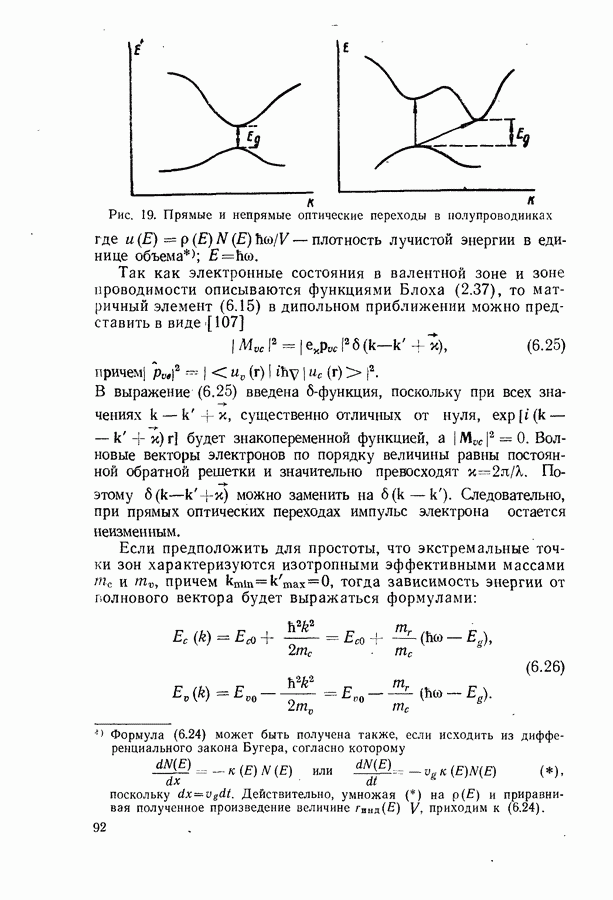
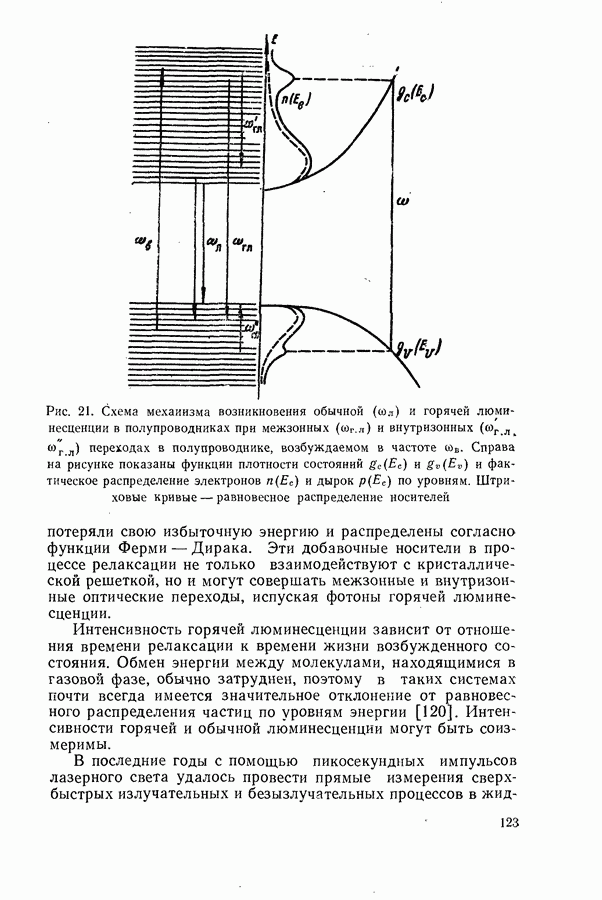
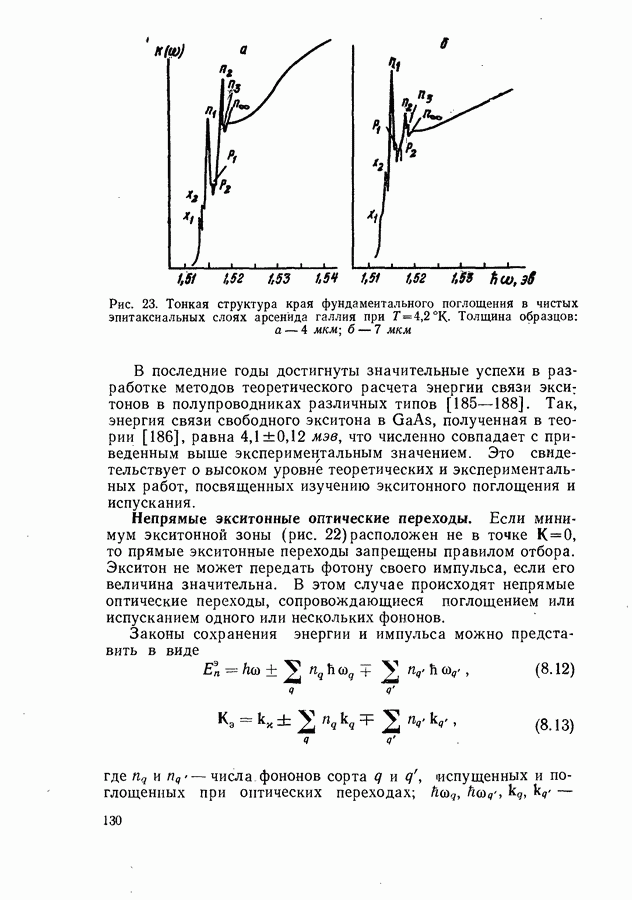
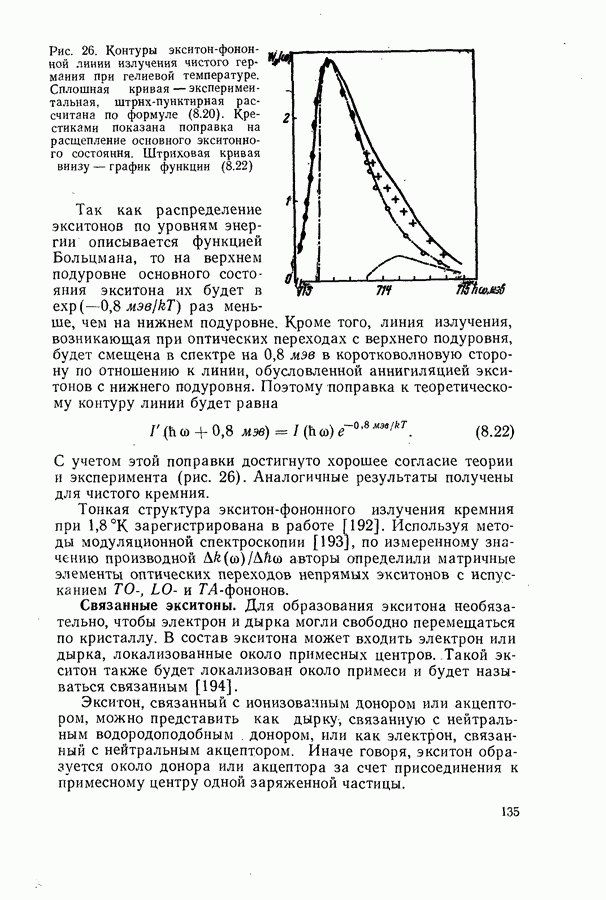
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
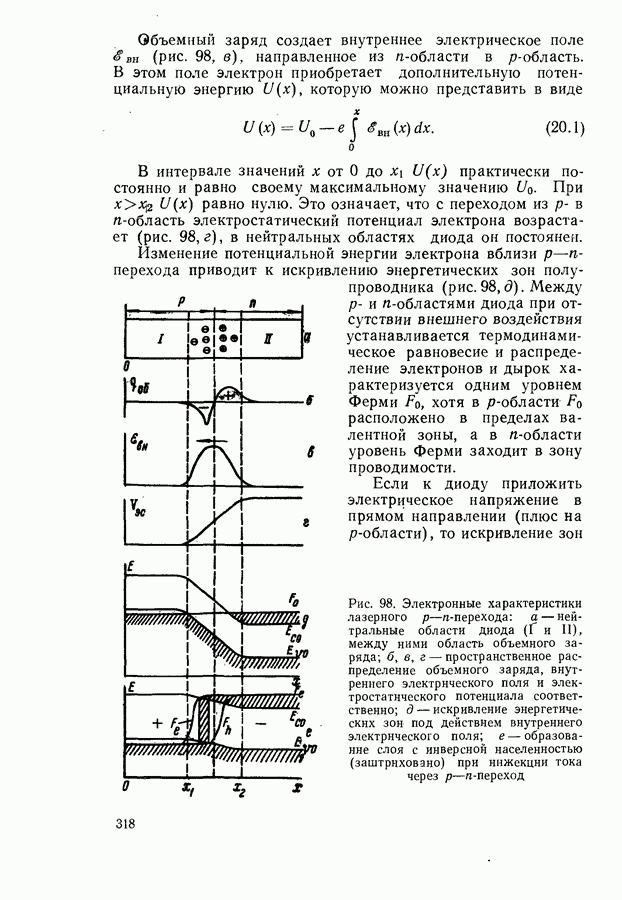
Модуляционная спектроскопия.
До середины 50-х годов основные исследования по оптике полупроводников относились к области спектра вблизи края фундаментального поглощения и к более длинноволновому участку спектра. Для более коротких длин волн коэффициент поглощения достигает больших значений — порядка  Чтобы измерить пропускание в этой области, необходимо брать образцы с толщиной от долей микрона до нескольких микрон. В таких тонких слоях большую роль играет приповерхностный слой (§ 11), и трудно получить надежные воспроизводимые результаты.
Чтобы измерить пропускание в этой области, необходимо брать образцы с толщиной от долей микрона до нескольких микрон. В таких тонких слоях большую роль играет приповерхностный слой (§ 11), и трудно получить надежные воспроизводимые результаты.
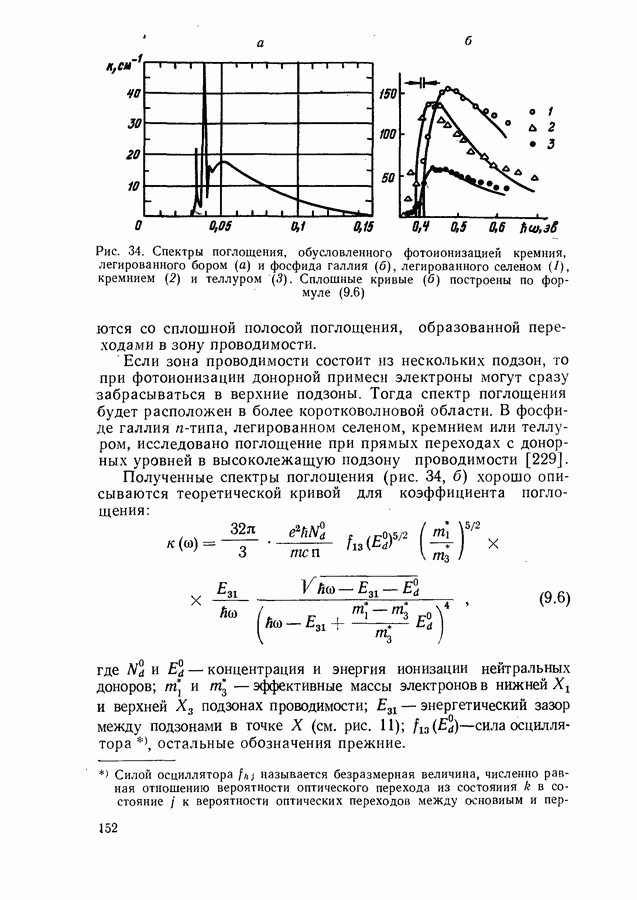
Тонкая структура полосы поглощения, соответствующая оптическим переходам в глубь зоны проводимости,
затушевывается сплошным фоном интенсивного поглощения, чтане позволяет извлекать всей необходимой информации о зонной структуре. Поэтому изучение оптических свойств полупроводников в области их металлического поглощения развивалось медленно.
В последние годы произошли решительные изменения. Это направление исследований начало бурно развиваться. Решающую роль сыграла разработка новых дифференциальных методов измерения тонкой структуры в спектрах поглощения и отражения. Коэффициент поглощения и ранее рассчитывался на основании соотношения Крамерса-Кронига по измеренному спектру отражения. Однако только после разработки методов дифференциальной или модуляционной спектроскопии это соотношение стало эффективным средством изучения оптических свойств полупроводников.
Если обозначить действительную и мнимую части комплексной диэлектрической проницаемости  через
через  соответственно, то соотношения Крамерса-Кронига можно представить в виде [2, 111]:
соответственно, то соотношения Крамерса-Кронига можно представить в виде [2, 111]:

где  главная часть интеграла в смысле Коши. Приравнивая по отдельности действительные и мнимые части равенства
главная часть интеграла в смысле Коши. Приравнивая по отдельности действительные и мнимые части равенства  находим связь между оптическими постоянными вещества:
находим связь между оптическими постоянными вещества:

Хотя при измерении показателя преломления и коэффициента поглощения на заданной частоте  можно получить для них любые значения, согласно соотношениям (12.21) и (12.22), функции
можно получить для них любые значения, согласно соотношениям (12.21) и (12.22), функции  в целом не являются независимыми. Если измерена (или задана) одна из них во всем интервале частот от
в целом не являются независимыми. Если измерена (или задана) одна из них во всем интервале частот от  до
до  то тем самым полностью определена и другая.
то тем самым полностью определена и другая.
Трудность в пользовании соотношениями Крамерса-Кронига связана с тем, что для расчета неизвестной функции хотя бы в одной точке, необходимо знать вторую для всех частот. Для преодоления этой трудности обычно широко пользуются экстраполяцией и приближенным заданием
значений  Так, если концентрация свободных носителей пренебрежимо мала, то для частот
Так, если концентрация свободных носителей пренебрежимо мала, то для частот  можно положить [402]
можно положить [402]

Для частот, превышающих среднюю частоту междузонных переходов  справедлива формула
справедлива формула 

Чтобы определить показатель преломления и коэффициент поглощения в области металлического поглощения на опыте, измеряется коэффициент отражения  при нормальном падении света. На основании (10.22) его можно представить как квадрат модуля комплексной отражательной способности
при нормальном падении света. На основании (10.22) его можно представить как квадрат модуля комплексной отражательной способности

Изменение фазы волны  при отражении связано с
при отражении связано с  дисперсионным соотношением [403]
дисперсионным соотношением [403]

Измерение  на опыте и расчет
на опыте и расчет  по формуле (12.26) позволяет решить уравнение (12.25) и определить
по формуле (12.26) позволяет решить уравнение (12.25) и определить  а следовательно, и коэффициент поглощения.
а следовательно, и коэффициент поглощения.
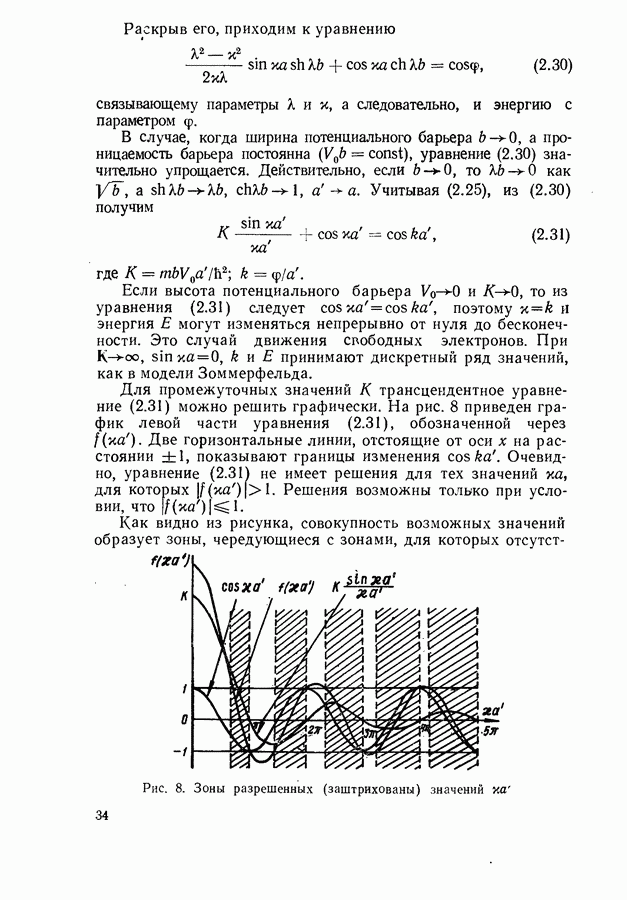
Сущность дифференциальной спектроскопии состоит в том, чтобы измерять ее первую или вторую производную по некоторому параметру  Это позволяет исключить сплошной фон и необычайно заострить все детали спектральных характеристик.
Это позволяет исключить сплошной фон и необычайно заострить все детали спектральных характеристик.
Пусть, например, на фоне практически постоянного значения коэффициента отражения  имеется небольшой пичок или ступенька
имеется небольшой пичок или ступенька 

При непосредственном измерении  тонкая структура будет едва различима. Если же взять производную от
тонкая структура будет едва различима. Если же взять производную от  по
по 

то величина  исчезает, а (12.28) может изменяться в больших пределах, в принципе от
исчезает, а (12.28) может изменяться в больших пределах, в принципе от  до
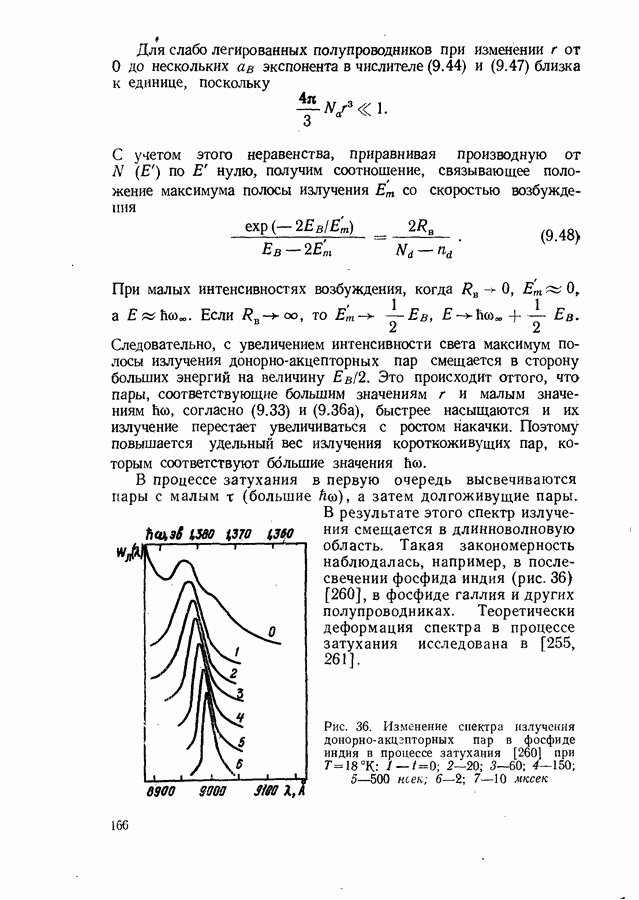
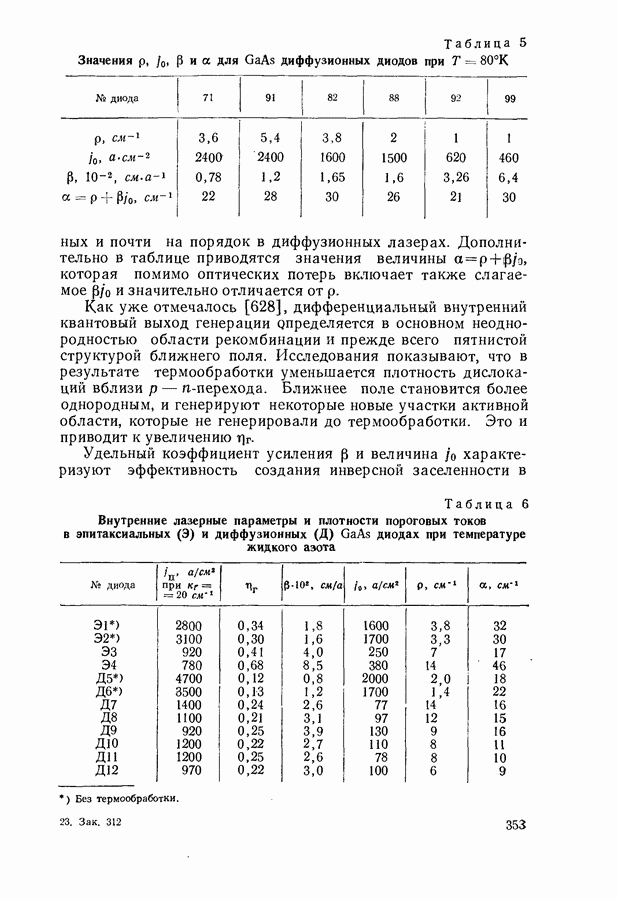
до  Например, в обычном спектре поглощения дублета двуокиси углерода (рис. 59, кривая 1)
Например, в обычном спектре поглощения дублета двуокиси углерода (рис. 59, кривая 1)

Рис. 59. Спектры поглощения  первой (2) и второй (3) производной для дублета
первой (2) и второй (3) производной для дублета  Кривые 2 и 3 получены с помощью дифференциального спектрометра
Кривые 2 и 3 получены с помощью дифференциального спектрометра
структура линии совершенно не разрешается. О наличии дублета можно только догадываться по различному наклону кривой справа и слева от максимума поглощения. На графике первой производной от  по
по  (кривая 2) дублетная структура линии становится очевидной. Еще более нагляден график второй производной.
(кривая 2) дублетная структура линии становится очевидной. Еще более нагляден график второй производной.
В качестве параметра  в формулах типа (12.28) берутся различные внешние силы, изменяющие оптические свойства полупроводников: температура, одноосное и гидростатическое давление, электрические и магнитные поля, концентрация примесей и т. п. Производная
в формулах типа (12.28) берутся различные внешние силы, изменяющие оптические свойства полупроводников: температура, одноосное и гидростатическое давление, электрические и магнитные поля, концентрация примесей и т. п. Производная  дает скорость изменения положения в спектре исследуемой особой точки зонной структуры, например ширины запрещенной зоны от параметра
дает скорость изменения положения в спектре исследуемой особой точки зонной структуры, например ширины запрещенной зоны от параметра  Если эта производная известна из теории или из независимых опытов, то по измеренному значению
Если эта производная известна из теории или из независимых опытов, то по измеренному значению  легко рассчитать структуру
легко рассчитать структуру 
Модулирование любого оптического параметра по частоте можно осуществить с помощью частотномодулированного света. Пусть частота света изменяется по косинусоидальному закону

Тогда диэлектрическая проницаемость будет равна

При малых  из (12.29) и (12.30) находим
из (12.29) и (12.30) находим

Если  то измеренное на опыте значение
то измеренное на опыте значение  будет пропорционально производной
будет пропорционально производной 
Модулирование длины волны можно осуществить, в частности, механическими колебаниями входной или выходной щелей монохроматора, колебаниями зеркала монохроматора и т. п. Созданы спектральные приборы, в которых дифференцирование спектра по времени производится вычислительным устройством, а длина волны линейно изменяется во времени.
Достаточно полный обзор методов дифференциальной спектроскопии изложен в книге М. Кардоны [402] и в [404].
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
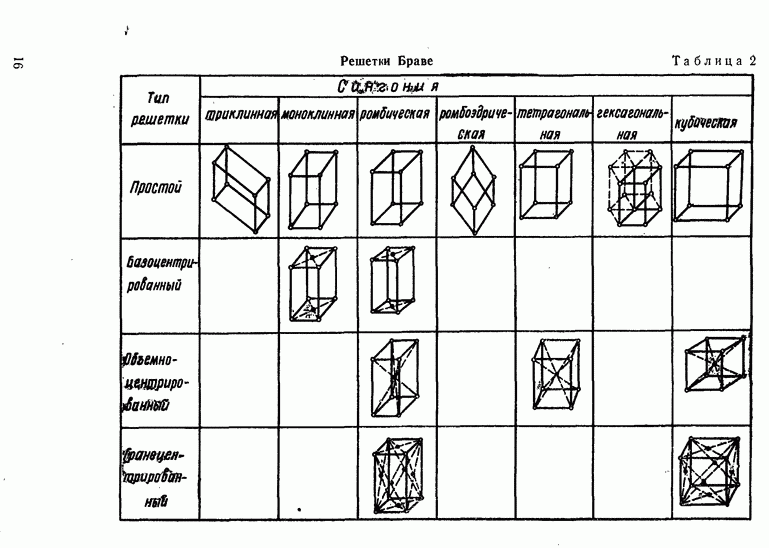
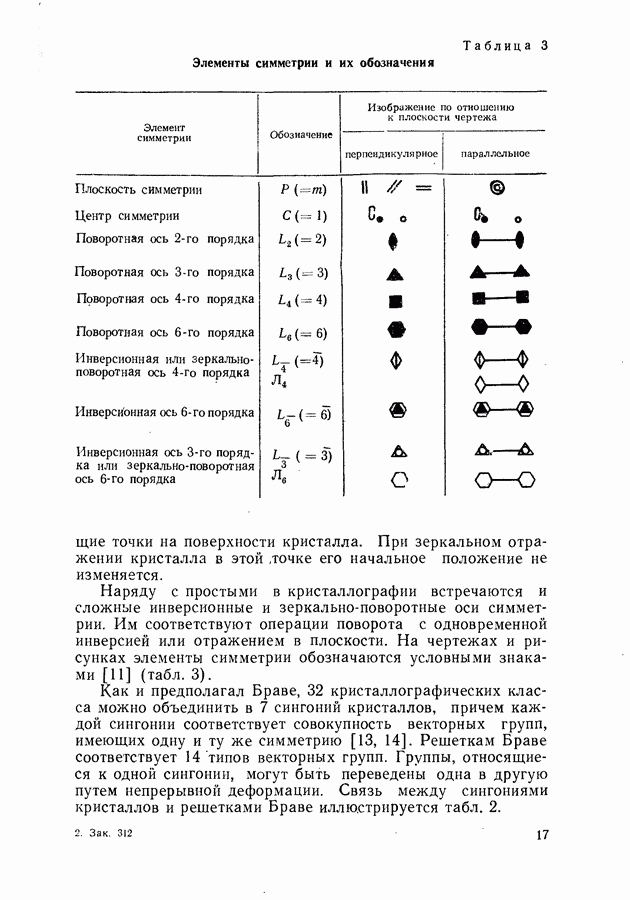
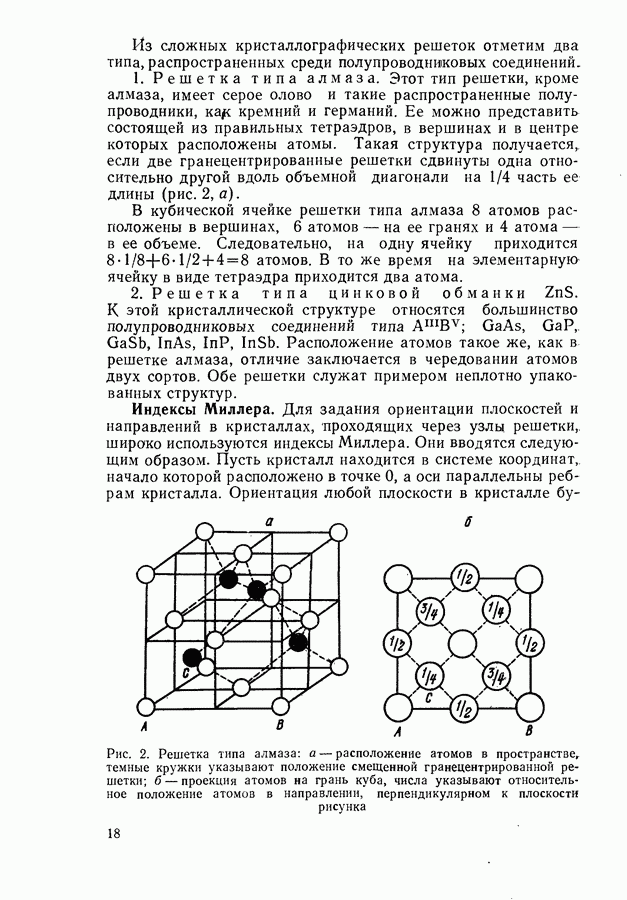
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
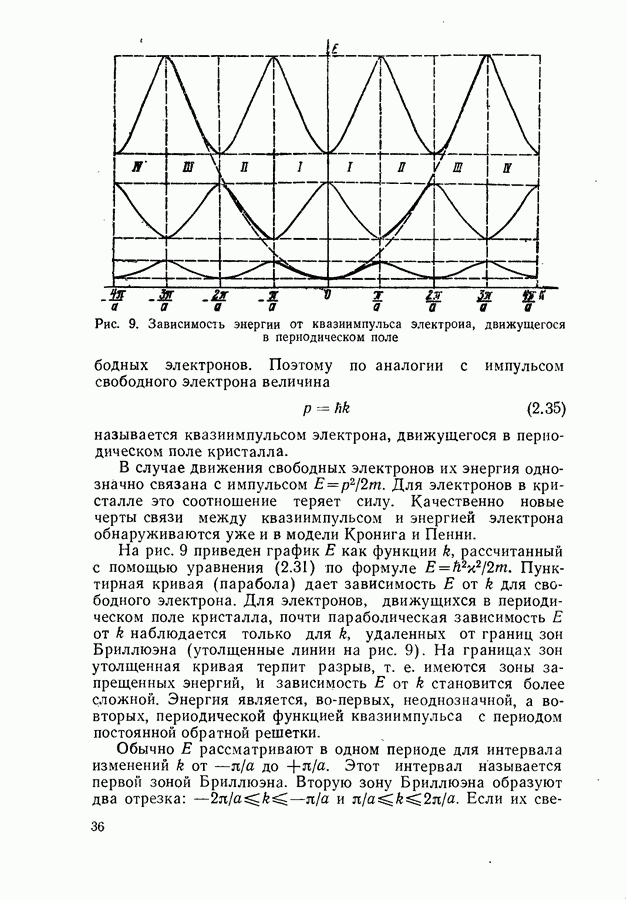
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
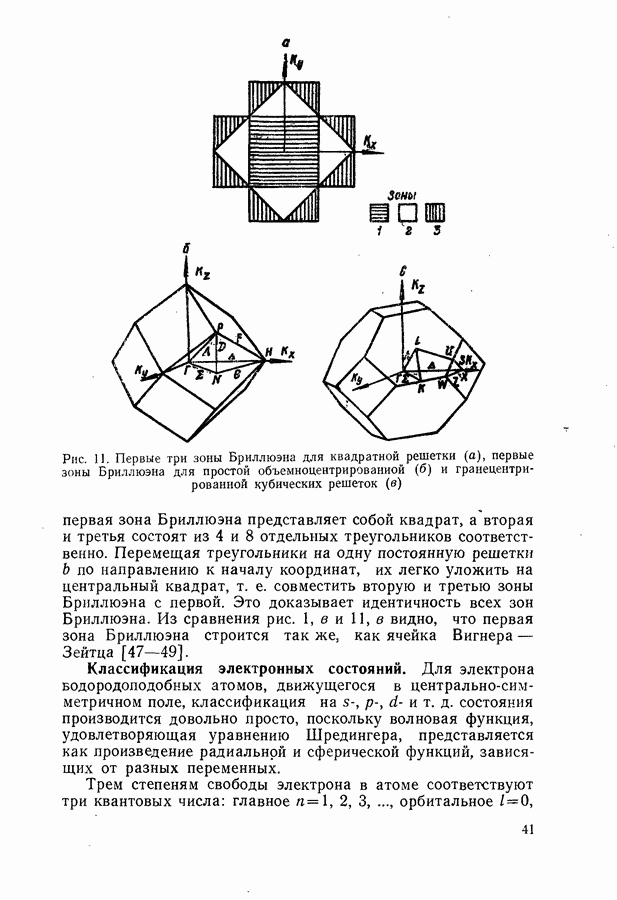
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
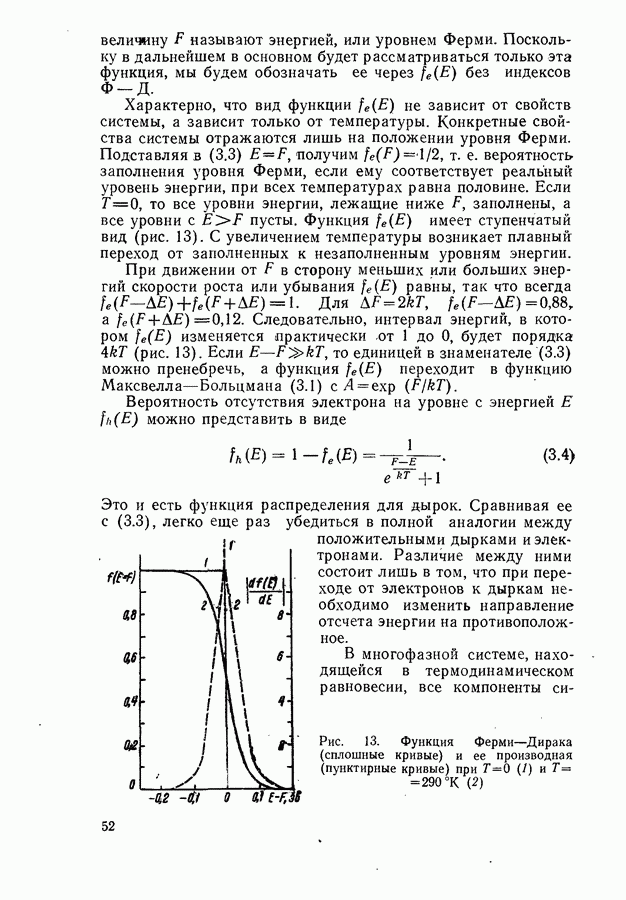
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
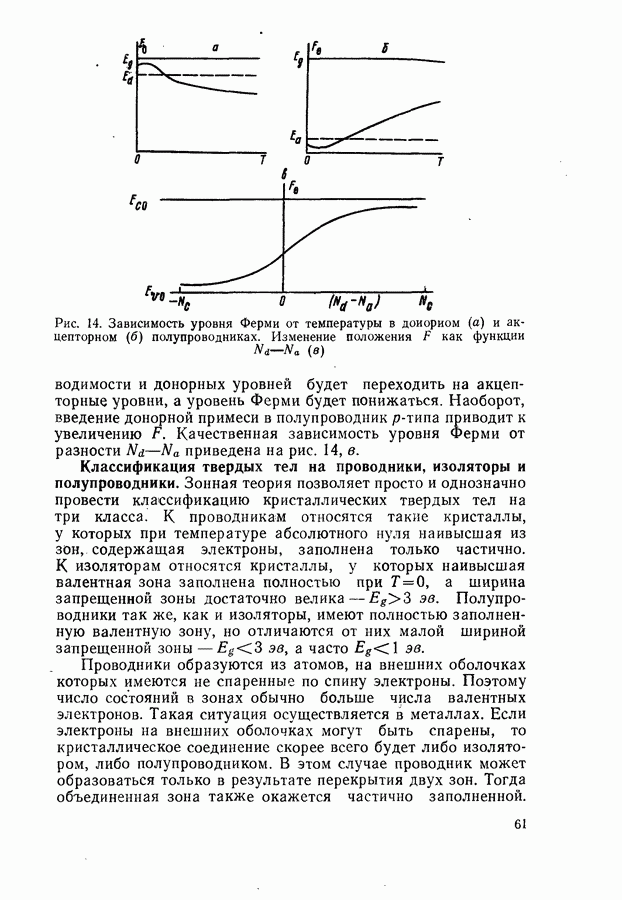
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
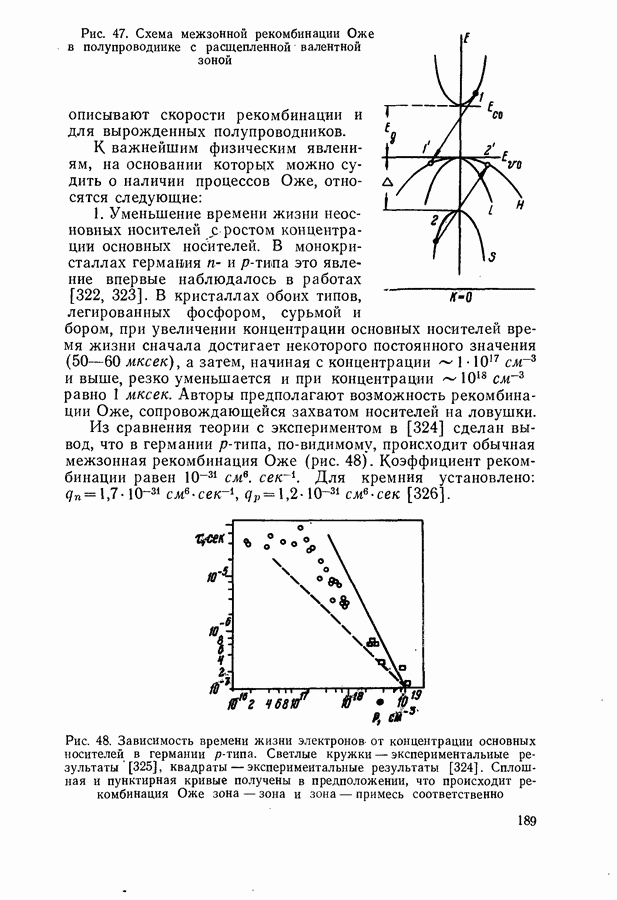
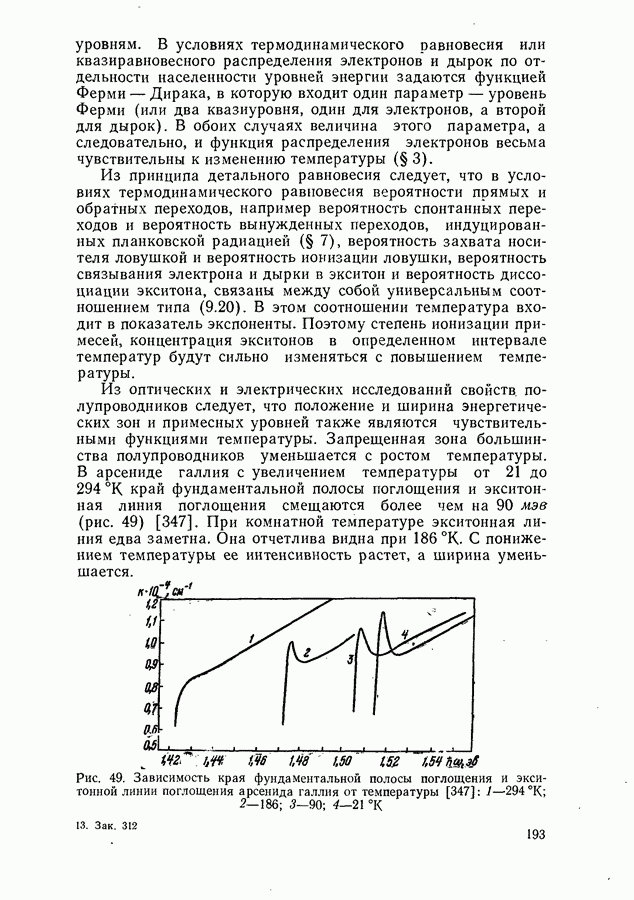
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
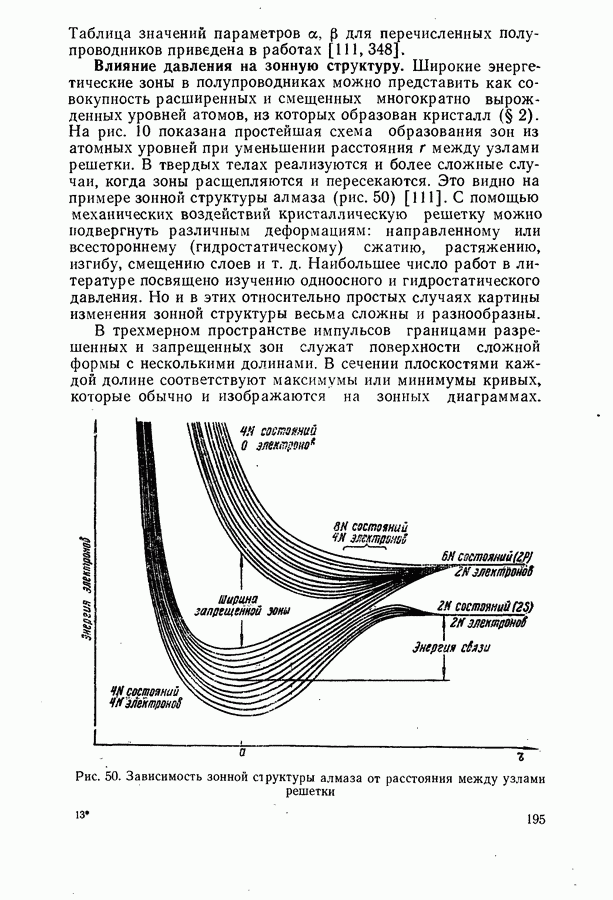
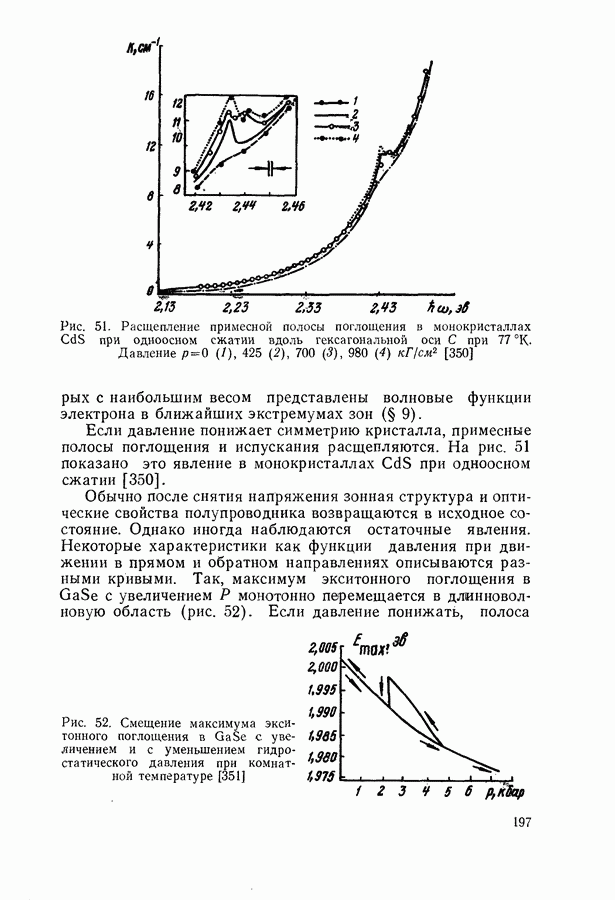
- Влияние давления на зонную структуру.
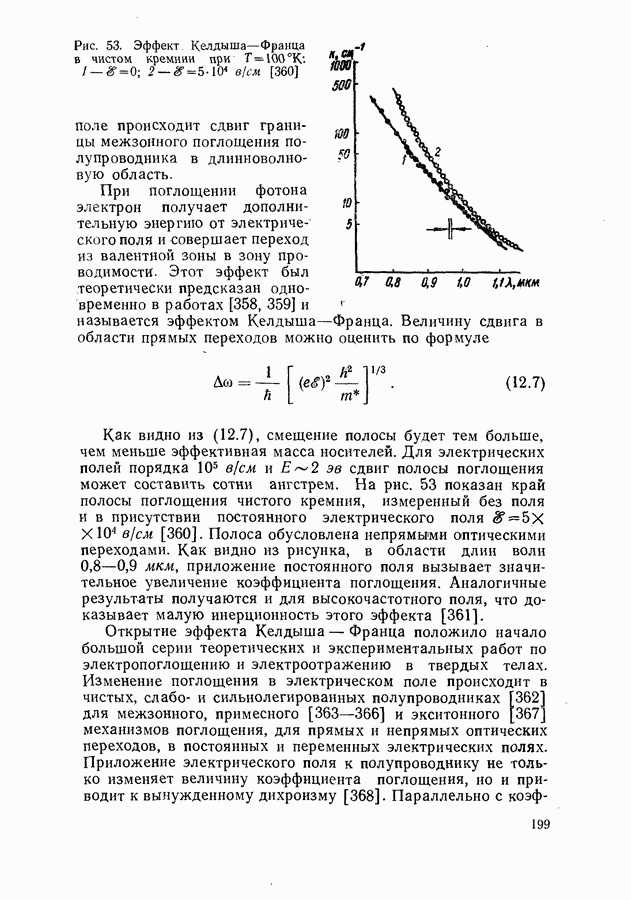
- Эффект Келдыша-Франца.
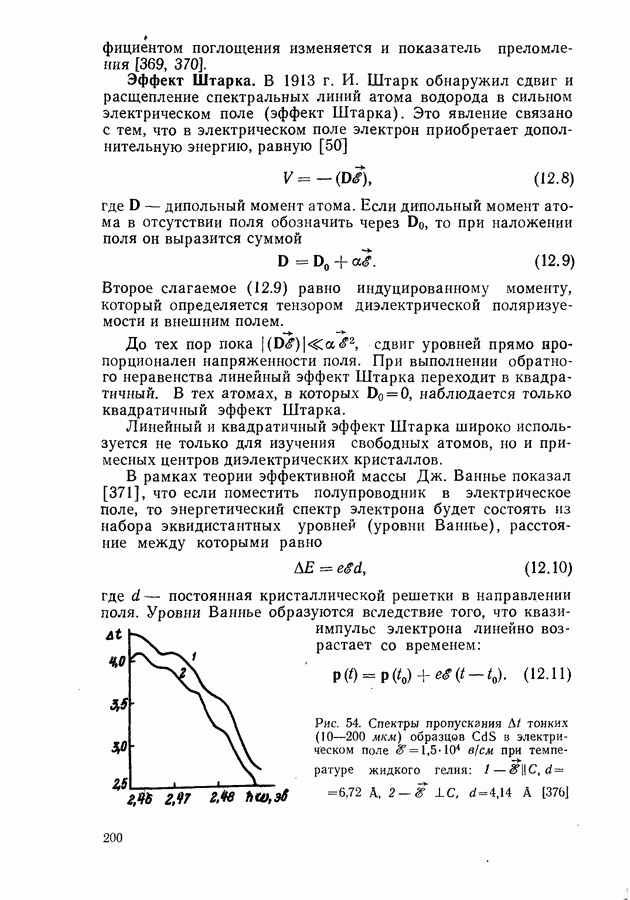
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
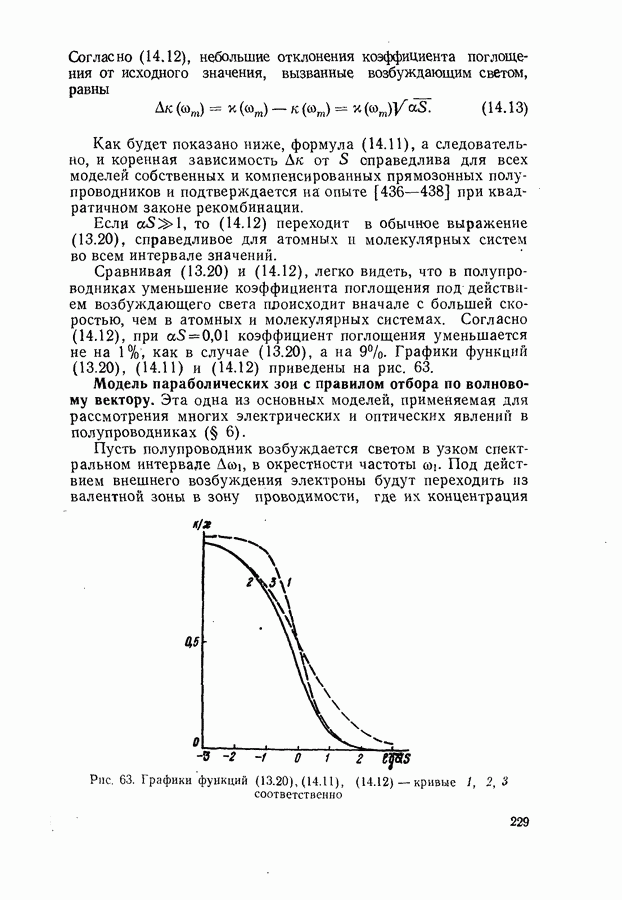
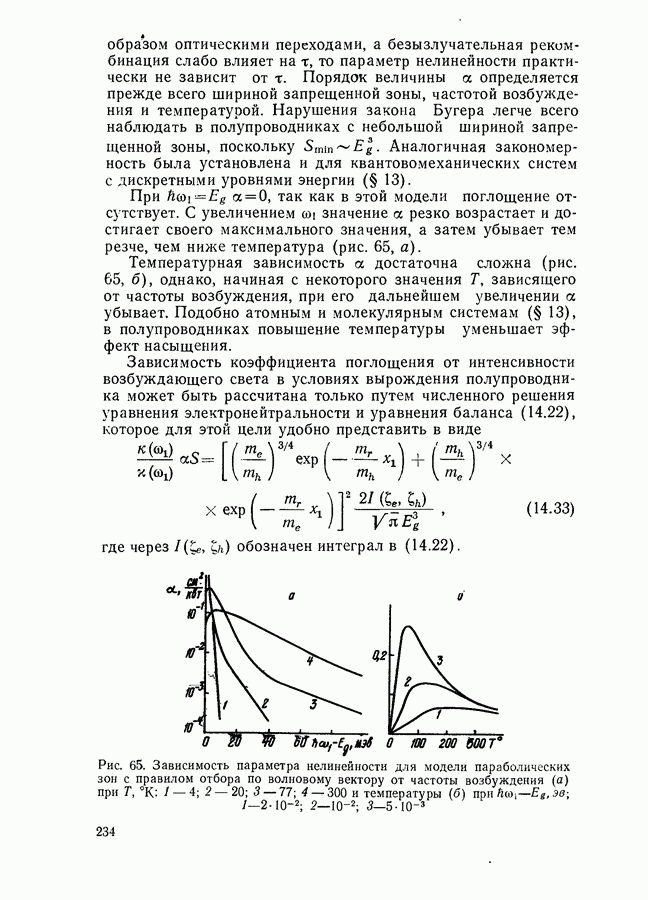
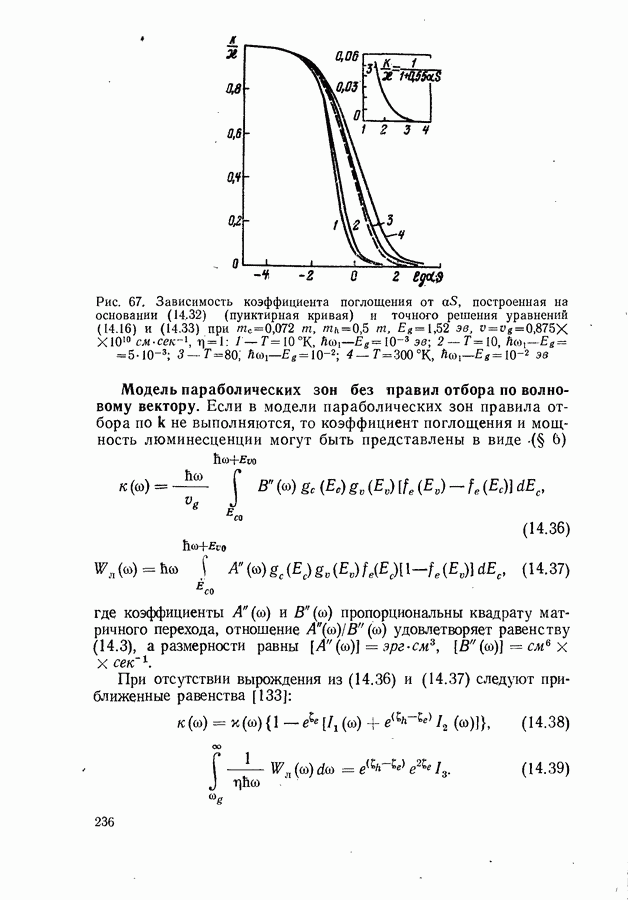
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
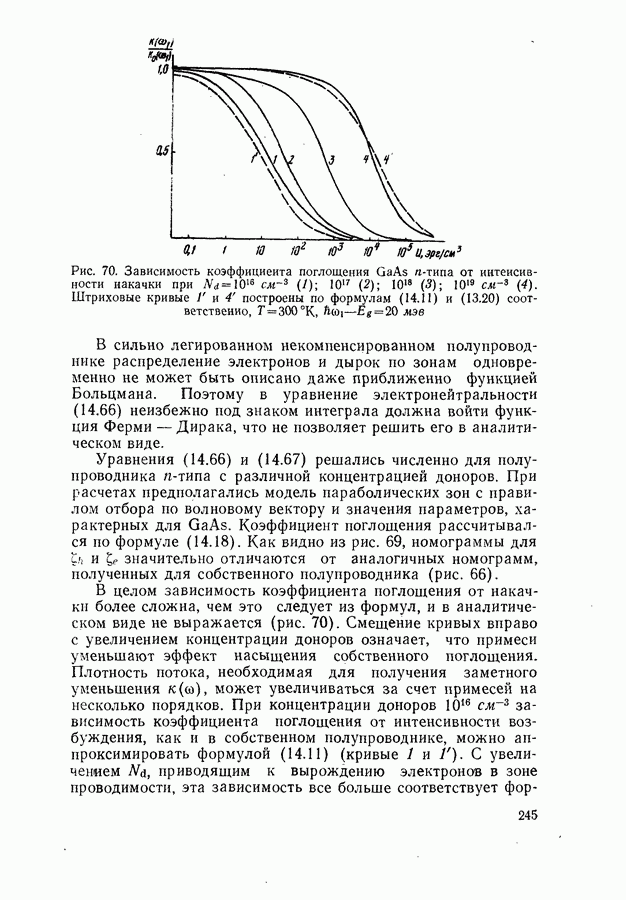
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
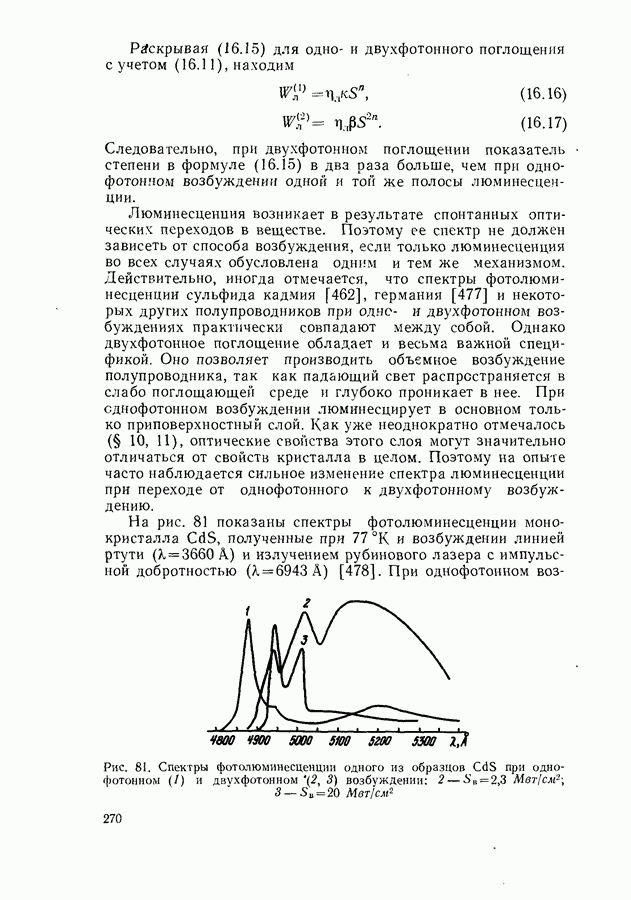
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
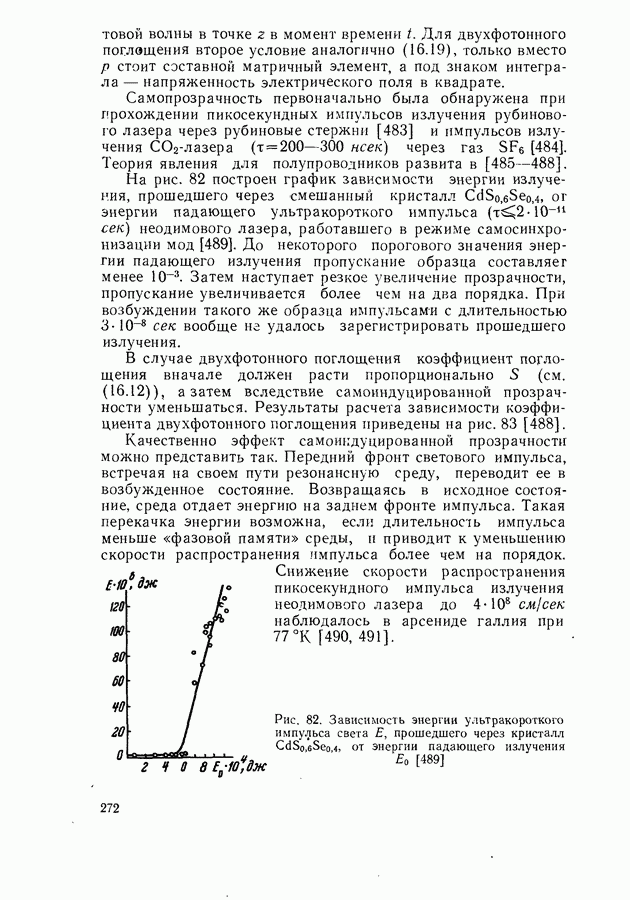
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
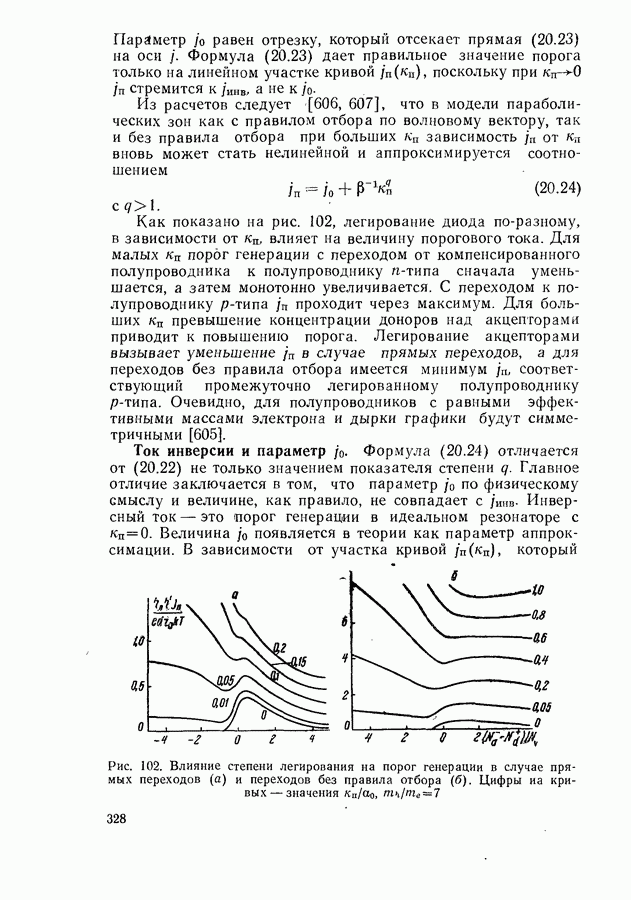
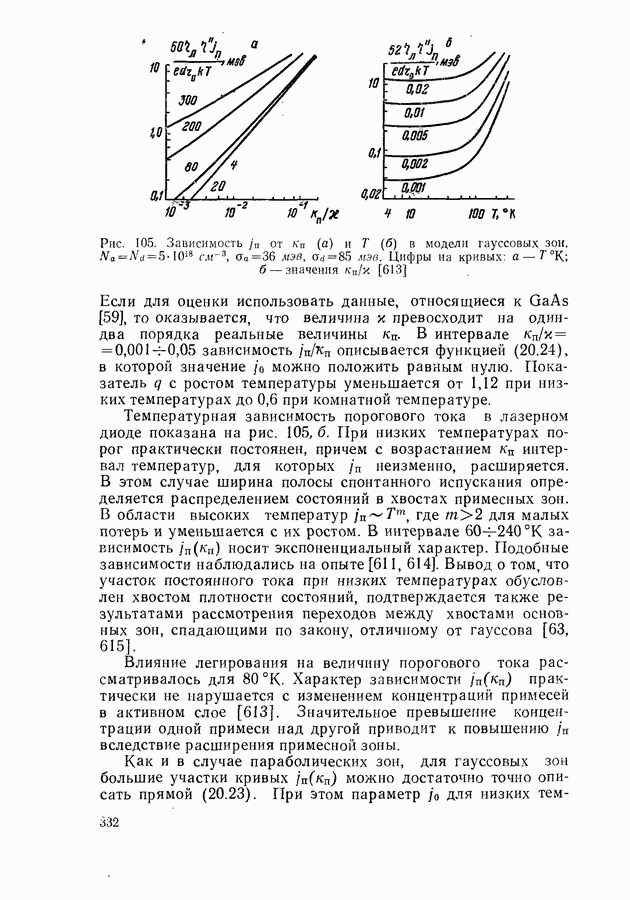
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
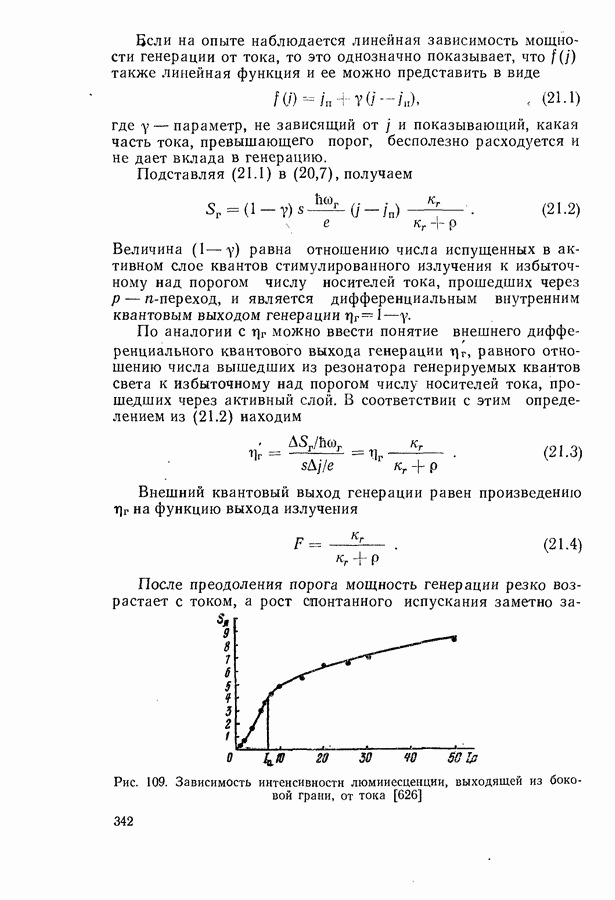
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
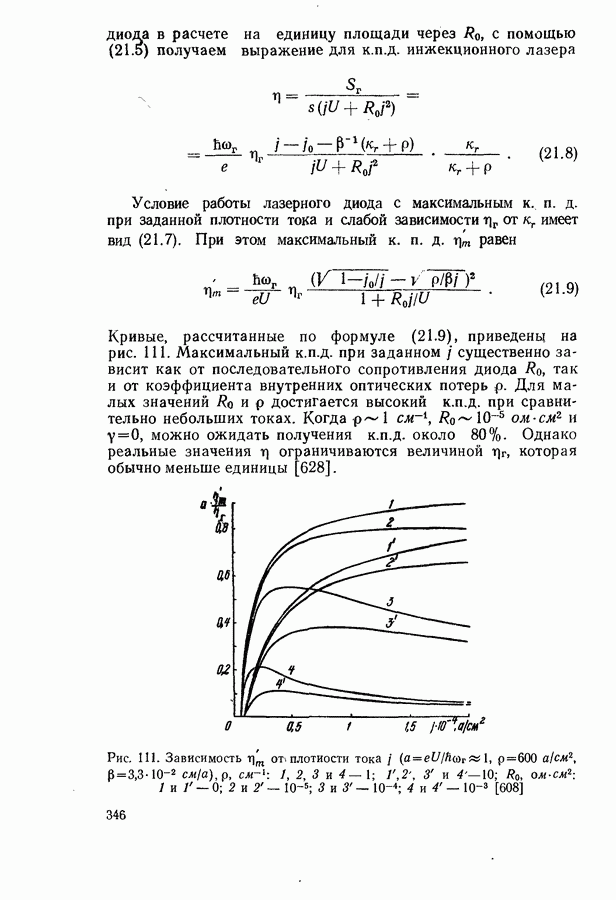
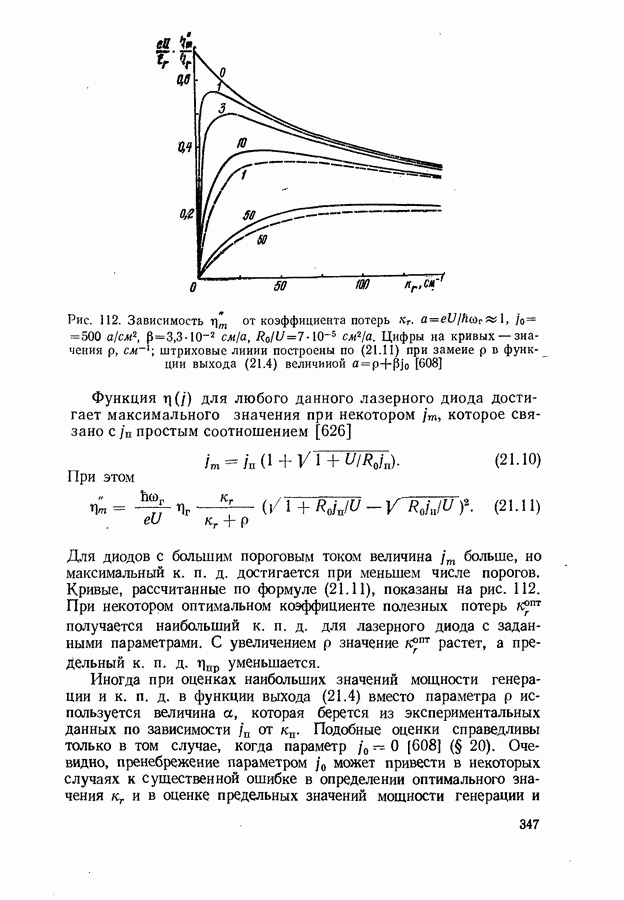
- Оптимальный режим генерации.
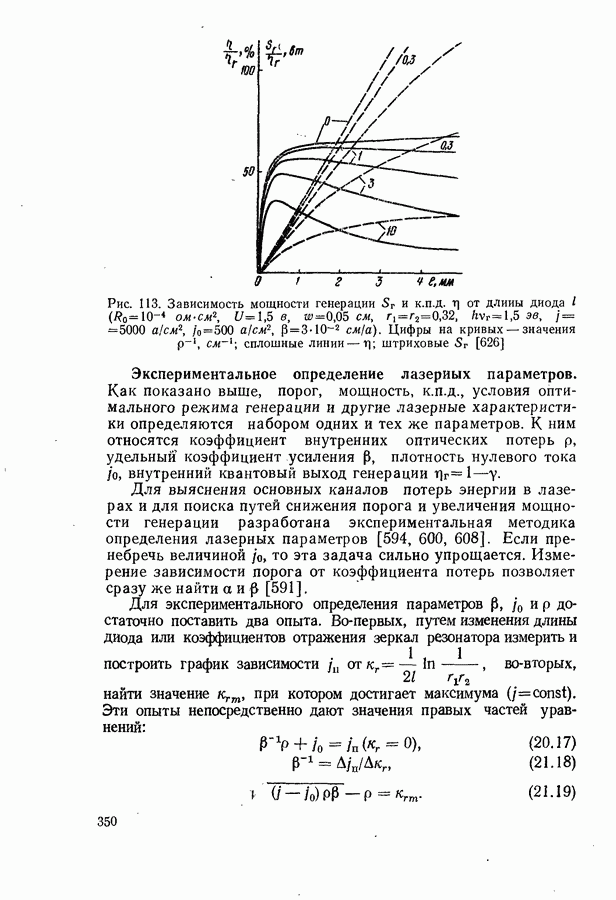
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
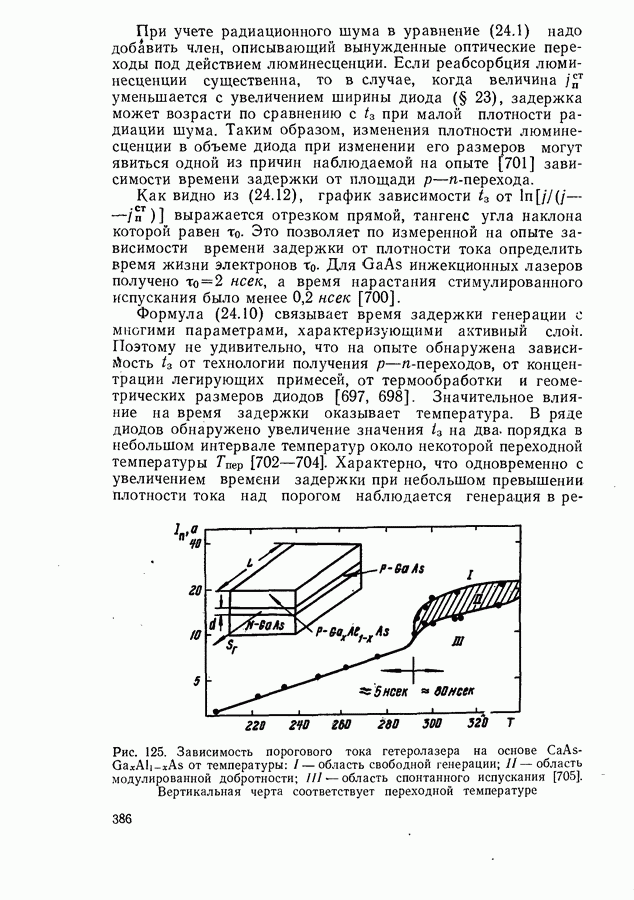
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
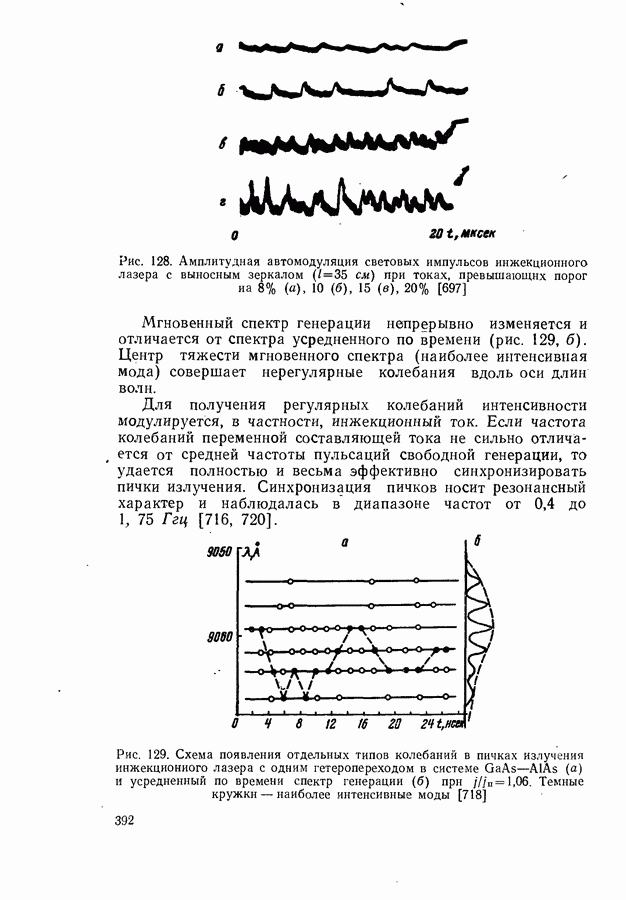
- Амплитудная и частотная автомодуляция излучения.
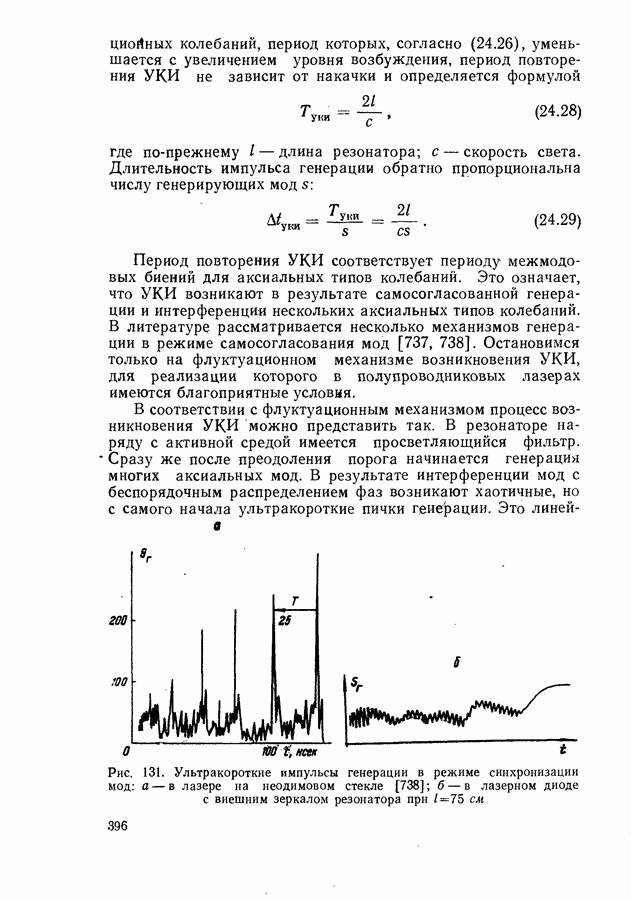
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
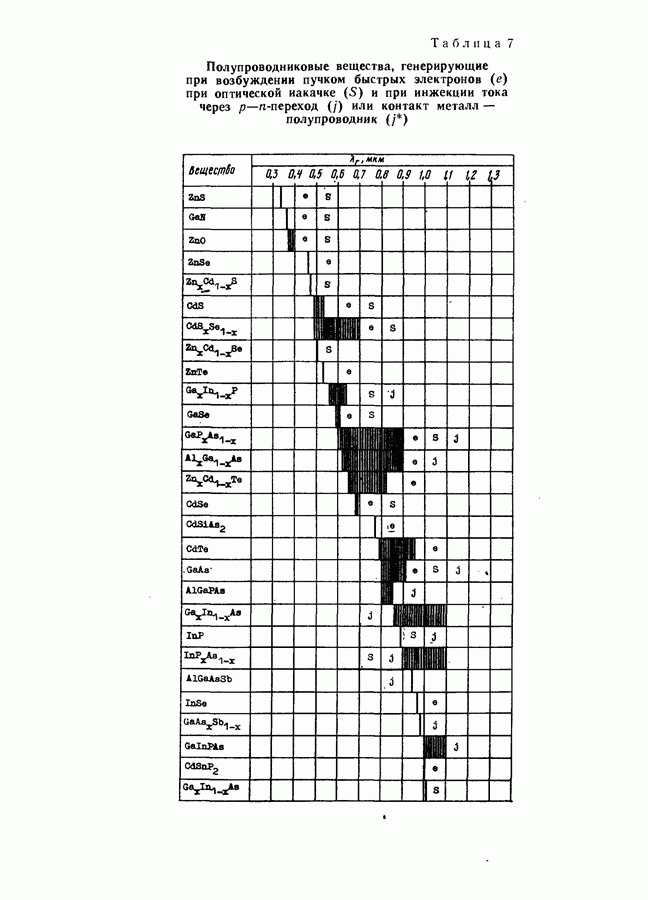
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
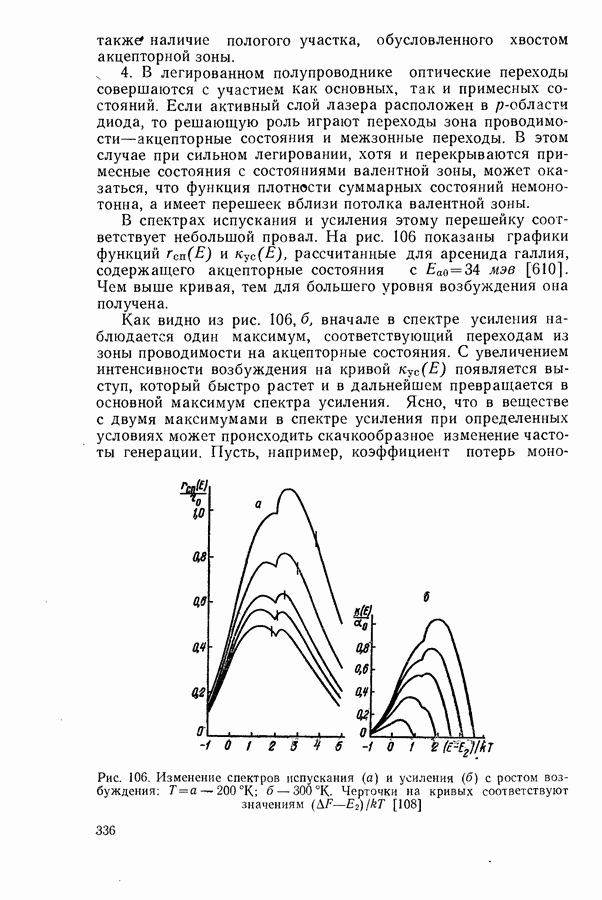
- Экситонный механизм генерации излучения.
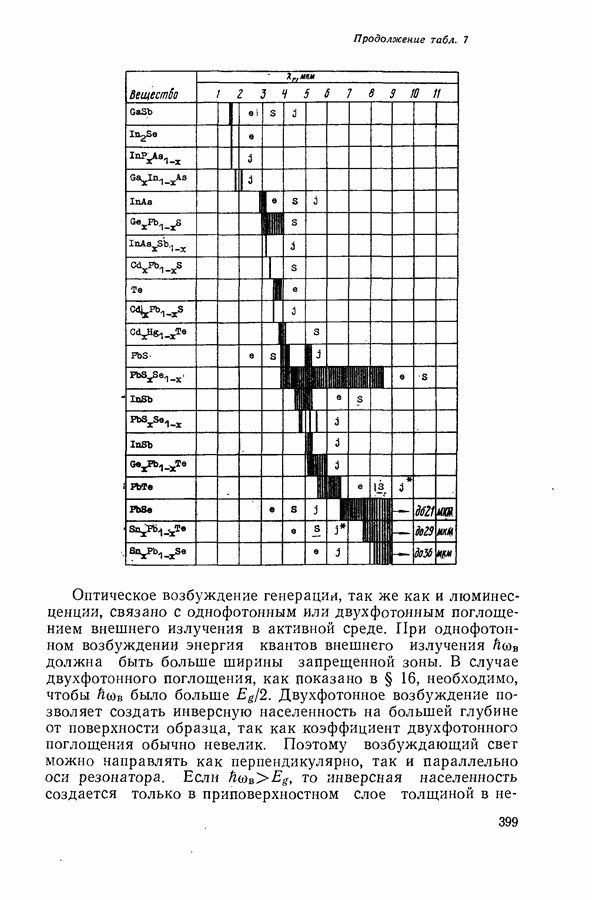
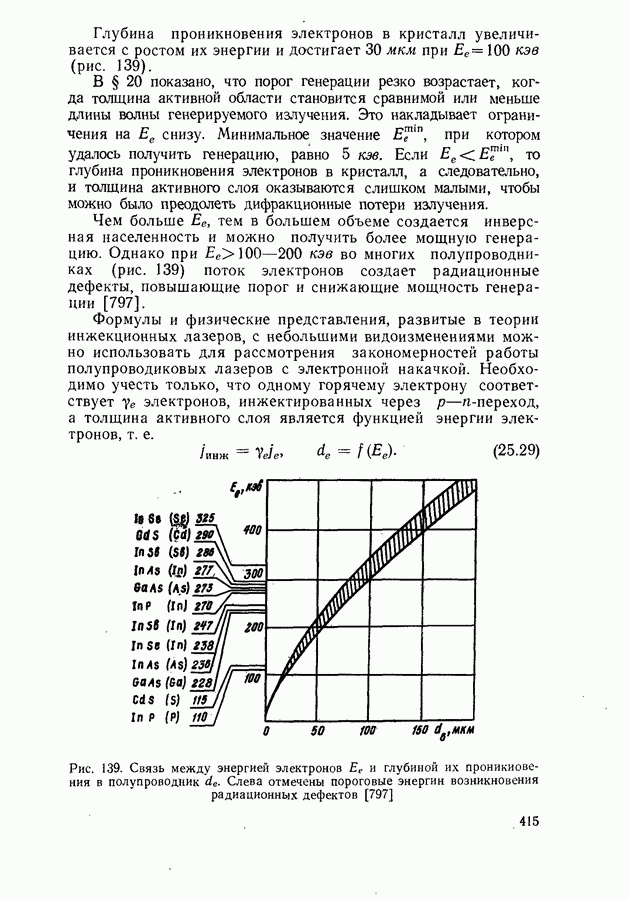
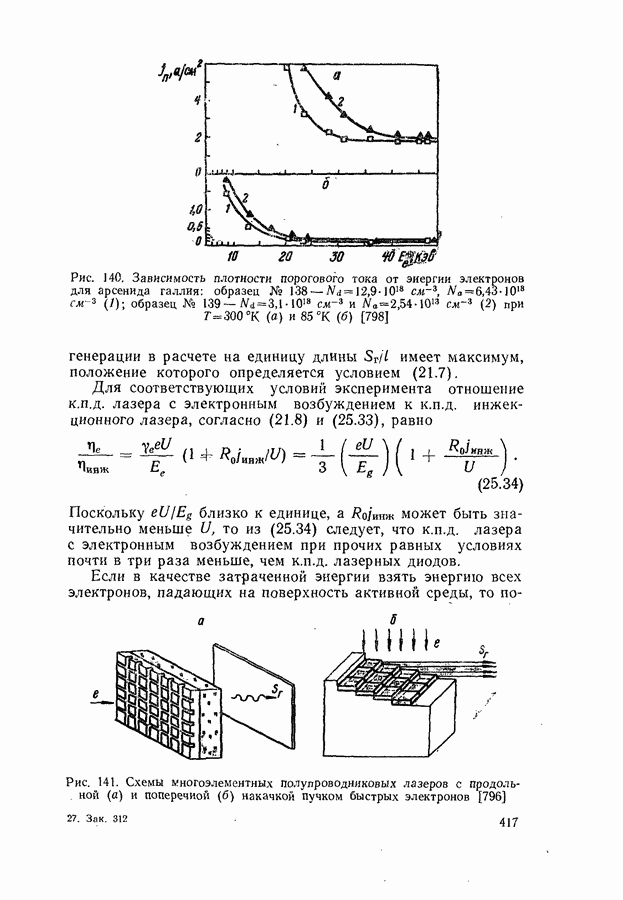
- Возбуждение генерации пучком быстрых электронов.