| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Линейная цепочка, состоящая из атомов двух сортов.
Если около каждого атома рассмотренной выше линейной цепочки разместить атом другого сорта с массой  то получится решетка с двумя атомами в элементарной ячейке. Номера новых атомов обозначим
то получится решетка с двумя атомами в элементарной ячейке. Номера новых атомов обозначим  Расстояние между соседними атомами
Расстояние между соседними атомами  равно постоянной решетки а. Коэффициенты квазиупругих сил между атомами
равно постоянной решетки а. Коэффициенты квазиупругих сил между атомами  обозначим
обозначим  а между атомами
а между атомами 
Тогда уравнения движения  атомов по аналогии с (4.8) представим в виде [38]:
атомов по аналогии с (4.8) представим в виде [38]:

Здесь по-прежнему учитывается взаимодействие только между соседними атомами: атом с номером  взаимодействует с
взаимодействует с  атомами, а атом
атомами, а атом 
Если подставить в (4.25) уравнения бегущих волн с одинаковыми волновыми векторами  и частотами
и частотами  но разными амплитудами
но разными амплитудами

получим после сокращения на 

Разделив (4.27) на (4.28), приходим к биквадратному уравнению относительно 

Если ввести обозначения

то решение (4.29) можно представить в виде

При любых значениях отношений  величина
величина  поэтому формула (4.30) дает два вещественных значения частоты колебаний для каждого значения волнового вектора
поэтому формула (4.30) дает два вещественных значения частоты колебаний для каждого значения волнового вектора  Если
Если  стремится к нулю, то
стремится к нулю, то  в то время как
в то время как  (рис. 15). По этому признаку все типы колебаний кристаллической решетки делятся на оптические
(рис. 15). По этому признаку все типы колебаний кристаллической решетки делятся на оптические  и акустические
и акустические  а кривые дисперсии соответственно называются оптическими и акустическими ветвями колебаний.
а кривые дисперсии соответственно называются оптическими и акустическими ветвями колебаний.
Как видно из (4.30), при всех значениях параметров частота оптических колебаний  больше частоты акустических колебаний
больше частоты акустических колебаний  При малых
При малых  различие особенно велико, а при больших
различие особенно велико, а при больших  частоты
частоты  сближаются.
сближаются.
Однако различие между оптическими и акустическими типами колебаний не сводится к количественно разным значениям частот  и Оно лежит глубже и связано с качественно. разным характером самого колебательного процесса. Это становится очевидным при рассмотрении некоторых частных случаев.
и Оно лежит глубже и связано с качественно. разным характером самого колебательного процесса. Это становится очевидным при рассмотрении некоторых частных случаев.

Рис. 15. Кривые (ветви) дисперсии для оптических  и акустических
и акустических  колебаний линейной цепочки, состоящей из атомов двух сортов
колебаний линейной цепочки, состоящей из атомов двух сортов
Согласно (4.26) и (4.27), отношение смещений соседних атомрв, принадлежащих к одной элементарной ячейке, равно

Для предельно длинных волн  Подставляя в (4.31) значения параметров, получим для акустических и оптических колебаний соответственно
Подставляя в (4.31) значения параметров, получим для акустических и оптических колебаний соответственно

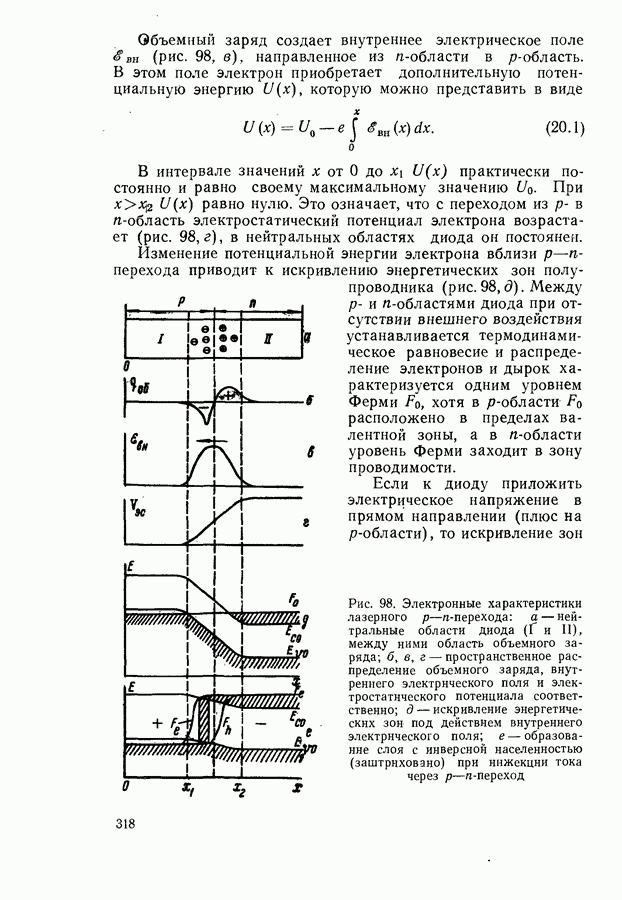
Из (4.32) следует, что в бесконечно длинной волне акустических колебаний все атомы движутся синхронно вправо или влево и смещения из положения равновесия для всех частиц равны. Синхронность смещения всех атомов одной элементарной ячейки сохраняется и для более коротких волн акустических колебаний. Это характерно для колебаний звуковых волн. Поэтому такой тип колебаний назван акустическим. При оптических колебаниях атомы одной ячейки либо движутся навстречу, либо удаляются друг от друга, а центр масс ячейки остается неподвижным, так как  В этом случае может происходить электрическая поляризация кристалла и возникнуть переменный дипольный момент, приводящий к поглощению или испусканию электромагнитных волн инфракрасного диапазона. Это послужило основанием назвать указанные колебания оптическими. Однако в принципе, если кристалл состоит из нейтральных атомов, оптические колебания могут и не сопровождаться появлением электрического дипольного момента.
В этом случае может происходить электрическая поляризация кристалла и возникнуть переменный дипольный момент, приводящий к поглощению или испусканию электромагнитных волн инфракрасного диапазона. Это послужило основанием назвать указанные колебания оптическими. Однако в принципе, если кристалл состоит из нейтральных атомов, оптические колебания могут и не сопровождаться появлением электрического дипольного момента.
Рассмотрим теперь отношение отклонений (4.31) в случае предельно коротких длин волн, для которых 
С учетом (4.30) формула (4.31) преобразуется к виду

Если  то числитель равен нулю, а знаменатель либо обращается в нуль, либо равен
то числитель равен нулю, а знаменатель либо обращается в нуль, либо равен  Он отличен от
Он отличен от
нуля для оптических колебаний, если  а для акустических при
а для акустических при  Следовательно, при оптических колебаниях тяжелые атомы неподвижны, а колеблются легкие атомы. В акустической волне наоборот, смещаются тяжелые атомы, а легкие неподвижны. Такой же результат получается, если рассмотреть случай, когда знаменатель обращается в ноль и необходимо раскрывать неопределенность
Следовательно, при оптических колебаниях тяжелые атомы неподвижны, а колеблются легкие атомы. В акустической волне наоборот, смещаются тяжелые атомы, а легкие неподвижны. Такой же результат получается, если рассмотреть случай, когда знаменатель обращается в ноль и необходимо раскрывать неопределенность 
В другом частном случае, когда  из (4.33) находим
из (4.33) находим

и, следовательно, в оптической волне с наименьшим значением  атомы движутся в противофазе, а в акустической волне — в фазе.
атомы движутся в противофазе, а в акустической волне — в фазе.
Численные оценки показывают [80], что частота акустических колебаний изменяется от  до 1013 гц и только незначительная их часть
до 1013 гц и только незначительная их часть  гц) приходится на звуковые волны.
гц) приходится на звуковые волны.
Рассмотренные оптические и акустические колебания называются продольными, потому что смещения атомов в них происходит вдоль направления распространения волны. Кроме продольных имеются и поперечные колебания, при которых атомы смещаются по направлениям, перпендикулярным к направлению распространения волны. Так же как и продольные, поперечные колебания делятся на оптические и акустические [82]. При оптических колебаниях атомы одной элементарной ячейки движутся в противофазе, в акустических колебаниях они смещаются синхронно (рис. 16). Поперечные

Рис. 16. Типы колебаний линейной цепочки: а — цепочка в положении равновесия;  продольные оптические колебания; в — продольные акустические колебания;
продольные оптические колебания; в — продольные акустические колебания;  поперечные оптические колебания;
поперечные оптические колебания;  поперечные акустические колебания
поперечные акустические колебания
колебания во всех направлениях можно свести к колебаниям в двух взаимно перпендикулярных плоскостях.
Гармонические колебания трехмерной решетки. Метод расчета, использованный при рассмотрении линейных цепочек, может быть применен и для изучения колебаний реальных кристаллов. Пусть кристалл состоит из большого числа  элементарных ячеек и в каждой ячейке содержится
элементарных ячеек и в каждой ячейке содержится  атомов. Массы атомов равны тк, где номер атома
атомов. Массы атомов равны тк, где номер атома  Проекцию смещения
Проекцию смещения  атома
атома  ячейки из положения равновесия на ось а обозначим через
ячейки из положения равновесия на ось а обозначим через  Индекс
Индекс  и относится к трем осям координат
и относится к трем осям координат 
В гармоническом приближении предполагается, что колебания атомов по всем  степеням свободы происходят независимо друг от друга и упругие силы, возникающие при смещении атома из положения равновесия, прямо пропорциональны величинам смещений
степеням свободы происходят независимо друг от друга и упругие силы, возникающие при смещении атома из положения равновесия, прямо пропорциональны величинам смещений  Это условие выполняется тем лучше, чем меньше амплитуды колебаний, в чем легко убедиться, если представить потенциальную функцию кристалла в виде разложения в ряд по степеням
Это условие выполняется тем лучше, чем меньше амплитуды колебаний, в чем легко убедиться, если представить потенциальную функцию кристалла в виде разложения в ряд по степеням  ].
].
Обозначая коэффициенты квазиупругих сил через  по аналогии с предыдущим, получим систему
по аналогии с предыдущим, получим систему  уравнений для такого же числа неизвестных икпа [83, 84]
уравнений для такого же числа неизвестных икпа [83, 84]

Уравнения (4.25) входят в (4.35) как частный случай при  В этой системе уравнений, как и ранее, учитывается взаимодействие только ближайших атомов.
В этой системе уравнений, как и ранее, учитывается взаимодействие только ближайших атомов.
Решение системы ищется в виде бегущих волн:

Переход к трехмерному случаю требует введения волнового вектора в общем виде, где  единичный вектор нормали
единичный вектор нормали

к плоской волне, длина которой равна  Величины являются проекциями на оси
Величины являются проекциями на оси  комплексной амплитуды колебаний
комплексной амплитуды колебаний  атома
атома 
Так же как и для одномерного случая, легко показать, что прибавление к волновому вектору  вектора обратной решетки
вектора обратной решетки  определяемого формулой (1.2), не изменяет волновую функцию (4.36). Поэтому произведение
определяемого формулой (1.2), не изменяет волновую функцию (4.36). Поэтому произведение  можно рассматривать только в первой зоне Бриллюэна
можно рассматривать только в первой зоне Бриллюэна  (см. (2.40а)).
(см. (2.40а)).
Подставляя (4.36) и (4.35) и сокращая на  находим
находим

где

Если ввести символы Кронекера  равные единице при
равные единице при  и равные нулю при
и равные нулю при  то (4.38) можно представить в виде
то (4.38) можно представить в виде

Система  дифференциальных уравнений (4.35) свелась к системе
дифференциальных уравнений (4.35) свелась к системе  однородных алгебраических уравнений. Эта система имеет ненулевое решение, если ее определитель равен нулю:
однородных алгебраических уравнений. Эта система имеет ненулевое решение, если ее определитель равен нулю:

Равенство (4.41) есть характеристическое или вековое  уравнение степени
уравнение степени  относительно квадрата частоты колебаний
относительно квадрата частоты колебаний 
В общем случае уравнение  степени имеет
степени имеет  различных корня, определяющих частоту колебаний как функцию волнового вектора (закон дисперсии):
различных корня, определяющих частоту колебаний как функцию волнового вектора (закон дисперсии):  где
где  Геометрически зависимость
Геометрически зависимость  от
от  представляется как гиперповерхность в четырехмерном пространстве. Форма этой поверхности зависит от симметрии кристалла, типа химической связи и числа атомов в элементарной ячейке. Сечение всех гиперповерхностей плоскостью в
представляется как гиперповерхность в четырехмерном пространстве. Форма этой поверхности зависит от симметрии кристалла, типа химической связи и числа атомов в элементарной ячейке. Сечение всех гиперповерхностей плоскостью в  пространстве изображается
пространстве изображается  кривыми линиями, форма которых зависит от ориентации секущей плоскости.
кривыми линиями, форма которых зависит от ориентации секущей плоскости.

Рис. 17. Кривые дисперсии для колебаний решетки йодистого натрия (а) и алмаза (б)
Учет симметрии кристаллов показывает, что некоторые ветви колебаний могут быть вырождены, тогда их общее число меньше  Например, в линейной цепочке, состоящей из атомов двух сортов, поперечные акустические и оптические колебания двукратно вырождены.
Например, в линейной цепочке, состоящей из атомов двух сортов, поперечные акустические и оптические колебания двукратно вырождены.
Среди  ветвей колебаний 3 всегда принадлежат акустическим ветвям: одна продольная и две (или одна двукратно вырожденная) поперечные. Частота акустических колебаний кристалла
ветвей колебаний 3 всегда принадлежат акустическим ветвям: одна продольная и две (или одна двукратно вырожденная) поперечные. Частота акустических колебаний кристалла  как и непрерывной упругой среды, стремится к нулю при
как и непрерывной упругой среды, стремится к нулю при  и в области малых значений
и в области малых значений  прямо пропорциональна
прямо пропорциональна 

где  коэффициент пропорциональности, зависящий только от направления вектора
коэффициент пропорциональности, зависящий только от направления вектора  Если в элементарной ячейке кристалла (например, натрия, калия, рубидия) содержится один атом, то
Если в элементарной ячейке кристалла (например, натрия, калия, рубидия) содержится один атом, то  и никаких других колебаний решетки, кроме акустических, не будет. Это подтверждается на опыте [77].
и никаких других колебаний решетки, кроме акустических, не будет. Это подтверждается на опыте [77].
Во всех кристаллах, для которых  может быть
может быть  оптических ветвей колебаний. Полупроводниковые кристаллы элементов IV группы (алмаз, кремний, германий, серое олово) имеют кристаллическую решетку типа алмаза, а соединения
оптических ветвей колебаний. Полупроводниковые кристаллы элементов IV группы (алмаз, кремний, германий, серое олово) имеют кристаллическую решетку типа алмаза, а соединения  типа цинковой обманки. И в том и в другом случае на элементарную ячейку приходится два либо одинаковых, либо разных атома. В таких кристаллах будет
типа цинковой обманки. И в том и в другом случае на элементарную ячейку приходится два либо одинаковых, либо разных атома. В таких кристаллах будет
3 акустических и 3 оптических ветви колебаний.
На рис. 17 приведены экспериментальные кривые дисперсии для колебаний решетки йодистого натрия и алмаза [86].
Обозначения ветвей колебаний общепринятые: LO и ТО - продольные и поперечные оптические, LA и ТА - продольные и поперечные акустические. Сокращения образованы первыми буквами английских слов: optical - оптический, acoustic - акустический, longitudinal - продольный, transversal - поперечный.
Как видно из рисунка, в обоих случаях поперечные оптические и акустические колебания двукратно вырождены. В йодистом натрии оптические и акустические ветви разделены запрещенной зоной. В алмазе на границе зоны Бриллюэна в направлении [100] ТО и LA ветви перекрываются. Это связано с тем, что в элементарной ячейке кристаллической решетки алмаза находятся два одинаковых атома.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
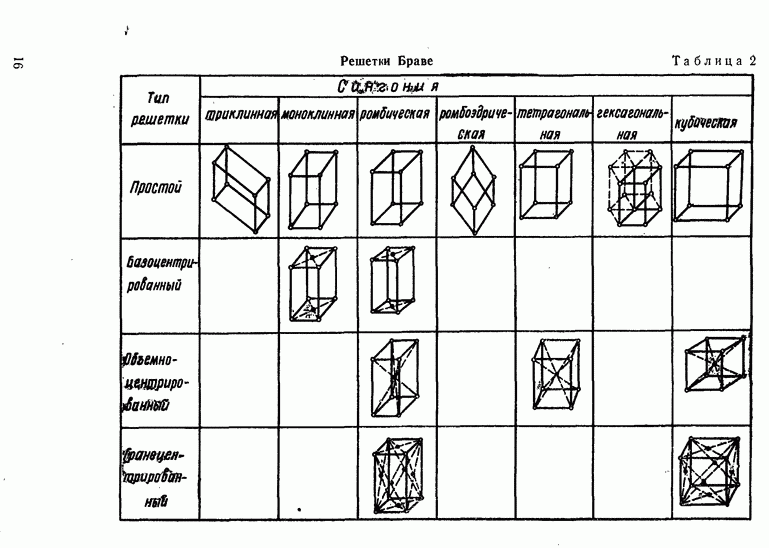
- Классификация кристаллических решеток.
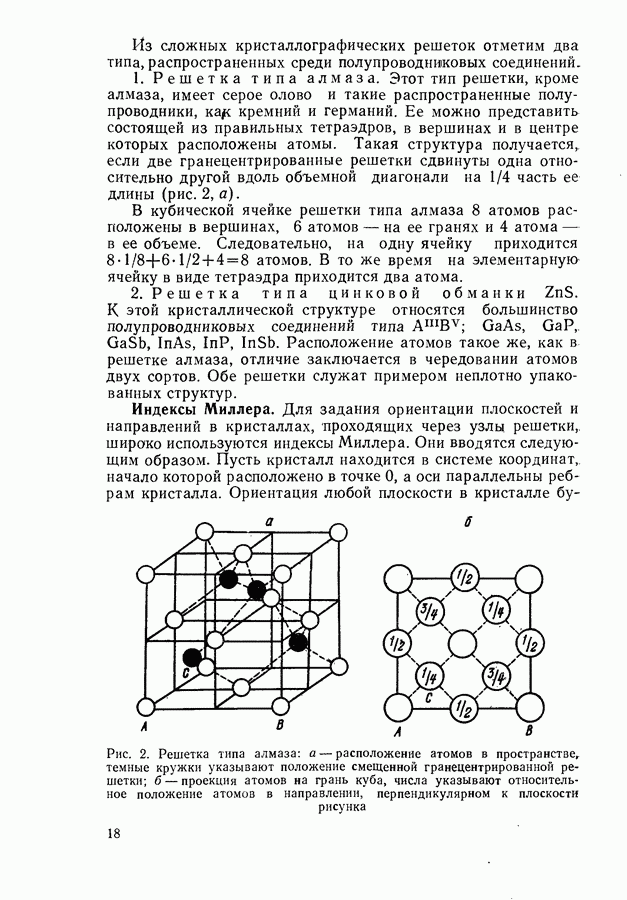
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
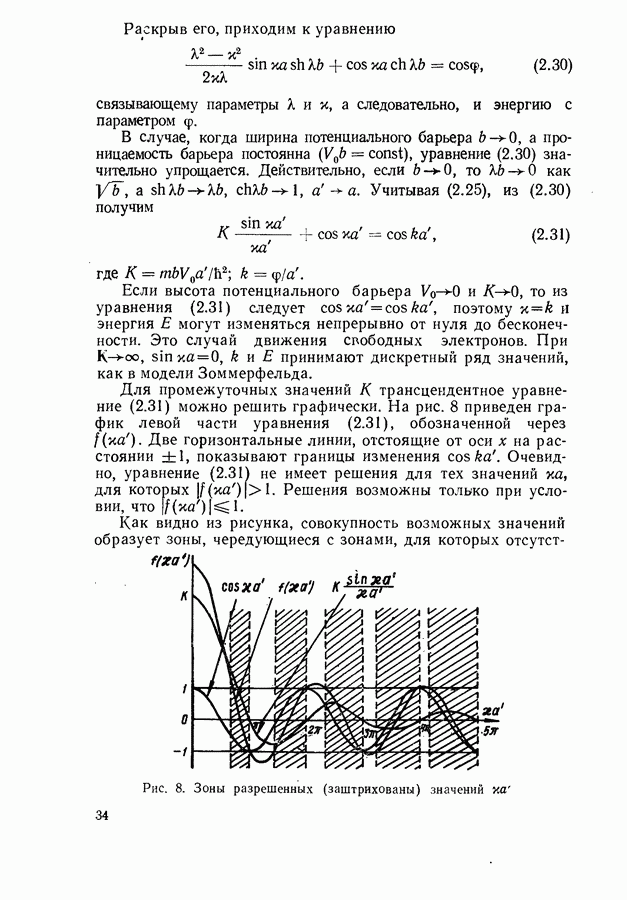
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
- Эффект Келдыша-Франца.
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
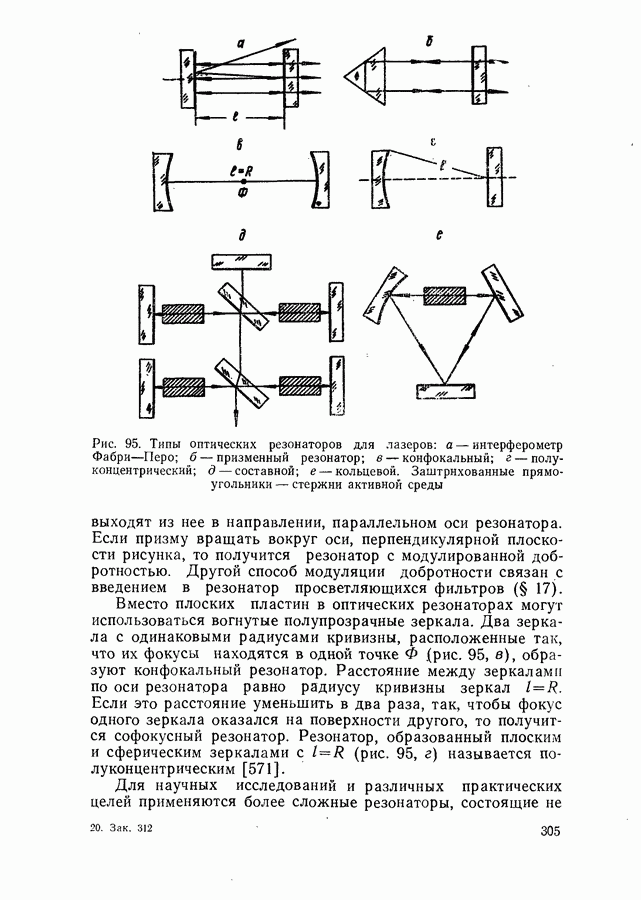
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
- Возбуждение генерации пучком быстрых электронов.