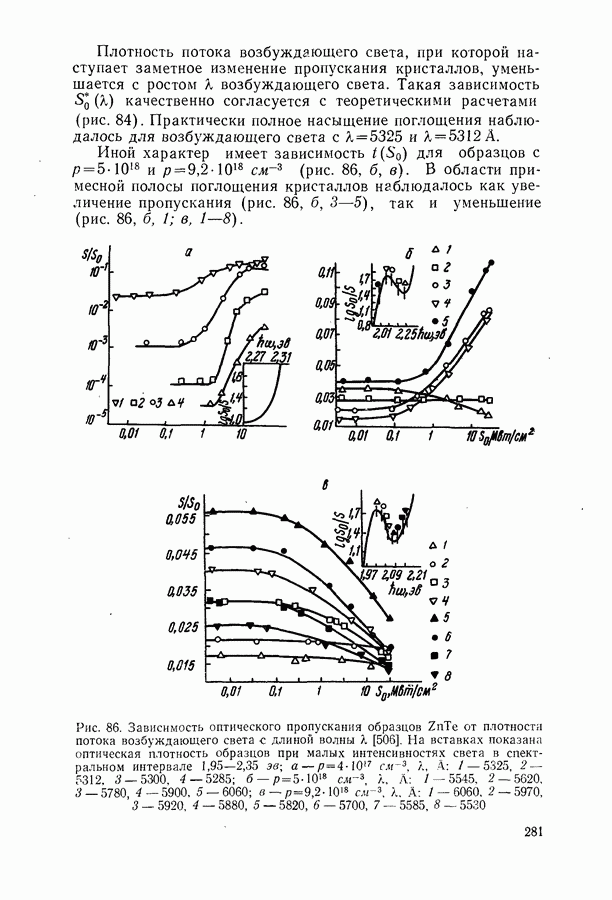
§ 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ

Типы электромагнитных колебаний в оптическом резонаторе.

Индикатриса и спектр излучения оптического квантового генератора определяются типами электромагнитных колебаний (модами), которые устанавливаются в оптическом резонаторе. Поэтому расчет спектральных и пространственных характеристик излучения, выходящего из резонатора, сводится в основном к решению уравнений Максвелла для нелинейной оптической среды с граничными условиями, определяемыми формой и поверхностью активного вещества и зеркалами резонатора.

Как правило, найти точные решения уравнений Максвелла для реального квантового генератора не удается. Однако свойства лазерного излучения можно изучить на основании решения совокупности упрощенных задач.

В качестве моделей резонаторов, поддающихся теоретическому расчету, рассматриваются бесконечно протяженные плоскопараллельные слои и волноводные трубки [497, 602], открытые резонаторы без боковых поверхностей и идеальные резонаторы с идеально проводящими металлическими стенками, наполненные диэлектриком с линейными оптическими свойствами и т. п. [636—638].

Простым примером идеального резонатора служит прямоугольный ящик, коэффициент отражения стенок которого равен единице. Если вещество, заполняющее резонатор, характеризуется постоянными значениями диэлектрической и магнитной проницаемости, то решения уравнения Максвелла для такого резонатора находятся легко.

Проекции на оси амплитуды электрического вектора электромагнитной волны

являющейся частным решением уравнений Максвелла

при токе смещения и плотности зарядов выражаются формулами

Здесь постоянные величины.

На поверхности стенок резонатора электрическое поле имеет только нормальную составляющую, а магнитное поле — только тангенциальную составляющую [638]. Если нормаль к поверхности, то граничное условие можно представить в виде

Из граничных условий следует, что волновые векторы принимают только дискретный ряд значений

где длина ребер прямоугольного резонатора вдоль осей а числа принимают значения 0, ±1, ±2, ...

Следовательно, в прямоугольном идеальном резонаторе, как и в резонаторах всех других типов, устанавливается дискретный набор электромагнитных колебаний с частотами

Последняя формула получена путем подстановки (22.5) в выражение для квадрата волнового вектора

вытекающее из уравнений Максвелла.

Одна из целей, преследуемых при создании оптических квантовых генераторов, заключается в том, чтобы получить остронаправленный луч света. Достижению этой цели способствует вытянутая форма резонатора, когда, например, значительно больше (способ получения направленного луча, где это условие необязательно, будет рассмотрен ниже).

С учетом выделенного направления в резонаторе, в рассматриваемом примере оси электромагнитные волны в резонаторе можно разделить на две группы: поперечно-электрические -волны) и поперечно-магнитные (ТМ-волны,

В электрическом векторе -волны отсутствует составляющая вдоль оси т. е. Колебания электрического вектора происходят в плоскости, перпендикулярной оси (ср. ТО- и ТА-фононы, § 4). Для ТМ-волн, наоборот, Вектор магнитного поля лежит в плоскости, перпендикулярной оси По наличию продольной составляющей -волны иногда называются магнитными, а ТМ-волны — электрическими.

Кроме указанных двух типов могут быть еще волны вырожденного типа, у которых отсутствует продольная составляющая как электрического, так и магнитного поля (ТЕМ-волны).

Многие характеристики излучения газовых и твердотельных лазеров хорошо описываются с помощью модели открытого резонатора, в которой не учитывается влияние боковых

Рис. 116. Распределение энергии в плоскости ТЕМ-волн оптического квантового генератора со сферическими зеркалами [640]

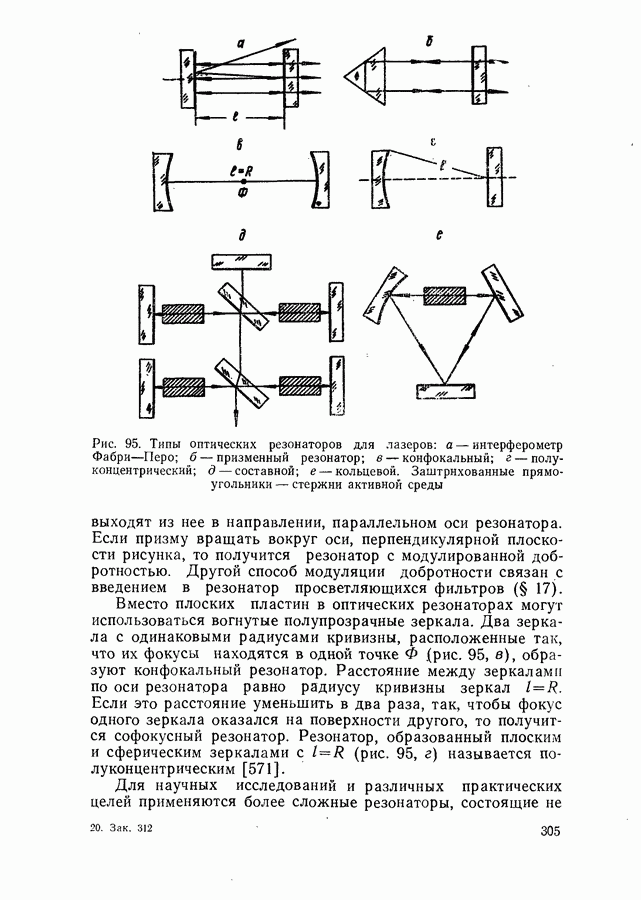
поверхностей активной среды, а граничные условия формулируются только для зеркал резонатора. Простейшим из таких резонаторов является интерферометр Фабри — Перо, состоящий из двух плоскопараллельных зеркал. А. Фокс и Ли показали, что в открытом резонаторе также устанавливаются вполне определенные типы колебаний, хотя плоская волна существовать в нем не может из-за дифракции на краях зеркал [639]. Расчет по методу А. Фокса и Ли основан на последовательном и многократном применении принципа Гюйгенса для электромагнитных волн.

Распределение энергии в плоскости для ТЕМ-волн легко экспериментально наблюдать в газовых лазерах. Особенно четкая картина получается для низших типов колебаний, т. е. для волн с небольшим значением чисел На рис. 116 приведены фотографии структуры поля излучения лазера со сферическими зеркалами, полученные в работе [640]. Ось х направлена горизонтально, а у — вертикально. Как видно из рисунка, только при нулевом типе колебаний ТЕМ вся энергия генерируемого излучения сосредоточена в одном центральном луче. Уже для поле излучения имеет довольно сложную структуру.

Все типы колебаний с волновым вектором параллельным оси резонатора называются аксиальными (осевыми) типами колебаний, или модами. ТЕМ-волны, у которых хотя бы один индекс или не равен нулю, относятся к неаксиальным (угловым) модам, поскольку у них волновой вектор направлен под некоторым углом к оси резонатора.

Ратояние в спектре излучения между ближайшими осевыми модами легко рассчитать, исходя из интерференционного условия генерации (19.14), вытекающего из граничных условий для уравнений Максвелла.

Если длины волн в вакууме, а соответствующие показатели преломления активной среды в резонаторе, то на основании (19.14) имеем

где целые числа; I — расстояние между зеркалами. Для соседних в спектре излучения типов аксиальных волн поскольку

Так как в пределах изменяется незначительно, то справедлива формула

Вычитая первое равенство (22.8) из второго и учитывая (22.9), находим

Обычно поэтому и индексы около можно опустить:

Для из (22.11) следует С увеличением длины резонатора уменьшается обратно пропорционально Справедливость формулы (22.11) подтверждена во многих экспериментальных работах.