| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
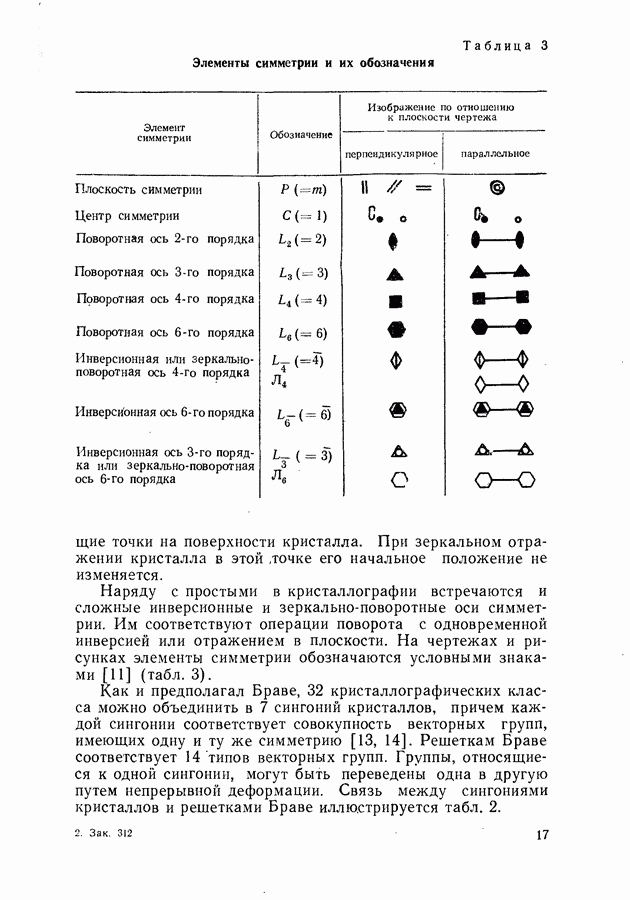
Прямая и обратная решетки.
При соблюдении определенных условий кристаллы растут в виде правильных многогранников. Плоскости, ограничивающие кристалл, называются его гранями, линии, разделяющие грани, — ребрами, а узловые точки, в которых пересекаются несколько граней, — вершинами. Из рентгеноструктурного анализа и из многих других опытов следует, что атомы и молекулы располагаются в кристалле строго закономерно в определенном порядке. При этом существует некоторая элементарная ячейка, с помощью которой путем многократного повторения можно сложить весь кристалл. Следовательно, физические свойства идеального кристалла периодически повторяются. Только благодаря периодической структуре кристаллов оказалось практически возможным создание теории твердого тела, состоящего из огромного количества частиц.
В теории для описания физических свойств кристаллов вводится понятие прямой и обратной решетки. Под прямой решеткой понимают совокупность точек, радиусы-векторы которых равны [10]

где  три не лежащих в одной плоскости (некомпло-нарных) вектора, называемых трансляционными, масштабными или основными (базисными) векторами, или трансляционными периодами кристаллической решетки;
три не лежащих в одной плоскости (некомпло-нарных) вектора, называемых трансляционными, масштабными или основными (базисными) векторами, или трансляционными периодами кристаллической решетки;  целые положительные и отрицательные числа. При смещении всего кристалла как целого на любой из этих векторов он совмещается сам с собою.
целые положительные и отрицательные числа. При смещении всего кристалла как целого на любой из этих векторов он совмещается сам с собою.
Очевидно, при перемещении кристалла на любой из векторов  он также будет совмещаться сам с собой. Поэтому вектор
он также будет совмещаться сам с собой. Поэтому вектор  называется вектором трансляции.
называется вектором трансляции.
Параллелепипед, построенный на базисных векторах, имеет объем, равный  и называется элементарной ячейкой. Перемещая (транслируя) элементарую ячейку в направлениях
и называется элементарной ячейкой. Перемещая (транслируя) элементарую ячейку в направлениях  можно заполнить все пространство. В этом и заключается трансляционная симметрия кристаллов.
можно заполнить все пространство. В этом и заключается трансляционная симметрия кристаллов.
Решетка, определенная формулой (1.1), является чисто геометрическим построением, ее узлами служат математические точки. Каждому узлу соответствует один или целая группа атомов. Из трансляционной симметрии кристалла следует, что если около начала координат расположены какие-то атомы, то точно такие же атомы находятся около любого другого узла решетки.
Выбор решетки неоднозначен. Для одного и того же кристалла можно выбрать различными способами тройку базисных векторов а. Пусть, например, атомы в кристалле располагаются в вершинах и в центре куба. Тогда, помещая начало координат в вершине куба, векторы а? молено выбрать вдоль осей х, у, z. Элементарная ячейка будет иметь форму куба (рис. 1, а). Если же начало координат поместить в центре куба, а векторы  направить к его вершинам, то элементарная ячейка будет иметь форму ромбоэдрического параллелепипеда. Более того, элементарная ячейка может быть построена не на векторах
направить к его вершинам, то элементарная ячейка будет иметь форму ромбоэдрического параллелепипеда. Более того, элементарная ячейка может быть построена не на векторах  совершенно иным способом, в частности в виде ячейки Вигнера — Зейтца.
совершенно иным способом, в частности в виде ячейки Вигнера — Зейтца.
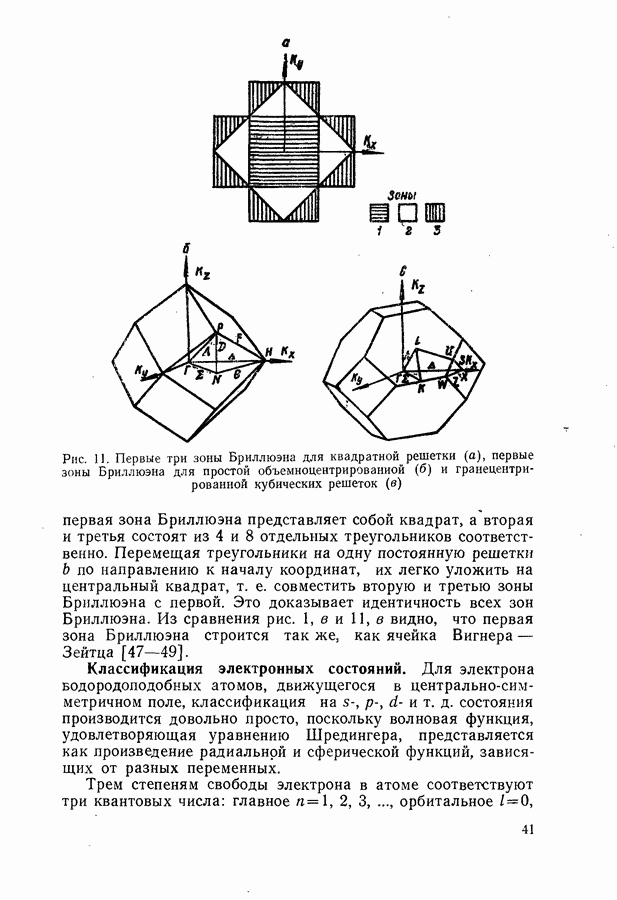
Соединим центр куба с его вершинами 8 отрезками. Через середину каждого отрезка проведем перпендикулярные к ним плоскости. Восемь таких плоскостей и ограничивают пространственную фигуру, называемую элементарной ячейкой Вигнера—Зейтца (рис. 1, в). Все пространство может быть заполнено такими ячейками, причем они обладают теми же элементами симметрии, что и куб. Ячейка Вигнера — Зейтца применяется для построения прямых решеток, однако она приобретает исключительно важное значение в пространстве обратной решетки, где она совпадает по существу с зоной Бриллюэна.
Как будет видно из дальнейшего, волновые функции, описывающие движение электрона в кристалле, отражают не

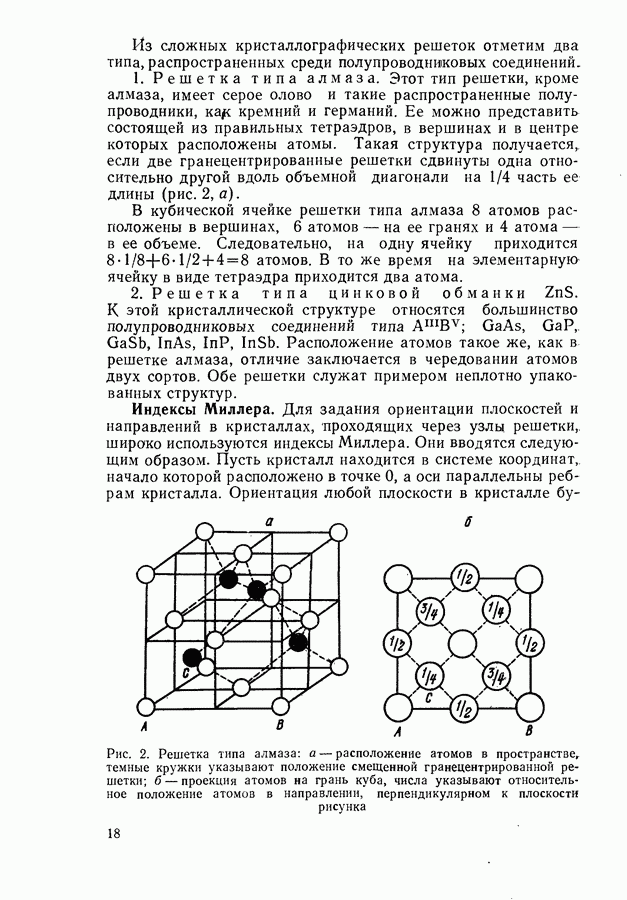
Рис. 1. Элементарные ячейки для кубического кристалла с одним атомом в центре куба: а — кубическая; б - ромбоэдрическая; в — ячейка, Вигнера-Зейтца
только симметрию прямой решетки, но и свойства обратной решетки. Именно в пространстве обратной решетки задается и исследуется волновой вектор электрона к. Поэтому изучение обратной решетки служит отправной точкой в теории твердого тела.
Вектор трансляции  обратной решетки равен
обратной решетки равен

где  целые числа;
целые числа;  базисные векторы обратной решетки.
базисные векторы обратной решетки.
Векторы  имеют размерность обратной длины и связаны с базисными векторами прямой решетки соотношениями
имеют размерность обратной длины и связаны с базисными векторами прямой решетки соотношениями

где  по-прежнему объем элементарной ячейки прямой решетки, равный
по-прежнему объем элементарной ячейки прямой решетки, равный  С помощью (1.3) легко убедиться, что
С помощью (1.3) легко убедиться, что  удовлетворяют соотношению
удовлетворяют соотношению

Здесь  символ Кронекера, равный 1, если
символ Кронекера, равный 1, если  и нулю при
и нулю при 
Параллелепипед, построенный на векторах  образует элементарную ячейку обратной решетки. Ее объем равен
образует элементарную ячейку обратной решетки. Ее объем равен  обратно пропорционален объему элементарной ячейки прямой решетки.
обратно пропорционален объему элементарной ячейки прямой решетки.
Согласно (1.3), любой из трех базисных векторов обратной решетки с индексом  перпендикулярен к двум основным векторам прямой решетки с индексами, отличными от Еслиаг образуют тройку взаимно перпендикулярных векторов, то
перпендикулярен к двум основным векторам прямой решетки с индексами, отличными от Еслиаг образуют тройку взаимно перпендикулярных векторов, то  тоже будут взаимно - перпендикулярны, причем
тоже будут взаимно - перпендикулярны, причем  В рлучае кубической решетки
В рлучае кубической решетки 
Если же элементарная ячейка прямой решетки является параллелепипедом произвольной формы, то для нахождения обратной решетки удобно векторы а рассматривать в некоторой прямоугольной системе координат. Тогда 9 проекций векторов  можно представить в виде матрицы А, а числа
можно представить в виде матрицы А, а числа  и
и  — как вектор-столбец
— как вектор-столбец  Положение узлов решетки будет определяться вектором трансляции, равным произведению матрицы на вектор [10]
Положение узлов решетки будет определяться вектором трансляции, равным произведению матрицы на вектор [10]

Вводя аналогичным образом матрицу В обратной решетки, имеем

На основании (1.4) приходим к равенству

где  единичная матрица, все элементы которой равны 1. Для нахождения компонент матрицы В равенство (1.7) можно представить в виде системы 9 уравнений
единичная матрица, все элементы которой равны 1. Для нахождения компонент матрицы В равенство (1.7) можно представить в виде системы 9 уравнений

Матрицы  полностью определяют прямую и обратную решетки. В случае простой кубической решетки они имеют вид:
полностью определяют прямую и обратную решетки. В случае простой кубической решетки они имеют вид:

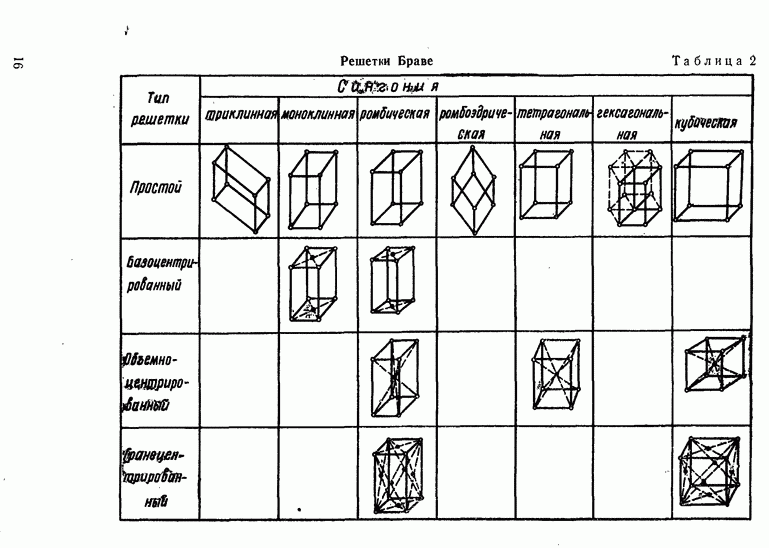
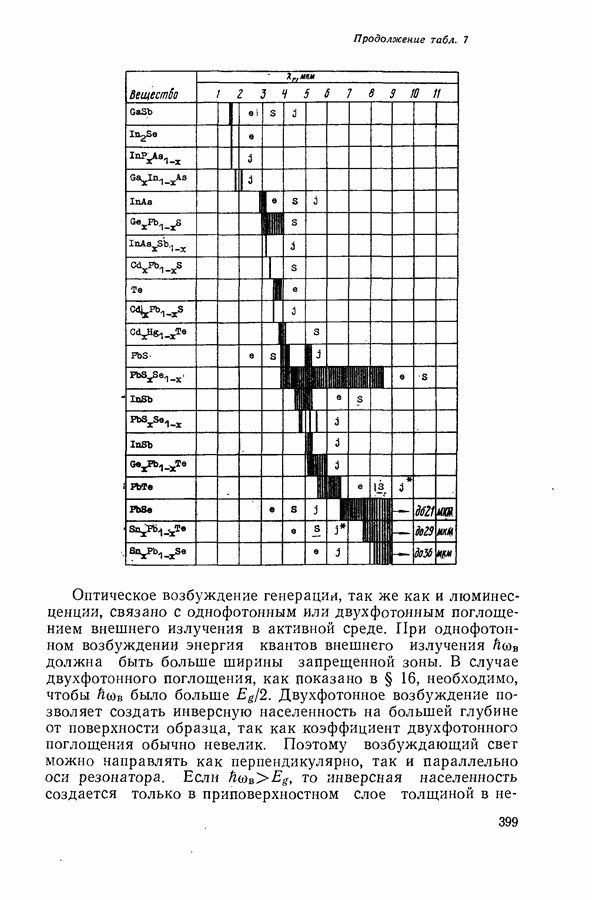
Таблица 1 (см. скан) Сингонии кристаллов
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
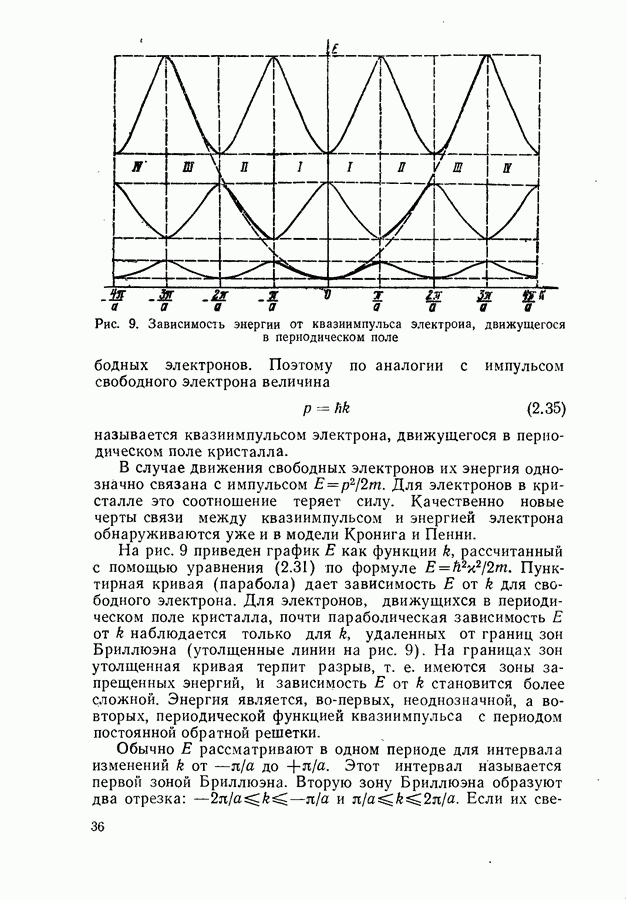
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
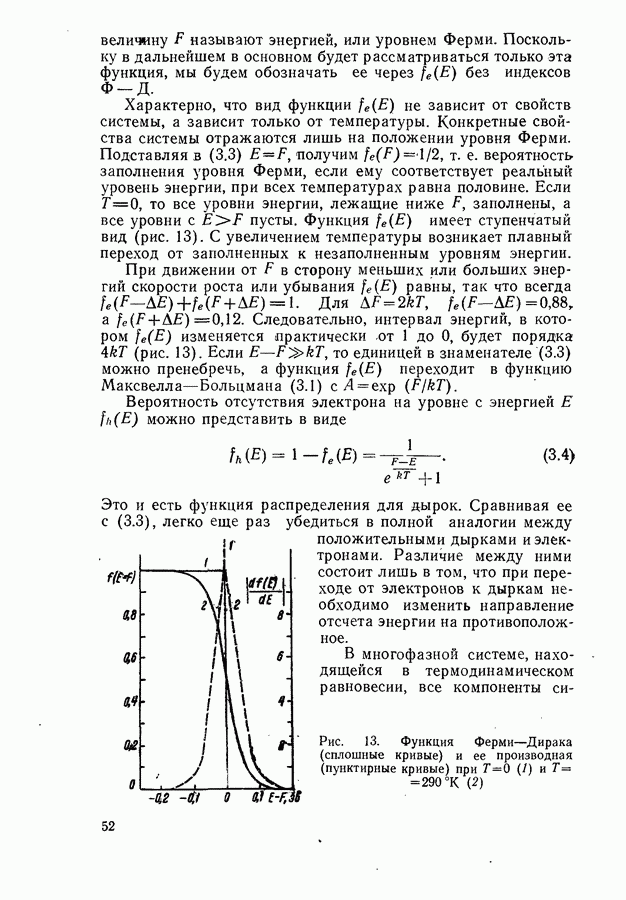
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
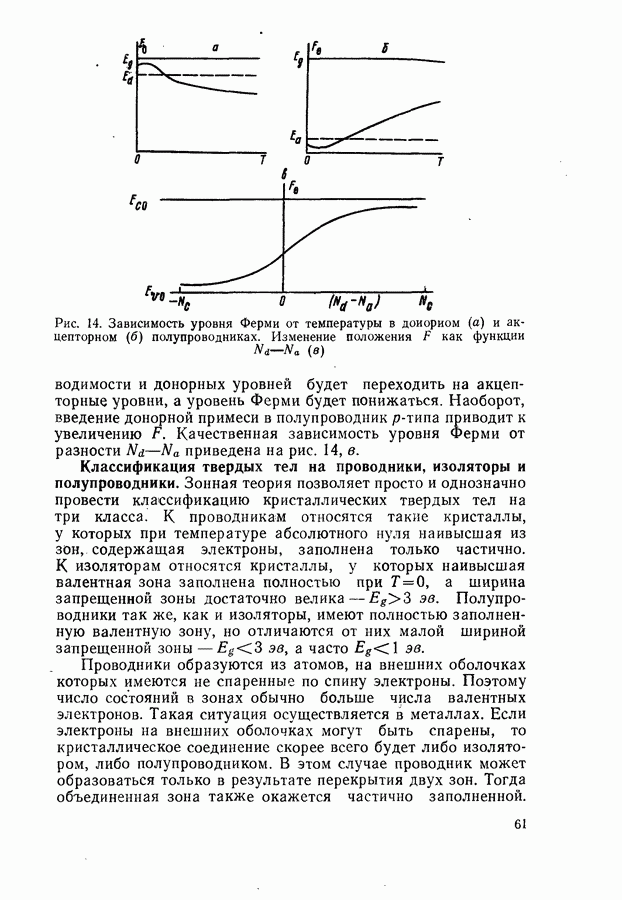
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
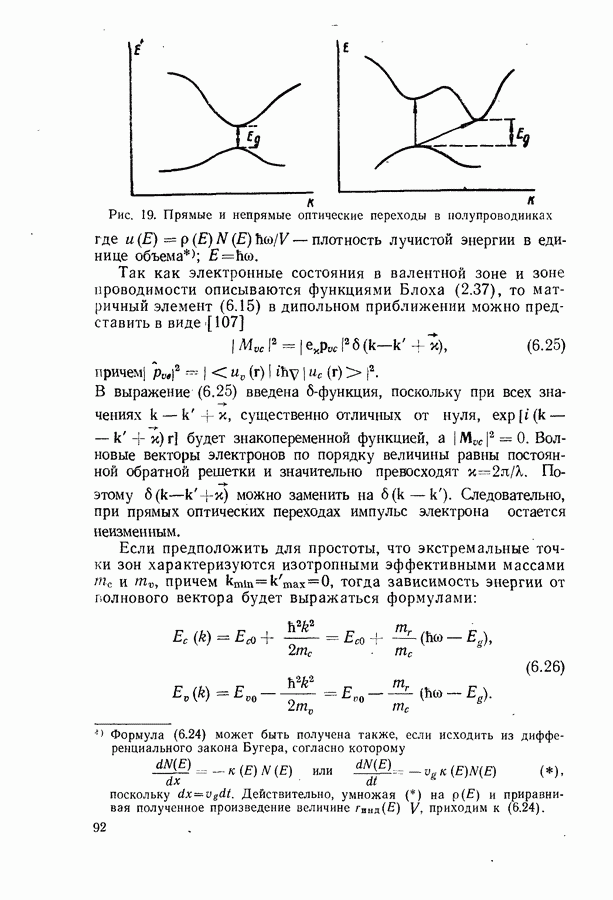
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
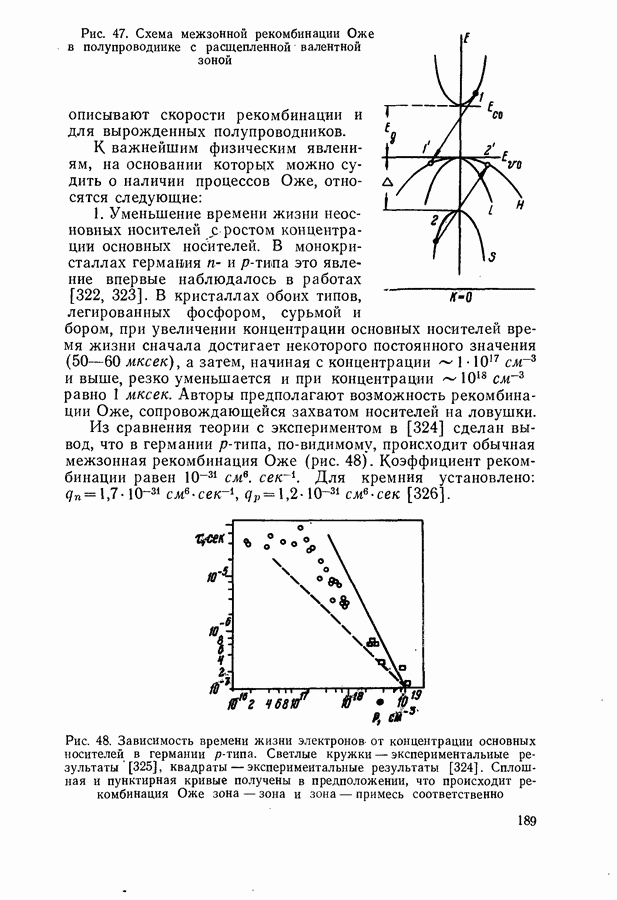
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
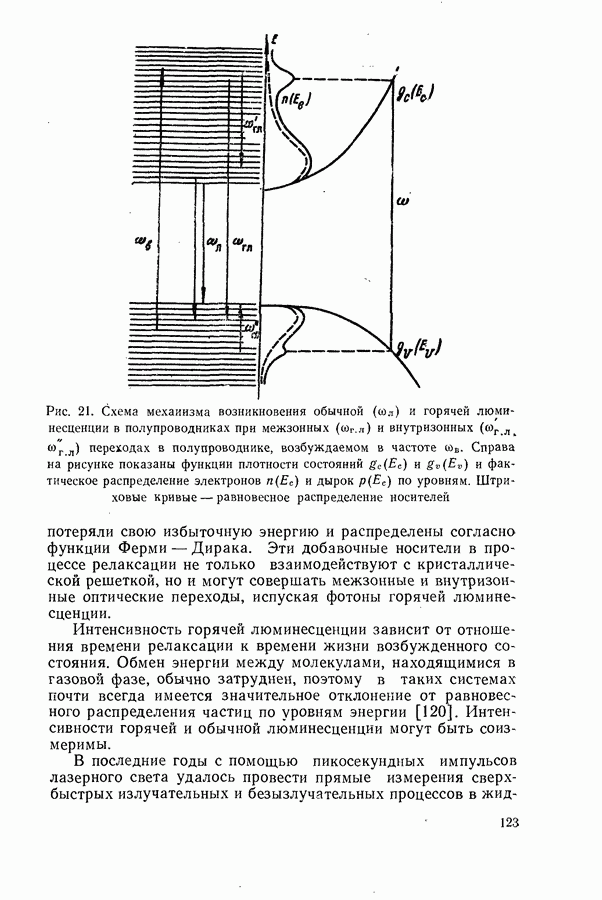
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
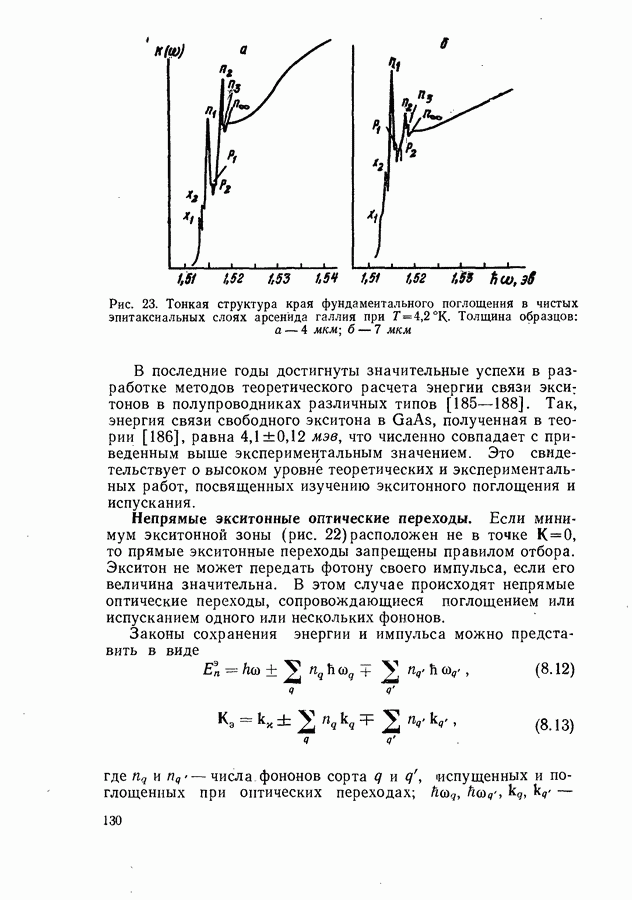
- Непрямые экситонные оптические переходы.
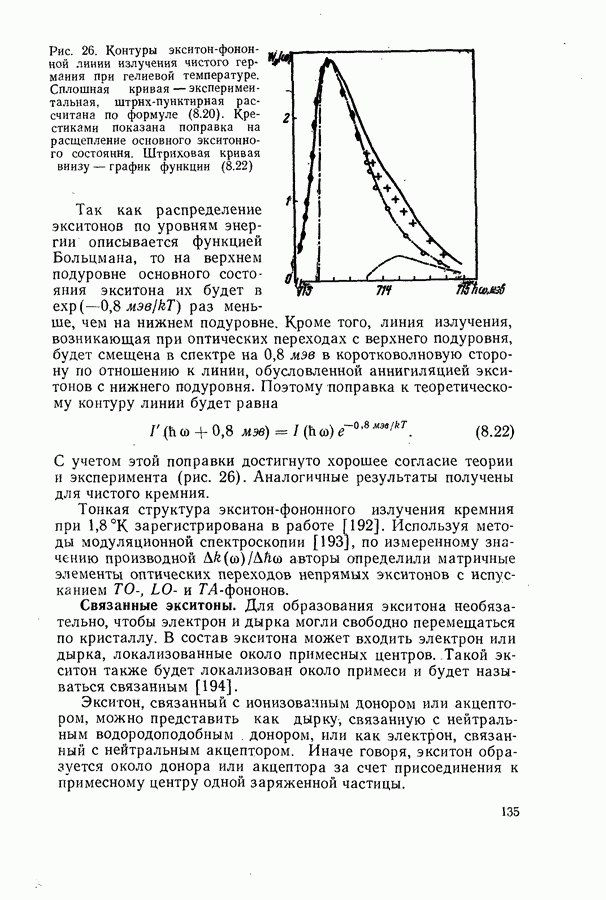
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
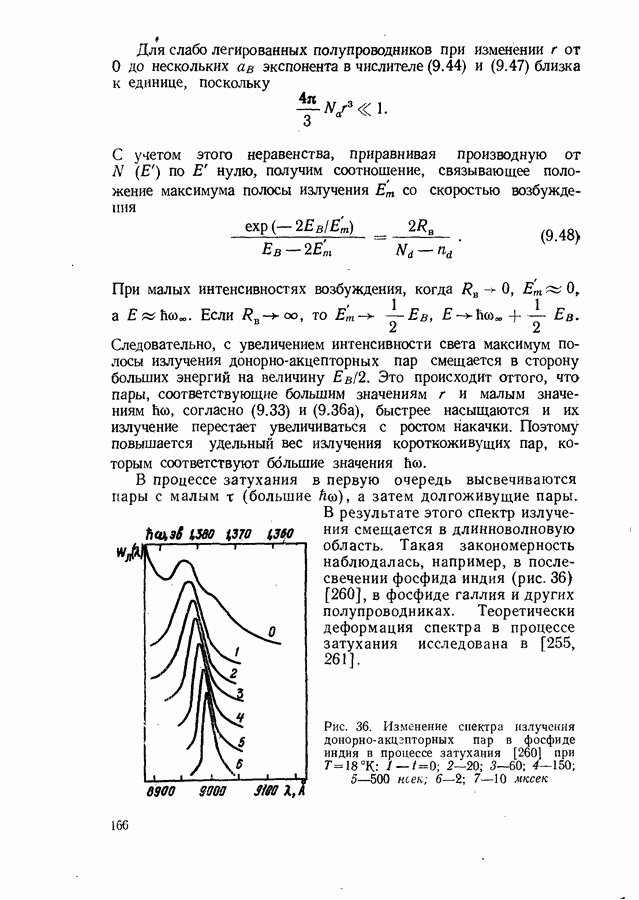
- Рекомбинация донорно-акцепторных пар.
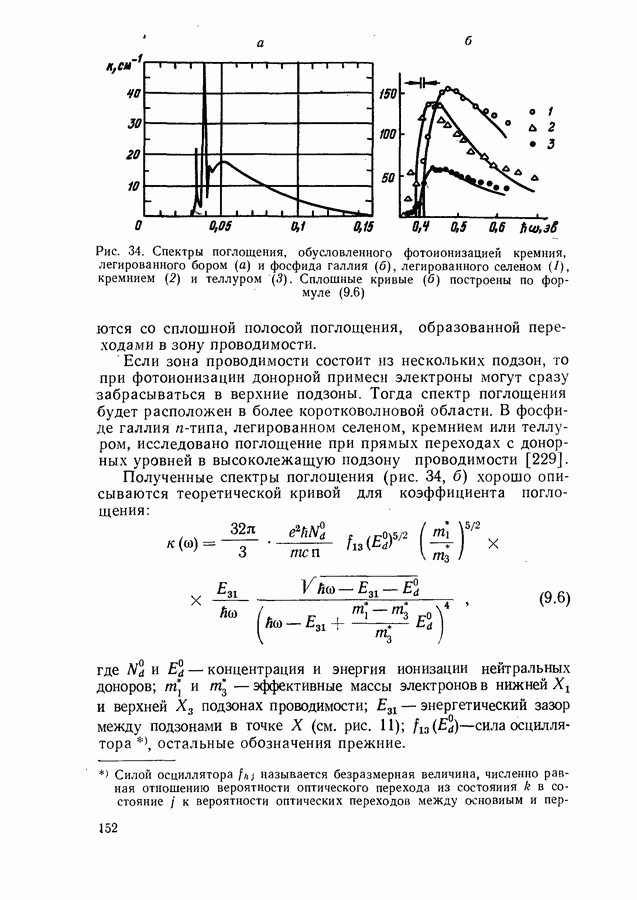
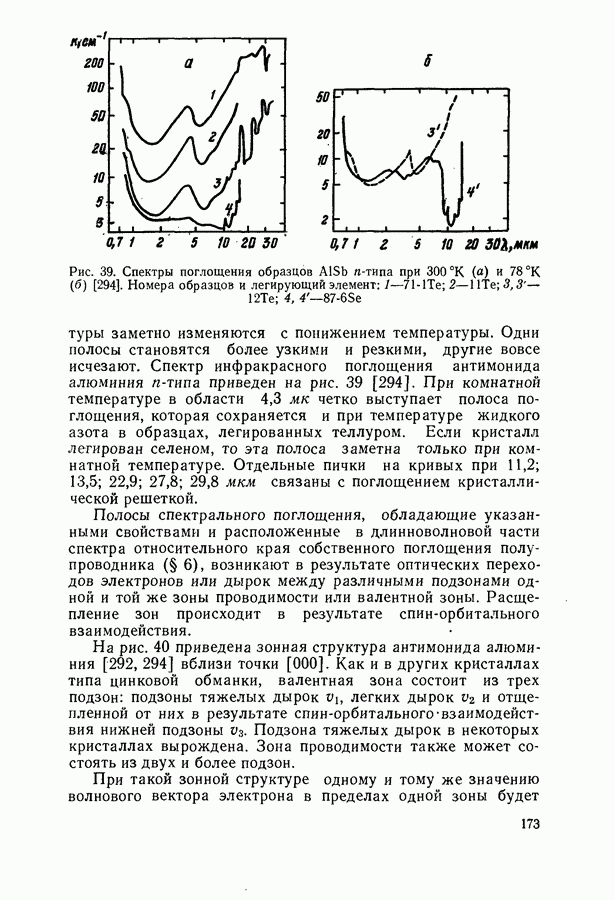
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
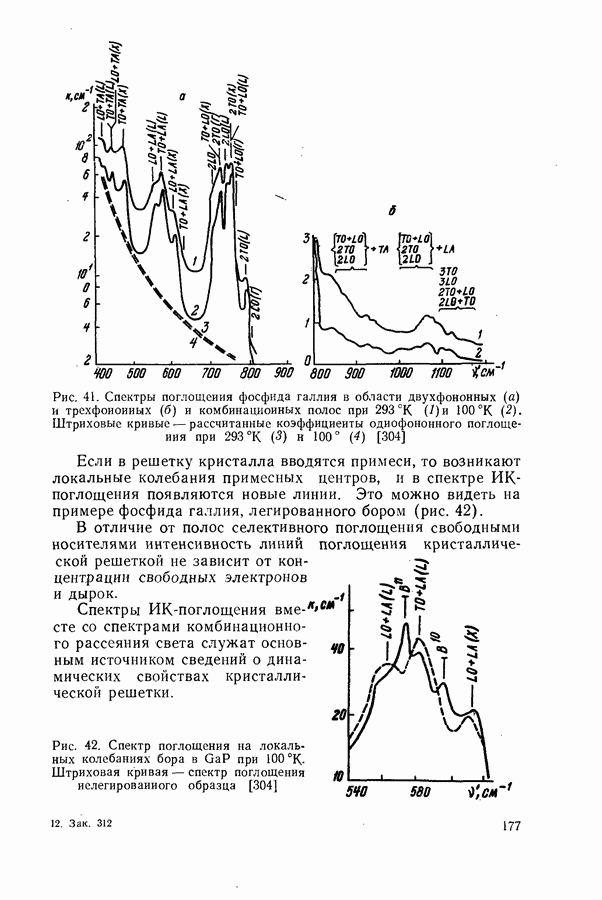
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
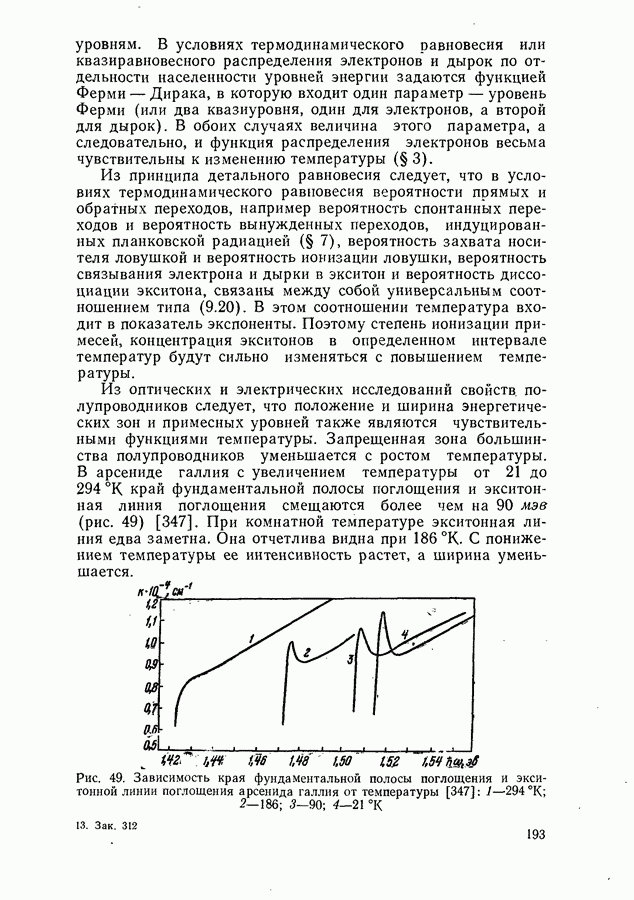
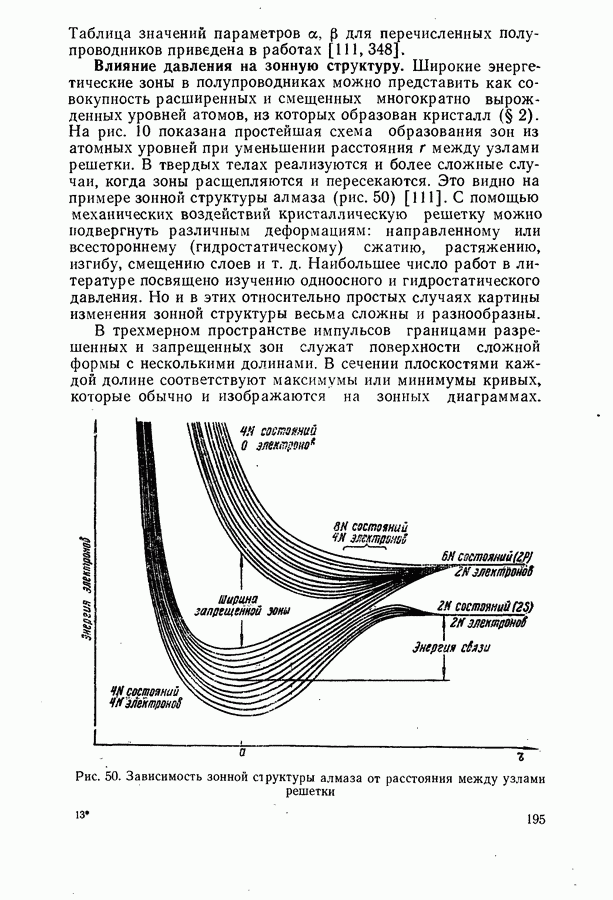
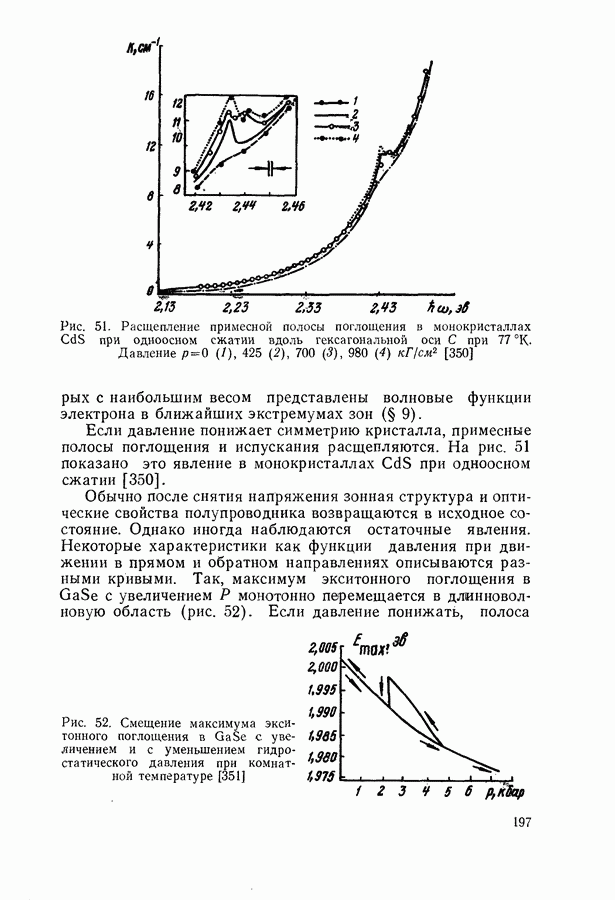
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
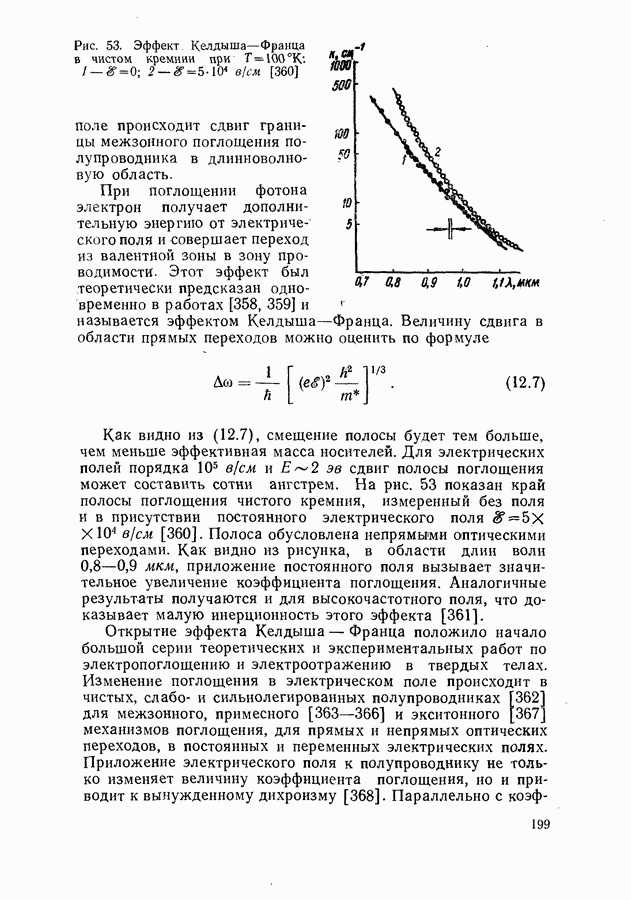
- Эффект Келдыша-Франца.
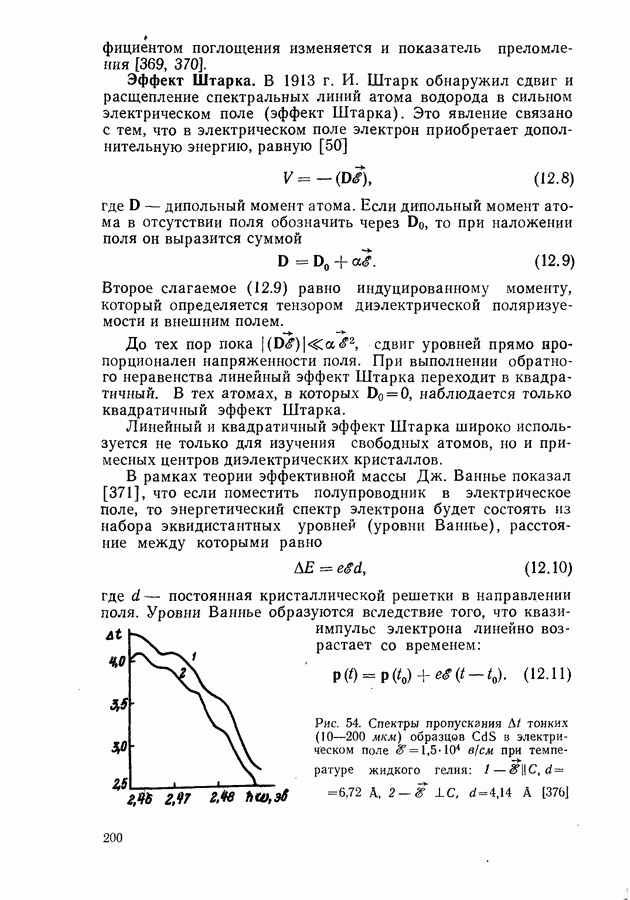
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
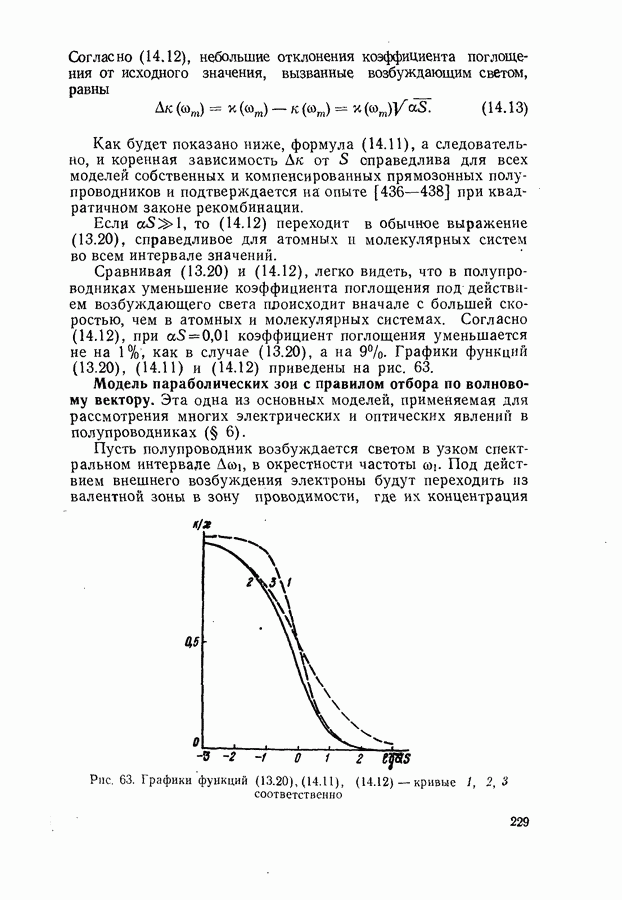
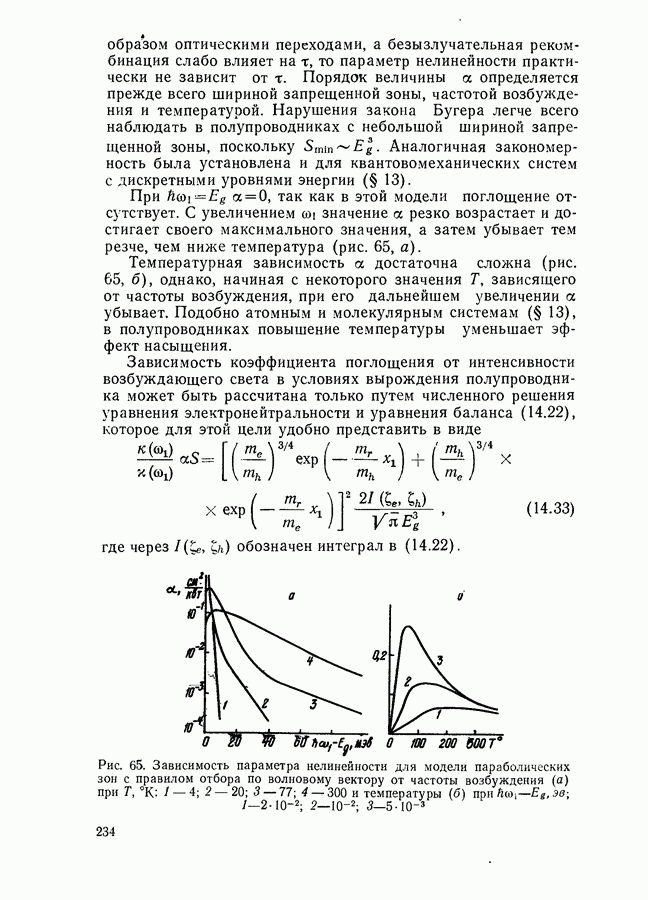
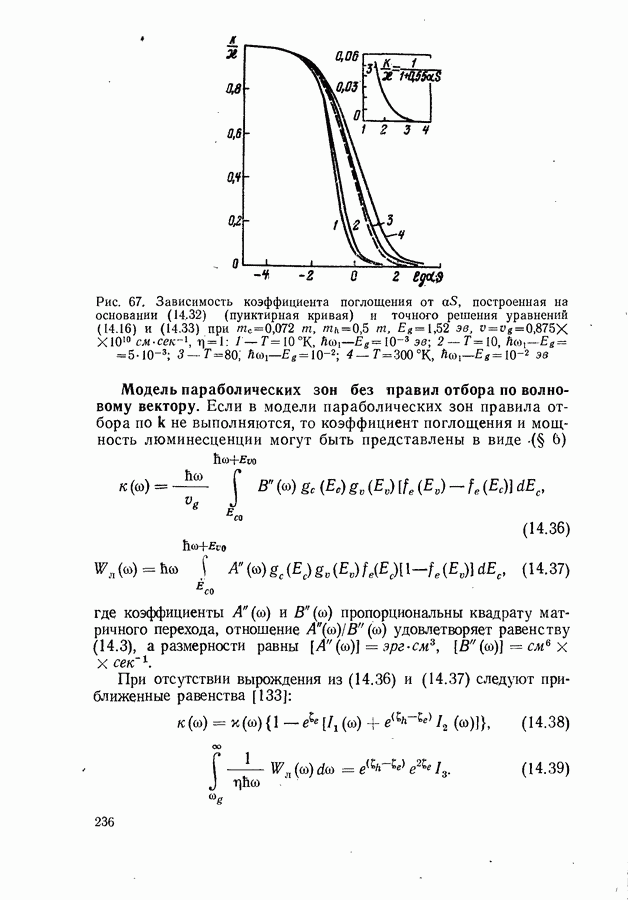
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
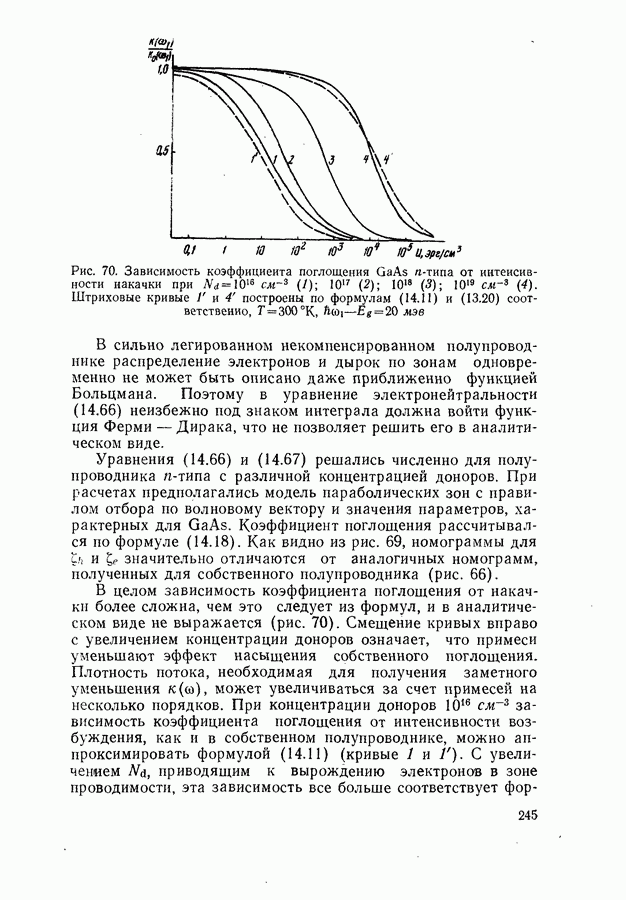
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
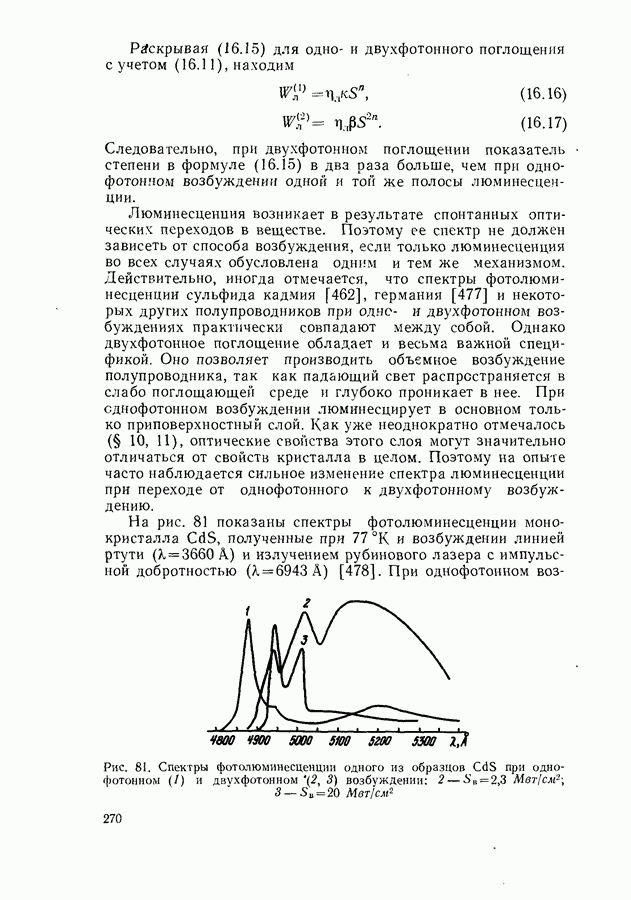
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
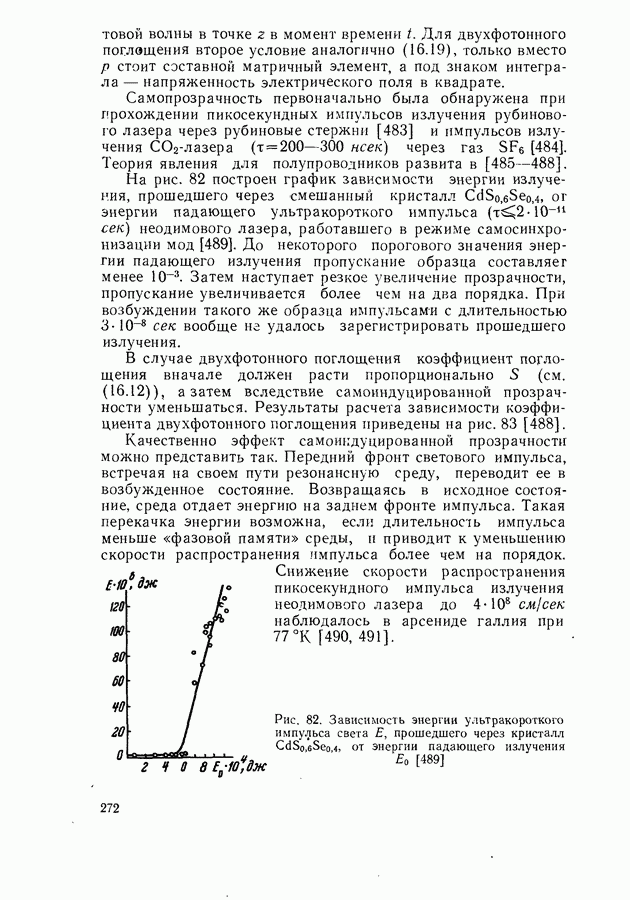
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
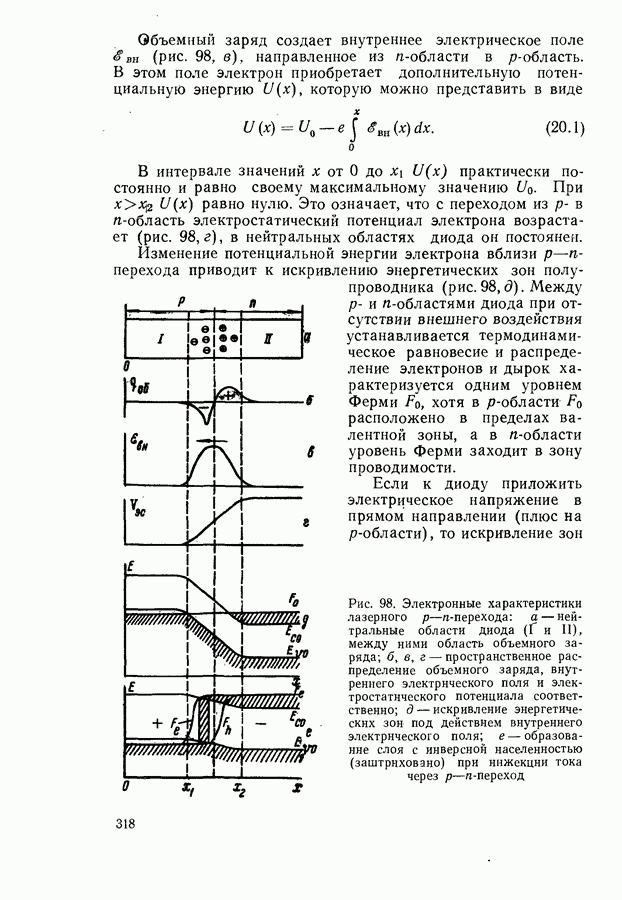
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
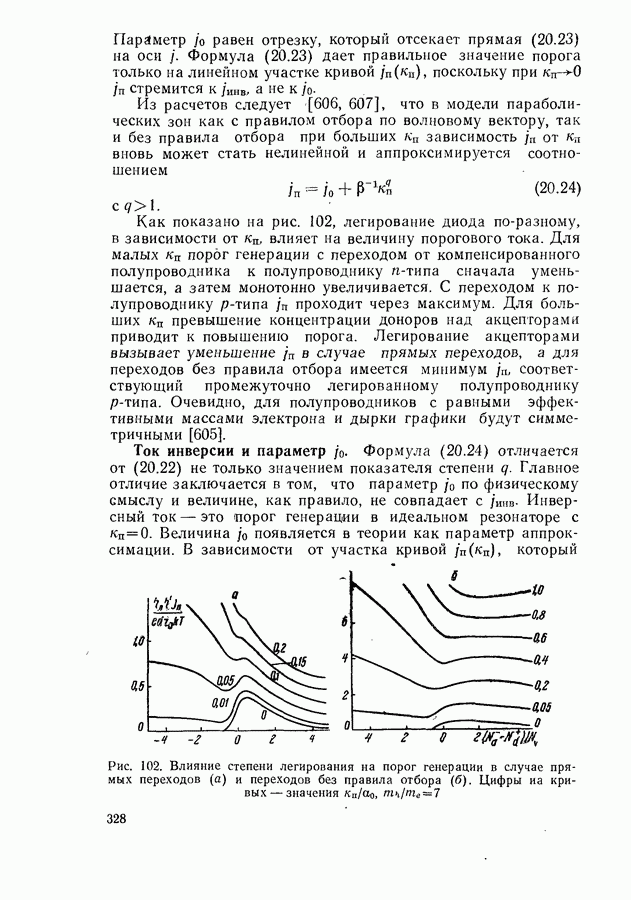
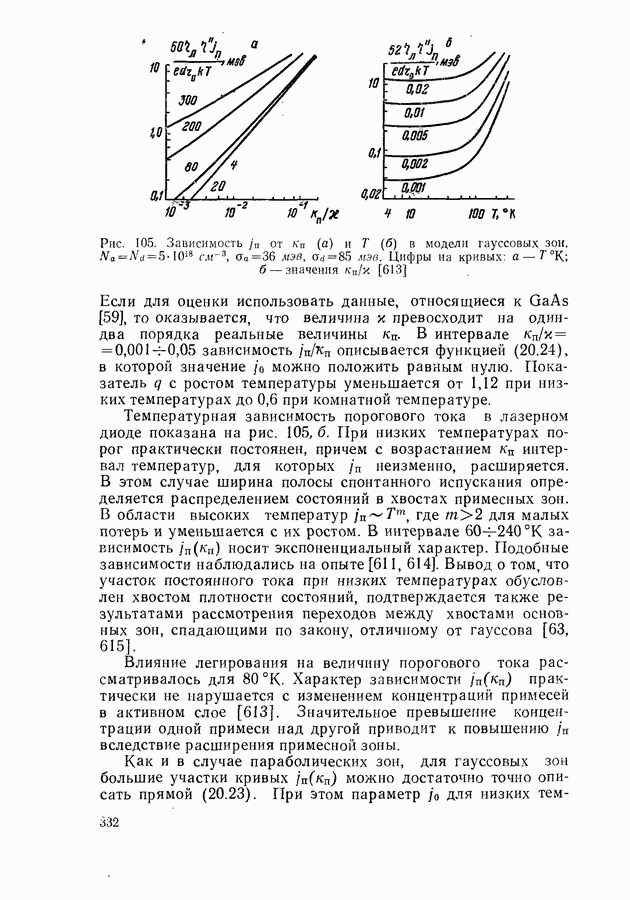
- Ток инверсии и параметр j0
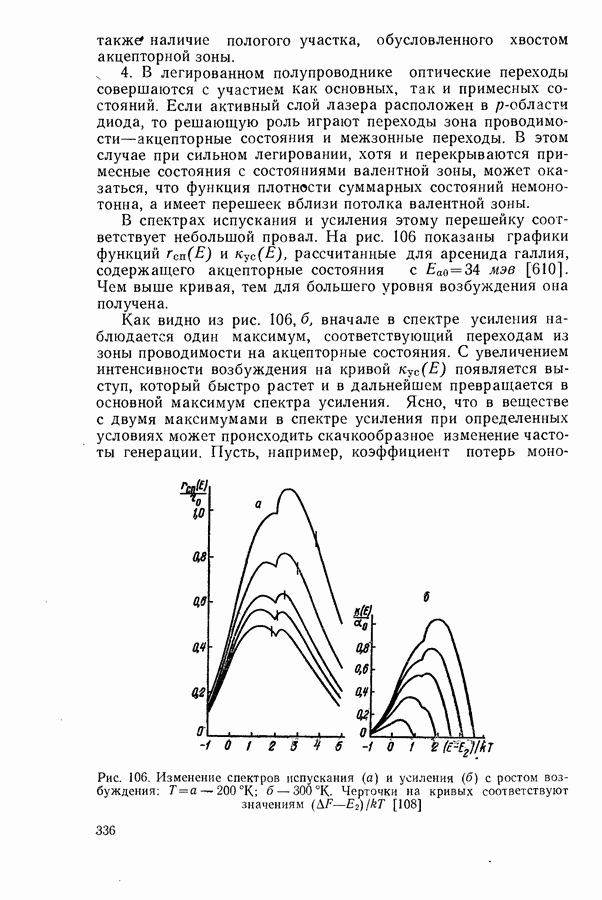
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
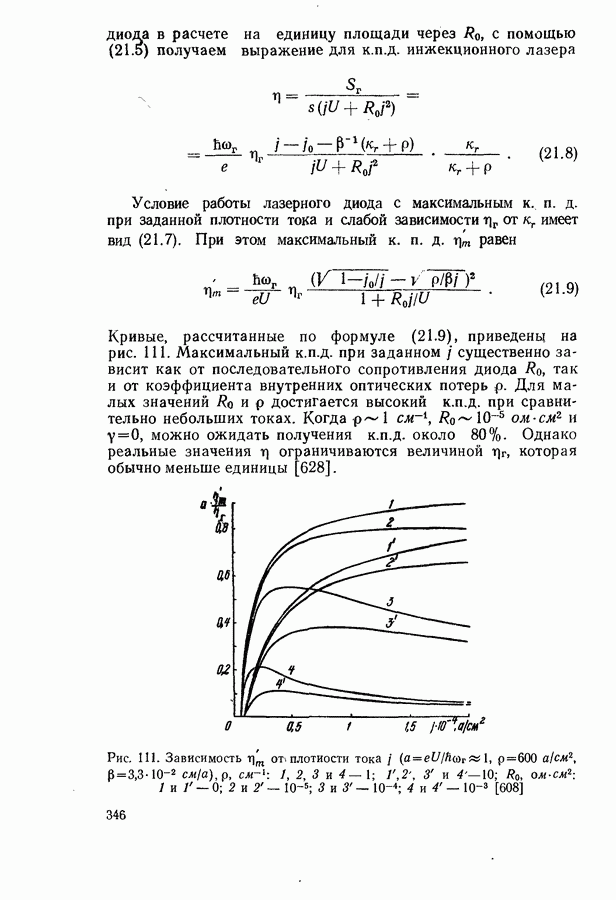
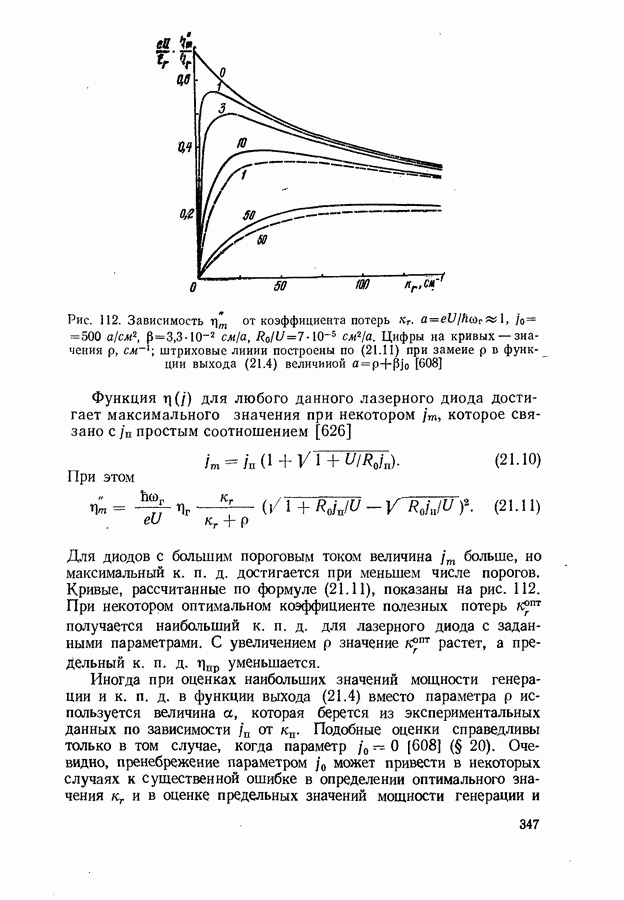
- Оптимальный режим генерации.
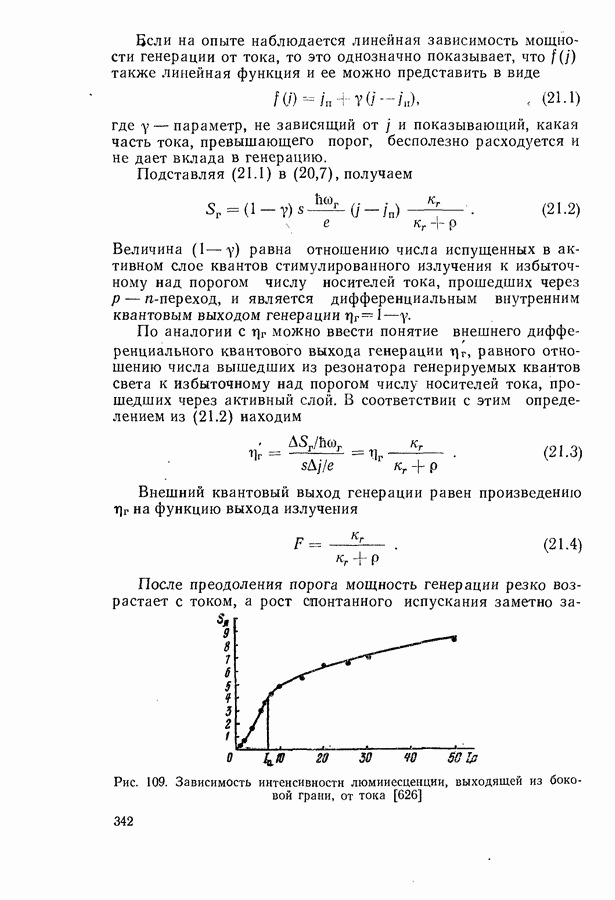
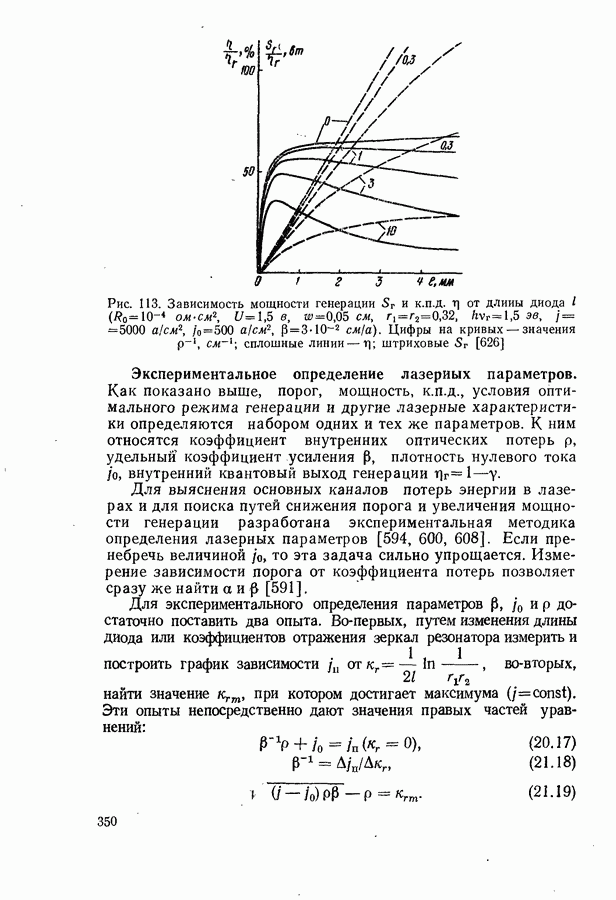
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
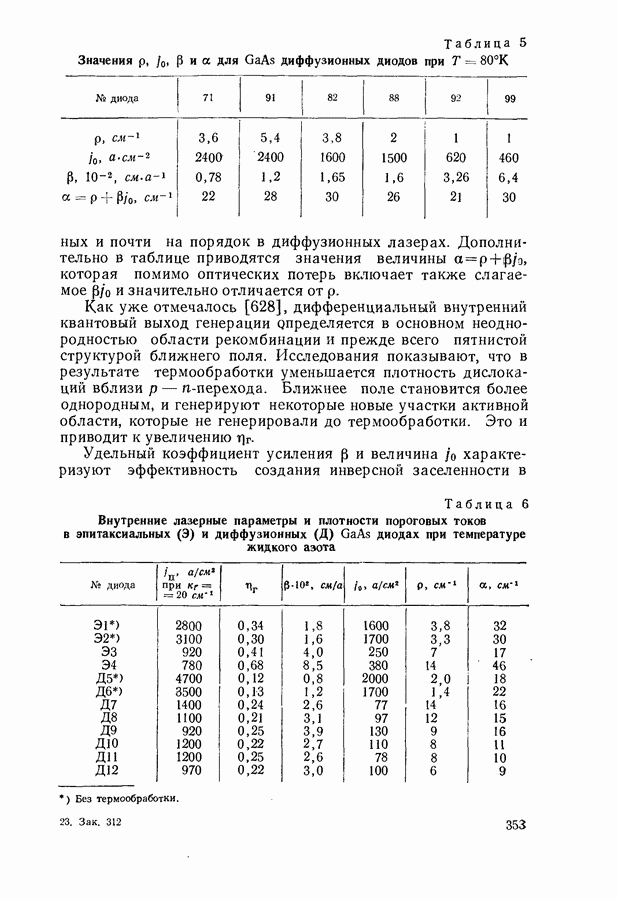
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
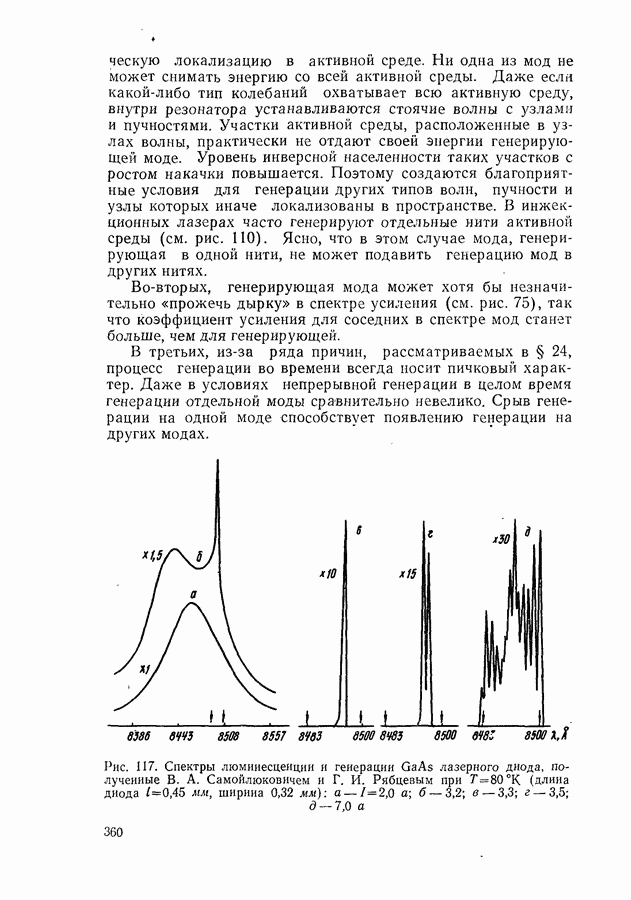
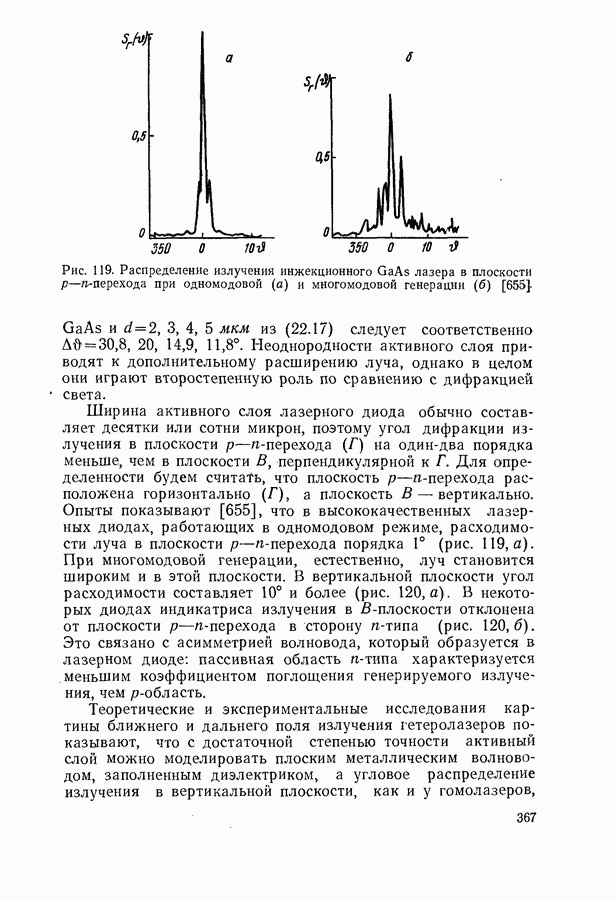
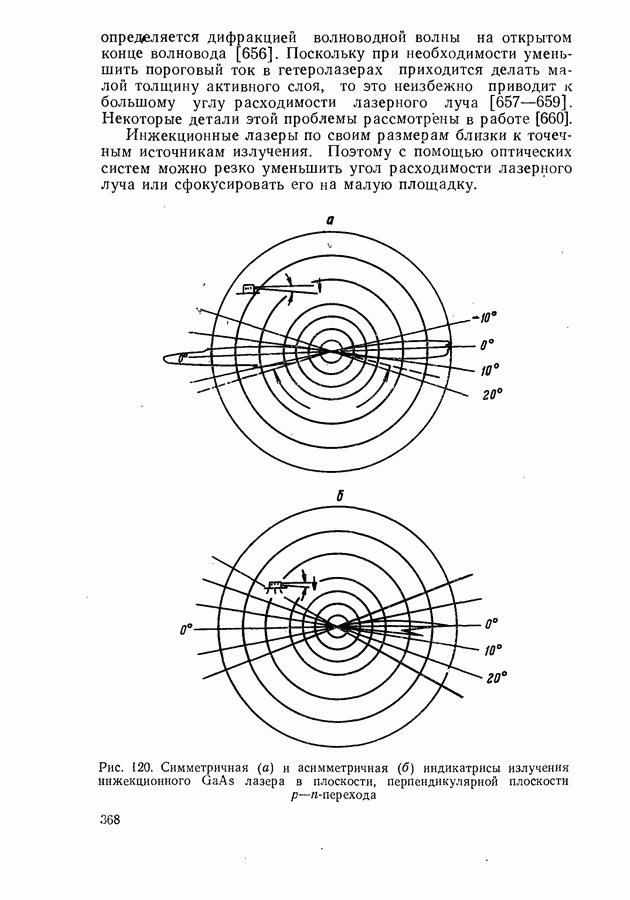
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
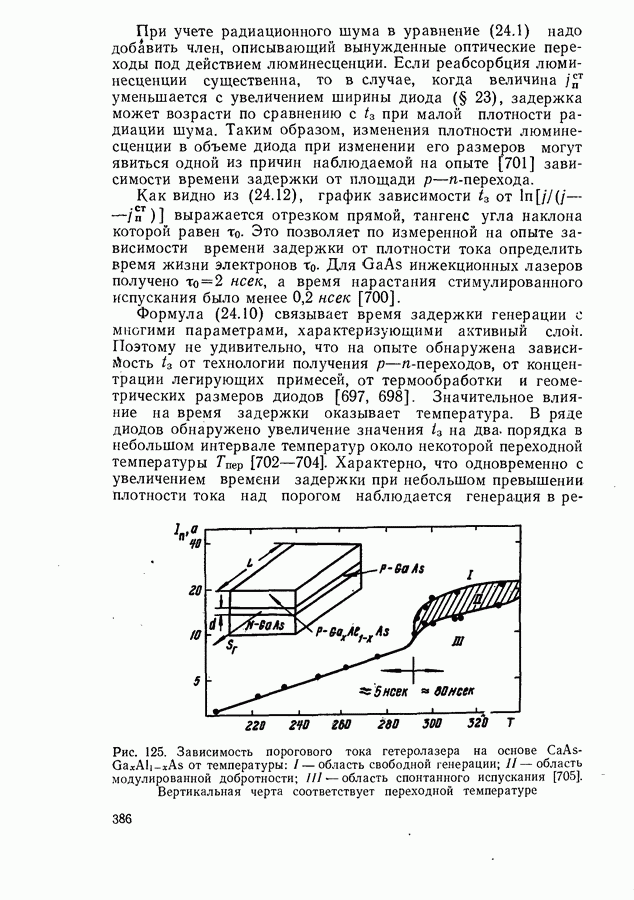
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
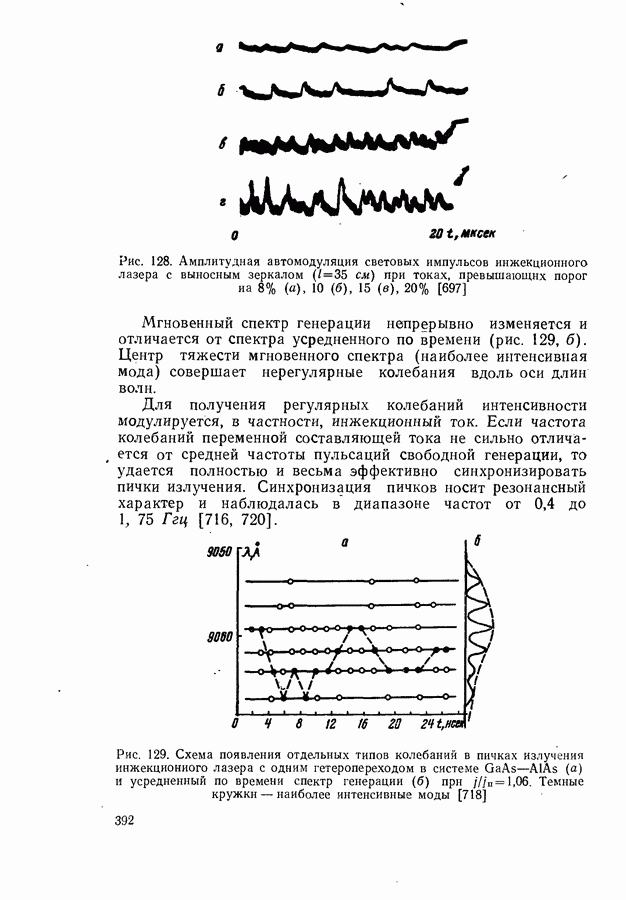
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
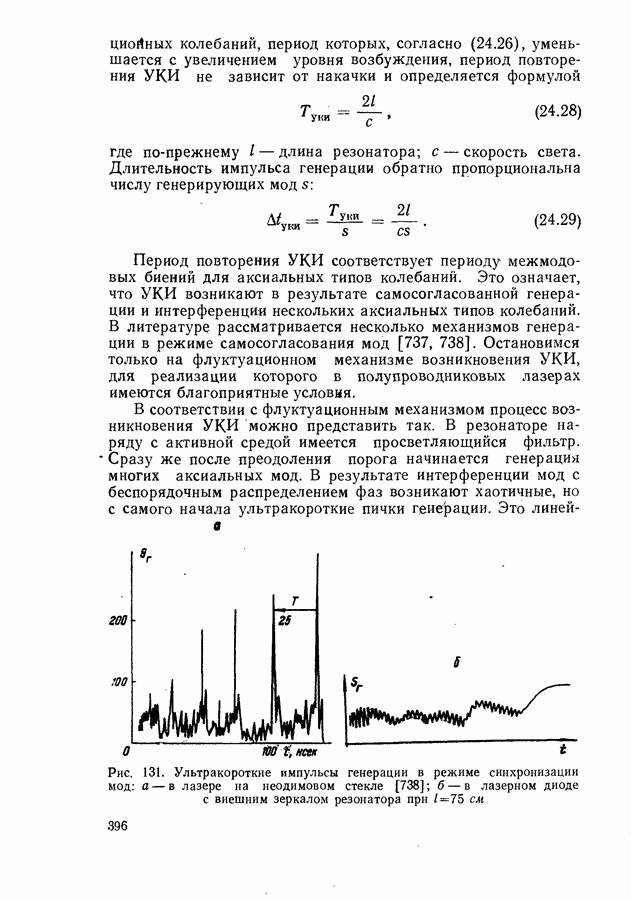
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
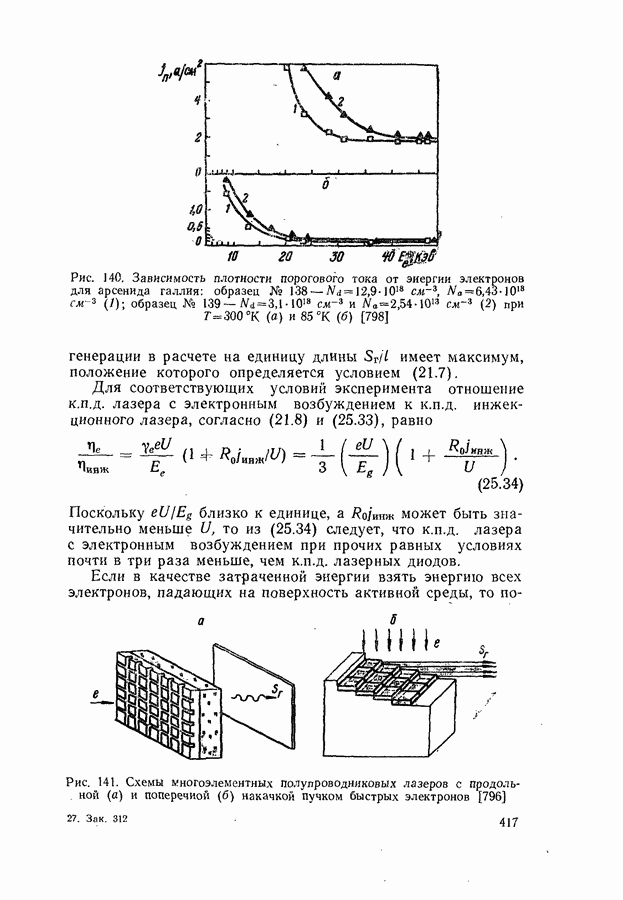
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
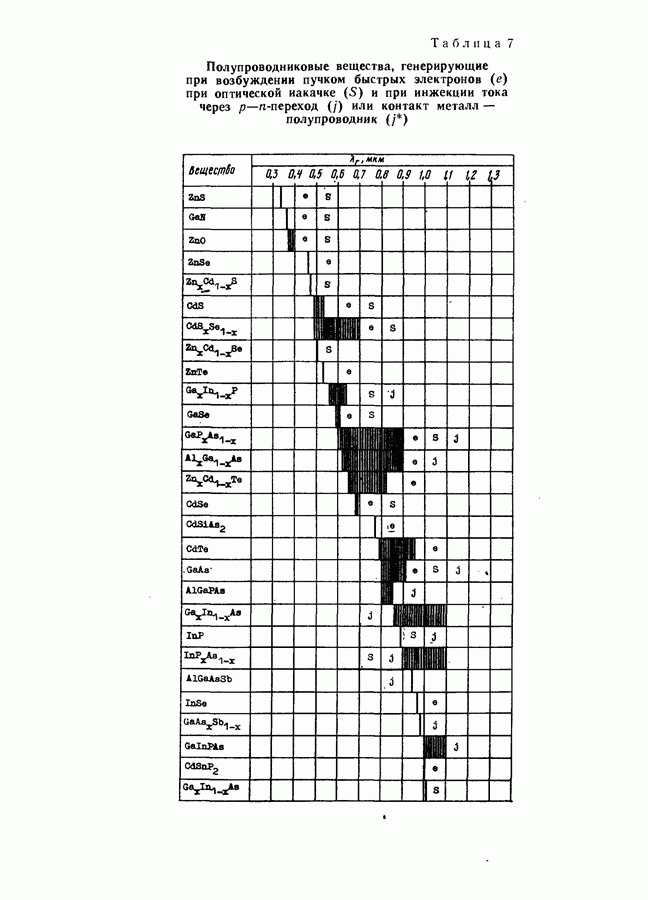
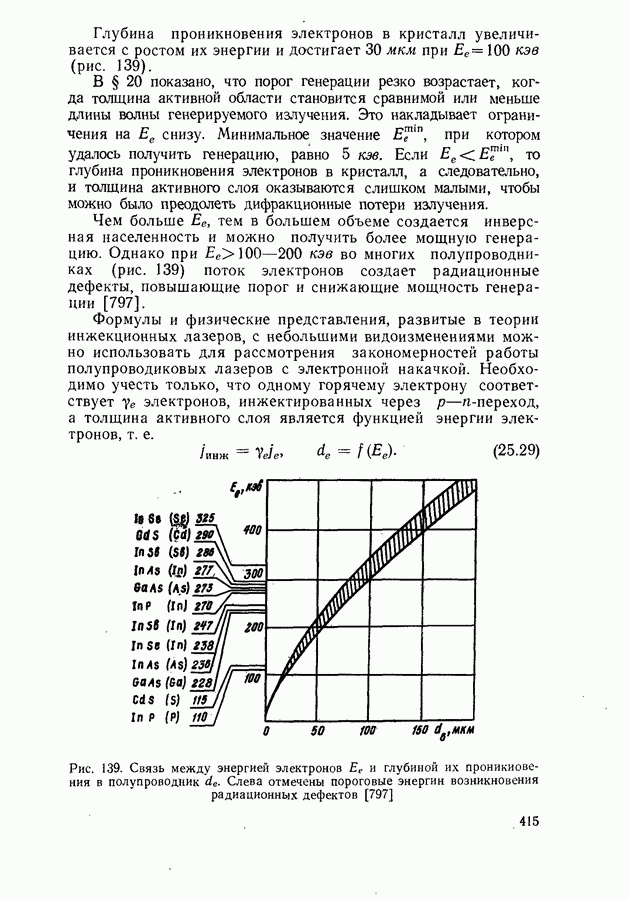
- Возбуждение генерации пучком быстрых электронов.