| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Фононы.
Хотя решение уравнения движения атомов в кристалле в гармоническом приближении выражается формулой плоских волн типа (4.9), это не означает, что узлы решетки совершают простое колебательное движение с заданной частотой  В любом кристалле одновременно происходят колебания всевозможных частот и направлений распространения волн. Так как один и тот же атом участвует во всех типах движения сразу, то его траектория движения может быть весьма сложной. Для линейной цепочки вещественную величину смещения можно представить в виде [38]
В любом кристалле одновременно происходят колебания всевозможных частот и направлений распространения волн. Так как один и тот же атом участвует во всех типах движения сразу, то его траектория движения может быть весьма сложной. Для линейной цепочки вещественную величину смещения можно представить в виде [38]

где  -величины, комплексно сопряженные
-величины, комплексно сопряженные  Как видио из (4.43), смещение атома является сложной функцией времени.
Как видио из (4.43), смещение атома является сложной функцией времени.
В теории колебаний молекул [85] и кристаллов движение частиц оказывается удобным представлять в некоторых обобщенных координатах, которые называются нормальнымн. Нормальные координаты выбираются так, чтобы уравнения движения, записанные в этих координатах, распадались на систему независимых уравнений типа

Ускорение частицы в нормальных координатах зависит только от значения этой же координаты. Следовательно, нормальные колебания полностью независимы. Если обычная координата  дает положение и состояние движения
дает положение и состояние движения  атома, то нормальная координата вместе с обобщенным импульсом
атома, то нормальная координата вместе с обобщенным импульсом
относится ко всему кристаллу в целом и характеризует колебательный процесс в этом кристалле с частотой  С помощью нормальных координат колебания кристаллической решетки представляются как суперпозиция простых гармонических колебаний. Это обстоятельство фактически и выражено формулой (4.43). Поэтому
С помощью нормальных координат колебания кристаллической решетки представляются как суперпозиция простых гармонических колебаний. Это обстоятельство фактически и выражено формулой (4.43). Поэтому  можно рассматривать как нормальную координату. Если в кристалле содержится
можно рассматривать как нормальную координату. Если в кристалле содержится  атомов, то число нормальных координат будет равно
атомов, то число нормальных координат будет равно 
Формально кристаллическая решетка заменяется набором гармонических осцилляторов, которые можно рассматривать не только в классической теории, но и в рамках квантовой механики. Из квантовой механики известно [44, 87, 88], что энергия гармонического осциллятора может принимать дискретный ряд значений:

где  целые положительные числа. В отличие от классической теории, согласно (4.45), минимальная энергия колебаний решетки не равна нулю, а выражается формулой
целые положительные числа. В отличие от классической теории, согласно (4.45), минимальная энергия колебаний решетки не равна нулю, а выражается формулой

Эта так называемая энергия нулевых колебаний. Исследование волновой функции осциллятора при  показывает, что она отлична от нуля в некоторой окрестности точки, соответствующей положению равновесия. Следовательно, «заморозить» неподвижно атомы кристалла в решетке невозможно даже при абсолютном нуле.
показывает, что она отлична от нуля в некоторой окрестности точки, соответствующей положению равновесия. Следовательно, «заморозить» неподвижно атомы кристалла в решетке невозможно даже при абсолютном нуле.
Поскольку колебательная энергия решетки может изменяться только отдельными порциями или квантами, то по аналогии с частицами света, фотонами, можно ввести понятие частиц колебательного движения — фононов. Энергия и импульс (точнее квазиимпульс) одного фонона сорта  равны соответственно
равны соответственно  где
где  волновой вектор плоской волны с частотой
волновой вектор плоской волны с частотой 
После этого воздействие колебаний решетки на движение электронов в кристалле можно описать как столкновение частиц — электронов и фононов, или электрон-фононное взаимодействие. Ангармонизм колебаний решетки и взаимное влияние одного типа колебаний на другой (ср. связанные маятники) на квантовомеханическом языке представляется
как рассеяние фононов на фононах, или фонон-фононное взаимодействие. Ангармонизм колебаний атомов необходимо учитывать при изучении многих процессов и прежде всего теплопроводности кристаллов. Если бы фононы не рассеивались на фононах, то их скорость была бы равна примерно скорости звука. Тогда от нагретого участка кристалла тепло передавалось бы к его холодным частям со скоростью порядка  см/сек. Из опыта известно, что распространение тепла в кристаллах происходит значительно медленнее. Одна из причин этого — фонон-фононное взаимодействие.
см/сек. Из опыта известно, что распространение тепла в кристаллах происходит значительно медленнее. Одна из причин этого — фонон-фононное взаимодействие.
Как будет показано в дальнейшем, фононы играют первостепенную роль при некоторых механизмах поглощения и испускания света в полупроводниках.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
- Химическая связь в кристаллах.
- Прямая и обратная решетки.
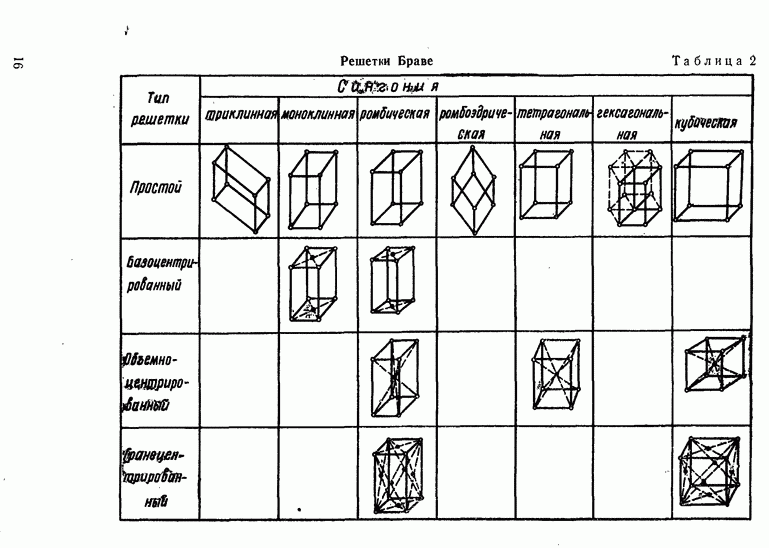
- Классификация кристаллических решеток.
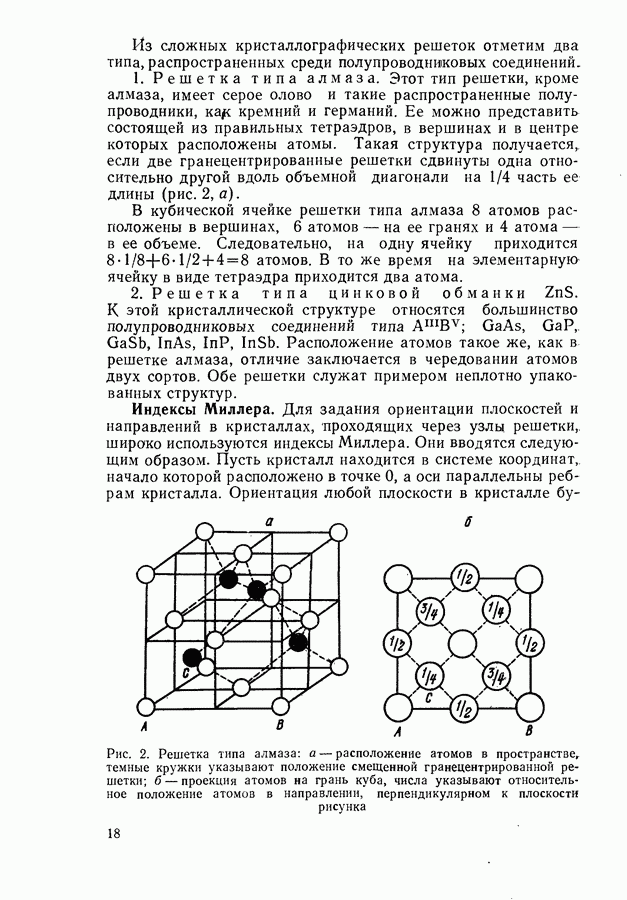
- Индексы Миллера.
- Определение ориентации кристаллов.
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
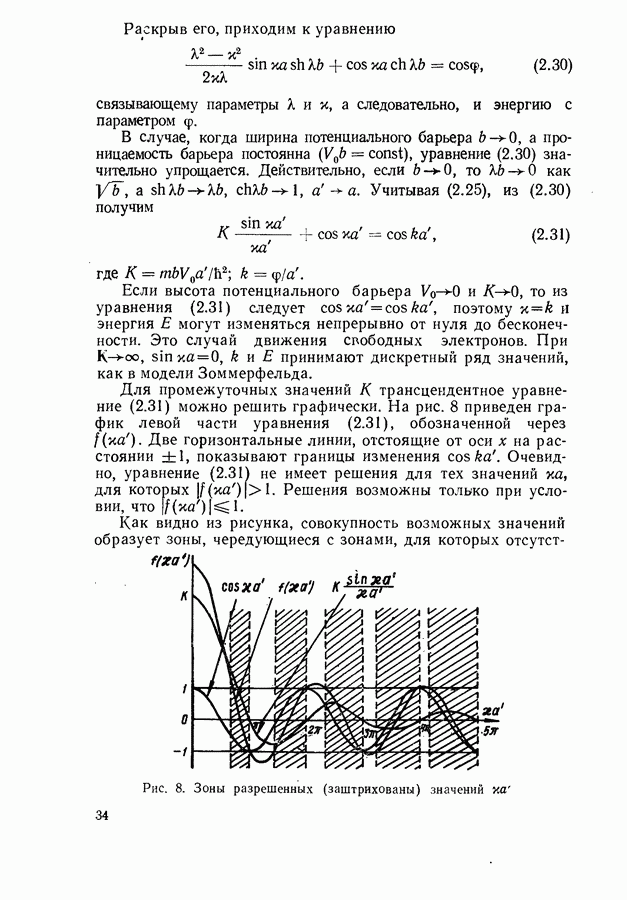
- Модель Зоммерфельда. Плотность состояний.
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
- Эффект Келдыша-Франца.
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
- Модель параболических зон с правилом отбора по волновому вектору.
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
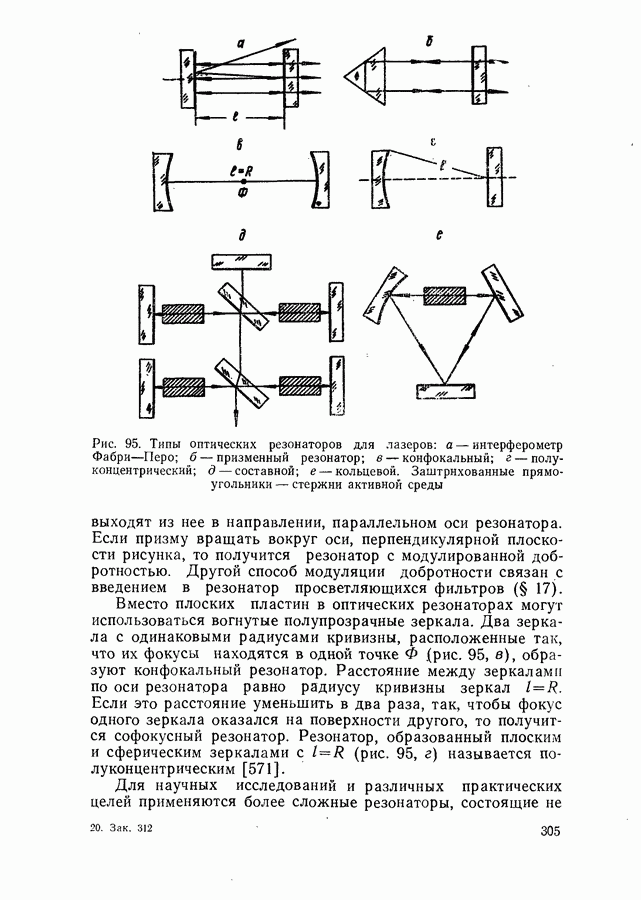
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
- Ток инверсии и параметр j0
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
- Оптимальный режим генерации.
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
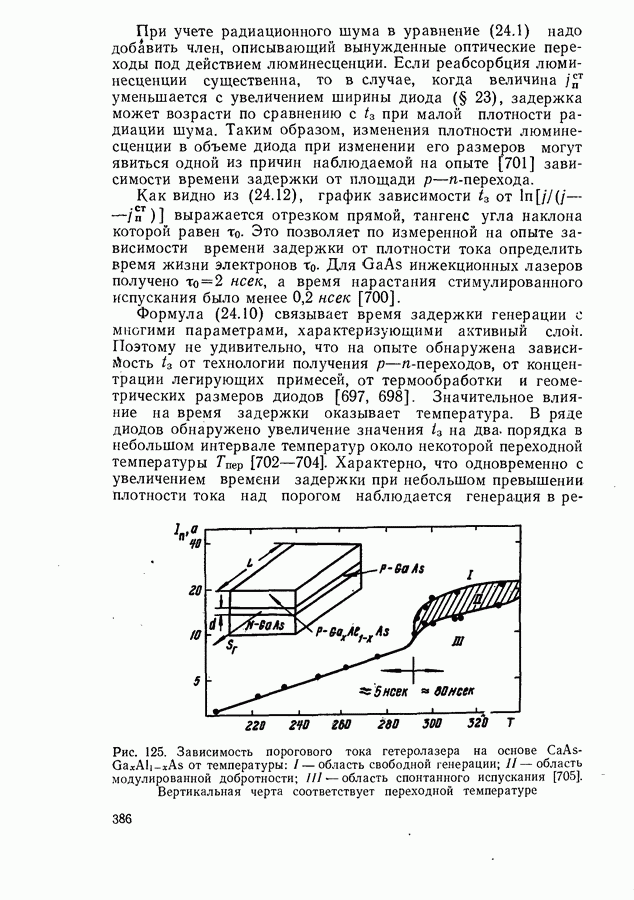
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
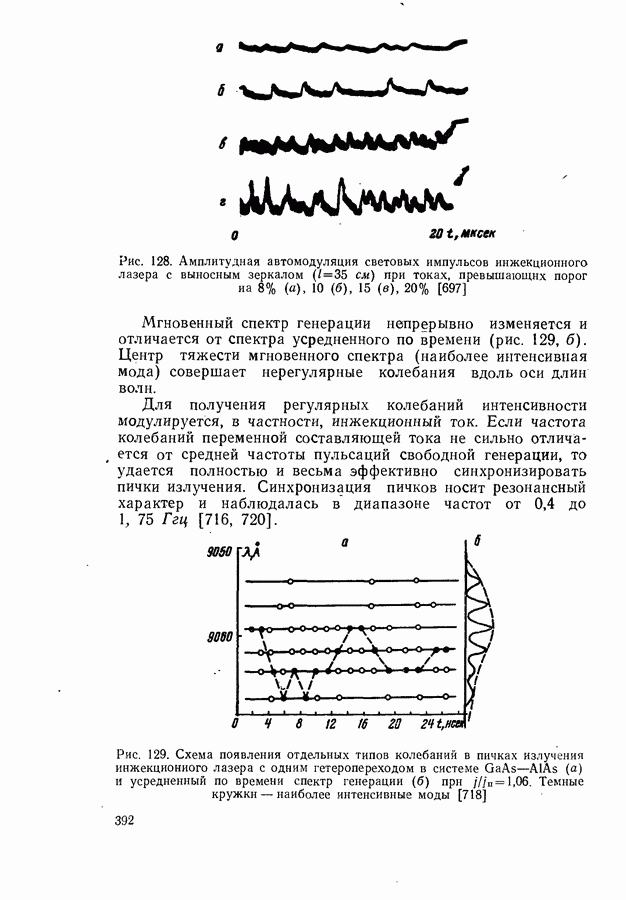
- Амплитудная и частотная автомодуляция излучения.
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
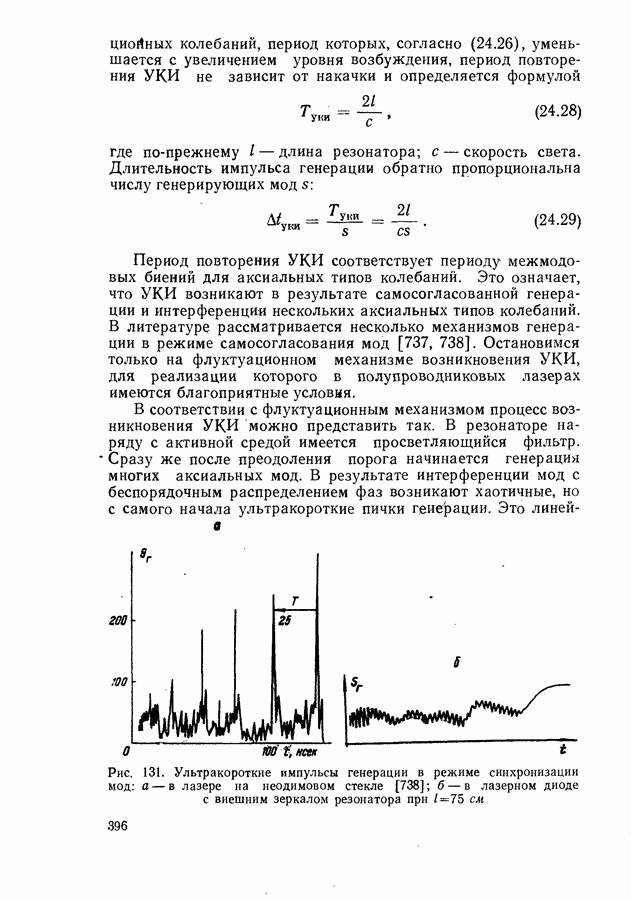
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
- Экситонный механизм генерации излучения.
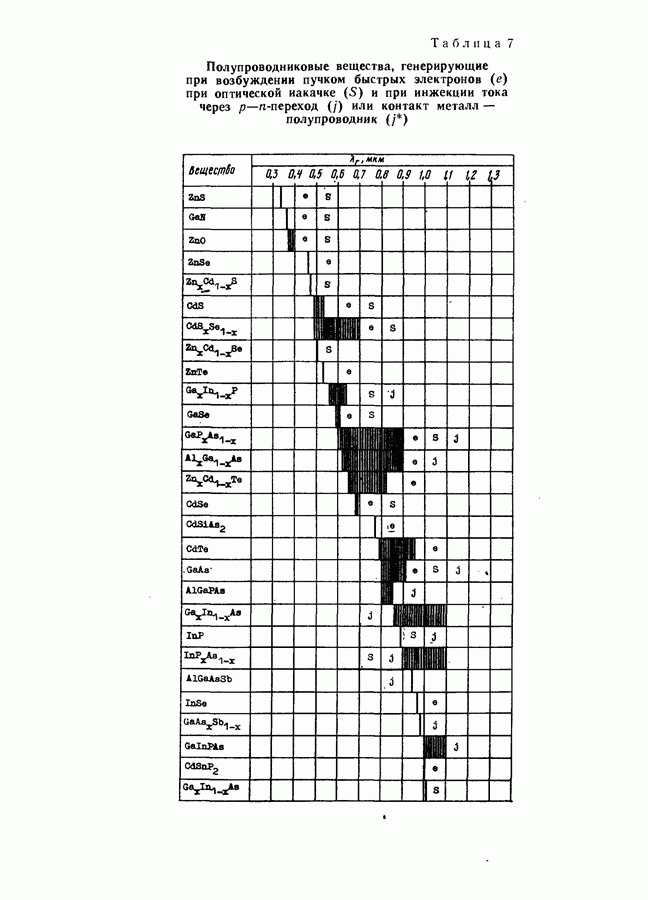
- Возбуждение генерации пучком быстрых электронов.