| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Непрямые экситонные оптические переходы.
Если минимум экситонной зоны (рис. 22) расположен не в точке  то прямые экситонные переходы запрещены правилом отбора. Экситон не может передать фотону своего импульса, если его величина значительна. В этом случае происходят непрямые оптические переходы, сопровождающиеся поглощением или испусканием одного или нескольких фононов.
то прямые экситонные переходы запрещены правилом отбора. Экситон не может передать фотону своего импульса, если его величина значительна. В этом случае происходят непрямые оптические переходы, сопровождающиеся поглощением или испусканием одного или нескольких фононов.
Законы сохранения энергии и импульса можно представить в виде

где  числа фононов сорта
числа фононов сорта  испущенных и поглощенных при оптических переходах;
испущенных и поглощенных при оптических переходах; 
энергии и волновые векторы испускаемых и поглощаемых фононов. Уравнения (8.12) и (8.13) с верхними знаками описывают процесс аннигиляции экситона, а с нижними знаками — рождение экситона.
Они справедливы и для случая, когда минимум экситонной зоны находится в точке  поскольку непрямые экситонные переходы происходят в обоих случаях. Если
поскольку непрямые экситонные переходы происходят в обоих случаях. Если  то в спектре экситонного излучения будут наблюдаться как бесфононные линии, так и их фононные повторения. Если же
то в спектре экситонного излучения будут наблюдаться как бесфононные линии, так и их фононные повторения. Если же  то бесфононных линий не будет.
то бесфононных линий не будет.
В § 4 было показано, Что при уменьшении до нуля волнового вектора фонона энергия акустических фононов стремится к нулю, а оптических — к некоторому постоянному значению  Это отличие имеет принципиальное значение для взаимодействия фононов с экситонами. Если волновой вектор экситона мал, то при его аннигиляции может испуститься или поглотиться только оптический фонон, поскольку значение его волнового вектора может быть пренебрежимо малым, чего нельзя сказать об акустических фононах. Следовательно, прямые экситоны, находящиеся при низких температурах на дне энергетической зоны, взаимодействуют прежде всего с оптическими фононами, у которых
Это отличие имеет принципиальное значение для взаимодействия фононов с экситонами. Если волновой вектор экситона мал, то при его аннигиляции может испуститься или поглотиться только оптический фонон, поскольку значение его волнового вектора может быть пренебрежимо малым, чего нельзя сказать об акустических фононах. Следовательно, прямые экситоны, находящиеся при низких температурах на дне энергетической зоны, взаимодействуют прежде всего с оптическими фононами, у которых
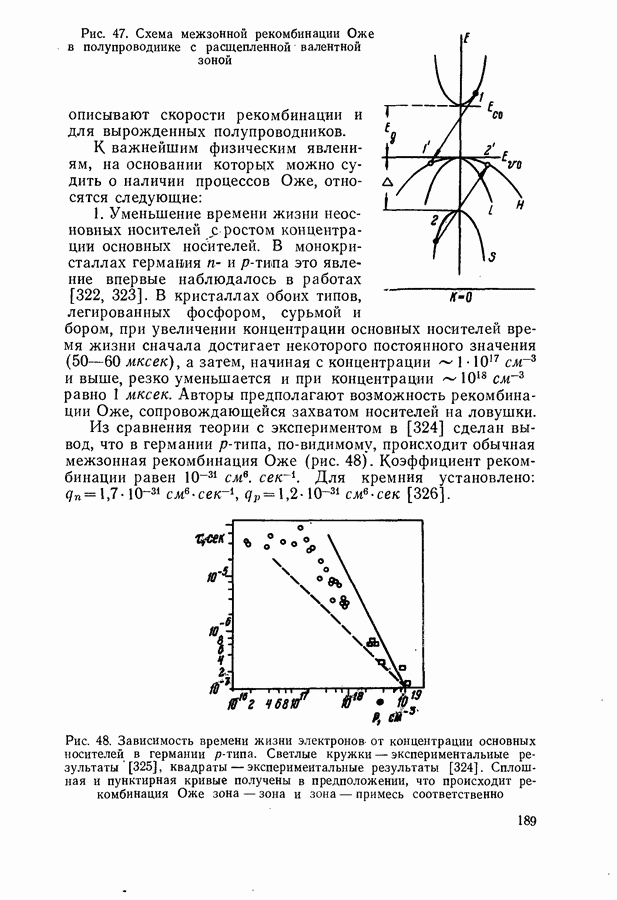
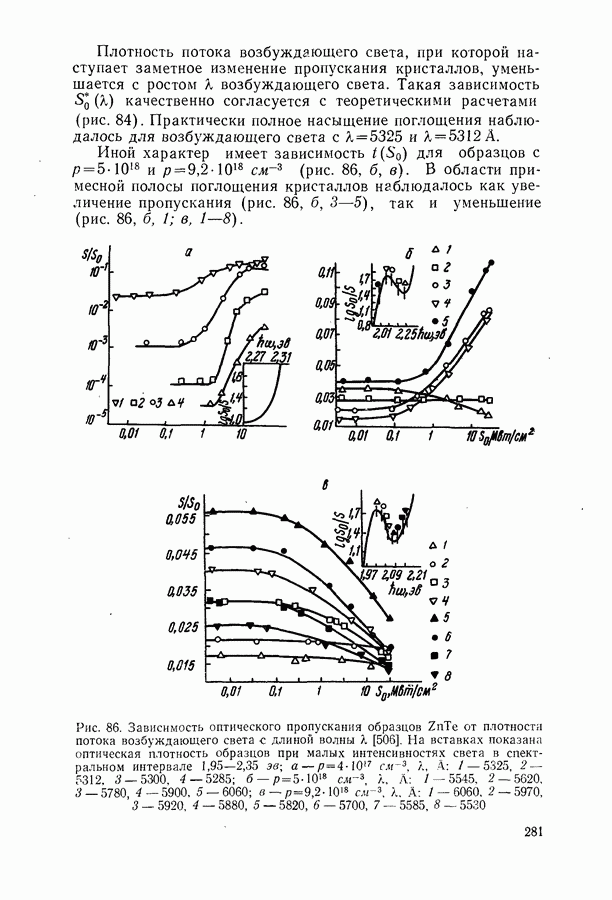
Рассмотрим закономерности непрямых экситонных переходов на примере кристалла  спектр люминесценции которого при температуре 60 К представлен на рис. 24. Первая узкая линия соответствует бесфононной аннигиляции экситонов из состояния
спектр люминесценции которого при температуре 60 К представлен на рис. 24. Первая узкая линия соответствует бесфононной аннигиляции экситонов из состояния  Ее положение в спектре практически совпадает с узкой линией экситонного поглощения. Две другие, более широкие, линии сдвинуты относительно первой в сторону меньших энергий на величину энергии одного или двух продольных оптических фононов
Ее положение в спектре практически совпадает с узкой линией экситонного поглощения. Две другие, более широкие, линии сдвинуты относительно первой в сторону меньших энергий на величину энергии одного или двух продольных оптических фононов  и
и 
При изменении температуры ширина бесфононной линии изменяется незначительно, а фононные линии заметно расширяются. Качественно контуры фононных линий напоминают асимметричный график функции максвелловского распределения частиц по энергии (8.5). Однако более детальное изучение контуров одно- и двухфононных линий позволяет установить некоторые тонкие детали механизма их образования [101].

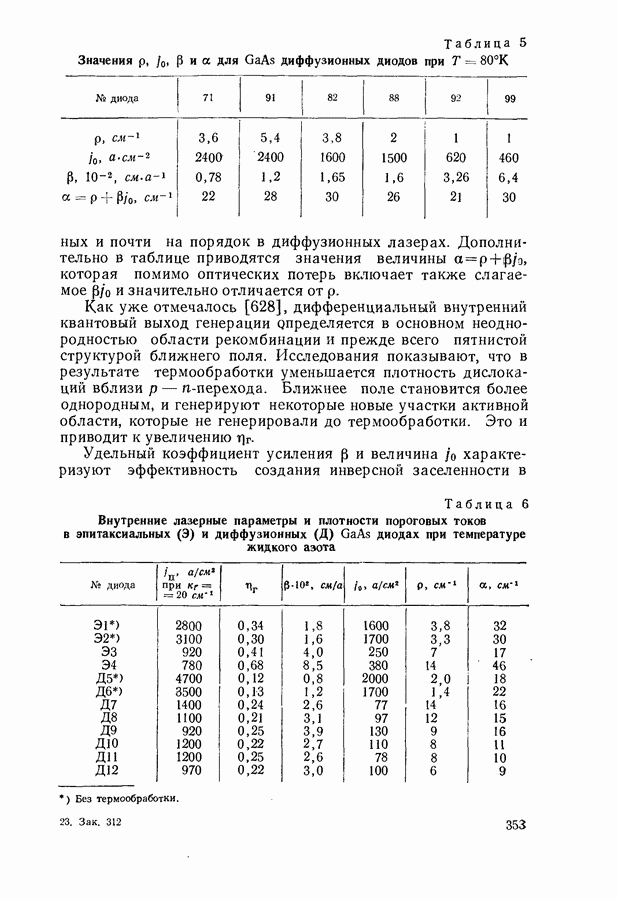
Рис. 24. Спектр экситонной люминесценции кристаллов CdS при  [101]
[101]

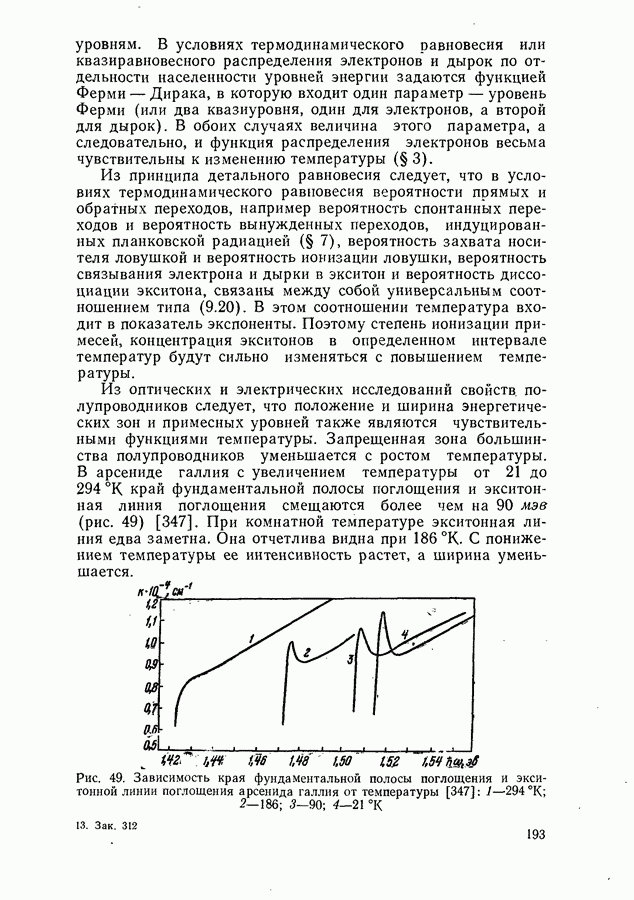
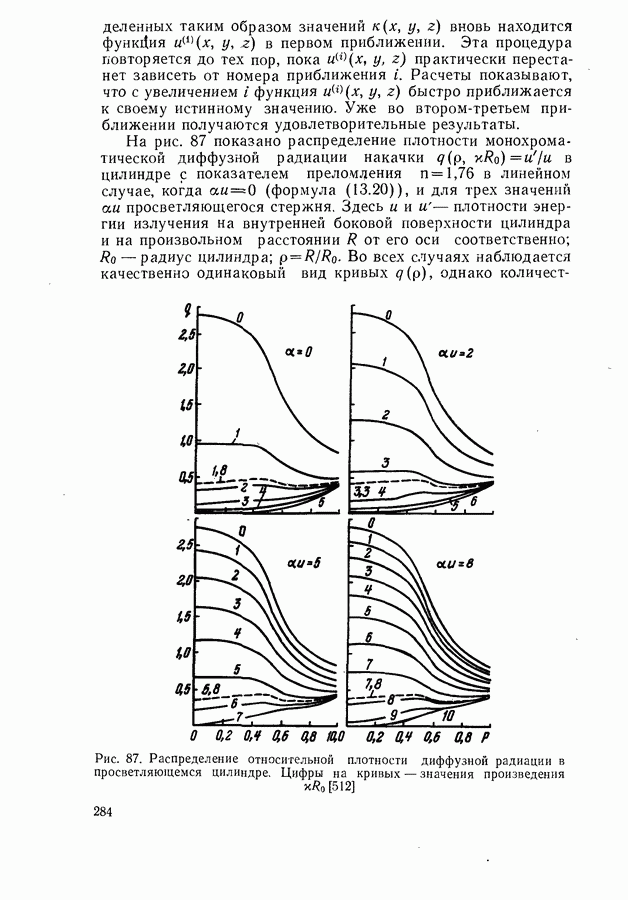
Рис. 25. Сравнение контуров линий однофононной (а) и двухфононной (б) аннигиляции экситонов в CdSe (сплошные кривые) с графиками функций  кривые);
кривые); 
Согласно (8.12), при аннигиляции экситона с испусканием одного фотона и возбуждением одного оптического фонона в спектре излучения должна появиться линия, сдвинутая относительно бесфононной линии в длинноволновую сторону на величину  В испускании этой линии могут участвовать экситоны с различным значением волнового вектора К. Импульс экситона при его аннигиляции передается фонону. Как было показано ранее (см. рис. 15, 17), частота и энергия квантов оптических фононов слабо зависит от величины волнового вектора. Поэтому все оптические фононы, возбуждаемые в процессе аннигиляции экситонов, будут иметь практически одну и ту же энергию, а вся избыточная кинетическая энергия экситонов будет передаваться фотонам. Если бы вероятность экситон-фононного взаимодействия не зависела от волнового вектора экситона, то контур линии однофононной аннигиляции совпадал бы с графиком максвелловского распределения частиц по энергиям. Расчеты показывают [189], что вероятность такого взаимодействия примерно пропорциональна
В испускании этой линии могут участвовать экситоны с различным значением волнового вектора К. Импульс экситона при его аннигиляции передается фонону. Как было показано ранее (см. рис. 15, 17), частота и энергия квантов оптических фононов слабо зависит от величины волнового вектора. Поэтому все оптические фононы, возбуждаемые в процессе аннигиляции экситонов, будут иметь практически одну и ту же энергию, а вся избыточная кинетическая энергия экситонов будет передаваться фотонам. Если бы вероятность экситон-фононного взаимодействия не зависела от волнового вектора экситона, то контур линии однофононной аннигиляции совпадал бы с графиком максвелловского распределения частиц по энергиям. Расчеты показывают [189], что вероятность такого взаимодействия примерно пропорциональна  т. е. линейно зависит от энергии. Поэтому можно ожидать, что контур однофононной линии будет описываться функцией Максвелла (8,5), умноженной на
т. е. линейно зависит от энергии. Поэтому можно ожидать, что контур однофононной линии будет описываться функцией Максвелла (8,5), умноженной на 
Действительно, сравнение экспериментального контура однофононной линии аннигиляции экситона в кристаллах CdSe при  с графиком функции
с графиком функции  показало их хорошее соответствие [101] (рис. 25, а). В то же время контур линии двухфононной аннигиляции лучше описывается функцией Максвелла (8,5), что свидетельствует о независимости вероятности одновременного возбуждения двух фононов от волнового вектора экситона. При двухфононной аннигиляции экситон возбуждает различные фононные пары.
показало их хорошее соответствие [101] (рис. 25, а). В то же время контур линии двухфононной аннигиляции лучше описывается функцией Максвелла (8,5), что свидетельствует о независимости вероятности одновременного возбуждения двух фононов от волнового вектора экситона. При двухфононной аннигиляции экситон возбуждает различные фононные пары.
Закон сохранения импульса выполняется для многочисленных комбинаций значений импульсов первого и второго фононов. Вероятность взаимодействия как бы усредняется по значению импульса и перестает от него зависеть. Этот вывод подтверждается теоретическими расчетами [190].
Полуширина двухфононной линии равна полуширине максвелловского распределения (8.5) и растет с температурой как  Полуширина однофононной линии растет еще быстрее, а именно как
Полуширина однофононной линии растет еще быстрее, а именно как  [101]. Изменение температуры не только по-разному деформирует контуры фононных линий, но и отражается на относительной их интенсивности.
[101]. Изменение температуры не только по-разному деформирует контуры фононных линий, но и отражается на относительной их интенсивности.
Обозначая интегральные по спектру интенсивности одно- и двухфононных линий через  зависимость отношения
зависимость отношения  от температуры можно представить в виде
от температуры можно представить в виде

где 
Такой линейный рост отношения интенсивностей фононных линий наблюдается в кристаллах CdS и CdSe [101].
Хорошее согласие теоретических и экспериментальных результатов, относящихся к экситонной люминесценции, служит прямым доказательством того, что экситоны в кристаллах совершают поступательное движение, характеризуются целым спином и подчиняются статистике Бозе — Эйнштейна.
В таких непрямозонных полупроводниках, как кремний и германий, образуются только непрямые экситоны с  Поэтому в спектре их экситонной люминесценции бесфононная линия не наблюдается.
Поэтому в спектре их экситонной люминесценции бесфононная линия не наблюдается.
Контур однофононной линии поглощения, согласно [181], выражается формулой

где А не зависит от 
При учете переходов со всех экситонных уровней зависимость суммарного коэффициента поглощения от частоты дается выражением [107, 126, 181]

где

Для энергий кванта  из (8.16) следует простая формула
из (8.16) следует простая формула

Если  то формула (8.16) переходит в выражение к
то формула (8.16) переходит в выражение к 

совпадающее с формулой для  полученной без учета экситонов (см. (6.35)).
полученной без учета экситонов (см. (6.35)).
Поскольку время жизни экситона достаточно велико для установления равновесного распределения по уровням энергии, то можно пользоваться универсальным соотношением между спектрами поглощения и люминесценции.
Если фоном теплового испускания можно пренебречь, а возбуждение не очень интенсивно  то на основании (7.18) и (8.15) спектр однофононной люминесценции можно выразить приближенной формулой
то на основании (7.18) и (8.15) спектр однофононной люминесценции можно выразить приближенной формулой

где 
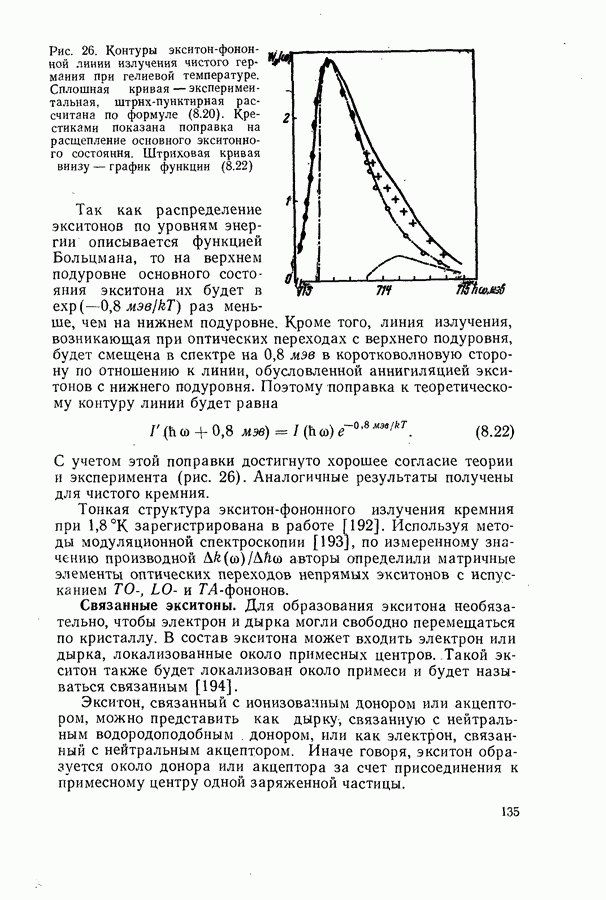
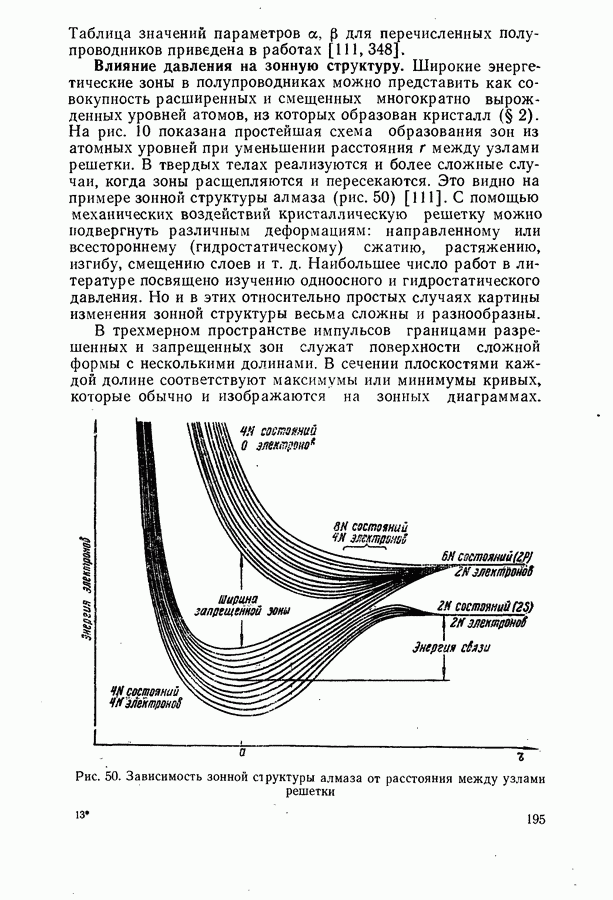
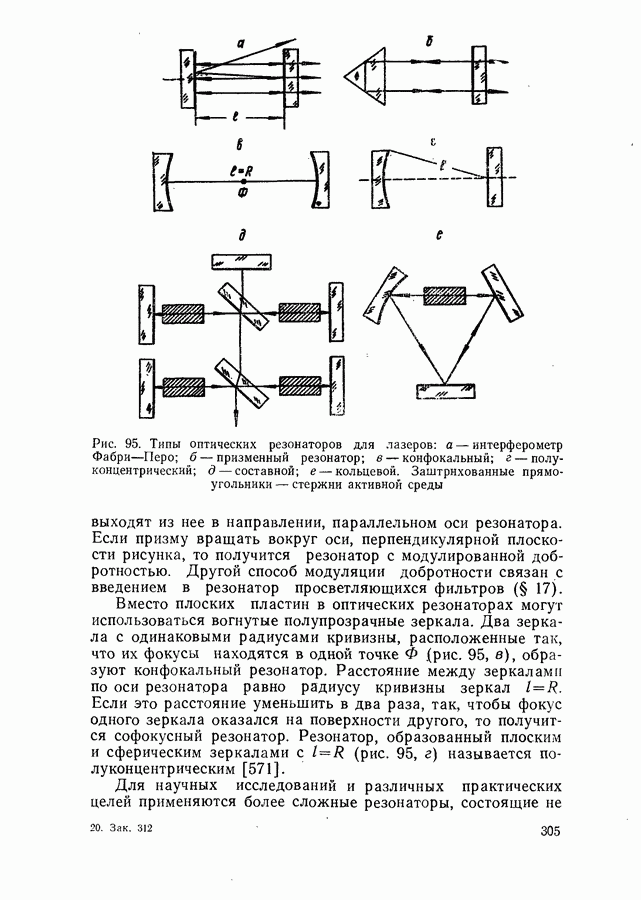
Недавно с большой точностью был снят контур экситон-фононной линии излучения в чистом германии при температуре жидкого геллия [191]. Авторы сравнили экспериментальные результаты с контуром линии, рассчитанным по формуле (8.20), в которой энергия фонона  взята со знаком минус (рис. 26).
взята со знаком минус (рис. 26).
Как видно, на коротковолновом крае контура линии имеется некоторое расхождение теории и эксперимента. Оно связано с расщеплением основного экситонного состояния. Расстояние между подуровнями равно  Чтобы внести поправку на это расщепление, теоретически рассчитанный контур линии аппроксимируется функцией
Чтобы внести поправку на это расщепление, теоретически рассчитанный контур линии аппроксимируется функцией

где 

Рис. 26. Контуры экситон-фононной линии излучения чистого германия при гелиевой температуре.
Сплошная кривая — экспериментальная, штрих-пунктирная рассчитана по формуле (8.20). Крестиками показана поправка на расщепление основного экситонного состояния. Штриховая кривая внизу — график функции (8.22)
Так как распределение экситонов по уровням энергии описывается функцией Больцмана, то на верхнем подуровне основного состояния экситона их будет в  раз меньше, чем на нижнем подуровне. Кроме того, линия излучения, возникающая при оптических переходах с верхнего подуровня, будет смещена в спектре на
раз меньше, чем на нижнем подуровне. Кроме того, линия излучения, возникающая при оптических переходах с верхнего подуровня, будет смещена в спектре на  в коротковолновую сторону по отношению к линии, обусловленной аннигиляцией экситонов с нижнего подуровня. Поэтому поправка к теоретическому контуру линии будет равна
в коротковолновую сторону по отношению к линии, обусловленной аннигиляцией экситонов с нижнего подуровня. Поэтому поправка к теоретическому контуру линии будет равна

С учетом этой поправки достигнуто хорошее согласие теории и эксперимента (рис. 26). Аналогичные результаты получены для чистого кремния.
Тонкая структура экситон-фононного излучения кремния при  зарегистрирована в работе [192]. Используя методы модуляционной спектроскопии [193], по измеренному значению производной
зарегистрирована в работе [192]. Используя методы модуляционной спектроскопии [193], по измеренному значению производной  авторы определили матричные элементы оптических переходов непрямых экситонов с испусканием
авторы определили матричные элементы оптических переходов непрямых экситонов с испусканием  и
и  -фононов.
-фононов.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВ
- § 1. КРИСТАЛЛИЧЕСКАЯ ПРИРОДА ПОЛУПРОВОДНИКОВ
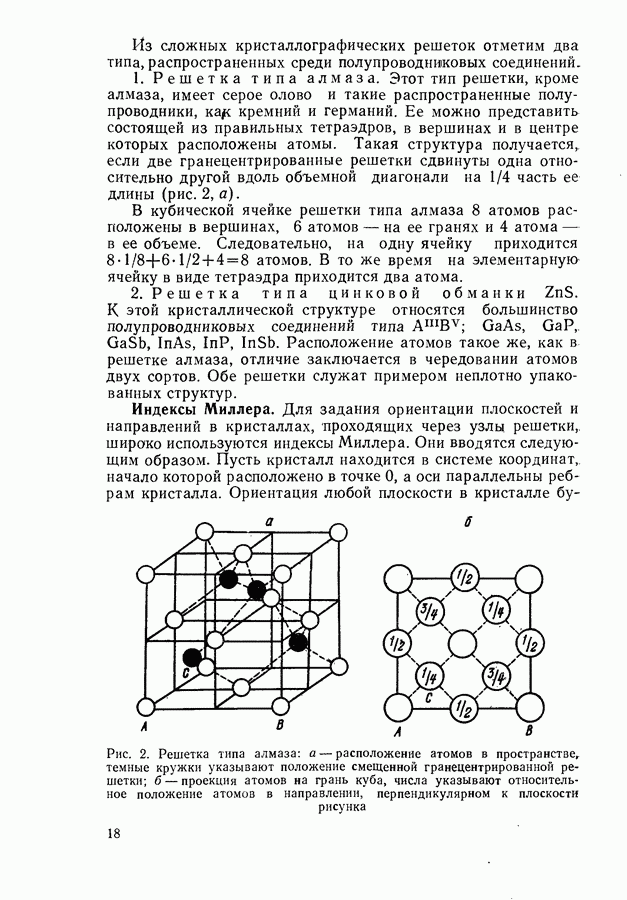
- Химическая связь в кристаллах.
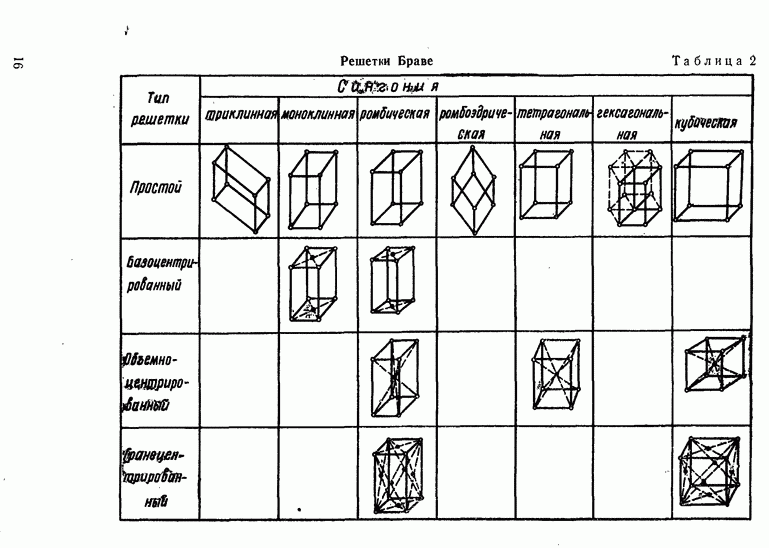
- Прямая и обратная решетки.
- Классификация кристаллических решеток.
- Индексы Миллера.
- Определение ориентации кристаллов.
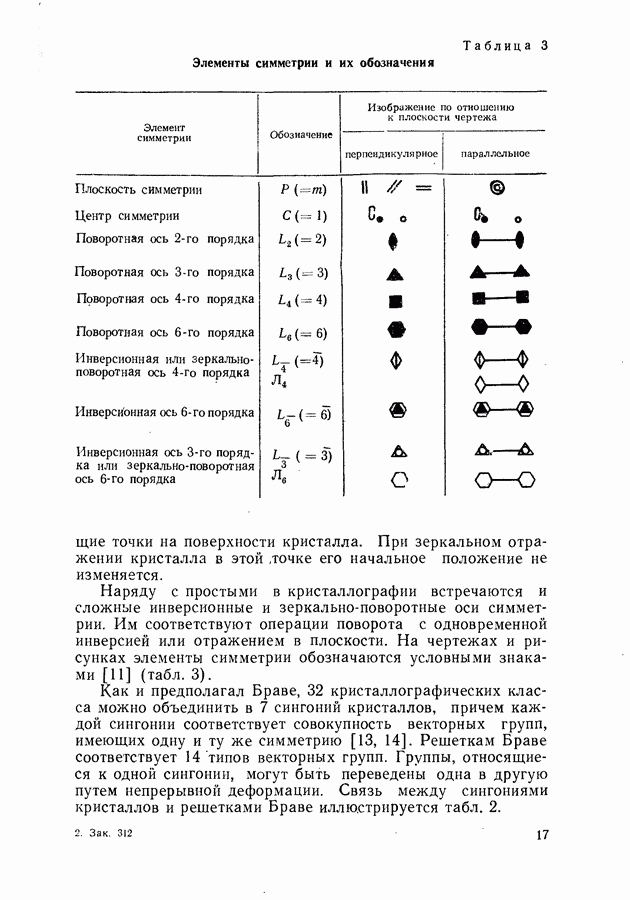
- Несовершенства в кристаллических структурах.
- § 2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
- Модель Зоммерфельда. Плотность состояний.
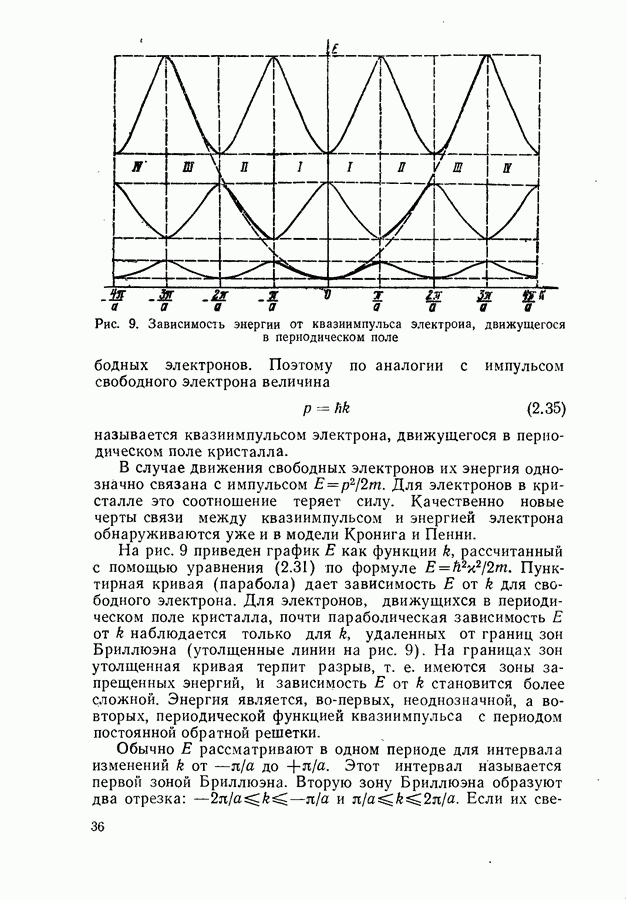
- Модель Кронига и Пенни. Энергетические зоны.
- Функции Блоха.
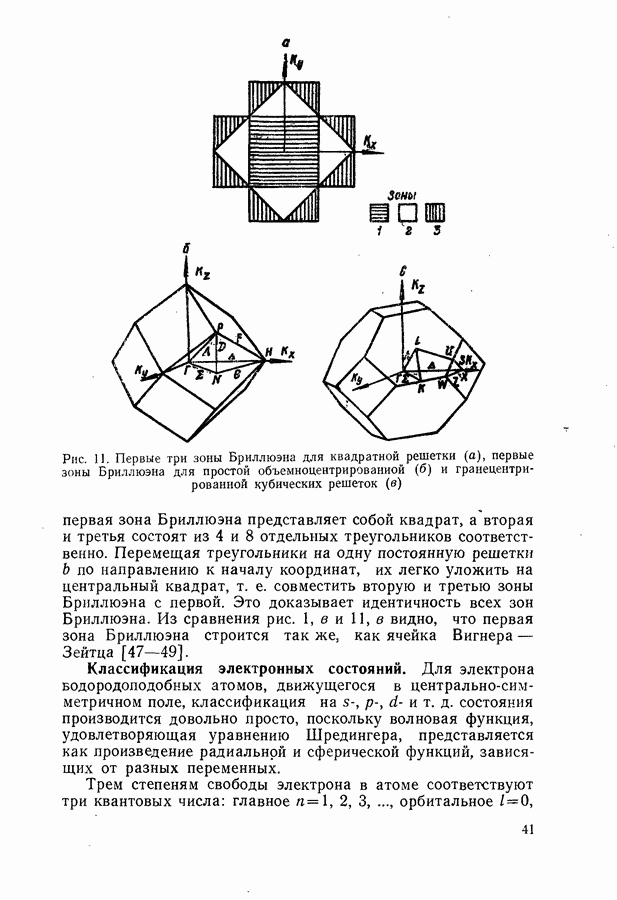
- Зоны Бриллюэна.
- Классификация электронных состояний.
- Эффективная масса.
- Дырки.
- Энергетические уровни примесей.
- § 3. СТАТИСТИКА ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКАХ
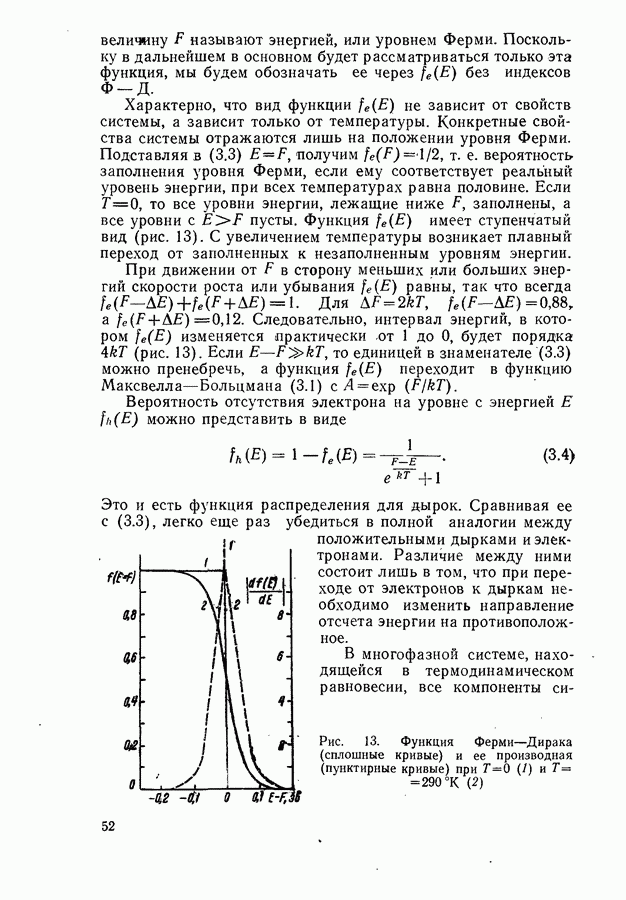
- Уровень Ферми в собственном невырожденном полупроводнике.
- Интегралы Ферми — Дирака.
- Произведение n0p0.
- Фактор спинового вырождения примесного уровня.
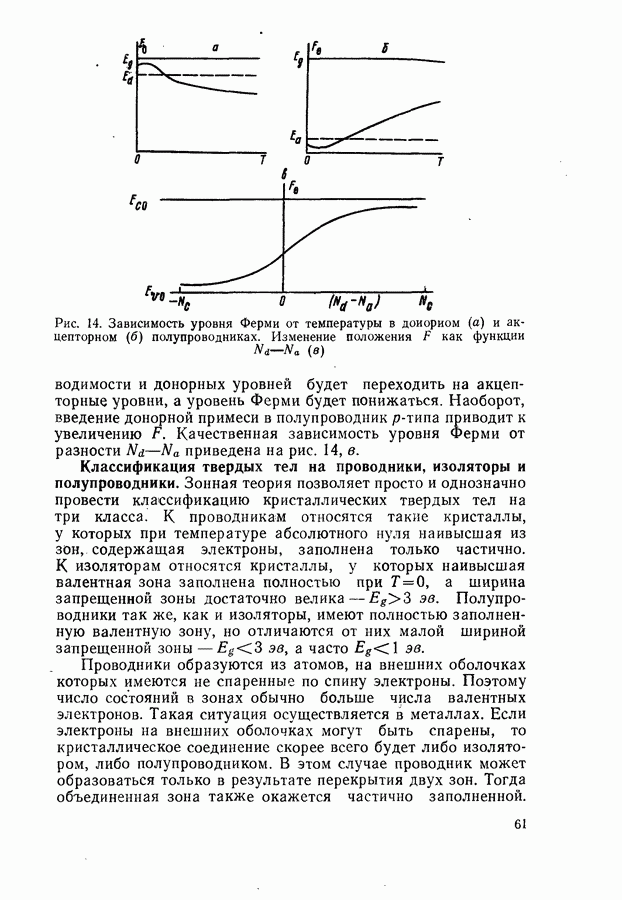
- Смещение уровня Ферми при легировании полупроводника.
- Классификация твердых тел на проводники, изоляторы и полупроводники.
- § 4. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Колебания одномерной решетки, состоящей из одинаковых атомов.
- Линейная цепочка, состоящая из атомов двух сортов.
- Фононы.
- § 5. ЭКСИТОНЫ И ПОЛЯРОНЫ
- Трансляционное и внутреннее движение экситонов большого радиуса.
- Поляроны.
- Глава II. ОСНОВНЫЕ МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ СВЕТА С ПОЛУПРОВОДНИКАМИ
- § 6. ОПТИЧЕСКИЕ ПЕРЕХОДЫ ЗОНА — ЗОНА
- Край полосы собственного поглощения.
- Скорость суммарной спонтанной рекомбинации.
- § 7. ЛЮМИНЕСЦЕНЦИЯ
- Универсальное соотношение между спектрами поглощения и люминесценции.
- Отрицательная люминесценция.
- Линейная и квадратичная скорости люминесценции.
- Энергетический и квантовый выход люминесценции.
- Длительность люминесценции и времена жизни избыточных носителей.
- Поляризация излучения.
- Горячая люминесценция.
- § 8. ЭКСИТОННЫЙ МЕХАНИЗМ ПОГЛОЩЕНИЯ И ИСПУСКАНИЯ СВЕТА
- Прямые оптические переходы свободных экситонов.
- Непрямые экситонные оптические переходы.
- Связанные экситоны.
- Светоэкситоны (поляритоны).
- Неравновесное распределение экситонов по кинетической энергии.
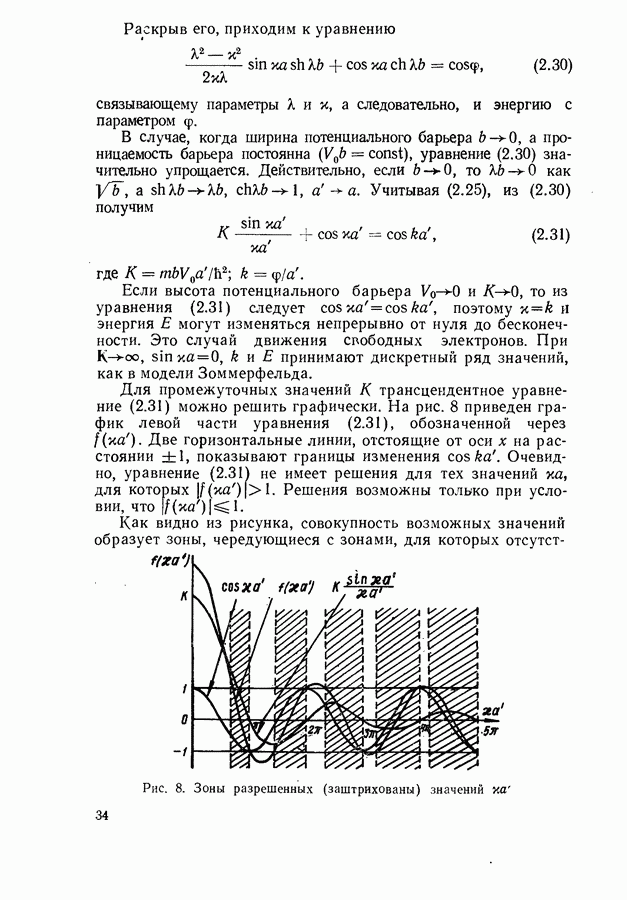
- Кинетические уравнения.
- Правило Урбаха.
- § 9. ОПТИЧЕСКИЕ ПЕРЕХОДЫ В ПРИМЕСНОМ ПОЛУПРОВОДНИКЕ
- Захват и эмиссия носителей заряда дефектами кристалла.
- Примесное краевое поглощение и испускание.
- Рекомбинация донорно-акцепторных пар.
- § 10. ПОГЛОЩЕНИЕ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ СВОБОДНЫМИ НОСИТЕЛЯМИ И КРИСТАЛЛИЧЕСКОЙ РЕШЕТКОЙ
- Поглощение света при переходах между подзонами одной вырожденной зоны.
- Поглощение света кристаллической решеткой.
- Собственные колебания плазмы.
- § 11. БЕЗЫЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ
- Поверхностная рекомбинация.
- § 12. ИЗМЕНЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВ ПОД ДЕЙСТВИЕМ ВНЕШНИХ СИЛ
- Влияние давления на зонную структуру.
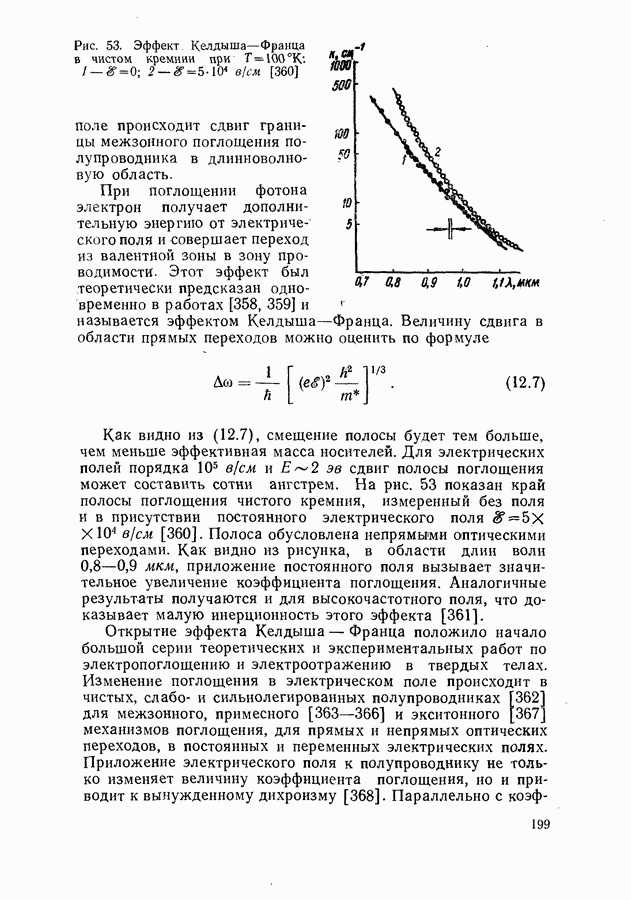
- Эффект Келдыша-Франца.
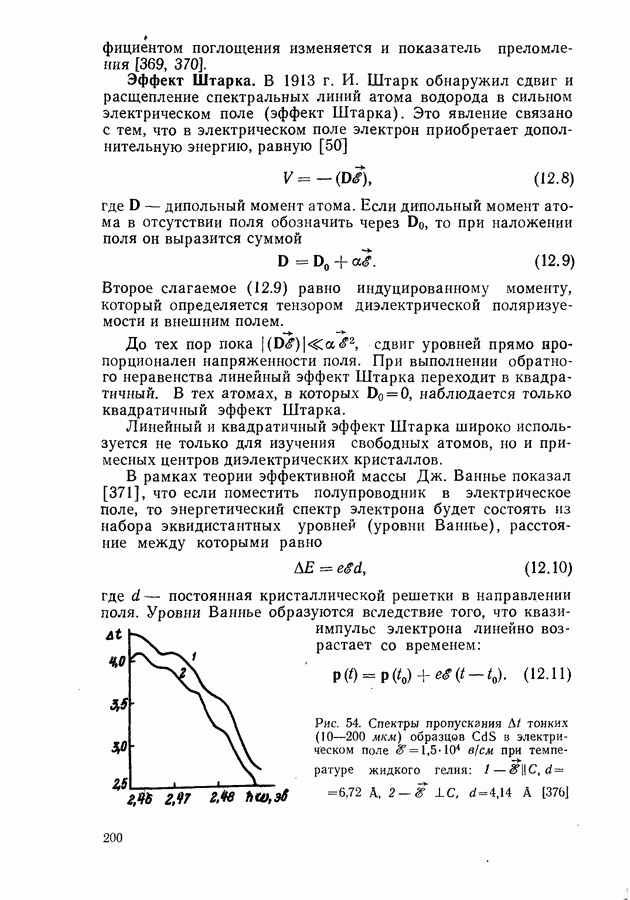
- Эффект Штарка.
- Ионизация экситонов в электрическом поле.
- Магнетооптические явления.
- Модуляционная спектроскопия.
- Глава III. ПОГЛОЩЕНИЕ СВЕТА И ФОТОЛЮМИНЕСЦЕНЦИЯ ПРИ ИНТЕНСИВНОМ ВОЗБУЖДЕНИИ
- § 13. ЭФФЕКТЫ НАСЫЩЕНИЯ В СИСТЕМАХ С ДИСКРЕТНЫМИ УРОВНЯМИ ЭНЕРГИИ
- Общее решение системы стационарных кинетических уравнений.
- Параметры нелинейности.
- Насыщение поглощения изотропной, линейно поляризованной и естественной радиации.
- Вынужденный дихроизм.
- Деполяризация люминесценции.
- Обобщение классической формулы Левшина.
- Гармонический осциллятор — уникальная модель вещества.
- § 14. ПРОСВЕТЛЕНИЕ ПОЛУПРОВОДНИКОВ НА ЧАСТОТЕ ВОЗБУЖДАЮЩЕГО СВЕТА
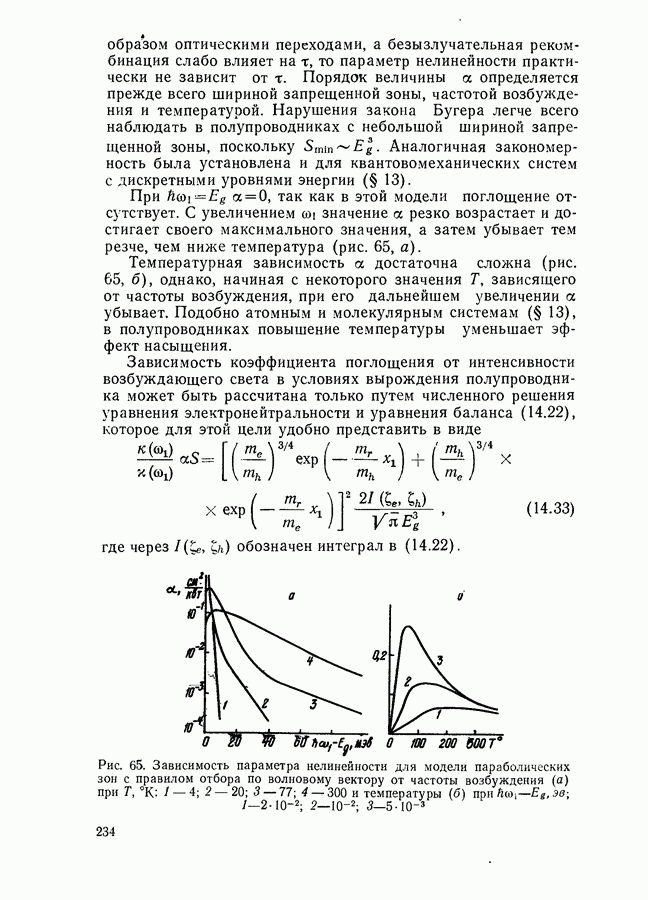
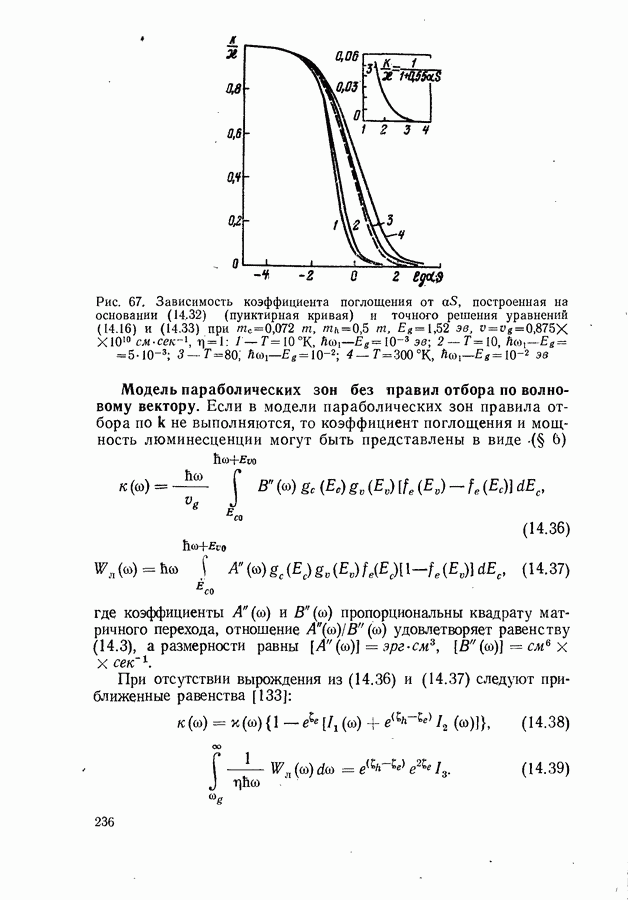
- Модель параболических зон с правилом отбора по волновому вектору.
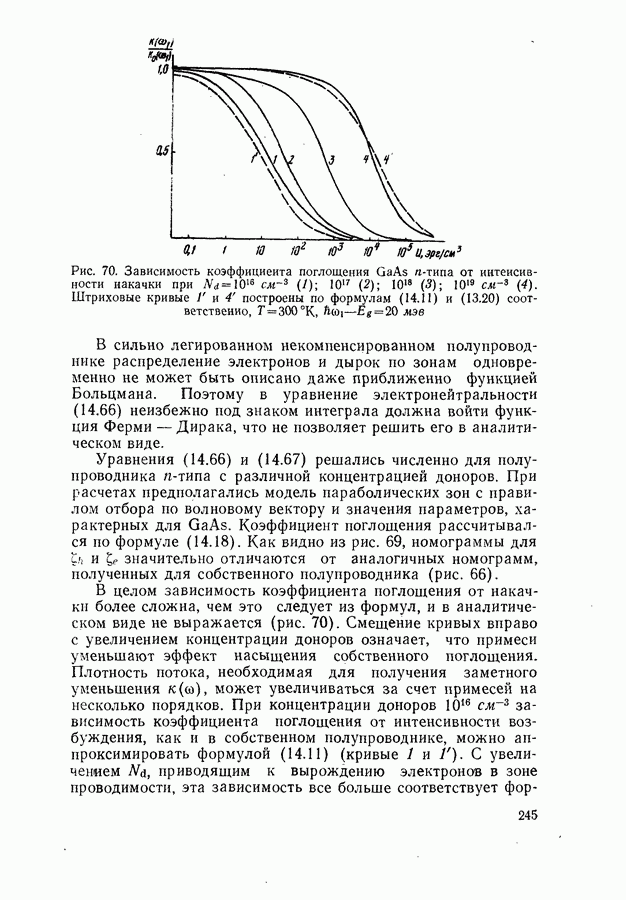
- Модель параболических зон без правил отбора по волновому вектору.
- Модель гауссовых примесных зон.
- Влияние легирующих примесей на характер зависимости коэффициента поглощения от накачки.
- Насыщение поглощения в условиях рекомбинации Оже.
- § 15. ДЕФОРМАЦИЯ СПЕКТРОВ ПОГЛОЩЕНИЯ И ЛЮМИНЕСЦЕНЦИИ. НАСЫЩЕНИЕ УСИЛЕНИЯ
- Начальный этап изменения спектров поглощения и люминесценции.
- Пределы деформации спектров поглощения и люминесценции.
- Общие закономерности насыщения усиления.
- Насыщение усиления в двухуровневой схеме.
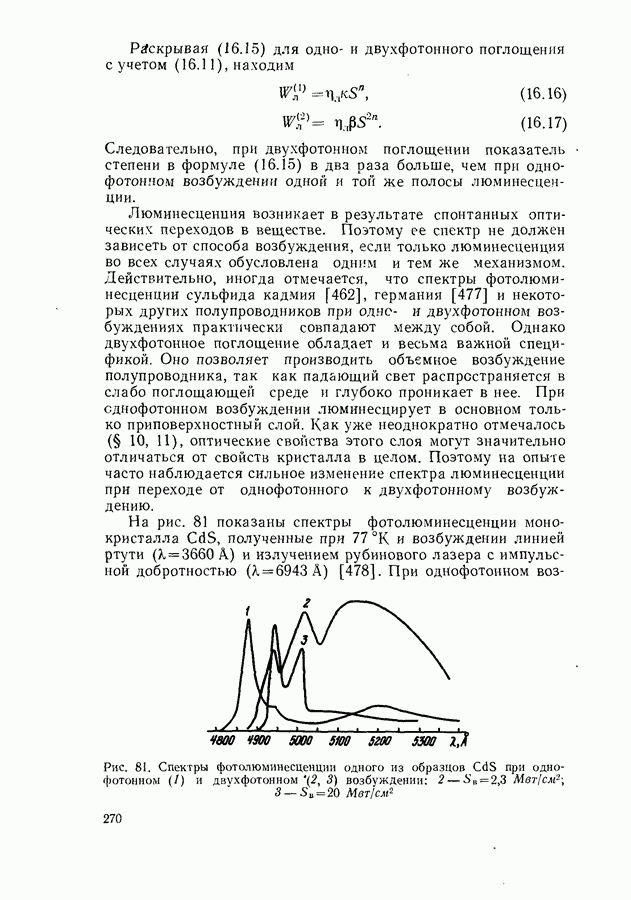
- § 16. ДВУХФОТОННОЕ ПОГЛОЩЕНИЕ
- Условия экспериментального наблюдения двухфотонного поглощения.
- Фотолюминесценция и фотопроводимость при двухфотонном возбуждении.
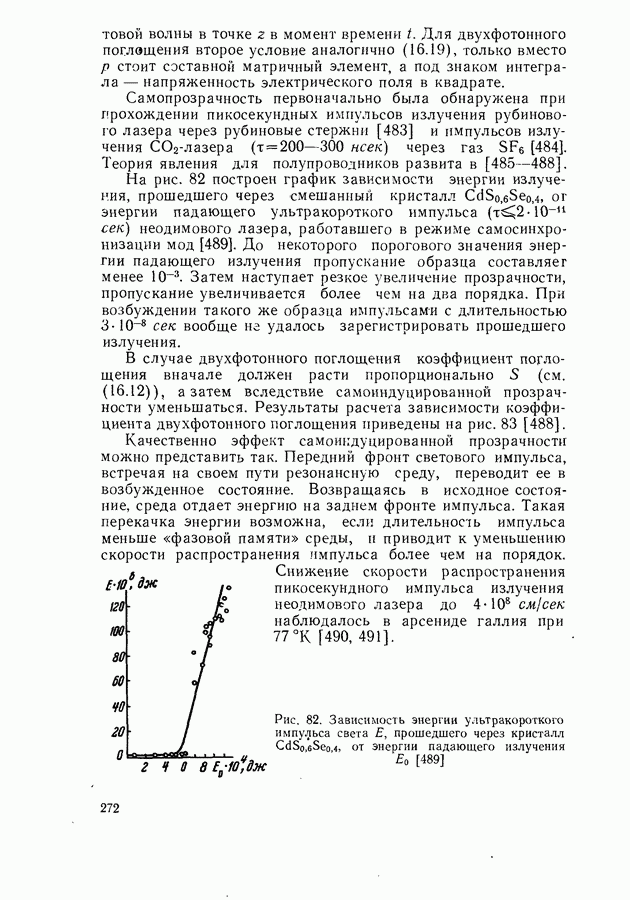
- Прохождение ультракоротких импульсов света через полупроводниковые кристаллы.
- § 17. НАСЫЩЕНИЕ ПОГЛОЩЕНИЯ В КОНЕЧНЫХ ОБЪЕМАХ ВЕЩЕСТВА
- Экспериментальные методы обнаружения эффектов насыщения.
- Расчет функции K(S) на основании экспериментальных данных.
- Условие равномерного возбуждения просветляющегося цилиндрического стержня.
- § 18. ЭКСИТОН-ЭКСИТОННОЕ ВЗАИМОДЕЙСТВИЕ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- Экситонные молекулы.
- Экситонная жидкость.
- Бозе-эйнштейновская конденсация экситонов и экситонных молекул.
- Многообразие форм коллективного взаимодействия носителей.
- Глава IV. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ
- § 19. ИСХОДНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ЭЛЕКТРОНИКИ
- Активные среды.
- Способы накачки.
- Оптические резонаторы.
- Энергетическое и интерференционное условия получения генерации.
- Генерация по трехуровневой и четырехуровневой схемам.
- Влияние резонатора на поглощение света и люминесценцию.
- § 20. ЗАВИСИМОСТЬ ПОРОГОВОГО ТОКА ОТ СПЕКТРОСКОПИЧЕСКИХ ХАРАКТЕРИСТИК ВЕЩЕСТВА И ПАРАМЕТРОВ РЕЗОНАТОРА
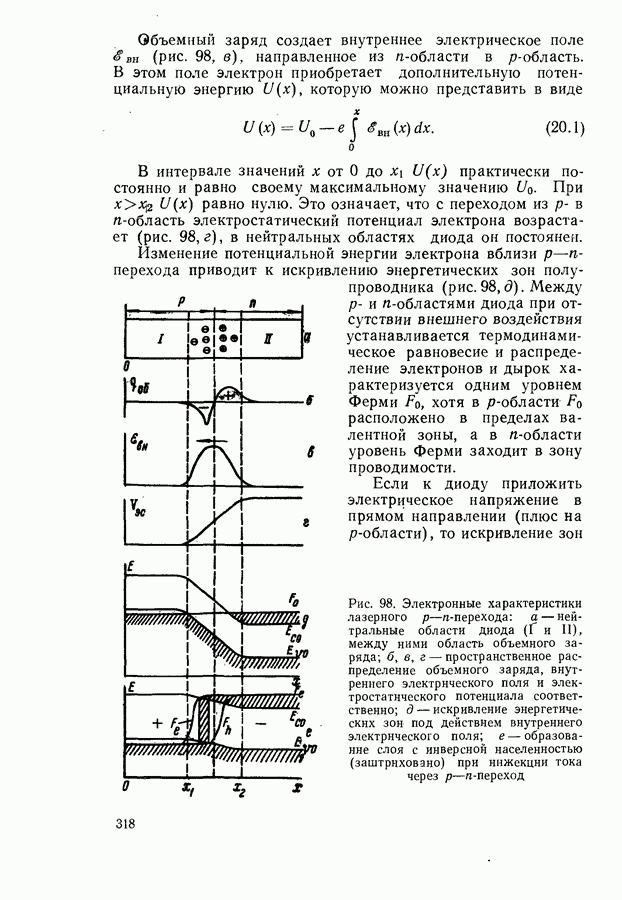
- Соотношение между пороговым током, мощностью и квантовым выходом люминесценции.
- Зависимость порога генерации от толщины активного слоя.
- Зависимость порогового тока от коэффициента потерь в модели параболических зон.
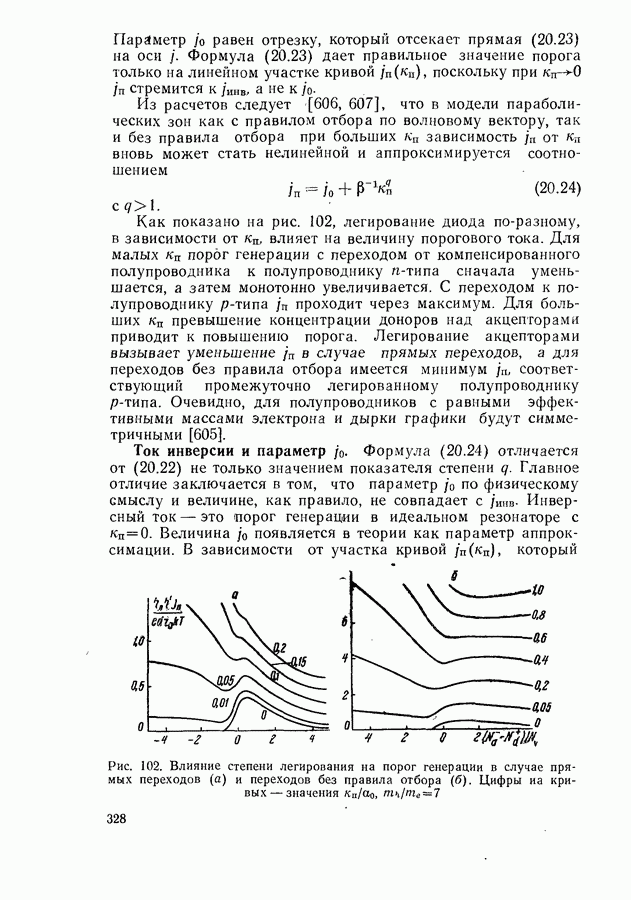
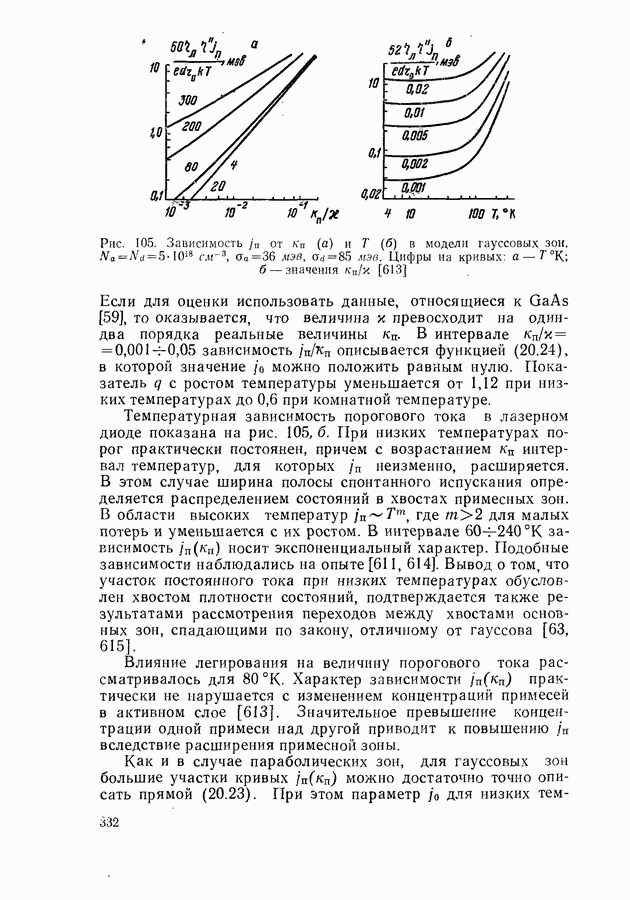
- Ток инверсии и параметр j0
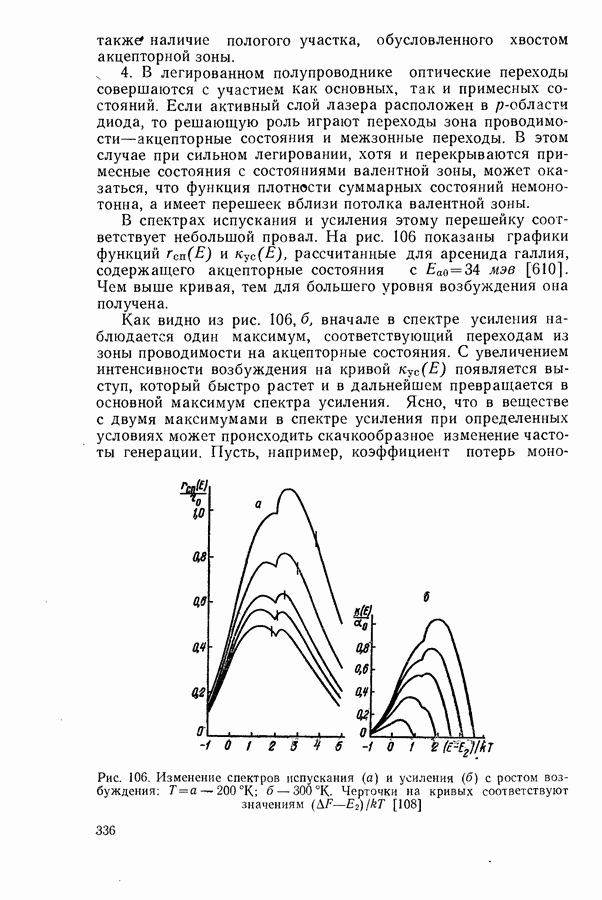
- Стимулированное испускание с участием хвостов зон и примесных зон.
- Поглощение излучения свободными носителями в активном слое.
- Температурная зависимость порогового тока для неоднородного активного слоя.
- Учет зависимости функции плотности состояний от уровня заполнения зон.
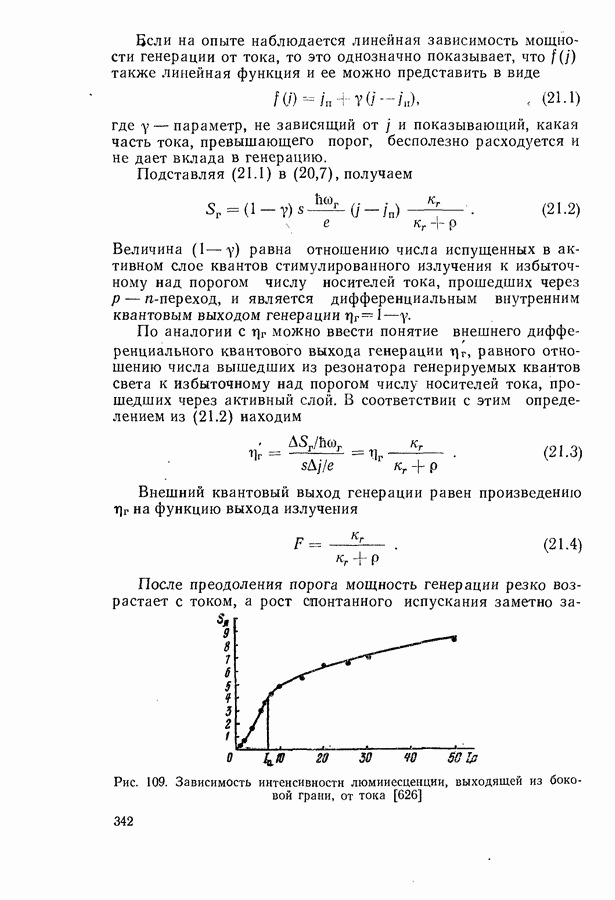
- § 21. МОЩНОСТЬ И К.П.Д. ГЕНЕРАЦИИ ЛАЗЕРНЫХ ДИОДОВ
- Внутренний квантовый выход генерации.
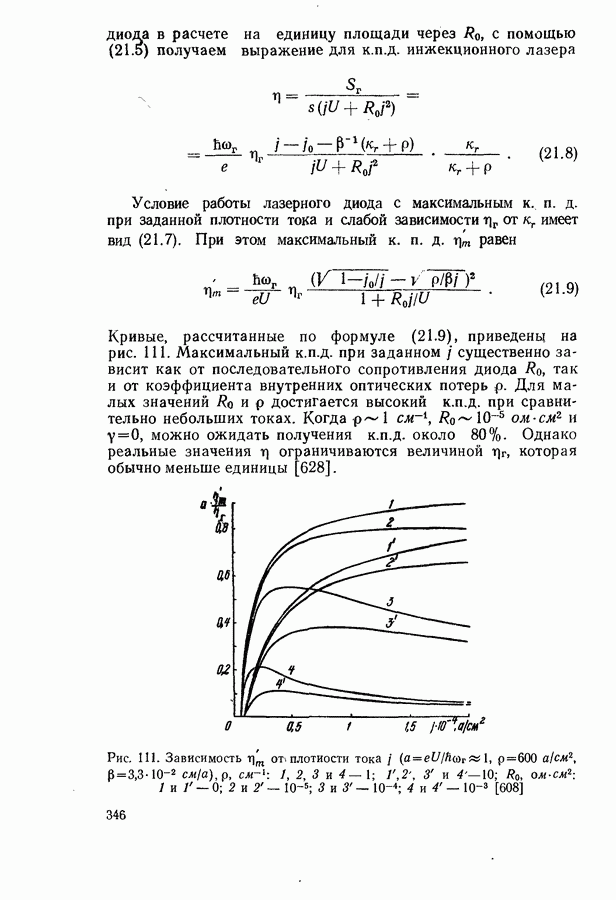
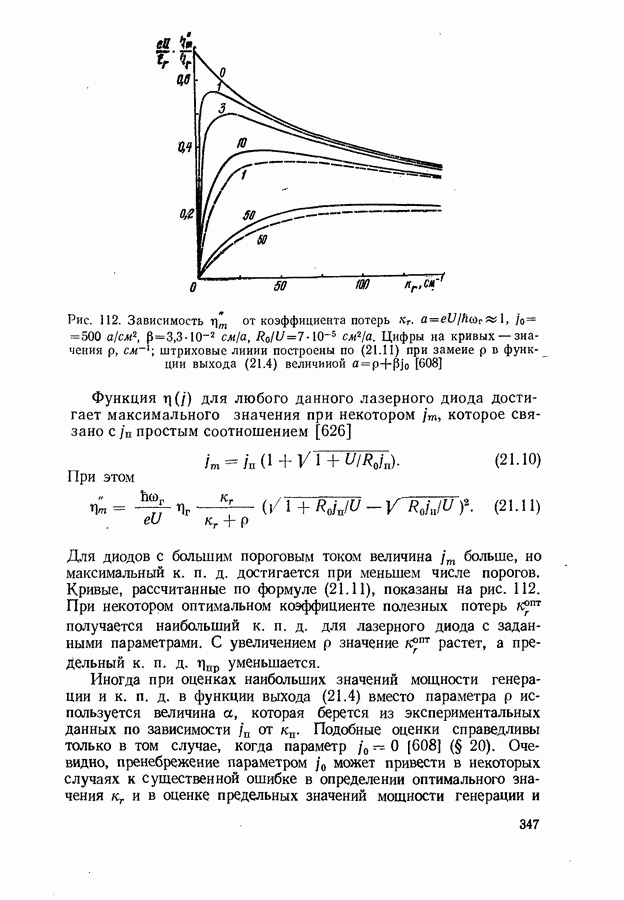
- Оптимальный режим генерации.
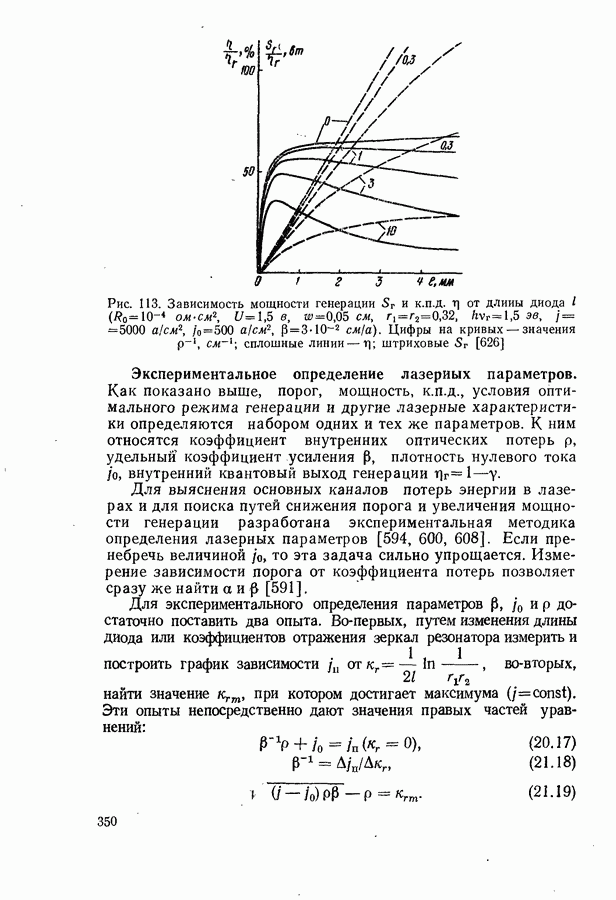
- Экспериментальное определение лазерных параметров.
- § 22. СПЕКТРАЛЬНЫЕ И ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМОГО ИЗЛУЧЕНИЯ
- Одномодовый и многомодовый режимы генерации.
- Экспериментальное определение спектра усиления активной среды на основании универсального соотношения (7.18).
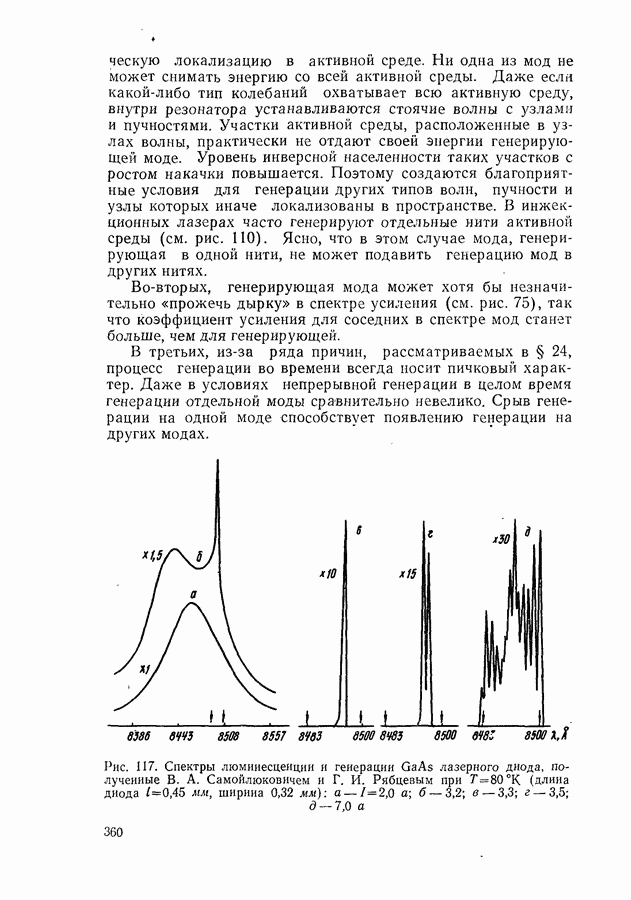
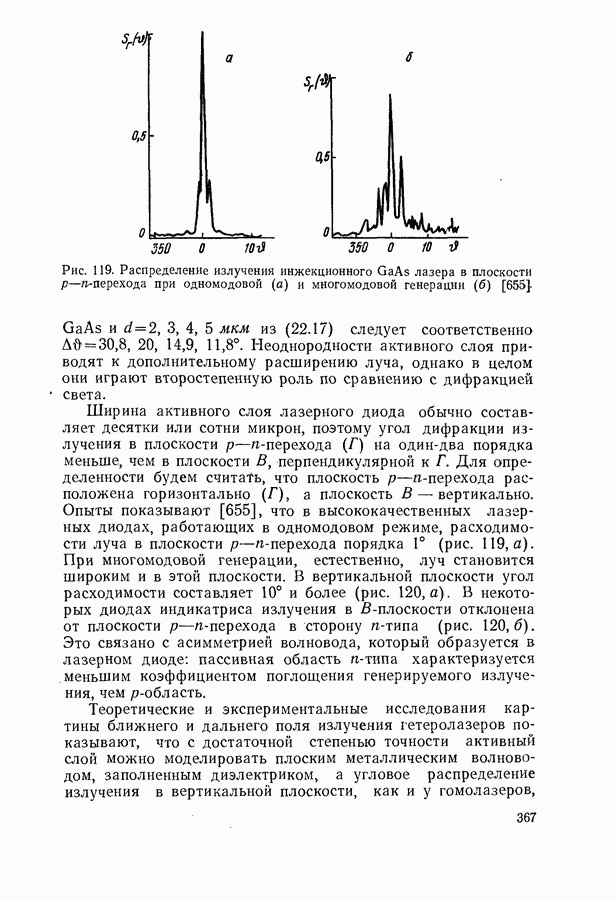
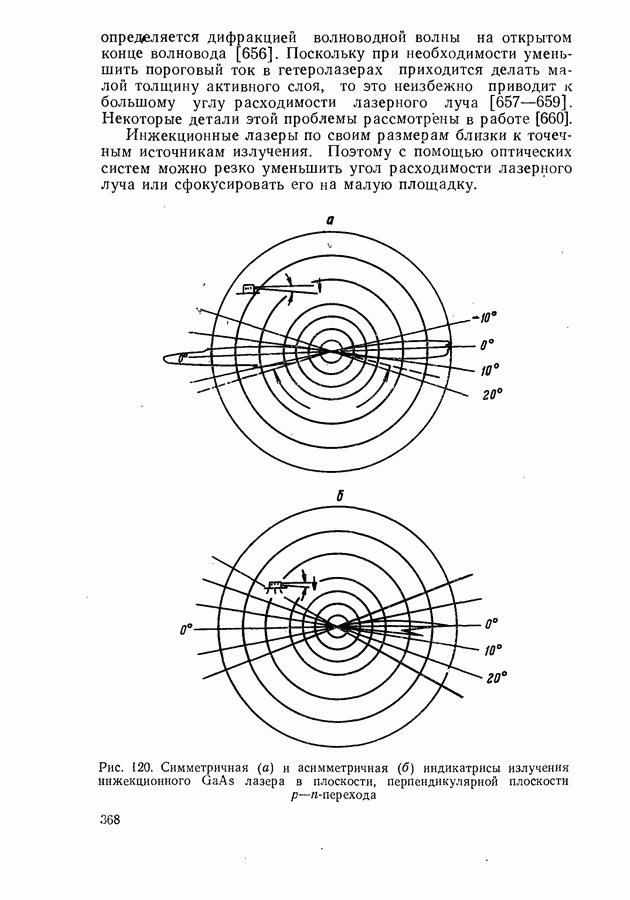
- Угол расходимости лазерного луча.
- Лазеры с распределенной обратной связью.
- § 23. РАДИАЦИОННЫЙ ШУМ В ЛАЗЕРАХ
- Коэффициент потерь радиации шума.
- Влияние шума на порог генерации.
- Рассеяние генерируемого излучения в активной среде.
- Инжекционный лазер с непланарным p-n-переходом.
- § 24. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЦИИ
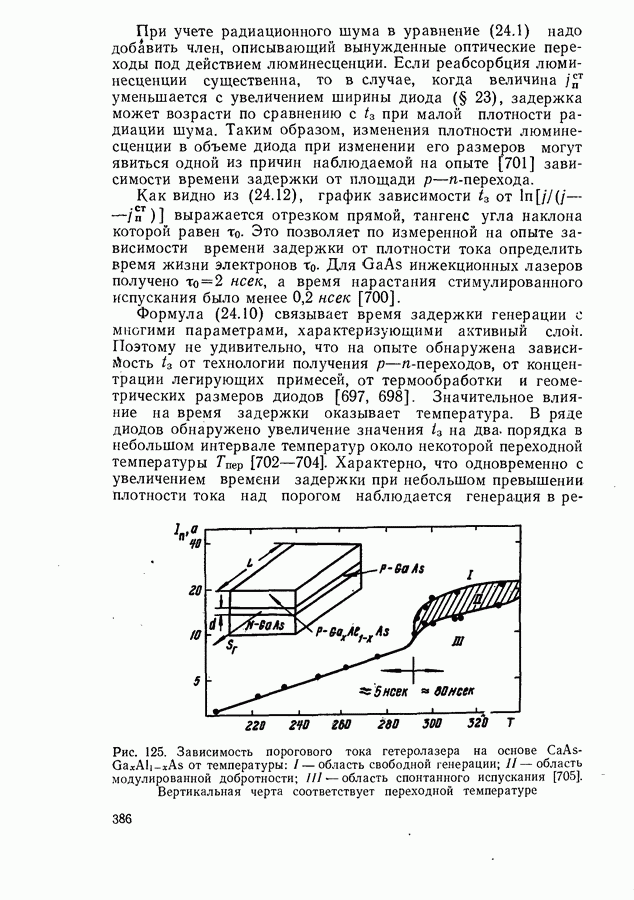
- Время задержки генерации.
- Зависимость порогового тока от длительности возбуждающего импульса.
- Переходный режим генерации.
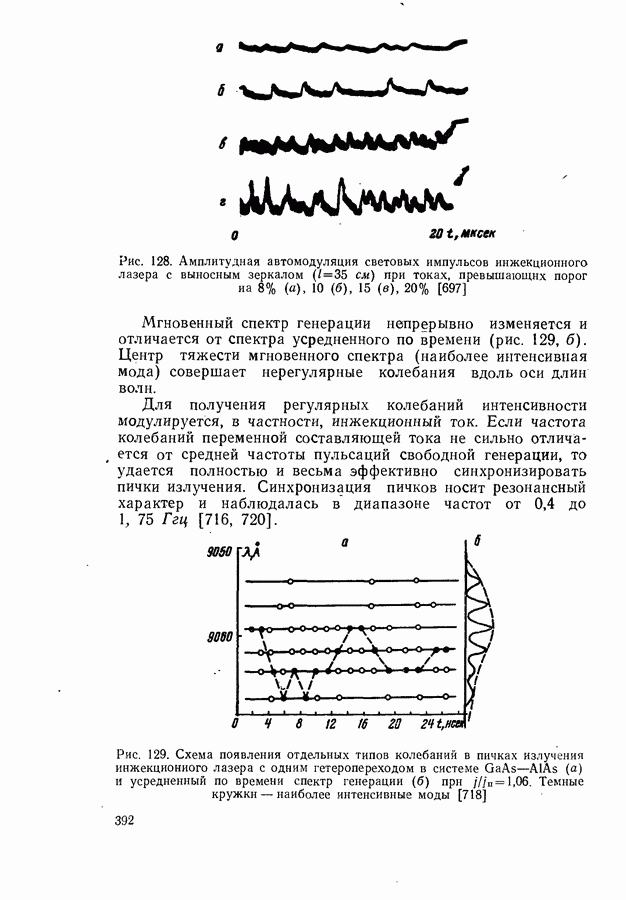
- Амплитудная и частотная автомодуляция излучения.
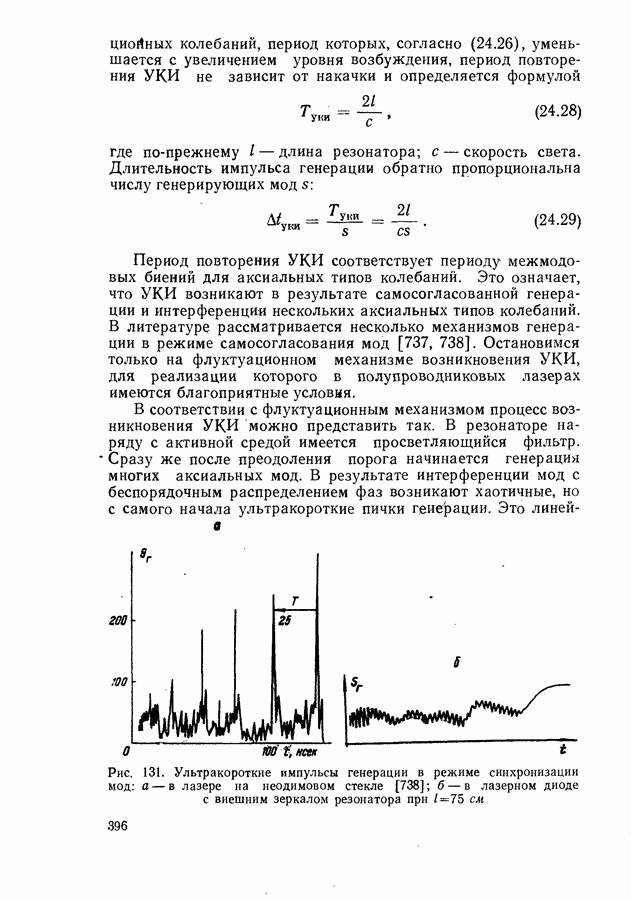
- Генерация наносекундных импульсов излучения в режиме модулированной добротности.
- Генерация пикосекундных импульсов излучения в режиме самосинхронизации мод.
- § 25. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ С ОПТИЧЕСКИМ И ЭЛЕКТРОННЫМ ВОЗБУЖДЕНИЕМ
- Порог генерации с учетом насыщения поглощения возбуждающего света [768].
- Мощность и к.п.д. генерации.
- Просветление пассивных областей пластинчатых лазеров [769].
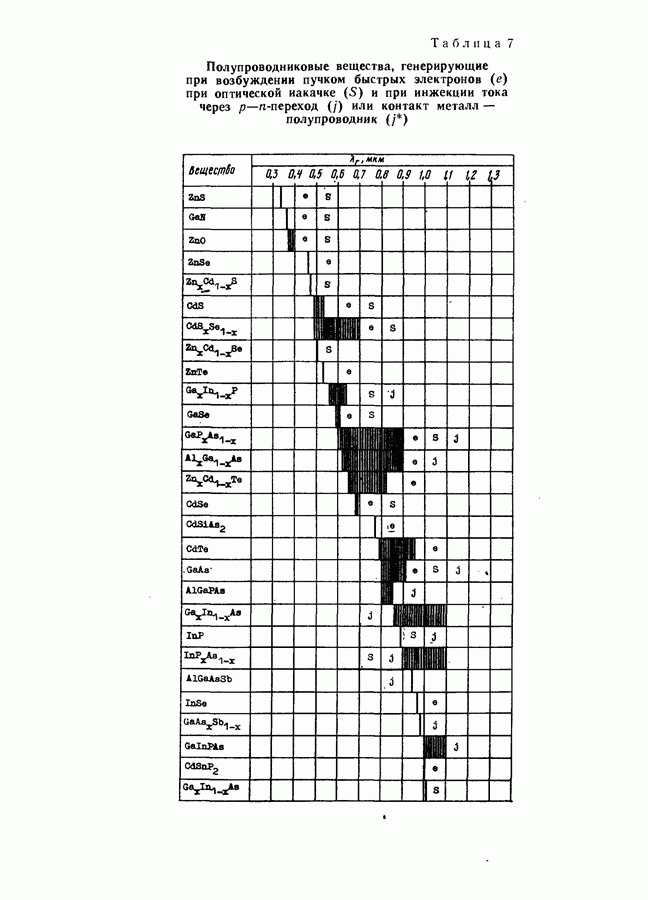
- Экситонный механизм генерации излучения.
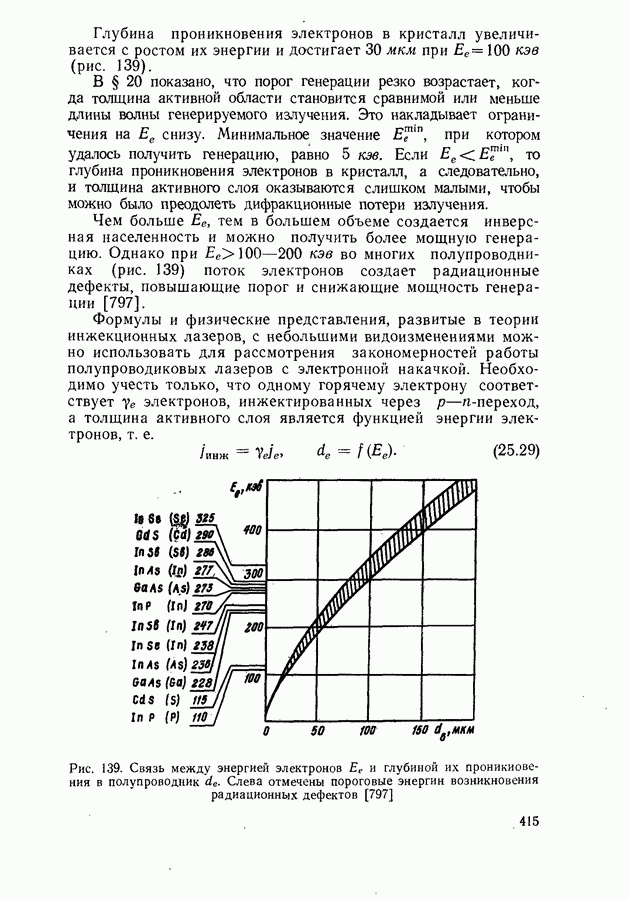
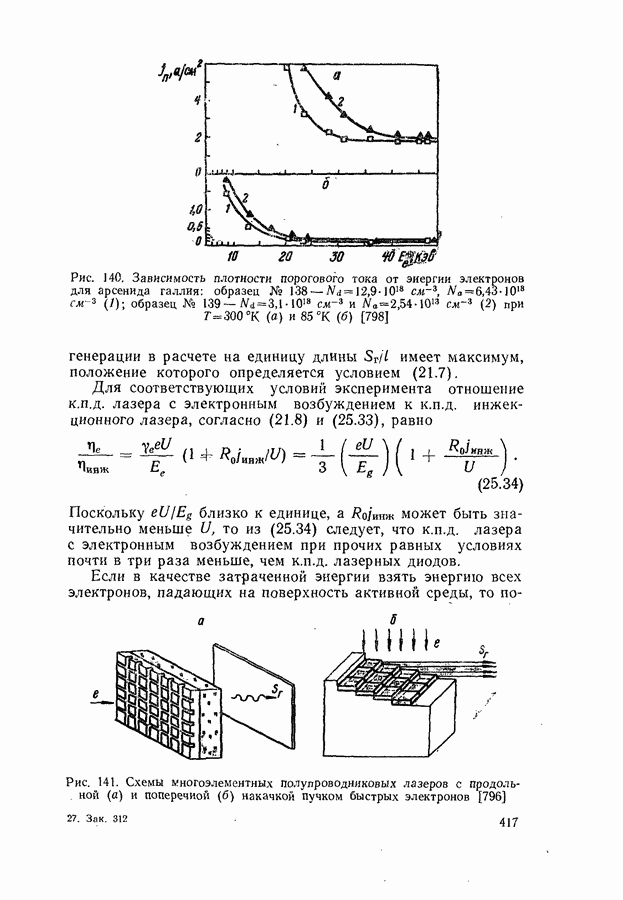
- Возбуждение генерации пучком быстрых электронов.