| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
Влияние погрешности оценки корреляционной функции.
Пусть  - оценка корреляционной функции
- оценка корреляционной функции  Функцию
Функцию  можно записать в виде
можно записать в виде

где  - погрешность оценки. Переходя в пространство частот, будем иметь
- погрешность оценки. Переходя в пространство частот, будем иметь

В практических расчетах ограничиваются вычислением  при
при  Значения при отрицательных х получаются на основе свойства четности функции
Значения при отрицательных х получаются на основе свойства четности функции  Рассмотрим
Рассмотрим 
 Так как
Так как  вещественная четная функция, то
вещественная четная функция, то

Пусть  — длина промежутка интегрирования, тогда импульсная характеристика интегрирующего фильтра будет равна 1 на промежутке
— длина промежутка интегрирования, тогда импульсная характеристика интегрирующего фильтра будет равна 1 на промежутке  и 0 вне промежутка, т. е.
и 0 вне промежутка, т. е.  . В пространстве частот имеем
. В пространстве частот имеем  .
.
Теперь находим  Простые, но громоздкие вычисления величин
Простые, но громоздкие вычисления величин  для гауссова процесса [1] дают
для гауссова процесса [1] дают

где  — ширина эквивалентного фильтра, равная
— ширина эквивалентного фильтра, равная  — максимальный сдвиг для коррелометра. Из полученного соотношения определяем
— максимальный сдвиг для коррелометра. Из полученного соотношения определяем

Так как максимальное и минимальное значения отношения  равны соответственно
равны соответственно  , то
, то

откуда

В результате получаются оценки дисперсии  и среднеквадратичного отклонения
и среднеквадратичного отклонения  Можно принять
Можно принять

Мы приходим к тому же результату, что и в случае измерения спектральной плотности методом фильтрации [выражение (9.48)].
Важное примечание.
Сравнение формул (9.48) и (9.37) показывает, что мы имеем в одном случае  а в другом
а в другом  Если В — ширина полосы,
Если В — ширина полосы,  — точность анализа, то
— точность анализа, то  где
где  — число точек спектра. Следовательно, для корреляции
— число точек спектра. Следовательно, для корреляции  а для спектральной плотности
а для спектральной плотности  так что
так что 
Предположим, например, что корреляционная функция измерена с точностью  (это позволяет определить «на глаз» вид графика функции). Если теперь рассчитать 100 точек спектра (коррелометр со 100 точками), то получим
(это позволяет определить «на глаз» вид графика функции). Если теперь рассчитать 100 точек спектра (коррелометр со 100 точками), то получим  Для коррелометра с 400 точками
Для коррелометра с 400 точками  .
.
Таким образом, для спектрального анализа необходимо вычислить корреляционную функцию на промежутке длиной Т, соответствующей  а не
а не 
Опыт показывает, что эти результаты внушают пессимизм и кажутся парадоксальными в том смысле, что спектральный анализ с помощью корреляции приводит к большей погрешности оценки, чем методы прямого преобразования Фурье или фильтрации.
Влияние систематической ошибки при определении корреляционной функции на спектральную плотность, полученную преобразованием Фурье [1].
Исследуем теперь случай, когда автокорреляционная функция задана  значениями, каждое из которых определено с ошибкой
значениями, каждое из которых определено с ошибкой  Будем предполагать, что ошибки, соответствующие разным значениям, между собой независимы. Здесь идет речь о систематических ошибках (разд. 10.4). Допустим, что коррелометр дает значения
Будем предполагать, что ошибки, соответствующие разным значениям, между собой независимы. Здесь идет речь о систематических ошибках (разд. 10.4). Допустим, что коррелометр дает значения

где  — приращение сдвига (период дискретизации корреляционной функции). Пусть
— приращение сдвига (период дискретизации корреляционной функции). Пусть  . Применим преобразование Фурье к обеим частям соотношения (13.30):
. Применим преобразование Фурье к обеим частям соотношения (13.30):

По предположению ошибки независимы, следовательно, некоррелированы, поэтому

Отсюда вытекает оценка

Учитывая соотношение  , где
, где  ширина эквивалентного фильтра, получим
ширина эквивалентного фильтра, получим

Допустим, что дисперсия  не зависит от индекса
не зависит от индекса  (это предположение хорошо выполняется в случае систематических ошибок):
(это предположение хорошо выполняется в случае систематических ошибок):  для всех
для всех  Следовательно,
Следовательно, 
Положим

тогда 

Эти соотношения были экспериментально проверены Фоком 
Трудно сделать общие выводы из последнего соотношения, так как величина ошибки зависит от точности анализа  Отметим все же, что если при уменьшении
Отметим все же, что если при уменьшении  (в рамках теоремы Шеннона) точность анализа возрастает, ошибка значительно увеличивается, так как уменьшается избыточность дискретных значений
(в рамках теоремы Шеннона) точность анализа возрастает, ошибка значительно увеличивается, так как уменьшается избыточность дискретных значений 
Частные случаи. Белый шум. В этом случае  Поскольку
Поскольку  то
то 
Итак, ошибка пропорциональна числу точек коррелометра, но корреляционная функция равна нулю всюду, кроме  поэтому все эти точки не играют никакой роли.
поэтому все эти точки не играют никакой роли.
Корреляционная функция почти совпадает с синусоидой (фильтр с очень узкой полосой). В этом случае  Ошибка уменьшается с ростом числа точек. Это естественно, так как чем дольше длится периодический сигнал, тем точнее удается определить его характеристики — частоту и амплитуду.
Ошибка уменьшается с ростом числа точек. Это естественно, так как чем дольше длится периодический сигнал, тем точнее удается определить его характеристики — частоту и амплитуду.
Между этими крайними случаями имеются всевозможные промежуточные. В частности, моделирование показало, что для осциллирующих и «умеренно» затухающих  имеет место соотношение
имеет место соотношение  т. е. нет зависимости от
т. е. нет зависимости от 
В заключение отметим, что влияние ошибки при переходе от корреляционной функции к спектральной плотности в очень большой степени определяется формой спектра. Сомнительным является утверждение, что ошибка пропорциональна  так как в ряде практических случаев такая зависимость от
так как в ряде практических случаев такая зависимость от  не дает даже правильного порядка величины.
не дает даже правильного порядка величины.
Важное примечание.
Приведенные выше рассуждения имеют непосредственное отношение к процедуре перехода от сигнала  к его фурье-образу
к его фурье-образу  (разд. 13.2). Если значения функции
(разд. 13.2). Если значения функции  определены с систематической ошибкой 1%, какое влияние окажет эта ошибка на фурье-образ
определены с систематической ошибкой 1%, какое влияние окажет эта ошибка на фурье-образ  Проведенные рассуждения служат лишь первым приближением решения проблемы. Для более точного ответа на поставленный вопрос потребовались бы значительные усилия.
Проведенные рассуждения служат лишь первым приближением решения проблемы. Для более точного ответа на поставленный вопрос потребовались бы значительные усилия.
Вычисления, выполненные в этом и предыдущем разделах, показывают, что ошибка в определении корреляционной функции проявляется впоследствии по-разному в зависимости от того, систематическая ли это ошибка, или погрешность оценки. Однако гипотезы о характеристиках этих ошибок мало отличаются. Оба результата совпадают только для белого шума. Что касается других случаев, то замечание, приведенное выше, подтверждает, по-видимому, выводы, сделанные здесь для общего случая. По всей вероятности, ошибка в расчете спектральной плотности окажется существенно меньше, если находить спектр с помощью преобразования Фурье корреляционной функции.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
- 2.7. Несколько функций и их фурье-образы
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
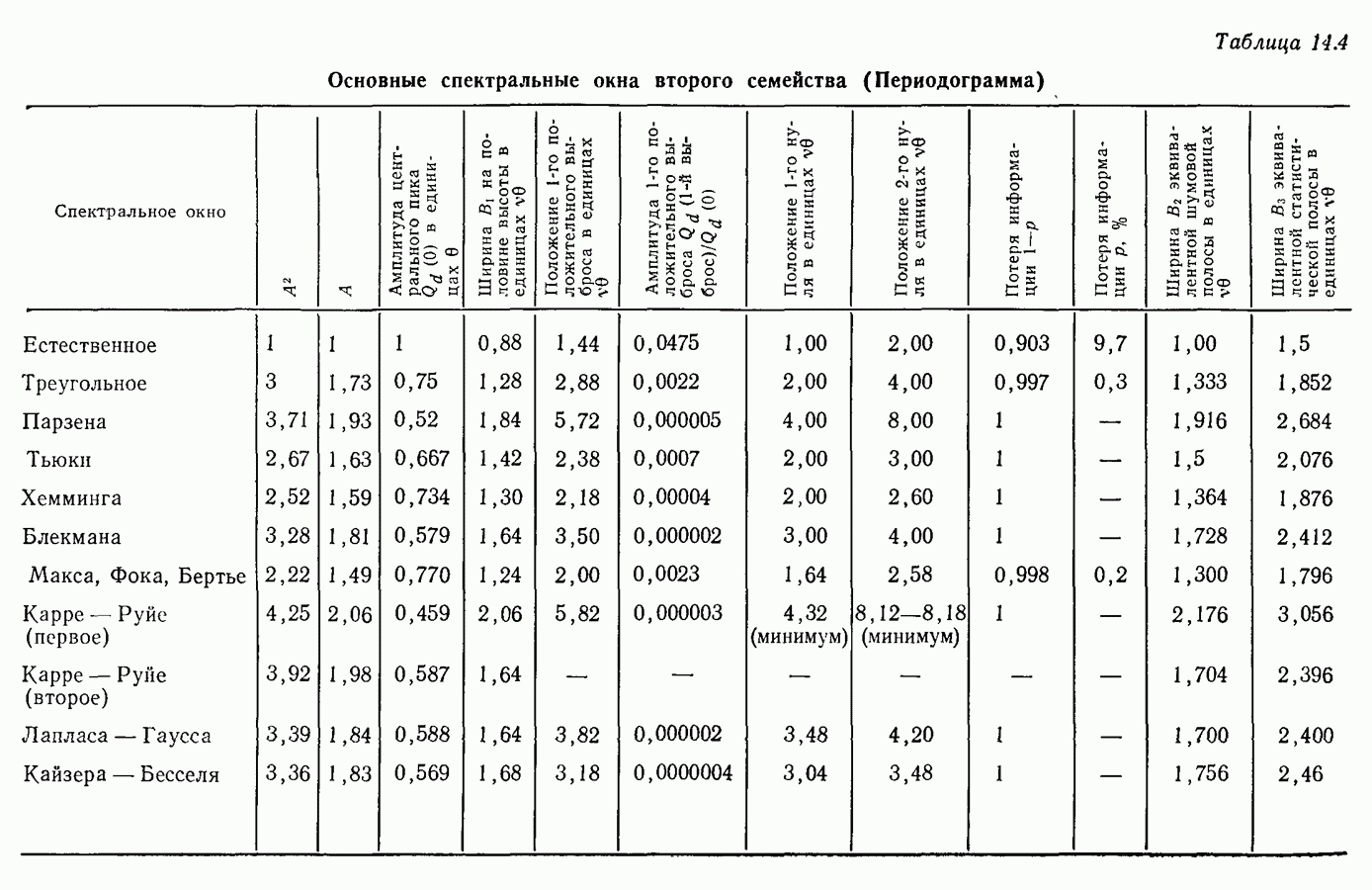
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
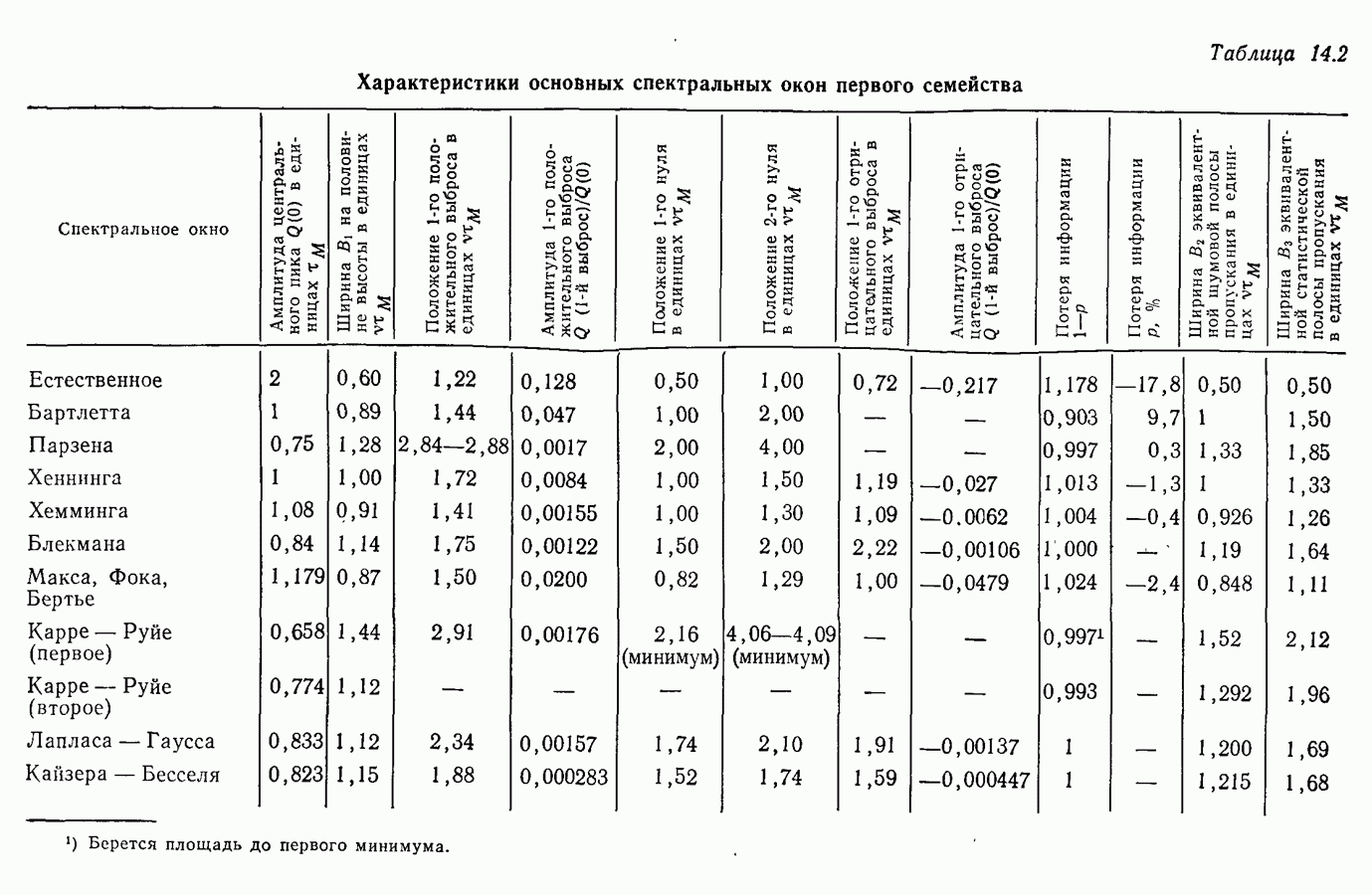
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции