| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
Сигналы с конечной энергией (и малым значением ВТ).
В данном случае фурье-образы сигналов существуют и спектральные плотности находятся непосредственно из соответствующих преобразований Фурье:

Здесь предполагается, что можно найти фурье-образ любого сигнала  однако при современном уровне аппаратуры это не всегда можно сделать. Мы в состоянии определить фурье-образ лишь коротких сигналов, т. е. сигналов, определяемых небольшим числом точек (обычно не больше 4096), т. е. произведение
однако при современном уровне аппаратуры это не всегда можно сделать. Мы в состоянии определить фурье-образ лишь коротких сигналов, т. е. сигналов, определяемых небольшим числом точек (обычно не больше 4096), т. е. произведение  много меньше 2048. Действительно, если
много меньше 2048. Действительно, если  частота дискретизации, то
частота дискретизации, то  при
при  следовательно, верхняя граница В спектра связана с
следовательно, верхняя граница В спектра связана с  соотношением
соотношением  Отсюда
Отсюда  Так как а всегда больше 1, а нередко много больше 1, то произведение
Так как а всегда больше 1, а нередко много больше 1, то произведение  невелико.
невелико.
Когда мы на практике используем численный расчет, то в блок вычислительного устройства помещаем  слов закодированного сигнала. Если Те — период дискретизации, то может показаться, что длина
слов закодированного сигнала. Если Те — период дискретизации, то может показаться, что длина  этих слов равна длине сигнала, однако не очевидно, что произведение
этих слов равна длине сигнала, однако не очевидно, что произведение  совпадает с длительностью сигнала до его кодирования. Действительно, пусть
совпадает с длительностью сигнала до его кодирования. Действительно, пусть  — группа слов сигнала
— группа слов сигнала  длина которой
длина которой  тогда
тогда

Хотя спектр  ограничен, тем не менее из-за множителя
ограничен, тем не менее из-за множителя  спектр
спектр  имеет бесконечную протяженность. Поэтому теоретически невозможно дискретизировать усеченный сигнал.
имеет бесконечную протяженность. Поэтому теоретически невозможно дискретизировать усеченный сигнал.
Как же поступают при отыскании фурье-образа  слов, находящихся в блоке вычислительного устройства? Рассмотрим
слов, находящихся в блоке вычислительного устройства? Рассмотрим  последовательных дискретных значений сигнала
последовательных дискретных значений сигнала  дискретизованного с частотой
дискретизованного с частотой  Фурье-образ этой группы из
Фурье-образ этой группы из  слов определяется формулой
слов определяется формулой

По определению  данному в теореме Шеннона, частоты,
данному в теореме Шеннона, частоты,
большие  не дают существенного вклада в спектр
не дают существенного вклада в спектр  и мы их не учитываем, принимая
и мы их не учитываем, принимая  для
для  Итак,
Итак,  для
для  Но поскольку
Но поскольку  служит фурье-образом функции
служит фурье-образом функции  то
то  является фурье-образом функции
является фурье-образом функции 
Поэтому

или

Таким образом,  является фурье-образом сигнала
является фурье-образом сигнала  , который определен выражением
, который определен выражением

Так как носитель функции  не ограничен, то из полученного выражения следует, что носитель сигнала
не ограничен, то из полученного выражения следует, что носитель сигнала  также не ограничен, т. е. его длительность бесконечна. Это означает, что
также не ограничен, т. е. его длительность бесконечна. Это означает, что  не может быть частью длины
не может быть частью длины  ограниченного по длительности сигнала
ограниченного по длительности сигнала 
В работе [8] показано, что среднеквадратичное отклонение разности  равно по порядку величины
равно по порядку величины  где В — протяженность спектра сигнала для положительных частот. Если
где В — протяженность спектра сигнала для положительных частот. Если  то
то  так что среднеквадратичное отклонение
так что среднеквадратичное отклонение

Таким образом, этой ошибкой не всегда можно пренебречь; если положить, например,  , а частоту дискретизации увеличить в 5 раз, то
, а частоту дискретизации увеличить в 5 раз, то  . Следует отметить, что это среднеквадратичное отклонение не оценивает наибольшее значение разности функций
. Следует отметить, что это среднеквадратичное отклонение не оценивает наибольшее значение разности функций 
Случайные стационарные сигналы и сигналы с большим значением ВТ.
Среднее значение  . Рассмотрим случайный стационарный двумерный процесс
. Рассмотрим случайный стационарный двумерный процесс  обладающий свойством эргодичности. Пусть
обладающий свойством эргодичности. Пусть  — какая-нибудь реализация
— какая-нибудь реализация
этого процесса. Выделим временной участок длительностью 0 реализации 

или 
Вычислим математическое ожидание величины 

Следовательно, «среднее» значение по участкам  равно среднему значению по реализациям
равно среднему значению по реализациям  при этом предполагается, что число участков бесконечно велико. Вследствие эргодичности процесса среднее значение можно найти, производя усреднение по последовательным участкам одной и той же реализации
при этом предполагается, что число участков бесконечно велико. Вследствие эргодичности процесса среднее значение можно найти, производя усреднение по последовательным участкам одной и той же реализации 
Дисперсия  Имеем
Имеем

Учитывая, что

найдем

или

Спектральная плотность. 1. Среднее значение фурье-образов. Пусть  . Очевидно, что участок конечной длительности
. Очевидно, что участок конечной длительности  всегда имеет фурье-образ:
всегда имеет фурье-образ:

так что

Меняя порядок операций усреднения и суммирования (в
предположении, что выполняются условия квадратичной сходимости), получим

Итак, если реализация  — центрированная функция, то среднее значение фурье-образов функций
— центрированная функция, то среднее значение фурье-образов функций  равно нулю. Если среднее значение
равно нулю. Если среднее значение  отлично от нуля, то среднее значение фурье-образов равно функции
отлично от нуля, то среднее значение фурье-образов равно функции  (центрированной в нуле) с множителем
(центрированной в нуле) с множителем 
2. Среднее значение квадратов модулей фурье-образов. По определению имеем

Меняя порядок операций усреднения и интегрирования, получим 

Но  является автокорреляционной функцией
является автокорреляционной функцией 

поэтому

При

Положим  тогда
тогда

Запишем полученное соотношение в виде

Свертка двух одинаковых прямоугольных функций шириной 9 дает треугольную функцию шириной  (см. разд. 2.14):
(см. разд. 2.14):

Следовательно,

или  .
.
В итоге получаем

Итак, среднее значение последовательности спектральных плотностей участков длительностью  (вследствие предположения об эргодичности процесса можно считать, что они принадлежат одной и той же реализации) равно свертке истинной спектральной плотности
(вследствие предположения об эргодичности процесса можно считать, что они принадлежат одной и той же реализации) равно свертке истинной спектральной плотности  и функции
и функции 

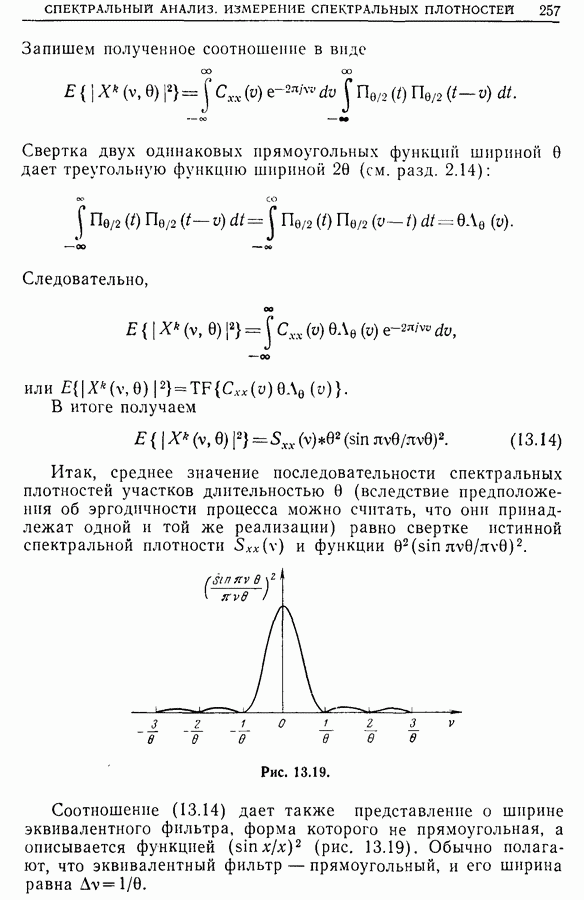
Рис. 13.19.
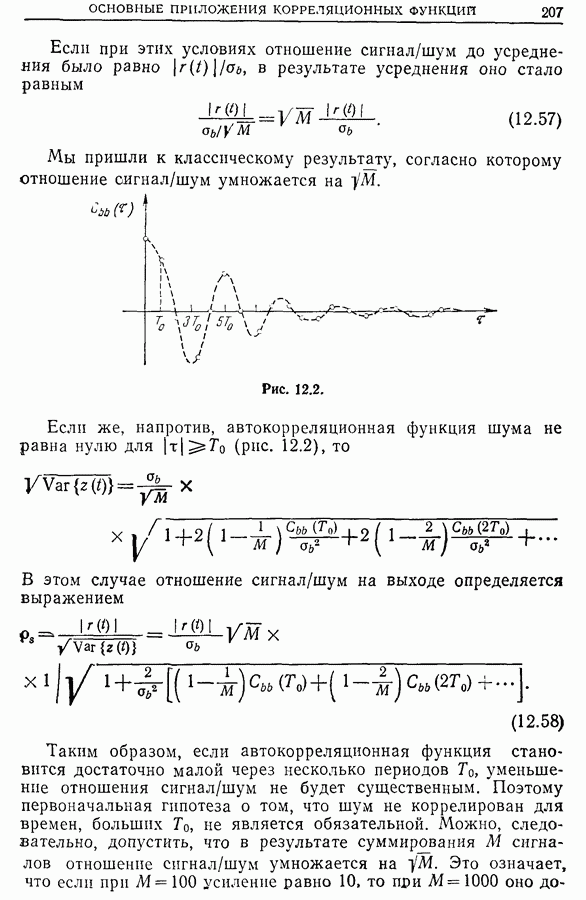
Соотношение (13.14) дает также представление о ширине эквивалентного фильтра, форма которого не прямоугольная, а описывается функцией  (рис. 13.19). Обычно полагают, что эквивалентный фильтр — прямоугольный, и его ширина равна
(рис. 13.19). Обычно полагают, что эквивалентный фильтр — прямоугольный, и его ширина равна 
Очевидно, что результат

применим лишь при 
Примечание. Если  мало меняется в интервале
мало меняется в интервале

Отсюда 
Естественно, что всякий раз, когда выполняется какая-либо оценка, необходимо иметь представление о погрешности этой оценки. С этой целью вычислим дисперсию  Имеем
Имеем

Выражение для  записывается в виде
записывается в виде

Чтобы вычислить моменты 4-го порядка, сделаем упрощающее предположение: допустим, что сигнал имеет гауссово распределение. Тогда можно найти моменты любого порядка, исходя из моментов 1-го и 2-го порядков. Вычисления дают следующий результат:

где  — число участков, по которым производится усреднение спектральных плотностей.
— число участков, по которым производится усреднение спектральных плотностей.
Здесь предполагается, что участки не коррелированы. Подобное допущение можно считать верным благодаря тому, что современные системы дают возможность выбора длительности этих участков.
Так как длительность каждого участка равна 0, то полная продолжительность сигнала  поэтому
поэтому

Поскольку  является шириной полосы пропускания эквивалентного фильтра, получаем хорошо известную формулу
является шириной полосы пропускания эквивалентного фильтра, получаем хорошо известную формулу

Дискретизация.
Как показано в гл. 7, дискретизация временных сигналов должна осуществляться в соответствии с теоремой Шеннона. Аналогичная задача возникает при дискретизации спектра. При вычислении спектральных плотностей с помощью дискретного преобразования Фурье ширина полосы сигнала, которую можно обработать в реальное время, будет тем больше, чем быстрее вычисляется фурье-образ. Кроме того, точность анализа тем выше, чем больше длительность  участков сигнала. А так как
участков сигнала. А так как  то, очевидно, точность анализа возрастает с уменьшением частоты дискретизации временного сигнала, что находится в соответствии с теоремой Шеннона. Скорость вычисления фурье-образа зависит от числа точек, в которых определяются его значения. Поэтому для ускорения обработки сигнала желательно брать возможно меньшее число таких точек, руководствуясь при этом теоремой Шеннона.
то, очевидно, точность анализа возрастает с уменьшением частоты дискретизации временного сигнала, что находится в соответствии с теоремой Шеннона. Скорость вычисления фурье-образа зависит от числа точек, в которых определяются его значения. Поэтому для ускорения обработки сигнала желательно брать возможно меньшее число таких точек, руководствуясь при этом теоремой Шеннона.
Допустим, что взято  точек сигнала. Тогда, согласно алгоритму быстрого преобразования Фурье, нужно определить значения спектра в
точек сигнала. Тогда, согласно алгоритму быстрого преобразования Фурье, нужно определить значения спектра в  точках полосы
точках полосы  или вследствие симметрии — в
или вследствие симметрии — в  точках полосы
точках полосы  . Пусть частота дискретизации сигнала равна
. Пусть частота дискретизации сигнала равна  Тогда
Тогда  при
при  и мы находим
и мы находим

Следовательно, ширина полосы, на которую нужно настроить аппаратуру, составляет 
Можно ли утверждать, что дискретизация спектра сделана корректно? Для ответа на этот вопрос воспользуемся теоремой Шеннона. Пусть  — спектральная плотность, которую нужно рассчитать. Применяя преобразование Фурье к соотношению
— спектральная плотность, которую нужно рассчитать. Применяя преобразование Фурье к соотношению

получим

Если  для
для  где
где  то нужно выбрать шаг дискретизации
то нужно выбрать шаг дискретизации  пли
пли 
Таким образом, величина  или число слов, вводимых в вычислительное устройство, зависит от ширины спектра и
или число слов, вводимых в вычислительное устройство, зависит от ширины спектра и
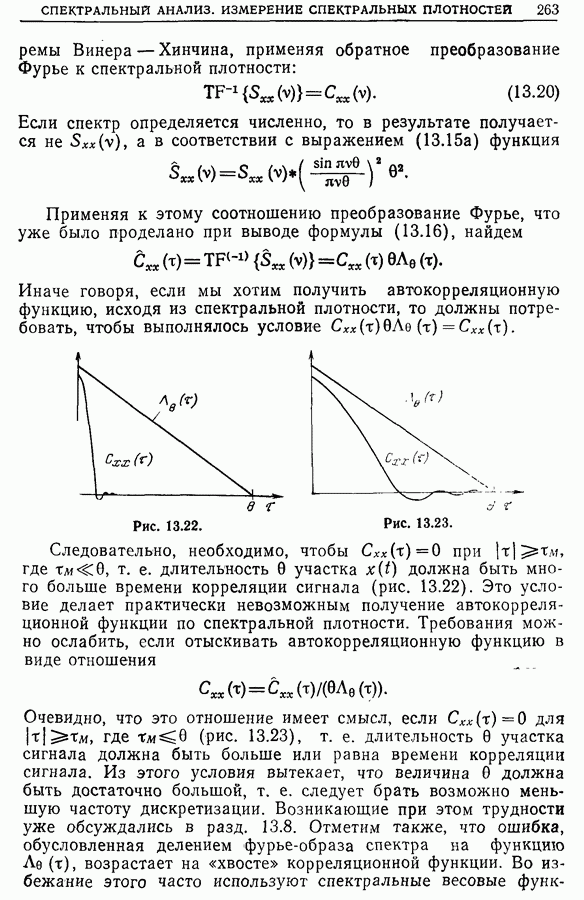
«ширины» корреляционной функции сигнала. Если значение  неизвестно и мы лишь знаем, что
неизвестно и мы лишь знаем, что  при
при  то
то  Следовательно,
Следовательно,  при
при 
В этом предельном (и, безусловно, реальном) случае нужно осуществить дополнительную дискретизацию временного сигнала, увеличив частоту по меньшей мере в 2 раза. Кроме того, не следует забывать, что речь идет об определении спектральной плотности  [см. выражения (13.3) и (13.14)].
[см. выражения (13.3) и (13.14)].
Визуализация спектра.
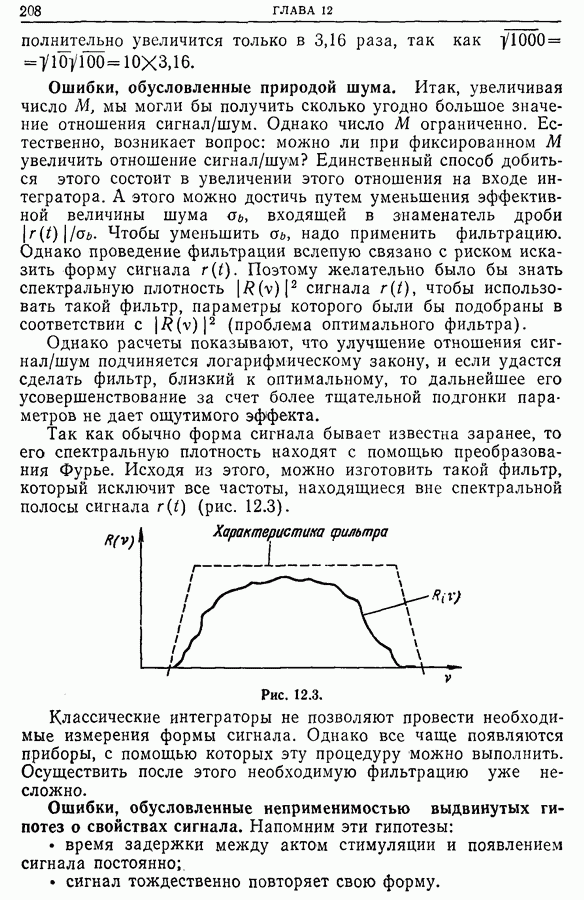
Очень часто возникает потребность «начертить» спектральную плотность в виде графика, чтобы «видеть» спектр. Однако следует помнить, что наш глаз — весьма несовершенный интерполятор (в основном 1-го порядка) и не способен выполнить интерполяцию Шеннона. Мы видели, что наибольшая точность анализа получается, если осуществить дискретизацию сигнала с частотой Шеннона, т. е. если брать коэффициент а как можно ближе к 1. В этом случае соответствующая дискретизация спектра оказывается такой, что коэффициент а также близок к 1. При таких условиях невозможно выполнить визуально качественную интерполяцию спектра, которая была бы близка к интерполяции Шеннона, т. е.
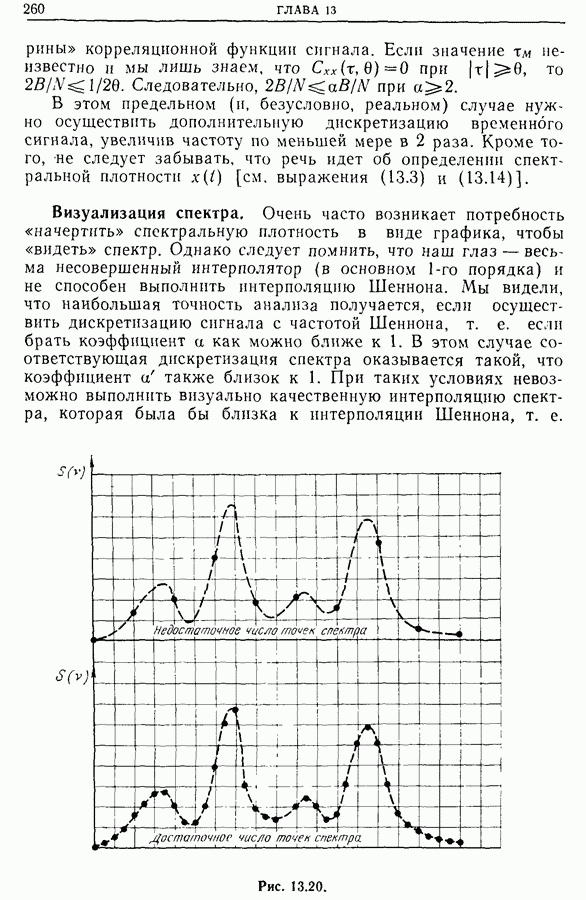
Рис. 13.20. (см. скан)
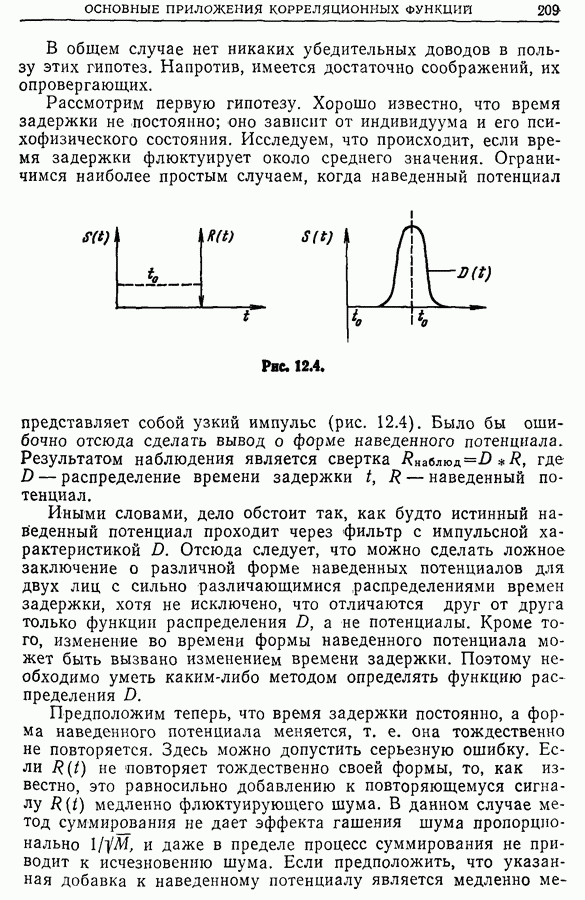
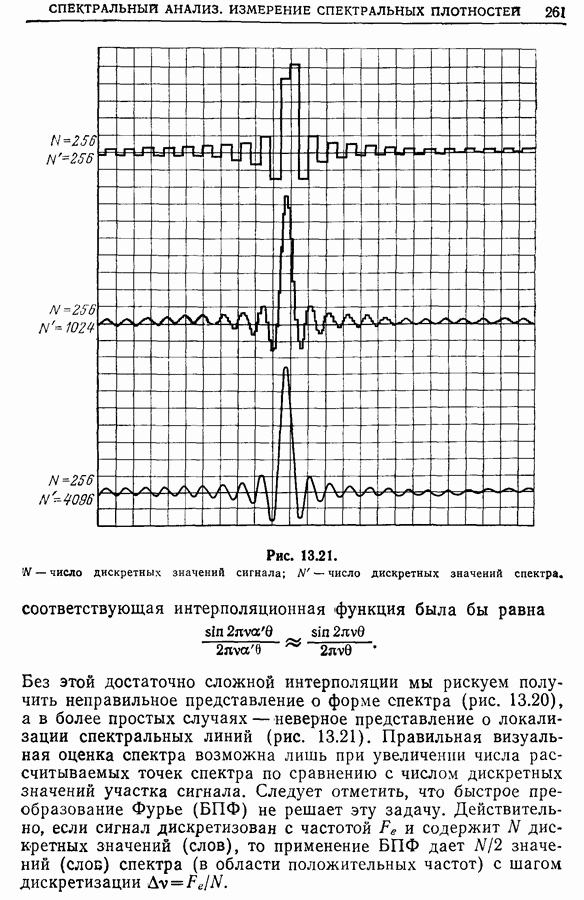
Рис. 13.21. W — число дискретных значений сигнала;  — число дискретных значений спектра. (см. скан)
— число дискретных значений спектра. (см. скан)
соответствующая интерполяционная функция была бы равна

Без этой достаточно сложной интерполяции мы рискуем получить неправильное представление о форме спектра (рис. 13.20), а в более простых случаях — неверное представление о локализации спектральных линий (рис. 13.21). Правильная визуальная оценка опектра возможна лишь при увеличении числа рассчитываемых точек спектра по сравнению с числом дискретных значений участка сигнала. Следует отметить, что быстрое преобразование Фурье (БПФ) не решает эту задачу. Действительно, если сигнал дискретизован с частотой  и содержит
и содержит  дискретных значений (слов), то применение БПФ дает
дискретных значений (слов), то применение БПФ дает  значений (слов) спектра (в области положительных частот) с шагом дискретизации
значений (слов) спектра (в области положительных частот) с шагом дискретизации 
Таким образом, для визуальной оценки спектральной плотности энергии следует использовать интерполятор либо рассчитывать больше точек спектра (в 4, 8, 16 раз) по сравнению с числом дискретных значений сигнала.
Увеличение частоты дискретизации временного сигнала не дает положительного результата из-за снижения точности анализа, так как  растет с ростом а. Наряду с этим при увеличении частоты дискретизации временного сигнала нужно уменьшить длительность 0 его участка, ибо число слов в вычислительном устройстве в общем постоянно, а это приводит к росту ошибки.
растет с ростом а. Наряду с этим при увеличении частоты дискретизации временного сигнала нужно уменьшить длительность 0 его участка, ибо число слов в вычислительном устройстве в общем постоянно, а это приводит к росту ошибки.
Измерение взаимных спектральных плотностей (взаимных спектров).
Рассмотрим сигналы  Для каждого участка
Для каждого участка  находим
находим

Затем определяем спектральные плотности

и аналогично  а также взаимные спектральные плотности
а также взаимные спектральные плотности

где

и аналогично 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
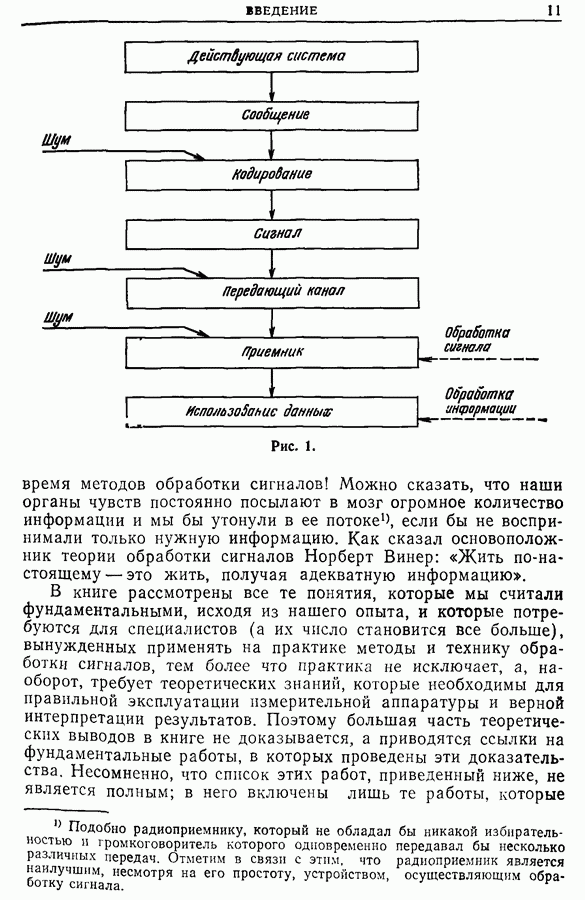
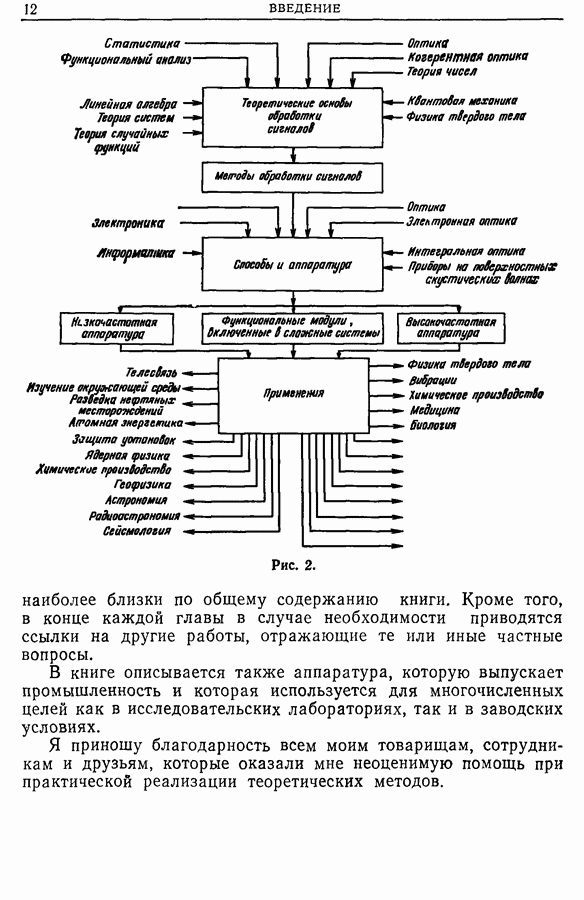
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
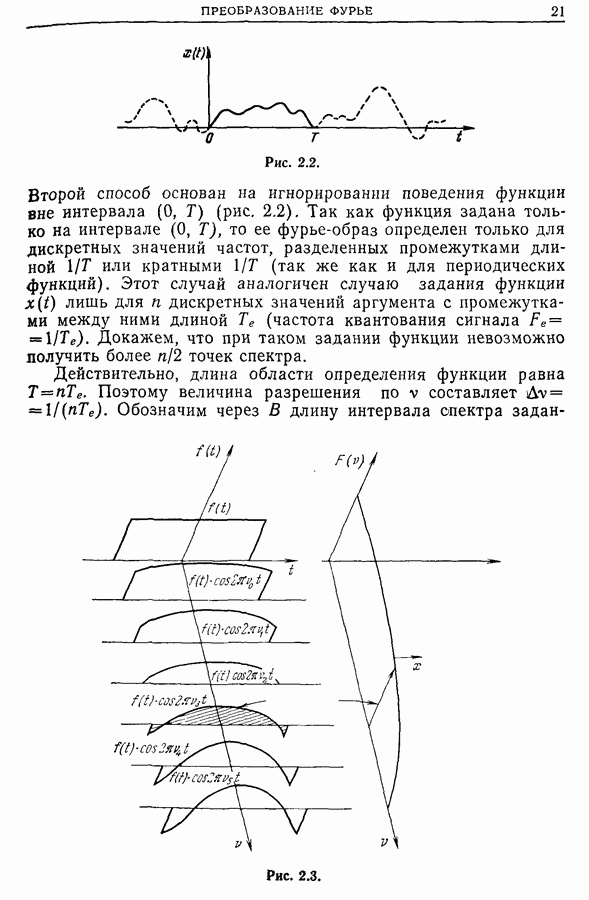
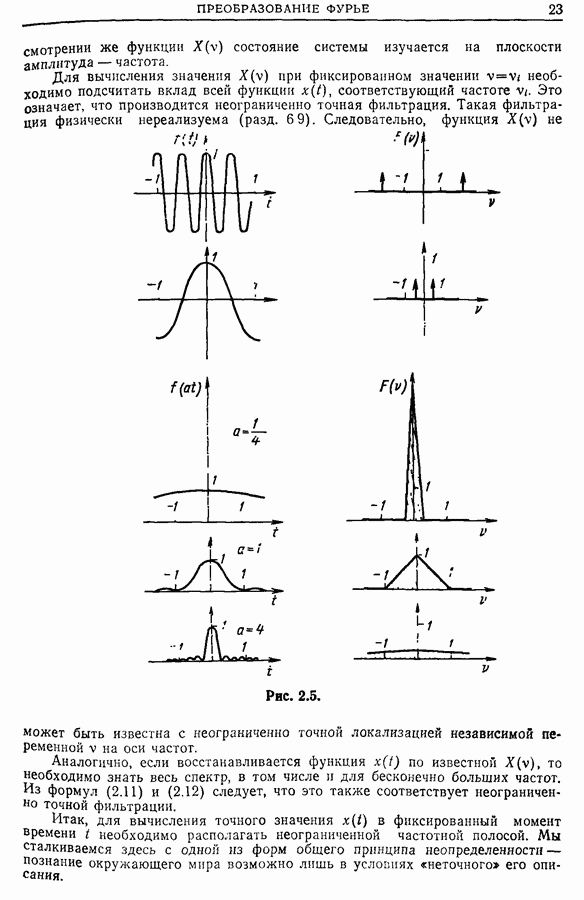
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
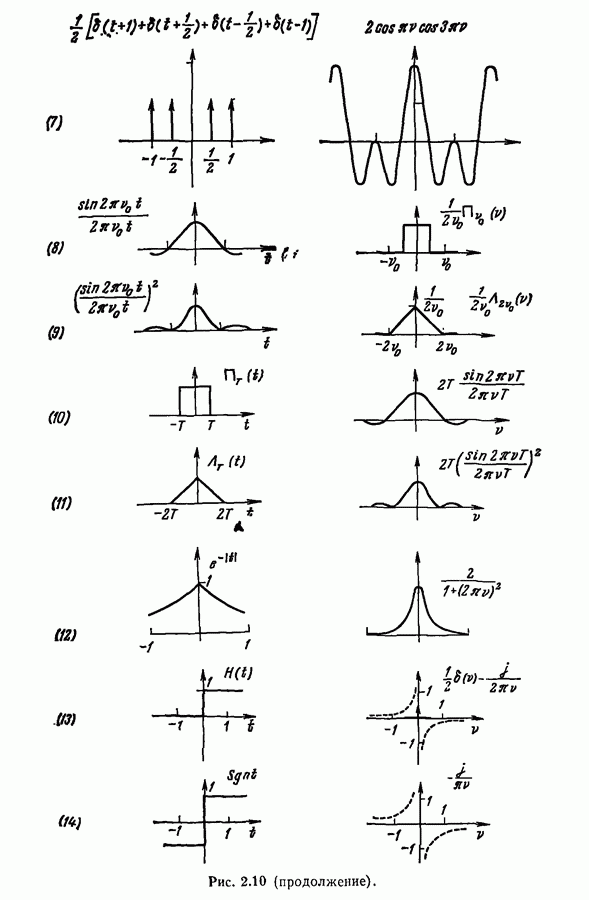
- 2.7. Несколько функций и их фурье-образы
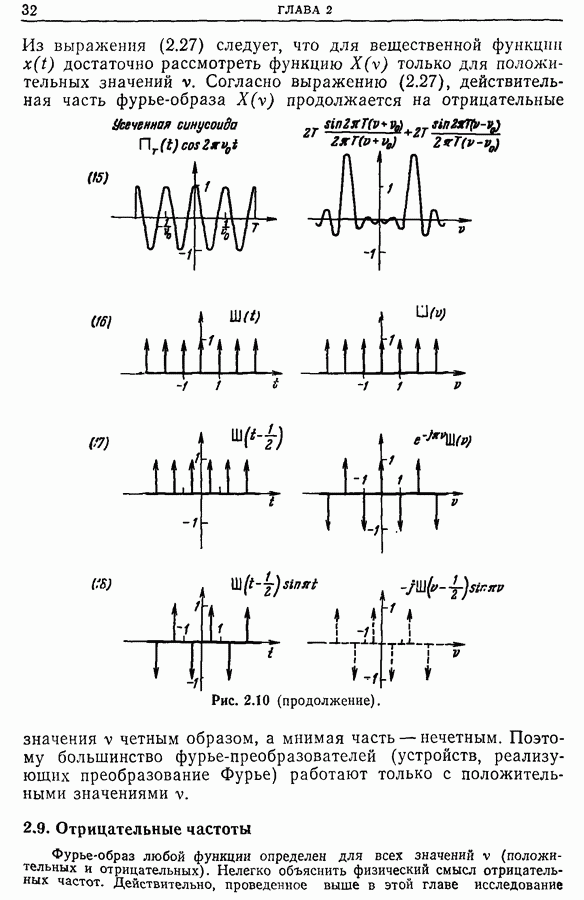
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
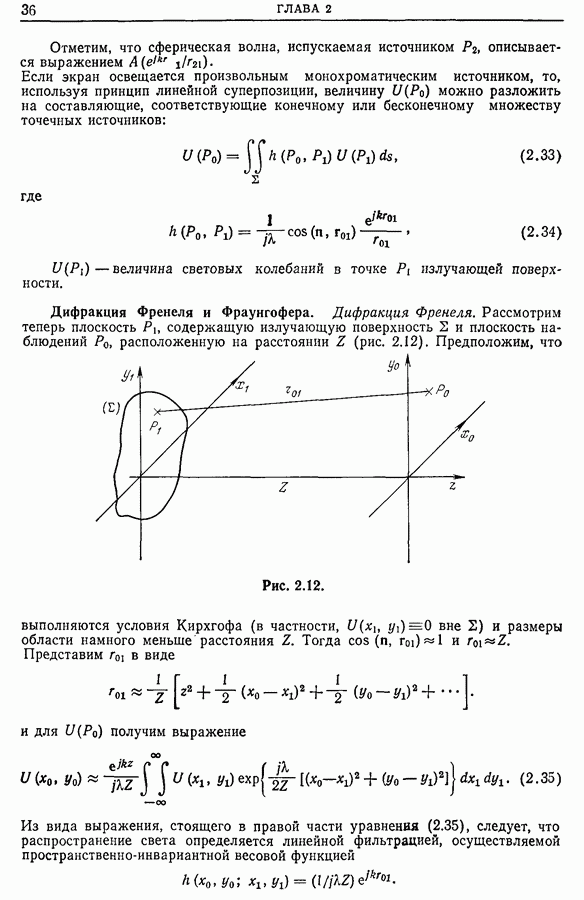
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
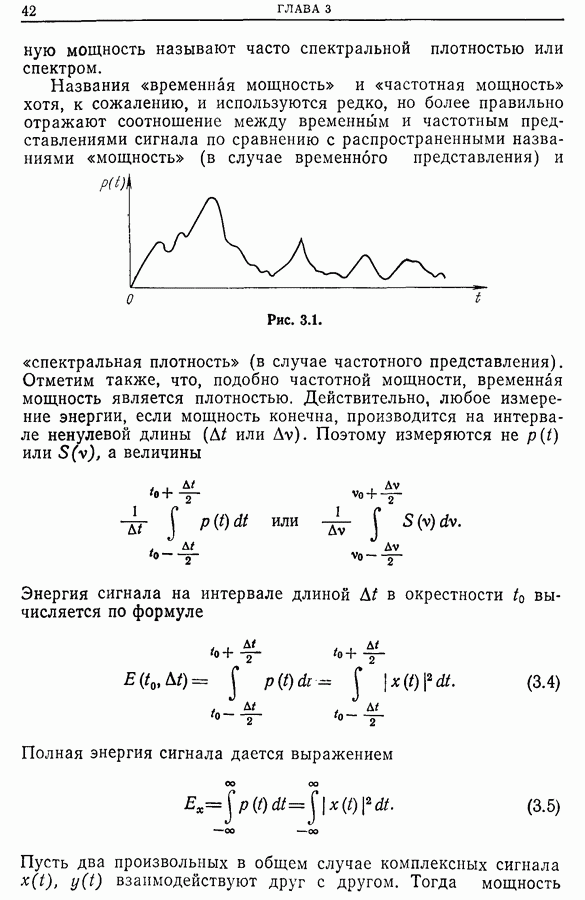
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
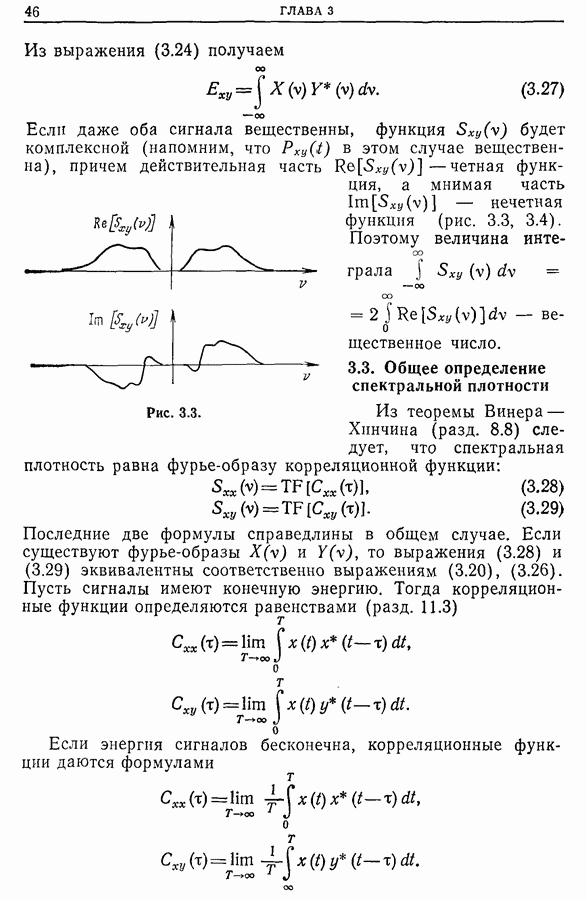
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
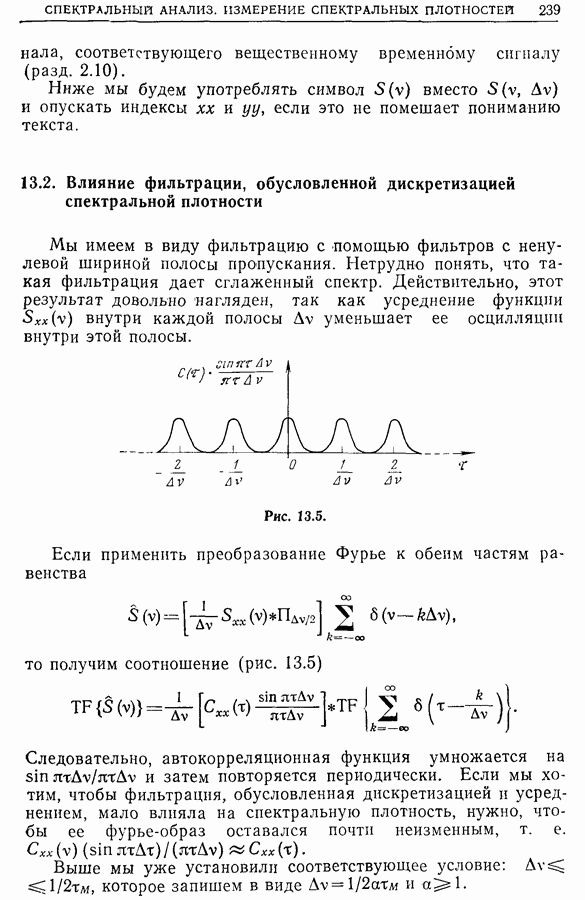
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
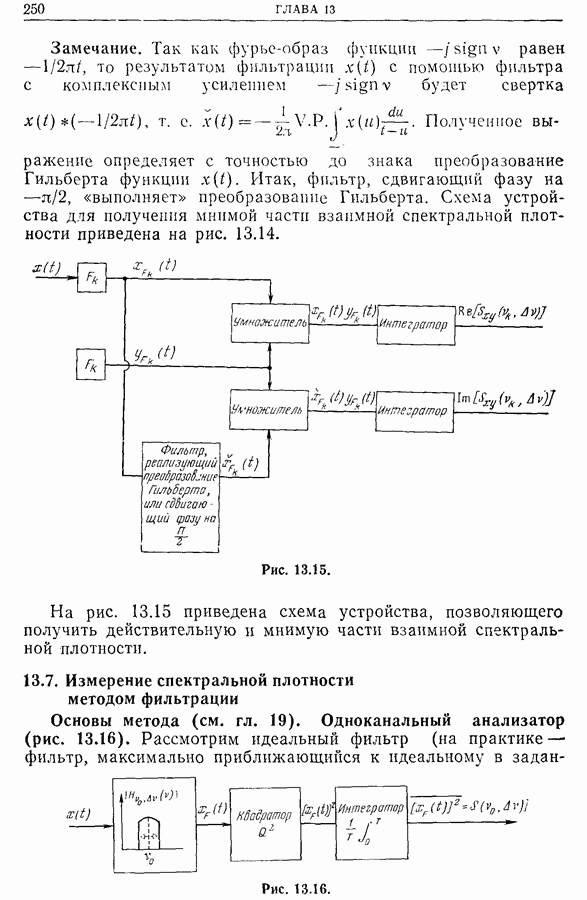
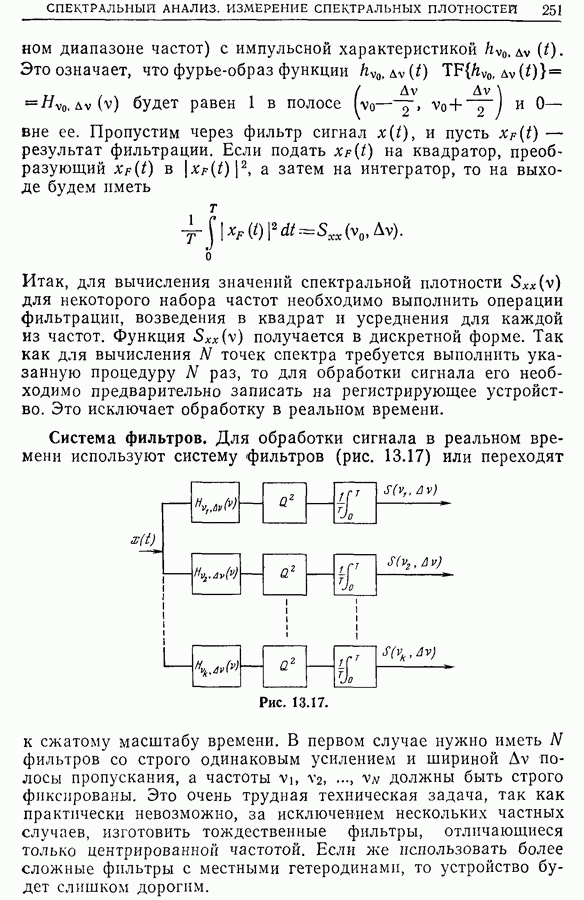
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
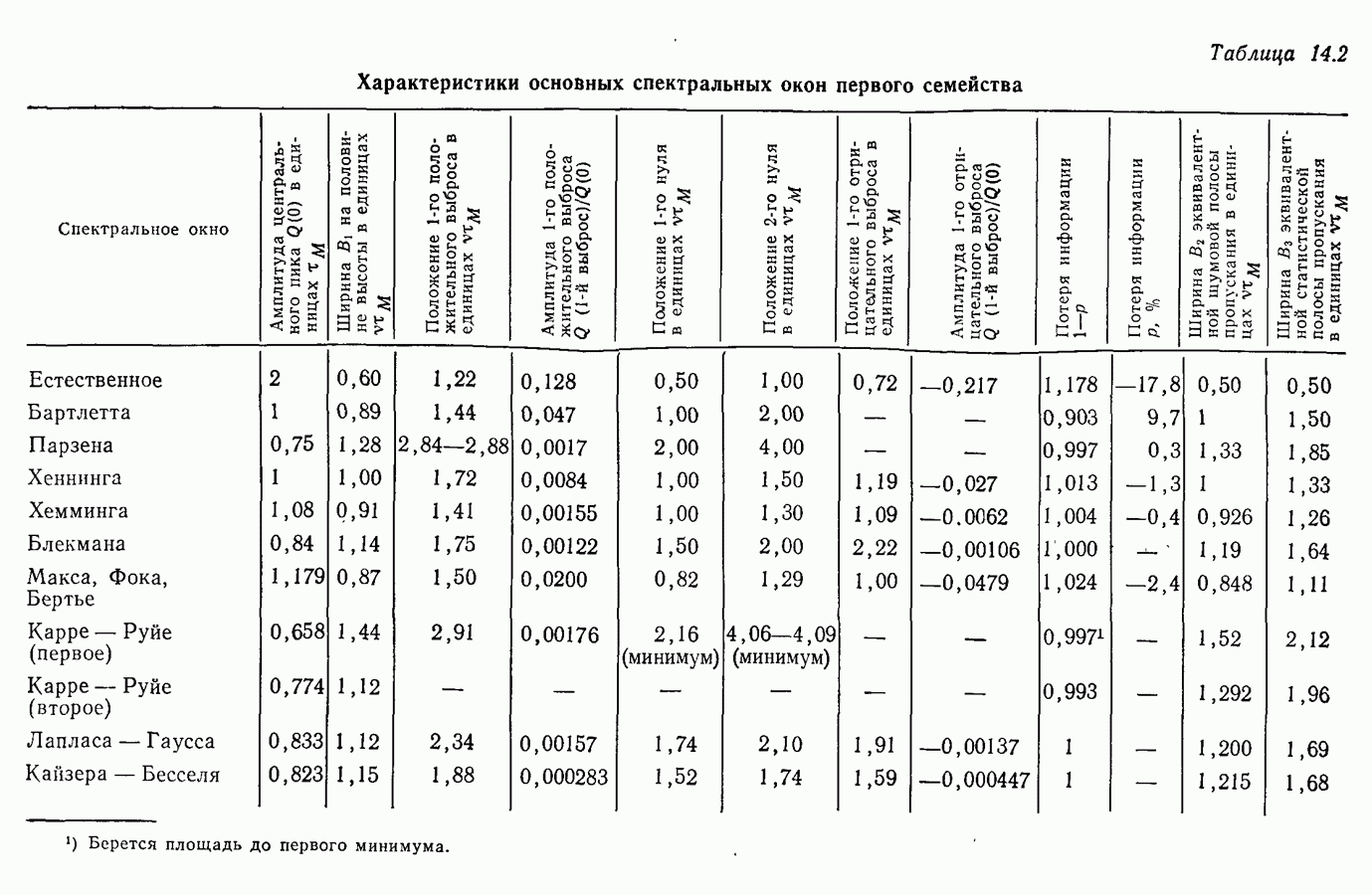
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
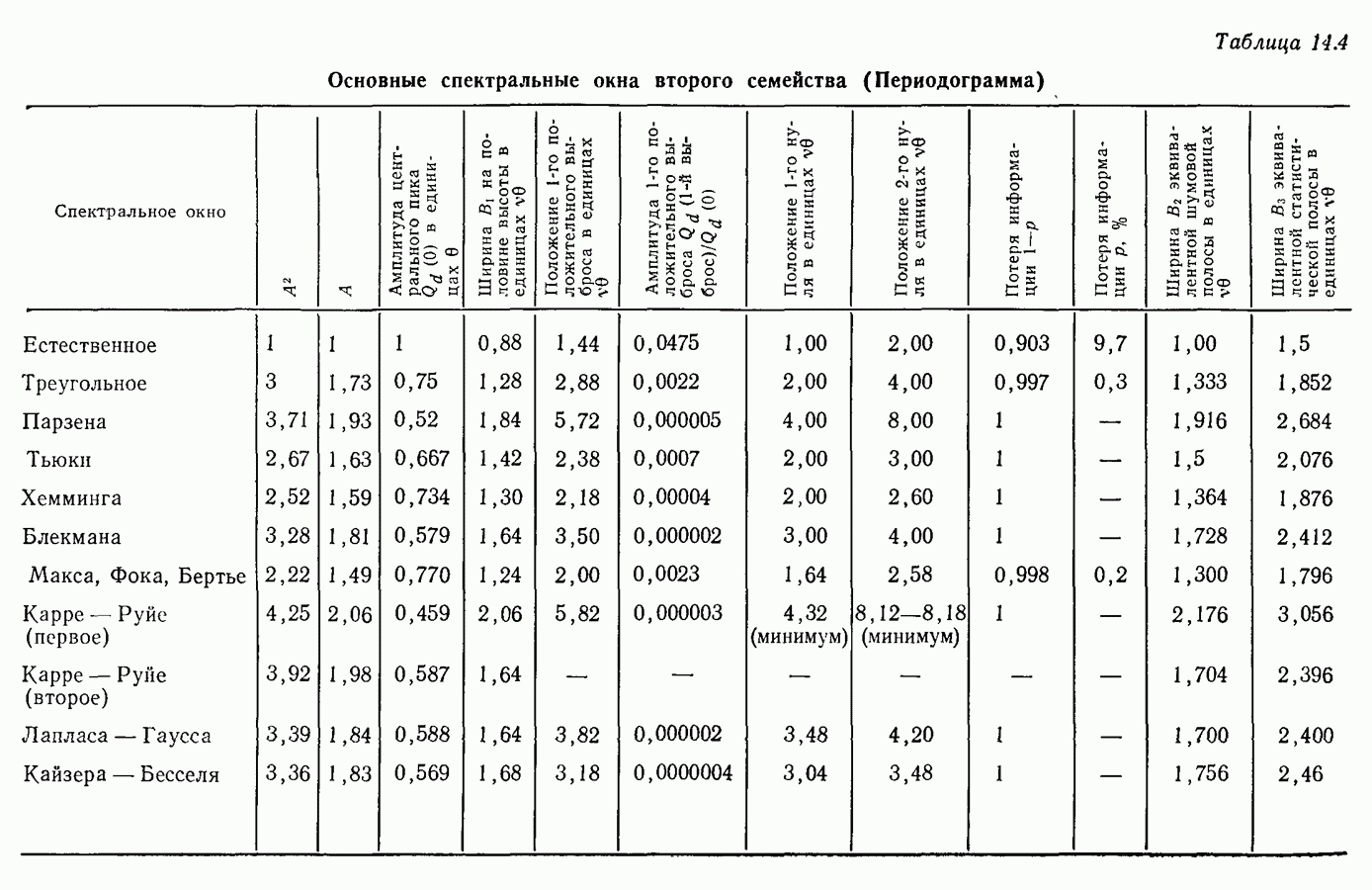
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции