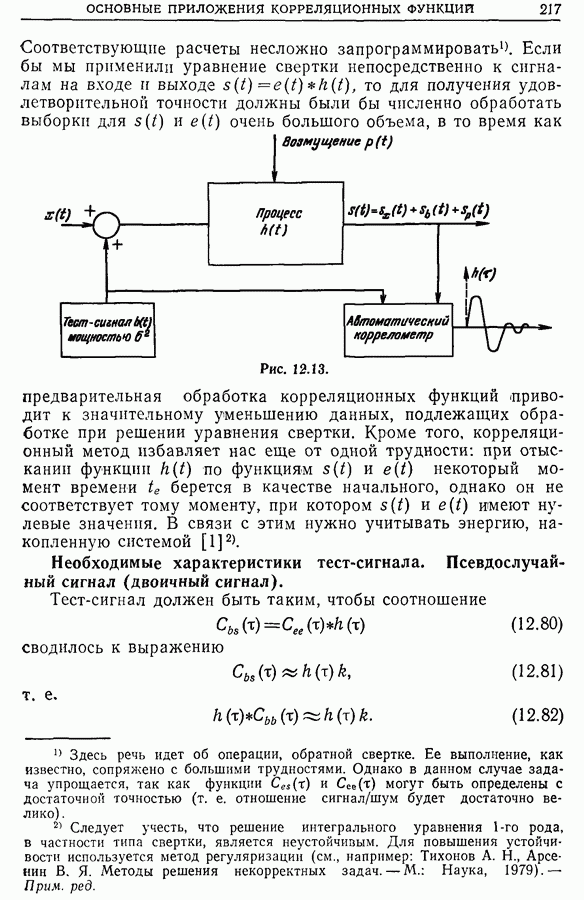
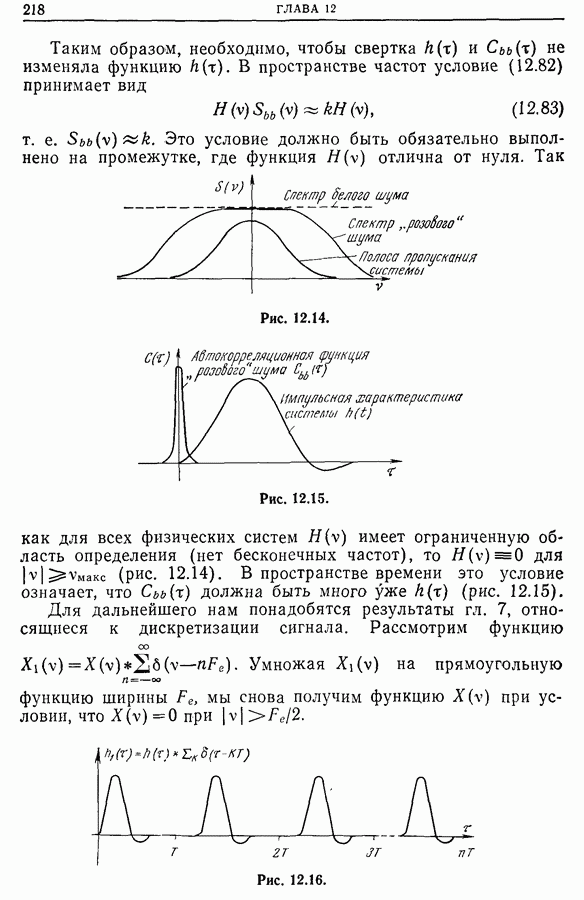
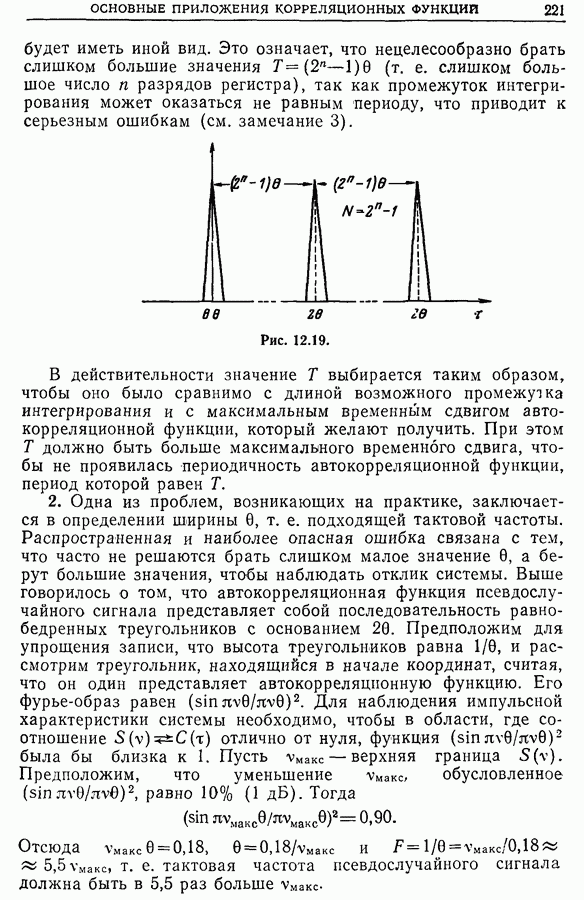
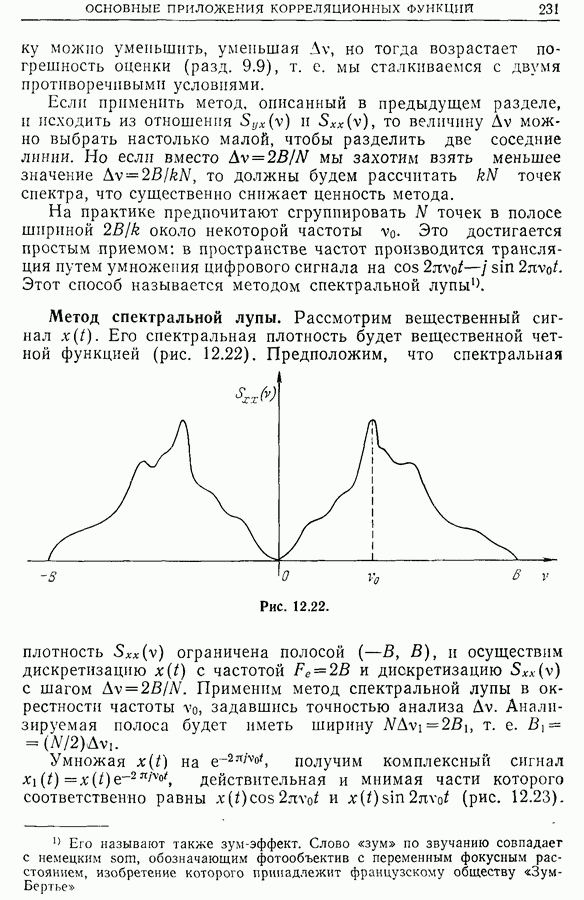
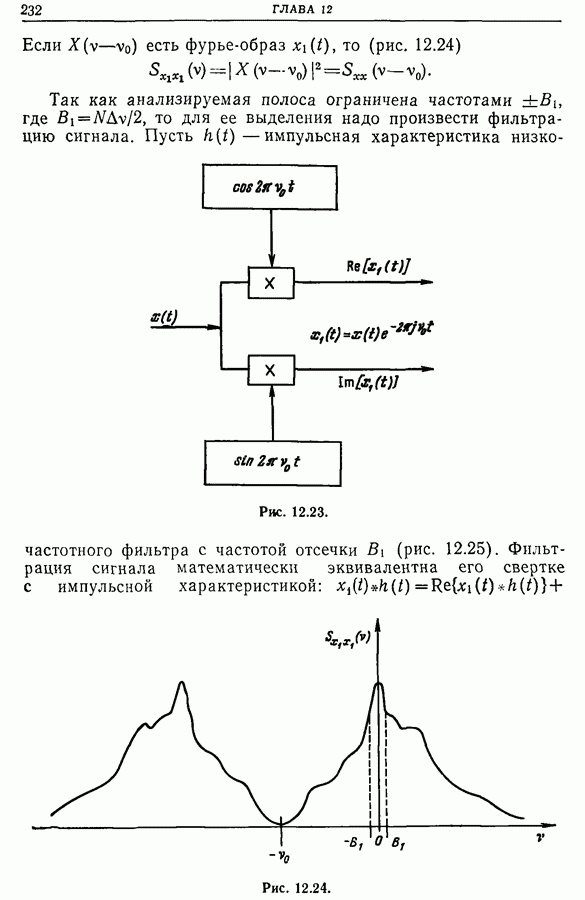
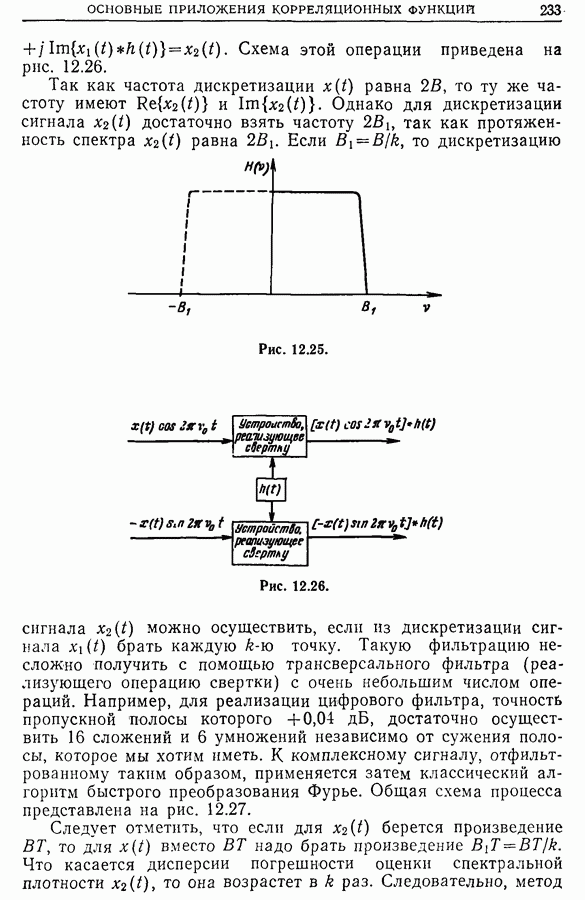
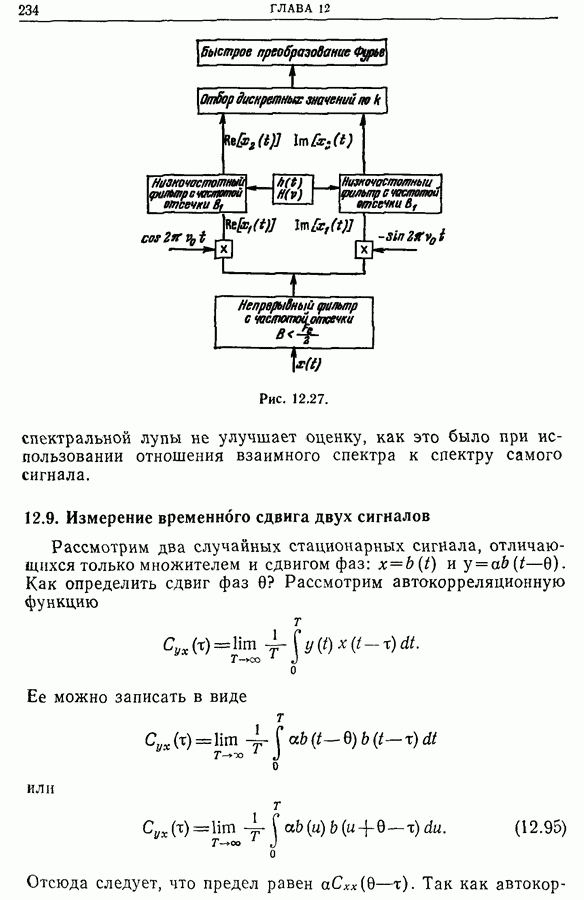
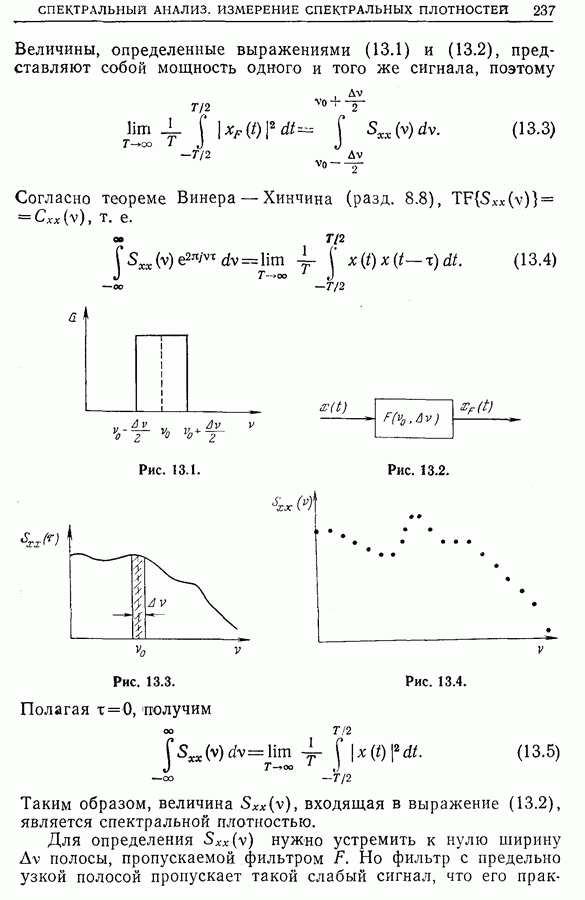
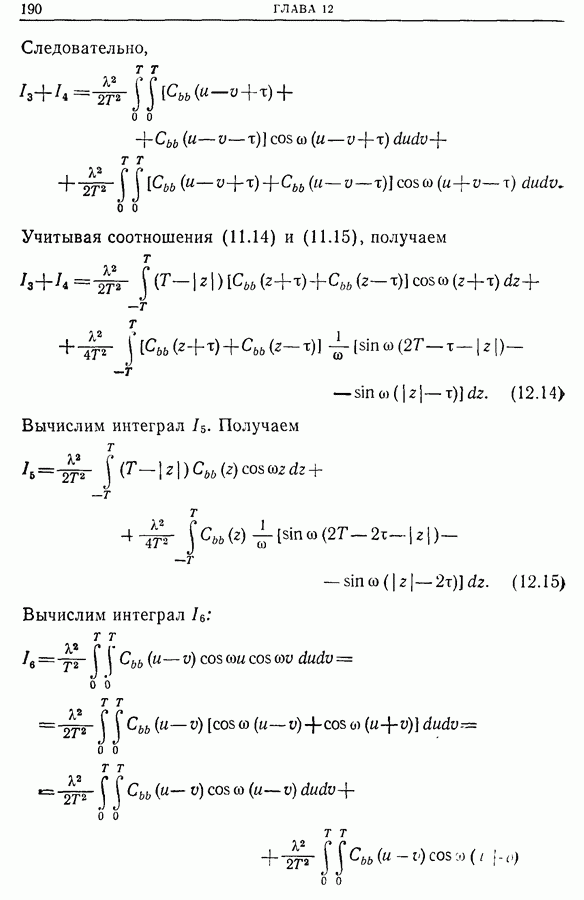| << Предыдущий параграф |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
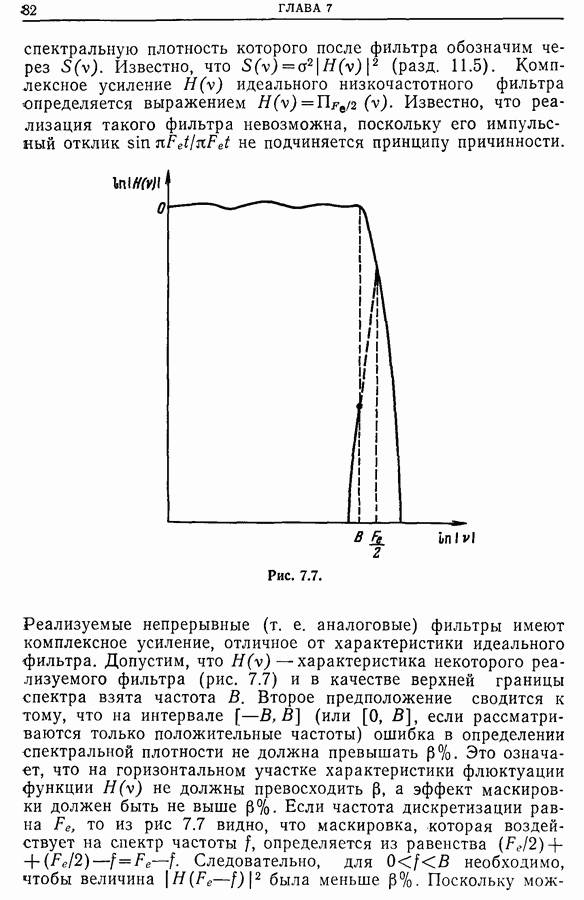
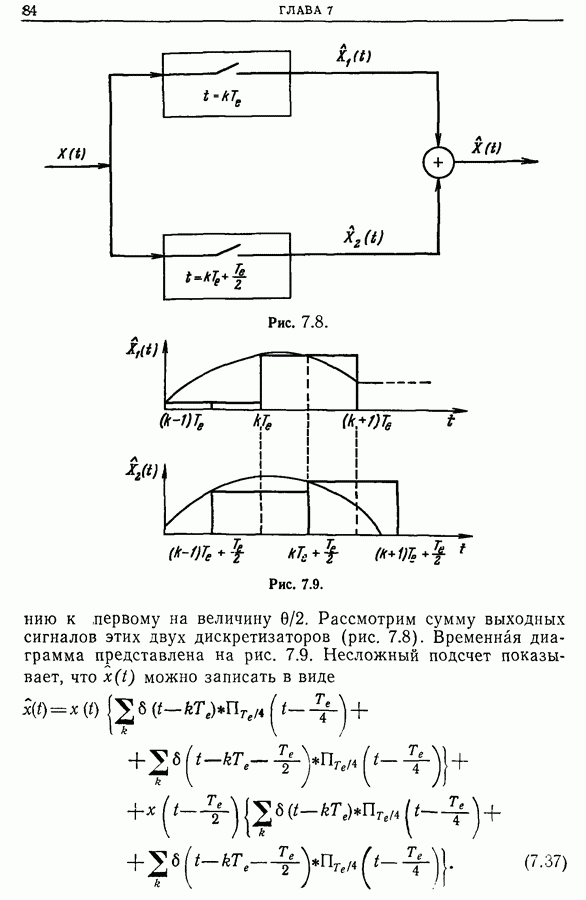
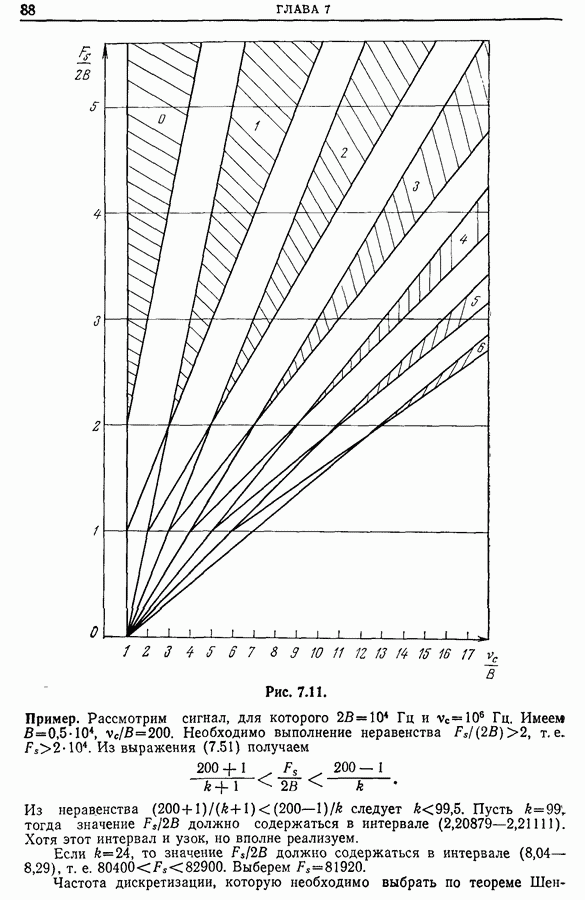
14.10. Выбор весовой функции
Выбор весовой функции представляет собой довольно трудную задачу, при решении которой определяющими факторами являются
• метод оценки спектра (коррелограммы, периодограммы);
• способ обработки спектра (аналоговый, цифровой, комбинированный);
• конечная цель (разделение по частоте соседних пиков, определение мощности резонанса, наибольшая статистическая точность измерений, минимальное искажение общей формы спектра, оценка функции когерентности).
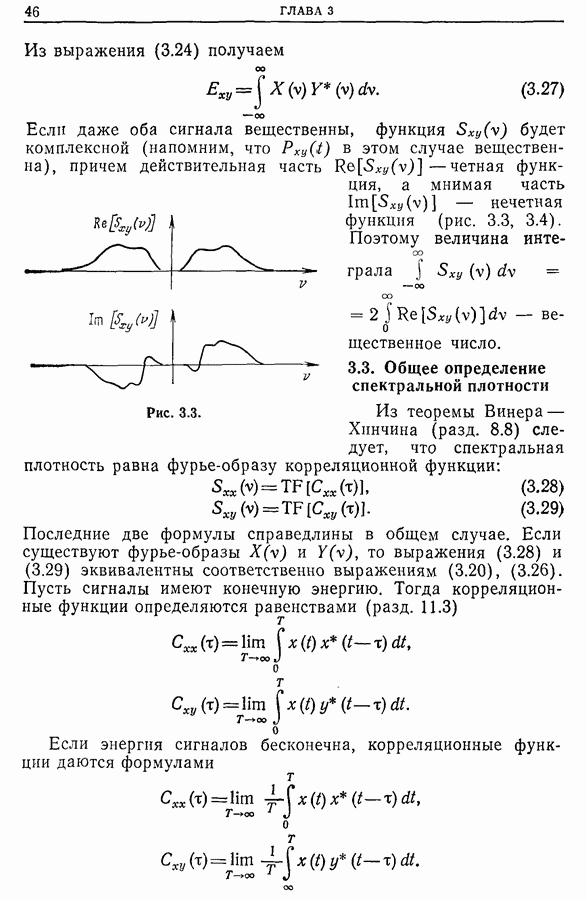
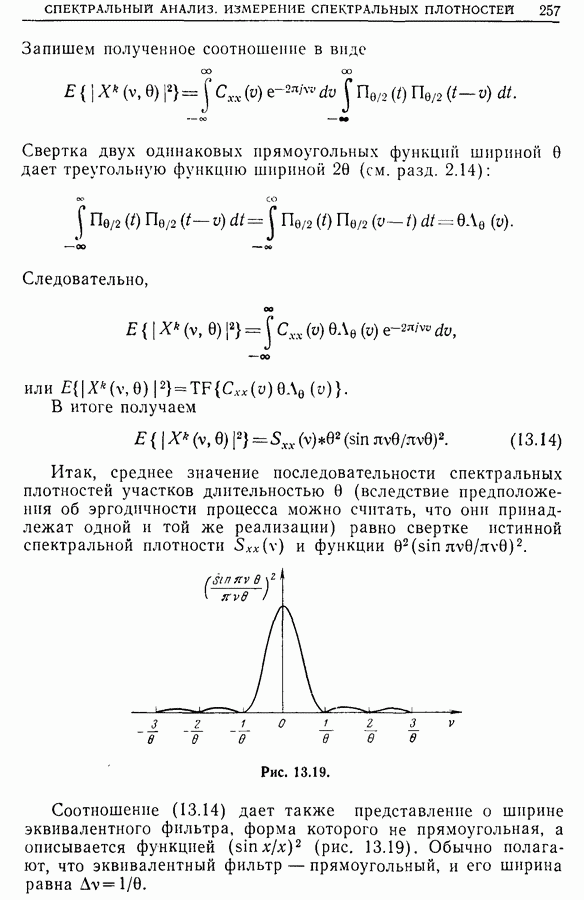
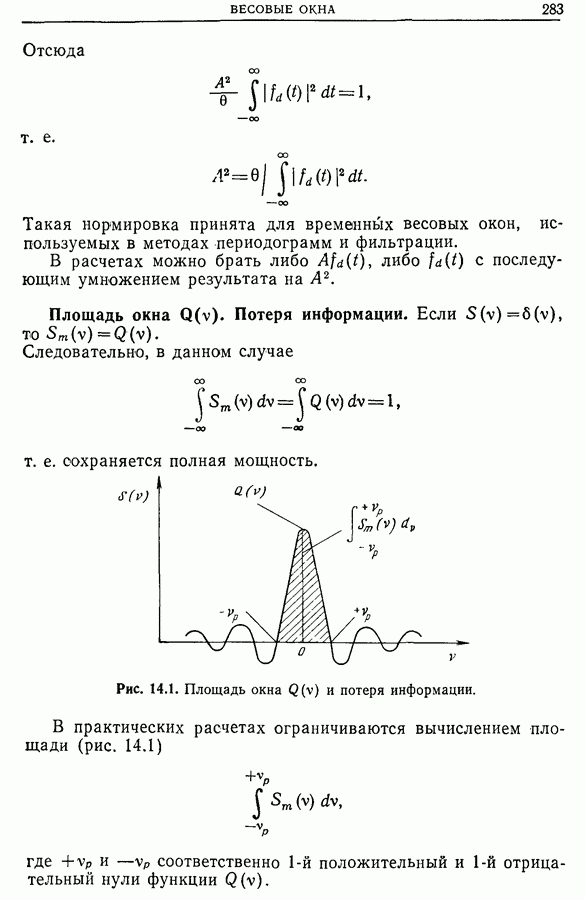
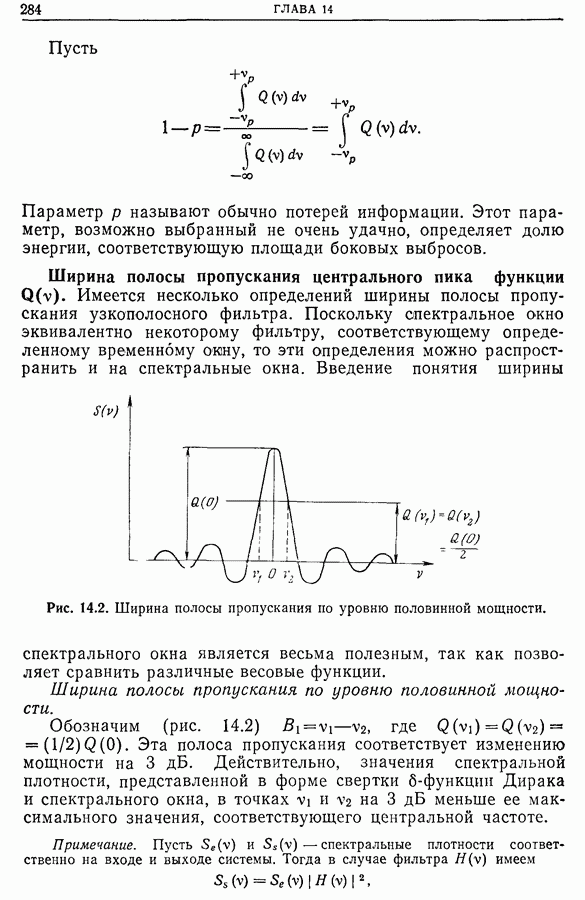
Следует помнить, что хотя большинство весовых окон имеют небольшие выбросы и обладают приемлемой разрешающей способностью, однако любое спектральное окно сглаживает спектральную плотность. Выбранное окно должно максимальным образом отвечать необходимым критериям. Если оценка спектральной плотности получается с помощью корреляционной функции или непосредственно преобразованием Фурье, то при одном и том же весовом окне влияние выбросов на форму
спектра в окрестности пика в 1-м случае будет больше, чем во 2-м. С другой стороны, ширина окна  на половине его высоты больше соответствующей ширины окна
на половине его высоты больше соответствующей ширины окна  при
при  Если применяется прямое преобразование Фурье, то одна из функций —
Если применяется прямое преобразование Фурье, то одна из функций —  или
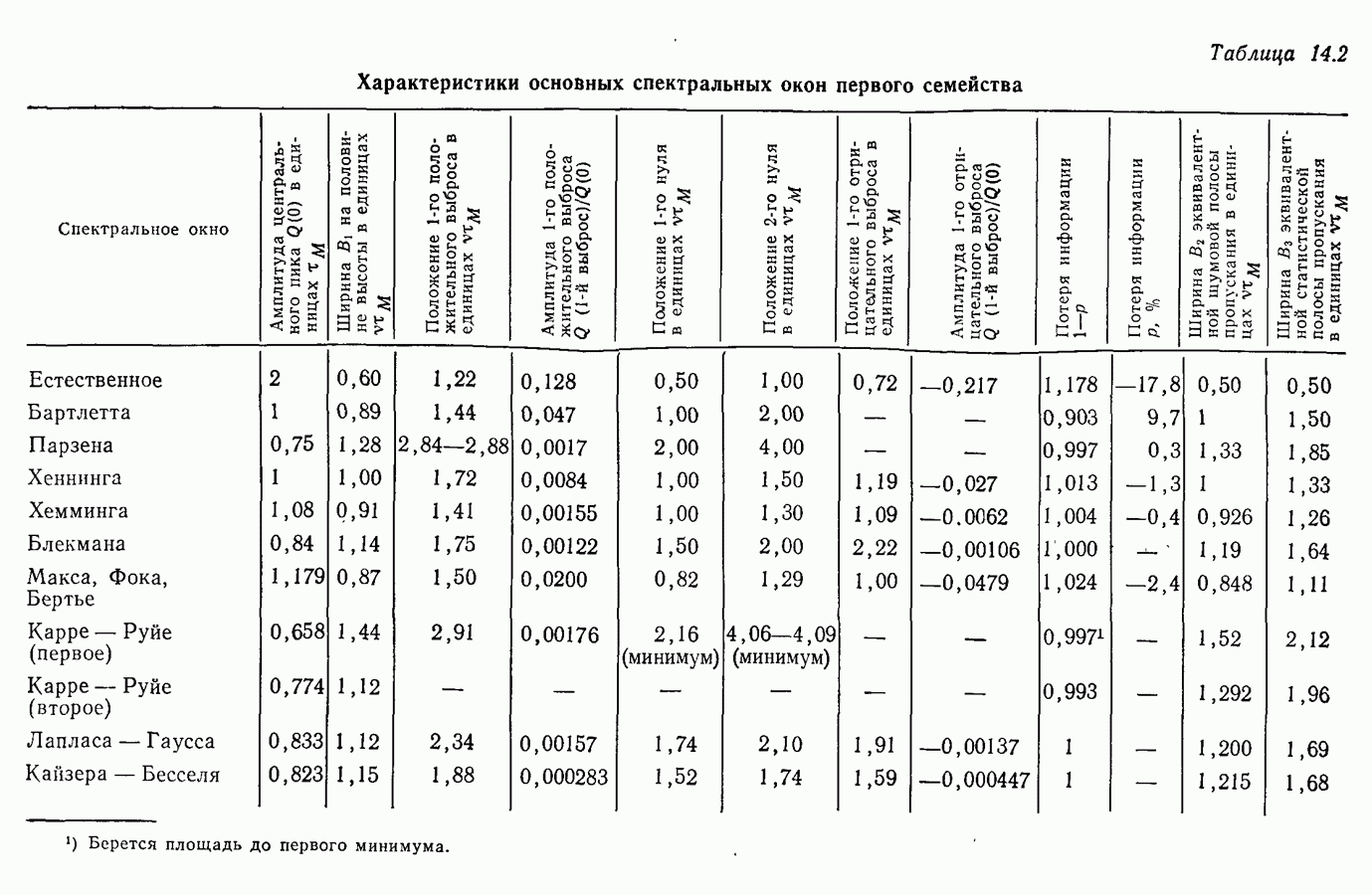
или  — должна быть нормирована, иначе теряется информация о мощности. Только несколько весовых окон — окна Бартлетта, Парзена и Карре — Руйе — используемых в методе коррелограмм, не имеют отрицательных выбросов.
— должна быть нормирована, иначе теряется информация о мощности. Только несколько весовых окон — окна Бартлетта, Парзена и Карре — Руйе — используемых в методе коррелограмм, не имеют отрицательных выбросов.
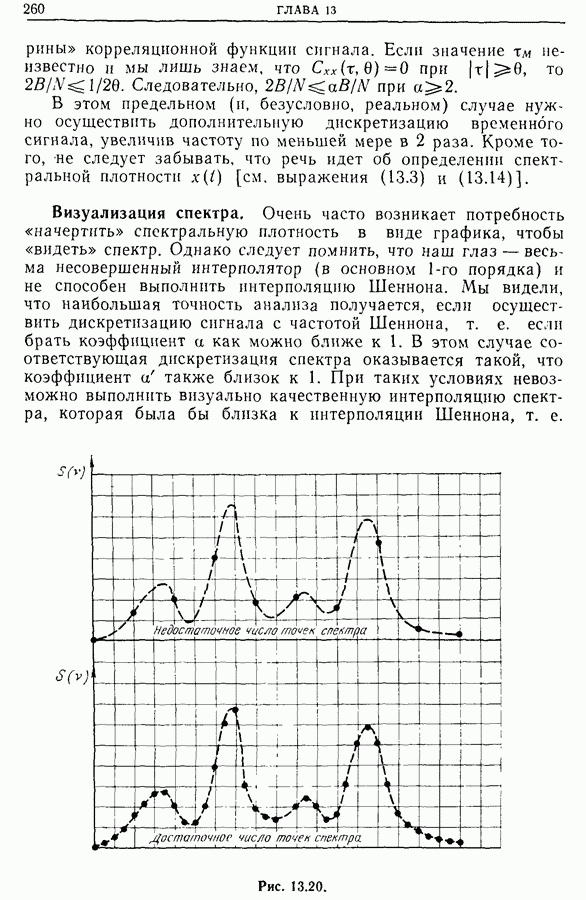
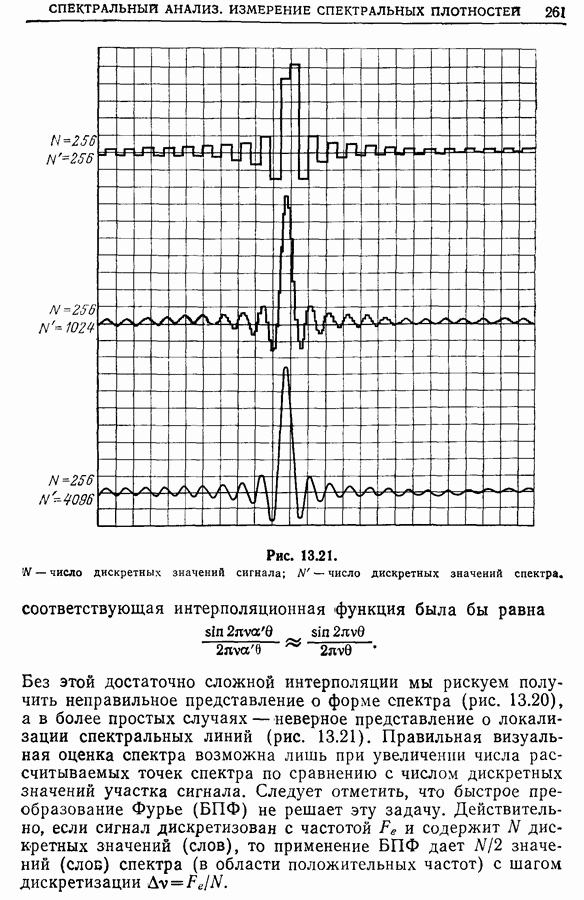
По характеристикам спектральных окон  и по характеристикам изучаемых явлений (требуемое разрешение пиков по частоте и по мощности и т. д.) — и только по этим характеристикам — можно выбрать весовую функцию, отвечающую наилучшим образом выбранному методу обработки. В качестве первого приближения часто используют естественное окно; оно обеспечивает наилучшее разрешение, хотя и искажает спектр из-за наличия выбросов. Затем, руководствуясь видом спектра и целью исследования, подбирают подходящее временное окно (или два, а иногда и несколько, если это возможно). При численной обработке спектра может оказаться, что узловая точка (целое число шагов по частоте) в точности совпадает с пиком. В этом случае лучше всего применить окно с плоской вершиной, помня, однако, что разрешающая способность при этом уменьшается.
и по характеристикам изучаемых явлений (требуемое разрешение пиков по частоте и по мощности и т. д.) — и только по этим характеристикам — можно выбрать весовую функцию, отвечающую наилучшим образом выбранному методу обработки. В качестве первого приближения часто используют естественное окно; оно обеспечивает наилучшее разрешение, хотя и искажает спектр из-за наличия выбросов. Затем, руководствуясь видом спектра и целью исследования, подбирают подходящее временное окно (или два, а иногда и несколько, если это возможно). При численной обработке спектра может оказаться, что узловая точка (целое число шагов по частоте) в точности совпадает с пиком. В этом случае лучше всего применить окно с плоской вершиной, помня, однако, что разрешающая способность при этом уменьшается.
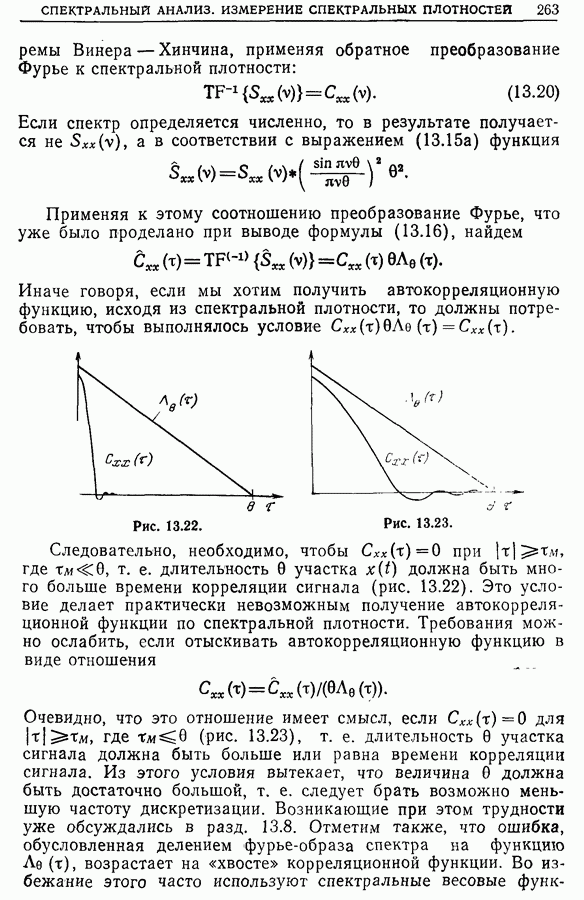
Для разделения пиков, сильно различающихся по мощности, но с не очень близкими частотами, целесообразно использовать временные весовые функции, которым соответствуют спектральные окна  с небольшим числом выбросов или без них. В большинстве случаев форма пиков на кривых спектральной плотности описывается функцией (резонанс 2-го порядка):
с небольшим числом выбросов или без них. В большинстве случаев форма пиков на кривых спектральной плотности описывается функцией (резонанс 2-го порядка):

При подборе наиболее подходящей весовой функции было бы весьма целесообразно руководствоваться не только методикой обработки спектра, но и зависимостью от параметров А и В, которую надо предварительно изучить.
Следует исключить оценку функции когерентности по спектральным плотностям, которые имеют отрицательные значения, обусловленные выбросами функции  . В этом случае надо применять окна Бартлетта, Парзена и окна Карре-—Руйе.
. В этом случае надо применять окна Бартлетта, Парзена и окна Карре-—Руйе.
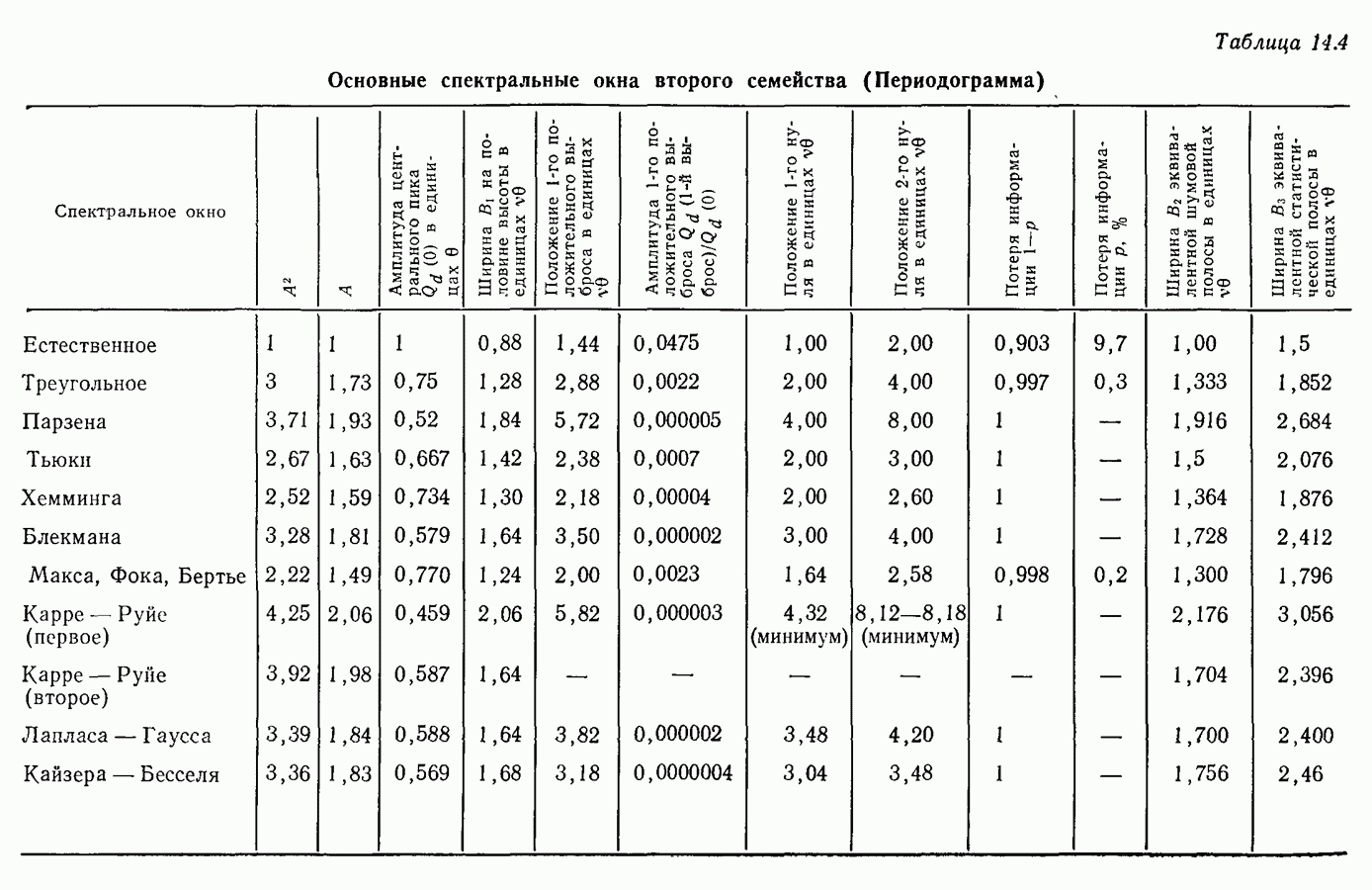
В заключение отметим, что нет общего практического правила выбора весовых функций. Эту задачу надо решать в каждом конкретном случае в соответствии с поставленной целью, руководствуясь характеристиками спектральных окон (табл. 14.1-14.4).
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
- 2.7. Несколько функций и их фурье-образы
- 2.8. Частный случай вещественных сигналов
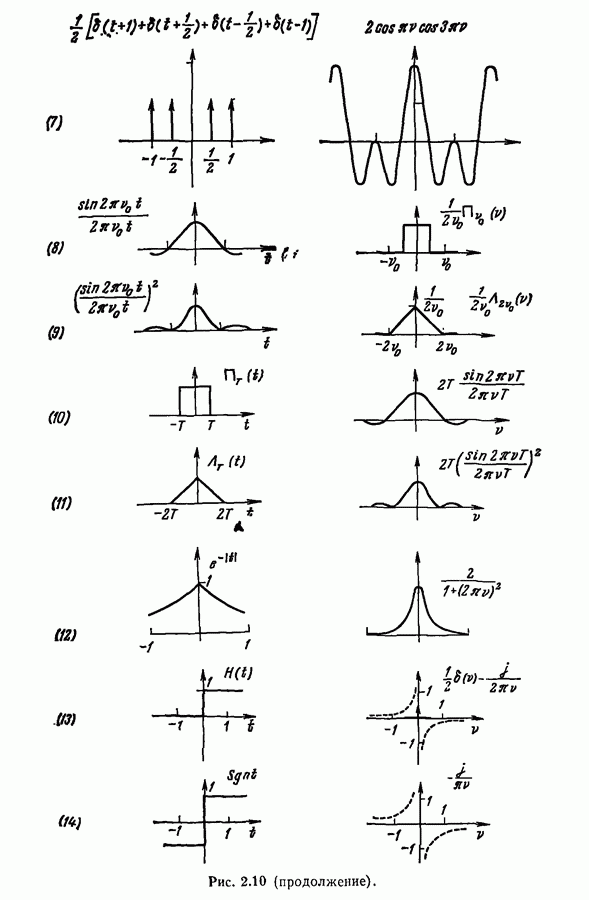
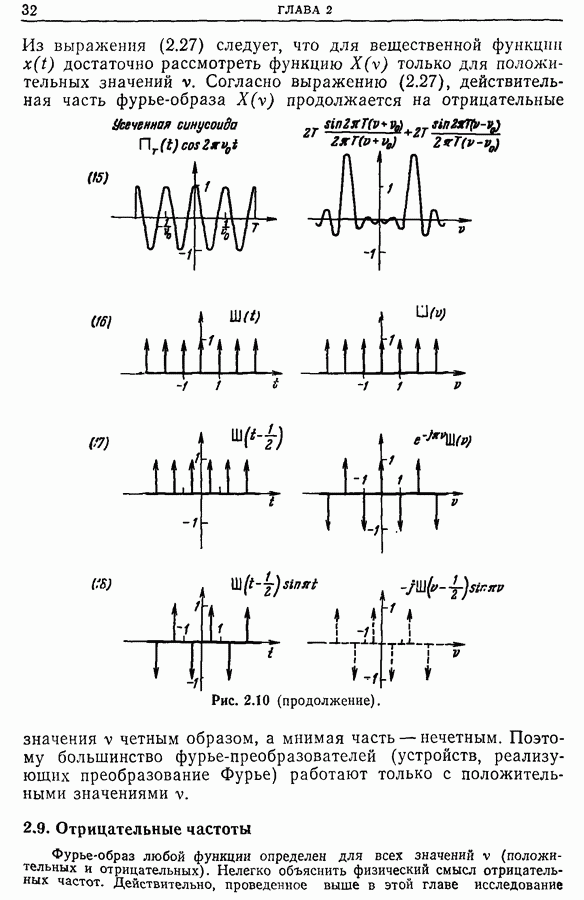
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
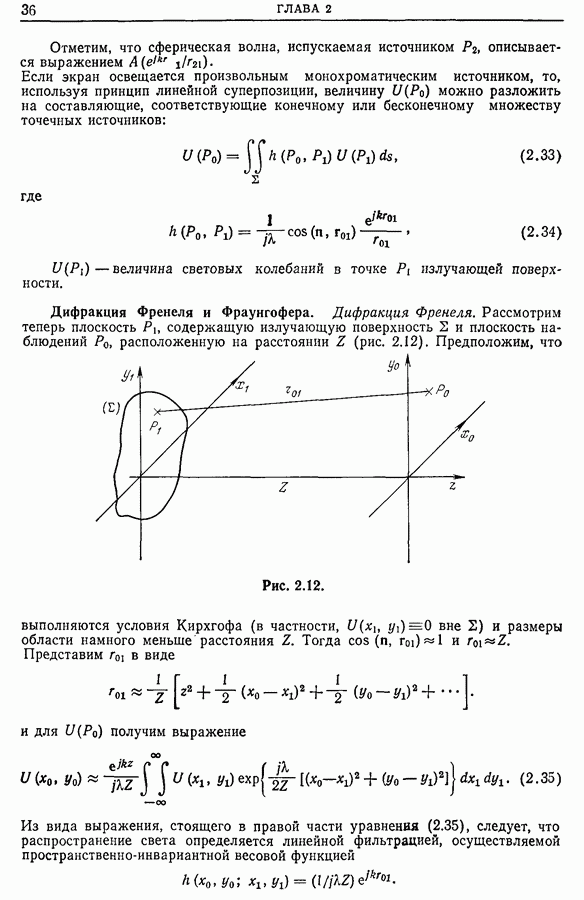
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
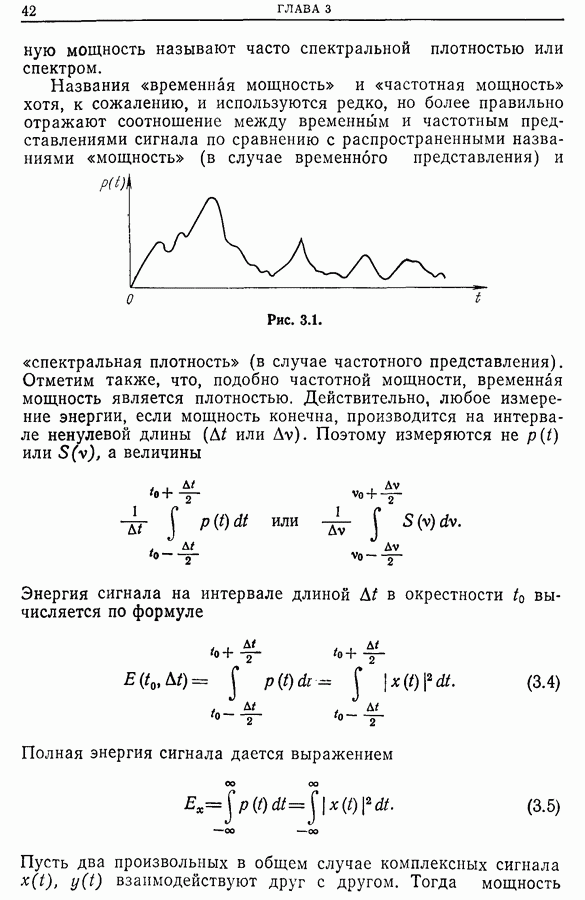
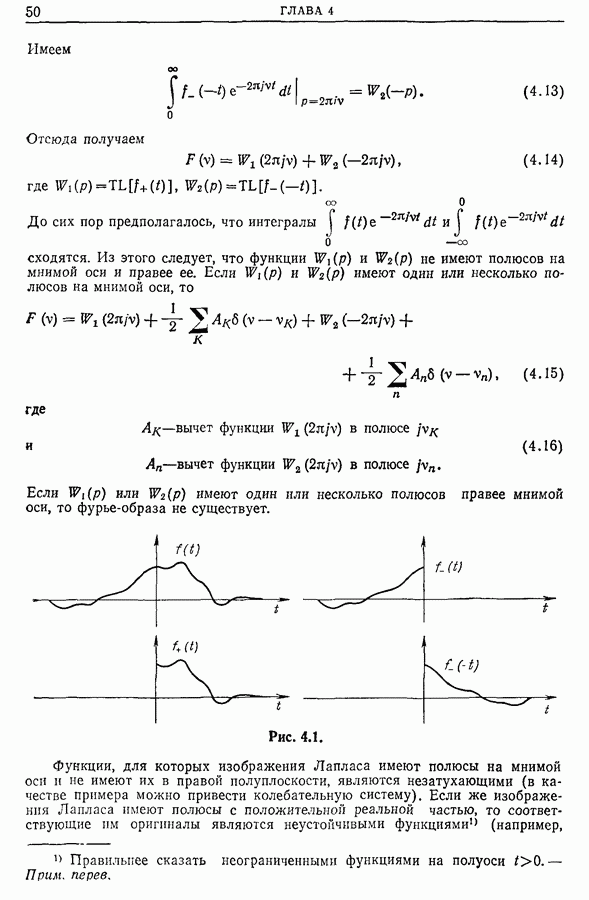
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
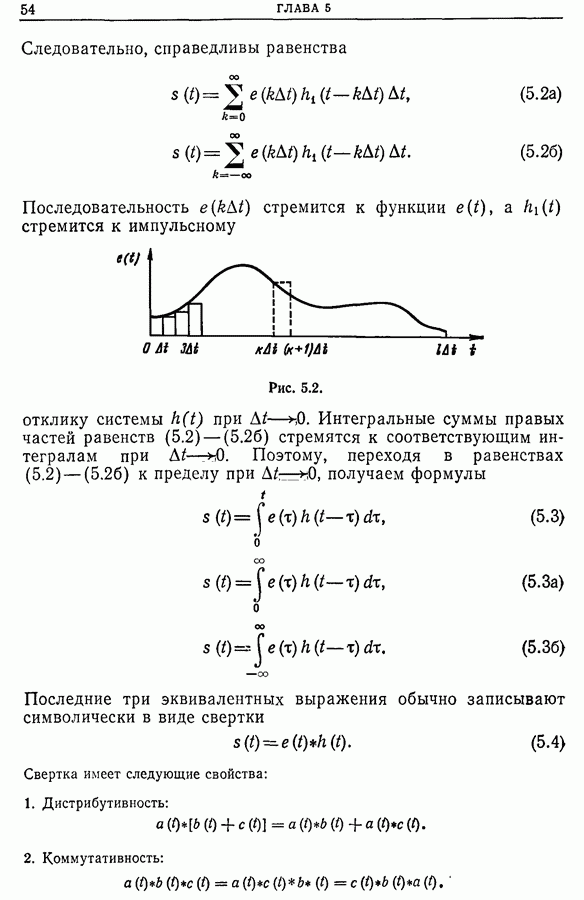
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
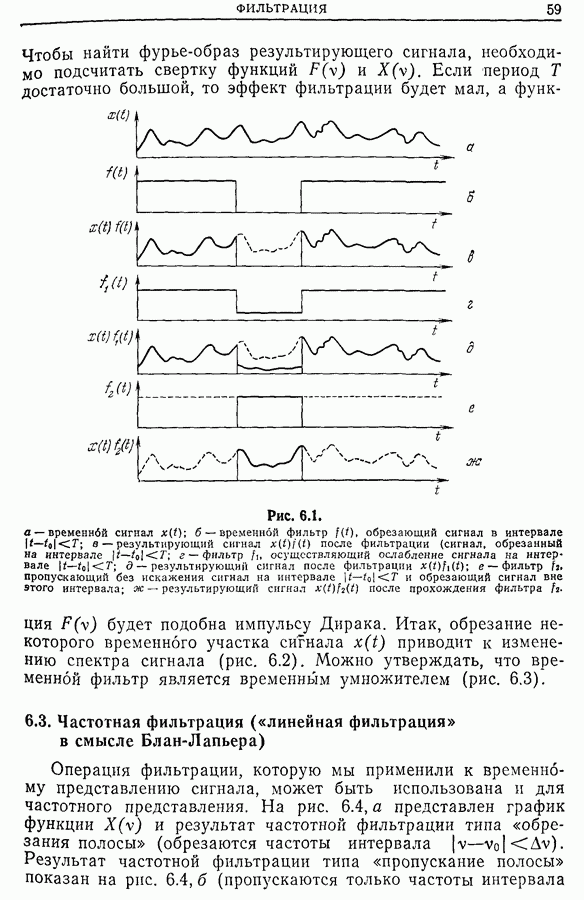
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
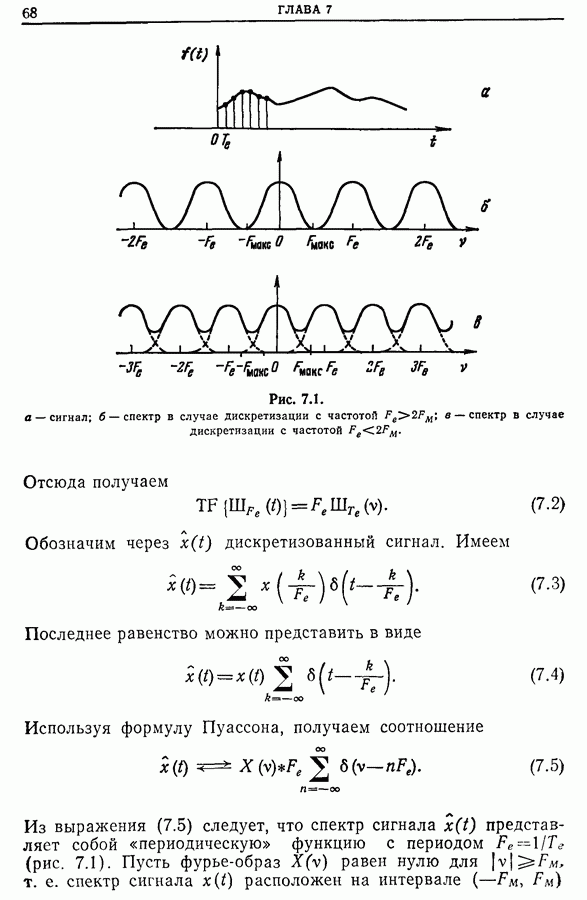
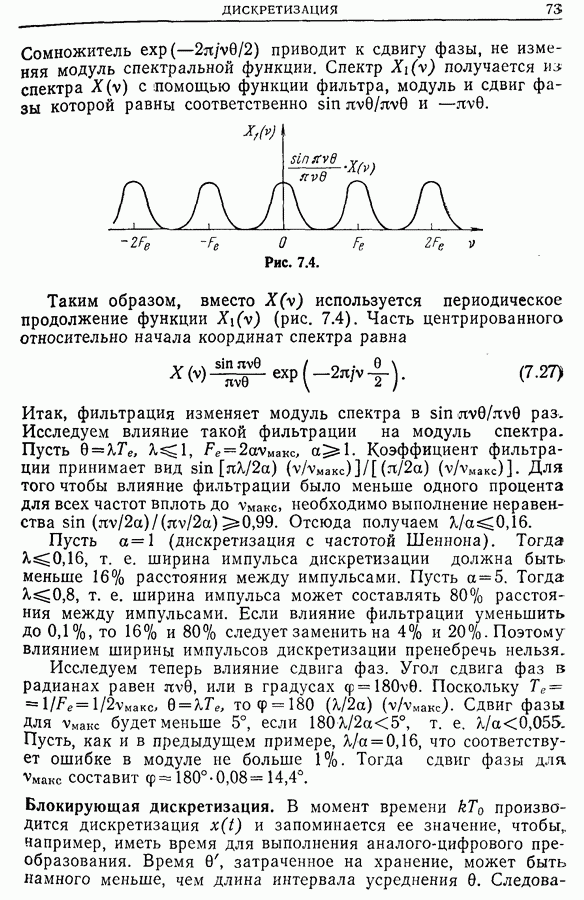
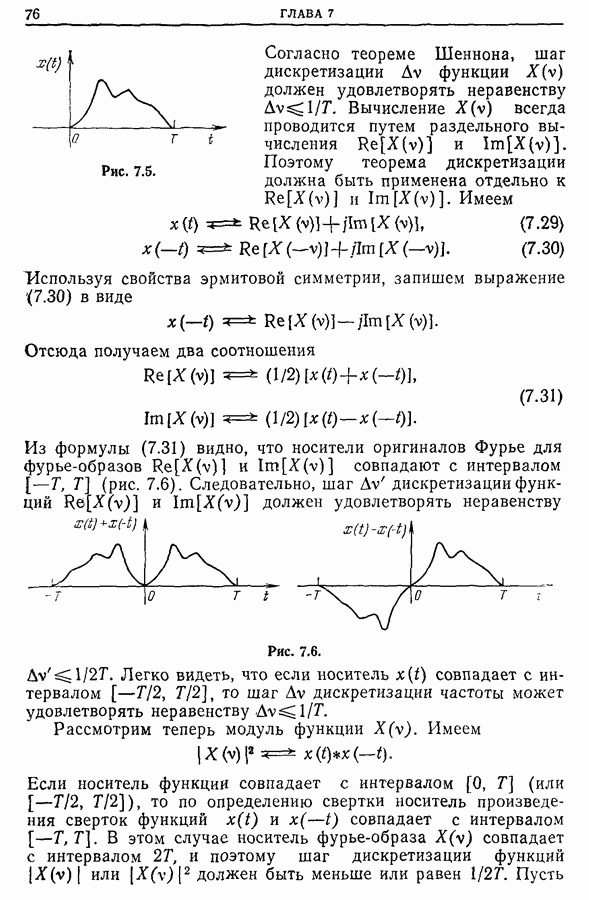
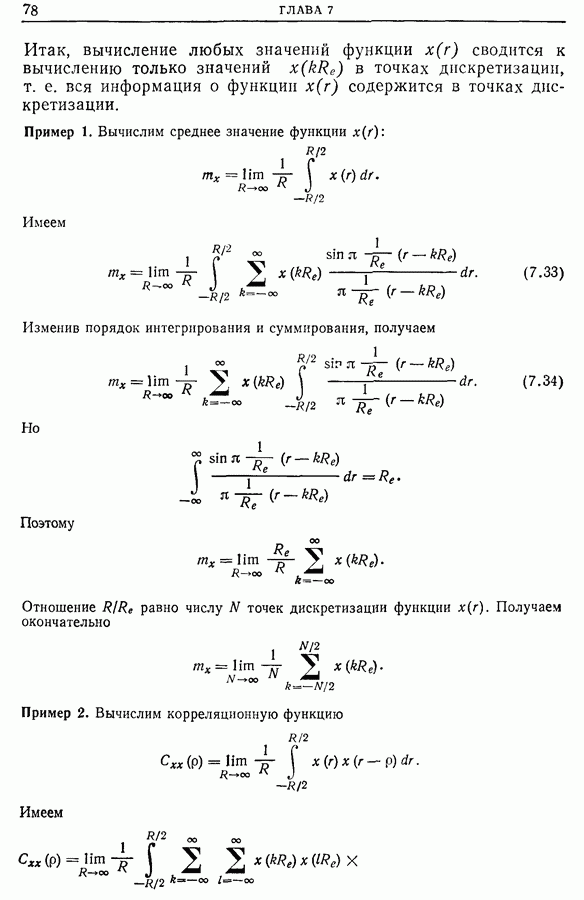
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
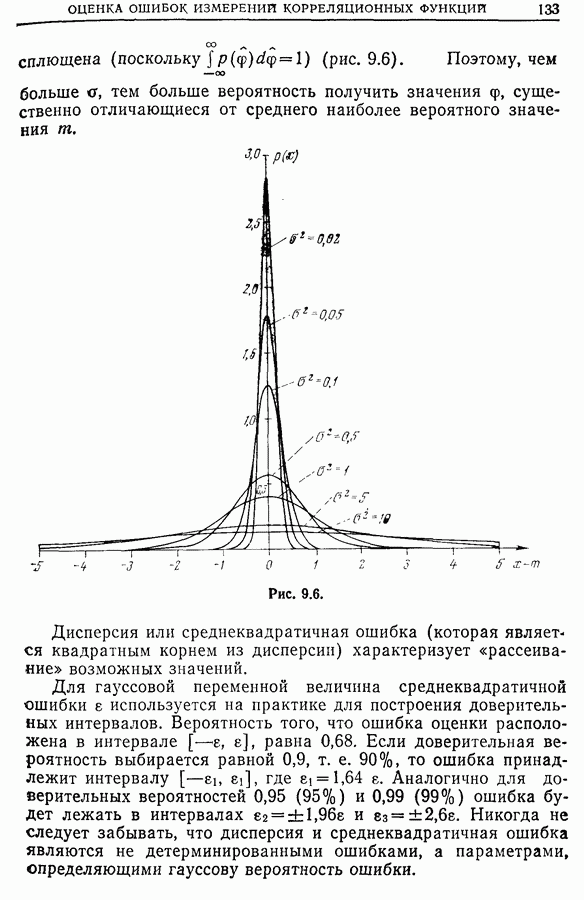
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
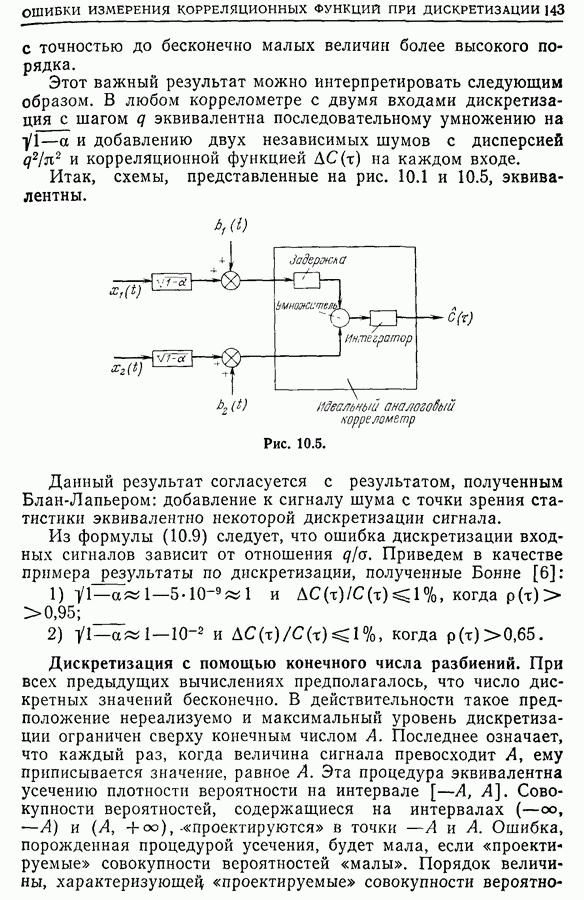
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
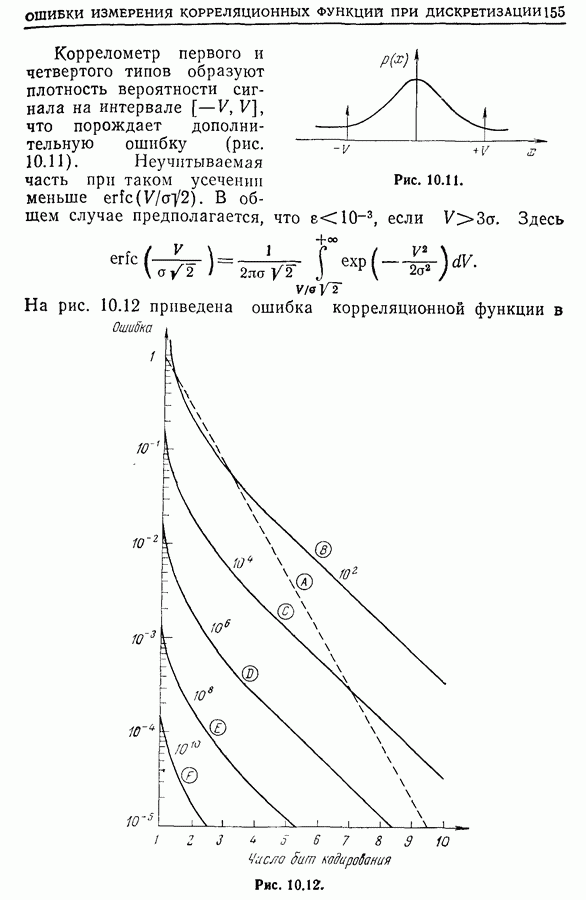
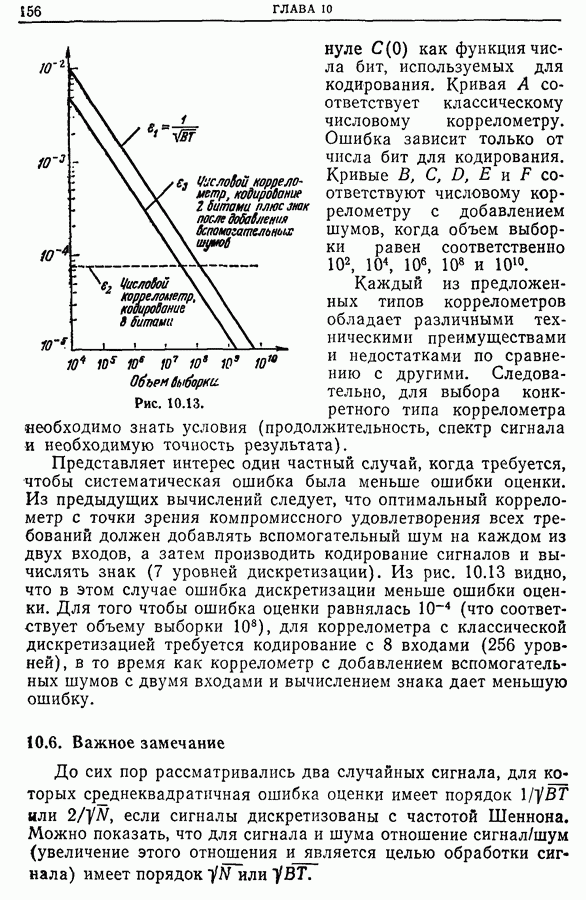
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
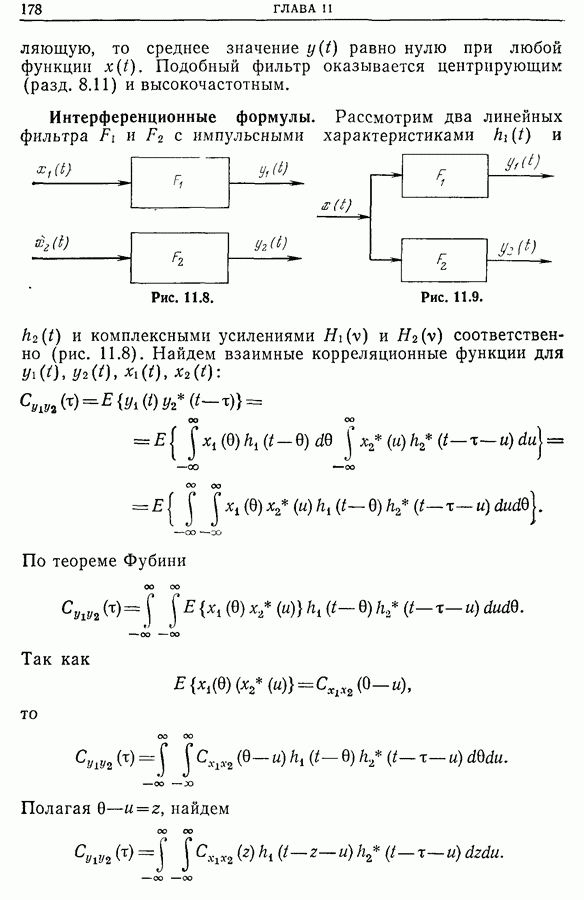
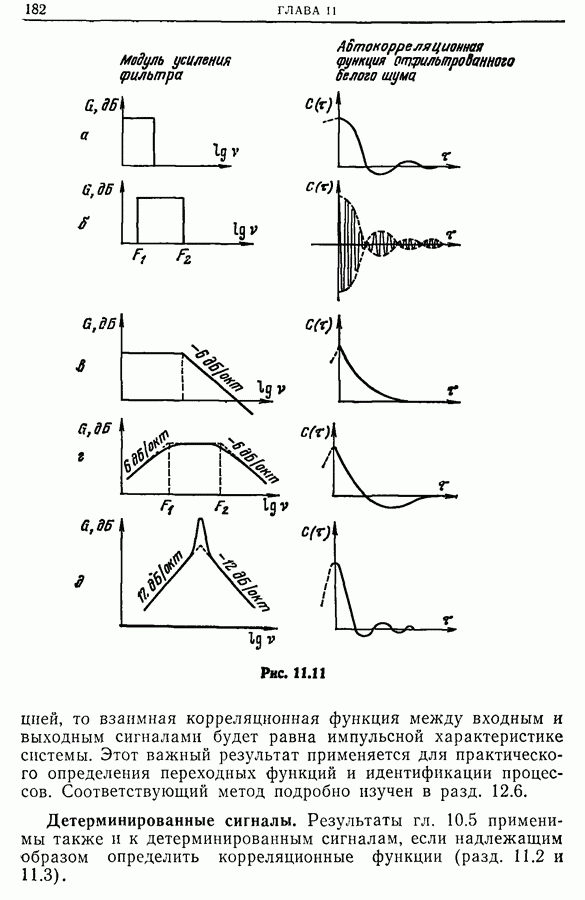
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
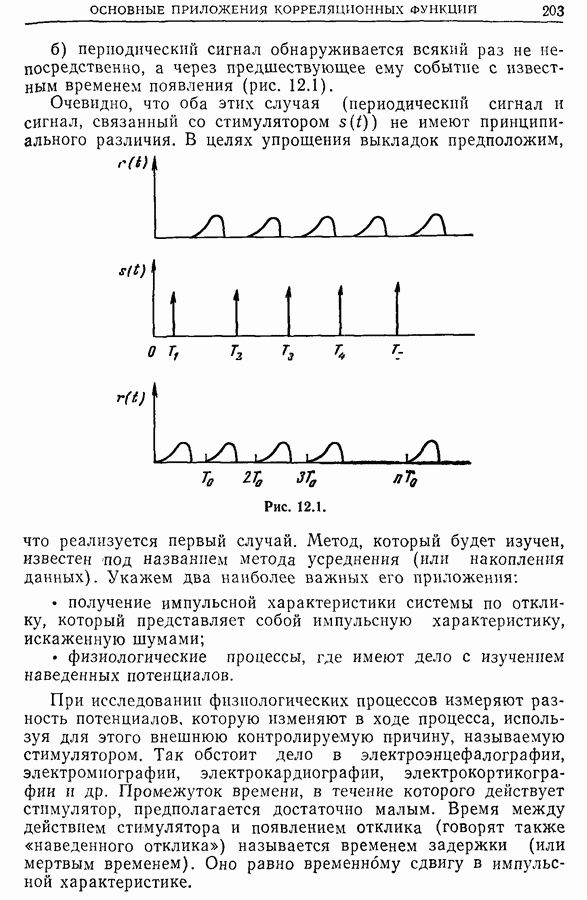
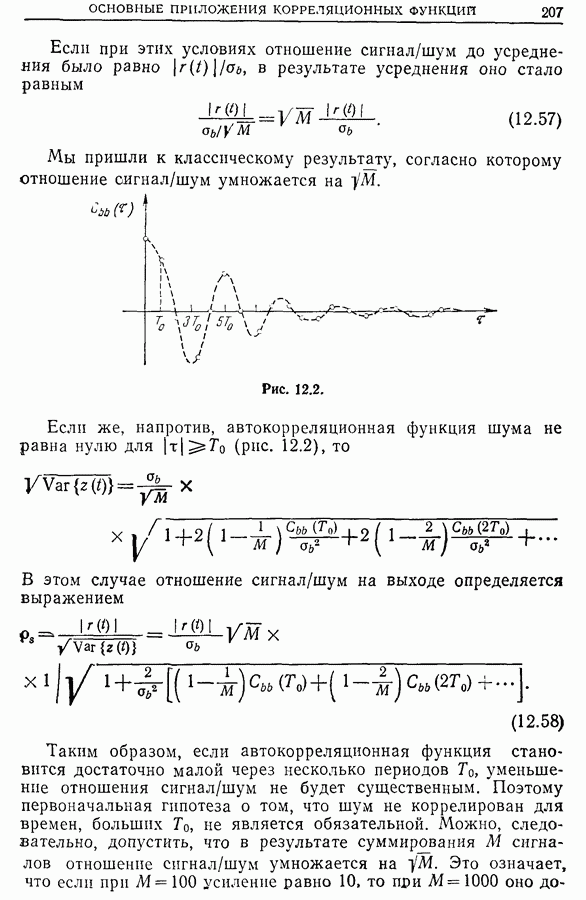
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
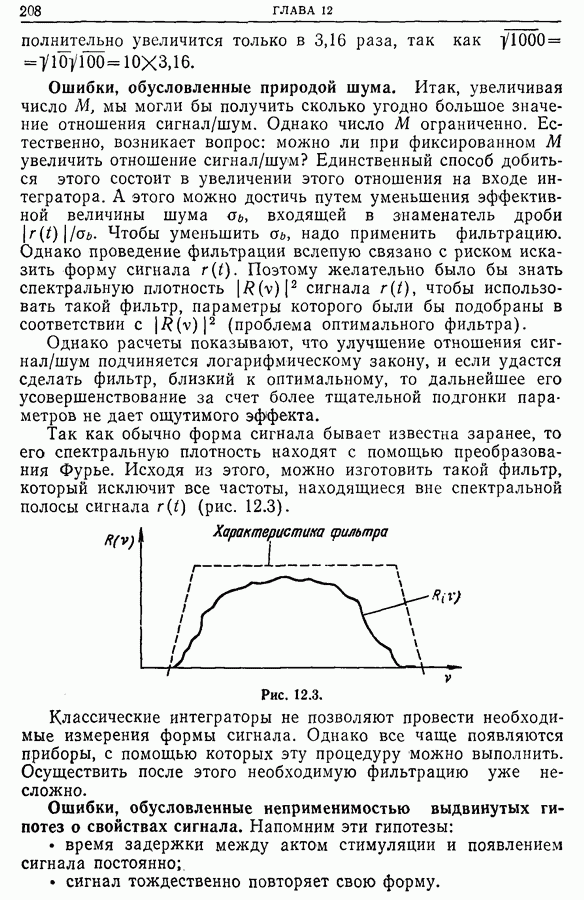
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
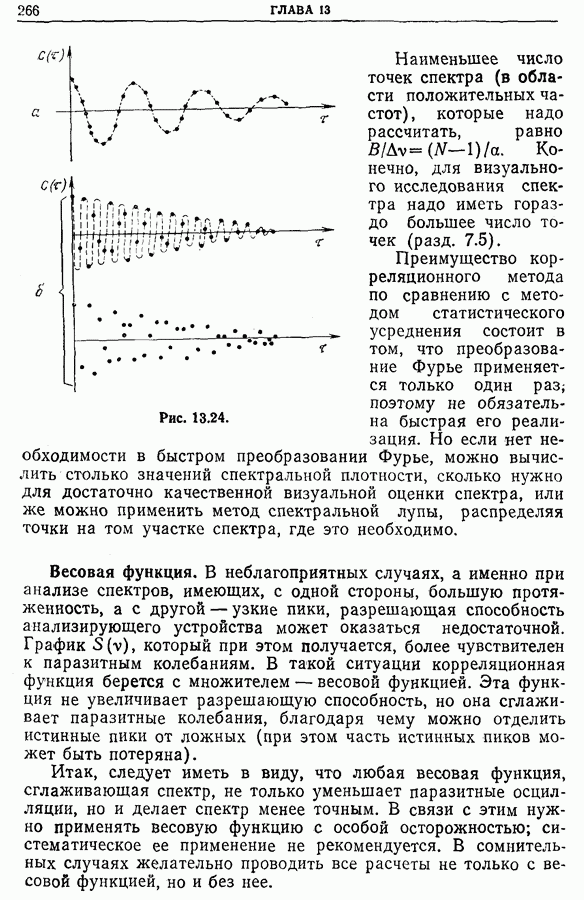
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
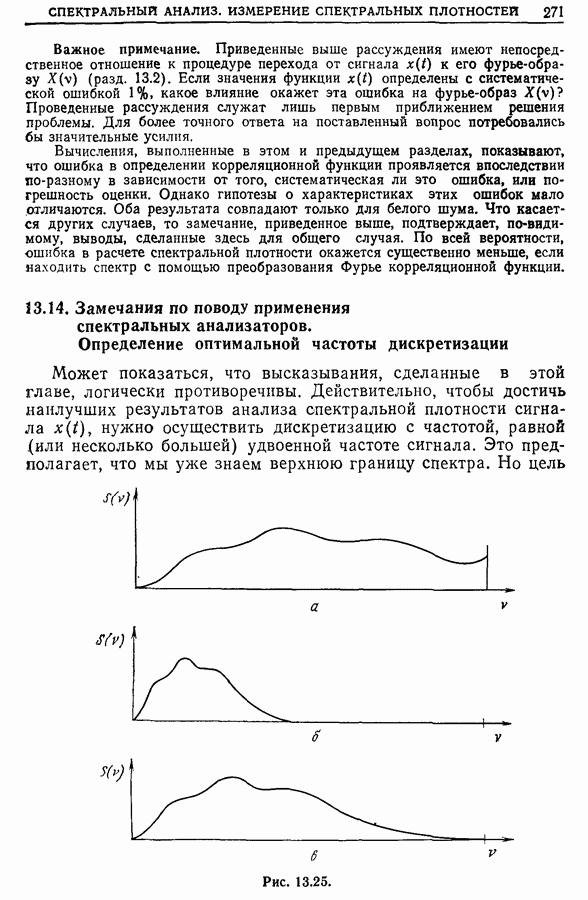
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции