| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
Физическая величина определяется более точно уравнением, чем измерением. Но, определяя ее из уравнения, мы, по сути дела, отказываемся от познания истинного значения данной величины. Сохранение в то же время ее названия влечет за собой неточности и недоразумения. (Макс Планк)
8.1. Поиск «связи» между двумя физическими процессами (явлениями), которые заданы физической величиной, выражающей один из параметров процессов. Случай, когда параметр может быть измерен, если задано большое число реализаций процессов. Средние значения ансамбля
Примеры физических процессов и их реализации.
Рассмотрим семейство числовых функций одной и той же переменной (например, времени), которые соответствуют физическим процессам одной природы. Пусть  — функция этого семейства. Функция
— функция этого семейства. Функция  может быть, например, напряжением шума в электронной трубке. Тогда каждая функция
может быть, например, напряжением шума в электронной трубке. Тогда каждая функция  представляет напряжение шума в
представляет напряжение шума в  трубке одной партии трубок. Функция
трубке одной партии трубок. Функция  может быть также электроэнцефалограммой людей с одной и той же болезнью или представлять скорость ветра как функцию высоты
может быть также электроэнцефалограммой людей с одной и той же болезнью или представлять скорость ветра как функцию высоты  Наряду с семейством
Наряду с семейством  можно рассмотреть другое семейство функций
можно рассмотреть другое семейство функций  например напряжение шумов в трубках другого типа, или электрокардиограммы больных, или, наконец, температуры в момент времени
например напряжение шумов в трубках другого типа, или электрокардиограммы больных, или, наконец, температуры в момент времени  на высоте
на высоте  Требуется установить связь между физическим процессом
Требуется установить связь между физическим процессом  порождающим семейство функций
порождающим семейство функций  (называемых реализациями процесса
(называемых реализациями процесса  и физическим процессом
и физическим процессом  порождающим семейство функций
порождающим семейство функций  (называемых реализациями процесса
(называемых реализациями процесса 
Среднее значение ансамбля. Связь с математическим ожиданием.
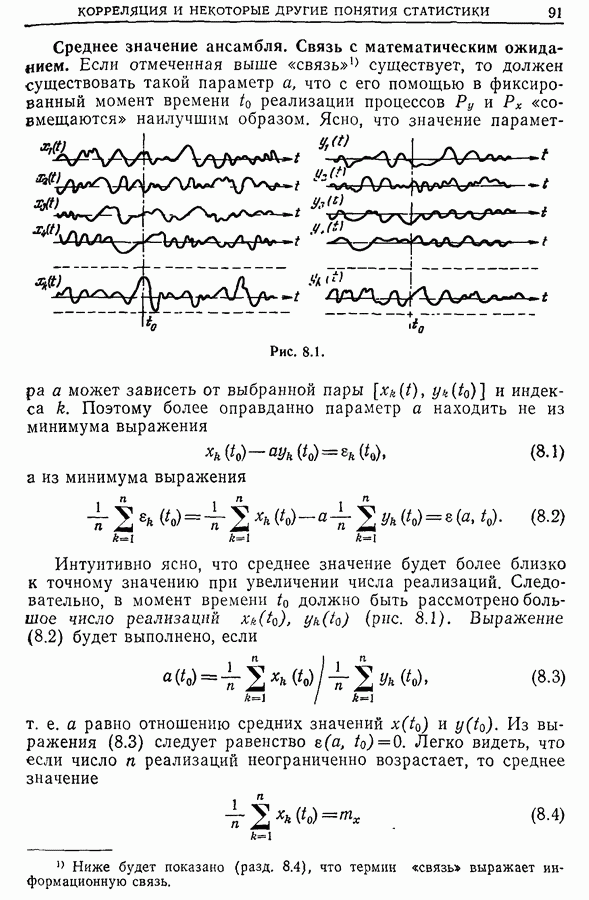
Если отмеченная выше «связь» существует, то должен существовать такой параметр а, что с его помощью в фиксированный момент времени  реализации процессов
реализации процессов  «совмещаются» наилучшим образом.
«совмещаются» наилучшим образом.

Рис. 8.1.
Ясно, что значение параметра а может зависеть от выбранной пары  и индекса
и индекса  Поэтому более оправданно параметр а находить не из минимума выражения
Поэтому более оправданно параметр а находить не из минимума выражения

а из минимума выражения

Интуитивно ясно, что среднее значение будет более близко к точному значению при увеличении числа реализаций. Следовательно, в момент времени  должно быть рассмотрено большое число реализаций
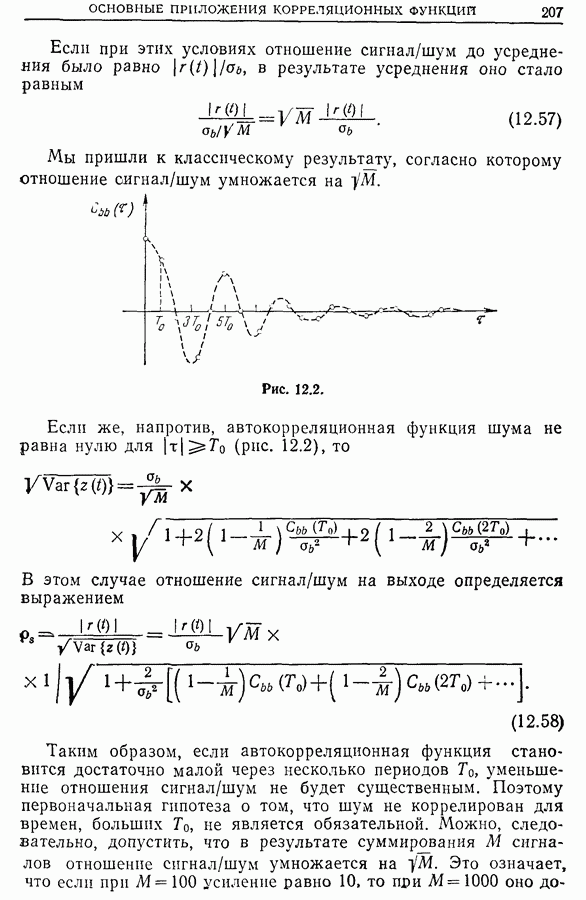
должно быть рассмотрено большое число реализаций  (рис. 8.1). Выражение (8.2) будет выполнено, если
(рис. 8.1). Выражение (8.2) будет выполнено, если

т. е. а равно отношению средних значений  Из выражения (8.3) следует равенство
Из выражения (8.3) следует равенство  Легко видеть, что если число
Легко видеть, что если число  реализаций неограниченно возрастает, то среднее значение
реализаций неограниченно возрастает, то среднее значение

стремится к математическому ожиданию  Если область изменения
Если область изменения  разбита на равные интервалы длины q (т. е. произведена операция дискретизации), то переменная
разбита на равные интервалы длины q (т. е. произведена операция дискретизации), то переменная  заменяется дискретной переменной, которая принимает только значения, кратные
заменяется дискретной переменной, которая принимает только значения, кратные  По определению математического ожидания имеем
По определению математического ожидания имеем


Рис. 8.2.
Выражение (8.5) можно записать также в виде

Одномерная плотность вероятности.
Рассмотрим вероятность того, что значение  принадлежит промежутку
принадлежит промежутку  (выражение
(выражение  Если
Если  стремится к нулю, то выражение (8.5) представляет собой плотность вероятности. Обозначим через
стремится к нулю, то выражение (8.5) представляет собой плотность вероятности. Обозначим через  вероятность нахождения значений случайной величины X на промежутке
вероятность нахождения значений случайной величины X на промежутке  Пусть
Пусть  Функция
Функция  называется плотностью вероятности. Такое определение плотности вероятности широко используется в теории вероятности. Поскольку всегда существует минимальная возможная величина
называется плотностью вероятности. Такое определение плотности вероятности широко используется в теории вероятности. Поскольку всегда существует минимальная возможная величина  определяемая разрешающей способностью прибора, то на практике возможна регистрация вероятности
определяемая разрешающей способностью прибора, то на практике возможна регистрация вероятности  Имеем
Имеем

где  — плотность вероятности (рис. 8.2).
— плотность вероятности (рис. 8.2).

Рис. 8.3.
Функция  всегда удовлетворяет условию нормировки
всегда удовлетворяет условию нормировки

Величина  является, очевидно, результатом «дискретизации с усреднением» плотности вероятности (рис. 8.2).
является, очевидно, результатом «дискретизации с усреднением» плотности вероятности (рис. 8.2).
Можно дать наглядную физическую интерпретацию такой дискретизации плотности вероятности (рис. 8.3). Рассмотрим некоторую функцию, график которой представлен набором шариков, свободно насаженных на решетку из горизонтальных и параллельных стержней. Для более точной реализации графика функции можно уменьшить расстояние между стержнями и размеры шариков. Если повернуть решетку на 90° в вертикальное положение, то шарики, скользя вдоль стержней, упадут вниз и совокупность шариков на всех стержнях даст аппроксимацию графика плотности вероятности. По существу аналогичная операция реализуется при построении гистограммы амплитуд с помощью комбинированного селектора (гл. 16).
Двумерная плотность вероятности.
Можно рассмотреть вероятность  того, что значения случайных величин
того, что значения случайных величин  содержатся соответственно в интервалах
содержатся соответственно в интервалах  Пусть
Пусть 
Тогда

Математическое ожидание произведения 

Вероятность  события
события 
 для двух случайных процессов
для двух случайных процессов  можно вычислить по формуле
можно вычислить по формуле

Многомерная плотность вероятности.
Аналогично определяется трехмерная, четырехмерная,  -мерная плотность вероятности. Можно доказать, что с возрастанием размерности
-мерная плотность вероятности. Можно доказать, что с возрастанием размерности  растет объем информации о случайном процессе, содержащейся в n-мерной плотности вероятности.
растет объем информации о случайном процессе, содержащейся в n-мерной плотности вероятности.
Среднеквадратичное отклонение.
Введенный выше параметр а обладает одним существенным недостатком. Пусть средние значения функций  равны нулю. Тогда, если даже значения
равны нулю. Тогда, если даже значения  различны, функция
различны, функция  равна нулю для всех значений а. Поэтому введем другой критерий сравнения. Чтобы критерий отражал суть явлений, он должен быть связан с энергией, содержащейся в разности сигналов
равна нулю для всех значений а. Поэтому введем другой критерий сравнения. Чтобы критерий отражал суть явлений, он должен быть связан с энергией, содержащейся в разности сигналов  (разд. 8.7), поскольку в конечном счете нас интересует в сигнале его энергия или мощность. Итак, рассмотрим величину
(разд. 8.7), поскольку в конечном счете нас интересует в сигнале его энергия или мощность. Итак, рассмотрим величину 
 , или
, или

Минимизация среднеквадратичного отклонения. Коэффициент корреляции.
Найдем значение коэффициента  , минимизирующее
, минимизирующее  . Имеем
. Имеем

т. е.

Из выражения (8.13) получаем

Минимальное значение  определяется из выражения
определяется из выражения 

Обозначим

Тогда

Из выражения (8.17) следует, что  для
для  . В случае
. В случае  говорят, что процессы
говорят, что процессы  полностью коррелируют в момент времени
полностью коррелируют в момент времени  . Если
. Если  то
то  . В этом случае говорят, что процессы
. В этом случае говорят, что процессы  не коррелируют в момент времени
не коррелируют в момент времени  Величина
Величина  характеризующая «связь» между двумя процессами, называется коэффициентом корреляции. Величину
характеризующая «связь» между двумя процессами, называется коэффициентом корреляции. Величину

принято называть ковариацией.
Связь коэффициента корреляции с математическим ожиданием произведения и квадратов случайных величин.
При  ковариация —
ковариация —  стремится к математическому ожиданию произведения
стремится к математическому ожиданию произведения 

где 
Аналогично величины  стремятся к математическим ожиданиям
стремятся к математическим ожиданиям 
До сих пор значения случайных функций  рассматривались для одного и того же момента времени
рассматривались для одного и того же момента времени  Можно исследовать связь между этими значениями и для разных моментов времени, например
Можно исследовать связь между этими значениями и для разных моментов времени, например  Тогда ковариация будет зависеть от смещения
Тогда ковариация будет зависеть от смещения 

 называется корреляционной функцией. Обычно вместо
называется корреляционной функцией. Обычно вместо  рассматриваются центрированные случайные величины
рассматриваются центрированные случайные величины  , где
, где  . Математические ожидания центрированных случайных величин равны нулю, т. е.
. Математические ожидания центрированных случайных величин равны нулю, т. е. 
Имеем

Отсюда

Итак, корреляционная функция двух случайных процессов  равна сумме корреляционной функции центрированных случайных процессов и произведения математических ожиданий. Если процессы стационарны, то математические ожидания
равна сумме корреляционной функции центрированных случайных процессов и произведения математических ожиданий. Если процессы стационарны, то математические ожидания  зависят от момента времени, т. е.
зависят от момента времени, т. е.  ту — постоянные величины). Поэтому для стационарных случайных процессов
ту — постоянные величины). Поэтому для стационарных случайных процессов

Ниже, за исключением специально оговоренных случаев, предполагается, что рассматриваемые случайные величины центрированы.
Стационарные процессы. Для многих случайных процессов в пределах заданной точности можно предполагать, что средние значения, дисперсии, коэффициенты корреляции и
корреляционные функции не зависят от рассматриваемого момента времени. Поэтому, если перечисленные выше характеристики вычислены в момент времени  то они будут известны для всего временного интервала задания процесса, т. е. имеется возможность «предсказания» величии некоторых характеристик процесса. В этом случае можно в определенной степени предсказать изменение процесса. Процессы, статистические характеристики которых не изменяются с течением времени, называются стационарными. Почти во всех случаях под стационарностью процесса подразумевают независимость от времени одномерных и двумерных статистических характеристик процесса.
то они будут известны для всего временного интервала задания процесса, т. е. имеется возможность «предсказания» величии некоторых характеристик процесса. В этом случае можно в определенной степени предсказать изменение процесса. Процессы, статистические характеристики которых не изменяются с течением времени, называются стационарными. Почти во всех случаях под стационарностью процесса подразумевают независимость от времени одномерных и двумерных статистических характеристик процесса.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
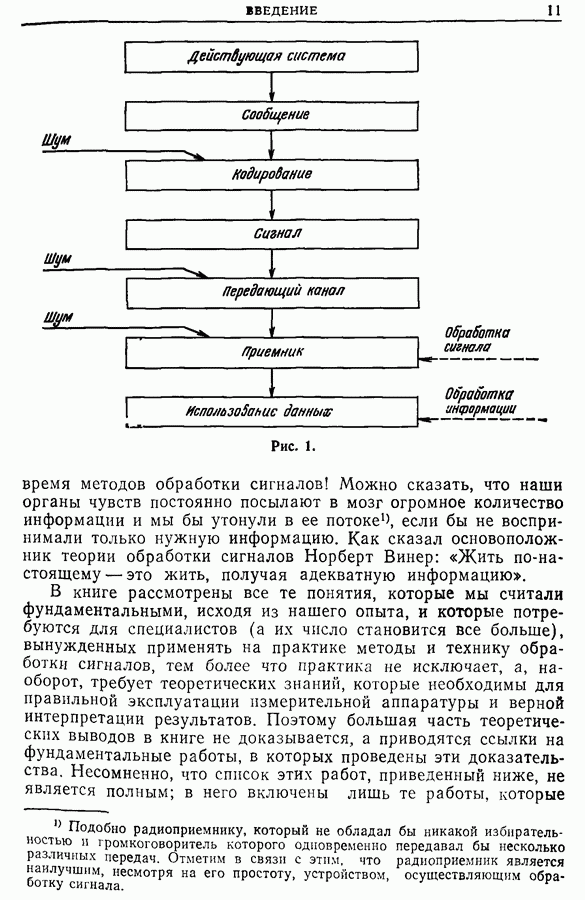
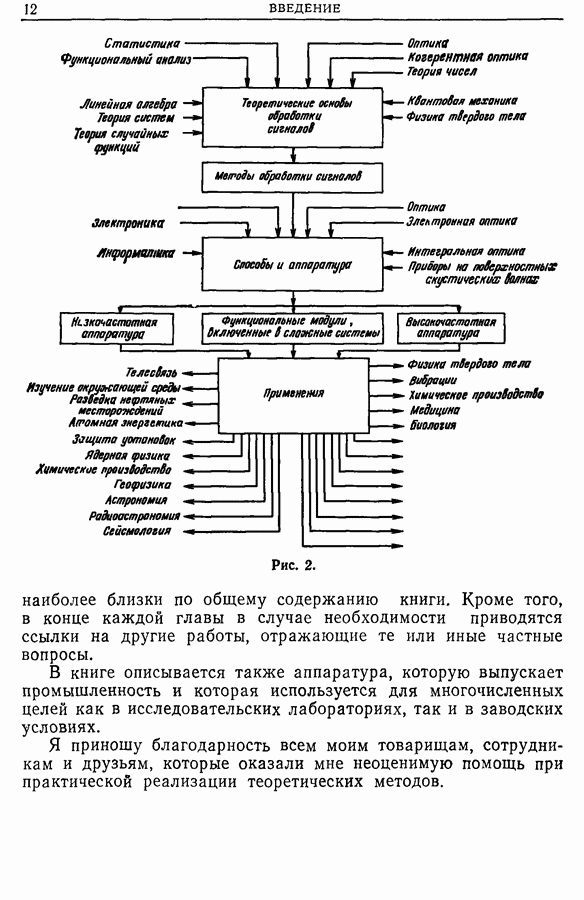
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
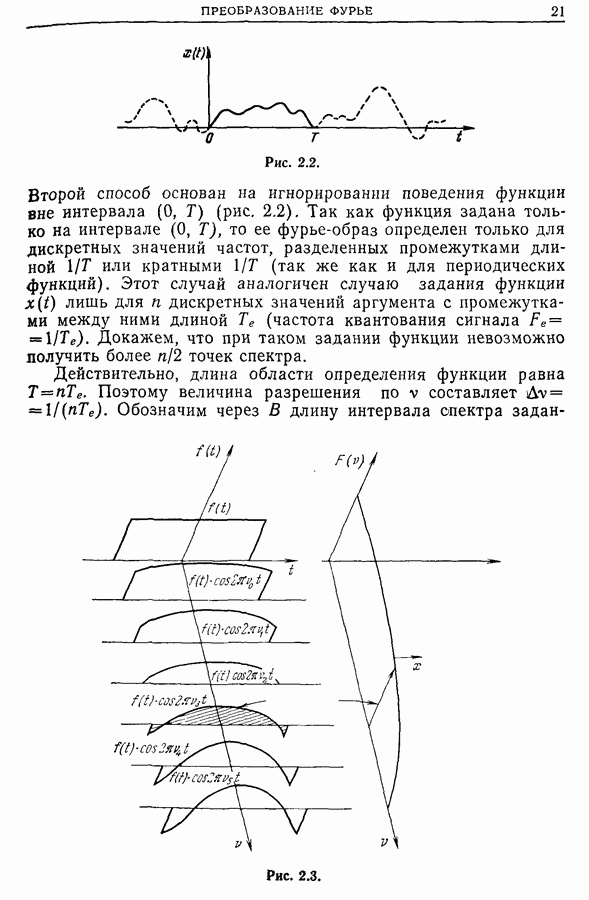
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
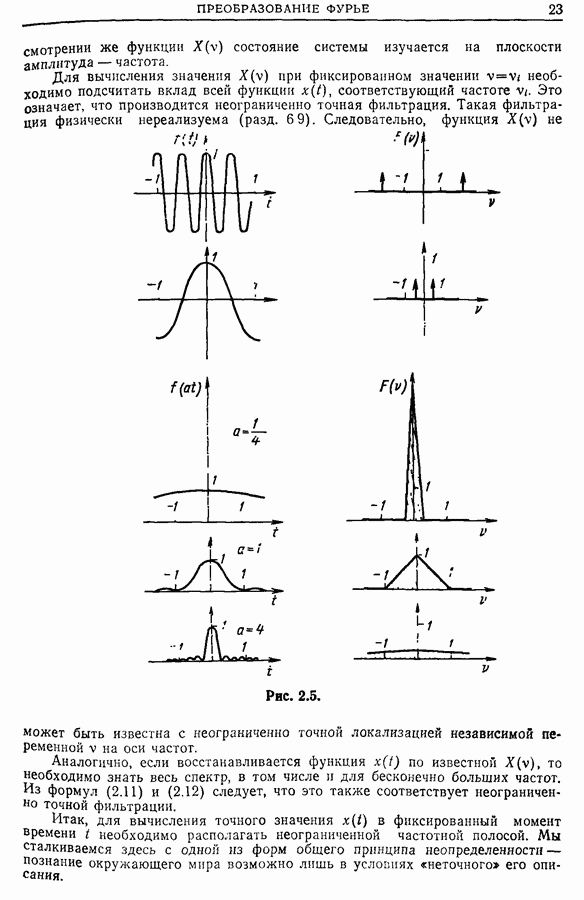
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
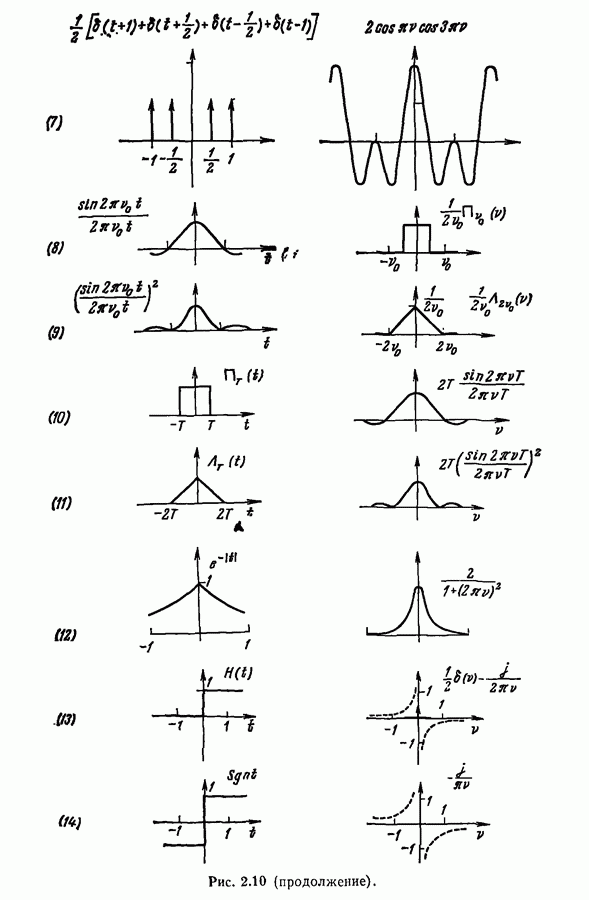
- 2.7. Несколько функций и их фурье-образы
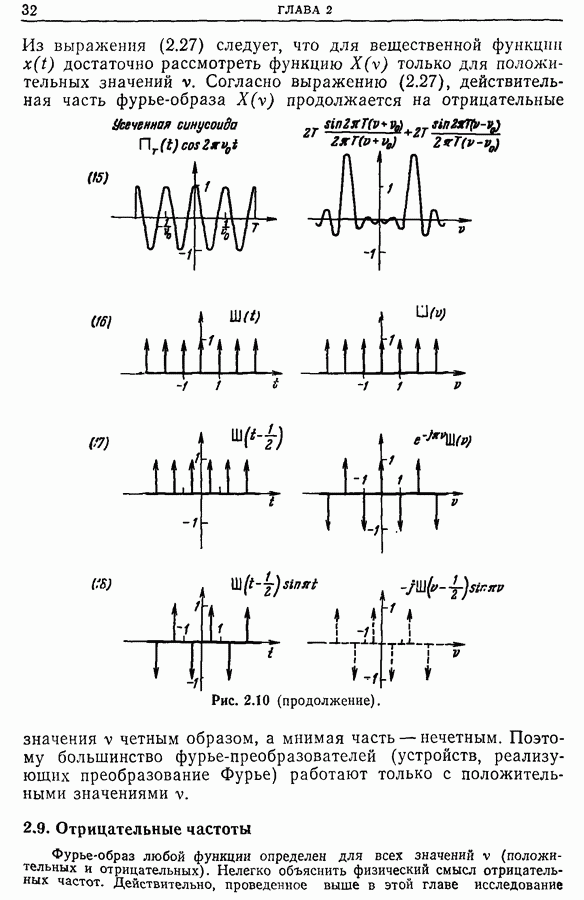
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
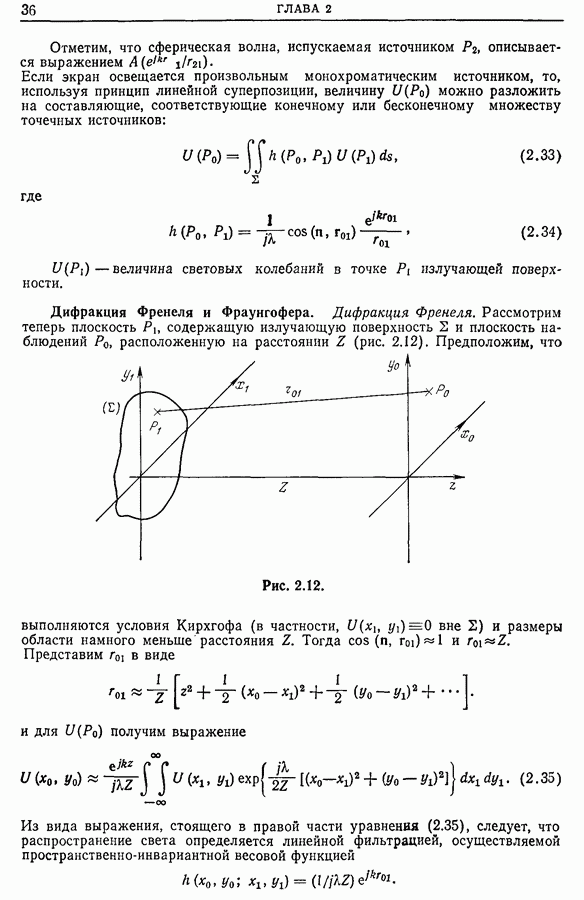
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
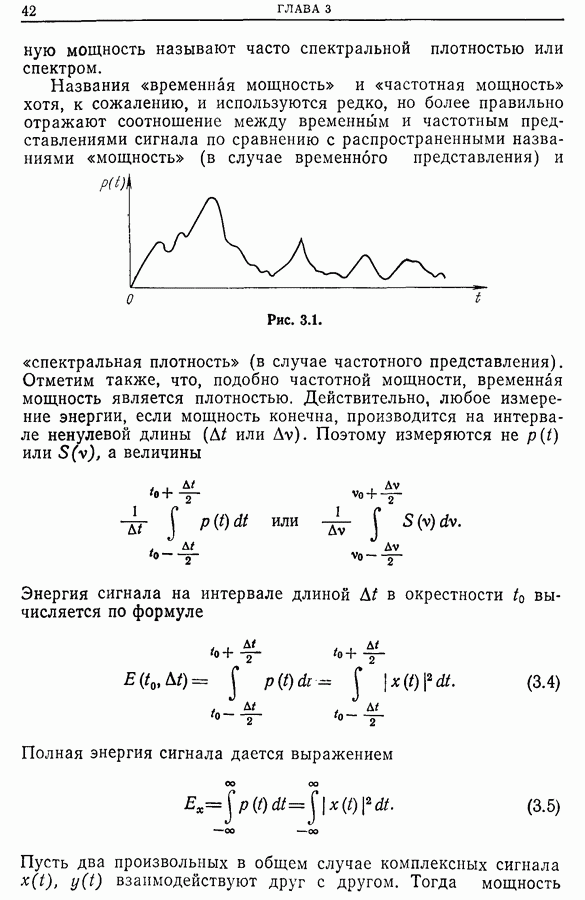
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
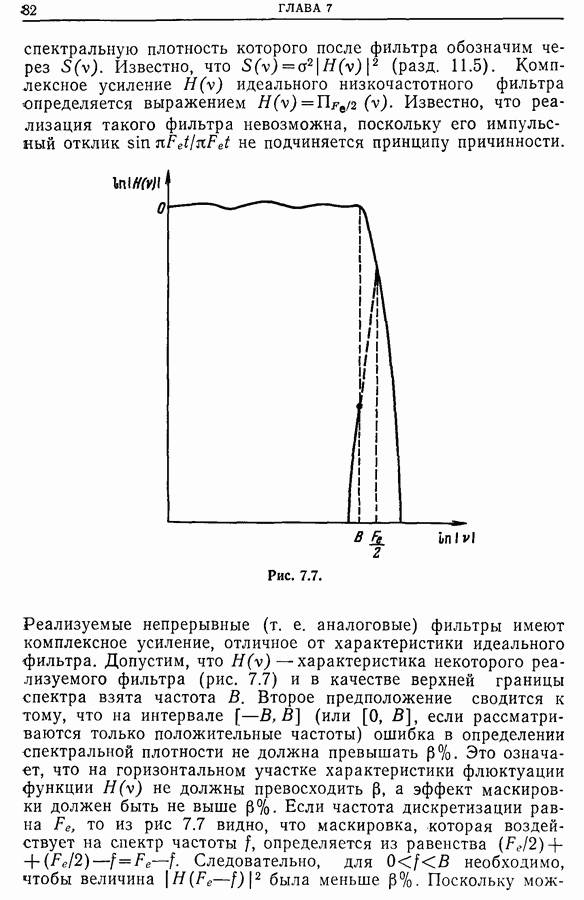
- 7.6. Противомаскировочный фильтр
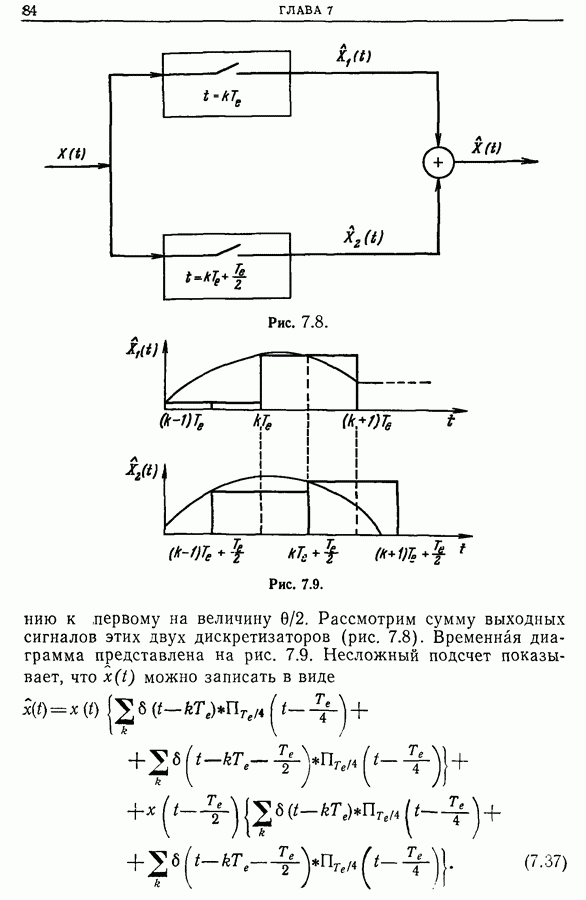
- 7.7. Физическая дискретизация. Комбинированная дискретизация
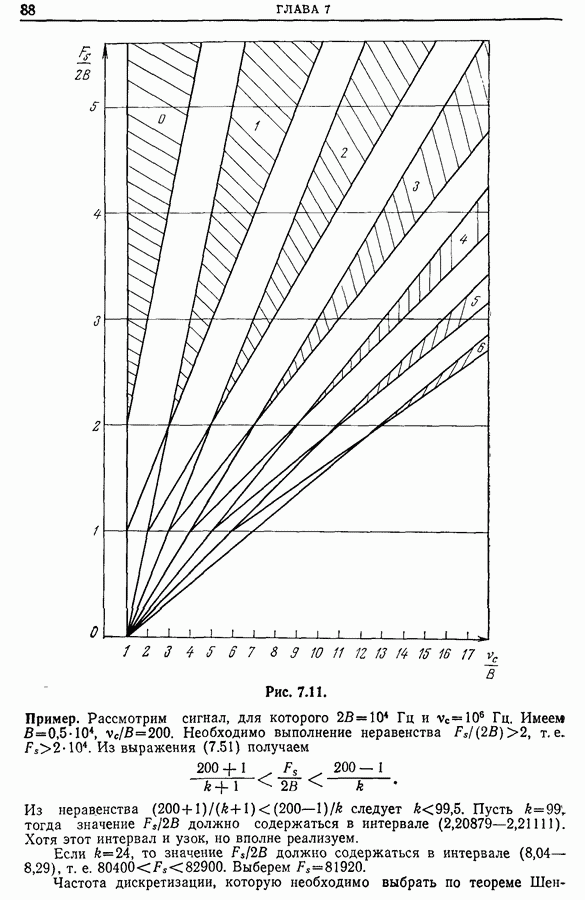
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
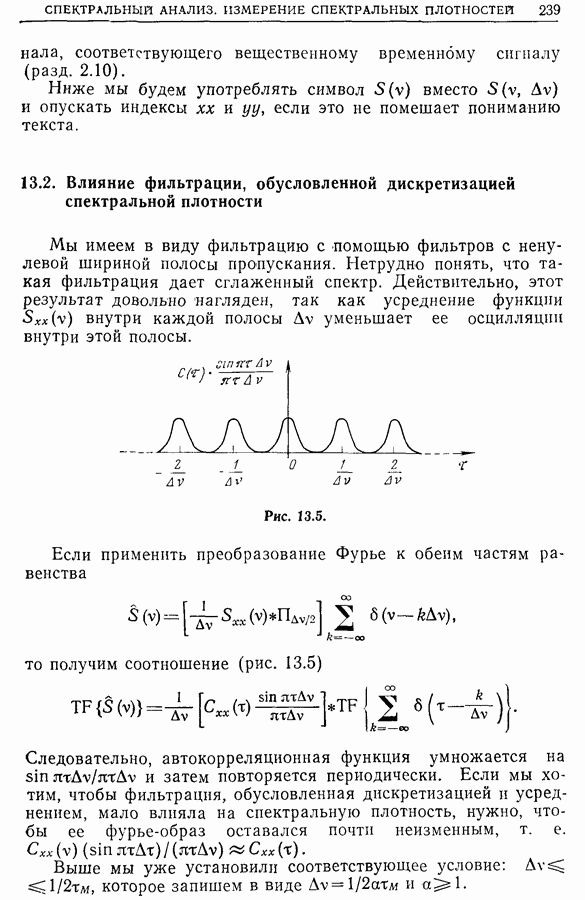
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
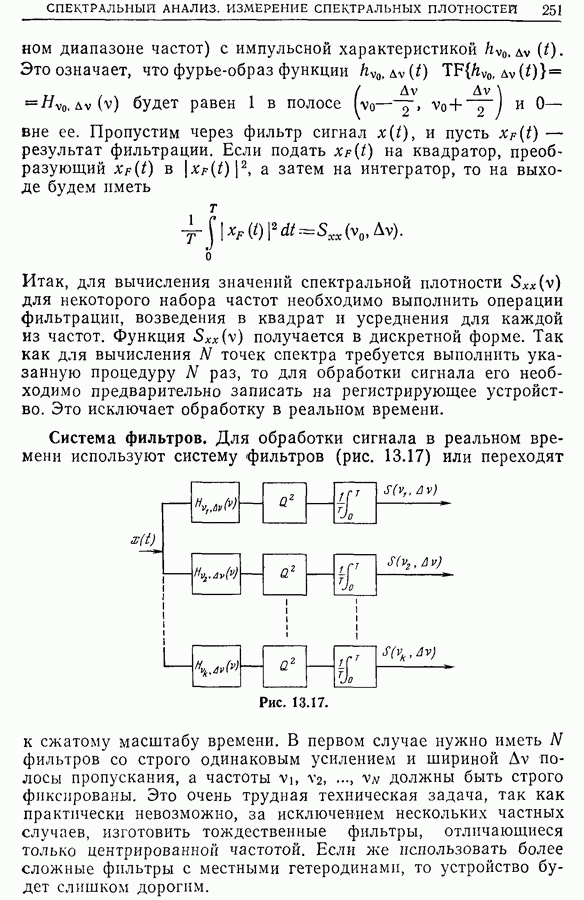
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
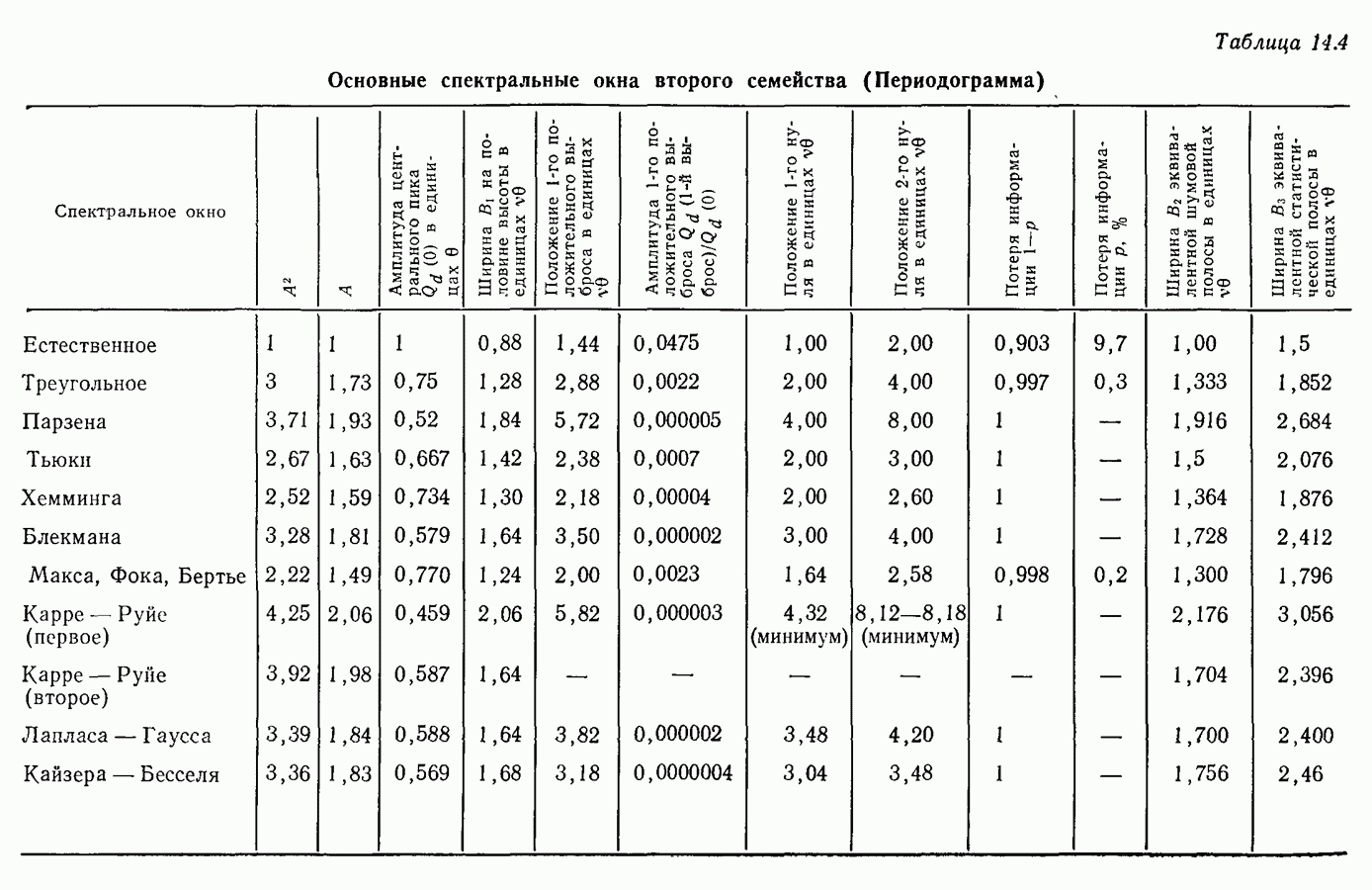
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
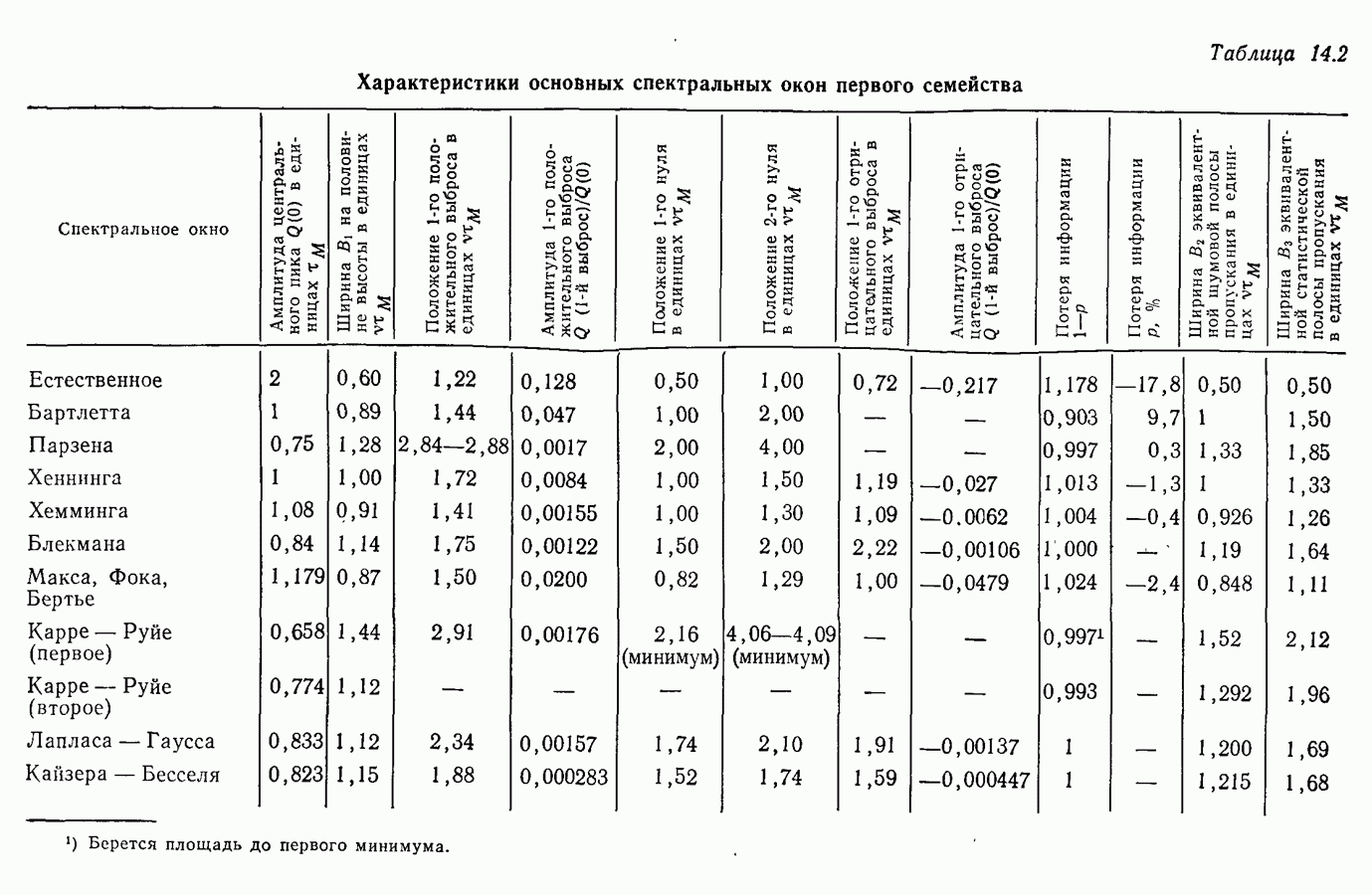
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции