| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
Те, кто обладает здравым суждением, знают, какая существует разница между двумя похожими словами в зависимости от того, в каком месте и при каких обстоятельствах эти слова употребляются. (Паскаль)
Поскольку основные физические процессы, для исследования которых используются методы обработки сигналов и методы корреляционного анализа, являются случайными, рассмотрим здесь представления о случайных процессах (они не так уж просты, как могут показаться с первого взгляда).
Существует множество физических процессов, для которых зависимость наблюдаемых величин от внешних условий устанавливается с помощью легко обнаруживаемых законов. Например, напряжение на выходе линейного фильтра может быть представлено в виде функции параметров фильтра и эволюции входной величины, причем значение напряжения на выходе, вычисленное на основе этой функции, будет тем более точным, чем точнее известны параметры фильтра и эволюция входной величины.
Движение частицы под действием некоторых сил можно легко вычислить и полностью «предсказать», если известны начальные условия и «движущие силы».
Однако в отличие от процессов, рассмотренных выше, существуют такие процессы (и они многочисленны), для которых наблюдаемые величины не могут быть выражены через начальные условия и «движущие силы» с помощью простых законов.
Рассмотрим, например, шум в электрическом контуре. Если мы попытаемся связать мгновенную величину напряжения шума с движением электронов (явлением, которое порождает этот шум), то сразу же столкнемся с проблемой, неразрешимой в настоящее время и теоретически (из-за соотношения неопределенности, например), и практически (из-за огромного числа одновременно решаемых уравнений). Если же мы хотим
количественно оценить шум, то будем вынуждены характеризовать его величинами, отличающимися от мгновенных значений напряжения. Этими величинами являются статистические характеристики шума.
Рассмотрим другой пример случайного процесса — игру в кости. Теоретически можно «предсказать» результат бросания игральных костей, но для этого необходимо знать полный набор физических и геометрических характеристик игральных костей и поверхности, на которую их бросают, начальные условия бросания и т. д. Если бы все эти исходные данные можно было легко измерить, а вычисления достаточно быстро выполнить, то в игре не было бы элемента случайности. Возможно, что в сравнительно недалеком будущем исключение случайности в этой игре станет реальностью. Именно невозможность на практике получить все исходные данные и на их основе вычислить простым способом конечное состояние системы заставляют нас рассматривать результат бросания игральных костей как случайный процесс.
Аналогичная ситуация возникает в термодинамике при рассмотрении поведения газа, заключенного в оболочку. Газ состоит из огромного числа элементарных частиц, движущихся за счет взаимных столкновений. Движение каждой частицы теоретически может быть определено, если известны начальные положения и скорости всех частиц. В настоящее время получить такой объем исходной информации о частицах газа практически нельзя, но, если бы мы даже и располагали этой информацией, ее дальнейшее использование невозможно, так как полученная система уравнений оказывается чрезвычайно сложной.
Итак, процессы, точные законы которых не могут быть использованы для их описания, мы вынуждены рассматривать как случайные. Следовательно, название «случайный» носит в определенном смысле временный характер, поскольку процесс перестает быть случайным, как только для его описания можно использовать точные законы, которым он подчиняется.
Теория случайных функций дает нам мощное средство для исследования явлений, точные законы которых не могут быть использованы непосредственно, путем изучения результата действия точных законов. Такие явления встречаются во всех областях науки: метеорологии, медицине, экономике, биологии и т. д.
Рассмотрим речь — процесс, существенно отличающийся от предыдущих. Образование звуковых волн, с помощью которых передается речь, является процессом сложным и не подчиняется простым законам, что придает ему характер случайного. Но слово «случайный» здесь может принимать и другое значение, поскольку речь предназначена для передачи информации. Начиная фразу, говорящий полностью знает, что он скажет в
дальнейшем. Поэтому продолжение фразы не является случайным для говорящего. Слушатель же не знает, что будет произнесено говорящим, он не может «предвидеть» фраз говорящего, кроме окончания некоторых слов. Для слушателя фразы, произносимые говорящим, носят характер случайного.
Отметим, что эта невозможность предсказания непосредственно связана с определением информации. Сообщение, которое могло бы быть полностью предсказуемо адресатом, не дало бы последнему никакой информации и считалось бы шумом. Следовательно, сообщение будет сигналом или шумом для адресата в зависимости от того, может или не может адресат извлечь из сообщения информацию. Из этого следует, что физически чрезвычайно трудно отличить шум от сигнала. Важно заранее определить, как будет извлекаться информация из сообщения, а это зависит от выбранного кода, с помощью которого передается информация от отправителя к адресату.
Таким образом, всякий сигнал при определенных обстоятельствах может быть рассмотрен как случайный, в то же время шум может содержать много информации.
В заключение рассмотрим еще один пример. Ток ионизационной камеры, помещенной в активную зону ядерного реактора, позволяет измерять уровень мощности реактора. Точное измерение осложняется тем, что на ток, определяемый уровнем мощности реактора, накладываются флюктуации. В этом случае непрерывный уровень тока есть сигнал, а флюктуации тока являются шумом, который и порождает ошибки в измерениях. Если же исследовать только флюктуации тока ионизационной камеры, то можно извлечь очень полезную информацию о динамических характеристиках реактора, например вычислить модуль передаточной функции. В этом случае флюктуации представляют собой источник, богатый информацией, т. е. будут выполнять роль сигнала.
Из приведенного примера следует, насколько определения информации и случайности являются двусмысленными и неточными. Определение, которое удовлетворит математика, будет непригодным для физика; определение, которое могло бы одновременно удовлетворить и математика, и физика, не будет приемлемым для биолога, и т. д. Читатель может быть удивлен и даже разочарован тем, что здесь не приводятся четкие и точные определения, но не будем забывать, что «любое сжатое определение часто несет в себе причину его деградации...» (Буланже).
Можно сказать, что сигнал отличается от шума наличием полезной информации, шум же содержит лишь такую информацию, которая нас не интересует по крайней мере в настоящий момент. Поэтому перед каждым измерением и обработкой сигнала необходимо ответить на вопрос: что будет приниматься в качестве сигнала, а что — в качестве шума?
Попытаемся определить, что будем понимать в дальнейшем под случайным процессом или случайной функцией (хотя в математике эти два понятия различаются). Назовем процесс случайным, если невозможна его полностью идентичная повторная реализация. Согласно этому определению, периодический и переходный процессы (например, импульсный отклик фильтра) не являются случайными, а шум усилителя относится к случайным процессам.
Необходимо отметить, что на практике трудно четко разделить процессы на случайные и неслучайные (детерминированные). Например, на импульсный отклик усилителя и на выходной сигнал генератора часто накладываются шумы. Поэтому теоретики попытались использовать ранее разработанные методы исследования случайных процессов для изучения детерминированных процессов. Оказалось, что методы и техника обработки сигналов применимы как к случайным процессам, так и к неслучайным.
В своей книге «Theorie des Fonctions Aleatoires» Андре Блан-Лапьер и Робер Форте указали на связь между интуитивными представлениями и теоретическими понятиями в этой области. Приведем отрывок из их предисловия к книге:
«В определенном смысле можно сказать, что введение понятия случайной функции было продиктовано практикой. Изучение метеорологических процессов, турбулентности жидкости, явления флюктуаций в электрических цепях, известных под названием фоновых шумов, и т. д. привело к необходимости расширения понятия функции, используемого в классическом математическом анализе, для учета случайного характера явлений. Такое расширение привело к понятию случайной функции.
Случайная функция х, зависящая от параметра  и определенная на некотором множестве испытаний, для каждого фиксированного испытания
и определенная на некотором множестве испытаний, для каждого фиксированного испытания  есть классическая функция”. Но эта функция изменяется от испытания к испытанию, что и порождает ее случайный характер. Если зафиксировать величину параметра
есть классическая функция”. Но эта функция изменяется от испытания к испытанию, что и порождает ее случайный характер. Если зафиксировать величину параметра  то значения х будут зависеть только от испытания, т. е. в этом случае х — случайная величина. Часто используемая запись
то значения х будут зависеть только от испытания, т. е. в этом случае х — случайная величина. Часто используемая запись  обозначает двойную зависимость х от параметра
обозначает двойную зависимость х от параметра  и от испытания е.
и от испытания е.
Специалисты по метеорологии, гидродинамике, радиоэлектронике и другие нередко применяют неслучайные функции, прибавляя к ним некоторое случайное слагаемое. Например, физик, регистрируя на осциллографе напряжение слабых токов как функцию времени, отмечает появление фонового шума в виде функций с иррегулярным изменением, который накладывается на регулярные сигналы, соответствующие сильным токам.
Специалисты в области теории вероятностей использовали другой подход. Они искали такое расширение понятия случайной величины, которое было бы применимо к случайным процессам достаточно общей природы, что и привело к введению понятия случайной функции.
Из сказанного выше следует, что в изучении теории случайных функций заинтересованы специалисты многих областей науки и техники»
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
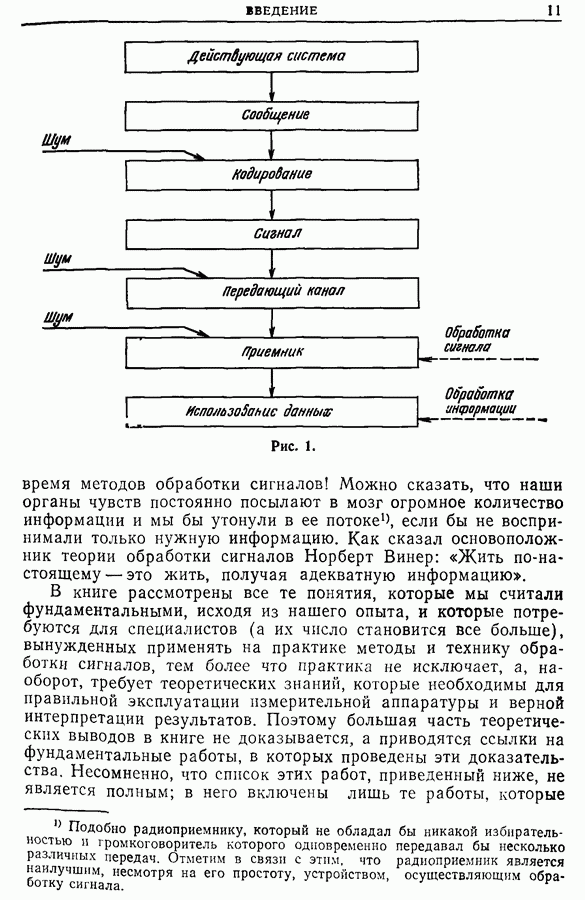
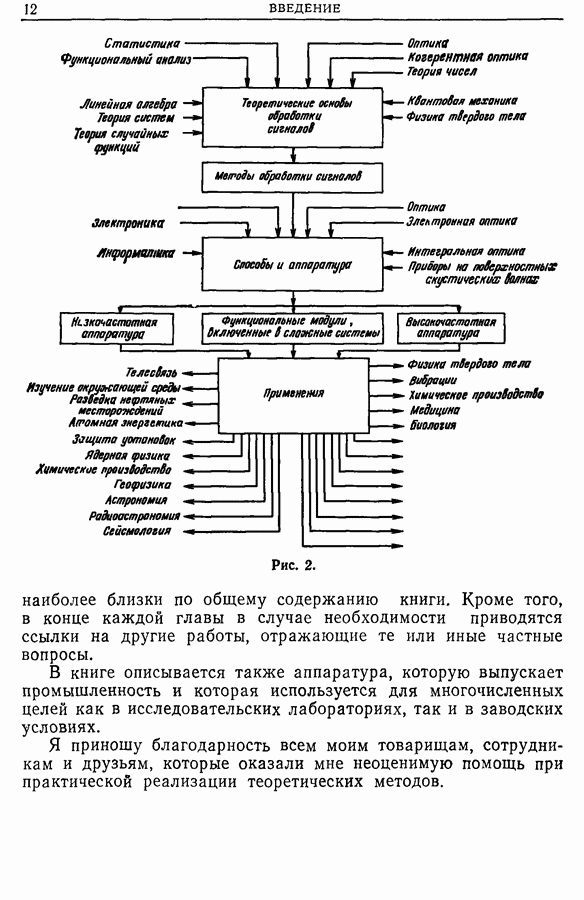
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
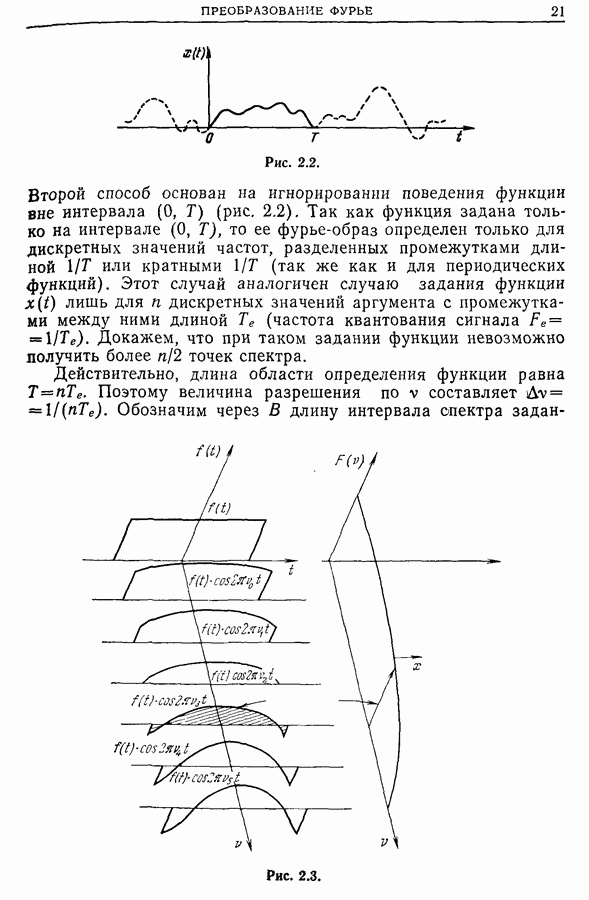
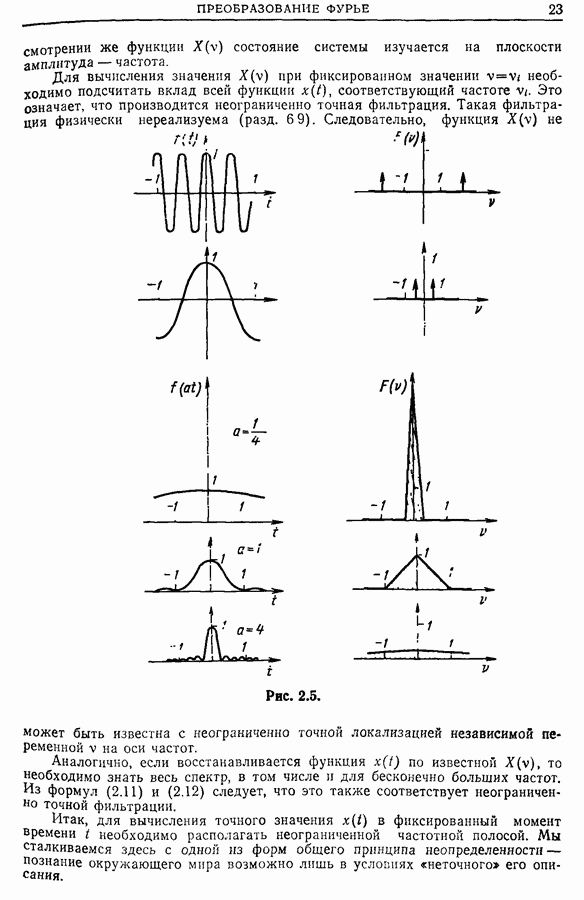
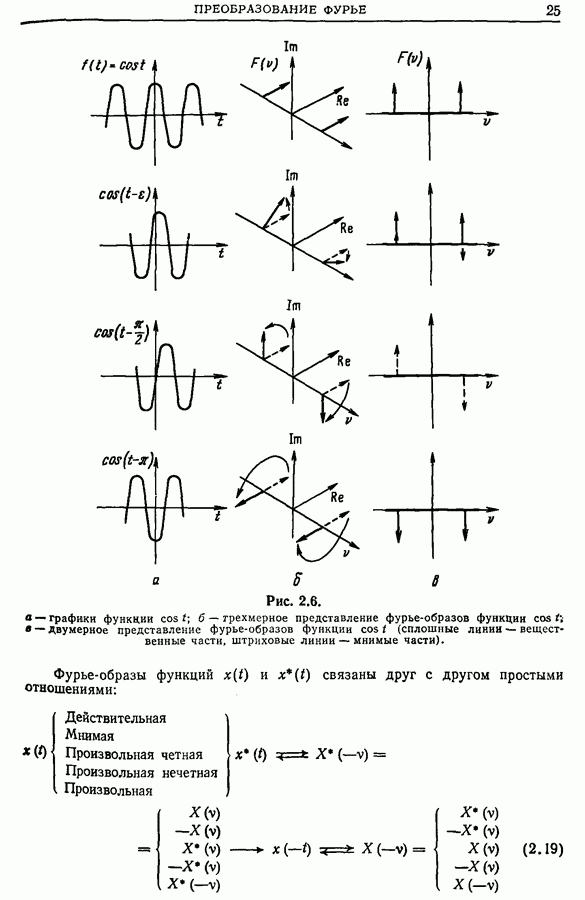
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
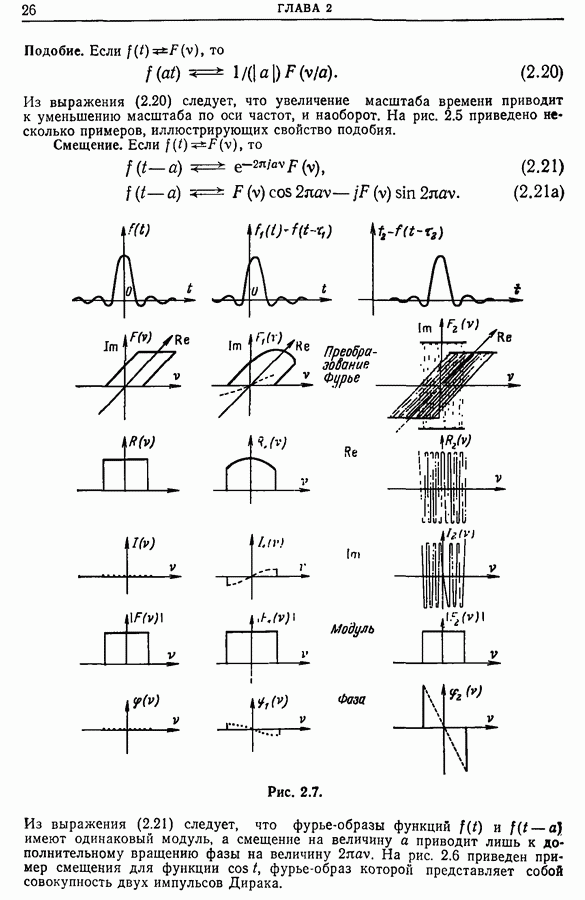
- 2.6. Некоторые свойства преобразования Фурье
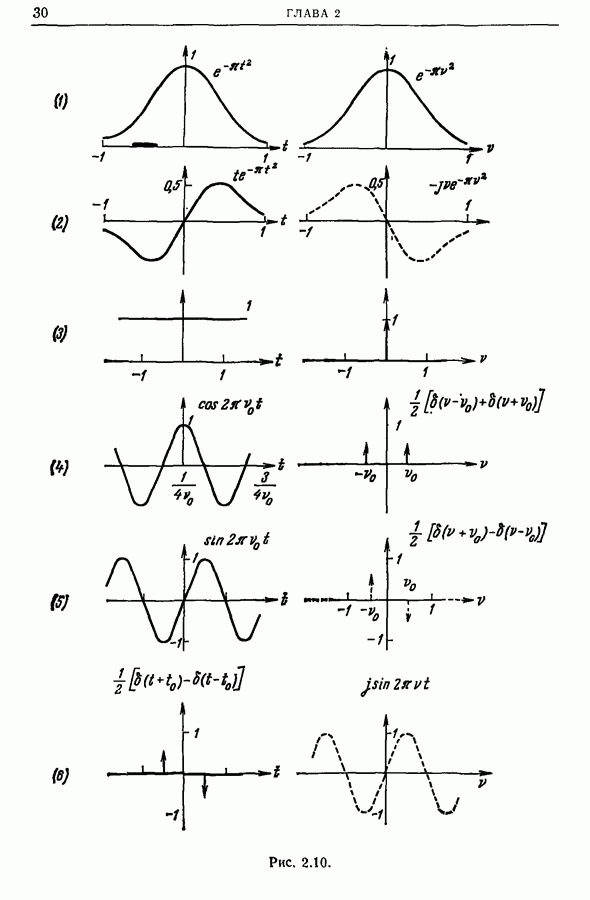
- 2.7. Несколько функций и их фурье-образы
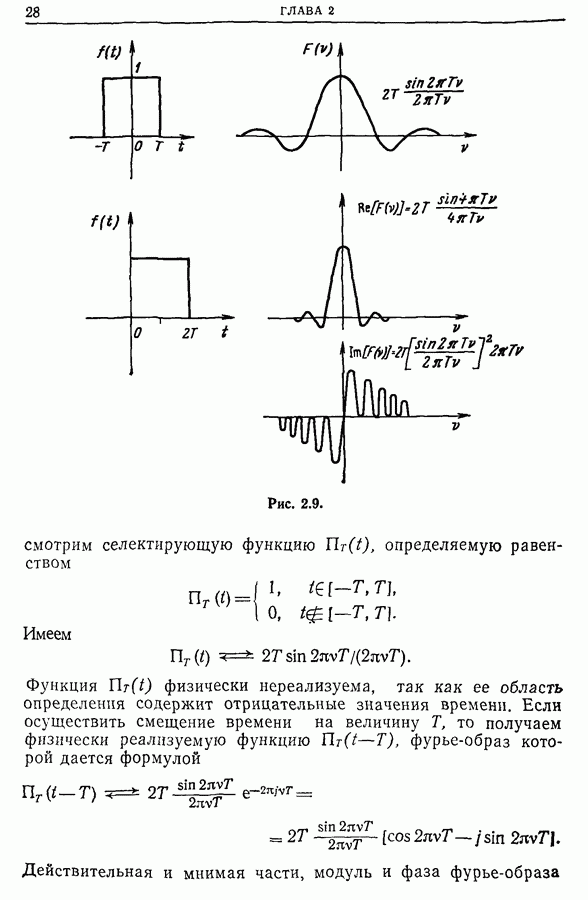
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
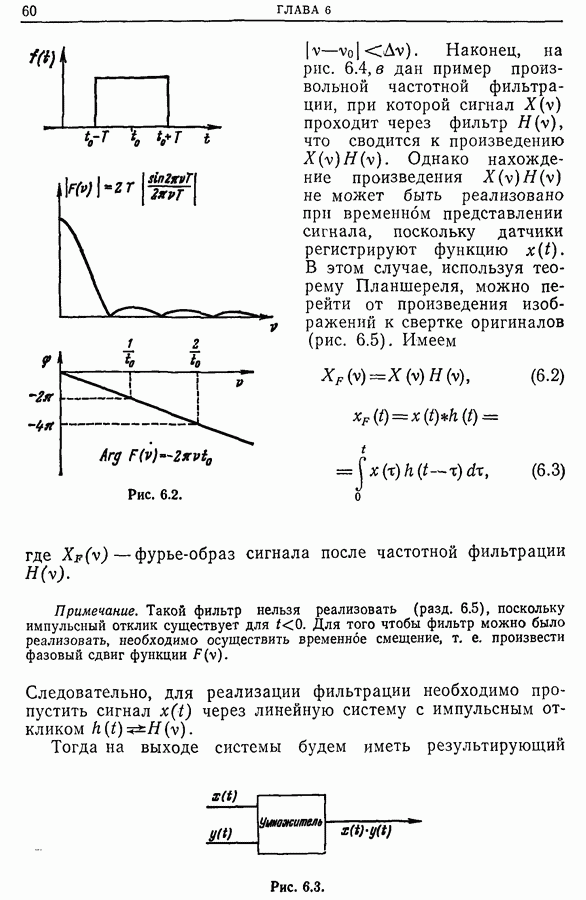
- 6.2. Временная фильтрация
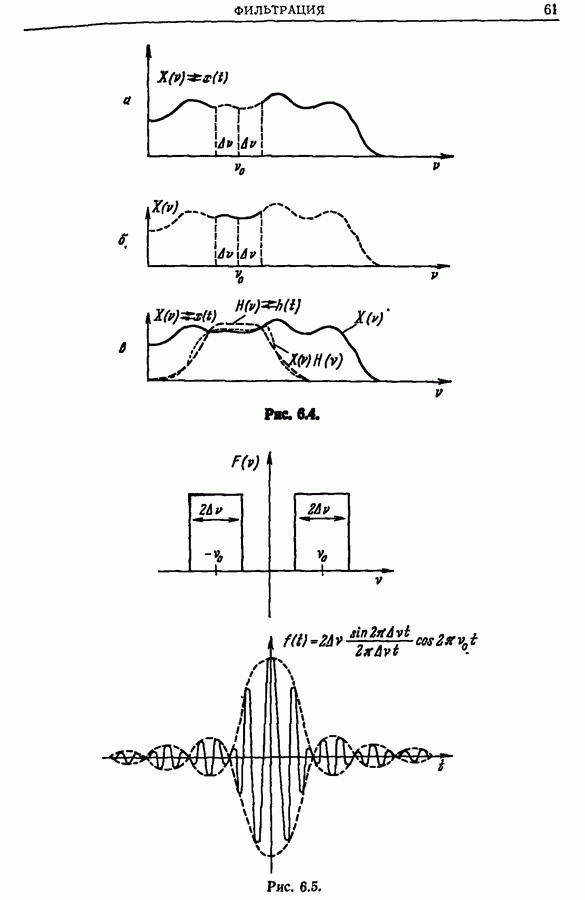
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
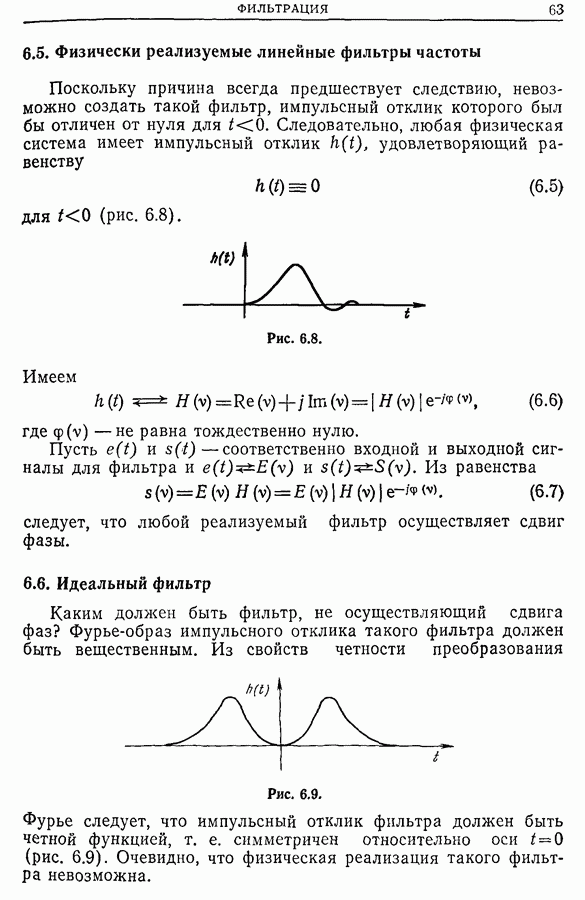
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
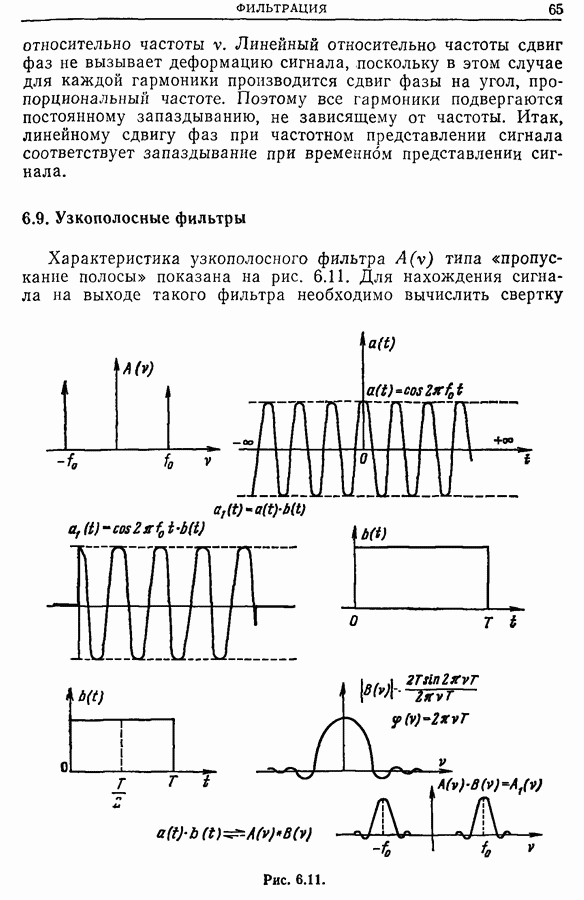
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
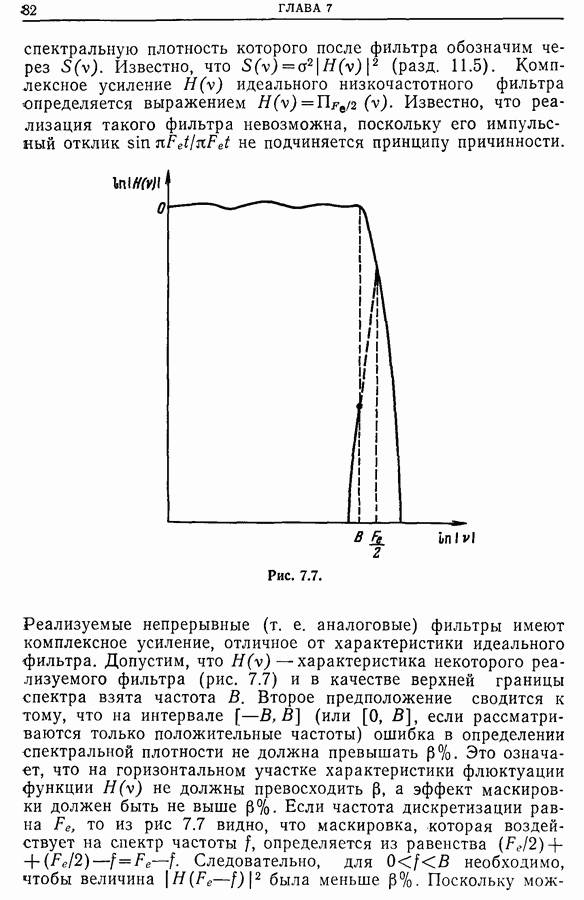
- 7.6. Противомаскировочный фильтр
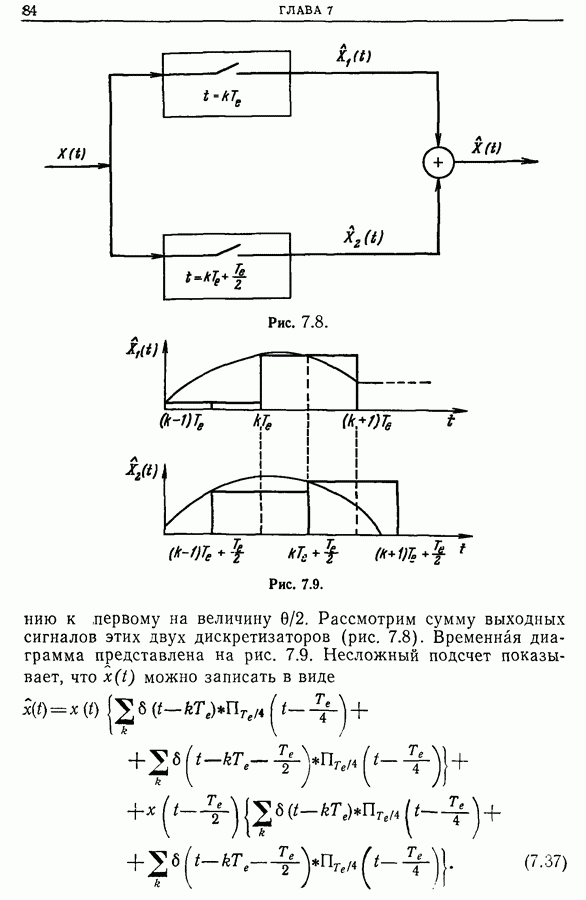
- 7.7. Физическая дискретизация. Комбинированная дискретизация
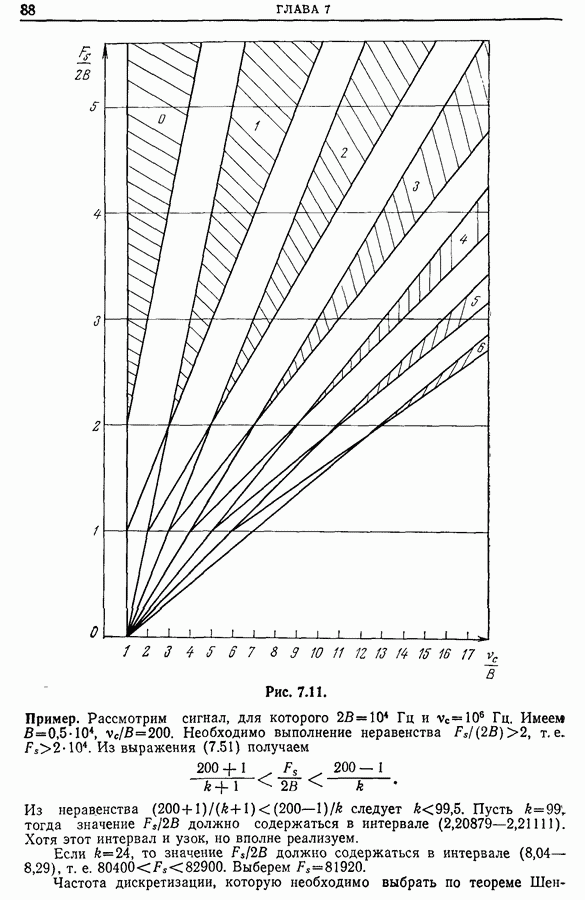
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
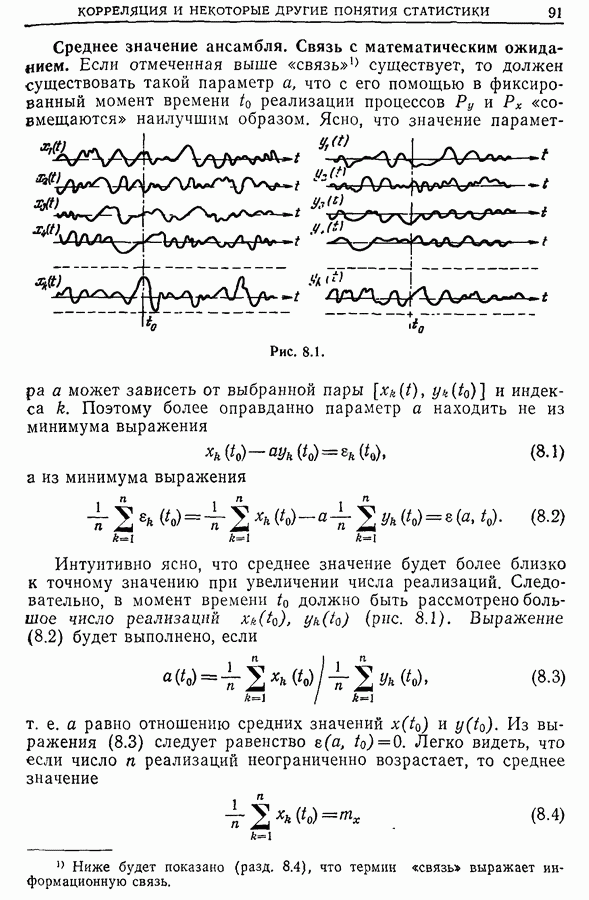
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
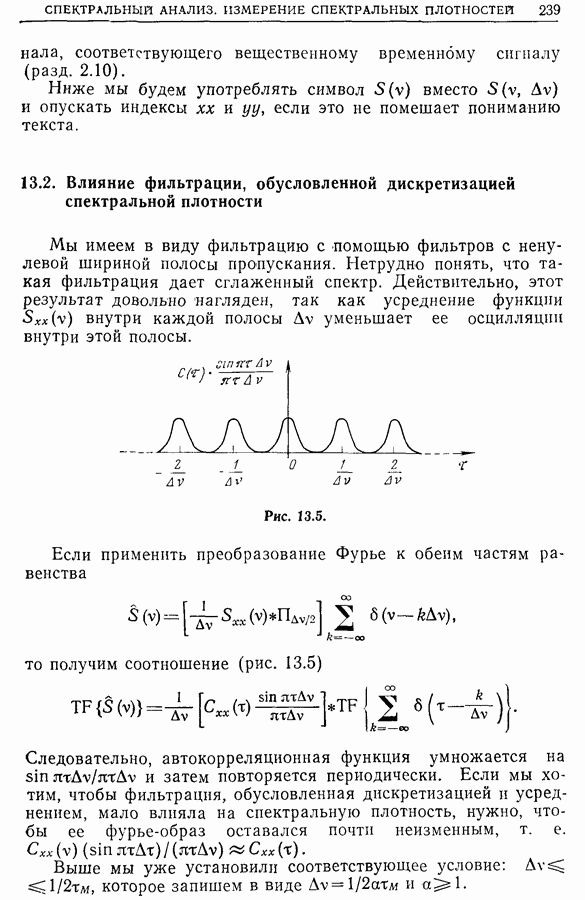
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
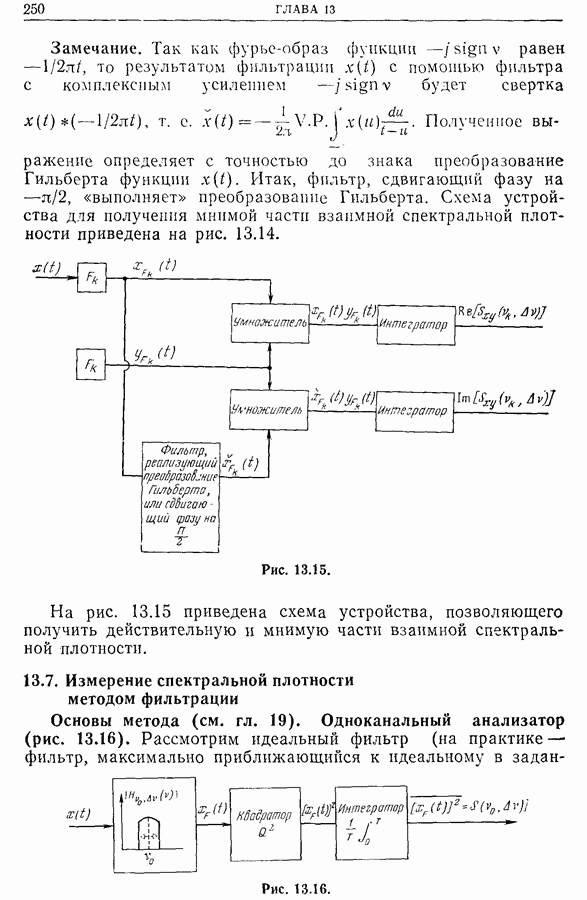
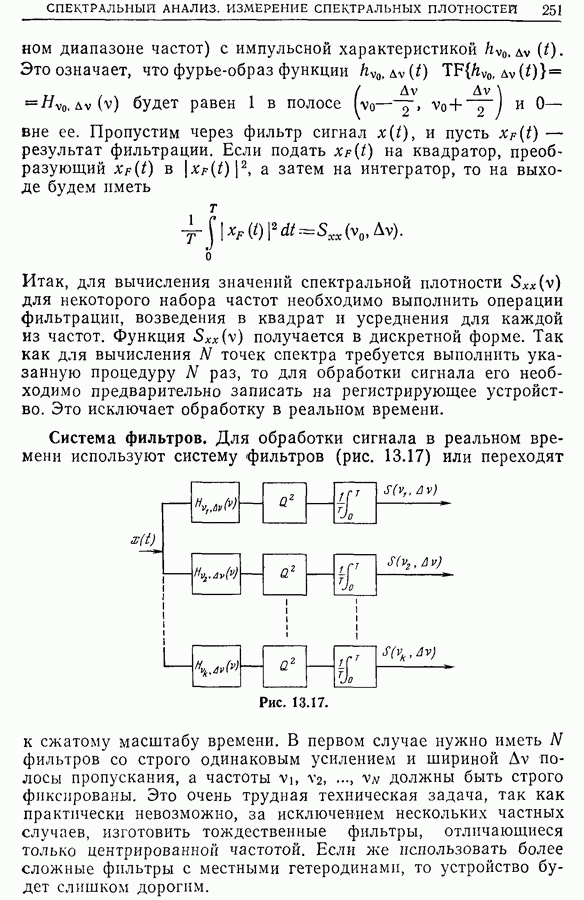
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
- 14.6. Основные характеристики временных и спектральных окон
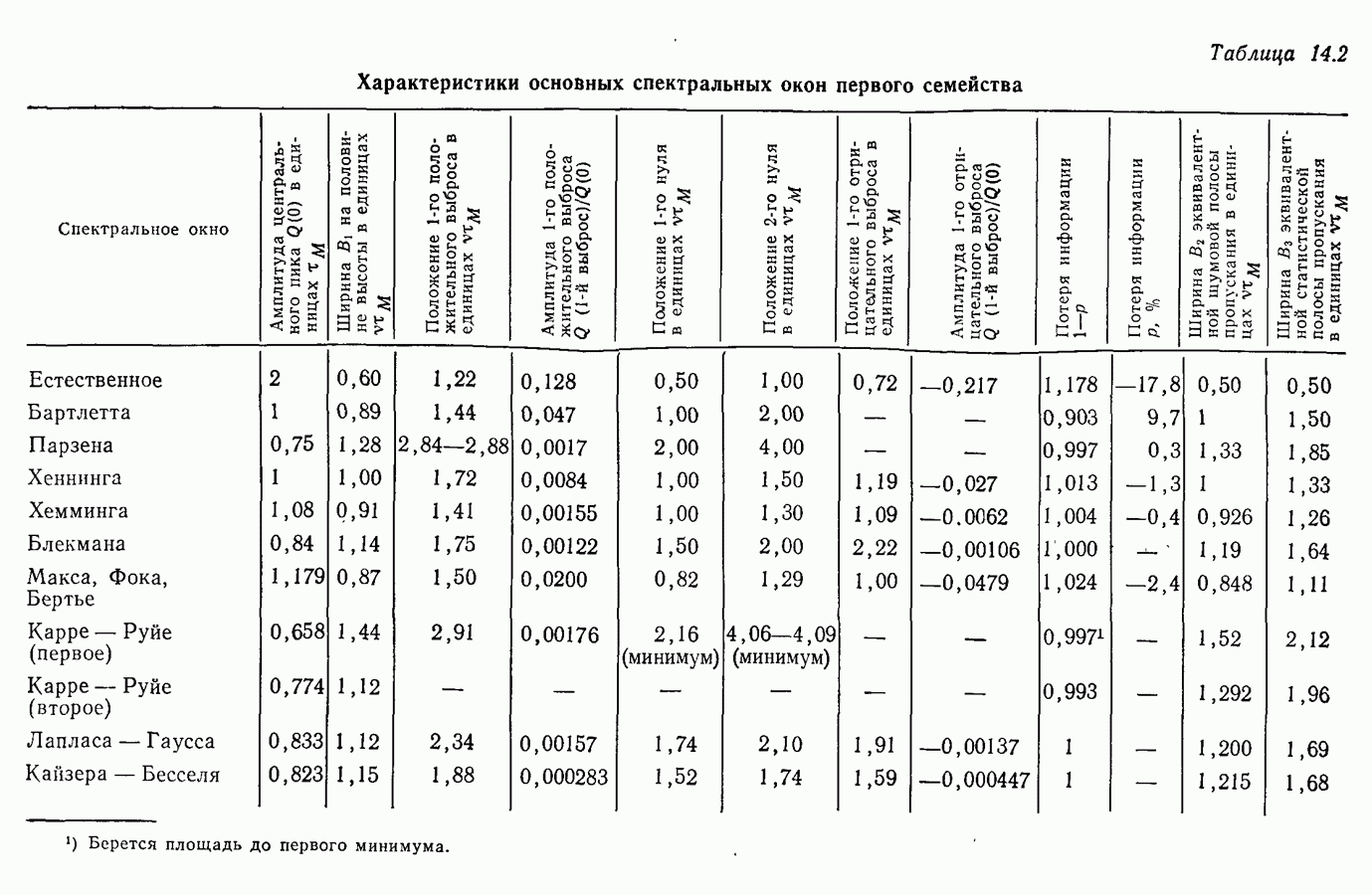
- 14.7. Первое семейство временных весовых окон
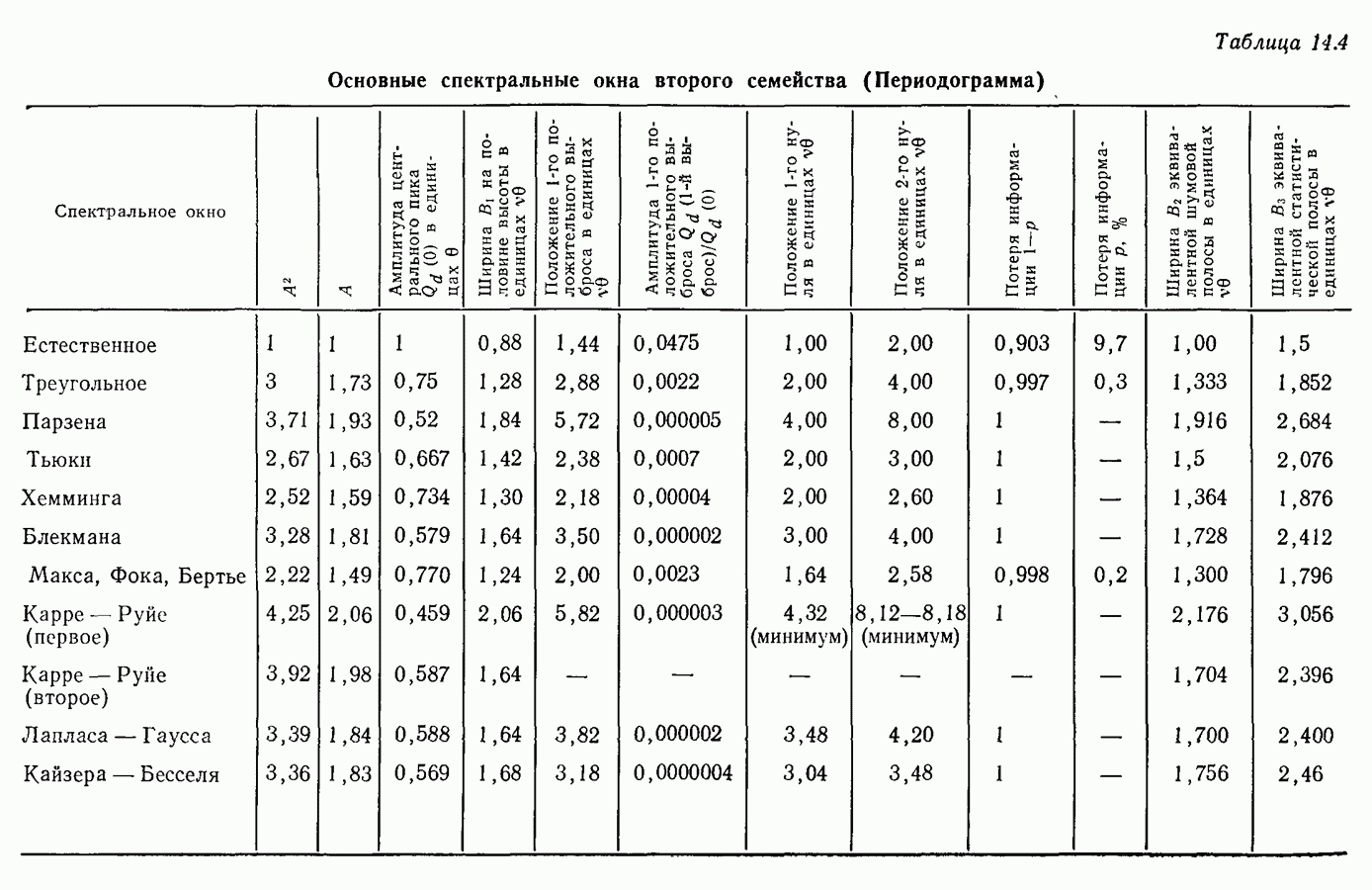
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции