| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
Высокая степень развития рационального интеллекта у человека привела к значительной и печальной потере возможностей его интуиции, которая так необходима сегодня для дальнейшего развития. (Жак Моно, Случайность и необходимость)
Тот, кто не допускает ошибок, не способен познать истину.
Рабиндранат Тагор
В гл. 9 предполагалось, что необходимые для вычислений математические операции реализуются идеально. Когда мы записывали выражение

то молчаливо предполагали, что операции умножения  (идеального аналогового умножения) и интегрирования осуществляются без ошибок. Однако известно, что на практике все чаще и чаще аналоговые операции умножения и интегрирования заменяются численным умножением и интегрированием (после аналого-цифрового преобразования). При огромном количестве исходных данных (когда величина ВТ равна
(идеального аналогового умножения) и интегрирования осуществляются без ошибок. Однако известно, что на практике все чаще и чаще аналоговые операции умножения и интегрирования заменяются численным умножением и интегрированием (после аналого-цифрового преобразования). При огромном количестве исходных данных (когда величина ВТ равна  и более) для вычисления корреляции необходимо найти способ уменьшения числа символов для записи каждого слова, т. е. осуществлять кодирование с минимальным общим числом символов. Следовательно, очень важно изучить влияние дискретизации.
и более) для вычисления корреляции необходимо найти способ уменьшения числа символов для записи каждого слова, т. е. осуществлять кодирование с минимальным общим числом символов. Следовательно, очень важно изучить влияние дискретизации.
10.1. Статистическое изучение влияния дискретизаций
Постановка проблемы.
Прежде всего мы изучим влияние дискретизации на корреляционную функцию, а затем покажем, что некоторые полученные результаты применимы и в более
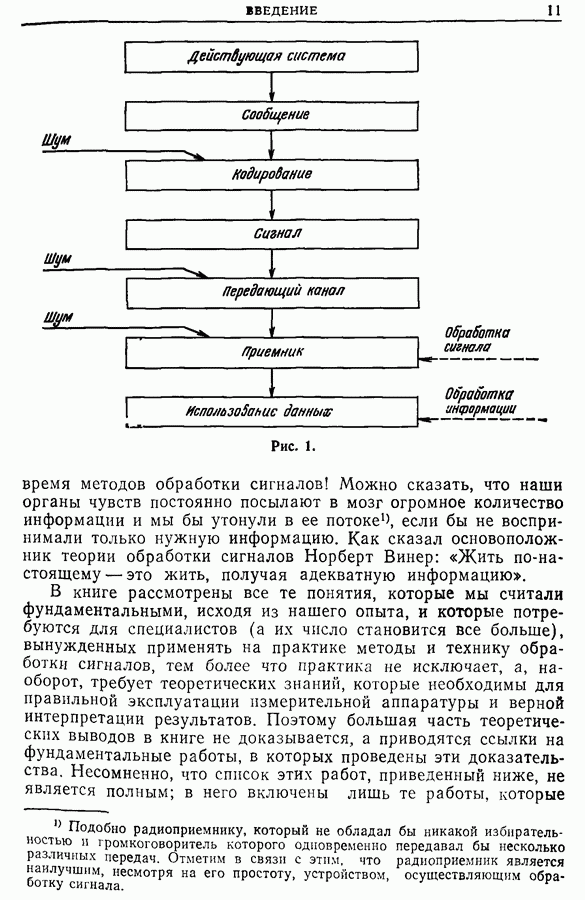
общем случае. Общая структура дискретного коррелометра может быть представлена в виде блок-схемы, приведенной на рис. 10.1. Это устройство осуществляет оценку  истинной автокорреляционной функции
истинной автокорреляционной функции 

Рис. 10.1.
Оценка отлична в общем случае от истинного значения по двум причинам:
1. Поскольку сигнал x(t) по предположению стационарен и эргодичен, то

Однако при вычислении оценки интервал интегрирования Т не может быть бесконечным, и, следовательно, мы получаем  . Ошибка, порожденная такой заменой, была изучена в гл. 9.
. Ошибка, порожденная такой заменой, была изучена в гл. 9.
2. Очень трудно реализовать запаздывание для непрерывных сигналов и очень легко — для дискретизованных сигналов. Поэтому наиболее часто рассматриваются дискретные сигналы. В этой главе мы изучим ошибку, обусловленную дискретизацией сигналов.
Дискретизация случайной величины.
Определение. Пусть х - случайная величина. Дискретизацией величины х называется шаг дискретизации и  — натуральное число.
— натуральное число.
Плотность вероятности дискретизованной случайной величины. Пусть  - плотность вероятности величины х. Изучим влияние дискретизации на
- плотность вероятности величины х. Изучим влияние дискретизации на 
По определению величины х имеем

Но

где

Отсюда

Следовательно, плотность вероятности дискретизованной случайной величины х записывается в виде

Отсюда

Из последнего выражения следуют два эффекта (рис. 10.2) влияния дискретизации на  :
:
1) эффект фильтрации с помощью фильтра-интегратора на интервале  импульсный отклик которого равен
импульсный отклик которого равен 
2) эффект дискретизации с шагом  т. е. влияние дискретизации с помощью дискретизатора-интегратора.
т. е. влияние дискретизации с помощью дискретизатора-интегратора.
Характеристическая функция дискретизованной случайной величины.
Напомним, что характеристическая функция случайной величины х определяется равенством

Из этого равенства следует соотношение между фурье-образом  плотности вероятности и характеристической функции
плотности вероятности и характеристической функции 

Рис. 10.2.
 . Используя формулу (10.2), вычислим характеристическую функцию
. Используя формулу (10.2), вычислим характеристическую функцию  дискретизованной случайной величины. Запишем выражение (10.2) в виде
дискретизованной случайной величины. Запишем выражение (10.2) в виде

Используя теорему Парсеваля и фурье-образ гребневой функции Дирака, получим

Перейдем в равенстве (10.3) к фурье-образам:

Положив  , получаем искомое выражение
, получаем искомое выражение

Выражение (10.4) позволяет обнаружить по спектру плотности вероятности два эффекта влияния дискретизации, о которых говорилось выше в связи с дискретизацией плотности вероятности:
• эффект фильтрации (рис. 10.3), соответствующий умножению функции  на величину
на величину  ;
;
• эффект дискретизации, соответствующий суммированию спектра после фильтрации с периодичностью 

Очевидно, что дискретизация не изменяет существенно  в окрестности точки
в окрестности точки  кроме случая, когда
кроме случая, когда  для
для  т. е. когда повторяемый таким образом спектр не восстанавливается через промежуток, длина которого больше половины периода (рис. 10.4). Это замечание будет нами использовано в дальнейшем, когда мы распространим его на случай двух случайных величин.
т. е. когда повторяемый таким образом спектр не восстанавливается через промежуток, длина которого больше половины периода (рис. 10.4). Это замечание будет нами использовано в дальнейшем, когда мы распространим его на случай двух случайных величин.

Рис. 10.3.

Рис. 10.4.
Дискретизация двух случайных величин.
Обобщения. Для того чтобы получить сведения о влиянии дискретизации на момент второго порядка (с целью использования их для корреляционной функции), мы изучим статистические воздействия дискретизации на двумерную случайную величину  Необходимые выкладки аналогичны выкладкам предыдущего раздела. Поэтому мы даем лишь окончательные формулы и обращаем внимание на интересующие нас результаты.
Необходимые выкладки аналогичны выкладкам предыдущего раздела. Поэтому мы даем лишь окончательные формулы и обращаем внимание на интересующие нас результаты.
Совместная плотность вероятности и характеристическая функция двух дискретизованных случайных величин. Используя предыдущие обозначения для двух случайных величин  дискретизованных с шагами
дискретизованных с шагами  получаем формулы
получаем формулы

Влияние дискретизации на момент второго порядка и на корреляцию двух случайных величин. Воздействие фильтрации и дискретизации. Поскольку выражение (10.6) аналогично выражению (10.4), то справедливы все предыдущие заключения о
воздействии фильтрации и дискретизации на характеристическую функцию.
Достаточное условие равенства нулю ошибки дискретизации для момента второго порядка. Согласно известной формуле теории вероятности, имеем

Из выражений (10.6) и (10.7) следует, что выполнение условия

для любых  и любых
и любых  достаточно для выполнения равенства
достаточно для выполнения равенства 
Связь между корреляционными функциями двух дискретизованных и недискретизованных сигналов. Если равенства (10.8) не выполнены, то между  существует более сложная связь. Рассмотрим два случайных стационарных процесса
существует более сложная связь. Рассмотрим два случайных стационарных процесса  Для нахождения соотношения между истинной корреляционной функцией
Для нахождения соотношения между истинной корреляционной функцией

и корреляционной функцией дискретизованных сигналов  можно использовать полученные выше формулы (10.6) и
можно использовать полученные выше формулы (10.6) и  (для сокращения записи иногда
(для сокращения записи иногда  обозначают
обозначают  если такое обозначение не может вызвать неоднозначного толкования).
если такое обозначение не может вызвать неоднозначного толкования).
Бонне, используя формулы (10.6) и (10.7), провел соответствующие вычисления и получил равенства

где 

В большинстве случаев коэффициентом а можно пренебречь, и предыдущая формула для  принимает вид
принимает вид

с точностью до бесконечно малых величин более высокого порядка.
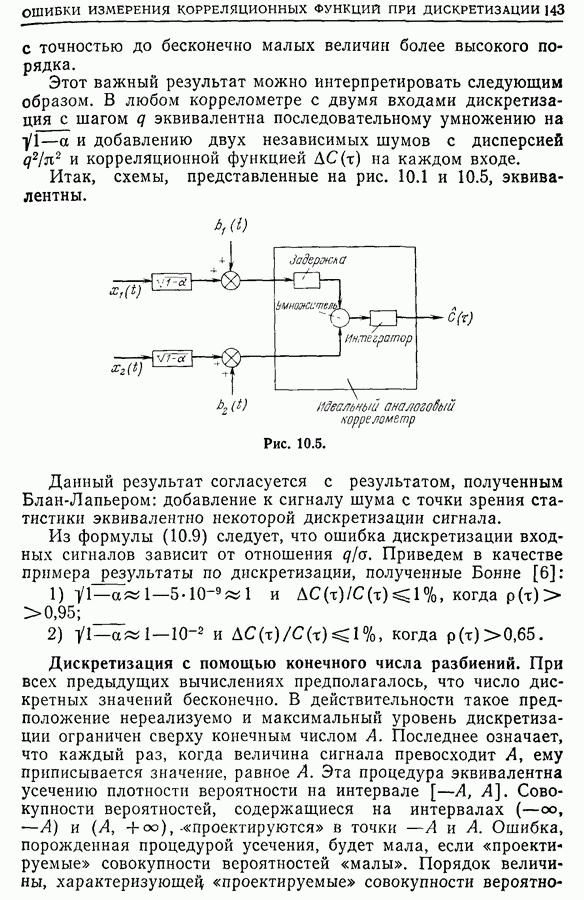
Этот важный результат можно интерпретировать следующим образом. В любом коррелометре с двумя входами дискретизация с шагом  эквивалентна последовательному умножению на
эквивалентна последовательному умножению на  и добавлению двух независимых шумов с дисперсией
и добавлению двух независимых шумов с дисперсией  и корреляционной функцией
и корреляционной функцией  на каждом входе.
на каждом входе.
Итак, схемы, представленные на рис. 10.1 и 10.5, эквивалентны.

Рис. 10.5.
Данный результат согласуется с результатом, полученным Блан-Лапьером: добавление к сигналу шума с точки зрения статистики эквивалентно некоторой дискретизации сигнала.
Из формулы (10.9) следует, что ошибка дискретизации входных сигналов зависит от отношения  Приведем в качестве примера результаты по дискретизации, полученные Бонне [6]:
Приведем в качестве примера результаты по дискретизации, полученные Бонне [6]:

Дискретизация с помощью конечного числа разбиений.
При всех предыдущих вычислениях предполагалось, что число дискретных значений бесконечно. В действительности такое предположение нереализуемо и максимальный уровень дискретизации ограничен сверху конечным числом А. Последнее означает, что каждый раз, когда величина сигнала превосходит А, ему приписывается значение, равное А. Эта процедура эквивалентна усечению плотности вероятности на интервале  . Совокупности вероятностей, содержащиеся на интервалах
. Совокупности вероятностей, содержащиеся на интервалах  , -«проектируются» в точки —А и А. Ошибка, порожденная процедурой усечения, будет мала, если «проектируемые» совокупности вероятностей «малы». Порядок величины, характеризующей «проектируемые» совокупности вероятно
, -«проектируются» в точки —А и А. Ошибка, порожденная процедурой усечения, будет мала, если «проектируемые» совокупности вероятностей «малы». Порядок величины, характеризующей «проектируемые» совокупности вероятно
стей, может быть оценен с помощью неравенства Чебышева  из которого следует, что ошибка, обусловленная заменой бесконечного числа дискретных значений конечным числом, зависит от отношения
из которого следует, что ошибка, обусловленная заменой бесконечного числа дискретных значений конечным числом, зависит от отношения  Согласно Бонне [6], этой ошибкой можно пренебречь, если
Согласно Бонне [6], этой ошибкой можно пренебречь, если 
Итак, мы показали, что ошибка, порожденная дискретизацией, уменьшается с уменьшением отношения  Кроме того, ошибка, порожденная конечностью числа дискретных значений, уменьшается с возрастанием отношения
Кроме того, ошибка, порожденная конечностью числа дискретных значений, уменьшается с возрастанием отношения  Следовательно, уменьшение полной ошибки всегда соответствует увеличению отношения
Следовательно, уменьшение полной ошибки всегда соответствует увеличению отношения  которое равно общему числу уровней дискретизации.
которое равно общему числу уровней дискретизации.
Частный случай.
Коррелометр с двумя уровнями дискретизации (коррелометр с совпадением полярности, коррелометр с подрезанием, коррелометр Фарана и Хилла). В этом частном случае предыдущие формулы принимают относительно простой вид [8]:

где  — нормированная корреляционная функция:
— нормированная корреляционная функция:

В тех случаях (они довольно многочисленны), когда достаточно вычислить нормированные корреляционные функции, переход от  осуществляется с помощью простого соотношения
осуществляется с помощью простого соотношения

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
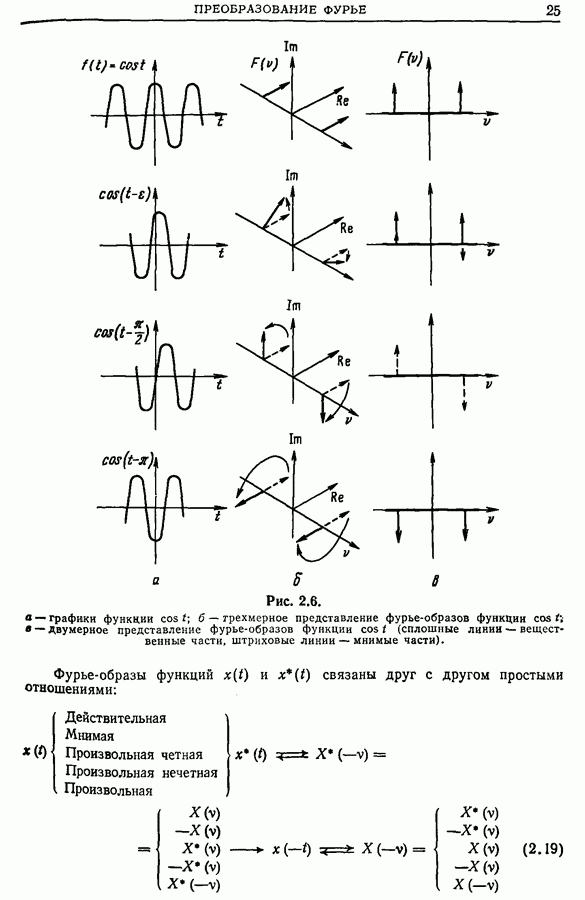
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
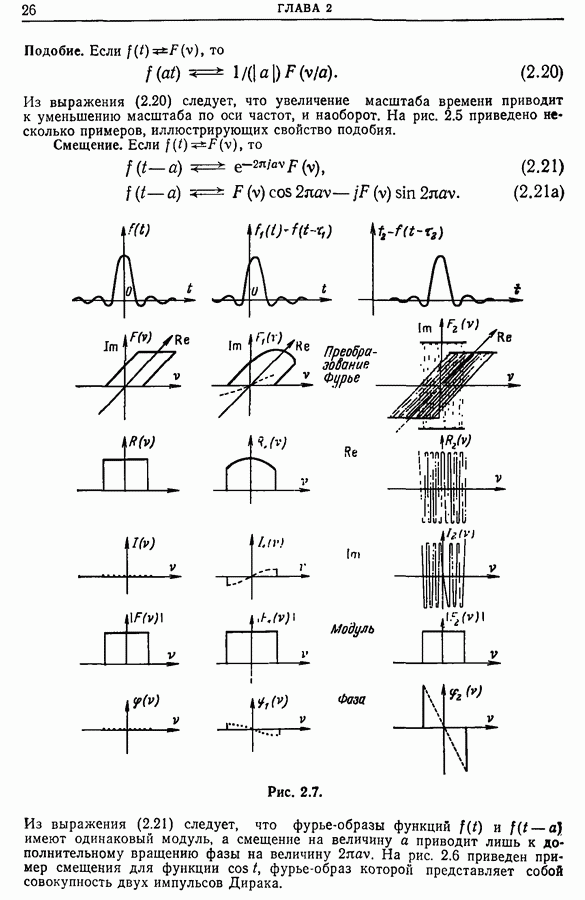
- 2.6. Некоторые свойства преобразования Фурье
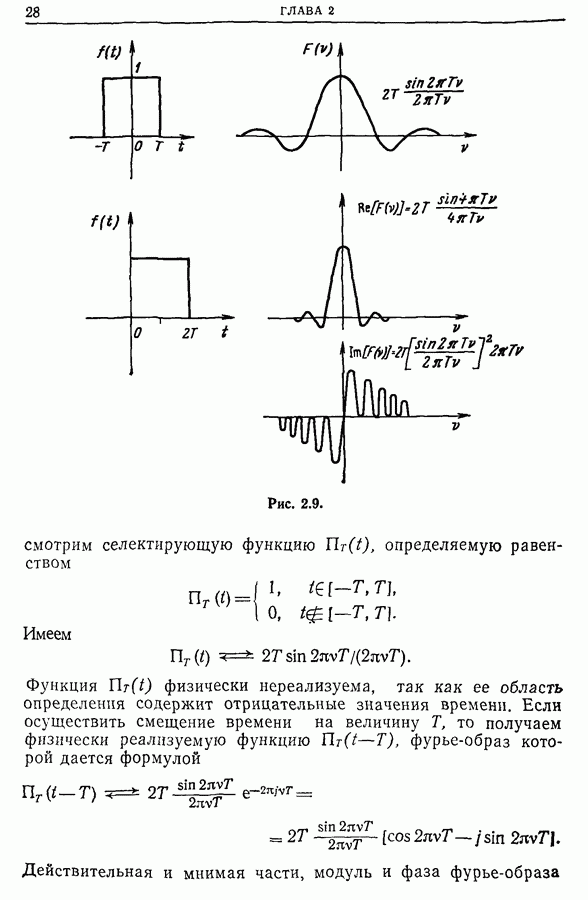
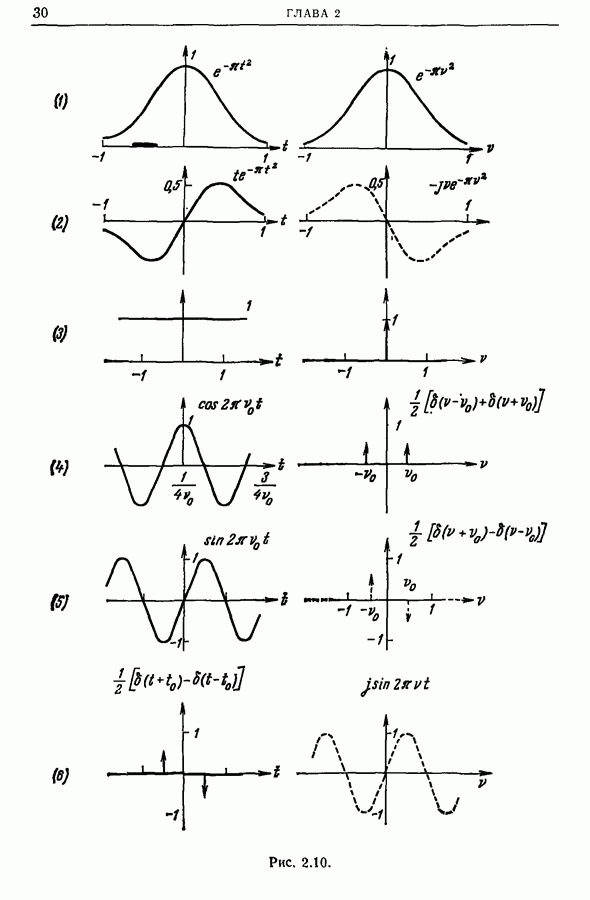
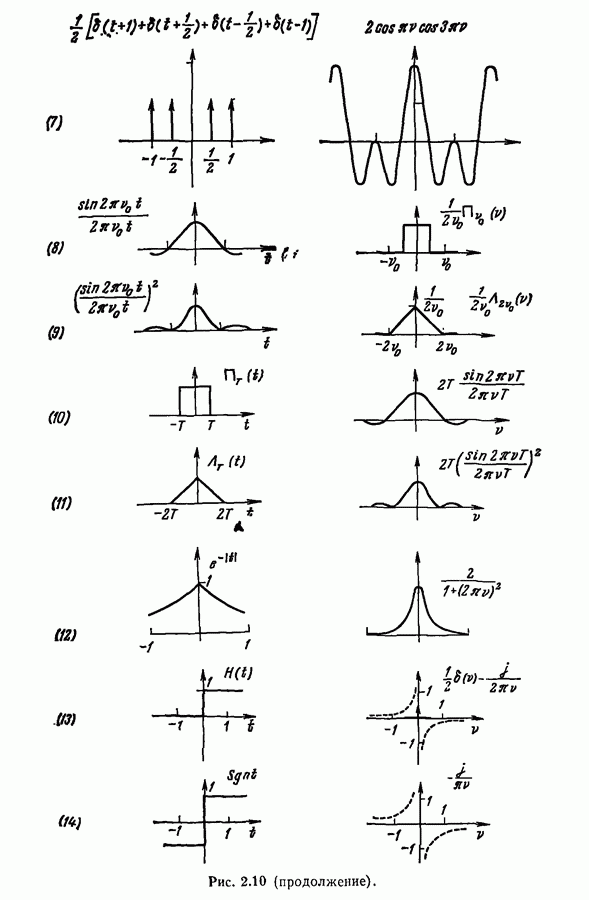
- 2.7. Несколько функций и их фурье-образы
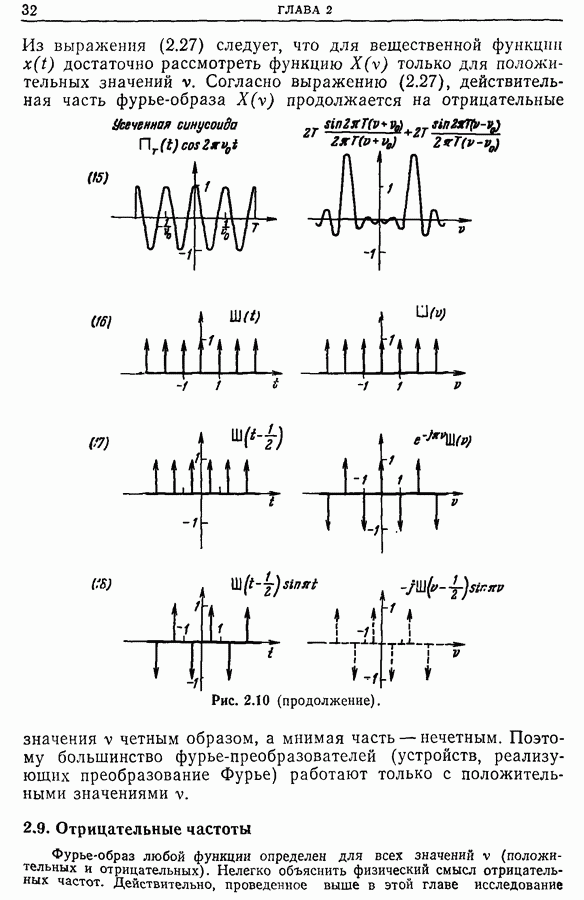
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
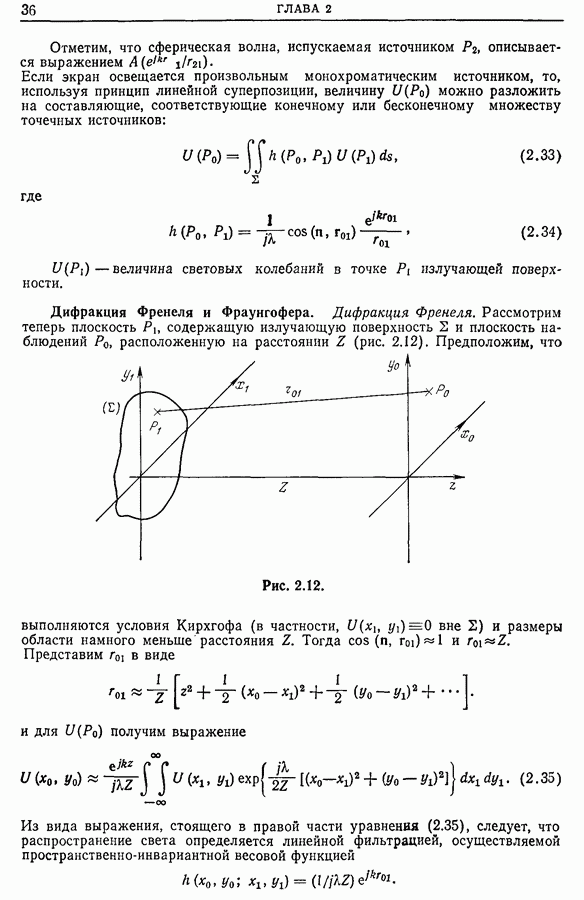
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
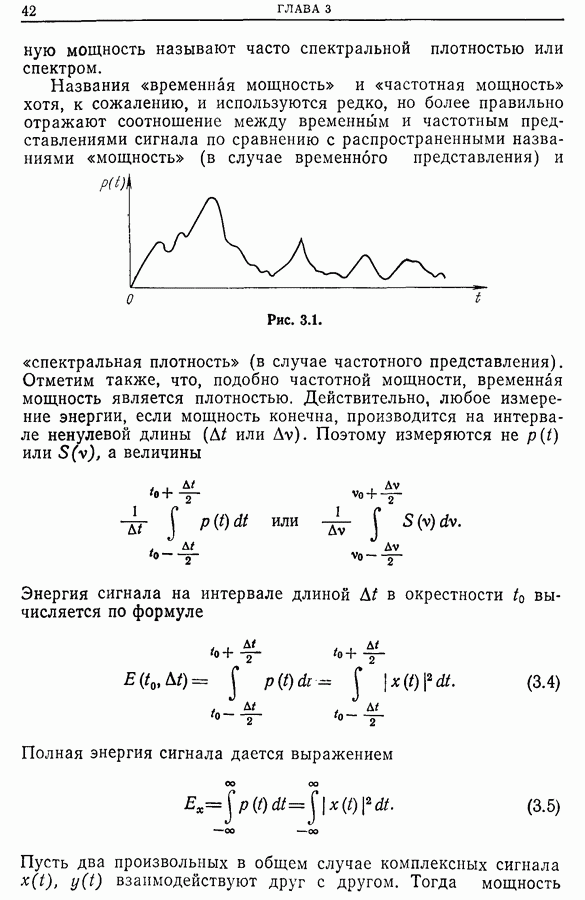
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
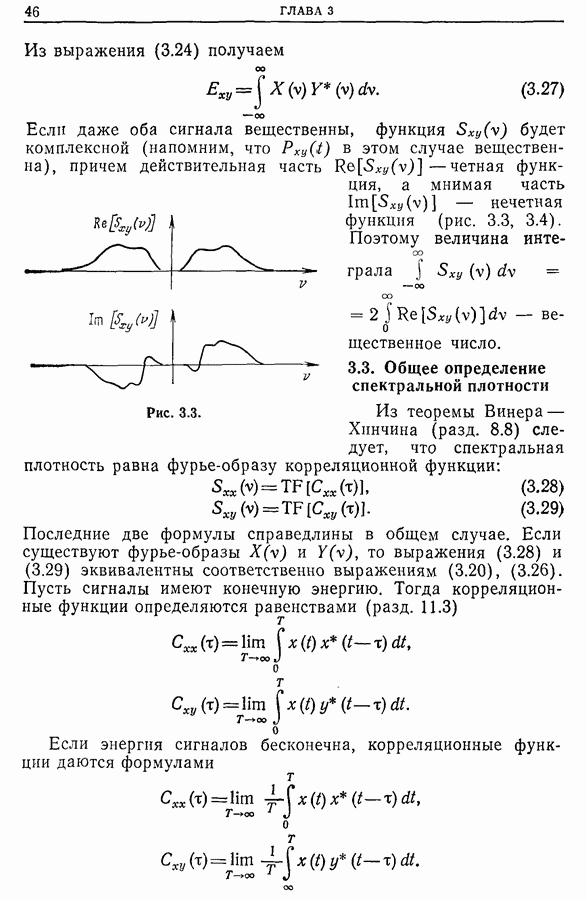
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
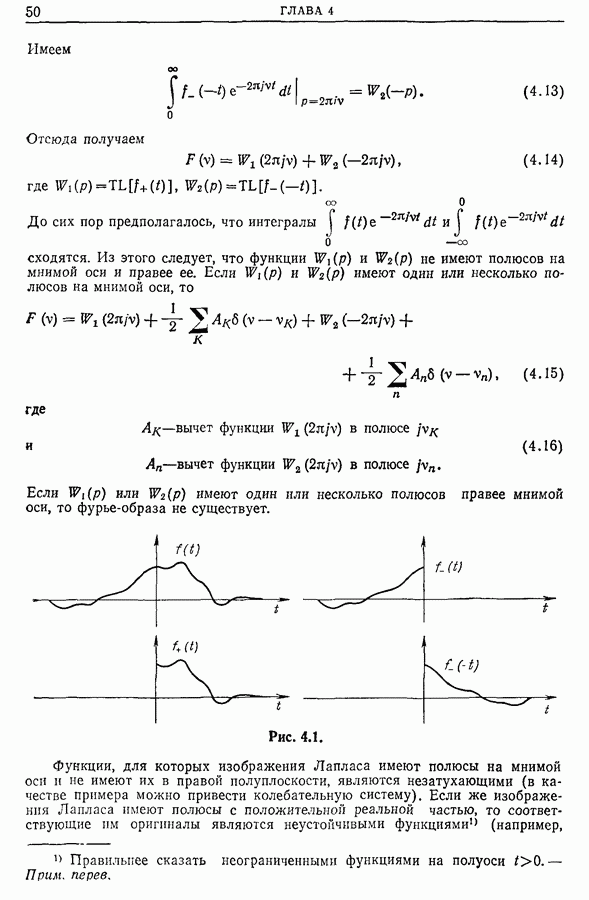
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
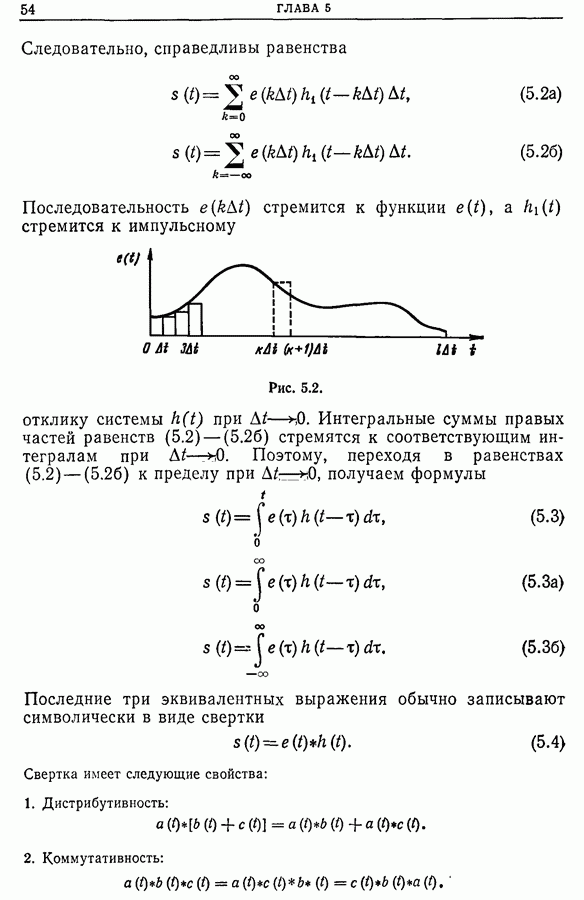
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
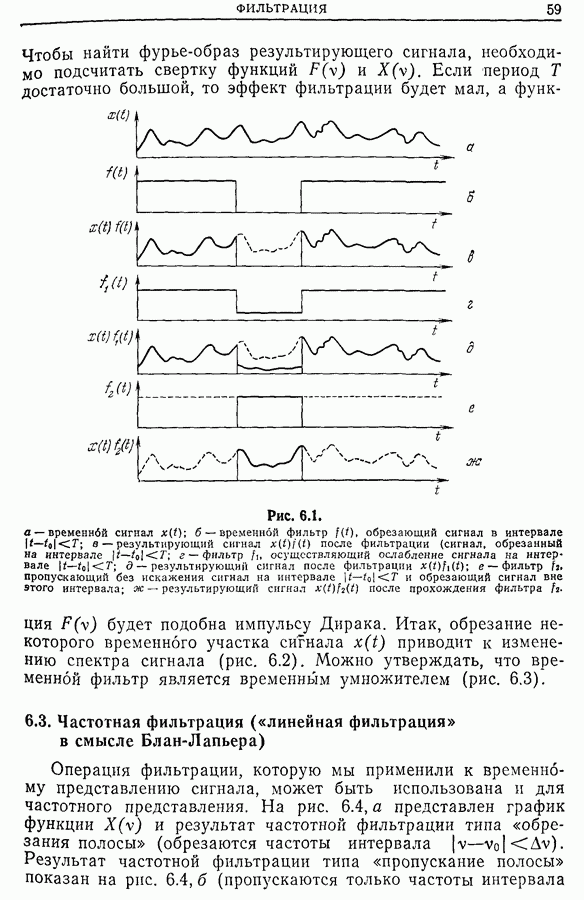
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
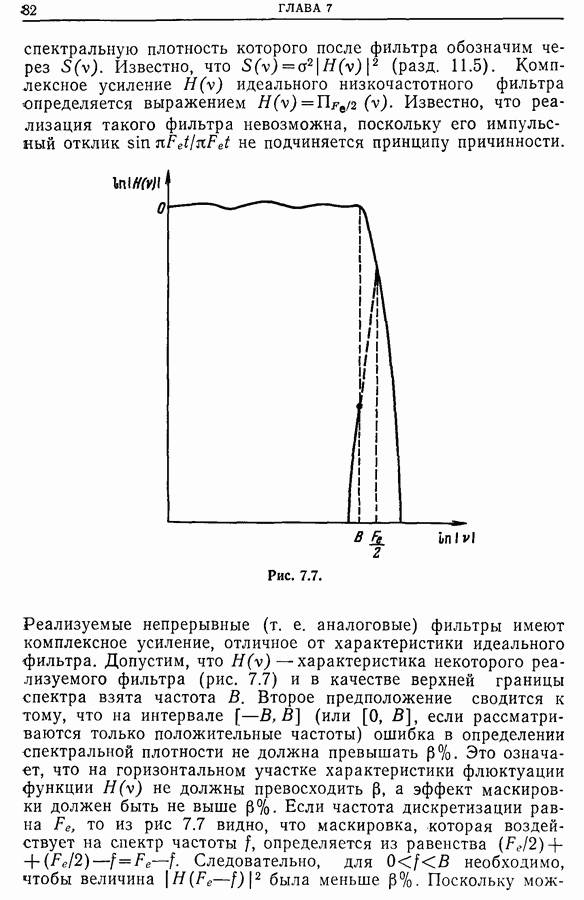
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
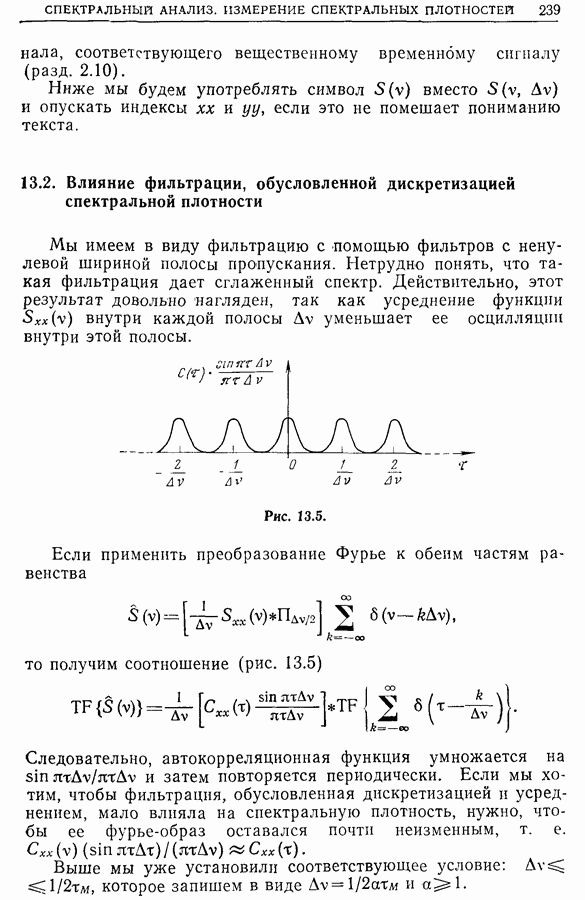
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
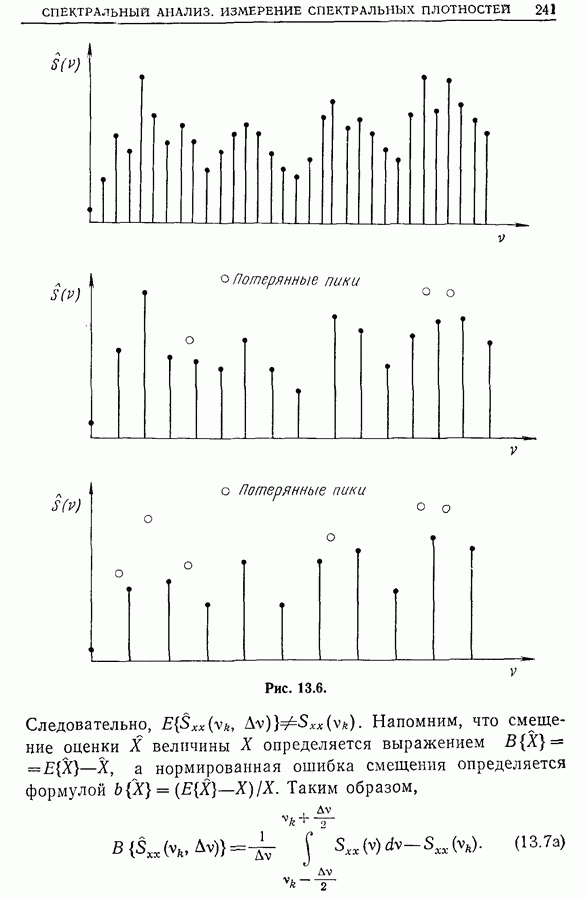
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
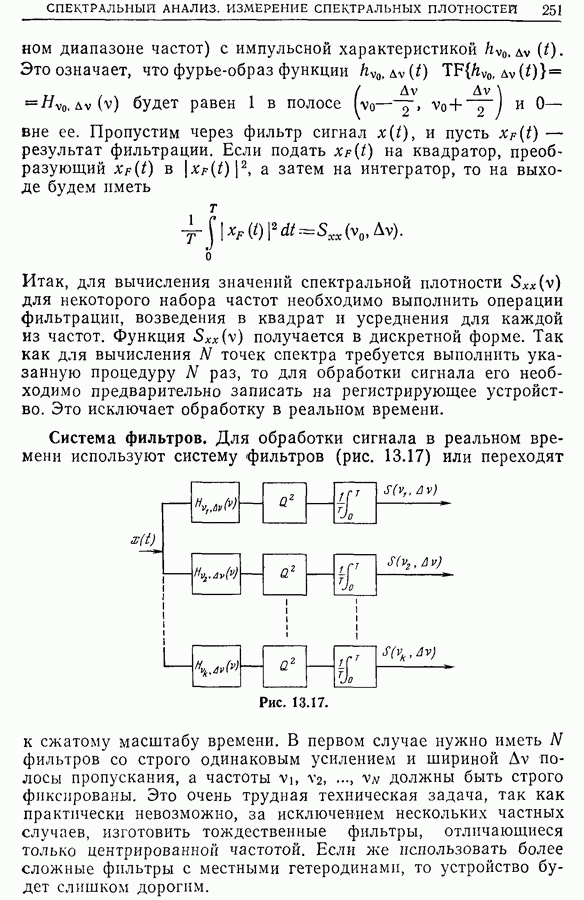
- 13.6. Спектральный анализ методом фильтрации
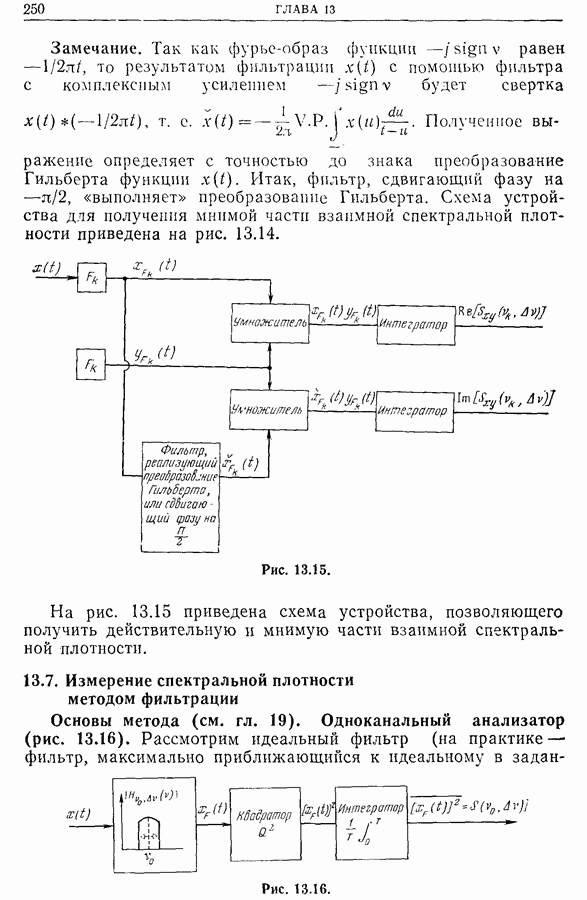
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
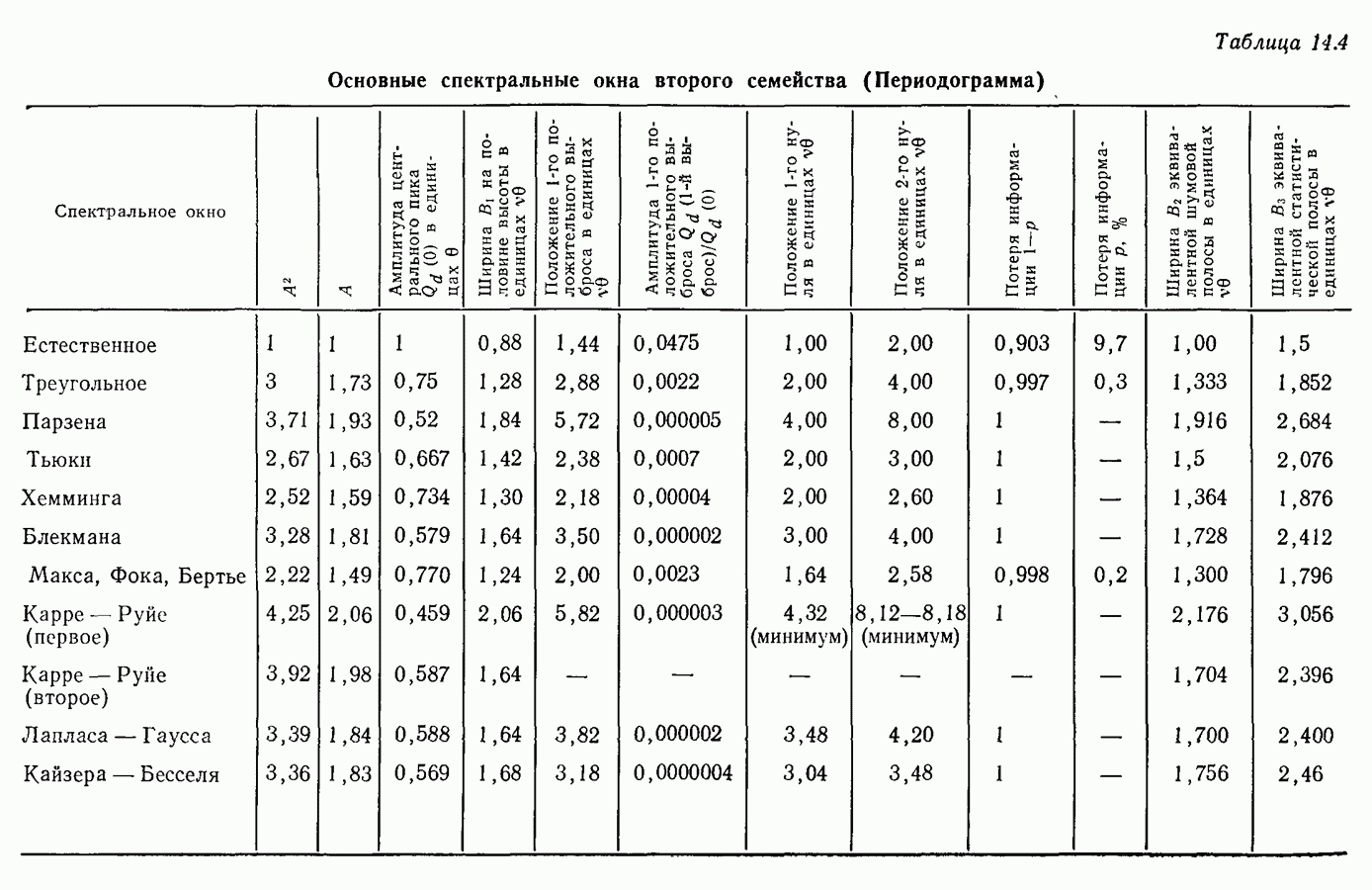
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
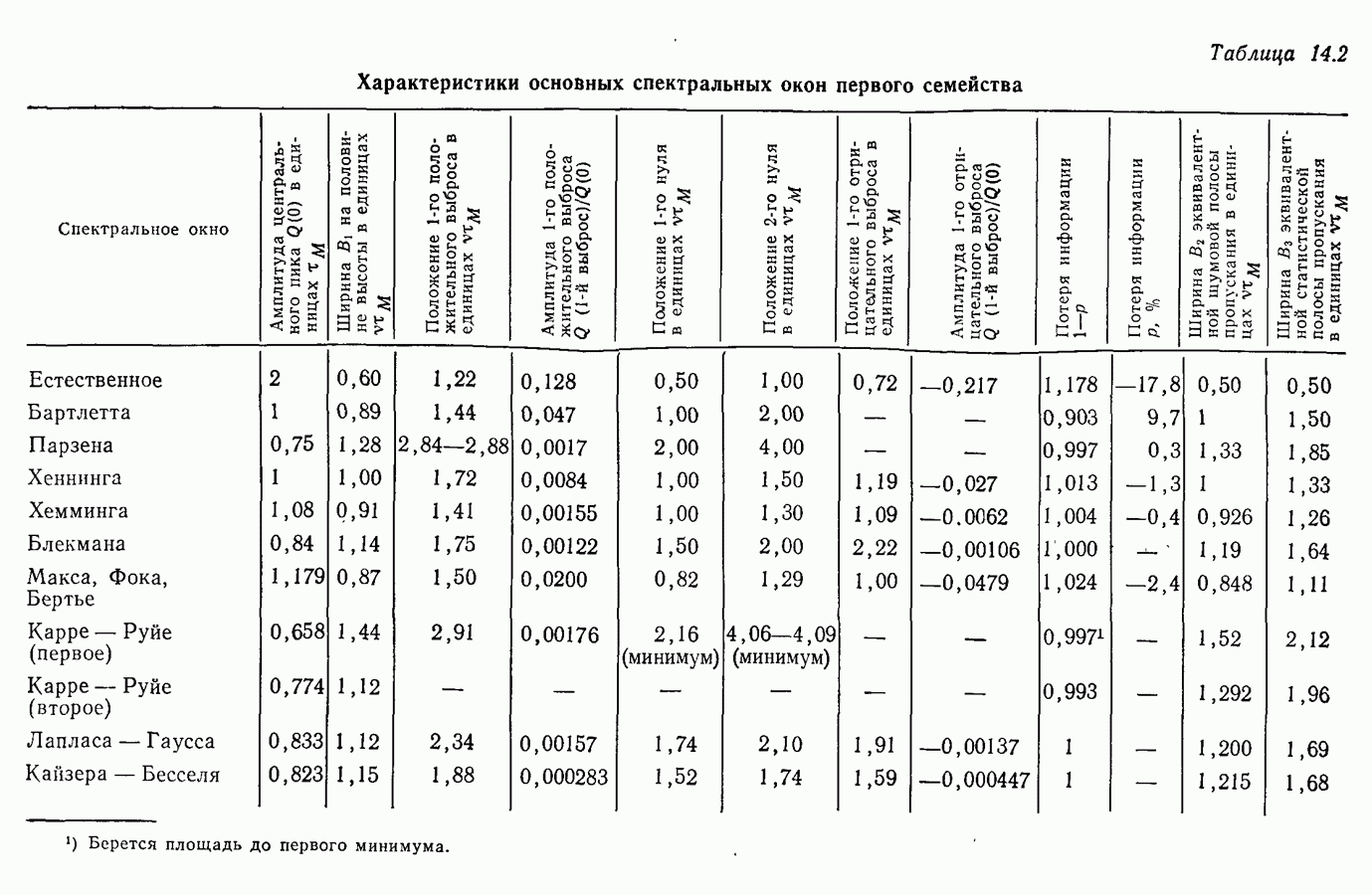
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции