| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
Прежде чем перейти к решению практических задач, рассмотрим основные приложения корреляционных функций и спектральных плотностей. Хотя число основных приложений сравнительно невелико, последние служат источником решения разнообразных практических задач. Мы рассмотрим следующие основные приложения: обнаружение и выделение сигнала на фоне шума; обнаружение скрытых периодичностей; получение спектральных плотностей энергии на основе корреляционной функции с помощью теоремы Винера — Хинчина (и наоборот); определение динамических характеристик линейных систем, когерентности и сдвига между сигналами.
Важное замечание.
Дуальность времени и частоты приводит к тому, что любой результат, полученный путем использования корреляционных функций, может быть получен также с помощью спектральных плотностей. При проведении практических расчетов требуется выбрать одну из переменных — время или частоту. Во многих случаях можно сделать этот выбор, руководствуясь простым соображением: «узкий» во времени сигнал является протяженным по частоте, и наоборот.
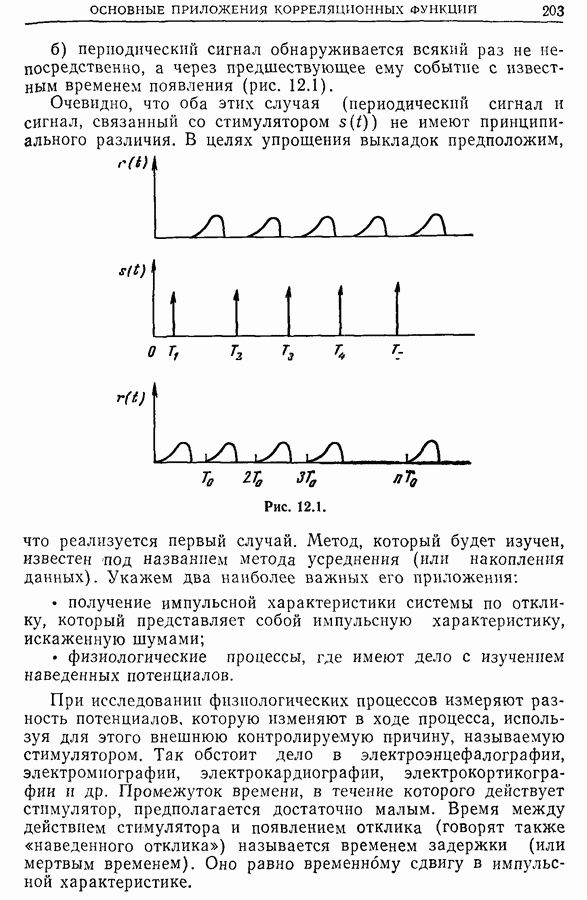
12.1. Обнаружение периодического сигнала на фоне помех с помощью автокорреляции
Обнаружить сигнал на фоне помех означает ответить на вопрос: существует сигнал или нет? Задача определения его формы при этом не ставится.
Основы метода.
Пусть  — периодический сигнал с неизвестным (основным) периодом
— периодический сигнал с неизвестным (основным) периодом  и
и  — шум. Рассмотрим суперпозицию
— шум. Рассмотрим суперпозицию

Для упрощения предположим, что  центрированы, т. е. их средние значения равны нулю, тогда сигнал
центрированы, т. е. их средние значения равны нулю, тогда сигнал  также будет центрирован. С точки зрения физики эта гипотеза вполне естественна, так как на практике всегда исключают постоянную компоненту, чтобы не «загромождать» измерительную аппаратуру, шкала (или динамический диапазон) которой всегда ограничена.
также будет центрирован. С точки зрения физики эта гипотеза вполне естественна, так как на практике всегда исключают постоянную компоненту, чтобы не «загромождать» измерительную аппаратуру, шкала (или динамический диапазон) которой всегда ограничена.
Автокорреляционная функция в данном случае определяется выражением

В силу свойства дистрибутивности корреляционного оператора имеем

Можно считать, что шум  и сигнал
и сигнал  независимы. При этом условии корреляционные функции
независимы. При этом условии корреляционные функции  тождественно равны нулю (с точностью до погрешностей оценок, обусловленных конечным временем интегрирования). Автокорреляционная функция шума
тождественно равны нулю (с точностью до погрешностей оценок, обусловленных конечным временем интегрирования). Автокорреляционная функция шума  стремится к нулю с возрастанием
стремится к нулю с возрастанием  (разд. 11.12); следовательно, для достаточно больших значений
(разд. 11.12); следовательно, для достаточно больших значений  (больших по модулю некоторого
(больших по модулю некоторого  величина
величина  практически равна нулю (с точностью до погрешности оценки). Значение
практически равна нулю (с точностью до погрешности оценки). Значение  начиная с которого автокорреляционную функцию
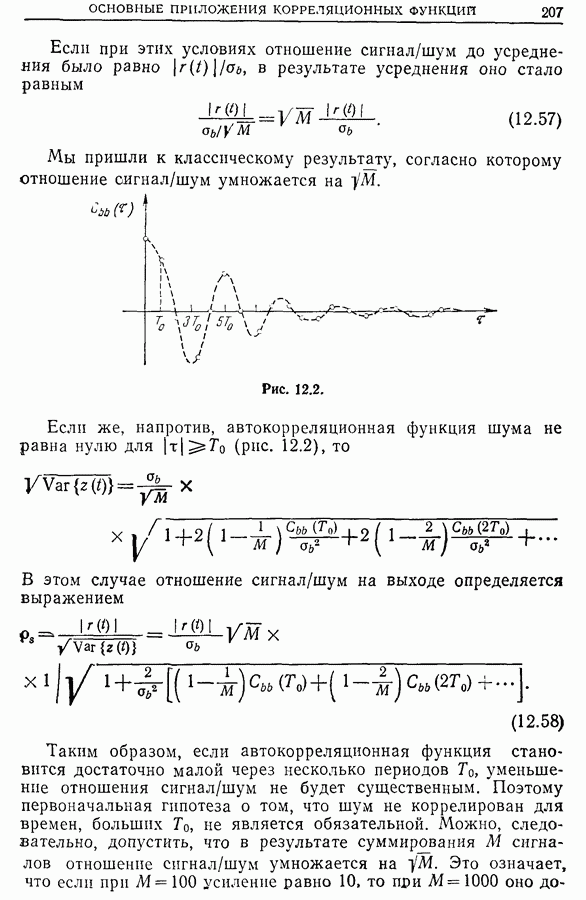
начиная с которого автокорреляционную функцию  можно положить равной нулю, зависит от характеристик шума, и в частности от его спектральной плотности: чем шире полоса частот шума при заданной полной мощности, тем быстрее убывает автокорреляционная функция. Итак, при
можно положить равной нулю, зависит от характеристик шума, и в частности от его спектральной плотности: чем шире полоса частот шума при заданной полной мощности, тем быстрее убывает автокорреляционная функция. Итак, при  в выражении для автокорреляционной функции периодического сигнала остается только одно слагаемое:
в выражении для автокорреляционной функции периодического сигнала остается только одно слагаемое:

В действительности

где ошибка  тем меньше, чем больше время интегрирования Т (или временная константа усредняющего низкочастотного фильтра).
тем меньше, чем больше время интегрирования Т (или временная константа усредняющего низкочастотного фильтра).
Итак, описанный метод позволяет обнаружить периодический сигнал на фоне шума.
В разд. 11.2 показано, что если периодический сигнал с периодом  разложить в ряд Фурье
разложить в ряд Фурье

то его автокорреляционная функция будет представлена рядом 

Из последнего выражения следует, что форму сигнала таким методом восстановить невозможно, так как в этом случае определяется лишь квадрат его модуля, а информация о фазе полностью теряется. Очевидно, что форма остается неизменной и может быть восстановлена, если  — синусоидальный сигнал.
— синусоидальный сигнал.
Увеличение отношения сигнал/шум при обнаружении сигнала с помощью корреляции.
Пусть  содержащий шум. Для упрощения записи обозначим
содержащий шум. Для упрощения записи обозначим  Будем считать, что шум
Будем считать, что шум  центрирован и является стационарным процессом 2-го порядка со спектральной плотностью
центрирован и является стационарным процессом 2-го порядка со спектральной плотностью  . Исходя из определения автокорреляционной функции
. Исходя из определения автокорреляционной функции 

находим ее оценку 

Вычислим теперь  (как в гл. 9). Вычисление
(как в гл. 9). Вычисление  . В данном случае выражение
. В данном случае выражение 

может быть представлено в виде суммы следующих трех слагаемых:


что можно также записать в виде

Так как шум  центрирован, то эти два последних слагаемых равны нулю.
центрирован, то эти два последних слагаемых равны нулю.

вследствие стационарности  Следовательно,
Следовательно,

или

Если произведение  , где
, где  — период сигнала, достаточно велико, то
— период сигнала, достаточно велико, то

Вычисление  . Согласно выражению (9.9),
. Согласно выражению (9.9),

Вычислим  По определению имеем
По определению имеем

что приводит к математическому ожиданию двойного интеграла:


Освобождаясь от скобок, получим 16 слагаемых, каждое из которых является математическим ожиданием одного из 16 двойных интегралов. Все эти интегралы вычисляются по ггеореме Фубини. Один из интегралов содержит детерминированную функцию  , а остальные содержат моменты 4-го порядков функции
, а остальные содержат моменты 4-го порядков функции  Поскольку шум
Поскольку шум  центрирован, моменты 1-го порядка обращаются в нуль. Если дополнительно предположить, что
центрирован, моменты 1-го порядка обращаются в нуль. Если дополнительно предположить, что  — гауссов шум, то обратятся в нуль все моменты нечетного порядка (разд. 8.10). В результате остается шесть моментов 2-го порядка и один момент 4-го порядка.
— гауссов шум, то обратятся в нуль все моменты нечетного порядка (разд. 8.10). В результате остается шесть моментов 2-го порядка и один момент 4-го порядка.
Таким образом, вычисление  сводится к вычислению восьми двойных интегралов:
сводится к вычислению восьми двойных интегралов:
(см. скан)
При этом  Нетрудно убедиться в том, что
Нетрудно убедиться в том, что

Поскольку  - гауссов шум, то, согласно выражению (9.28), получаем
- гауссов шум, то, согласно выражению (9.28), получаем

Вычислим теперь интеграл  . Так как
. Так как 

то

Этот интеграл был уже найден при вычислении математического ожидания  . Таким образом,
. Таким образом,

Вычислим интегралы  и
и  . Эти два интеграла имеют одно и то же значение:
. Эти два интеграла имеют одно и то же значение:

Вычислим сумму  . Имеем
. Имеем


(кликните для просмотра скана)
Применяя формулы (9.14) и (9.15), найдем 

Вычислим интеграл 

или, согласно выражению (9.14),

Итак, получаем в результате
(см. скан)

Три последних слагаемых входят в сумму дважды, но с противоположными знаками, поэтому они взаимно уничтожаются. Положим  , где
, где  . Если
. Если  достаточно велико, т. е. промежуток интегрирования содержит достаточно большое число периодов искомого сигнала, то можно пренебречь слагаемыми, содержащими
достаточно велико, т. е. промежуток интегрирования содержит достаточно большое число периодов искомого сигнала, то можно пренебречь слагаемыми, содержащими  Тогда
Тогда 

Поскольку (разд. 2.14)

то

Учитывая, что  стремится к нулю с увеличением Т, получаем в результате два слагаемых:
стремится к нулю с увеличением Т, получаем в результате два слагаемых:

Первое слагаемое можно записать в виде 00

или

Если предположить, что  мало изменяется в области, где величина
мало изменяется в области, где величина  существенно отлична от нуля, то
существенно отлична от нуля, то

Предполагая, что спектральная плотность шума  постоянна в полосе частот
постоянна в полосе частот  , получим
, получим  и
и

где  — дисперсия шума.
— дисперсия шума.
При тех же допущениях легко вычислить интеграл

Действительно, исходя из соотношений

и учитывая равенство Парсеваля

найдем

Отсюда вытекает соотношение

Окончательно имеем

Отношение сигнал/шум до вычисления корреляции было равно

Это отношение после вычисления корреляции оказывается равным

Увеличение отношения сигнал/шум по мощности, которое обозначим  определяется формулой
определяется формулой

Из последнего выражения следует, что увеличение отношения сигнал/шум, достигнутое путем вычисления автокорреляции, пропорционально  и зависит еще от отношения сигнал/шум на входе коррелометра. Если
и зависит еще от отношения сигнал/шум на входе коррелометра. Если  то
то  Из формулы (12.28) следует также, что автокорреляция увеличивает отношение сигнал/шум только при условии
Из формулы (12.28) следует также, что автокорреляция увеличивает отношение сигнал/шум только при условии 
Примечание. Усиление по «амплитуде» будет равно

Замечание.
Может показаться невозможным обнаружить периодический сигнал с помощью метода вычисления автокорреляции, если отношение сигнал/шум на входе коррелометра слишком мало. Тем не менее существует способ увеличить это отношение. Он состоит в разбиении всего спектра на полосы путем фильтрации. Предположим, что шум  мощности
мощности  имеет постоянную спектральную плотность в рассматриваемой спектральной полосе. Если эту полосу разделить на две равные части, то мощность шума в каждой из них будет равна
имеет постоянную спектральную плотность в рассматриваемой спектральной полосе. Если эту полосу разделить на две равные части, то мощность шума в каждой из них будет равна  при делении на четыре части мощность в одной части будет
при делении на четыре части мощность в одной части будет  Отсюда видно, что разбиение исходной полосы на четыре
Отсюда видно, что разбиение исходной полосы на четыре
равные части дает увеличение отношения сигнал/шум на входе на 12 дБ.
При работе в реальном масштабе времени необходимо, чтобы каждой полосе соответствовал свой коррелометр. Выполнение этого условия может показаться трудным и дорогостоящим, однако с появлением коррелометров на интегральных схемах это препятствие вполне преодолимо. Если предположить, что разбиение спектра на полосы осуществляет система из 10 или 100 параллельно соединенных коррелометров, то это приводит к увеличению отношения сигнал/шум на входе на 20 или соответственно на 40 дБ.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
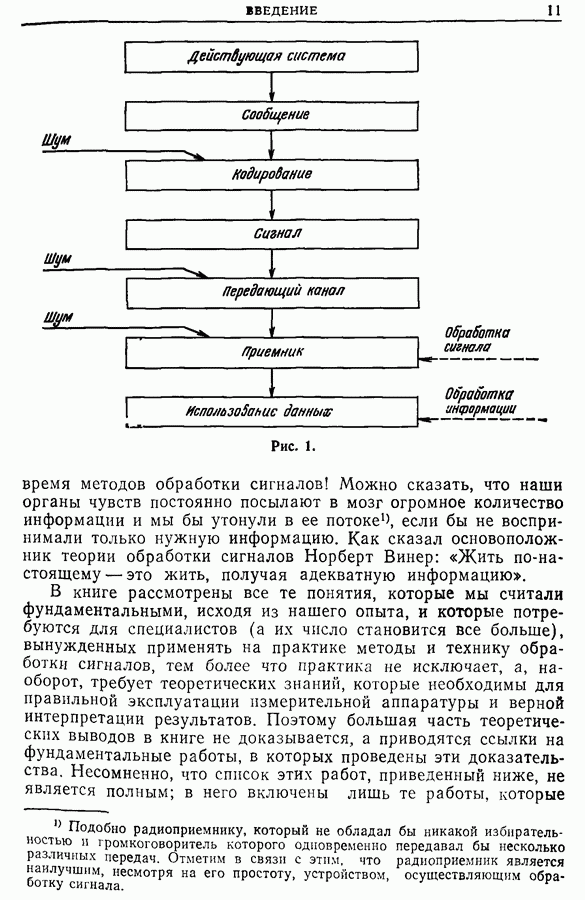
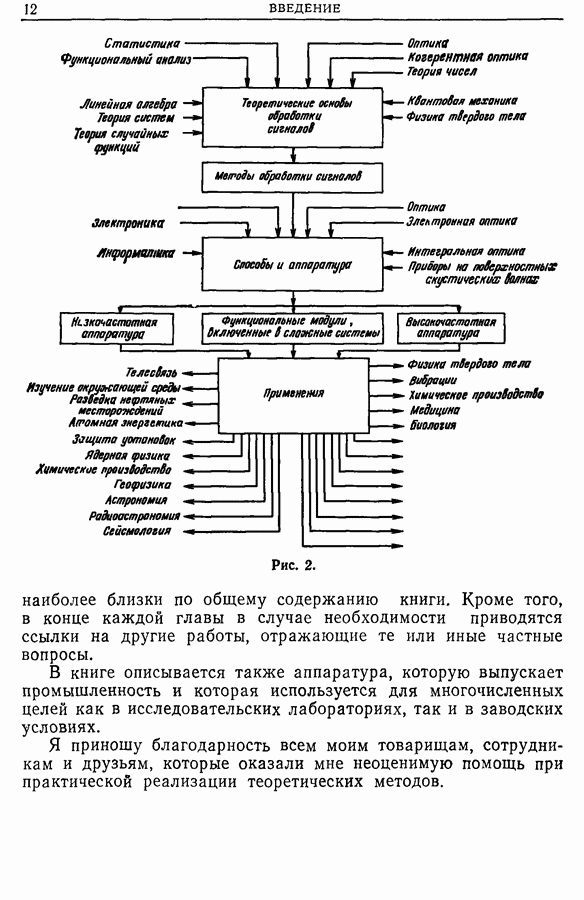
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
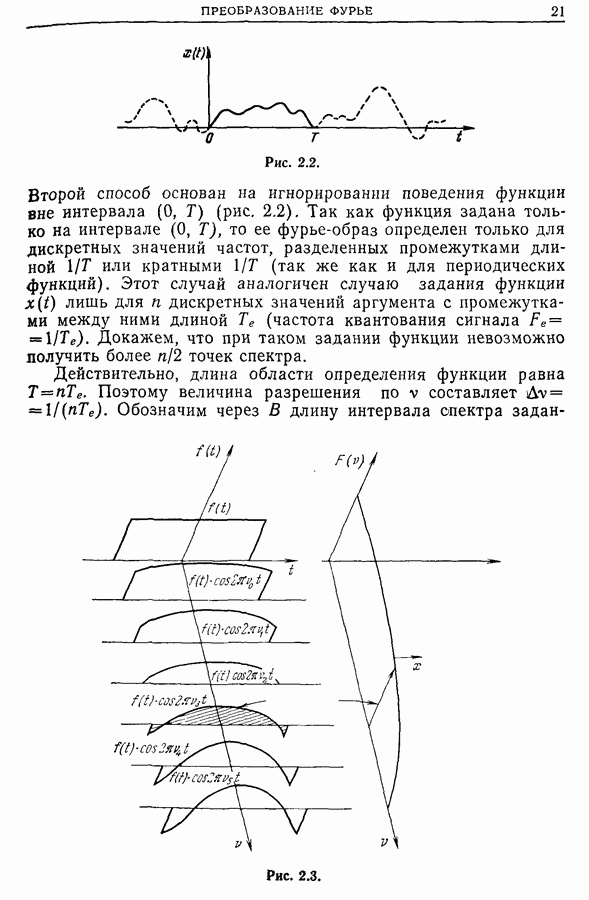
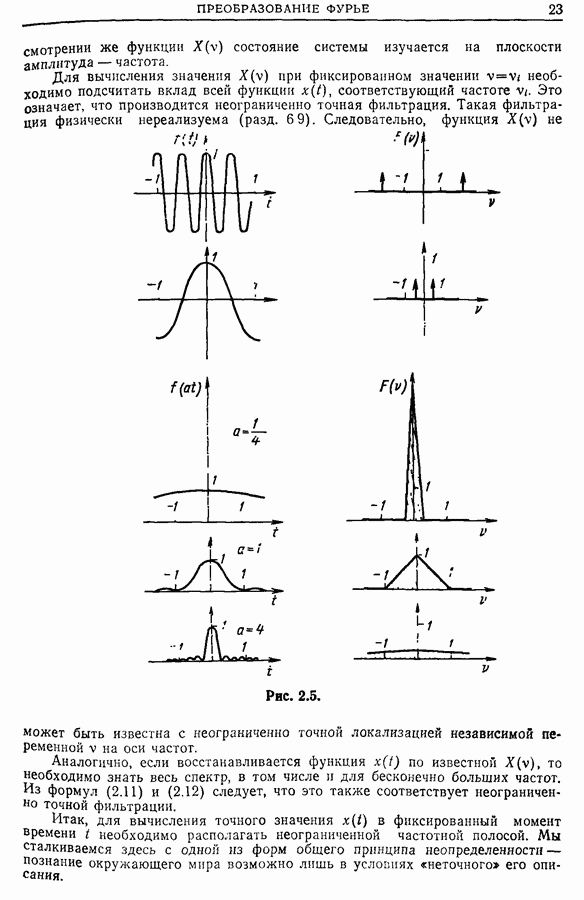
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
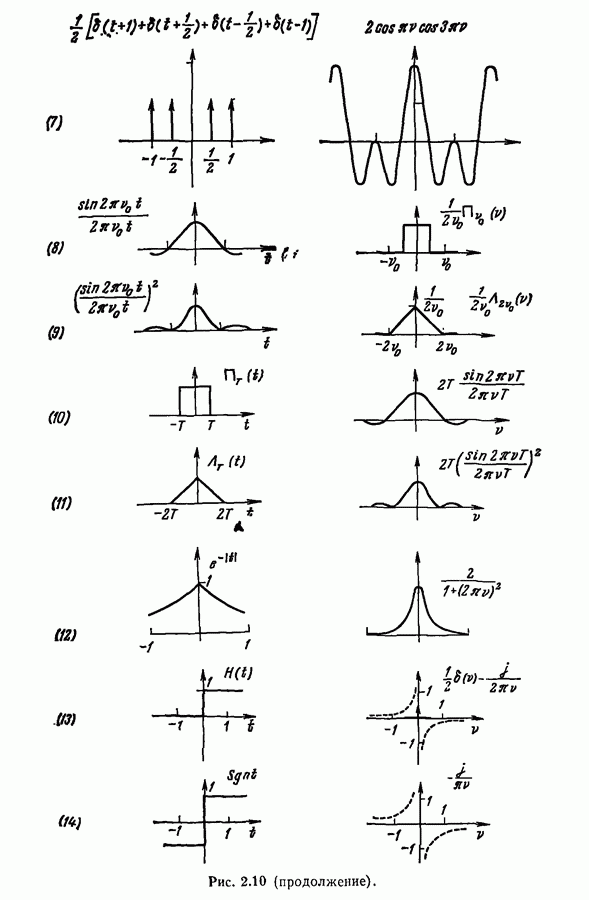
- 2.7. Несколько функций и их фурье-образы
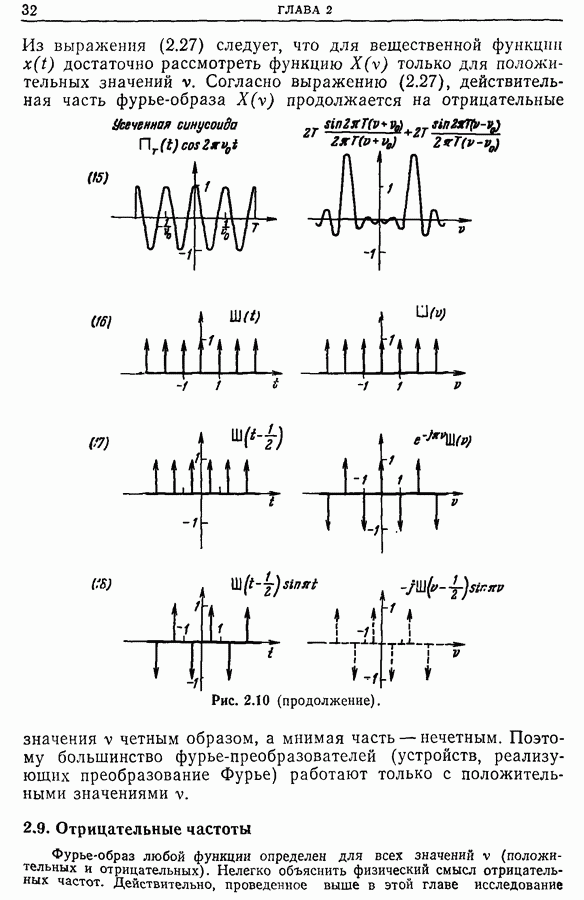
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
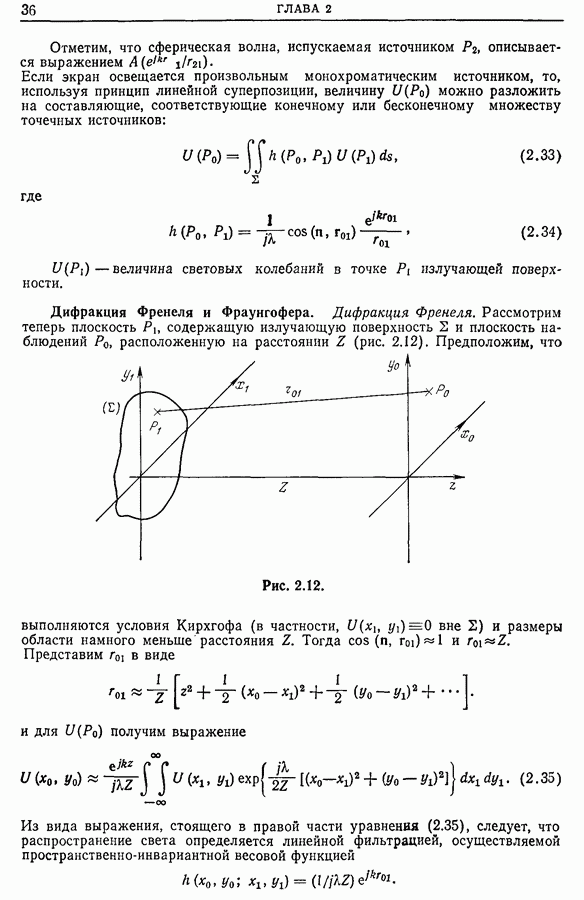
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
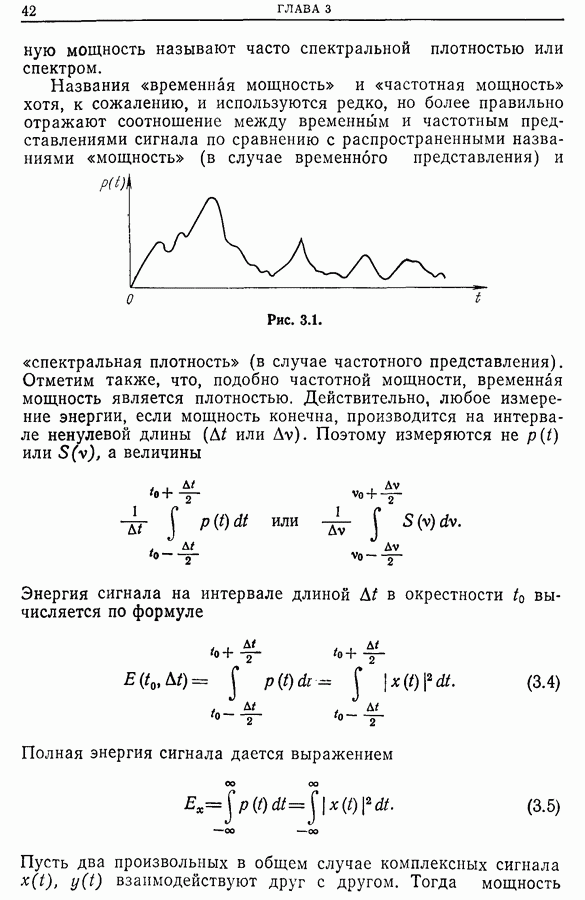
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
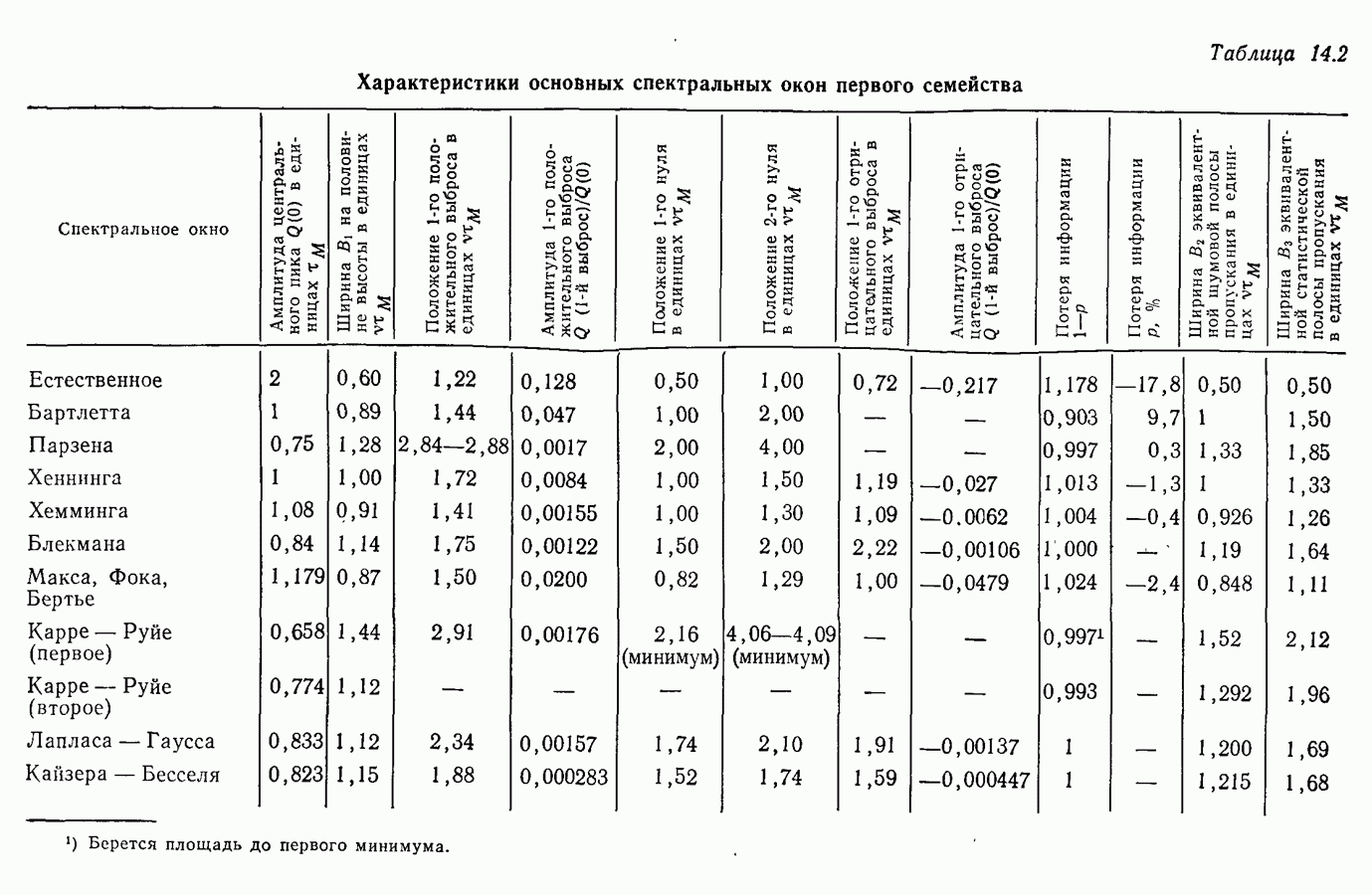
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
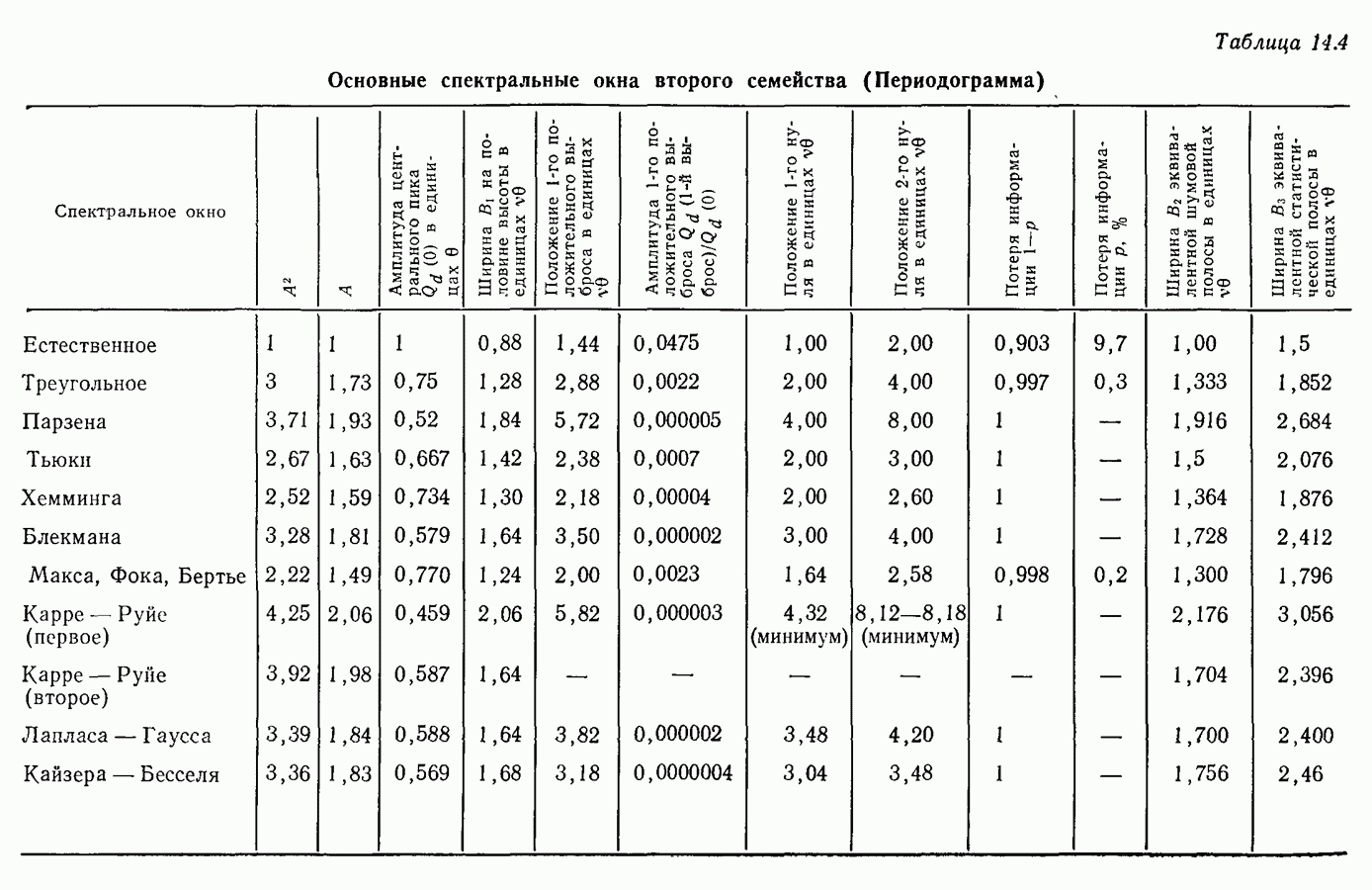
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции