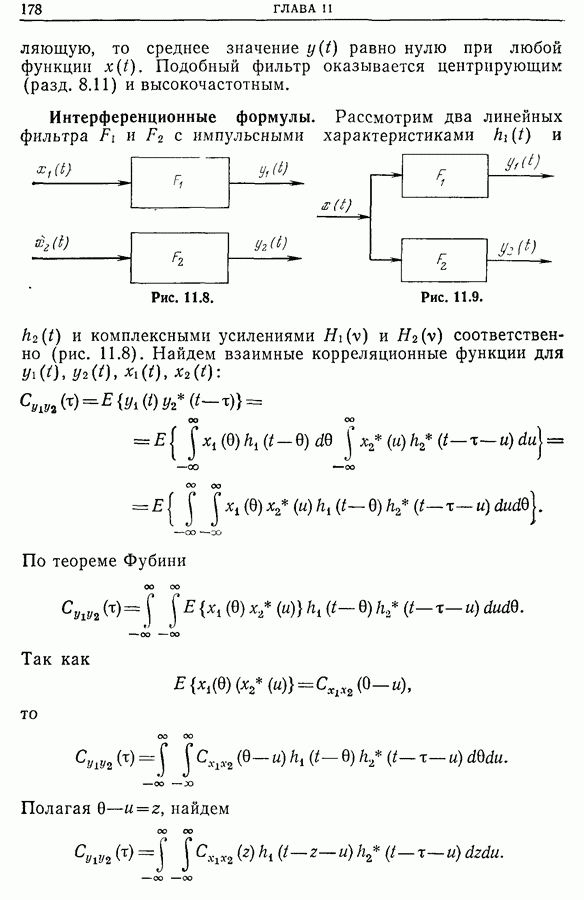
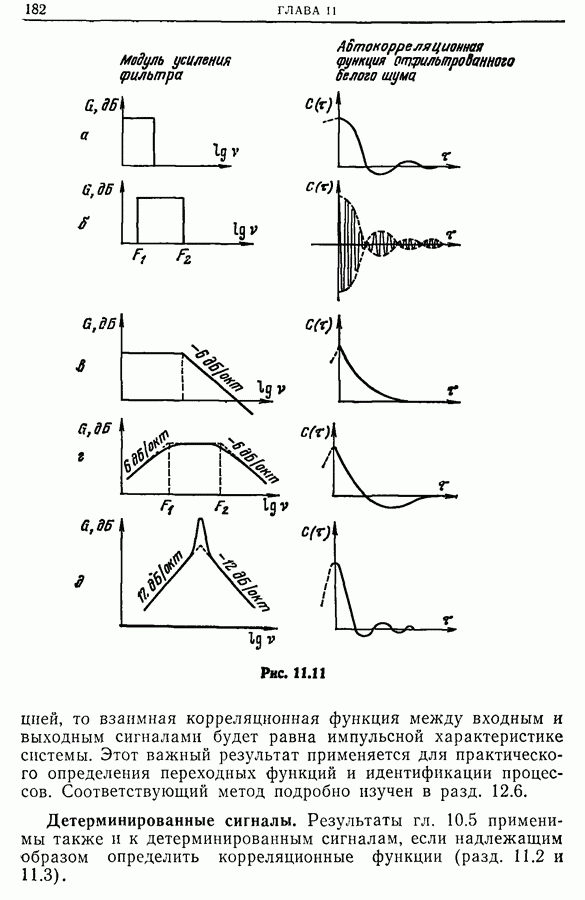
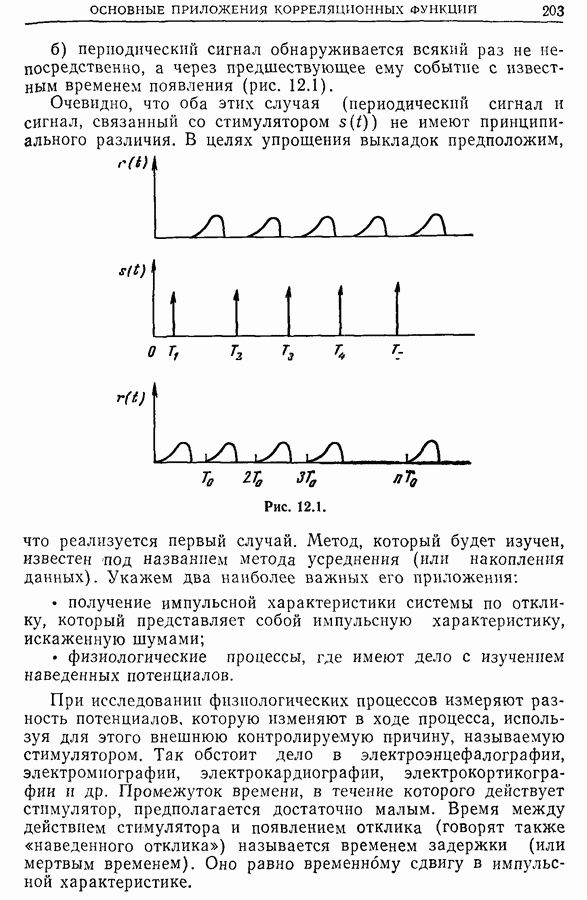
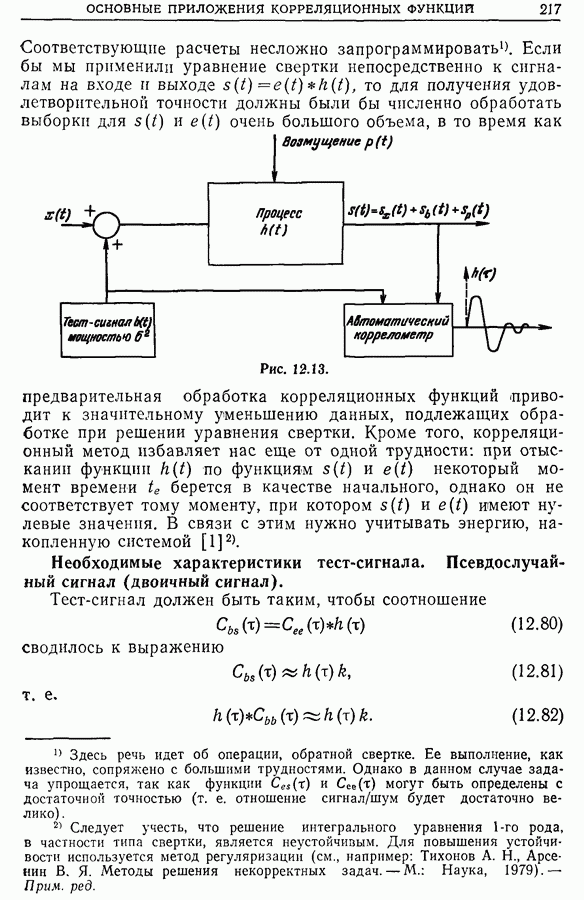
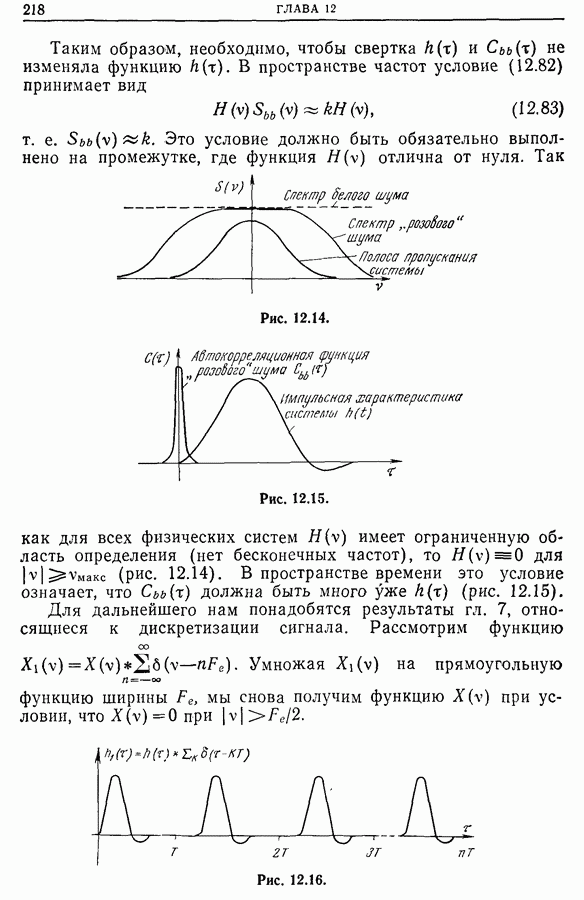
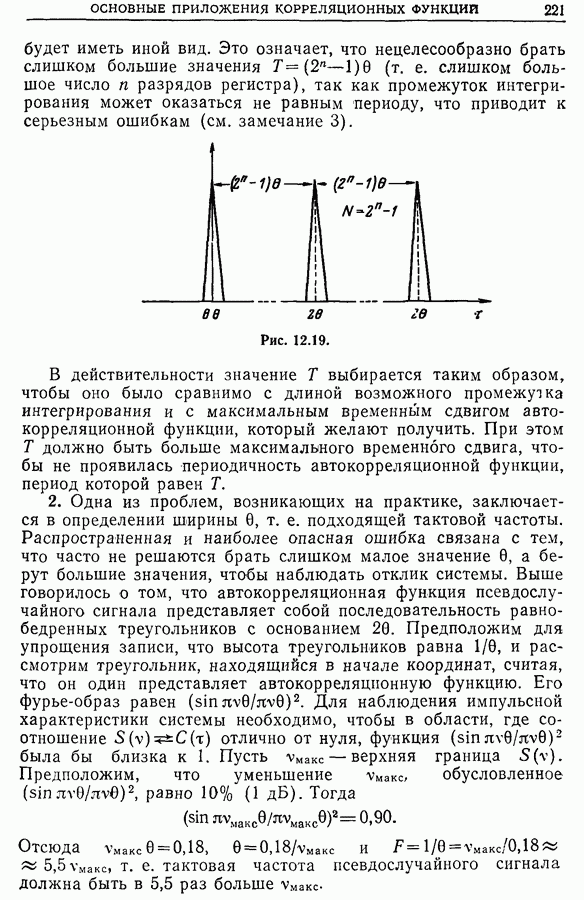
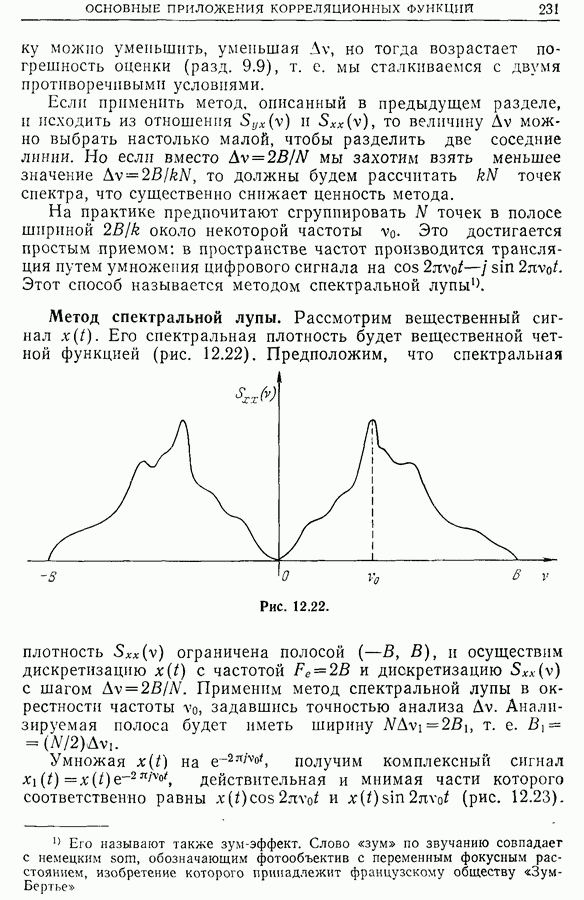
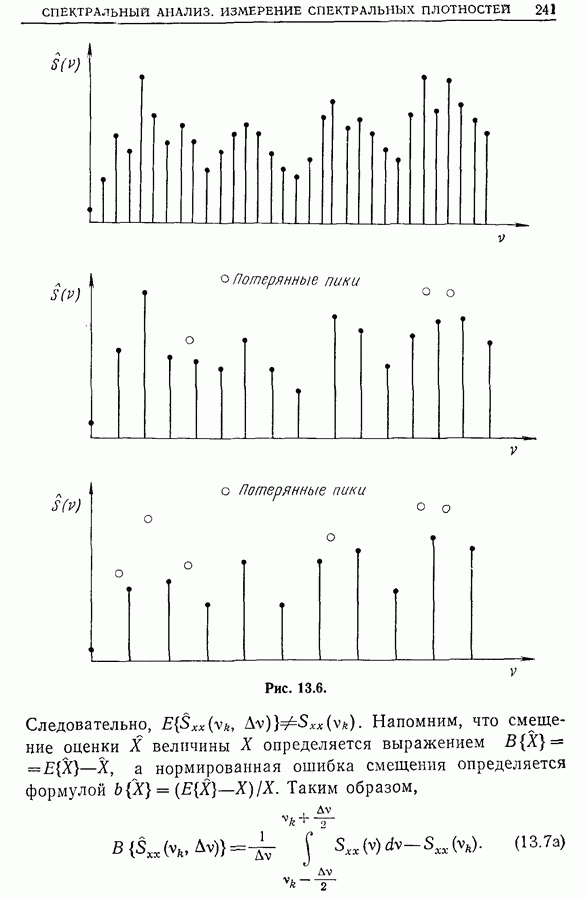
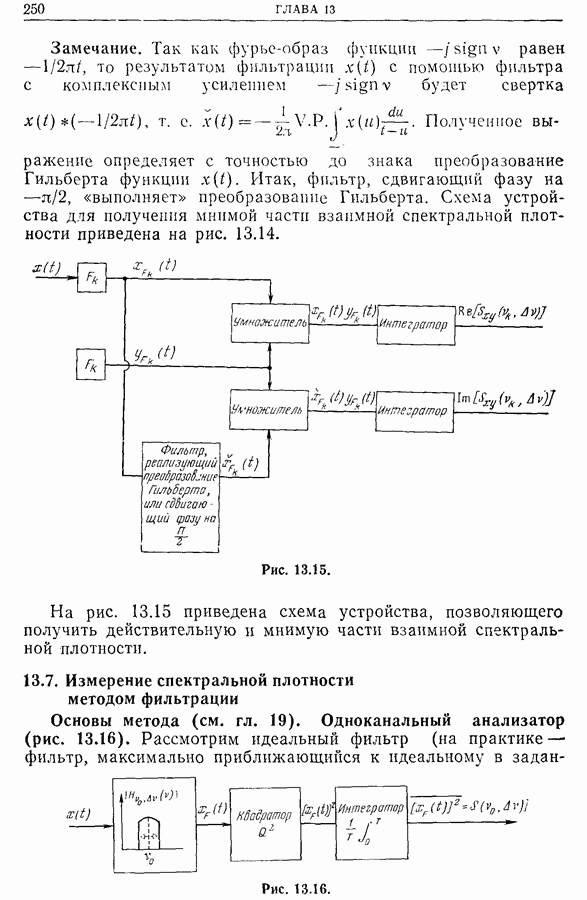
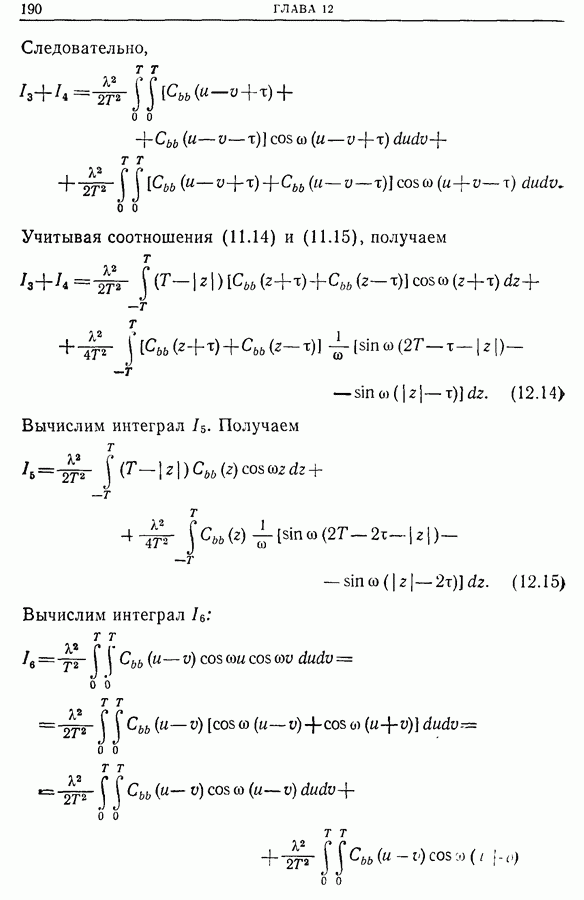| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Мой друг, что говорить о нас: Ни вы без меня, ни я без вас. (Мария Французская)
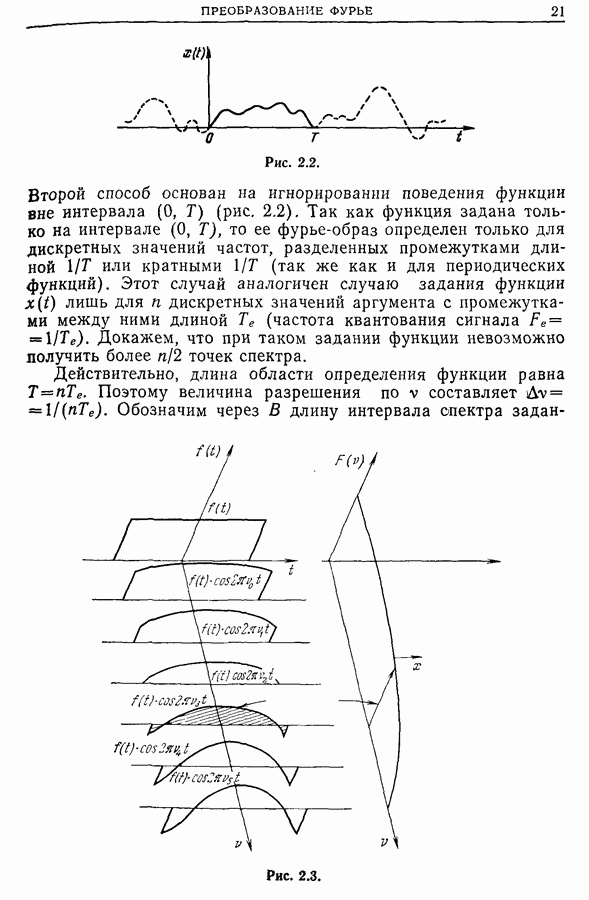
Существуют два способа описания произвольного сигнала. Первый способ основан на математическом представлении сигнала в виде  где независимая переменная
где независимая переменная  — время. Математическое представление сигнала по второму способу имеет вид
— время. Математическое представление сигнала по второму способу имеет вид  где независимая переменная
где независимая переменная  — частота (размерность
— частота (размерность  обратна размерности
обратна размерности  Эти два представления сигнала связаны друг с другом преобразованием Фурье. Следовательно, использование методов обработки сигнала требует знания свойств преобразования Фурье. Этим объясняется включение данной главы в книгу.
Эти два представления сигнала связаны друг с другом преобразованием Фурье. Следовательно, использование методов обработки сигнала требует знания свойств преобразования Фурье. Этим объясняется включение данной главы в книгу.
Отметим, что вводимое здесь преобразование Фурье над функциями времени может быть применено и для функций других переменных. Например, если независимая переменная — длина, то переменной, аналогичной частоте, будет величина, обратно пропорциональная длине и т. д.
2.1. Преобразование Фурье периодических функций
Если  — периодическая функция от
— периодическая функция от  с периодом Т, то ее можно представить в виде
с периодом Т, то ее можно представить в виде

или

где 
Коэффициенты  вычисляются по формулам
вычисляются по формулам

Если принять

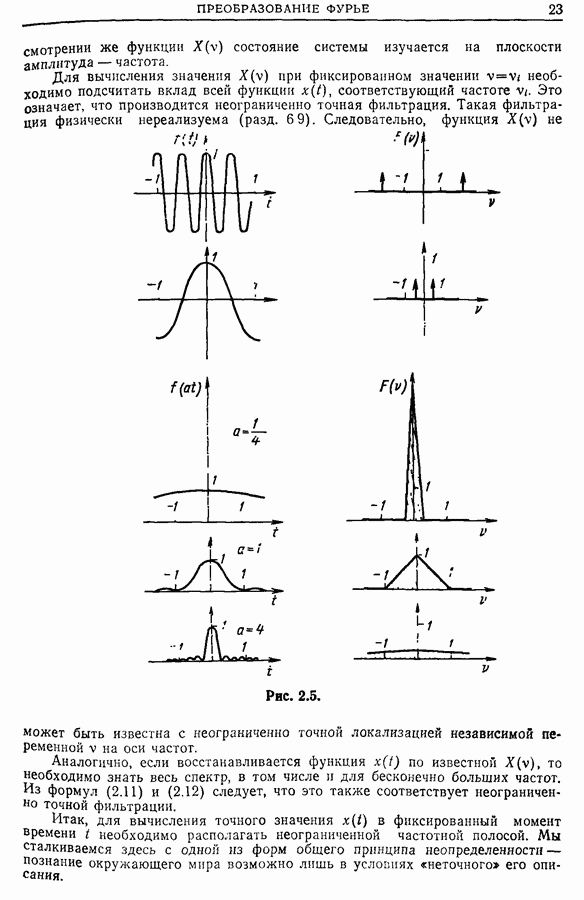
Спектральная функция  (в общем случае комплексная) может быть представлена в виде спектра амплитуд
(в общем случае комплексная) может быть представлена в виде спектра амплитуд

или спектра фаз

Справедливы также формулы

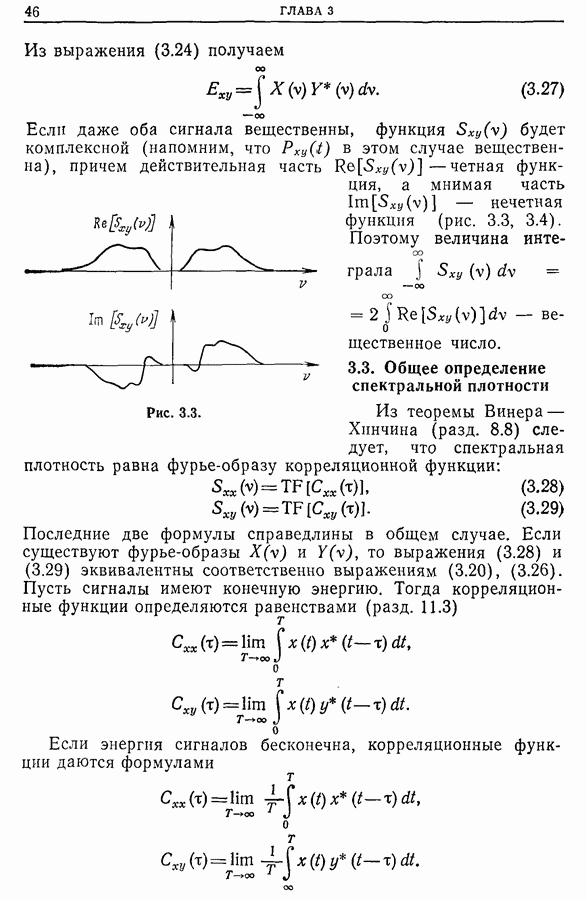
Отрицательные значения  введены с целью упрощения записи формул. Если
введены с целью упрощения записи формул. Если  — вещественная функция, то
— вещественная функция, то 

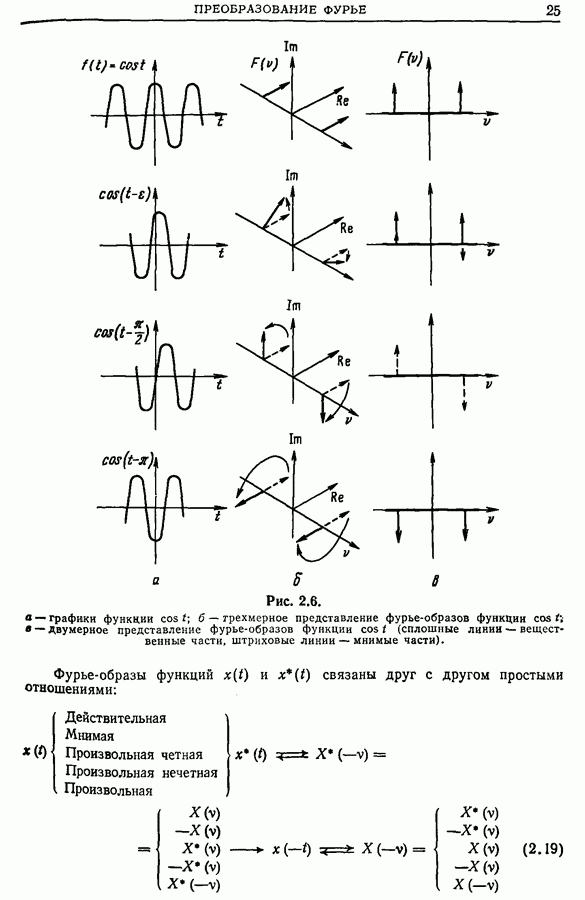
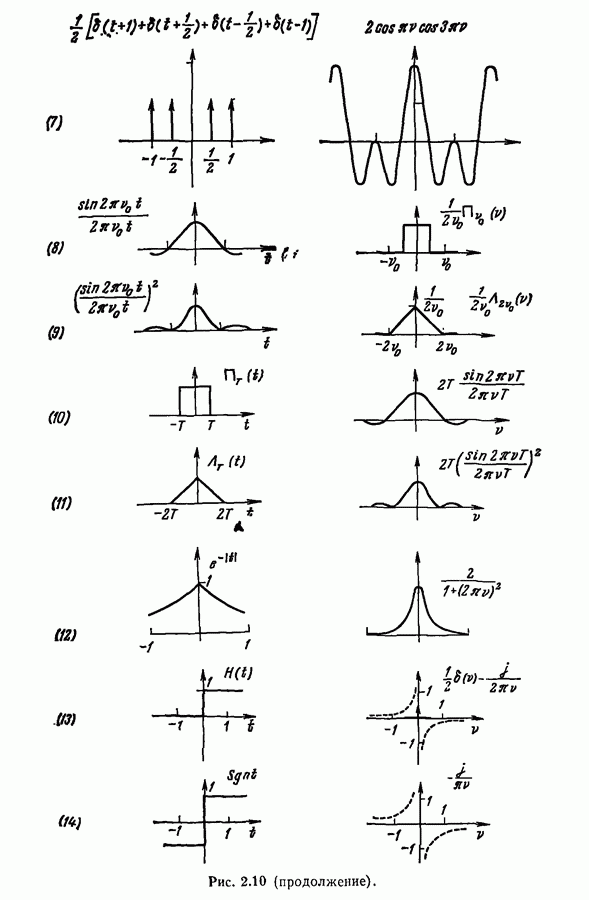
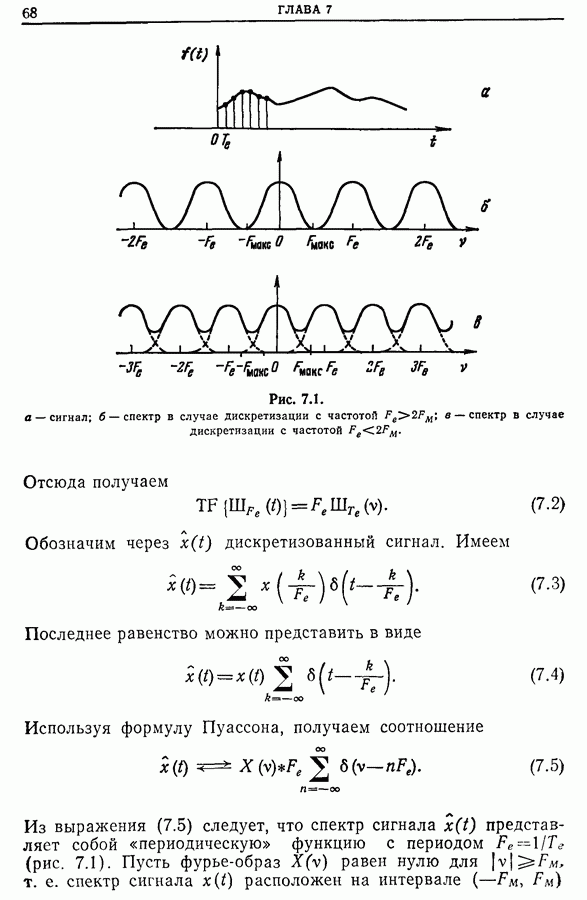
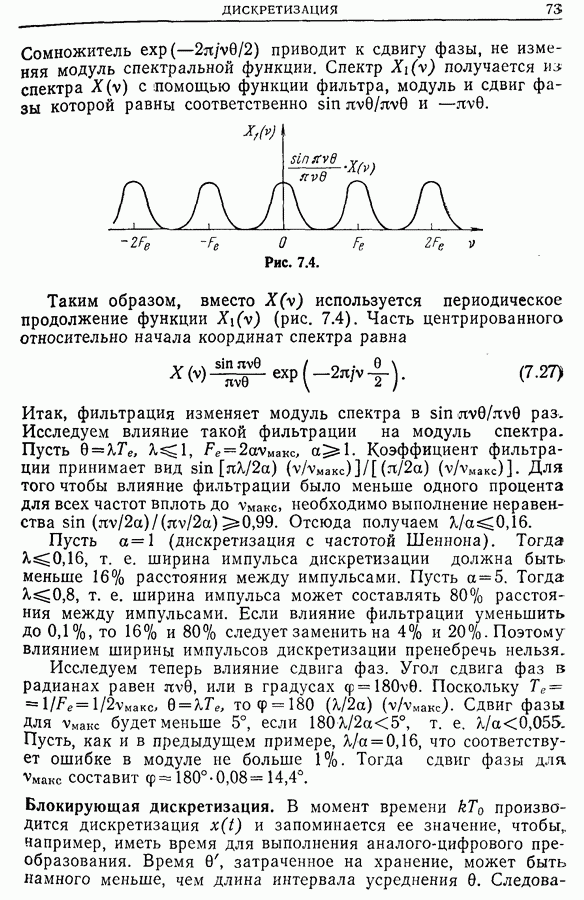
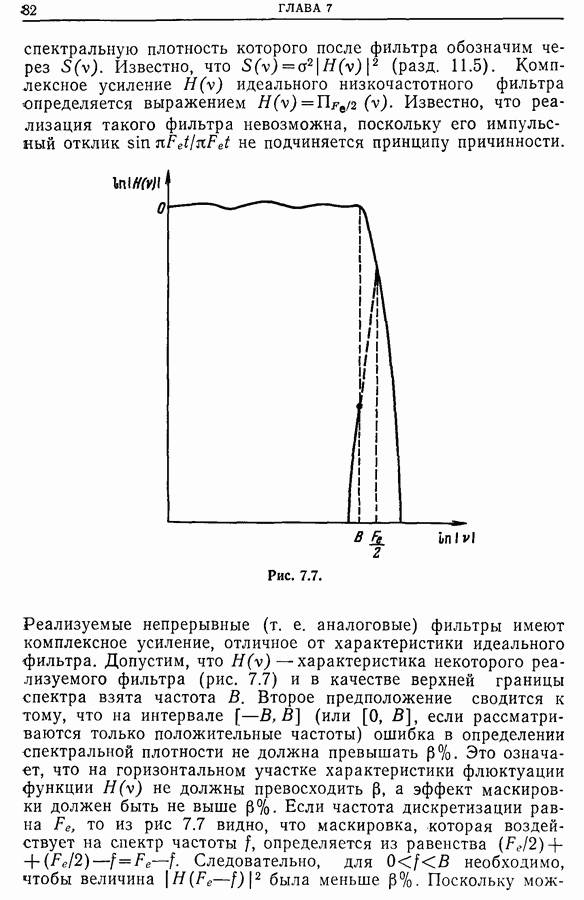
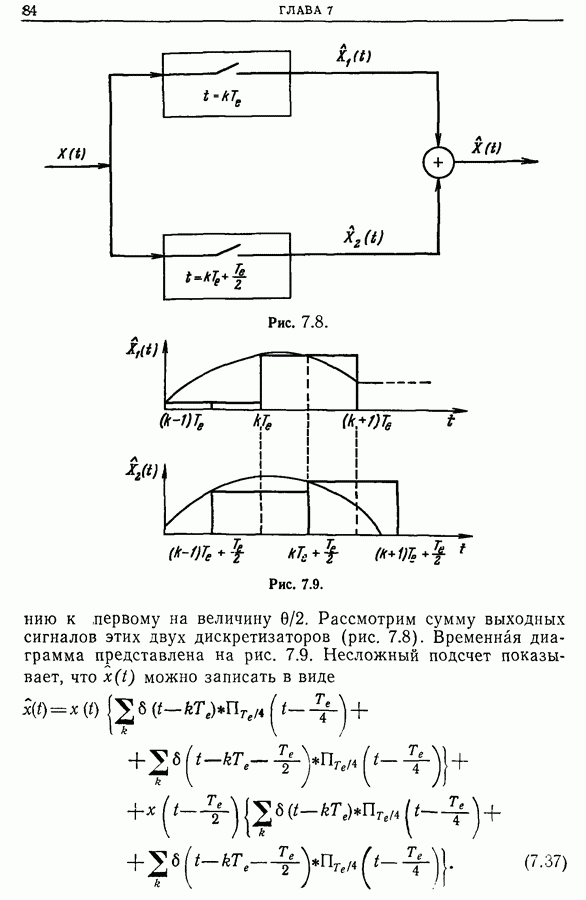
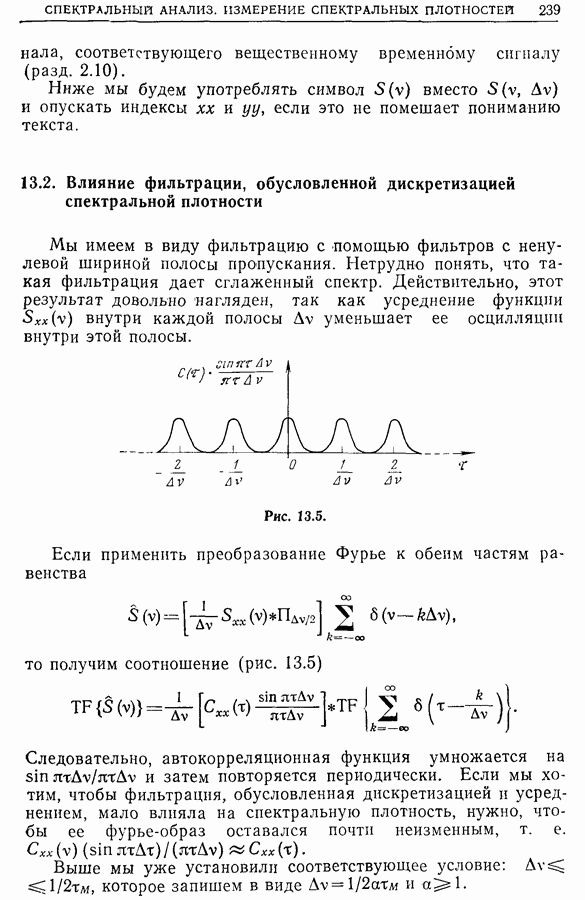
Важно отметить, что спектр периодической функции с периодом Т дискретен и минимальное расстояние между точками спектра на оси частот равно  Следовательно, спектр состоит из частот, кратных
Следовательно, спектр состоит из частот, кратных 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
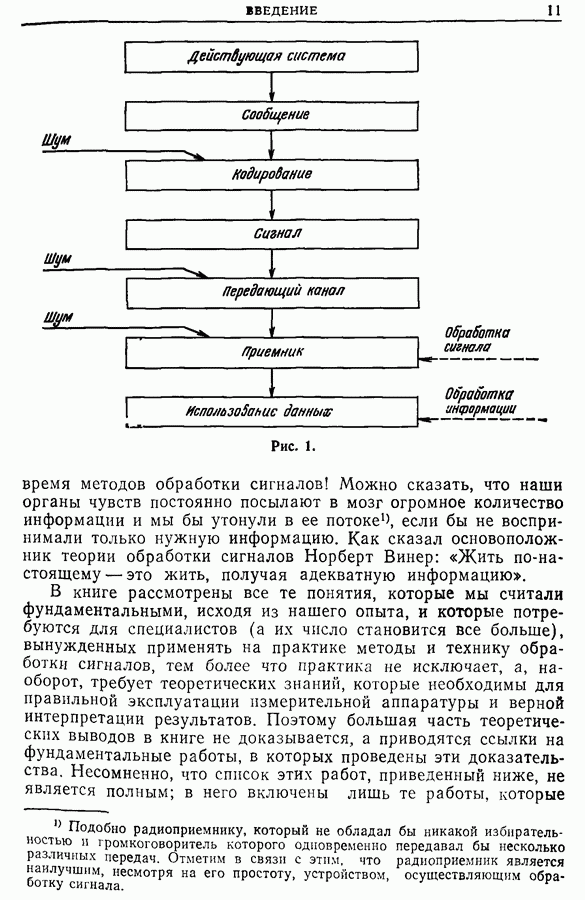
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
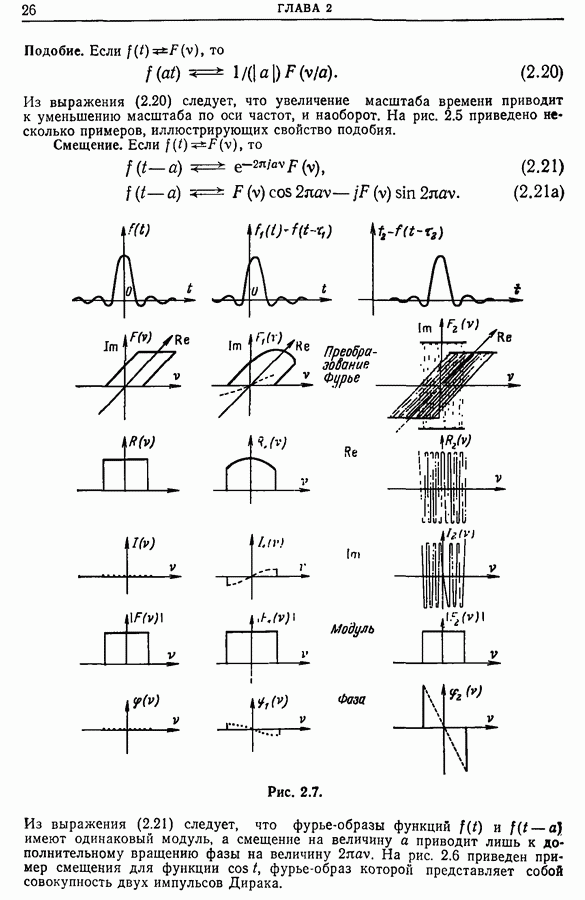
- 2.6. Некоторые свойства преобразования Фурье
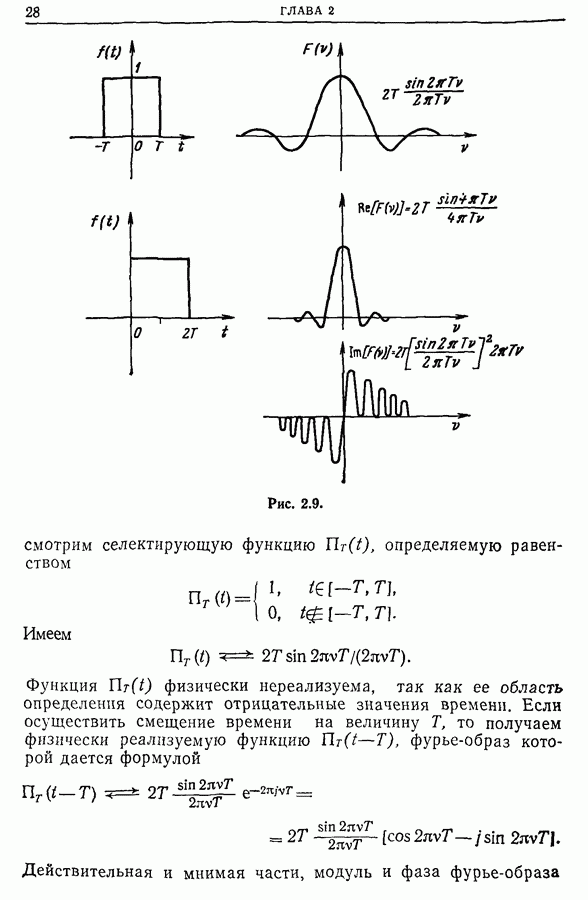
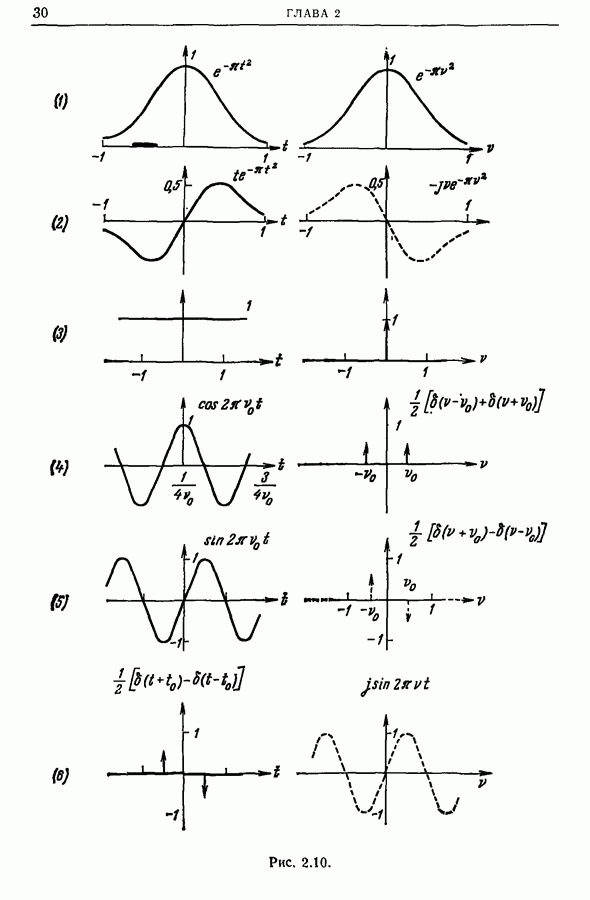
- 2.7. Несколько функций и их фурье-образы
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
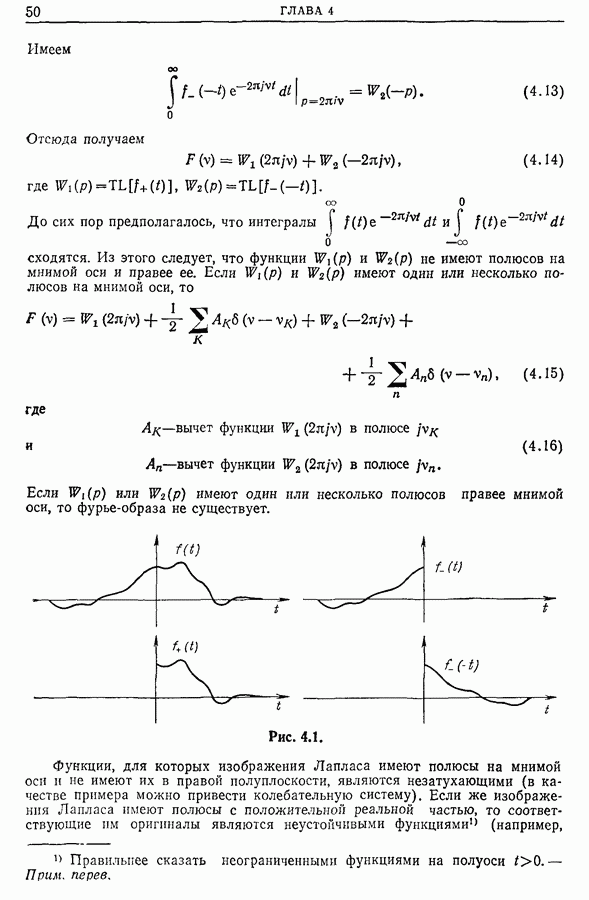
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
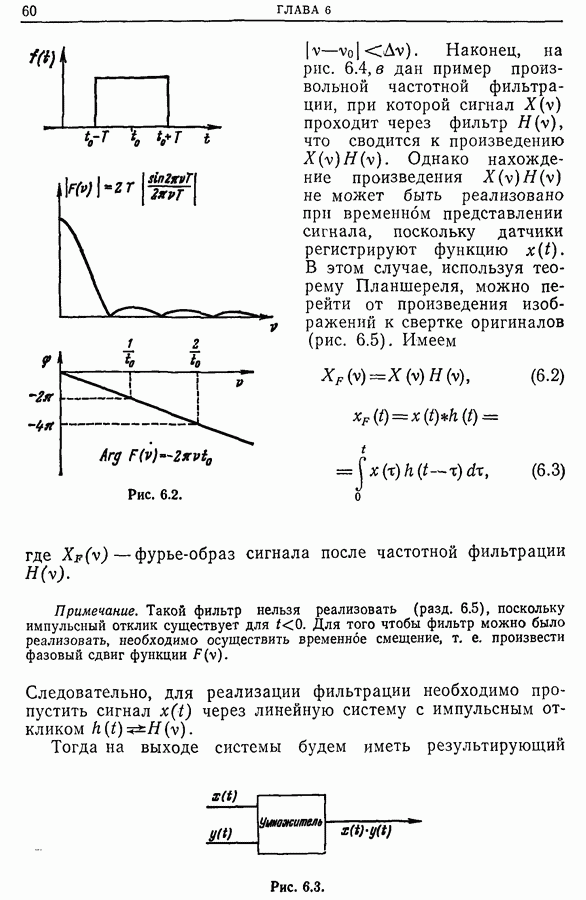
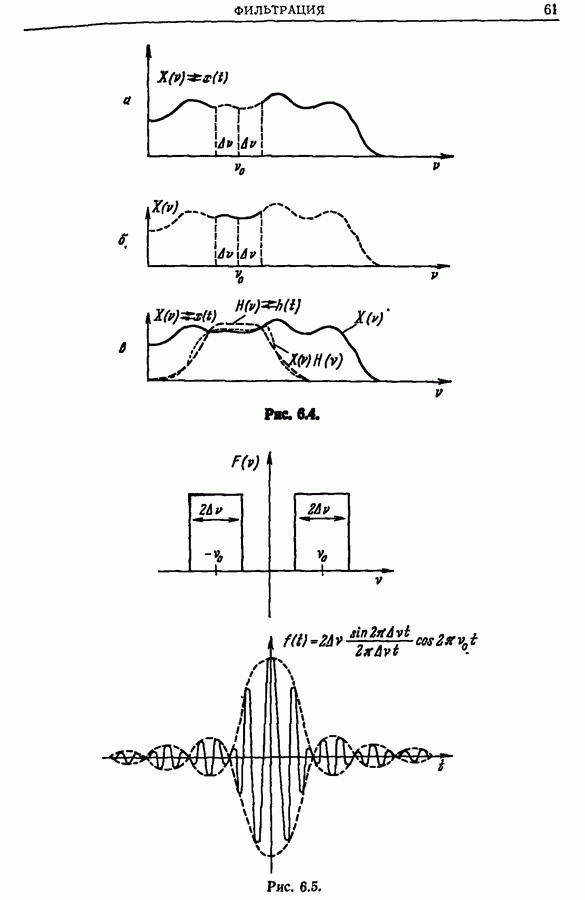
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
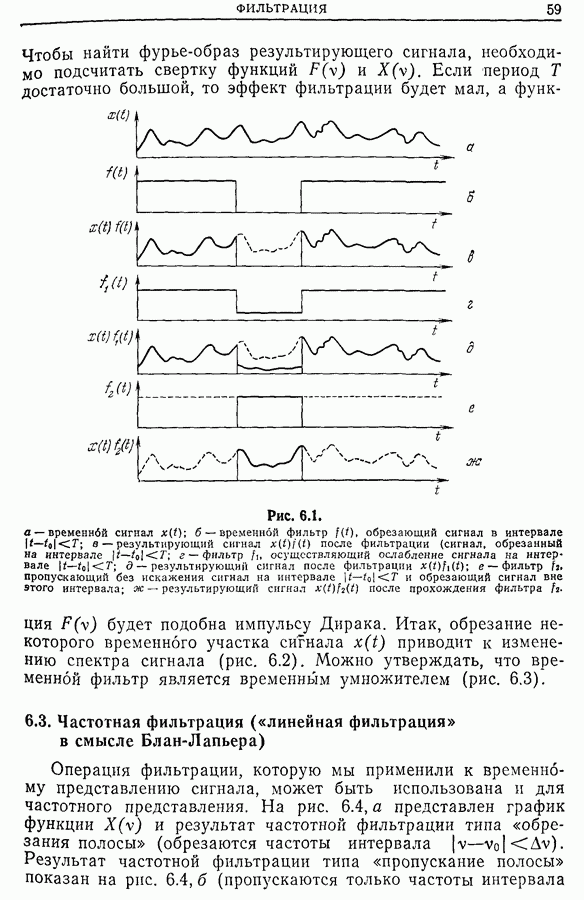
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
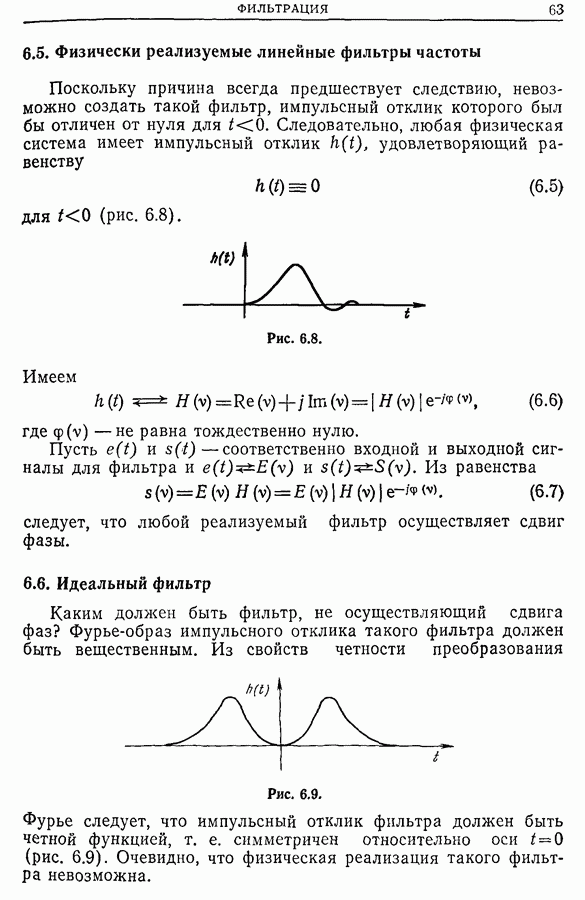
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
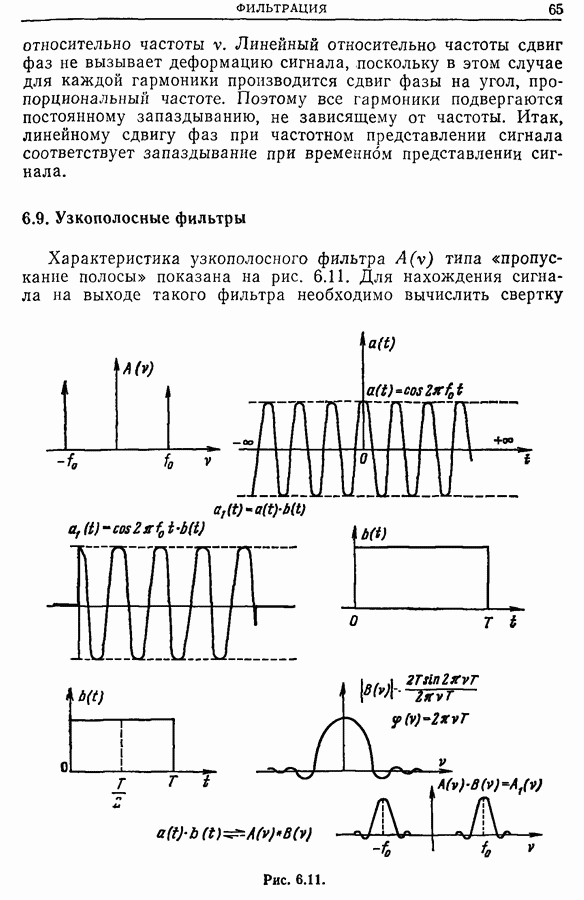
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
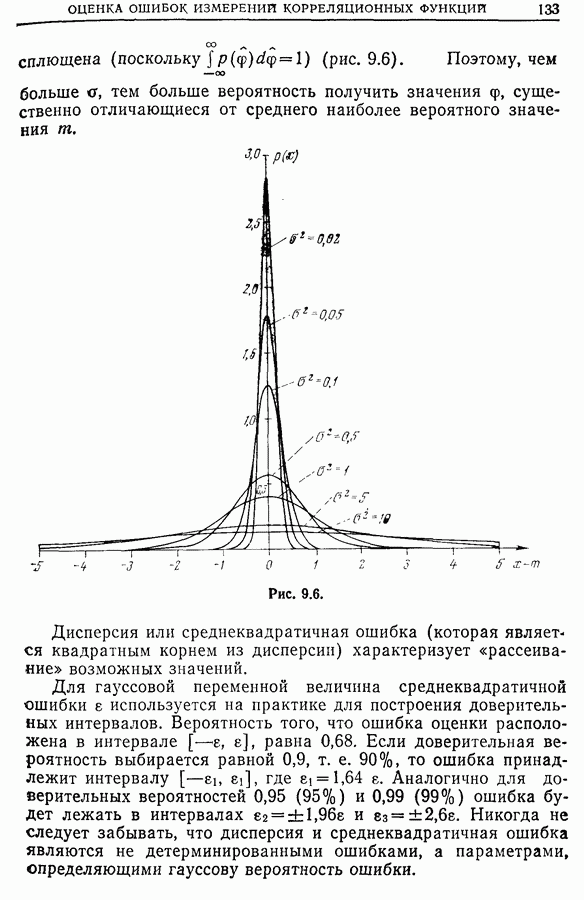
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
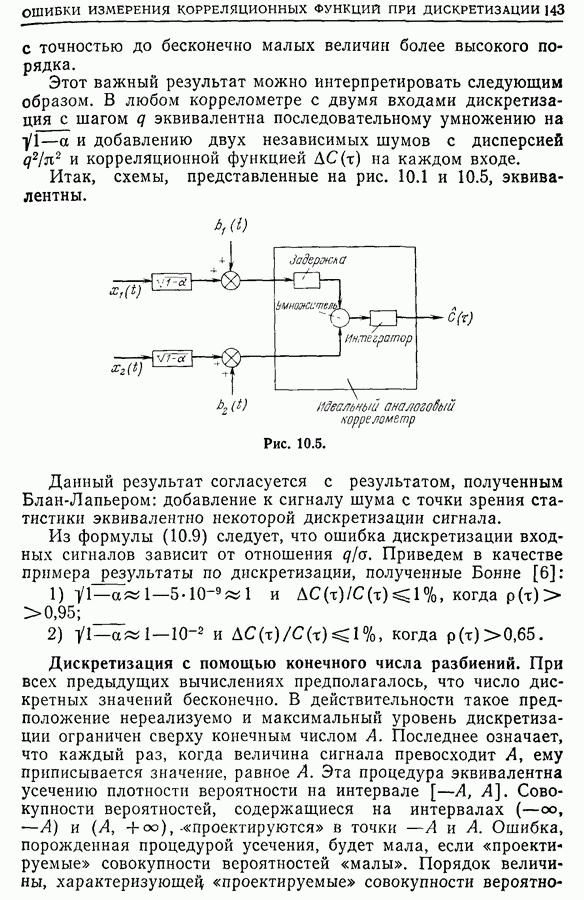
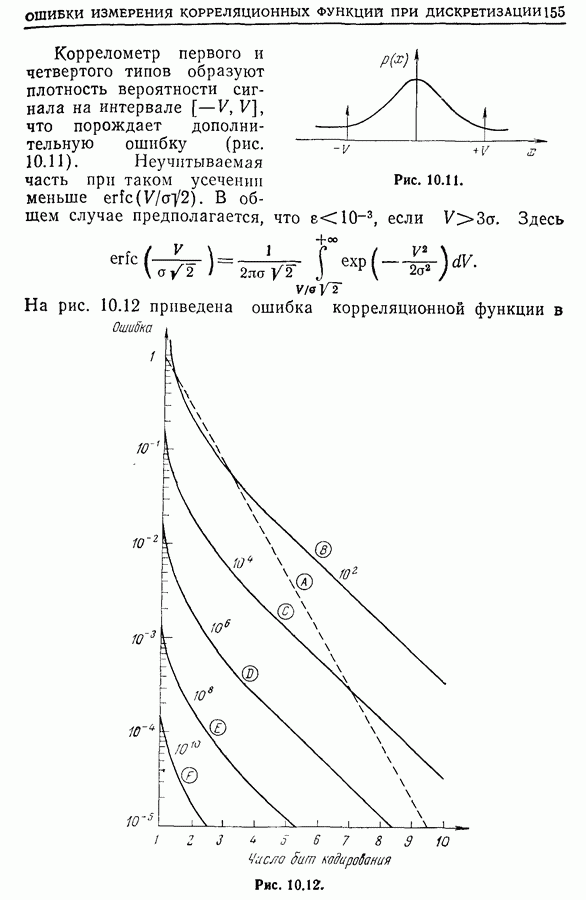
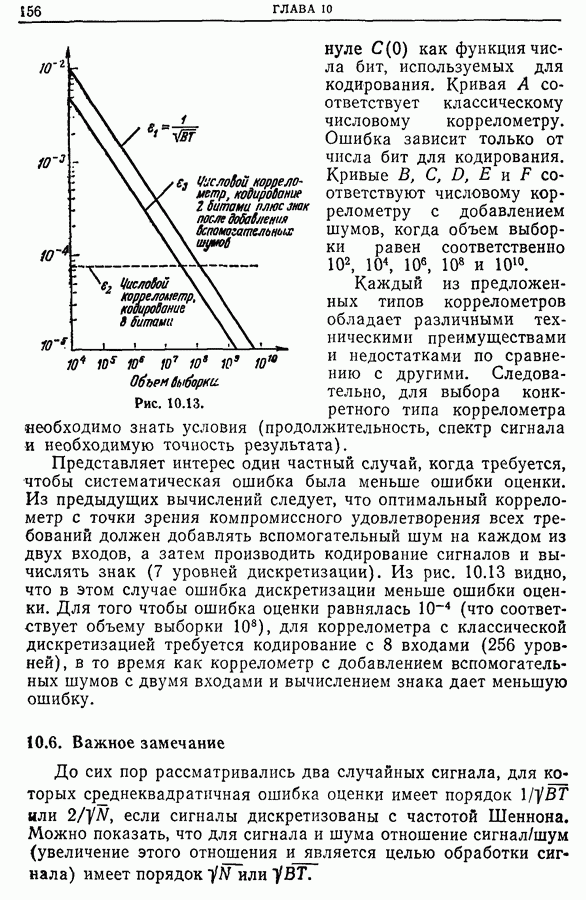
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
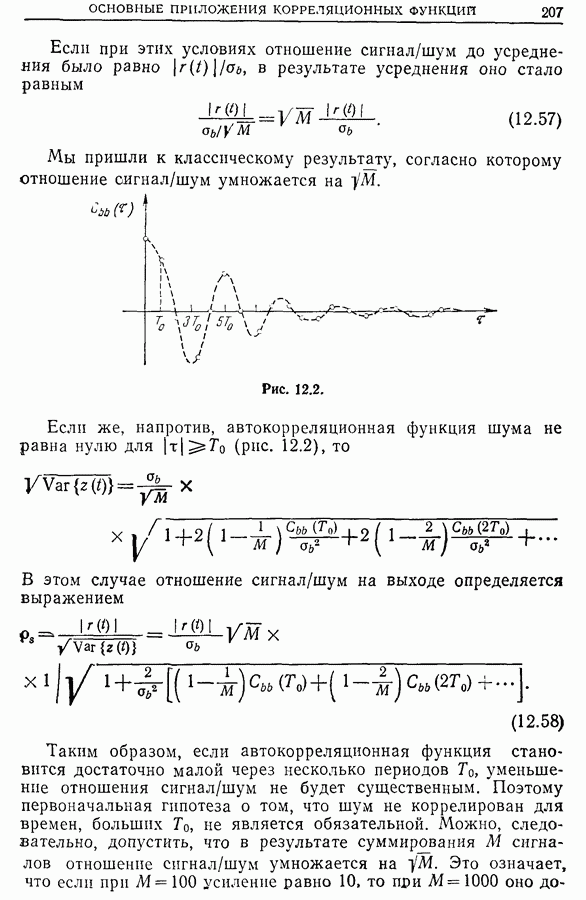
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
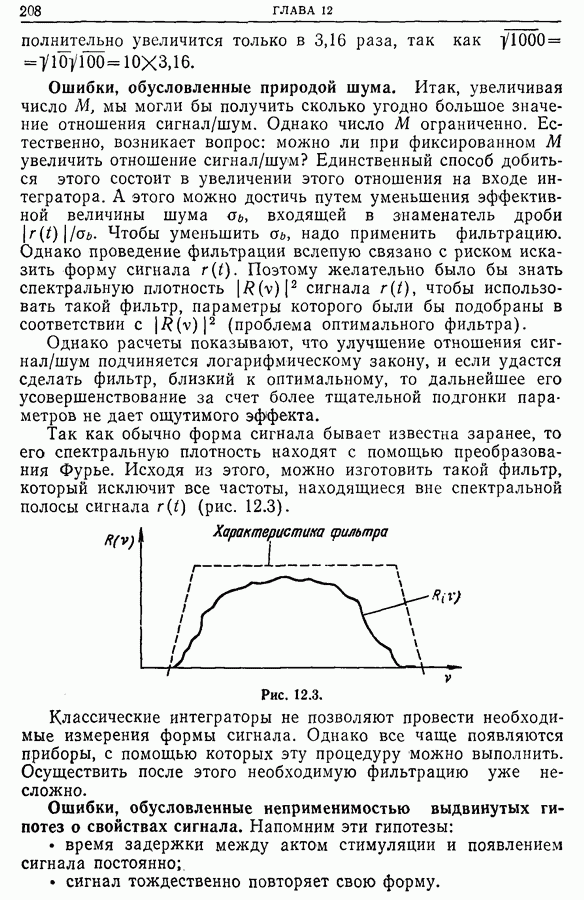
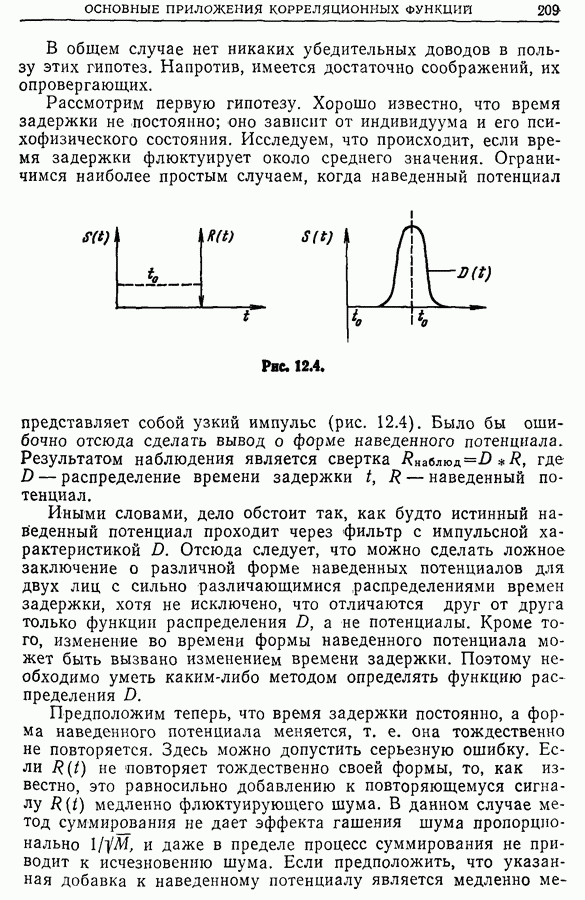
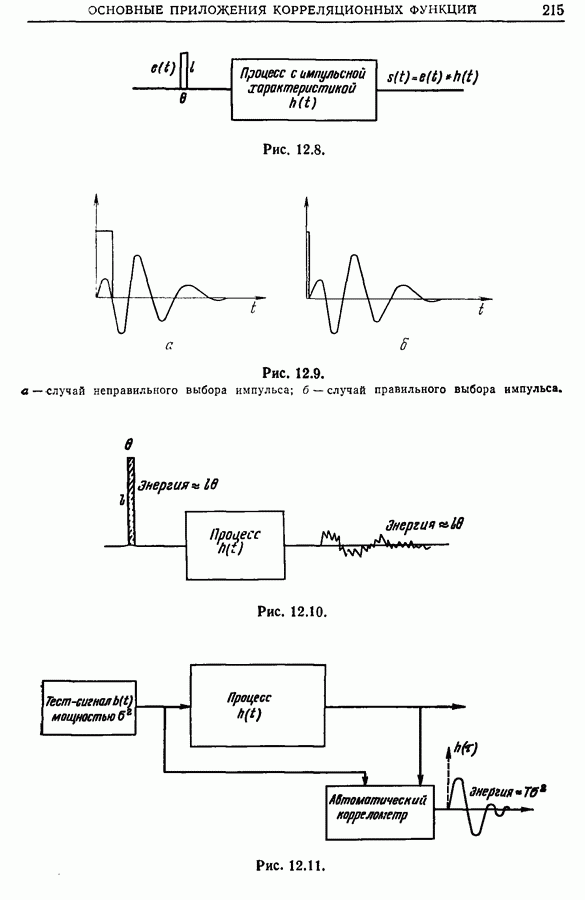
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
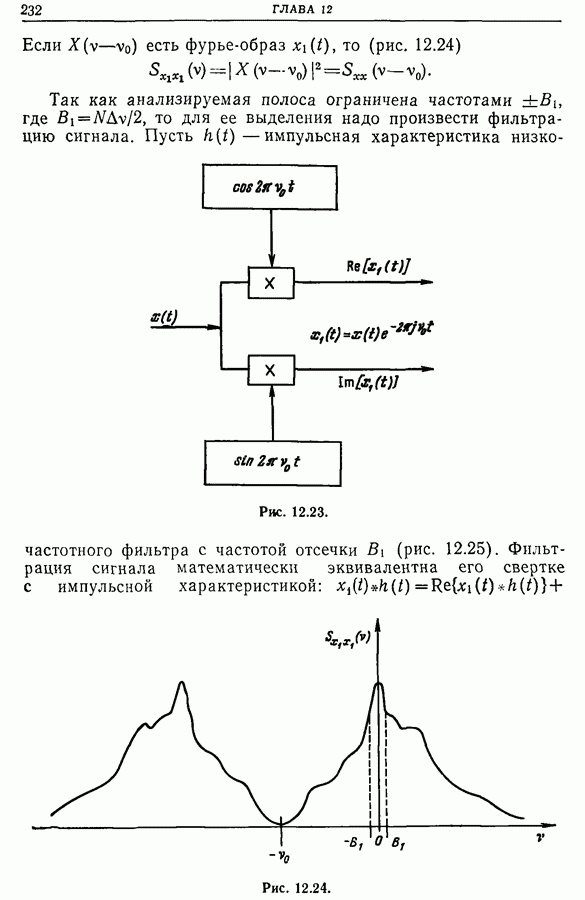
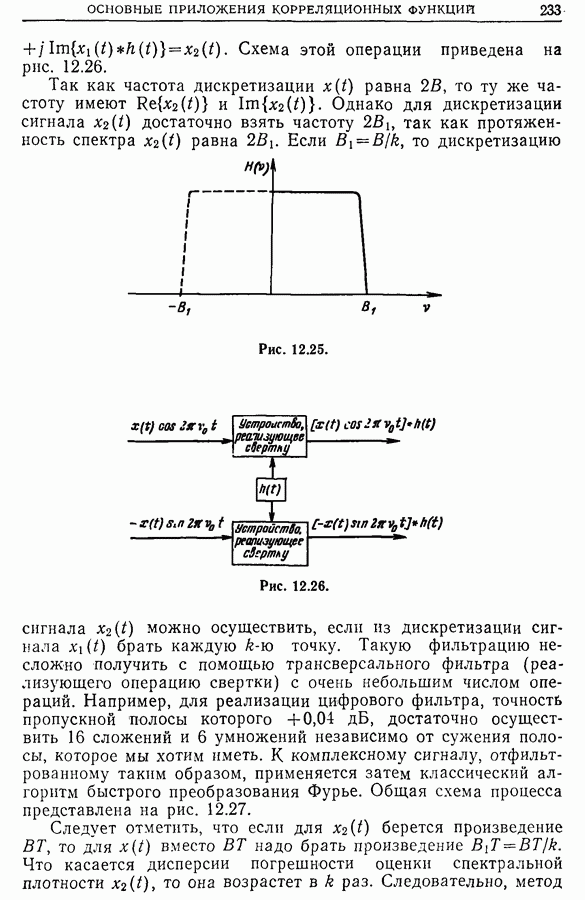
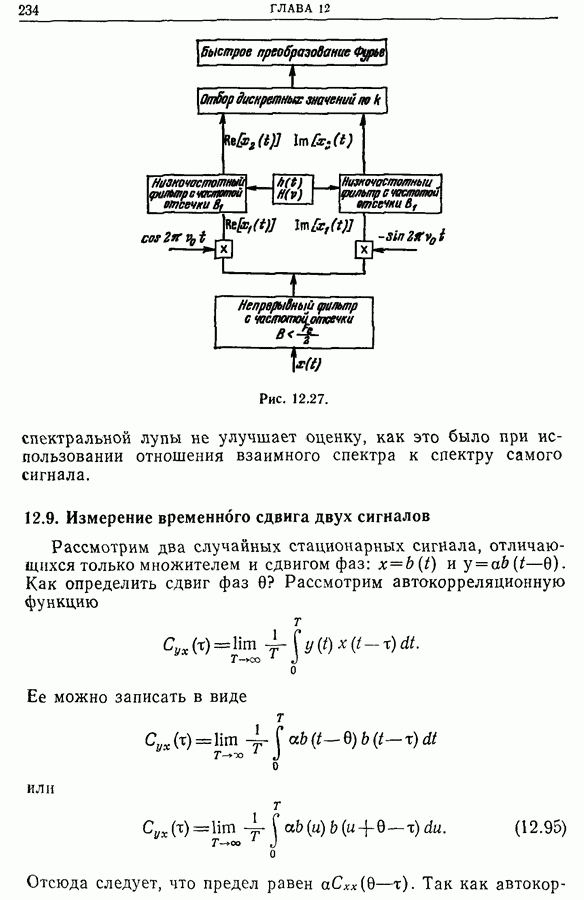
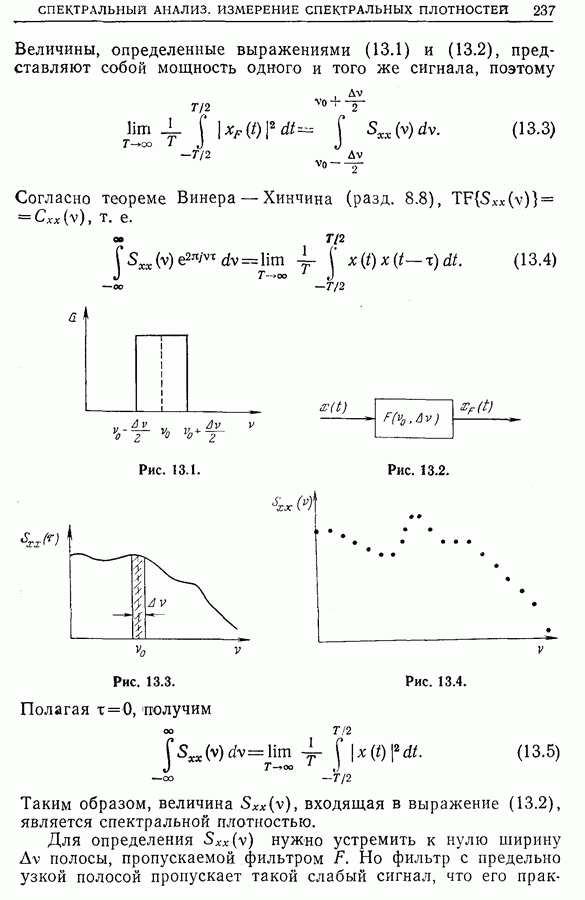
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
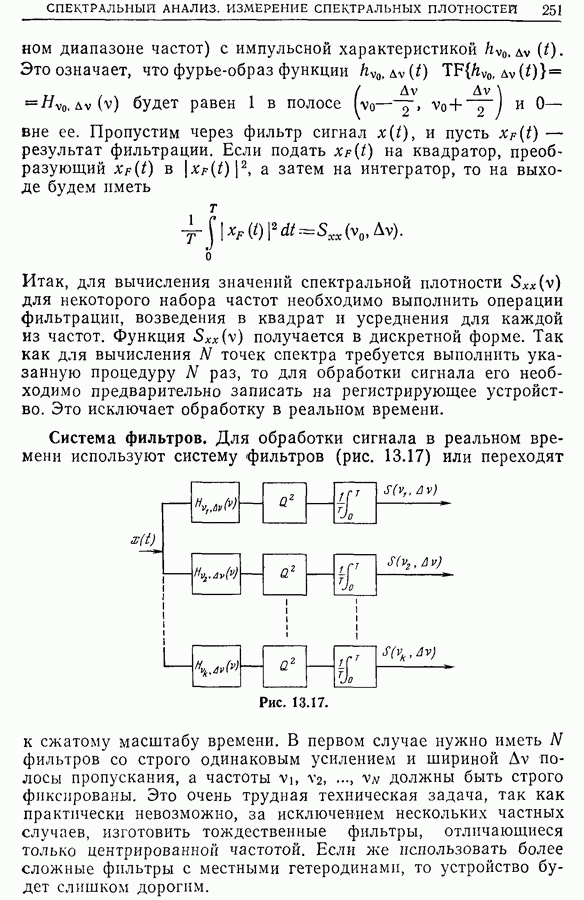
- 13.7. Измерение спектральной плотности методом фильтрации
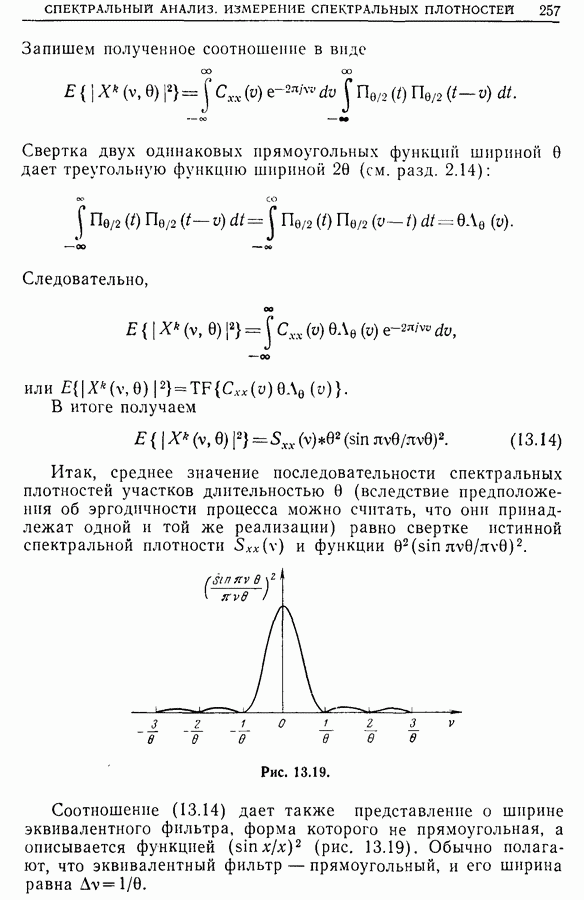
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
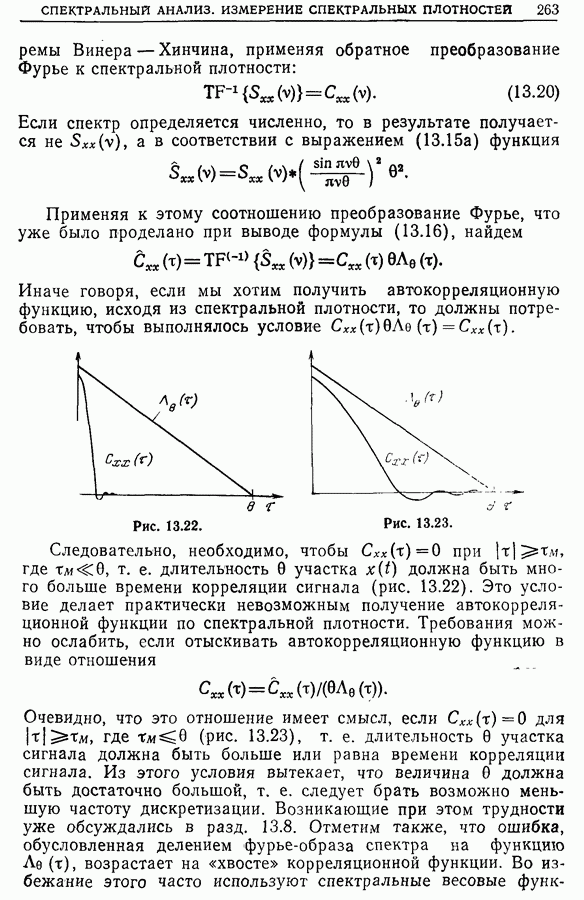
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
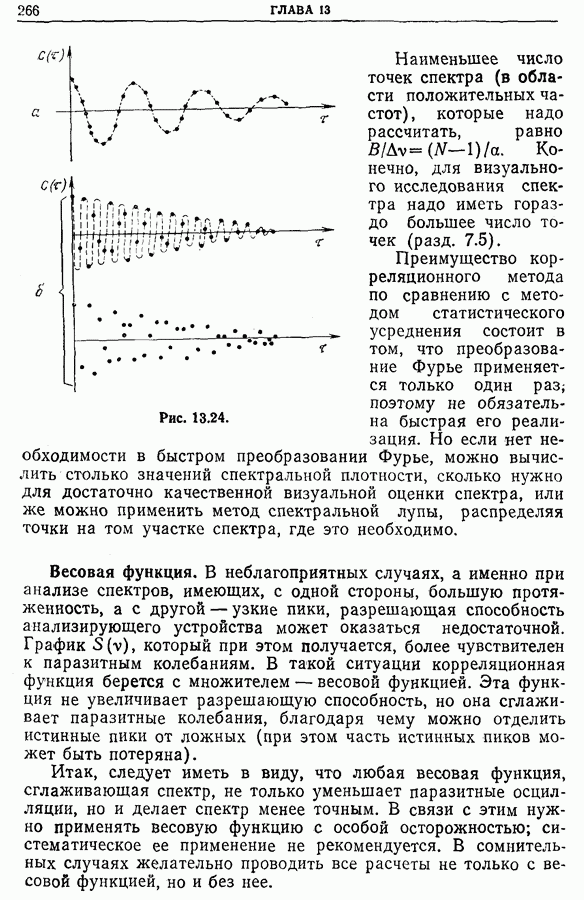
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
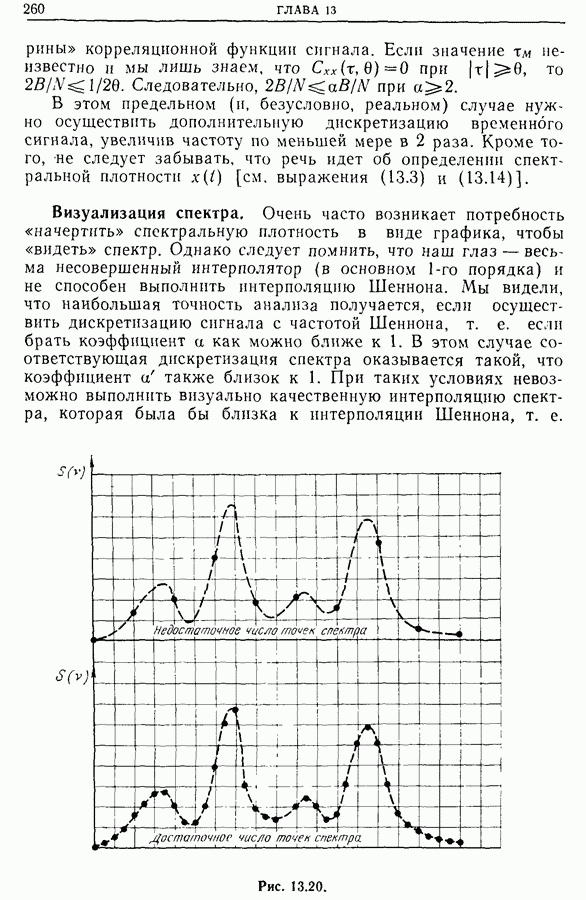
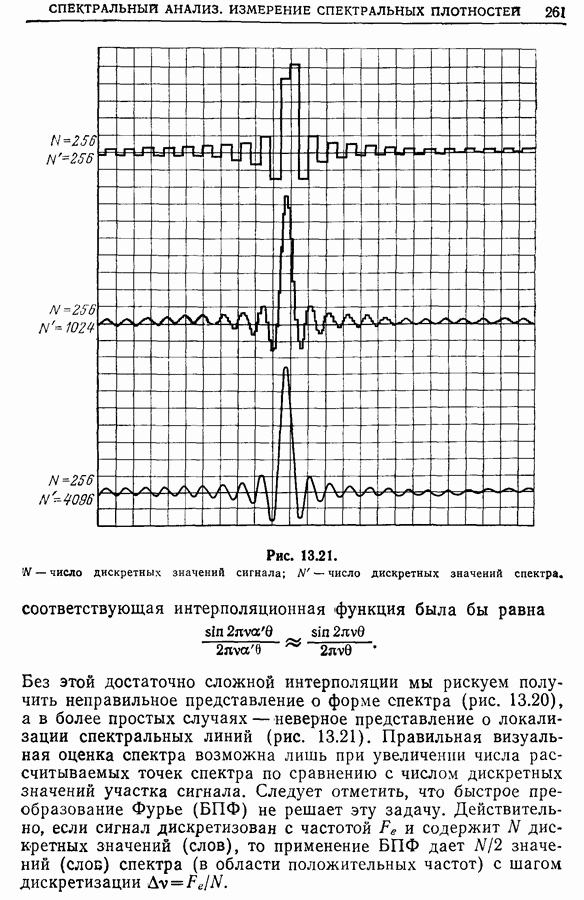
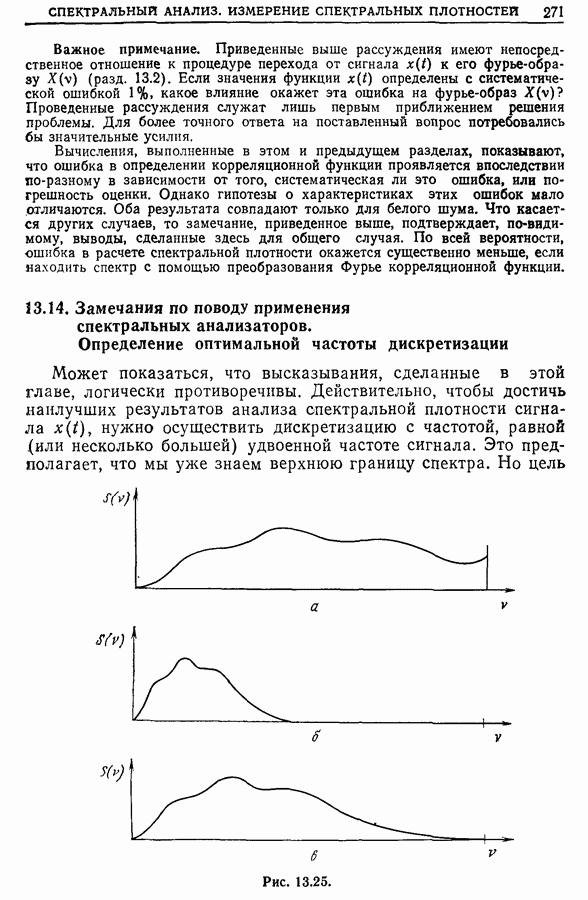
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
- 14.6. Основные характеристики временных и спектральных окон
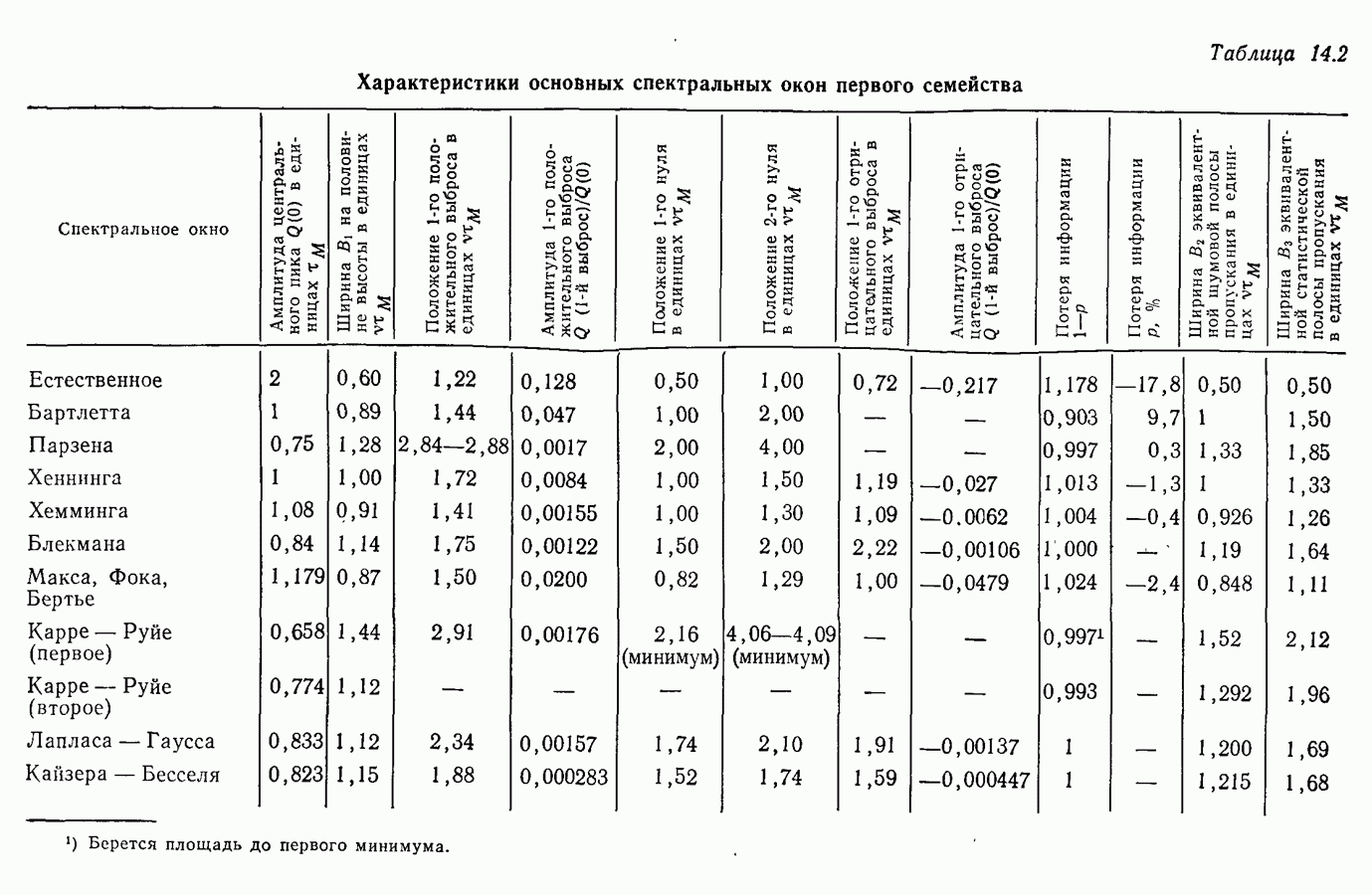
- 14.7. Первое семейство временных весовых окон
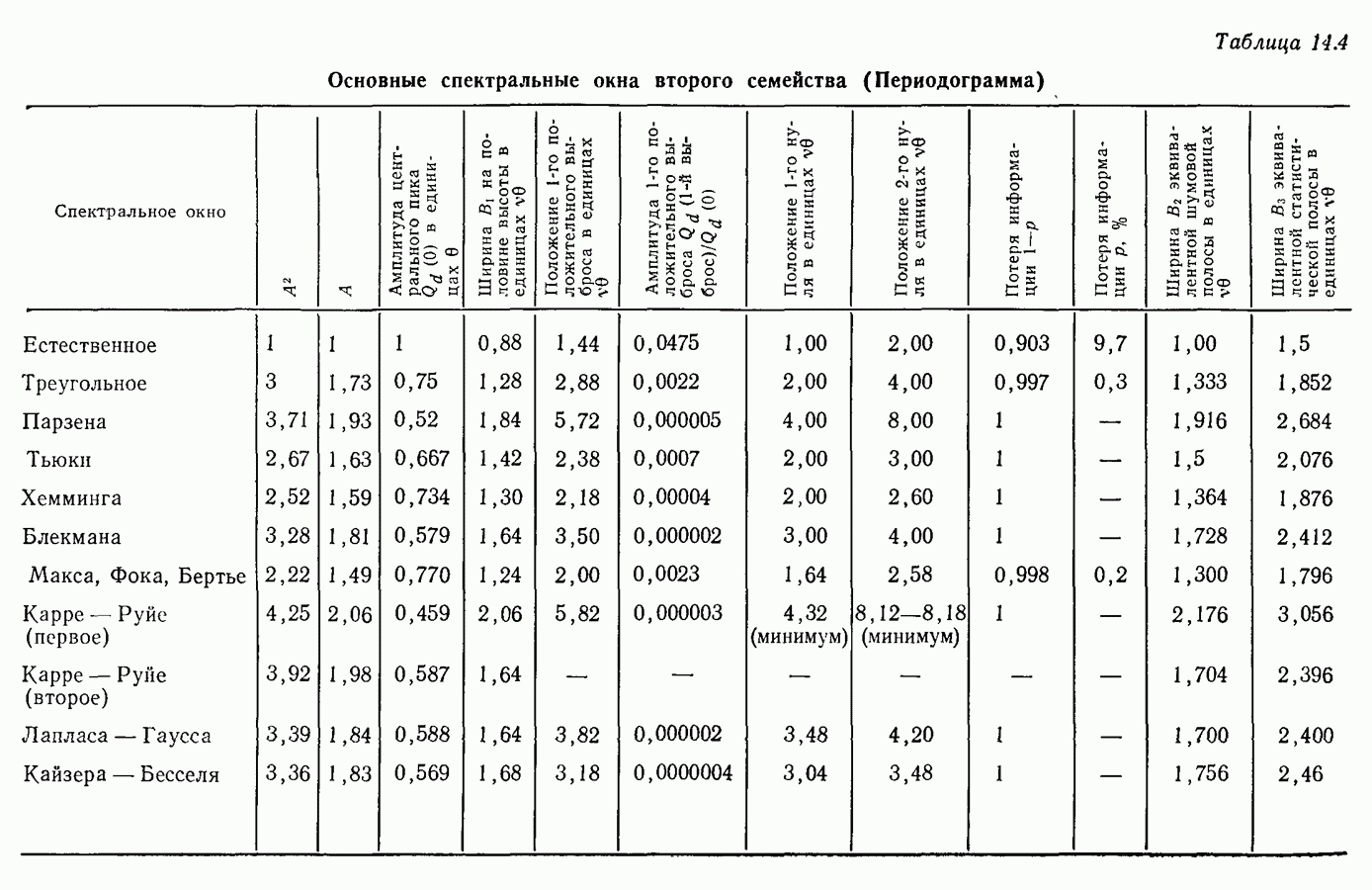
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции