| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
Линейная фильтрация.
В гл. 6 дано определение линейной фильтрации и соответствующей математической операции, которая называется сверткой. В случае линейного фильтра уравнение свертки связывает предшествующие по времени значения входного сигнала с его значением на выходе в данный момент посредством импульсной характеристики, которая полностью описывает линейную систему. Импульсная характеристика является откликом на мгновенный импульс единичной площади (фактически продолжительность импульса должна быть малой по сравнению с длительностью импульсной характеристики, т. е. переходной функции). Напомним, что преобразование Лапласа импульсной характеристики определяет передаточную функцию линейного фильтра. Напомним также, что свертке двух функций, зависящих от времени, соответствует обычное произведение в пространстве частот, и наоборот.
Формулы для средних значений.
Пусть  — импульсная характеристика фильтра, тогда
— импульсная характеристика фильтра, тогда

Следовательно,  . Таким образом, среднее значение y(t) равно среднему значению x(t), умноженному на алгебраическую площадь. Отсюда следует также, что линейный фильтр преобразует стационарный сигнал 1-го порядка таким образом, что свойство стационарности сигнала сохраняется. Кроме того, известно, что
. Таким образом, среднее значение y(t) равно среднему значению x(t), умноженному на алгебраическую площадь. Отсюда следует также, что линейный фильтр преобразует стационарный сигнал 1-го порядка таким образом, что свойство стационарности сигнала сохраняется. Кроме того, известно, что

Если  т. е. если фильтр отсекает постоянную
т. е. если фильтр отсекает постоянную
составляющую, то среднее значение  равно нулю при любой функции
равно нулю при любой функции  . Подобный фильтр оказывается центрирующим (разд. 8.11) и высокочастотным.
. Подобный фильтр оказывается центрирующим (разд. 8.11) и высокочастотным.
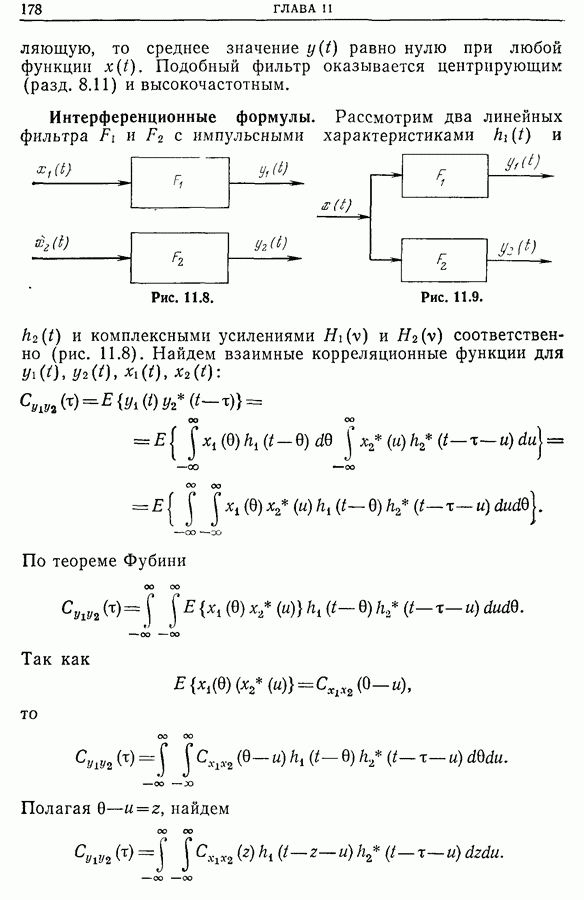
Интерференционные формулы.
Рассмотрим два линейных фильтра  с импульсными характеристиками
с импульсными характеристиками  и комплексными усилениями
и комплексными усилениями  соответственно (рис. 11.8).
соответственно (рис. 11.8).

Рис. 11.8.

Рис. 11.9.
Найдем взаимные корреляционные функции для 

По теореме Фубини

Так как

то

Полагая  , найдем
, найдем

Полученное выражение можно записать в виде

Отметим, что

Тогда

В результате находим

Аналогично выводятся формулы

Переходя к фурье-образам, найдем

Аналогично вычисляются функции вида

В итоге получаем следующие выражения:

Два параллельно соединенных фильтра (рис. 11.9).
Если в формулах (11.43) и (11.47) положить  то
то
получим

Аналогично выводятся соотношения

Соотношения между входным и выходным сигналами в линейной системе (рис. 11.10).
Если в соотношении (11.55) положить  , то оно примет вид
, то оно примет вид  или
или

а соотношение (11.59) запишется в виде

Переходя в пространство частот, получим

Соотношения (11.61) и (11.62) интерпретируются следующим образом. Автокорреляционная функция выходного сигнала представляет собой свертку автокорреляционной функции импульсной характеристики системы и автокорреляционной функции входного сигнала. Интеграл свертки, связывающий вход и выход системы, устанавливает такую же связь между автокорреляционной функцией входного сигнала и взаимной корреляционной функцией входного и выходного сигналов.
Напомним, что если фильтр стабильный, т. е. его передаточная функция  не имеет полюсов на мнимой оси и правее ее, то
не имеет полюсов на мнимой оси и правее ее, то 
Соотношения (11.61) — (11.64) упрощаются, если автокорреляционная функция входного сигнала является  -функцией Дирака, т. е. если
-функцией Дирака, т. е. если  При этом условии соотношения
При этом условии соотношения

Рис. 11.10.
(11.61) и (11.63) принимают вид

Иными словами, если автокорреляционная функция входного сигнала может быть представлена  -функцией, то фурье-образ автокорреляционной функции выходного сигнала равен квадрату модуля передаточной функции:
-функцией, то фурье-образ автокорреляционной функции выходного сигнала равен квадрату модуля передаточной функции:

Безусловно, методом, использующим автокорреляционную функцию входного сигнала, можно найти только модуль передаточной функции (этот метод не дает никакой информации о ее фазе). Фазу можно определить по кривой усиления, применяя метод Боде — Байяра. Этот способ не очень удобен, так как он требует много вычислений. Однако в ряде случаев, например для систем, в которых сдвиг фазы мал, вполне достаточно определить модуль передаточной функции (т. е. кривую усиления), так как знание модуля дает важную информацию о системе.
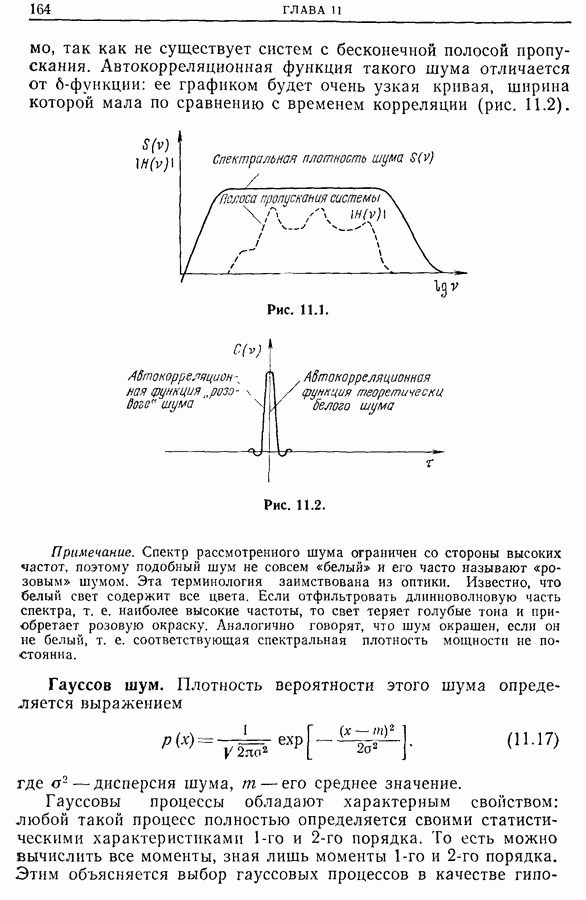
Фильтрация белого шума.
Из сказанного выше следует, что при прохождении белого шума через линейную систему с малым сдвигом фаз с передаточной функцией  автокорреляционная функция выходного сигнала, фурье-образ которой равен
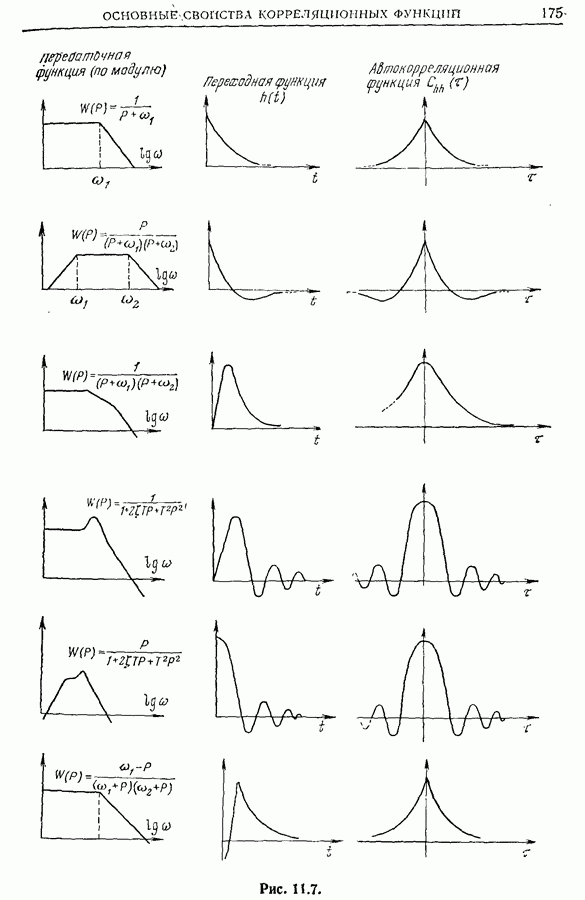
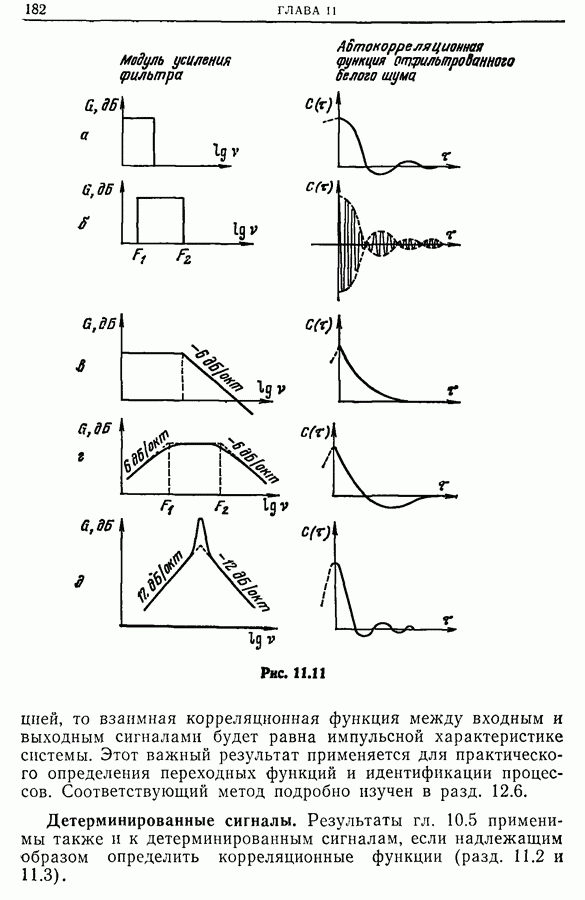
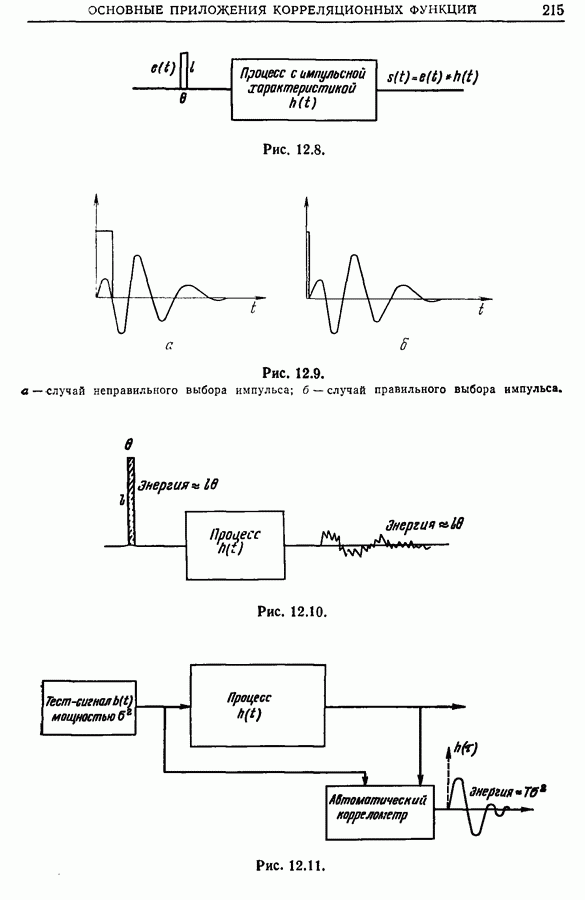
автокорреляционная функция выходного сигнала, фурье-образ которой равен  дает достаточную информацию о четырехполюснике. В связи с этим полезно иметь набор кривых усиления, отвечающих автокорреляционным функциям белого шума, пропущенного через стандартные фильтры. Несколько характерных кривых приведено на рис. 11.11. Часто оказывается удобным рассматривать стационарный шум
дает достаточную информацию о четырехполюснике. В связи с этим полезно иметь набор кривых усиления, отвечающих автокорреляционным функциям белого шума, пропущенного через стандартные фильтры. Несколько характерных кривых приведено на рис. 11.11. Часто оказывается удобным рассматривать стационарный шум  порядка (по предположению центрированный), заданный с помощью автокорреляционной функции
порядка (по предположению центрированный), заданный с помощью автокорреляционной функции  и спектральной плотности
и спектральной плотности  как белый шум, пропущенный через фильтр, модуль комплексного усиления которого удовлетворяет условию
как белый шум, пропущенный через фильтр, модуль комплексного усиления которого удовлетворяет условию  Автокорреляционная функция этого шума равна
Автокорреляционная функция этого шума равна 
Взаимная корреляция между входным и выходным сигналами. Идентификация процессов.
Если  , то соотношения (11.62) и (11.64) преобразуются к виду
, то соотношения (11.62) и (11.64) преобразуются к виду

Итак, если на вход линейной системы подать сигнал, автокорреляционную функцию которого можно представить  -функцией,
-функцией,
Рис. 11.11 (см. скан)
то взаимная корреляционная функция между входным и выходным сигналами будет равна импульсной характеристике системы. Этот важный результат применяется для практического определения переходных функций и идентификации процессов. Соответствующий метод подробно изучен в разд. 12.6.
Детерминированные сигналы.
Результаты гл. 10.5 применимы также и к детерминированным сигналам, если надлежащим образом определить корреляционные функции (разд. 11.2 и 11.3).
Нелинейные системы.
Методы, описанные выше, применимы только к линейным системам. В настоящее время ведутся работы по исследованию нелинейных систем. Однако еще слишком рано делать выводы о практическом значении полученных результатов.
Единственным методом изучения нелинейных систем пока является метод линеаризации в окрестности рабочей точки. При этом исследуется импульсная характеристика системы в малых окрестностях сначала одной рабочей точки, затем другой. Это дает возможность определить элемент характеристической кривой вместе с ее касательной в окрестности рабочей точки. В данном случае особенно полезен корреляционный метод, так как он позволяет возбуждать систему сигналом очень малой амплитуды и наблюдать за ней в течение большого промежутка времени.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
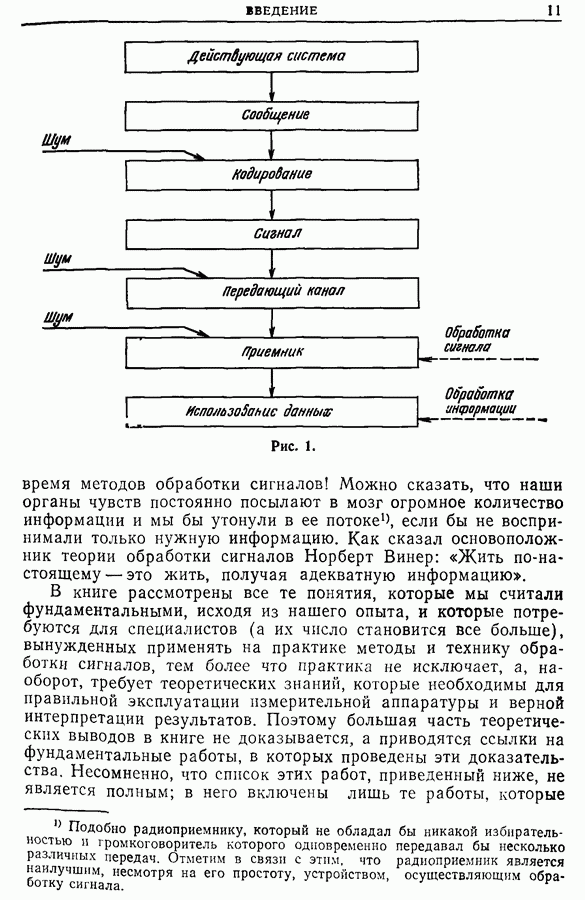
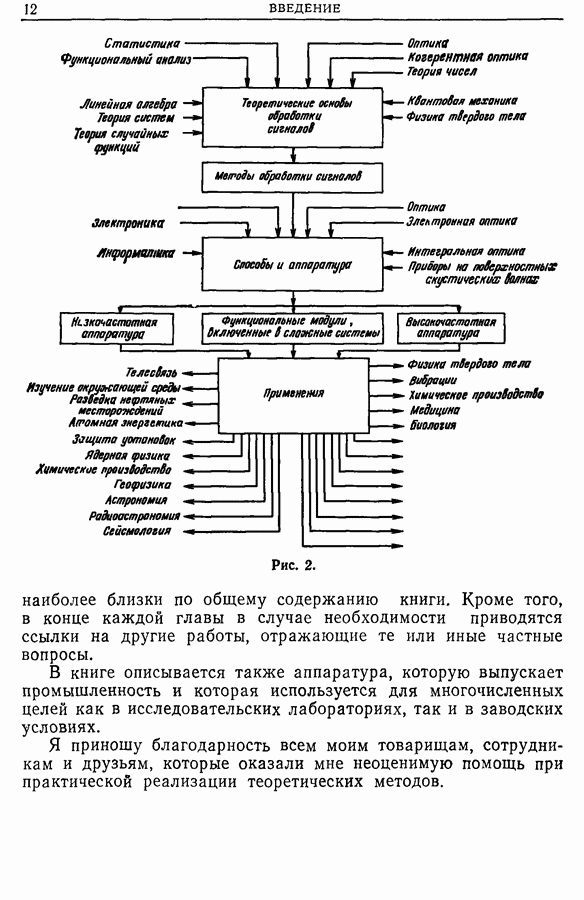
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
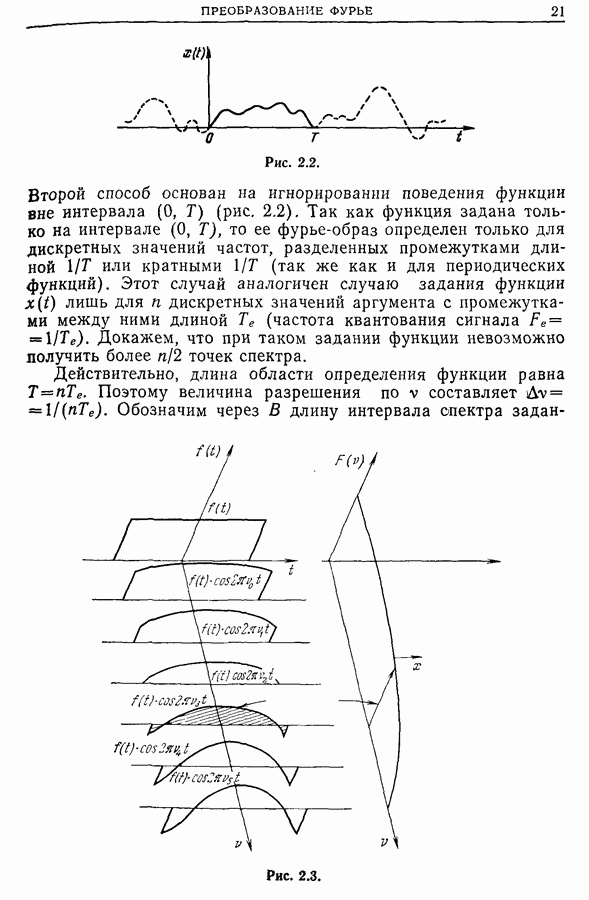
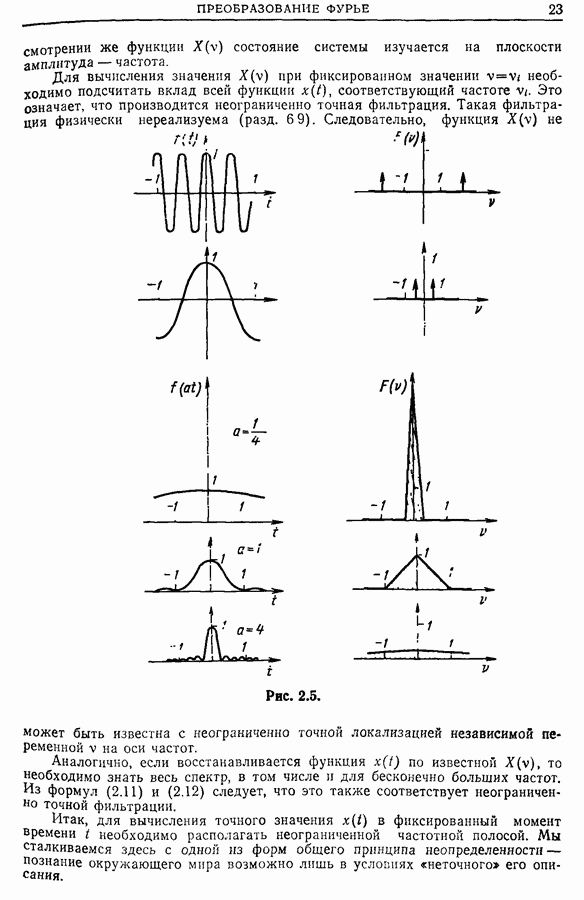
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
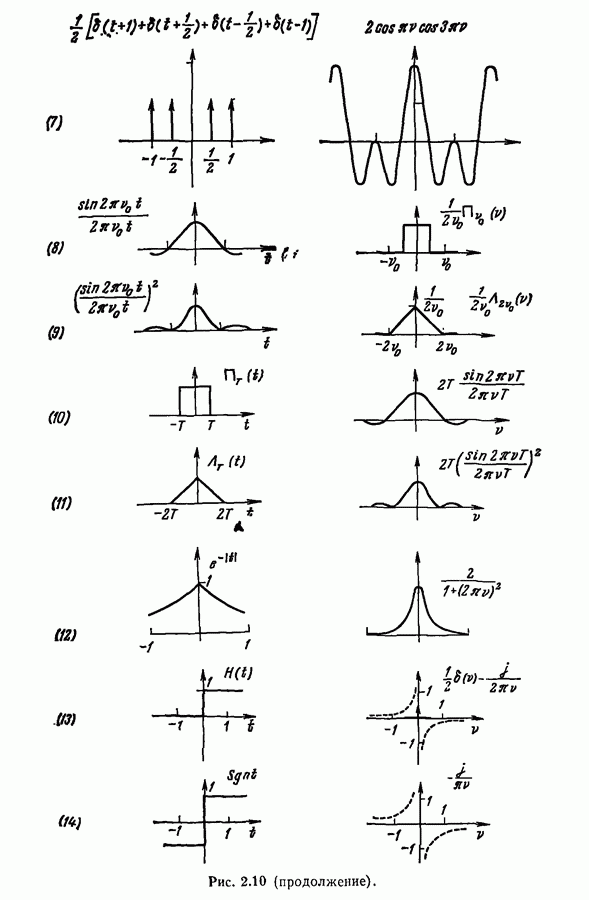
- 2.7. Несколько функций и их фурье-образы
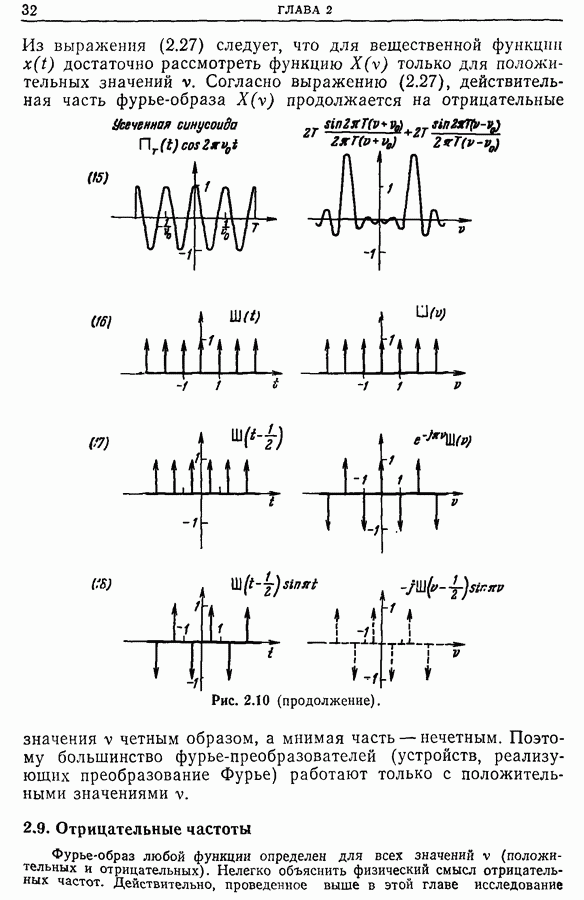
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
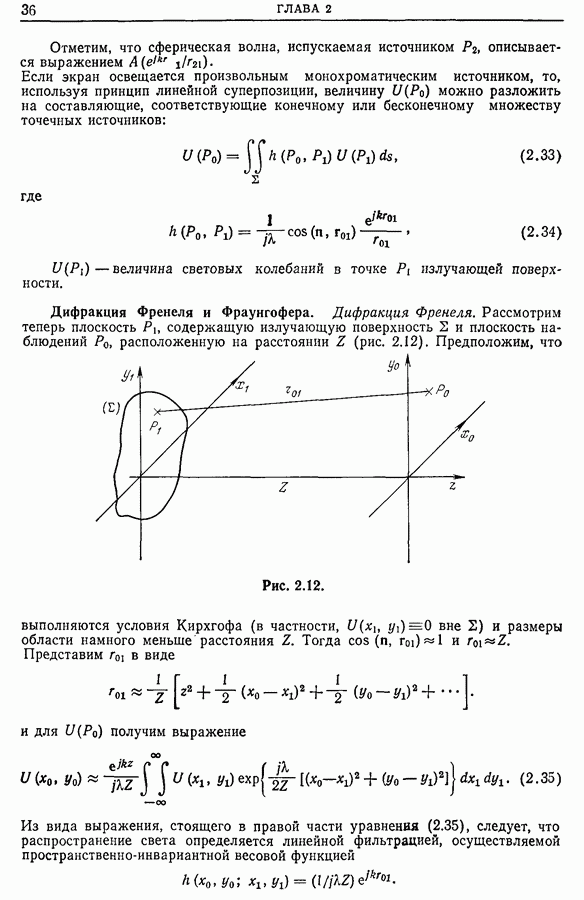
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
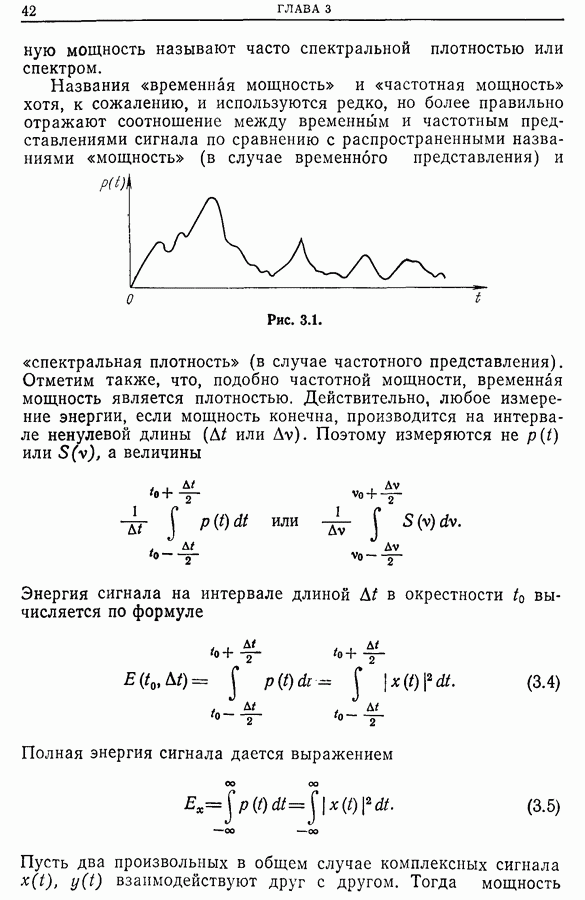
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
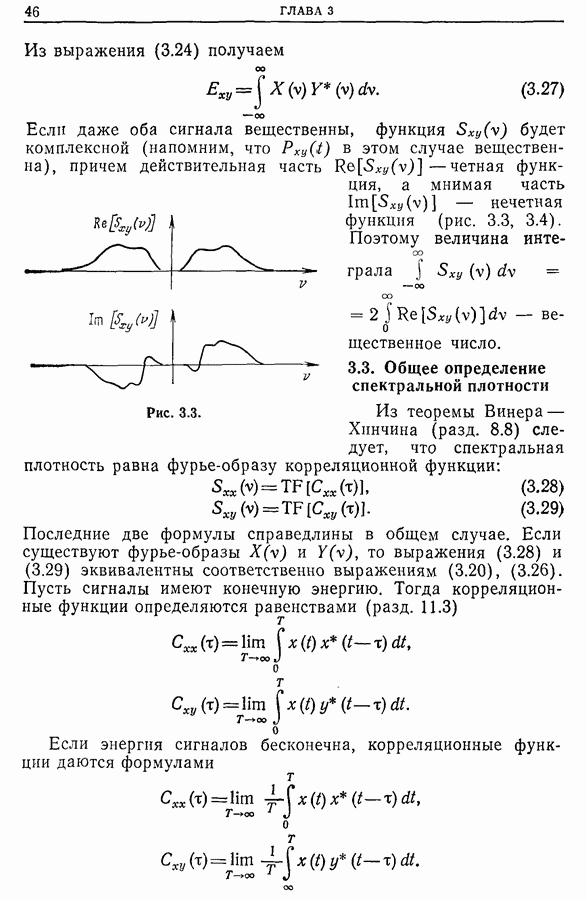
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
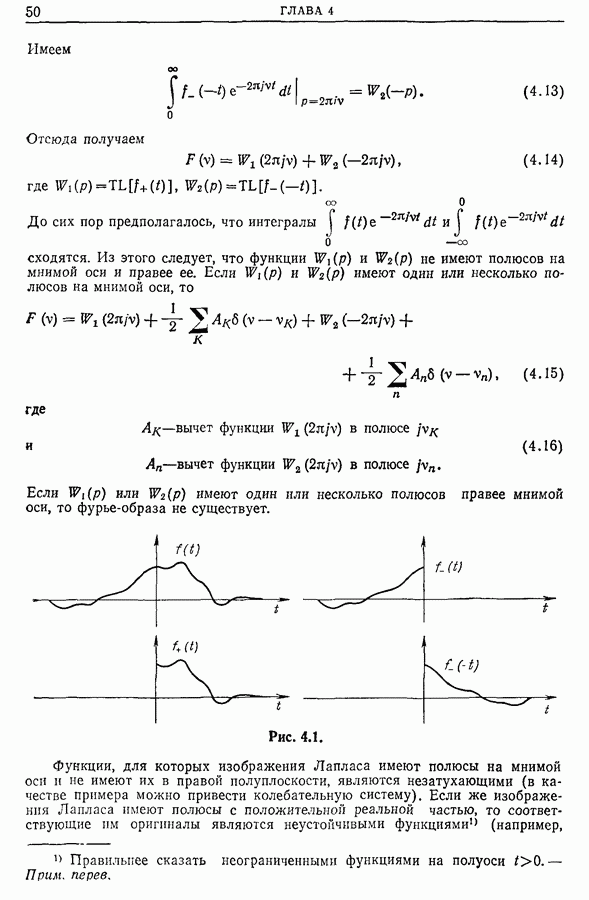
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
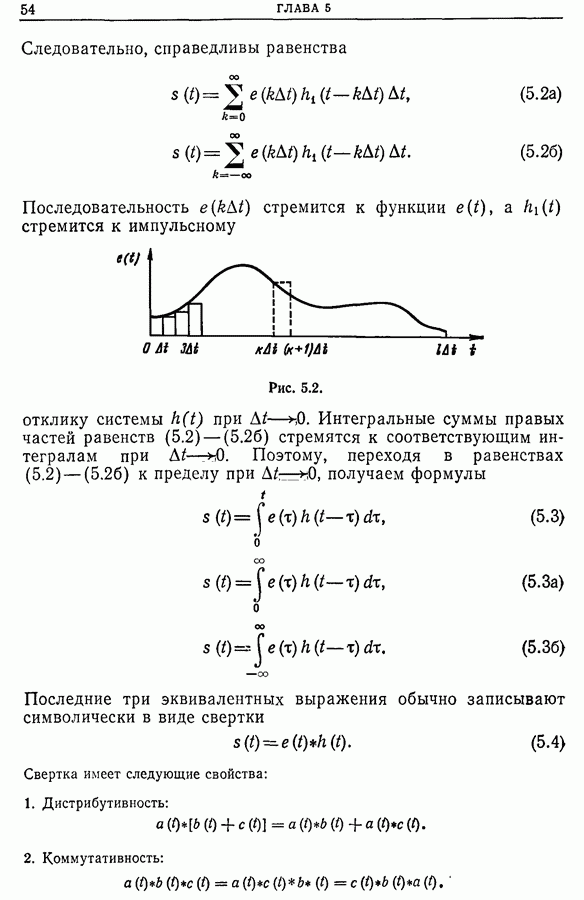
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
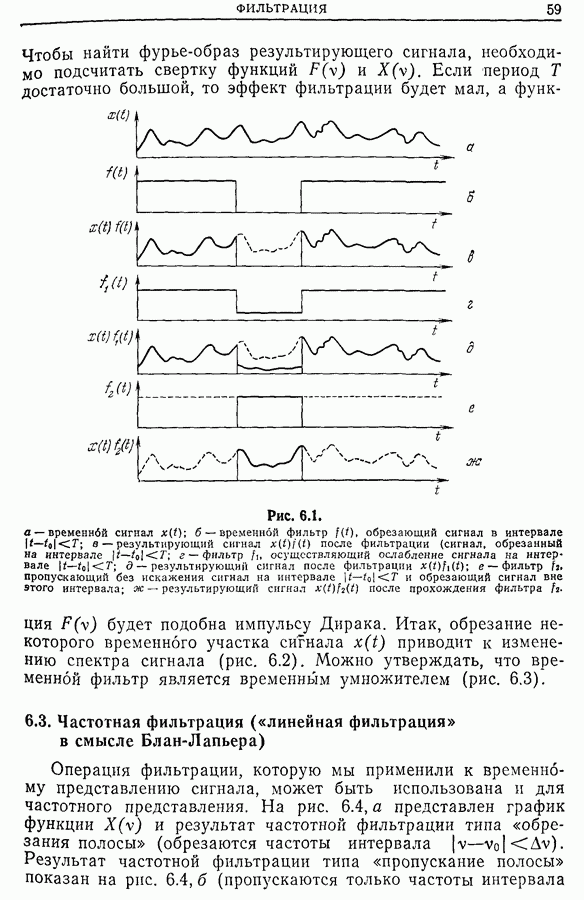
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
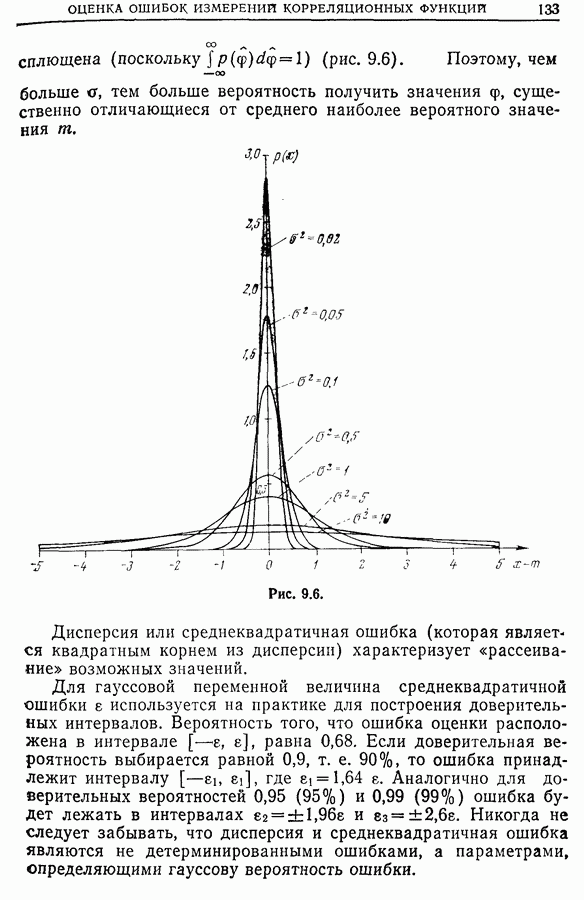
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
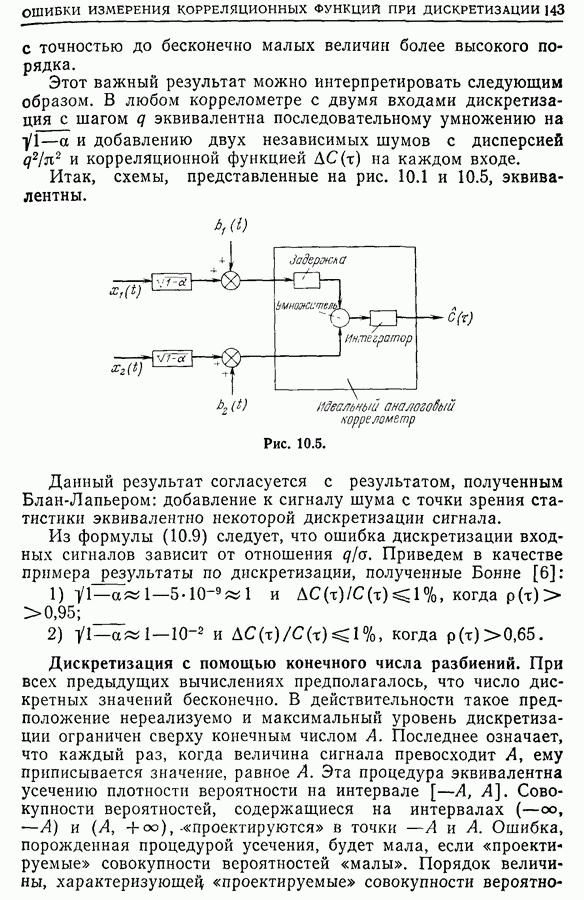
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
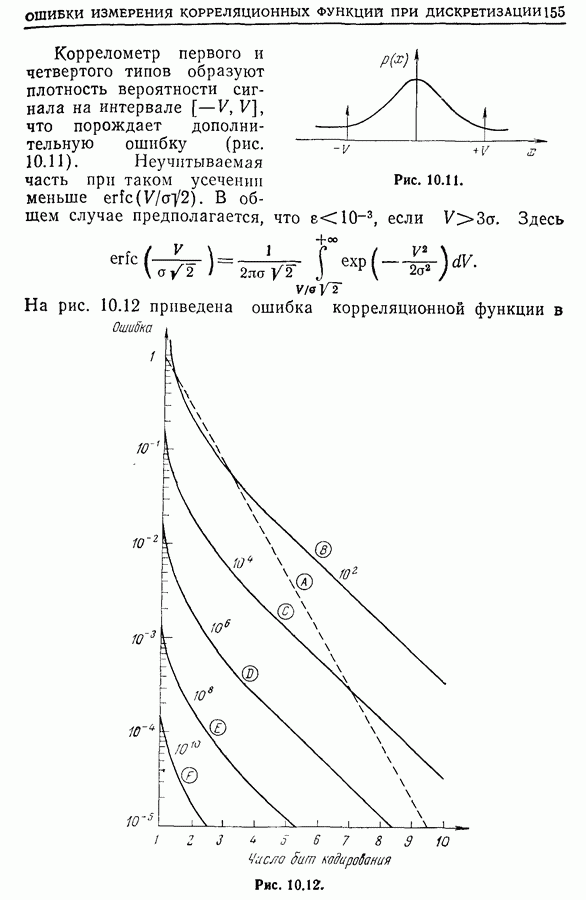
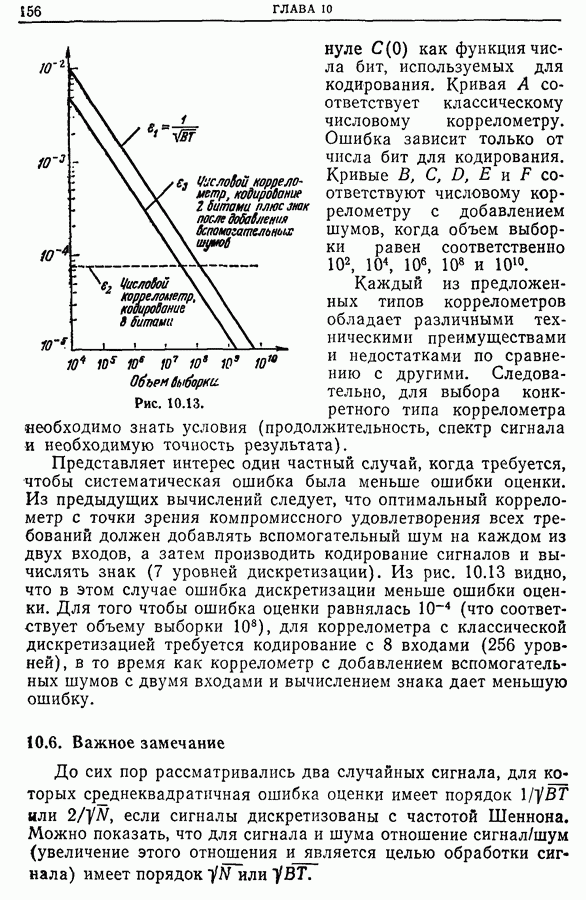
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
- 14.6. Основные характеристики временных и спектральных окон
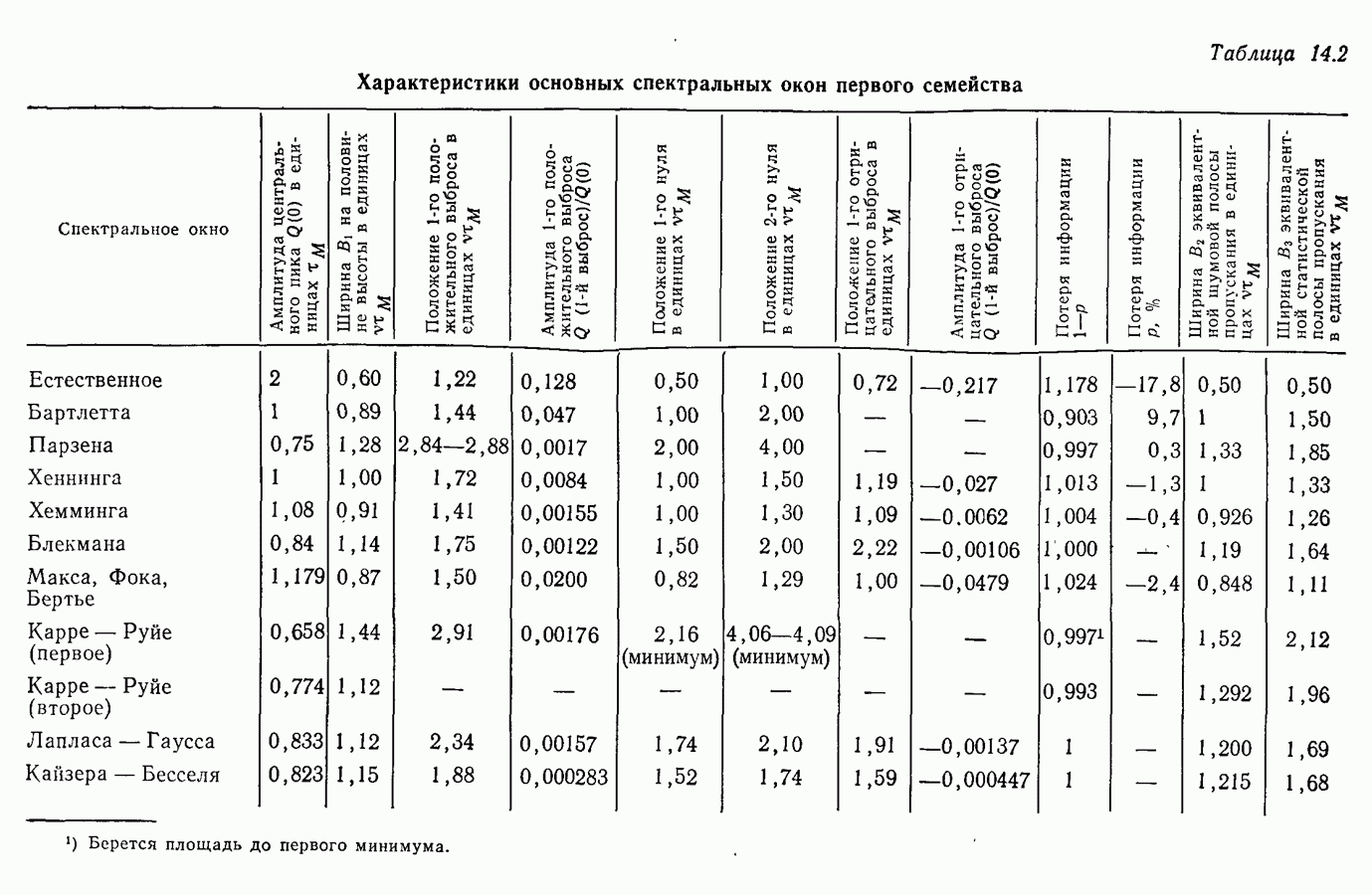
- 14.7. Первое семейство временных весовых окон
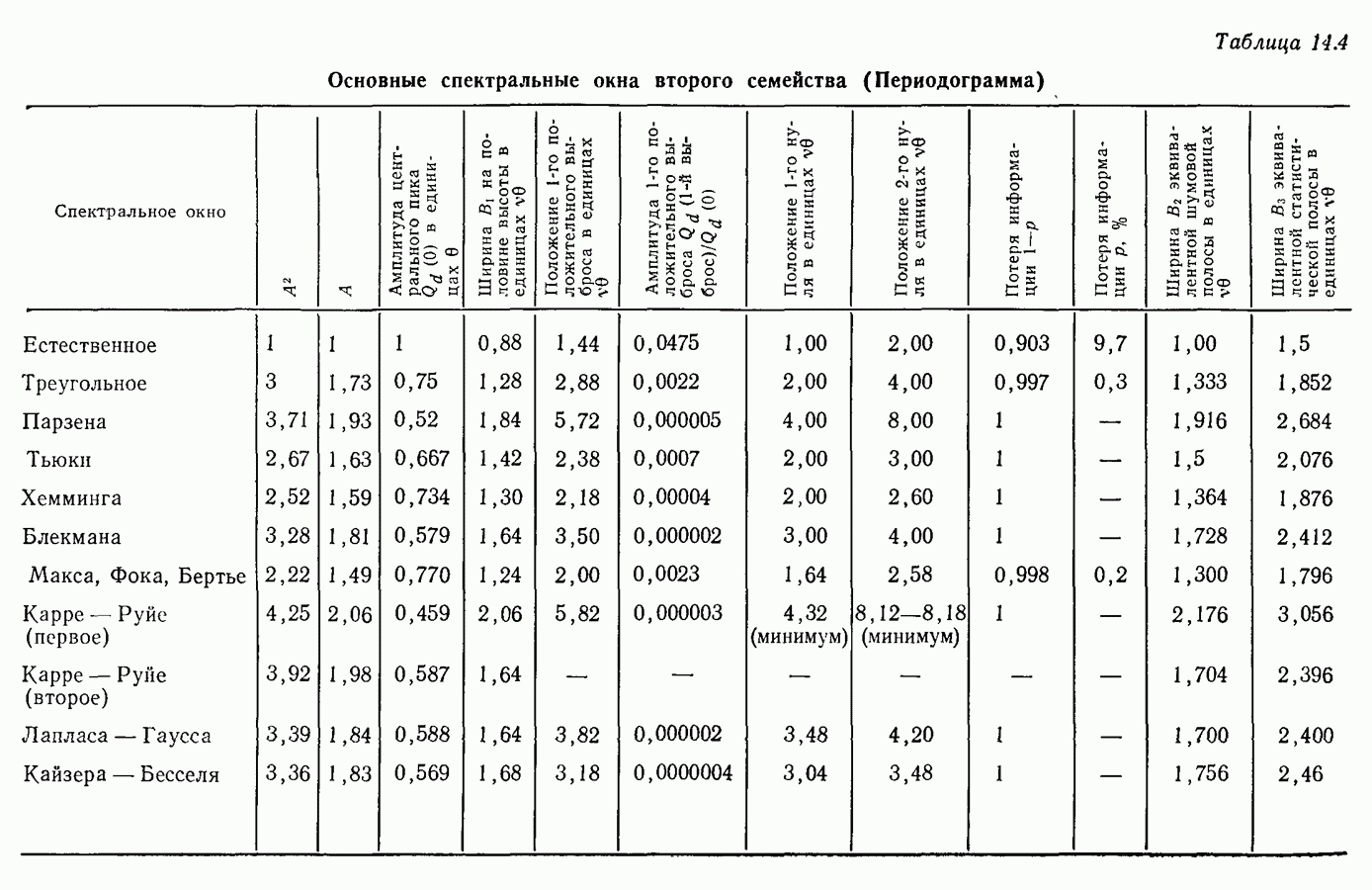
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции