| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
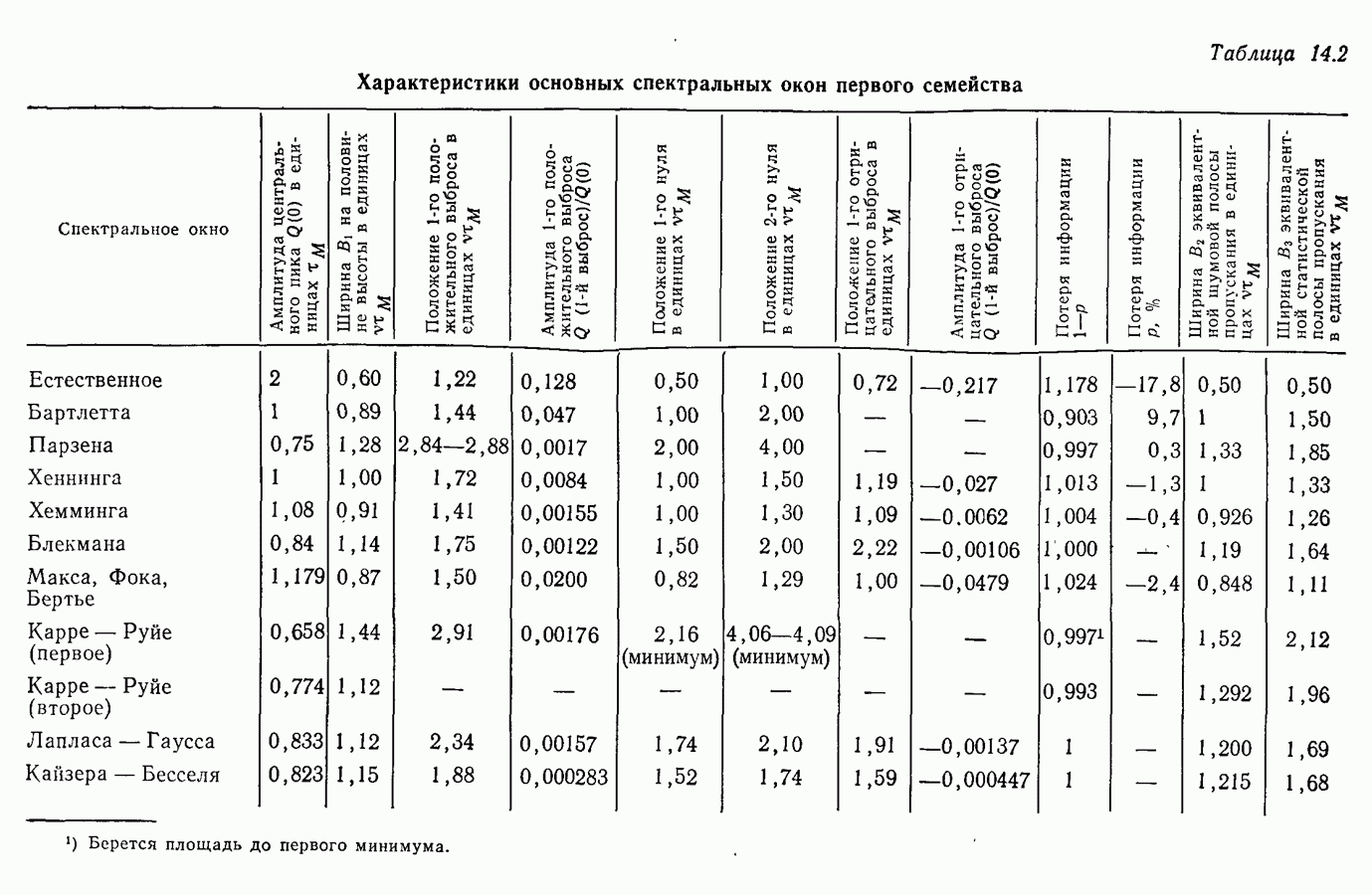
14.6. Основные характеристики временных и спектральных окон
Из изложенного выше следует, что три основных метода получения оценки  в которых используются естественные или временные весовые окна, приводят в пространстве частот к свертке функции
в которых используются естественные или временные весовые окна, приводят в пространстве частот к свертке функции  и спектрального окна
и спектрального окна  Чтобы иметь возможность сравнивать и выбирать весовые функции, необходимо ввести какие-либо простые параметры, характеризующие функции
Чтобы иметь возможность сравнивать и выбирать весовые функции, необходимо ввести какие-либо простые параметры, характеризующие функции  и особенно
и особенно  Прежде чем переходить к классическим определениям, напомним некоторые свойства окон, и в частности нормировку временных окон.
Прежде чем переходить к классическим определениям, напомним некоторые свойства окон, и в частности нормировку временных окон.
Нормировка временных весовых окон.
Пусть дана спектральная плотность, значения которой не зависят от частоты:  (белый шум). В этом случае
(белый шум). В этом случае  Отсюда вытекает следующее свойство весовых функций первого семейства:
Отсюда вытекает следующее свойство весовых функций первого семейства:

Именно в этом содержится объяснение того, что временная весовая функция должна принимать значение, равное 1 при  Мы примем такую нормировку для весовых функций, используемых в методе коррелограмм.
Мы примем такую нормировку для весовых функций, используемых в методе коррелограмм.
Рассмотрим вещественные и четные функции второго семейства. Пусть  — временное окно,
— временное окно,  — соответствующее спектральное окно, тогда
— соответствующее спектральное окно, тогда

Следовательно,

Отсюда

т. е.

Такая нормировка принята для временных весовых окон, используемых в методах периодограмм и фильтрации.
В расчетах можно брать либо  либо
либо  с последующим умножением результата на
с последующим умножением результата на 
Площадь окна Q(v). Потеря информации.
Если  то
то 
Следовательно, в данном случае

т. е. сохраняется полная мощность.

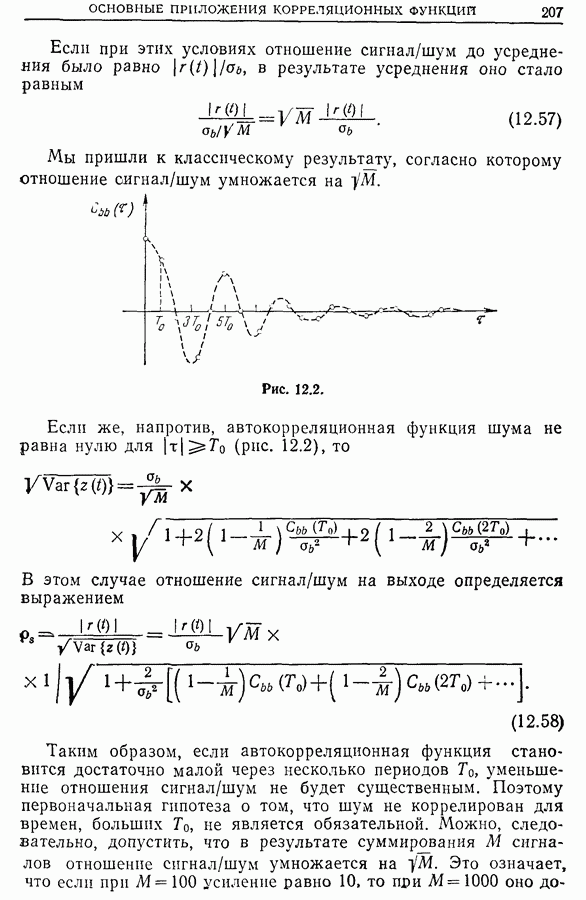
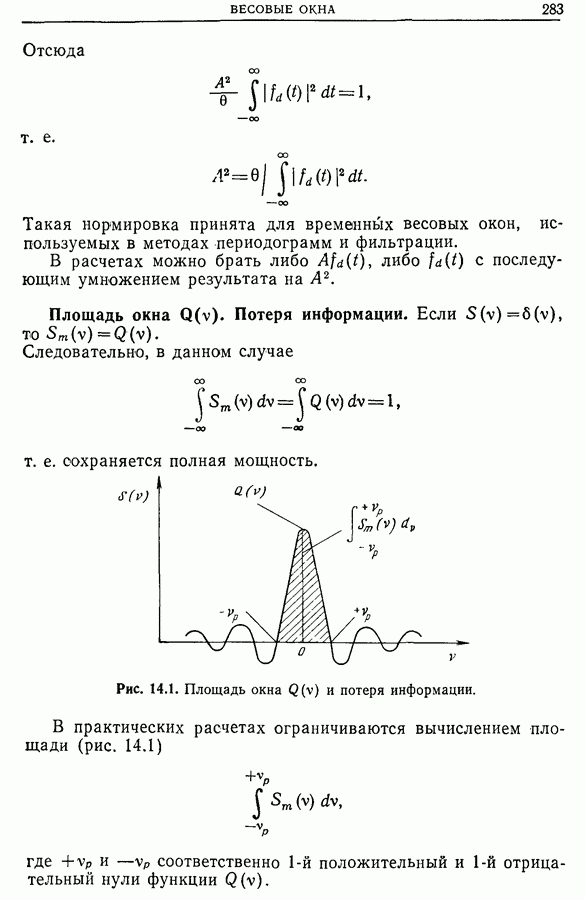
Рис. 14.1. Площадь окна  и потеря информации.
и потеря информации.
В практических расчетах ограничиваются вычислением площади (рис. 14.1)

где  соответственно 1-й положительный и 1-й отрицательный нули функции
соответственно 1-й положительный и 1-й отрицательный нули функции 
Пусть

Параметр  называют обычно потерей информации. Этот параметр, возможно выбранный не очень удачно, определяет долю энергии, соответствующую площади боковых выбросов.
называют обычно потерей информации. Этот параметр, возможно выбранный не очень удачно, определяет долю энергии, соответствующую площади боковых выбросов.
Ширина полосы пропускания центрального пика функции Q(v).
Имеется несколько определений ширины полосы пропускания узкополосного фильтра. Поскольку спектральное окно эквивалентно некоторому фильтру, соответствующему определенному временному окну, то эти определения можно распространить и на спектральные окна.

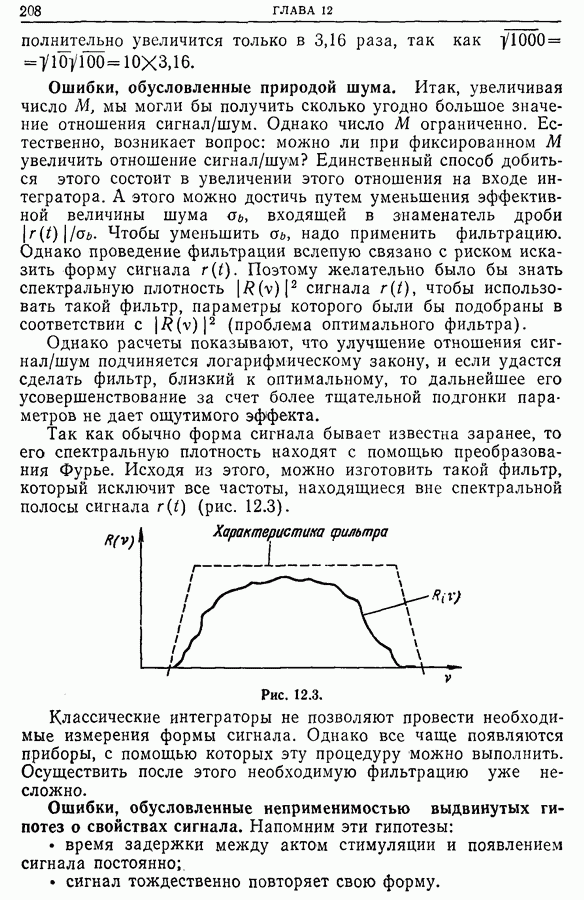
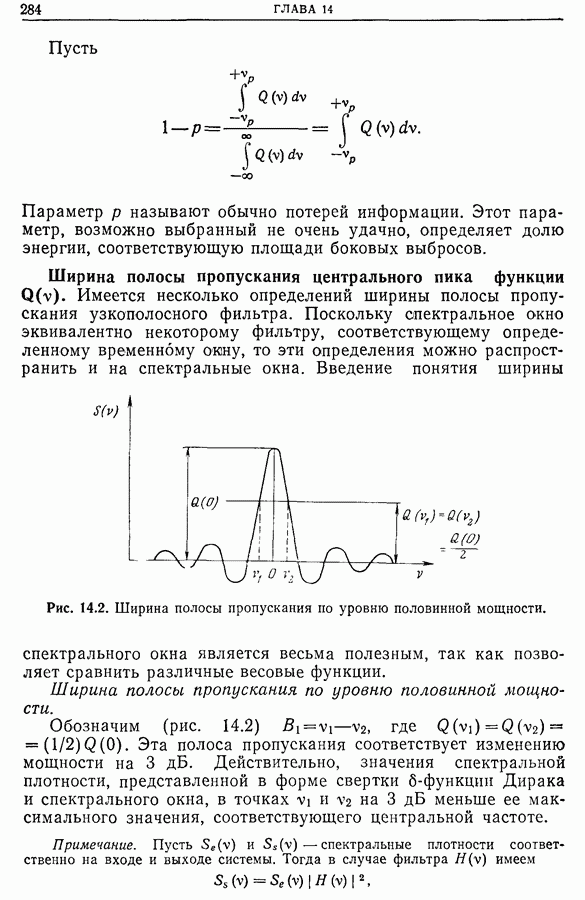
Рис. 14.2. Ширина полосы пропускания по уровню половинной мощности.
Введение понятия ширины спектрального окна является весьма полезным, так как позволяет сравнить различные весовые функции.
Ширина полосы пропускания по уровню половинной мощности.
Обозначим (рис. 14.2)  , где
, где  Эта полоса пропускания соответствует изменению мощности на 3 дБ. Действительно, значения спектральной плотности, представленной в форме свертки
Эта полоса пропускания соответствует изменению мощности на 3 дБ. Действительно, значения спектральной плотности, представленной в форме свертки  -функции Дирака и спектрального окна, в точках
-функции Дирака и спектрального окна, в точках  на 3 дБ меньше ее максимального значения, соответствующего центральной частоте.
на 3 дБ меньше ее максимального значения, соответствующего центральной частоте.
Примечание. Пусть  - спектральные плотности соответственно на входе и выходе системы. Тогда в случае фильтра
- спектральные плотности соответственно на входе и выходе системы. Тогда в случае фильтра  имеем
имеем

а в случае спектрального окна  имеем
имеем

Определяя ширину полосы, мы полагаем, что  - белый шум в случае фильтров и
- белый шум в случае фильтров и  -функция Дирака в случае спектральных окон.
-функция Дирака в случае спектральных окон.
Эквивалентная шумовая полоса пропускания. Эквивалентная шумовая полоса пропускания определяется выражением

где  — ширина полосы пропускания такого прямоугольного спектрального окна, которое пропускает сигнал с той же дисперсией, что и данное спектральное окно при воздействии на него сигналом со спектральной плотностью
— ширина полосы пропускания такого прямоугольного спектрального окна, которое пропускает сигнал с той же дисперсией, что и данное спектральное окно при воздействии на него сигналом со спектральной плотностью 

Эквивалентная статистическая полоса пропускания. Эквивалентная статистическая полоса пропускания определяется выражением

Это ширина полосы пропускания такого фиктивного прямоугольного окна, которое пропускает сигнал с той же статистической ошибкой, что и данное спектральное окно при воздействии на него сигналом со спектральной плотностью, представленной  -функцией.
-функцией.
Другие характеристики спектральных окон.
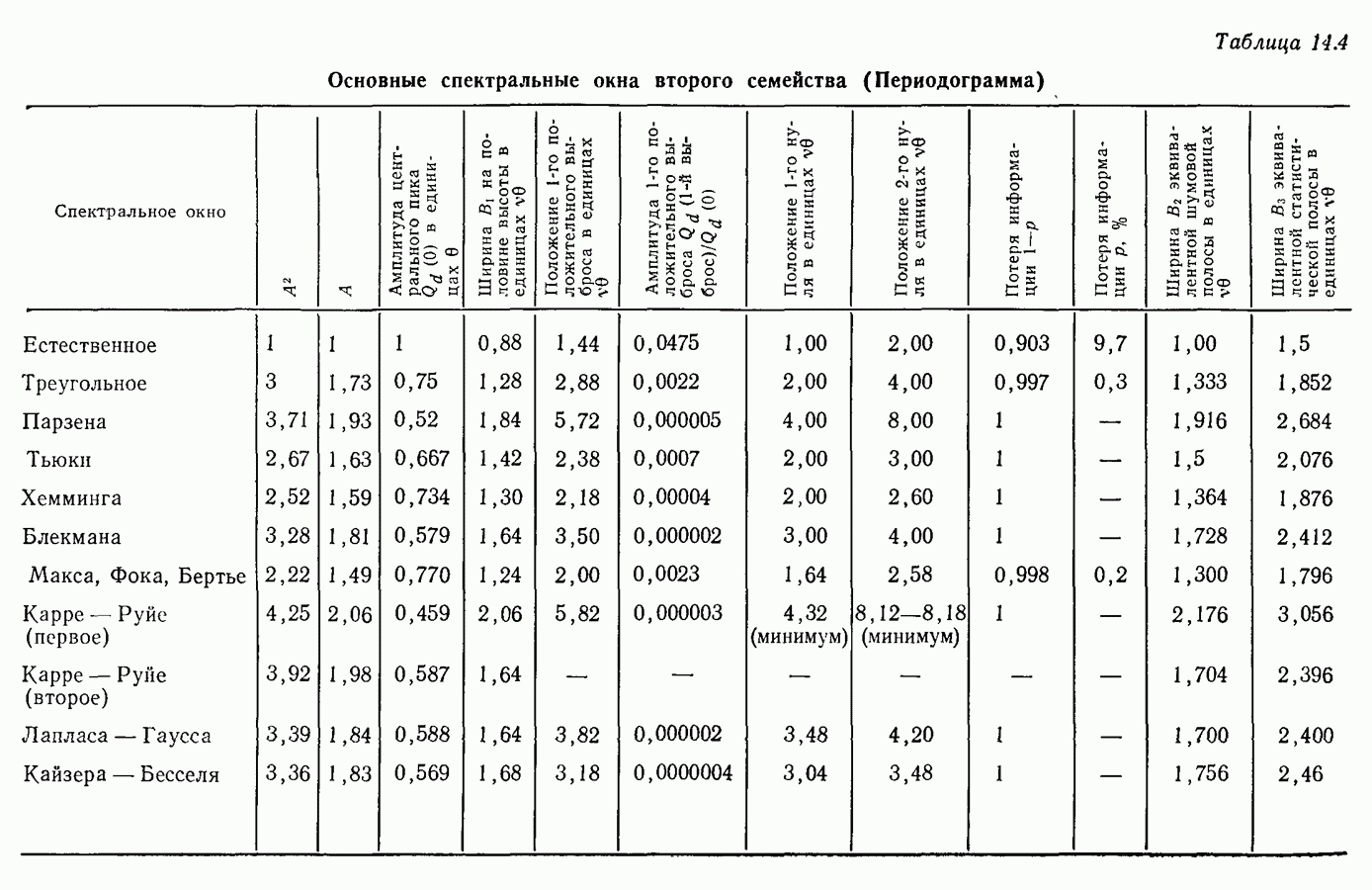
К основным характеристикам спектральных окон  относятся:
относятся:
• амплитуда  выраженная в безразмерных единицах (амплитуда, соответствующая центральной частоте);
выраженная в безразмерных единицах (амплитуда, соответствующая центральной частоте);
•  — ширина на половине высоты в безразмерных единицах;
— ширина на половине высоты в безразмерных единицах;
• положение 1-го положительного выброса в безразмерных единицах;
• относительная амплитуда 1-го положительного выброса:  (1-й положительный выброс
(1-й положительный выброс  ;
;
• положение  нуля (если он существует):
нуля (если он существует):  — в безразмерных единицах;
— в безразмерных единицах;
• положение  нуля (если он существует):
нуля (если он существует):  в безразмерных единицах;
в безразмерных единицах;
• положение  отрицательного выброса (если он существует) ;
отрицательного выброса (если он существует) ;
• относительная амплитуда  отрицательного выброса (если он существует):
отрицательного выброса (если он существует):  (1-й отрицательный выброс)
(1-й отрицательный выброс)  ;
;
• потеря информации

 потеря информации
потеря информации 
— ширина эквивалентной шумовой полосы пропускания;
 — ширина эквивалентной статистической полосы пропускания.
— ширина эквивалентной статистической полосы пропускания.
Безразмерной единицей для первого семейства является  а для второго семейства
а для второго семейства 
Существуют также и другие характеристические параметры.
Приведем некоторые из них:
 — ширина полосы пропускания центрального пика;
— ширина полосы пропускания центрального пика;

• отношение  выраженное в децибеллах, т. е.
выраженное в децибеллах, т. е. 
 потеря информации, выраженная в децибеллах:
потеря информации, выраженная в децибеллах:

 наклон огибающей боковых выбросов, выраженный в децибеллах на октаву;
наклон огибающей боковых выбросов, выраженный в децибеллах на октаву;
• центральный пик спектрального окна характеризуется также шириной и эксцессом, для оценки которых используются отношения  для спектральных окон первого семейства и отношениями
для спектральных окон первого семейства и отношениями  для спектральных окон второго семейства (эти отношения могут быть выражены в децибеллах).
для спектральных окон второго семейства (эти отношения могут быть выражены в децибеллах).
Замечание.
Отношение  иногда называемое «сглаженностью» спектрального окна, характеризует точность измерения амплитуды. Действительно, при обработке сигнала, например, методом периодограмм, точность анализа равна
иногда называемое «сглаженностью» спектрального окна, характеризует точность измерения амплитуды. Действительно, при обработке сигнала, например, методом периодограмм, точность анализа равна  . Отношение
. Отношение  = Измеренная амплитуда/Максимальная амплитуда служит характеристикой точности измерения амплитуды.
= Измеренная амплитуда/Максимальная амплитуда служит характеристикой точности измерения амплитуды.
Разделение двух пиков.
Разрешение. Разделение двух соседних пиков, или резонансных линий, зависит от качества оценки  функции
функции  , следовательно, от временного окна. Ширина основания центрального пика окна равна
, следовательно, от временного окна. Ширина основания центрального пика окна равна  Условие разрешения двух пиков с близкими амплитудами и центральными частотами
Условие разрешения двух пиков с близкими амплитудами и центральными частотами  записывается в виде неравенства [4]:
записывается в виде неравенства [4]:  . Этому условию удовлетворить труднее, если спектральное окно ближе к прямоугольному, и легче, если окно ближе к треугольному. Оно неприменимо, если две резонансные линии соответствуют существенно различным мощностям. Однако это скорее свойство применяемого временного весового окна, а не практическое правило.
. Этому условию удовлетворить труднее, если спектральное окно ближе к прямоугольному, и легче, если окно ближе к треугольному. Оно неприменимо, если две резонансные линии соответствуют существенно различным мощностям. Однако это скорее свойство применяемого временного весового окна, а не практическое правило.
Оценка спектральной плотности с помощью временного окна.
Смещение. Оценка спектральной плотности одним из трех классических методов имеет вид

Ей соответствует смещение

Полезно напомнить, что оценка называется сходящейся, или корректной, если  при
при  или
или  Если временному окну отвечает спектральное окно
Если временному окну отвечает спектральное окно  которое стремится к
которое стремится к  при
при  или
или  то
то  т. е. оценка корректна.
т. е. оценка корректна.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
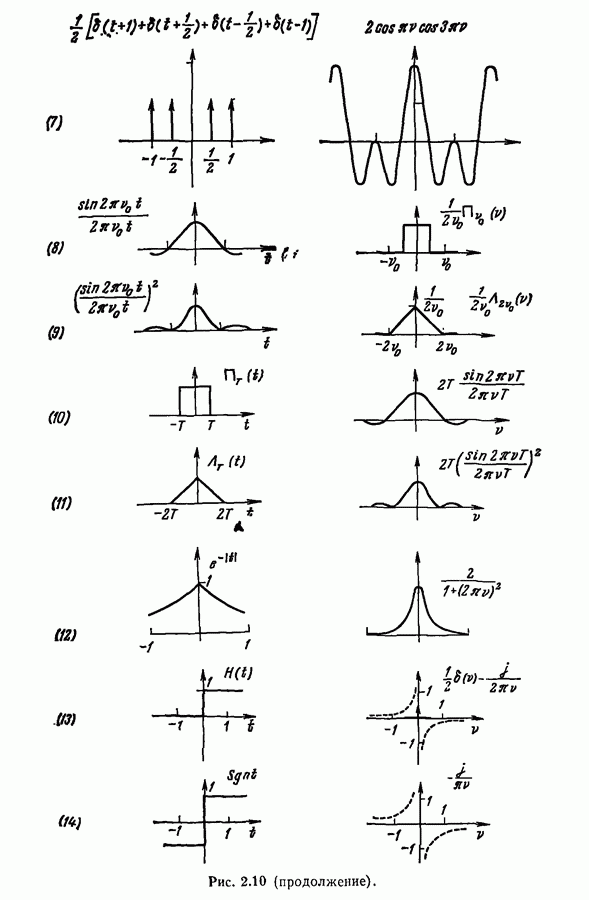
- 2.7. Несколько функций и их фурье-образы
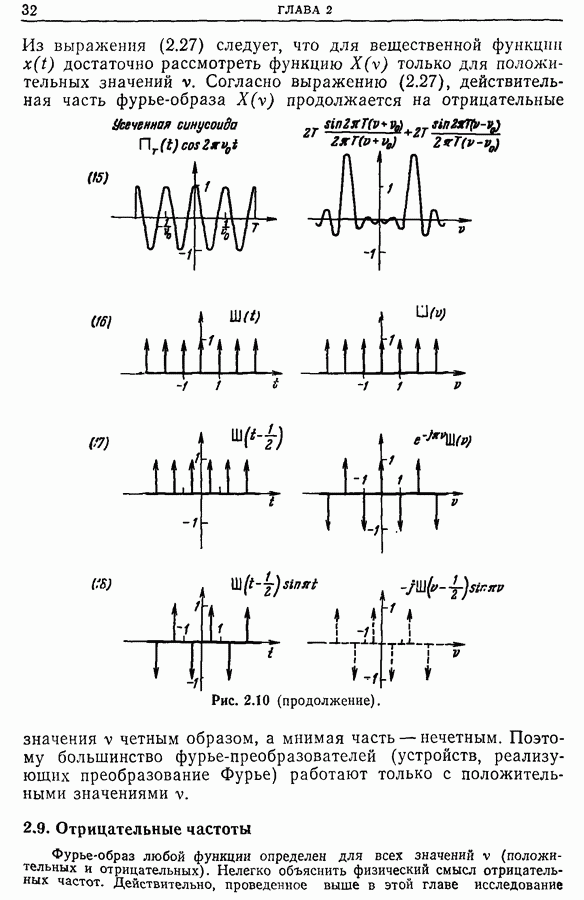
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
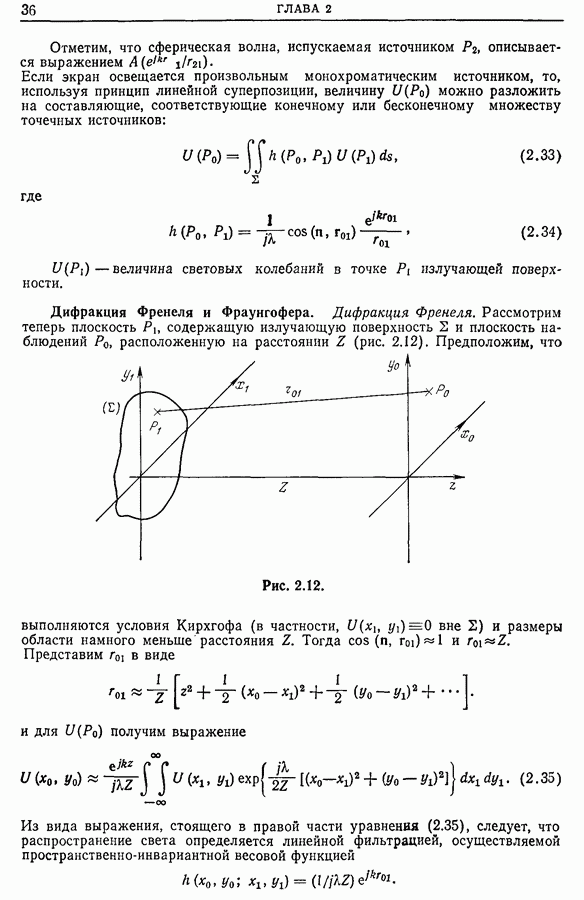
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
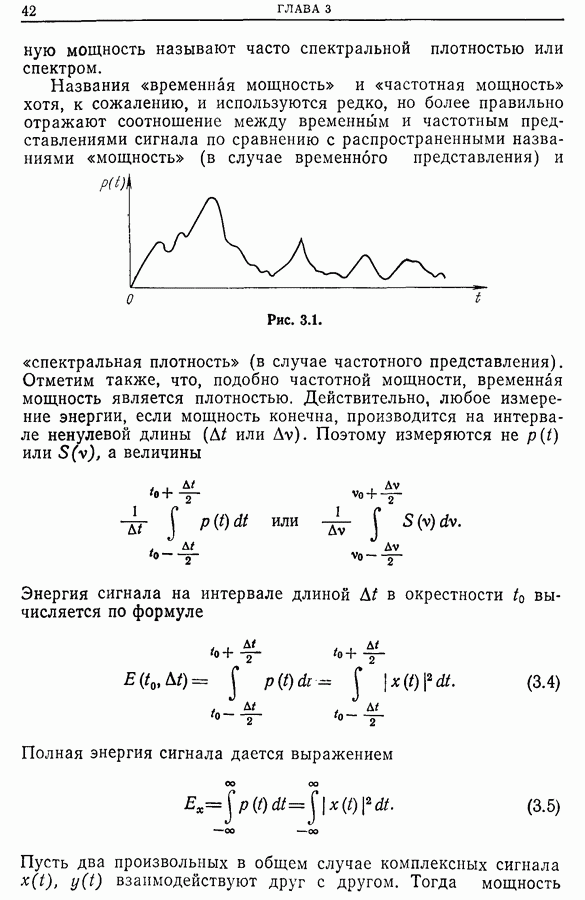
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
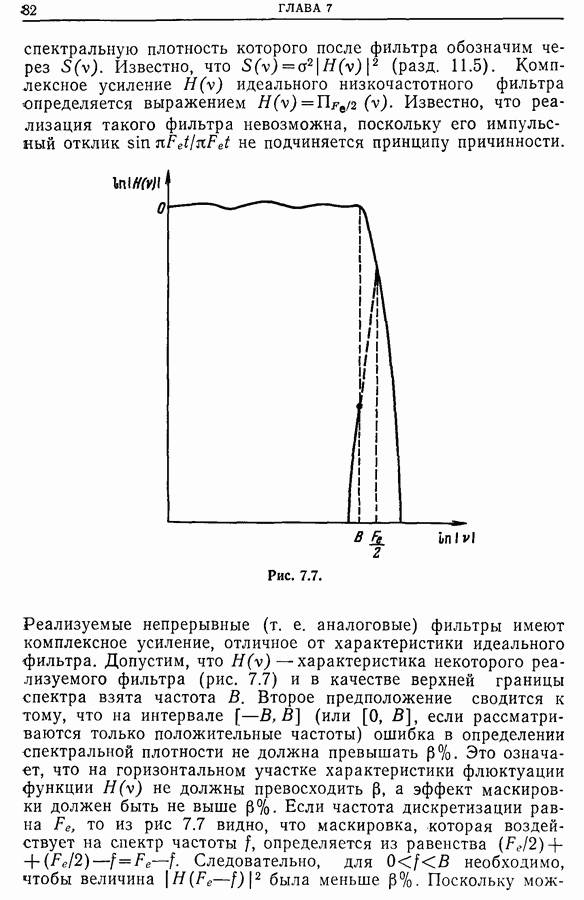
- 7.6. Противомаскировочный фильтр
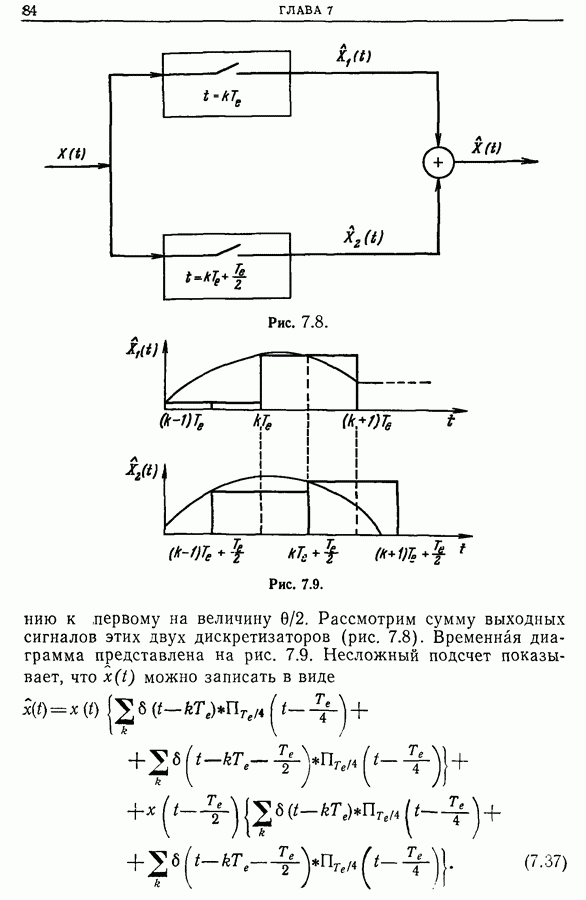
- 7.7. Физическая дискретизация. Комбинированная дискретизация
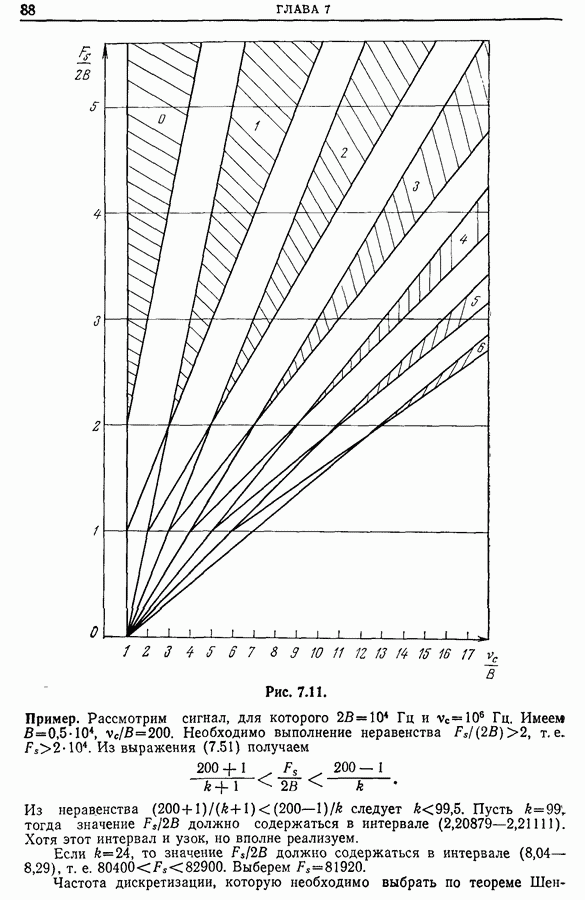
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
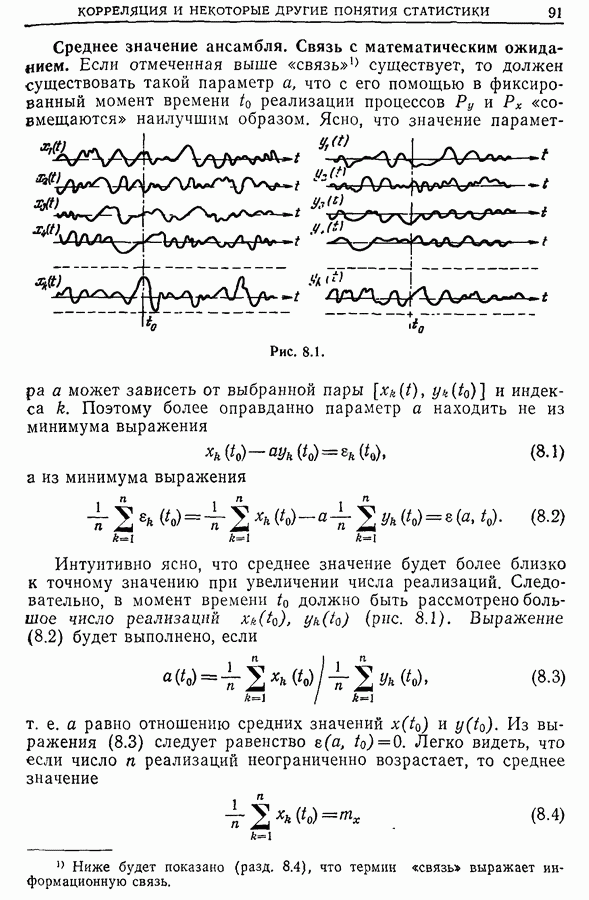
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции