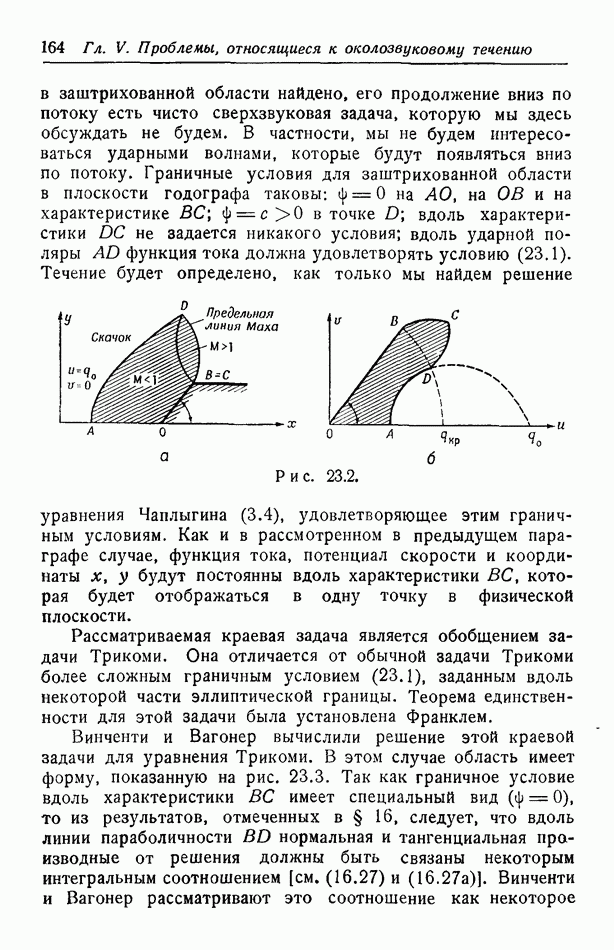
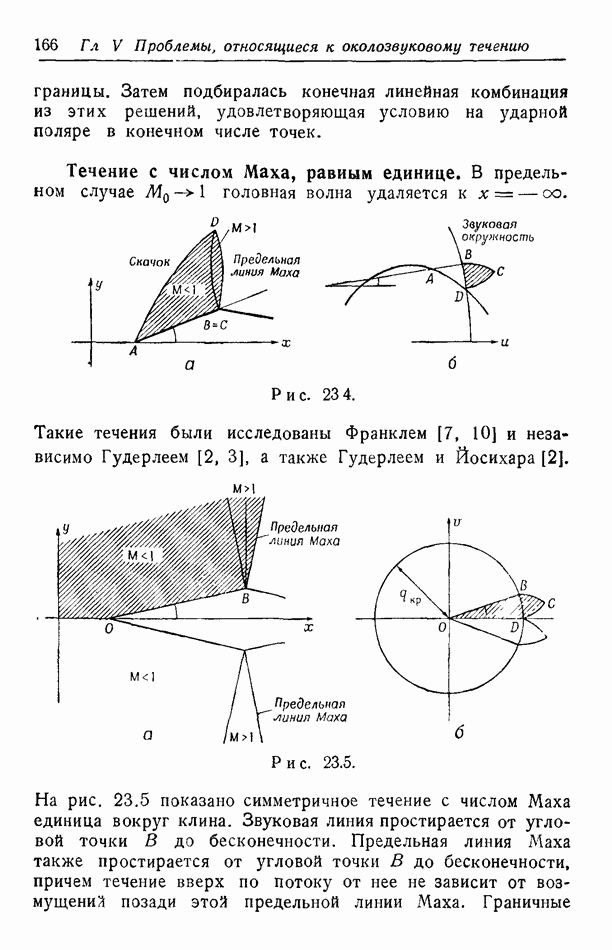
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 17. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ ДЛЯ УРАВНЕНИЙ СМЕШАННОГО ТИПА
Задача Трикоми.
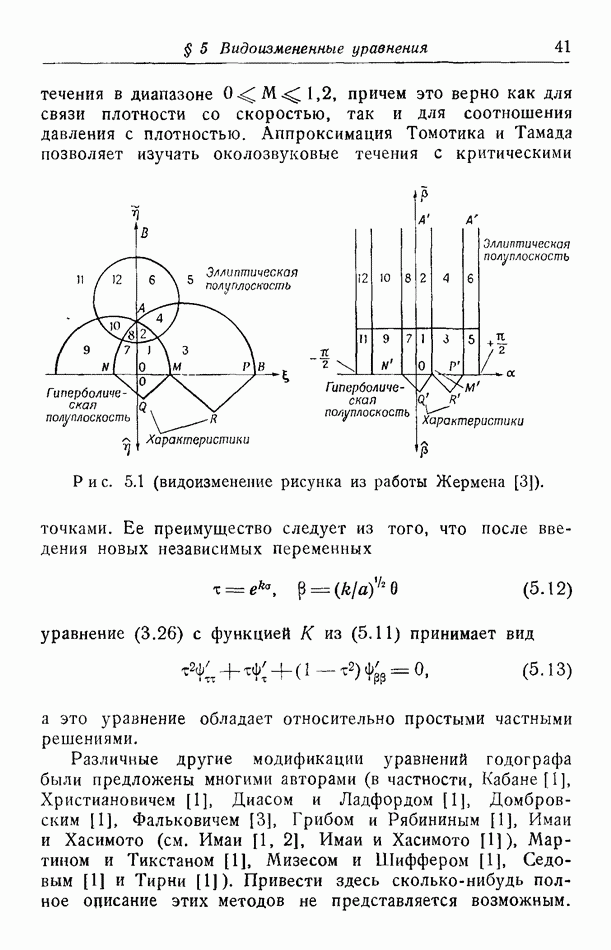
Трикоми был первым, поставившим корректную краевую задачу для уравнения смешанного типа в области, пересекаемой линией параболичности. Он показал, что уравнение (16.1) имеет единственное решение в области, ограниченной некоторой кривой  при
при  и двумя характеристиками
и двумя характеристиками  (рис. 17.1), если это решение принимает заданные граничные значения на эллиптической части границы
(рис. 17.1), если это решение принимает заданные граничные значения на эллиптической части границы  и на одной из двух характеристик. Эта же "задача Трикоми“ рассматривалась Геллерстедом [1,2] для уравнения (16.16). Мы будем рассматривать все краевые задачи для более общего уравнения (16.2).
и на одной из двух характеристик. Эта же "задача Трикоми“ рассматривалась Геллерстедом [1,2] для уравнения (16.16). Мы будем рассматривать все краевые задачи для более общего уравнения (16.2).

Рис. 17.1.
Геллерстед также заметил, что можно рассматривать области более общего вида, ограниченные  и различными характеристиками. Например, в случае области, показанной
и различными характеристиками. Например, в случае области, показанной
на рис. 17.2, граничные значения задаются на (30 и на двух характеристиках  и
и  Дальнейшие обобщения были предложены Халиловым [1, 2], Бицадзе [1], Кармановым [1] и другими. Мы приведем только один пример. Область показана на рис. 17.3; она многосвязна; граничные значения задаются на всей эллиптической части границы и на характеристиках
Дальнейшие обобщения были предложены Халиловым [1, 2], Бицадзе [1], Кармановым [1] и другими. Мы приведем только один пример. Область показана на рис. 17.3; она многосвязна; граничные значения задаются на всей эллиптической части границы и на характеристиках 

Рис. 17.2.

Рис. 17.3.
Другие краевые задачи.
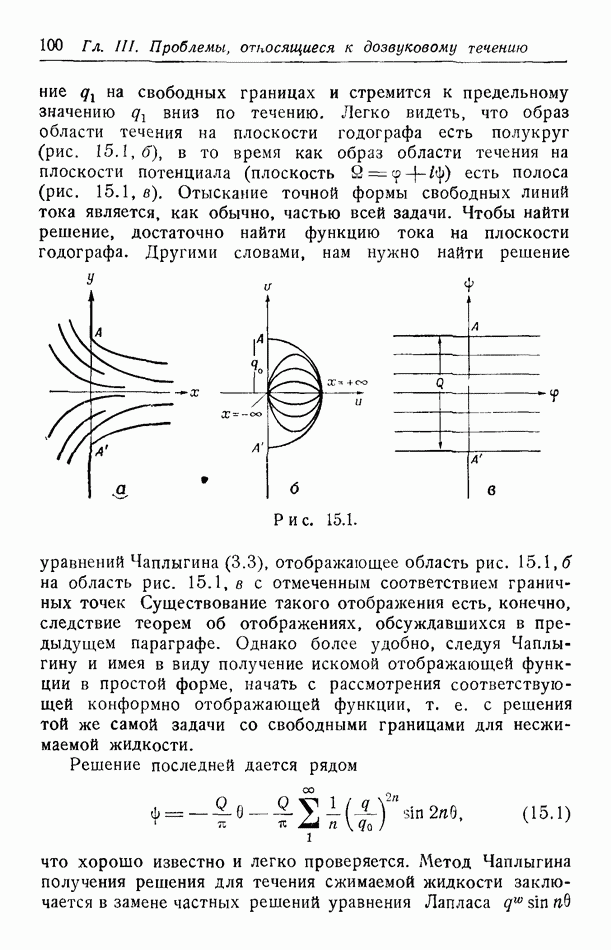
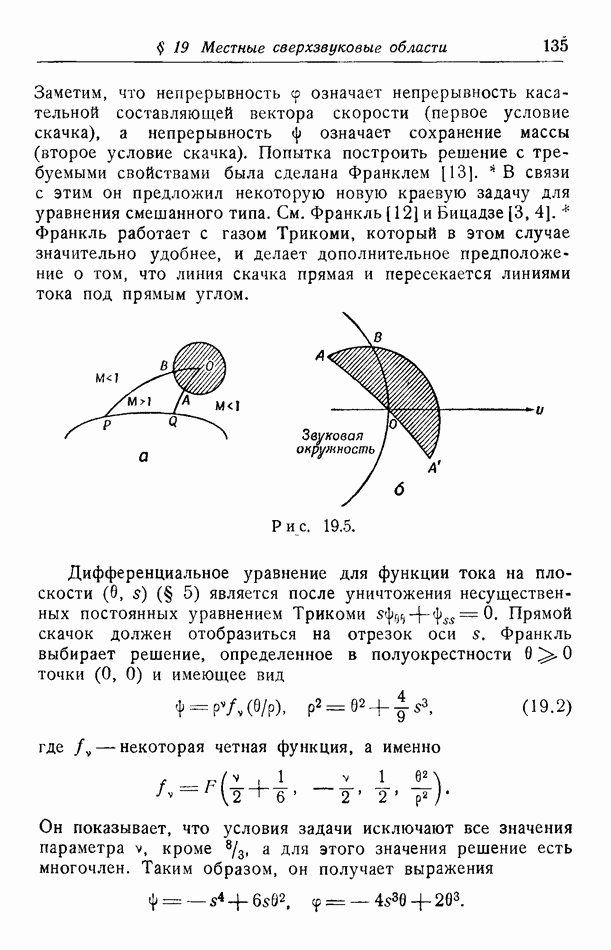
Важное обобщение задачи Трикоми было дано Франклем [3], Франкль заменил несущую граничные значения характеристику некоторой нехарактеристической кривой  расположенной внутри характеристического треугольника и пересекающей каждую характеристику "второго семейства" не более одного раза. Как показано на рис. 17.4, кривая
расположенной внутри характеристического треугольника и пересекающей каждую характеристику "второго семейства" не более одного раза. Как показано на рис. 17.4, кривая  может частично совпадать с характеристикой. Большой интерес представляет также область, показанная на рис. 17.5. Здесь граничные значения задаются на
может частично совпадать с характеристикой. Большой интерес представляет также область, показанная на рис. 17.5. Здесь граничные значения задаются на  и на двух нехарактеристических кривых
и на двух нехарактеристических кривых  На характеристиках
На характеристиках  никаких условий не задано. В дальнейшем мы будем предполагать, что
никаких условий не задано. В дальнейшем мы будем предполагать, что

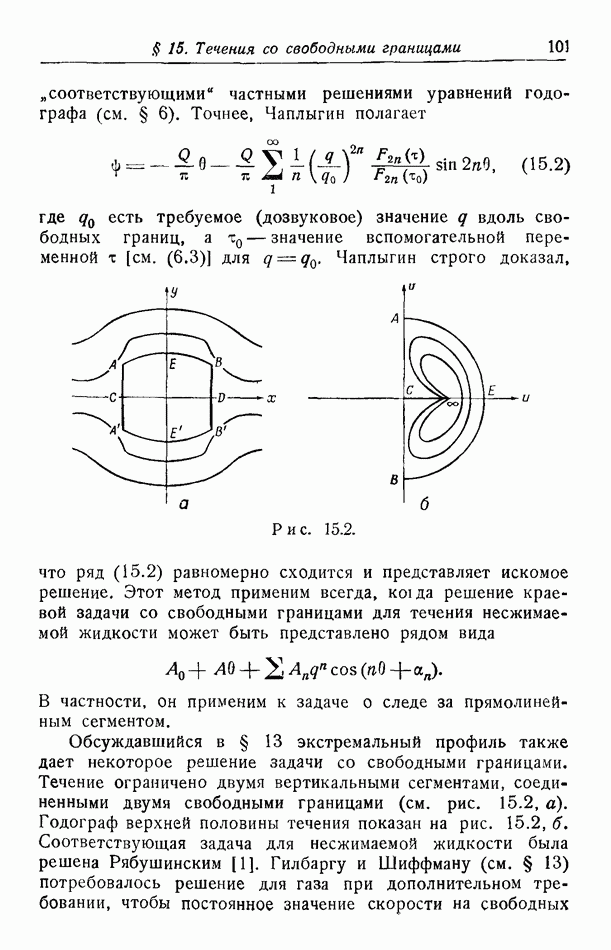
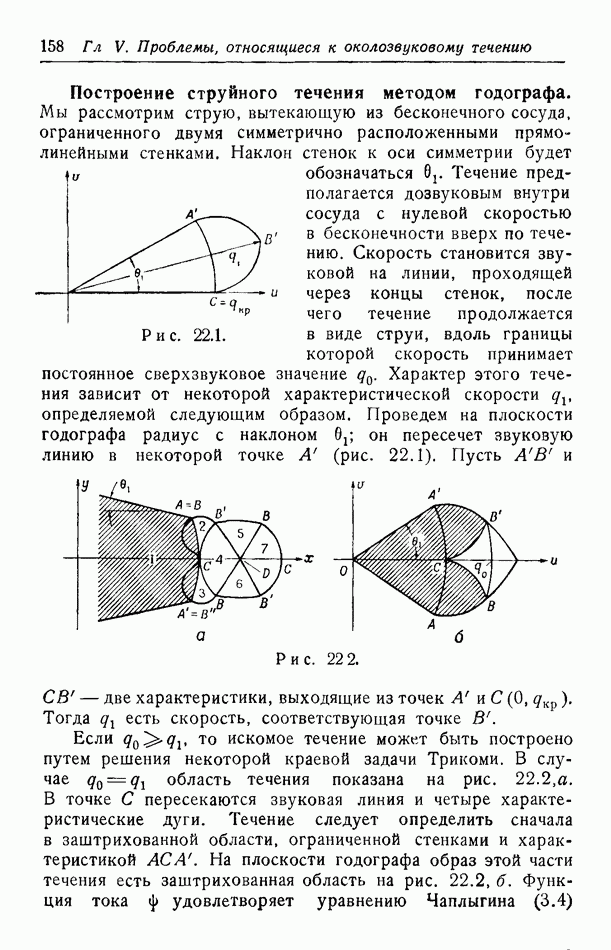
Все вышеупомянутые задачи аналогичны задаче Дирихле. Вопросы газовой динамики приводят также к задачам,
аналогичным задаче Неймана. Мы поставим ее для области, показанной на рис. 17.5. Граничное условие имеет вид

где  данная функция. Аналогия с задачей Неймана будет очевидна, если преобразовать уравнение к каноническому виду в эллиптической полуплоскости.
данная функция. Аналогия с задачей Неймана будет очевидна, если преобразовать уравнение к каноническому виду в эллиптической полуплоскости.

Рис. 17.4.

Рис. 17.5.
В переменных  где у определена в (16.7), это граничное условие на
где у определена в (16.7), это граничное условие на  принимает вид
принимает вид

Заметим, что Франкль [11] и Агмон [1] рассмотрели задачу, в которой условие (17.2) задается на эллиптической части границы, а значения искомой функции — на соответствующих кусках гиперболической части границы.
Проблема единственности.
Для того чтобы какую-нибудь из этих задач можно было считать корректно поставленной, необходимо прежде всего убедиться в том, что граничные условия определяют функцию  т. е. что решение рассматриваемого уравнения, удовлетворяющее однородным граничным условиям, есть тождественный нуль.
т. е. что решение рассматриваемого уравнения, удовлетворяющее однородным граничным условиям, есть тождественный нуль.
Первые доказательства единственности (Трикоми, Геллерстед) использовали специальные свойства уравнений (16.1)
и (16 16). Для общего уравнения (16 2) первое доказательство единственности для задачи Трикоми было дано Франклем [11]. В этом доказательстве требуется выполнение неравенства

в гиперболической части области. Заметим, что это неравенство выполнено всюду для уравнения (16.1), но, вообще говоря, оно не справедливо, если характеристический треугольник достаточно велик.
Ясно, что обсуждавшийся в § 16 принцип максимума дает доказательство единственности для задачи Трикоми, причем наиболее удовлетворительное доказательство, так как оно не требует условий регулярности на границе. К сожалению, условие (16.19) является даже более ограничительным, чем условие (17.3).
Метод abc.
Фридрихе заметил, что доказательство Франкля можно изложить в терминах "интеграла энергии", и с тех пор различные доказательства единственности были найдены так называемым методом  (Проттер [2], Моравец [1], У и Дин [1]; см. также Гудерлей [2]). В простой форме метод
(Проттер [2], Моравец [1], У и Дин [1]; см. также Гудерлей [2]). В простой форме метод  может быть описан так. Предположим, что
может быть описан так. Предположим, что  есть решение уравнения (16.2), определенное в области
есть решение уравнения (16.2), определенное в области  и удовлетворяющее однородным граничным условиям обсуждаемой задачи. Рассмотрим интеграл
и удовлетворяющее однородным граничным условиям обсуждаемой задачи. Рассмотрим интеграл

где а, b и с — достаточно гладкие функции от  Этот интеграл равен нулю. Попытаемся найти такие функции
Этот интеграл равен нулю. Попытаемся найти такие функции  чтобы после преобразования этого интеграла с помощью формулы Грина получилось положительно определенное выражение, которое может быть равно нулю, только если
чтобы после преобразования этого интеграла с помощью формулы Грина получилось положительно определенное выражение, которое может быть равно нулю, только если  Как только это сделано, доказательство заканчивается.
Как только это сделано, доказательство заканчивается.
Определение соответствующих функций  с может представить трудности, однако предложенное У и Дином и развитое Проттером обобщение приводит к полному доказательству единственности для задачи Трикоми. Проттер
с может представить трудности, однако предложенное У и Дином и развитое Проттером обобщение приводит к полному доказательству единственности для задачи Трикоми. Проттер
рассматривает для области  рис. 17.1 выражение где
рис. 17.1 выражение где

Здесь  некоторые функции, подлежащие определению, причем
некоторые функции, подлежащие определению, причем  есть эллиптическая часть, а
есть эллиптическая часть, а  гиперболическая часть области
гиперболическая часть области  Решение
Решение  уравнения (16.2) равно нулю на
уравнения (16.2) равно нулю на  Формула Грина показывает, что первый и последний интегралы в (17.5) равны нулю. Применение той же формулы ко второму и третьему интегралам дает слагаемое
Формула Грина показывает, что первый и последний интегралы в (17.5) равны нулю. Применение той же формулы ко второму и третьему интегралам дает слагаемое

которое также равно нулю, так как  на
на  . С другой стороны, если выполнить указанные в (17.5) дифференцирования и преобразовать интеграл I с помощью формулы Грина, то получится соотношение вида
. С другой стороны, если выполнить указанные в (17.5) дифференцирования и преобразовать интеграл I с помощью формулы Грина, то получится соотношение вида

где  представляют собой квадратичные формы от
представляют собой квадратичные формы от  Теорема единственности будет доказана, если функции
Теорема единственности будет доказана, если функции  могут быть выбраны так, что эти три квадратичные формы будут положительно определенными. Как показал Проттер, такой выбор возможен. Фактические выражения можно найти в его подготовленной для печати статье.
могут быть выбраны так, что эти три квадратичные формы будут положительно определенными. Как показал Проттер, такой выбор возможен. Фактические выражения можно найти в его подготовленной для печати статье.
Установленная здесь теорема единственности справедлива, если существуют все участвующие в рассуждении двойные интегралы и законны применения формулы Грина.
Пример.
Метод  можно применить также к обобщенной задаче Трикоми (иногда называемой задачей Франкля). В качестве
можно применить также к обобщенной задаче Трикоми (иногда называемой задачей Франкля). В качестве
примера мы рассмотрим данное Моравец доказательство теоремы единственности для области  показанной на рис. 17.5, при дополнительном предположении, что эллиптическая граничная кривая
показанной на рис. 17.5, при дополнительном предположении, что эллиптическая граничная кривая  звездообразна относительно начала координат. В аналитической форме это условие означает, что при движении вдоль
звездообразна относительно начала координат. В аналитической форме это условие означает, что при движении вдоль  против часовой стрелки
против часовой стрелки

Мы положим  Применив формулу Грина, находим, что интеграл I равен
Применив формулу Грина, находим, что интеграл I равен

Заметив, что  на
на  и используя уравнение (16.11), видим, что криволинейный интеграл преобразуется к виду
и используя уравнение (16.11), видим, что криволинейный интеграл преобразуется к виду

откуда сразу следует ввиду (17.1) и (17.6), что это выражение неотрицательно. Так как двойной интеграл, очевидно, положительно определенный, то доказательство единственности закончено. Мы молчаливо предполагали, что производные  непрерывны в замкнутой области. Это условие может быть ослаблено. Например, можно разрешить производным
непрерывны в замкнутой области. Это условие может быть ослаблено. Например, можно разрешить производным  обращаться в начале координат в бесконечность порядка не выше первого, а в концевых точках
обращаться в начале координат в бесконечность порядка не выше первого, а в концевых точках  порядка не выше 1/2.
порядка не выше 1/2.
Доказательство единственности для задачи Франкля без каких-либо предположений относительно кривой  до сих пор еще не получено.
до сих пор еще не получено.
Использование вспомогательной функций.
Другой подход к доказательствам единственности (Моравец [3]) заключается в сопоставлении каждому решению уравнения (16.2) функции

Этот криволинейный интеграл не зависит от пути интегрирования, а определяемая им функция удовлетворяет в эллиптической полуплоскости эллиптическому дифференциальному уравнению

Это означает, что не может достигать ни локального максимума, ни локального минимума во внутренней эллиптической точке, если только  не постоянна. Кроме того, вдоль характеристик (6.11) мы имеем
не постоянна. Кроме того, вдоль характеристик (6.11) мы имеем

так что если  и определены в области да рис. 17.5, то х принимает максимальное значение на
и определены в области да рис. 17.5, то х принимает максимальное значение на 

Рис. 17.6.
Для того чтобы показать применение этой функции к доказательствам единственности, мы рассмотрим аналог задачи Неймана. Для простоты исследуем уравнение (16.15). Область показана на рис. 17.6. В этом случае однородные граничные условия таковы:

Мы сделаем также следующие предположения относительно границы:  в точках
в точках  на (50; производная
на (50; производная  не обращается в нуль на
не обращается в нуль на  в эллиптической полуплоскости, за исключением одной точки
в эллиптической полуплоскости, за исключением одной точки 
Пусть  удовлетворяет (16.15) и (17.8), и пусть определена формулой (17.7) с
удовлетворяет (16.15) и (17.8), и пусть определена формулой (17.7) с  На
На  в силу (17.8) мы имеем
в силу (17.8) мы имеем

На  согласно (17.1), имеем
согласно (17.1), имеем  так что в силу (17.8)
так что в силу (17.8)

Отсюда следует, что максимум  достигается либо в точке
достигается либо в точке  либо в точке В. Предположим, что он достигается в
либо в точке В. Предположим, что он достигается в  -Приближаясь к этой точке сверху и используя условие (17.8). а также предполагаемую непрерывность производных
-Приближаясь к этой точке сверху и используя условие (17.8). а также предполагаемую непрерывность производных  мы видим, что
мы видим, что  . С другой стороны, согласно лемме Хопфа о граничной точке (см. § 7), производная
. С другой стороны, согласно лемме Хопфа о граничной точке (см. § 7), производная  должна быть отрицательна как производная в точке максимума, если только х не постоянна. Поэтому
должна быть отрицательна как производная в точке максимума, если только х не постоянна. Поэтому  постоянна, а значит, и
постоянна, а значит, и  постоянна в эллиптической области. Так как задача Коши для волнового уравнения имеет единственное решение, то
постоянна в эллиптической области. Так как задача Коши для волнового уравнения имеет единственное решение, то  также постоянна и в гиперболической области. Это завершает доказательство.
также постоянна и в гиперболической области. Это завершает доказательство.
Аналогичными рассуждениями, хотя и значительно более сложными, при определенных условиях можно получить теорему единственности для аналога задачи Неймана в случае общего уравнения (16.2). Эти условия относятся к граничным кривым и формулируются (Моравец [3]) следующим образом. Пусть

где  длина дуги кривой
длина дуги кривой  на плоскости
на плоскости  Предположим, что угол
Предположим, что угол  удовлетворяет условиям
удовлетворяет условиям

Функция К и граничные кривые предполагаются достаточно гладкими.
Геометрическое условие, наложенное на граничные кривые, является существенным, так как Моравец обнаружила контрпример, в котором условие (17.9) нарушается в точках  а задача Неймана с нулевыми данными обладает нетривиальным решением.
а задача Неймана с нулевыми данными обладает нетривиальным решением.
Систематический подход к краевым задачам смешанного типа.
Совсем недавно Фридрихе [7] сформулировал новый подход к методу  Мы очень кратко изложим здесь основные черты его подхода. Метод Фридрихса в принципе является весьма общим и дает систематический способ отыскания корректно поставленных краевых задач для широкого класса дифференциальных уравнений с частными производными.
Мы очень кратко изложим здесь основные черты его подхода. Метод Фридрихса в принципе является весьма общим и дает систематический способ отыскания корректно поставленных краевых задач для широкого класса дифференциальных уравнений с частными производными.
Технически удобнее работать с системами уравнений первого порядка при однородных краевых условиях. Заметим, что уравнение (16.2) может быть записано в виде системы двух уравнений первого порядка

где мы положили  То же самое уравнение можно записать в виде системы трех уравнений первого порядка
То же самое уравнение можно записать в виде системы трех уравнений первого порядка

где  произвольные функции. Нет необходимости подробно разъяснять, что однородное уравнение с неоднородными граничными условиями эквивалентно неоднородному уравнению с однородными граничными условиями.
произвольные функции. Нет необходимости подробно разъяснять, что однородное уравнение с неоднородными граничными условиями эквивалентно неоднородному уравнению с однородными граничными условиями.
Рассмотрим оператор

Здесь  - вектор-столбец из
- вектор-столбец из  неизвестных функций от х, у, а
неизвестных функций от х, у, а  матрицы размера
матрицы размера  с элементами, зависящими от
с элементами, зависящими от  Мы будем говорить, что уравнение
Мы будем говорить, что уравнение

где  данный вектор-столбец, записано в "подходящем" виде, если в рассматриваемой области матрицы
данный вектор-столбец, записано в "подходящем" виде, если в рассматриваемой области матрицы  симметричны, а матрица
симметричны, а матрица

является положительно определенной. Вообще говоря, данное уравнение не будет иметь "подходящего" вида. Однако его можно преобразовать к "подходящему" виду посредством умножения матриц  слева на некоторую матрицу
слева на некоторую матрицу  Определение такой матрицы
Определение такой матрицы  в сущности аналогично
в сущности аналогично
определению вспомогательных функций  и с в методе
и с в методе  Заметим, что два уравнения
Заметим, что два уравнения

будут эквивалентны только в том случае, если матрица  неособенная. Впрочем, для доказательства единственности иногда можно пользоваться и особенными матрицами
неособенная. Впрочем, для доказательства единственности иногда можно пользоваться и особенными матрицами 
Предположим, что оператор (17.10) уже записан в "подходящем” виде, и будем искать "подходящие” граничные условия. Формально сопряженный оператор  дается формулой
дается формулой

Заметим, что

так что формула Грина приводит к тождеству

Здесь  обозначает обычное скалярное произведение двух векторов, а криволинейный интеграл берется по границе
обозначает обычное скалярное произведение двух векторов, а криволинейный интеграл берется по границе  области
области 
Всякая квадратичная форма может быть записана в виде разности двух полуопределенных форм. Поэтому можно найти две симметричные полуопределенные неотрицательные матрицы  определенные на
определенные на  и такие, что
и такие, что  обозначает элемент длины дуги кривой
обозначает элемент длины дуги кривой 

Теперь (17.13) можно переписать так:

Это тождество приводит к двум теоремам единственности: одной для уравнения (17.11) с граничным "условием

и другой для задачи

В самом деле, допустив, что и есть решение (17.11) и (17.15) с  мы получим из (17.12) и (17.14), полагая там
мы получим из (17.12) и (17.14), полагая там 

что возможно, только если  Вторая теорема единственности доказывается аналогично.
Вторая теорема единственности доказывается аналогично.
В общем случае матрицы  могут обращаться в нуль на некоторой части границы, так что граничные условия
могут обращаться в нуль на некоторой части границы, так что граничные условия  будут относиться только к части границы, как это было в задаче Трикоми и ее обобщениях.
будут относиться только к части границы, как это было в задаче Трикоми и ее обобщениях.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- § 1. ВВЕДЕНИЕ
- Глава 1. Дифференциальные уравнения потенциального течения газа
- Скорость звука.
- Установившееся потенциальное течение.
- Плоские течения.
- Слабые разрывы и скачки уплотнения.
- Краевые условия.
- § 3. ГОДОГРАФ
- Отображение в плоскость годографа.
- Уравнения годографа.
- Преобразования уравнений годографа.
- Отображение в физическую плоскость.
- Уравнения в плоскости потенциала.
- § 4. ПРИБЛИЖЕННЫЕ УРАВНЕНИЯ
- Несжимаемое течение.
- Разложение по степеням числа Маха.
- Почти параллельное течение.
- Околозвуковое приближение.
- § 5. ВИДОИЗМЕНЕННЫЕ УРАВНЕНИЯ
- Газ Чаплыгина и минимальные поверхности.
- Неизменно дозвуковые течения.
- Газ Трикоми.
- Другие аппроксимации.
- Метод Лёвнера.
- § 6. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ГОДОГРАФА
- Сигма-интегрирование.
- Источник и вихрь.
- Продолжение в комплексную область.
- Решения с особенностями.
- Интегральные операторы Бергмана.
- ГЛАВА II. Математические основы теории дозвукового течения
- Условие Кутта — Жуковского.
- § 8. КВАЗИКОНФОРМНЫЕ ОТОБРАЖЕНИЯ
- Квазиконформность.
- Уравнения Бельтрами.
- Метрика течения.
- Теоремы о квазиконформных отображениях.
- Теорема о представлении.
- § 9. ПСЕВДОАНАЛИТИЧЕСКИЕ ФУНКЦИИ
- Псевдоаналитические функции.
- Принцип подобия.
- Течение вокруг профиля.
- § 10. ЗАМЕЧАНИЯ О КВАЗИЛИНЕЙНЫХ УРАВНЕНИЯХ
- Прямой метод вариационного исчисления.
- Решения как неподвижные точки.
- Сжатые отображения.
- Теорема Шаудера о неподвижной точке.
- Метод непрерывного продолжения.
- Степень отображения.
- Априорные оценки.
- Целые решения и особенности.
- ГЛАВА III. Некоторые проблемы, относящиеся к дозвуковому течению
- § 11. ПОВЕДЕНИЕ ДОЗВУКОВОГО ТЕЧЕНИЯ В БЕСКОНЕЧНОСТИ
- § 12. ДОЗВУКОВОЕ ТЕЧЕНИЕ ВОКРУГ ПРОФИЛЯ
- § 13. ТЕЧЕНИЕ ГАЗА ЧАПЛЫГИНА
- § 14. ДОЗВУКОВОЕ ТЕЧЕНИЕ В КАНАЛЕ И СООТВЕТСТВУЮЩИЕ ТЕОРЕМЫ ОБ ОТОБРАЖЕНИЯХ
- Обобщения теоремы Римана об отображении.
- § 15. ДОЗВУКОВЫЕ ТЕЧЕНИЯ СО СВОБОДНЫМИ ГРАНИЦАМИ
- Течение Гельмгольца около криволинейного препятствия.
- ГЛАВА IV. Математичесние основы околозвуковой газодинамики
- Частные решения уравнения Трикоми.
- Задача Коши для уравнения Трикоми.
- § 17. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ ДЛЯ УРАВНЕНИЙ СМЕШАННОГО ТИПА
- § 18. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ ДЛЯ УРАВНЕНИЙ СМЕШАННОГО ТИПА
- Метод гильбертова пространства.
- ГЛАВА V. Некоторые проблемы, относящиеся к околозвуковому течению
- Сверхзвуковое включение, ограниченное скачком.
- § 20. ОКОЛОЗВУКОВОЕ ОБТЕКАНИЕ ПРОФИЛЯ В ДОЗВУКОВОМ НЕВОЗМУЩЕННОМ ТЕЧЕНИИ
- Применение функций Чаплыгина.
- Другие методы.
- Предельная линия.
- Околозвуковая полемика.
- Формулировка теорем несуществования.
- Набросок доказательств несуществования.
- Нерешенные вопросы.
- Течения со скачками.
- Приближенная теория.
- Течение вокруг прямолинейного клина.
- § 21. ОКОЛОЗВУКОВОЕ ТЕЧЕНИЕ В КАНАЛЕ
- § 22. ОКОЛОЗВУКОВЫЕ ТЕЧЕНИЯ СО СВОБОДНЫМИ ГРАНИЦАМИ
- § 23. ТЕЧЕНИЯ ВОКРУГ ПРЕПЯТСТВИЯ СО СВЕРХЗВУКОВОЙ И ЗВУКОВОЙ СКОРОСТЯМИ НЕВОЗМУЩЕННОГО ПОТОКА
- Приложение
- § 24. ЗАМЕЧАНИЯ О ЧИСЛЕННЫХ МЕТОДАХ
- Библиография