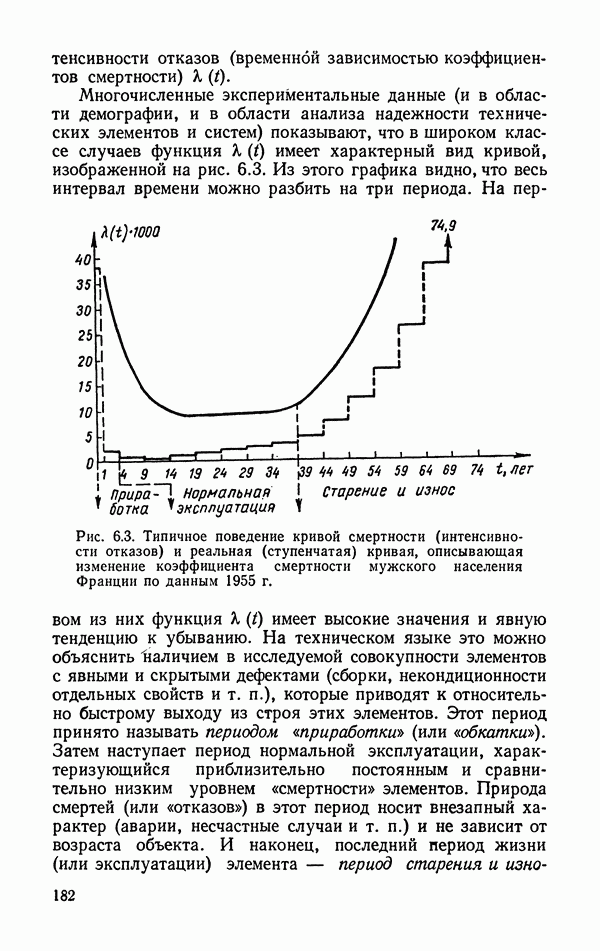
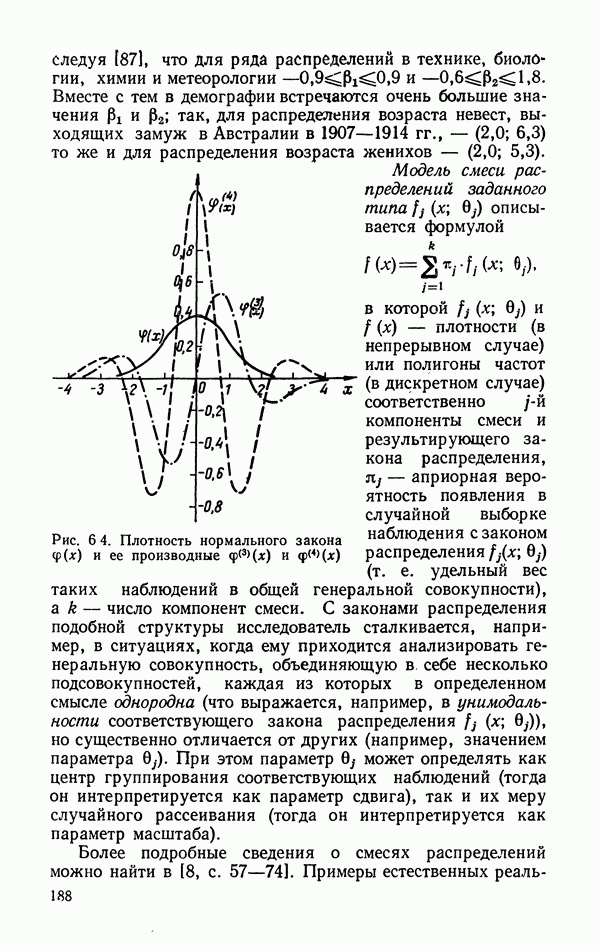
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Выводы
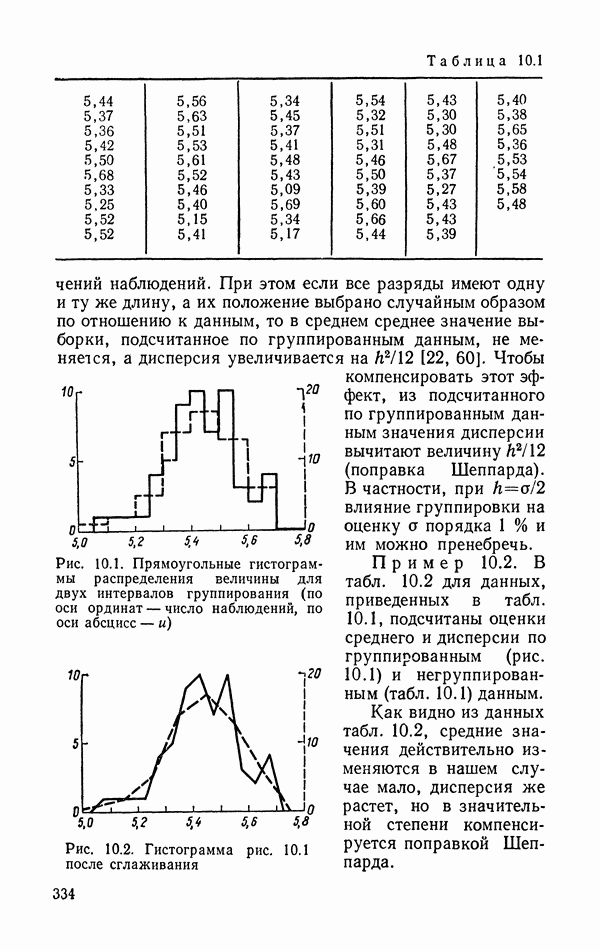
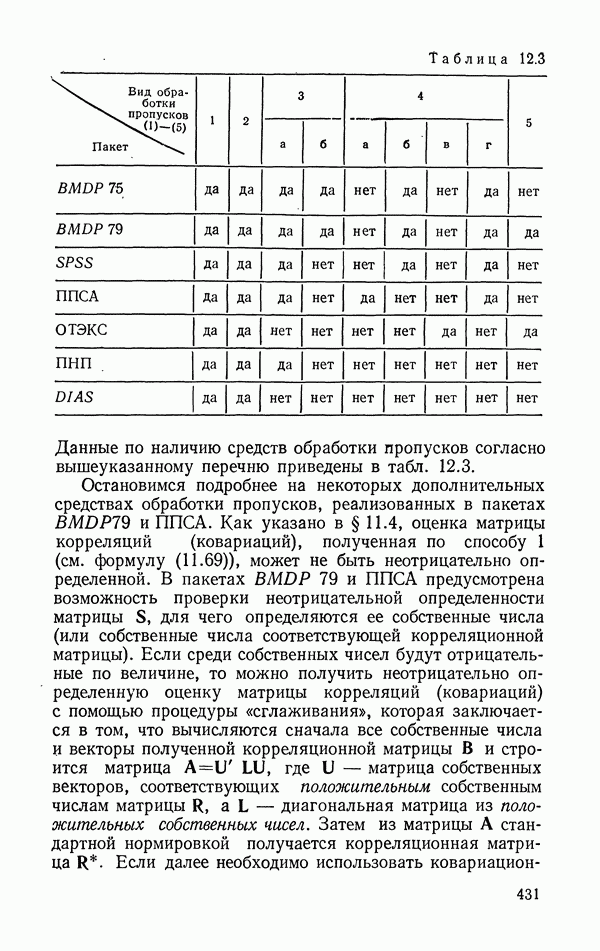
1. Тщательное ведение документации, описывающей организацию сбора данных, регистрируемые переменные и ход анализа, является одним из необходимых условий успешного выполнения исследования, особенно исследования большого объема. Современное состояние математического обеспечения ЭВМ позволяет достигнуть высокой степени автоматизации в выполнении этого процесса. Перед началом статистического анализа данные должны быть тщательно просмотрены и отредактированы.
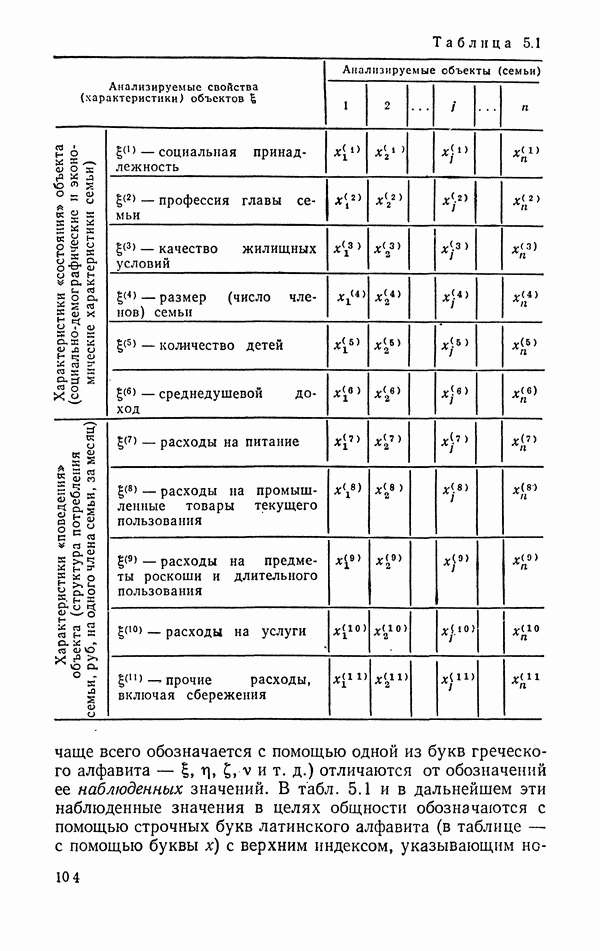
2. Измерения могут быть произведены в разных шкалах: номинальной, порядковой, интервалов и отношений. Каждому типу шкалы соответствует своя статистическая техника.
Существуют специальные математические методы, рассчитанные на использование многомерных данных, выраженных в шкалах разных типов. Однако более типичной для многомерного анализа является ситуация, когда шкалы однотипны. Чтобы достигнуть этого, либо переходят к переменным, принимающим только два значения: 0 и 1, либо производят так называемую оцифровку номинальных и порядковых величин.
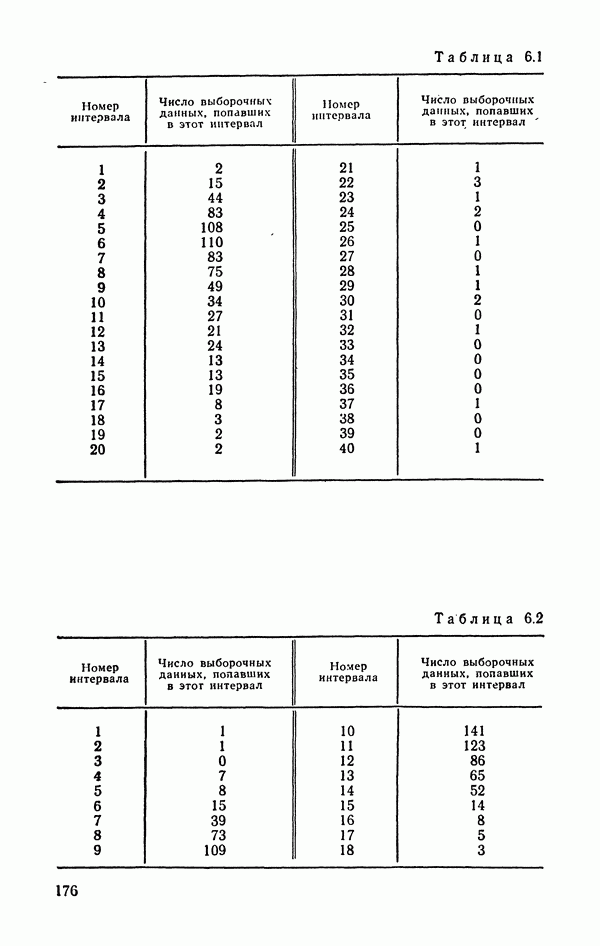
3. Наиболее распространенным методом оценки плотности распределения случайной величины является построение ее гистограммы или полигона частот. С помощью группированных данных можно оценивать также моменты распределения, но при этом приходится вводить поправки на группировку. При использовании ЭВМ доступны и так называемые непараметрические оценки плотности, основанные на усреднении «весов» отдельных наблюдений, «размазанных» в окрестности каждого наблюдения, с помощью специально выбранной весовой функции.
4. Часто используются специальные преобразования случайных величин для сведения их распределений к гауссовскому. В этом случае плотность распределения исходной величины равна нормальной плотности для соответствующего значения преобразованной величины, умноженной на якобиан преобразования (см. также (7.11)).
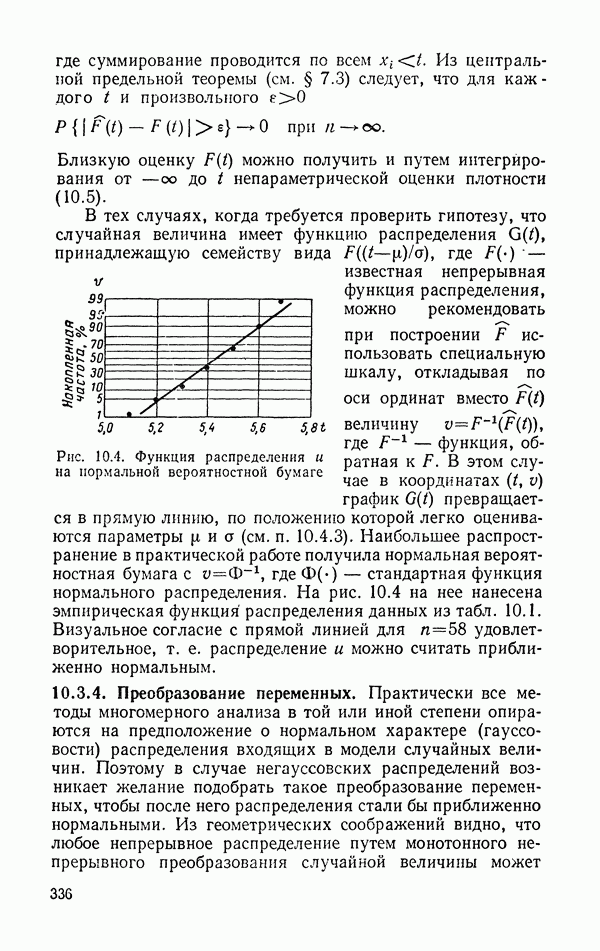
5. При графическом изображении функции распределения принято использовать специальные вероятностные бумаги, на которых распределения вида  , где F — известно, а
, где F — известно, а  — неизвестные параметры, изображаются в виде прямых линий. Наибольшее распространение получила нормальная вероятностная бумага.
— неизвестные параметры, изображаются в виде прямых линий. Наибольшее распространение получила нормальная вероятностная бумага.
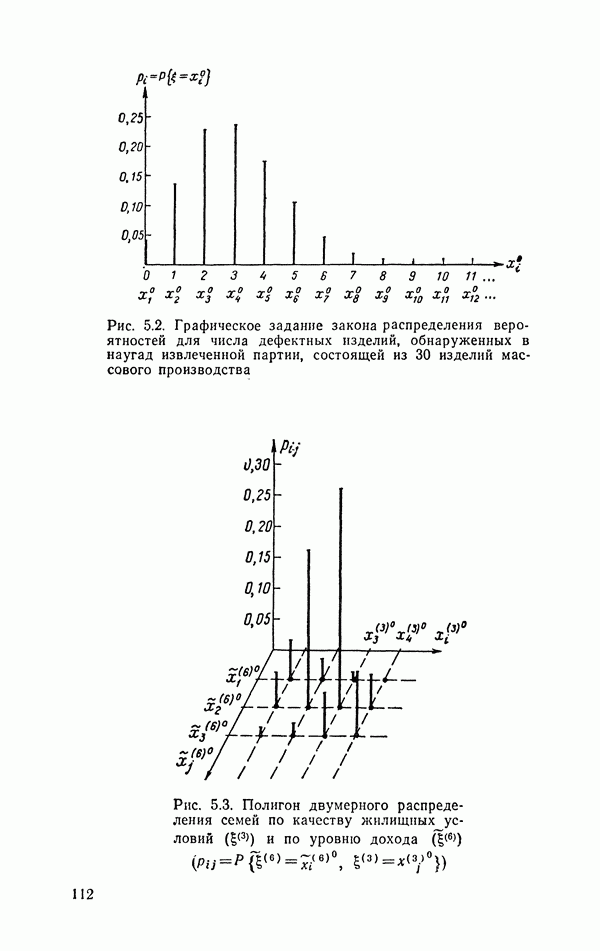
6. Для изображения многомерных распределений случайных величин, измеренных в номинальной и порядковых шкалах, широко используются таблицы сопряженности,  элемент которых показывает, сколько наблюдений в выборке имеют
элемент которых показывает, сколько наблюдений в выборке имеют  градацию первого признака,
градацию первого признака,  второго,
второго,  последнего. Наиболее часто проверяемая гипотеза в двумерных таблицах состоит в предположении независимости распределения первого и второго признаков.
последнего. Наиболее часто проверяемая гипотеза в двумерных таблицах состоит в предположении независимости распределения первого и второго признаков.
7. При работе с существенно многомерными данными часто возникает необходимость получения общего представления о взаимном расположении точек-наблюдений в соответствующем многомерном пространстве признаков. Все используемые
здесь методы опираются на понятие «расстояния» между точками. К наиболее распространенным приемам такого типа относится метод главных компонент, с помощью которого строятся проекции точек-наблюдений на направления наибольшей вытянутости данных.
В последние годы широкое распространение получили существенно опирающиеся на ЭВМ прямые методы поиска в пространстве невысокой размерности конфигурации точек, отождествляемых с наблюдаемыми объектами, такой, что расстояния между точками в этом пространстве в наибольшей степени (измеряемой с помощью специально выбранного функционала) соответствуют расстояниям между объектами. Эти методы получили название многомерного шкалирования. С теоретико-вероятностной и статистической точек зрения они изучены пока недостаточно.
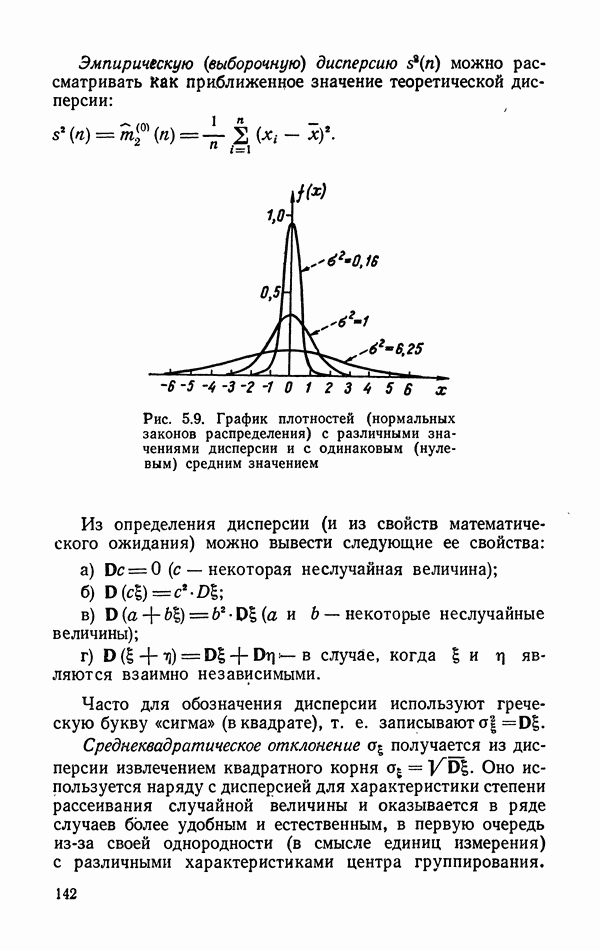
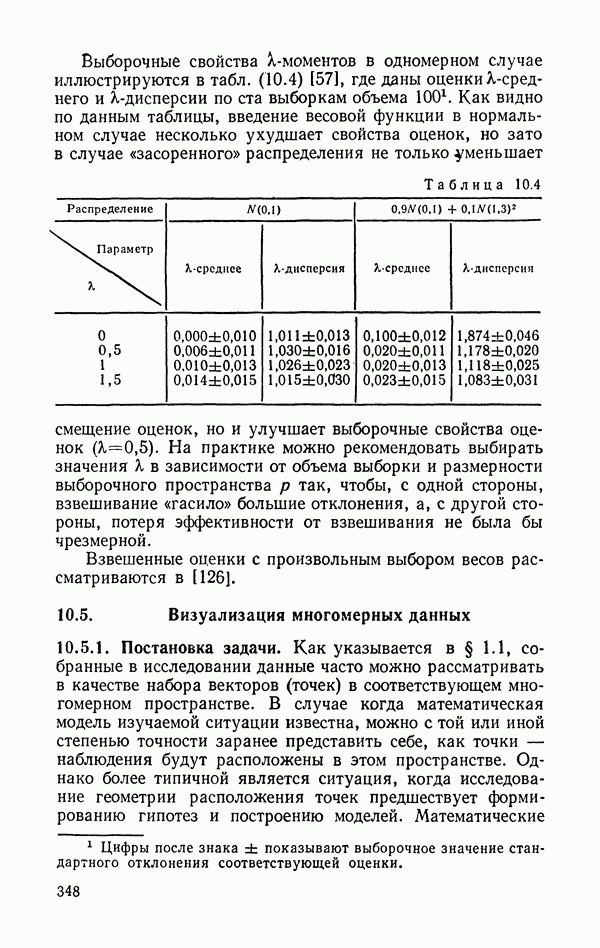
8. Для описания распределений, близких к гауссовским, традиционно используются среднее арифметическое и средний квадратический разброс. Однако этот подход не всегда удачен, поскольку указанные оценки быстро теряют свои оптимальные свойства при отклонениях распределений от нормального закона. В связи с этим приобретают значение методы хотя и менее эффективные в случае гауссовского распределения, но более устойчивые («робастные») к отклонениям от нормальности. В связи с этим следует вспомнить графические методы и давно забытую оценку параметра масштаба, основанную на среднем абсолютном отклонении.
В последние двадцать лет предложено и много других устойчивых оценок параметров. Среди них выделяются оценки, использующие при вычислении моментов взвешивание наблюдений с помощью степени плотности подходящим образом подобранного нормального закона.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.1.2. Два варианта интерпретации исходных данных и два подхода к их статистической обработке.
- 1.1.3. Основные этапы статистической обработки исходных данных.
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1. Теория вероятностей и условия ее применимости
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1. Для чего нужны математические модели
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей»
- 3.5.4. Геометрические модели.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1. Дискретное вероятностное пространство
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
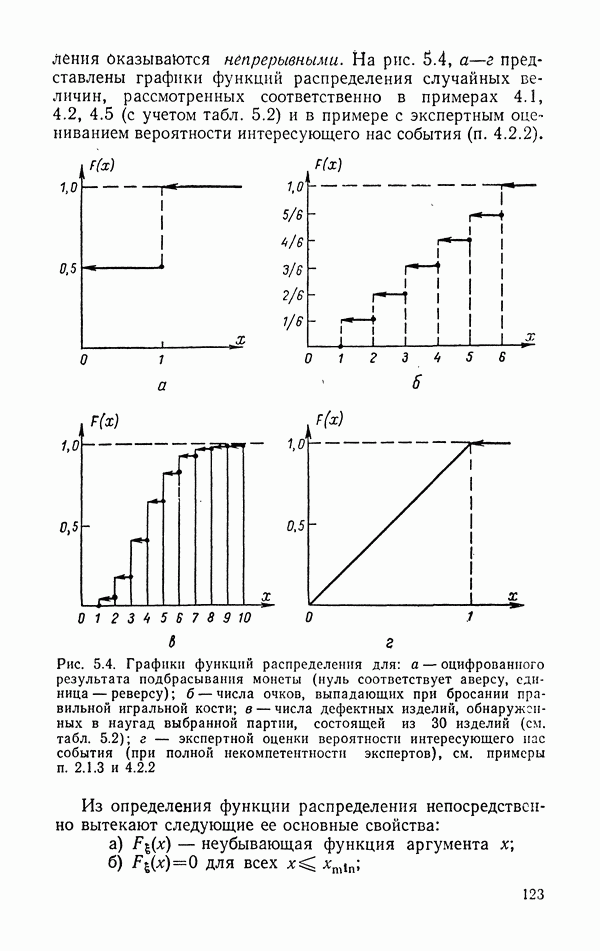
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.2. Характеристики центра группирования значений случайной величины.
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
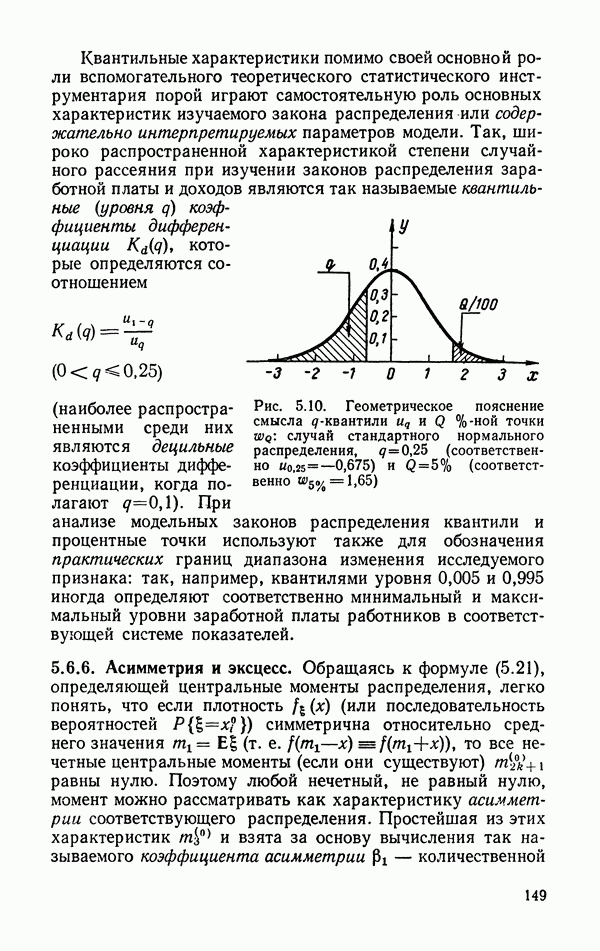
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
- 6.1.5. Нормальное (гауссовское) распределение.
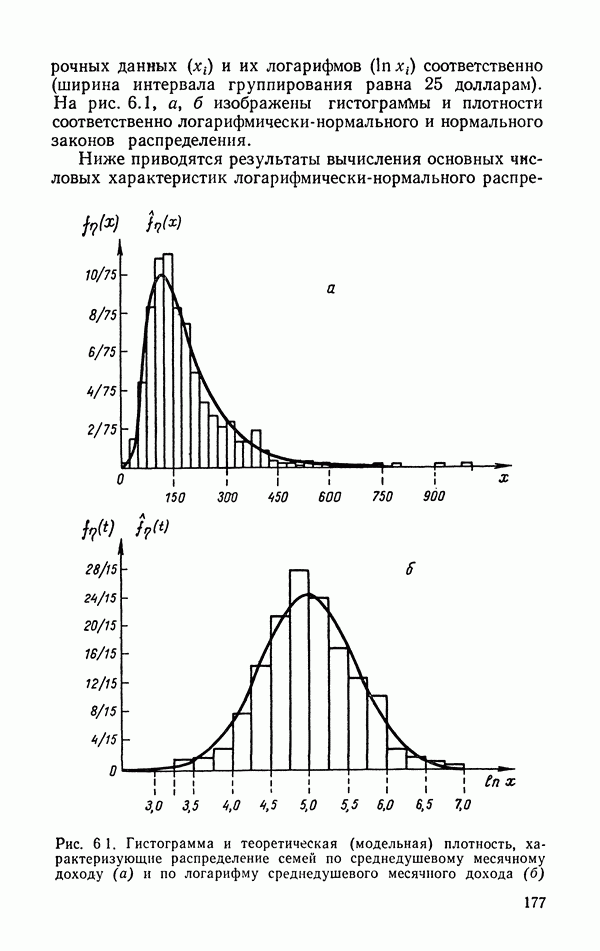
- 6.1.6. Логарифмически-нормальное распределение.
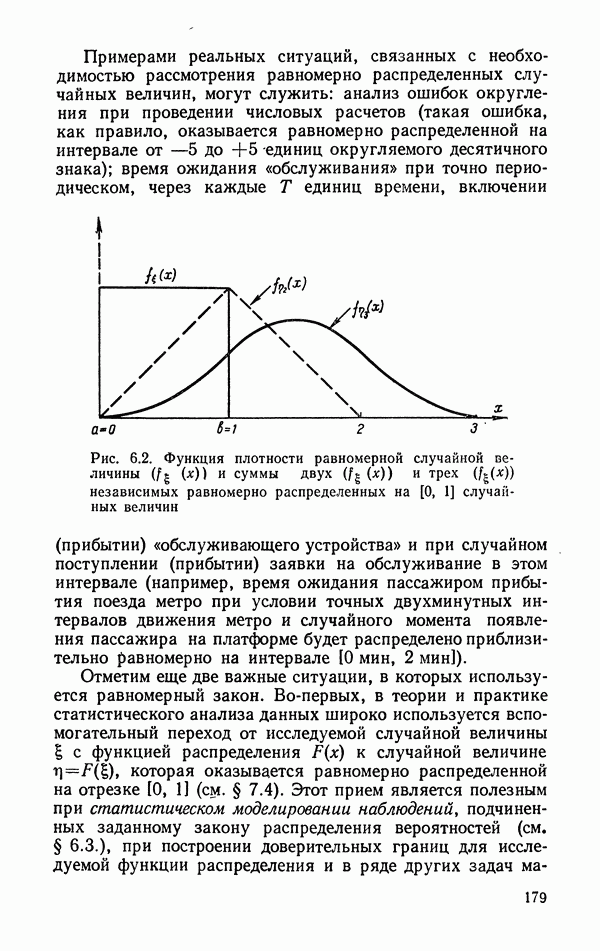
- 6.1.7. Равномерное (прямоугольное) распределение.
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
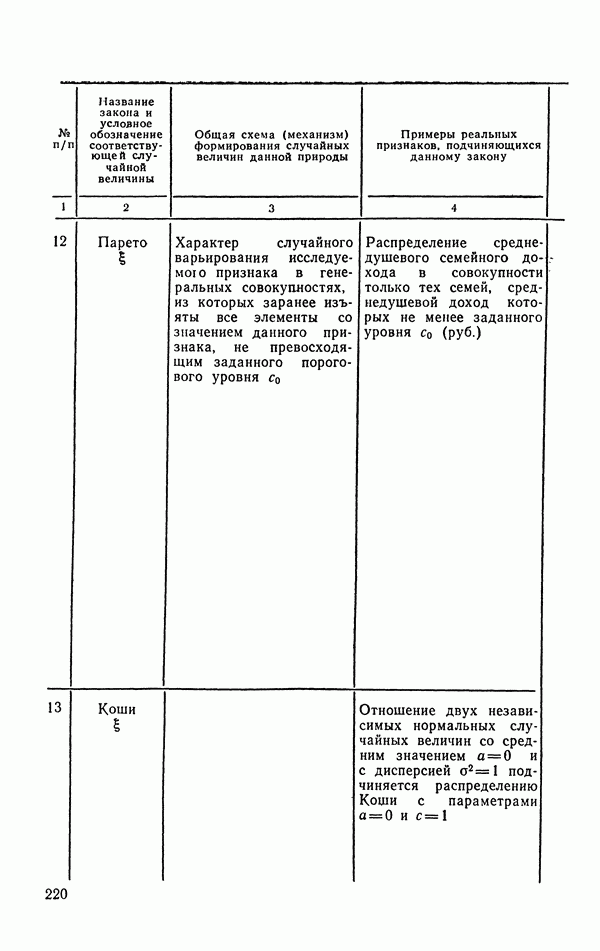
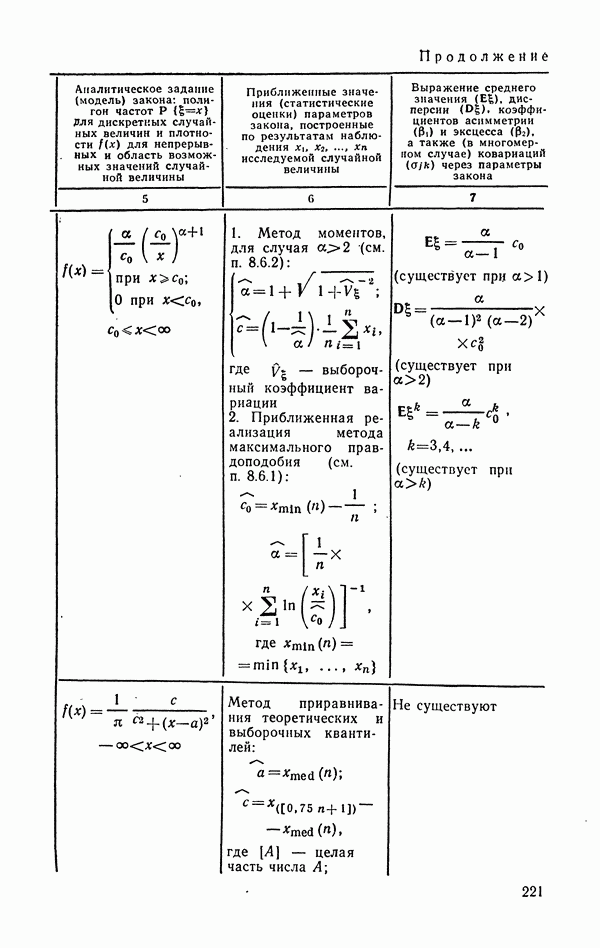
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
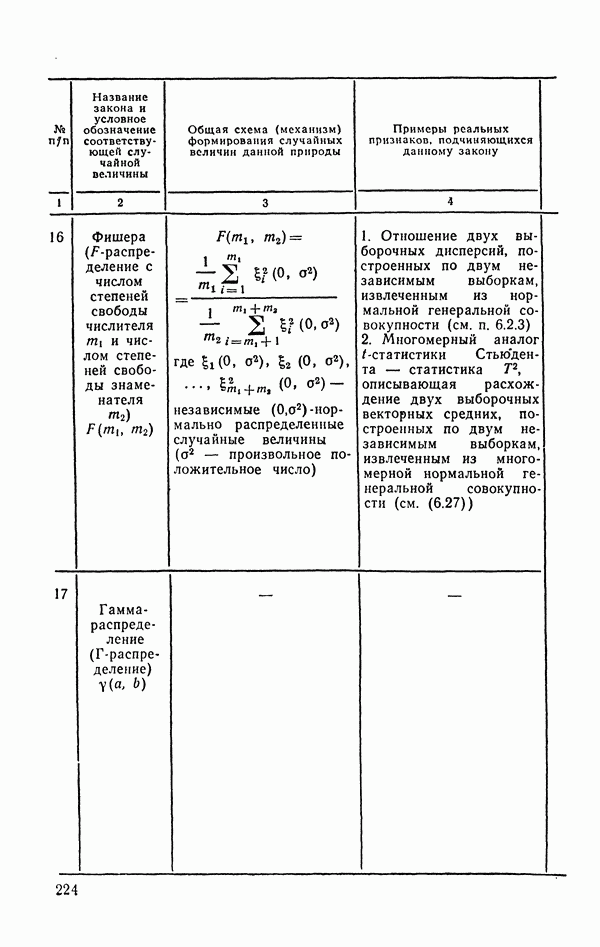
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
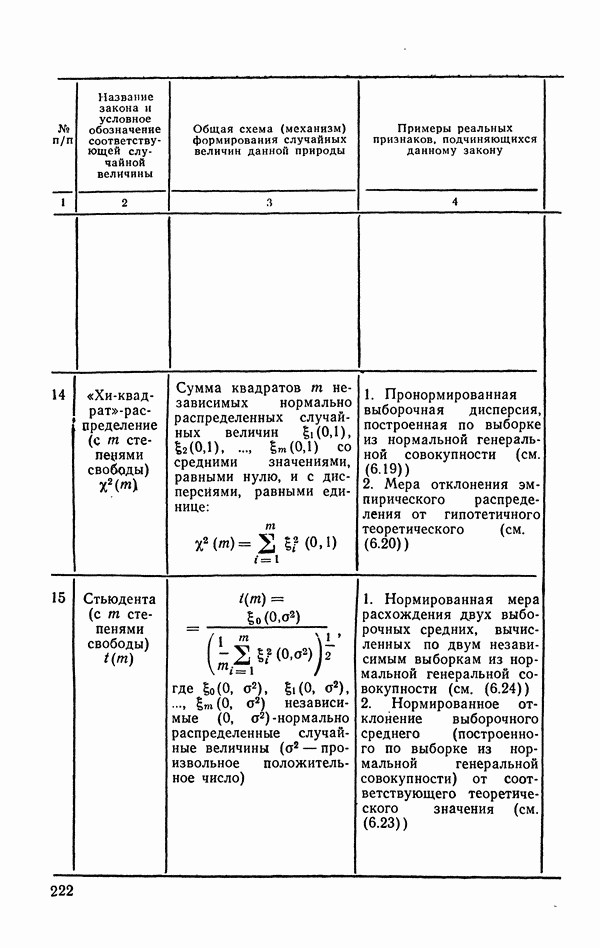
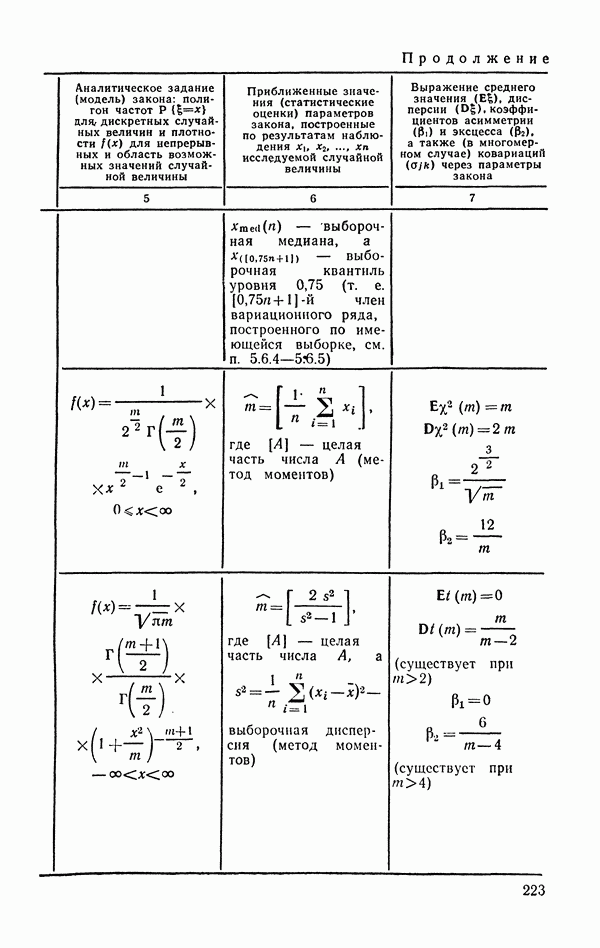
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных распределениях.
- 6.2.5. Г-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.2. Моделирование дискретных случайных величин. Стандартный метод.
- 6.3.3. Моделирование непрерывных распределений.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.2. Многомерная центральная предельная теорема (см. [12, с. 105]).
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
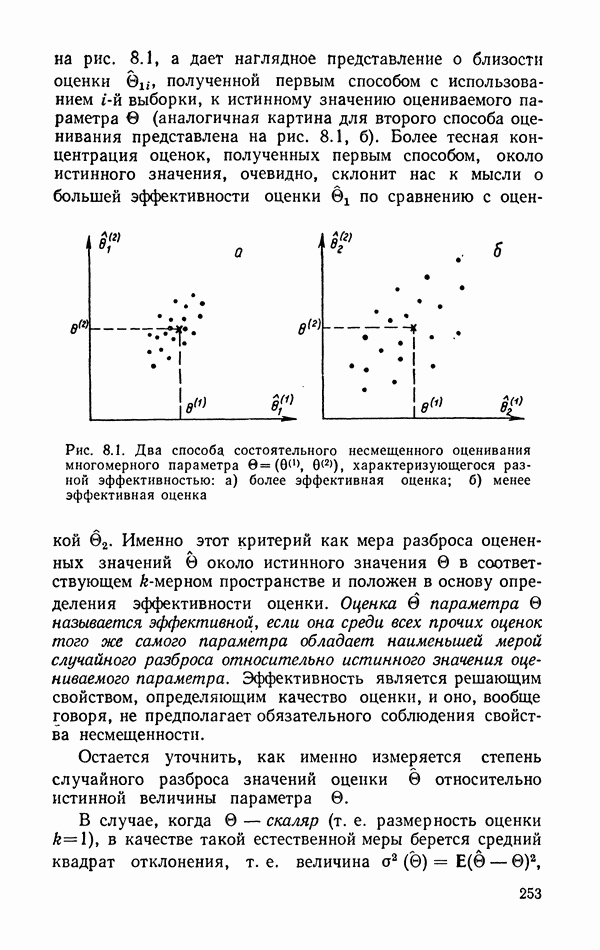
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия.
- 8.3. Неравенство Рао — Крамера — Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
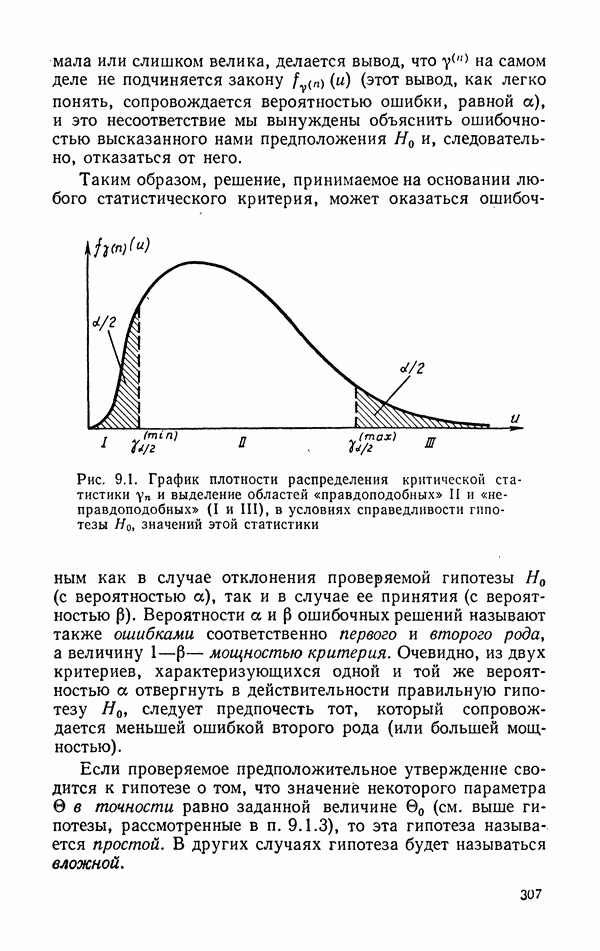
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.4. Оценивание параметров сдвига и масштаба
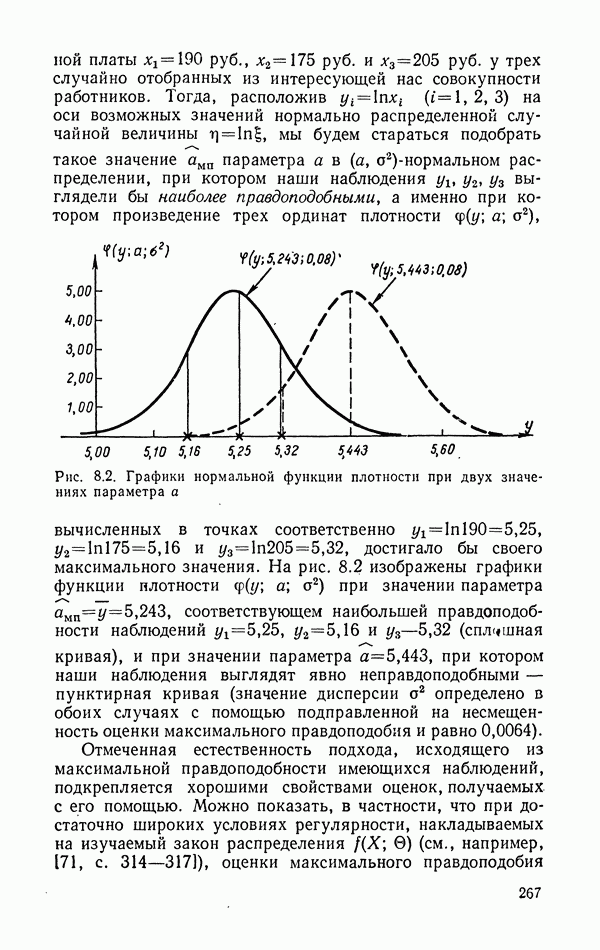
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4. Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1.1. Критерий «хи квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий w^2 (Крамера — Мнзеса — Смирнова).
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и w^2 для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- 11.1.7. Использование критериев согласия Колмогорова и w^2 в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.2. Критерий однородности «хи квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия.
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа w^2
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ