| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.6. Методы статистического оценивания неизвестных параметров
В предыдущем параграфе рассмотрены различные варианты использования функций от исходных наблюдений  в качестве оценок неизвестных параметров, анализировались их свойства. Однако пока не ясно, каким способом устанавливаются именно те комбинации результатов наблюдений (статистики), с помощью которых производится (да еще наилучшим в определенном смысле образом!) оценивание того или иного параметра. Каким образом, например, было установлено, что именно комбинации
в качестве оценок неизвестных параметров, анализировались их свойства. Однако пока не ясно, каким способом устанавливаются именно те комбинации результатов наблюдений (статистики), с помощью которых производится (да еще наилучшим в определенном смысле образом!) оценивание того или иного параметра. Каким образом, например, было установлено, что именно комбинации  (см. (8.3), (8.4)) лучше всего использовать в качестве оценок неизвестных параметров соответственно среднего значения
(см. (8.3), (8.4)) лучше всего использовать в качестве оценок неизвестных параметров соответственно среднего значения  ? и дисперсии
? и дисперсии  нормальной генеральной совокупности? И как конкретно строить
нормальной генеральной совокупности? И как конкретно строить
описанные выше доверительные интервалы и области для неизвестных значений параметров?
Описанию основных приемов, позволяющих получать ответы на данные вопросы, и посвящен настоящий параграф.
8.6.1. Метод максимального (наибольшего) правдоподобия.
В соответствии с этим методом оценка  неизвестного параметра
неизвестного параметра  по наблюдениям
по наблюдениям  случайной величины
случайной величины  (подчиненной закону распределения
(подчиненной закону распределения  , где
, где  — плотность или вероятность
— плотность или вероятность  определяется из условия
определяется из условия

где L — функция правдоподобия, определенная соотношением (8.5).
Таким образом, в формальной записи оценка максимального правдоподобия  параметра
параметра  по независимым наблюдениям
по независимым наблюдениям  может быть представлена в виде
может быть представлена в виде

Естественность подобного подхода к определению статистических оценок вытекает из смысла функции правдоподобия. Действительно, по определению (см. § 8.2), функция  при каждом фиксированном значении параметра
при каждом фиксированном значении параметра  является мерой правдоподобности получения системы наблюдений, равных
является мерой правдоподобности получения системы наблюдений, равных  Поэтому, изменяя значения параметра
Поэтому, изменяя значения параметра  при данных конкретных (имеющихся у нас) величинах
при данных конкретных (имеющихся у нас) величинах  мы можем проследить, при каких значениях
мы можем проследить, при каких значениях  эти наблюдения являются более правдоподобными у а при каких — менее и выбрать в конечном счете такое значение параметра
эти наблюдения являются более правдоподобными у а при каких — менее и выбрать в конечном счете такое значение параметра  при котором имеющаяся у нас система наблюдений
при котором имеющаяся у нас система наблюдений  выглядит наиболее правдоподобной (очевидно, что это значение
выглядит наиболее правдоподобной (очевидно, что это значение  определяется конкретными величинами наблюдений
определяется конкретными величинами наблюдений  , т. е. является некоторой функцией от них). Так, например, пусть
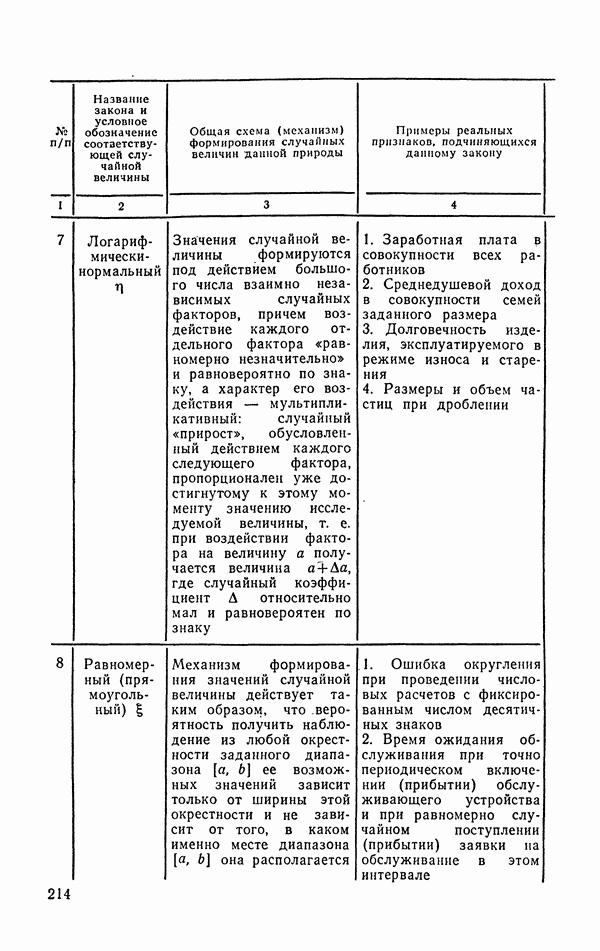
, т. е. является некоторой функцией от них). Так, например, пусть  — заработная плата работников, подчиненная логарифмически-нормальному распределению (см. п. 6.1.6). И пусть с целью приближенной оценки средней величины логарифма заработной платы работников
— заработная плата работников, подчиненная логарифмически-нормальному распределению (см. п. 6.1.6). И пусть с целью приближенной оценки средней величины логарифма заработной платы работников  мы зафиксировали значения заработной
мы зафиксировали значения заработной
платы  у трех случайно отобранных из интересующей нас совокупности работников. Тогда, расположив
у трех случайно отобранных из интересующей нас совокупности работников. Тогда, расположив  на оси возможных значений нормально распределенной случайной величины
на оси возможных значений нормально распределенной случайной величины  мы будем стараться подобрать такое значение
мы будем стараться подобрать такое значение  параметра а в
параметра а в  -нормальном распределении, при котором наши наблюдения
-нормальном распределении, при котором наши наблюдения  выглядели бы наиболее правдоподобными, а именно при котором произведение трех ординат плотности
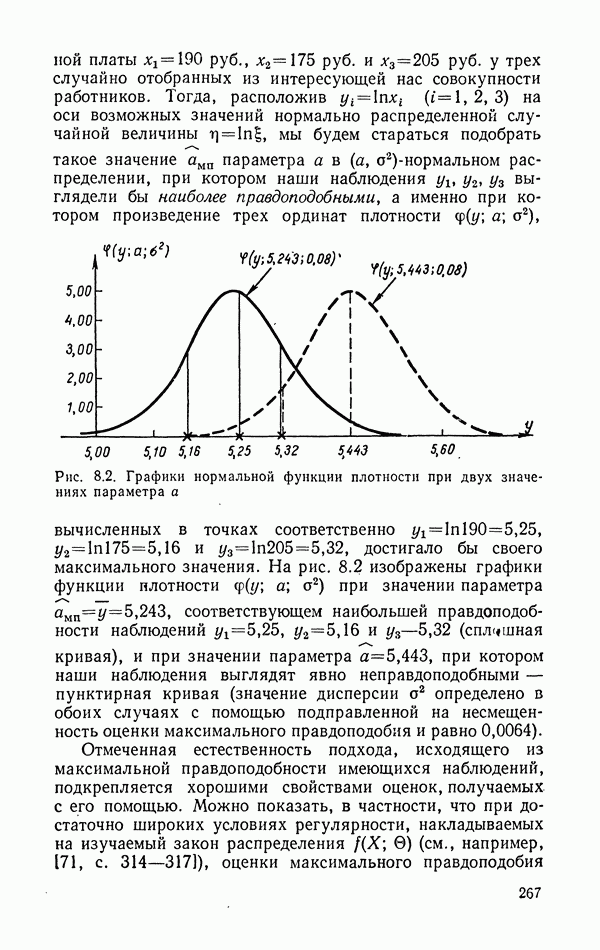
выглядели бы наиболее правдоподобными, а именно при котором произведение трех ординат плотности  вычисленных в точках соответственно
вычисленных в точках соответственно  достигало бы своего максимального значения.
достигало бы своего максимального значения.

Рис. 8.2. Графики нормальной функции плотности при двух значениях параметра а
На рис. 8.2 изображены графики функции плотности  при значении параметра
при значении параметра  соответствующем наибольшей правдоподобности наблюдений
соответствующем наибольшей правдоподобности наблюдений  (сплошная кривая), и при значении параметра
(сплошная кривая), и при значении параметра  при котором наши наблюдения выглядят явно неправдоподобными — пунктирная кривая (значение дисперсии
при котором наши наблюдения выглядят явно неправдоподобными — пунктирная кривая (значение дисперсии  определено в обоих случаях с помощью подправленной на несмещенность оценки максимального правдоподобия и равно 0,0064).
определено в обоих случаях с помощью подправленной на несмещенность оценки максимального правдоподобия и равно 0,0064).
Отмеченная естественность подхода, исходящего из максимальной правдоподобности имеющихся наблюдений, подкрепляется хорошими свойствами оценок, получаемых с его помощью. Можно показать, в частности, что при достаточно широких условиях регулярности, накладываемых на изучаемый закон распределения  (см., например, 171, с. 314-317]), оценки максимального правдоподобия
(см., например, 171, с. 314-317]), оценки максимального правдоподобия
 параметра
параметра  являются состоятельными, асимптотически-несмещенными, асимптотически-нормальными и асимптотически-эффективными (т. е. их ковариационная матрица
являются состоятельными, асимптотически-несмещенными, асимптотически-нормальными и асимптотически-эффективными (т. е. их ковариационная матрица  ) асимптотически имеет вид
) асимптотически имеет вид  где
где  информационная матрица Фишера, определенная соотношениями (8.7) применительно к единственному наблюдению, т. е. при
информационная матрица Фишера, определенная соотношениями (8.7) применительно к единственному наблюдению, т. е. при 
Однако из этого не следует, что оценки максимального правдоподобия будут наилучшими во всех сйтуациях. Во-первых, их хорошие свойства проявляются часто лишь при очень больших объемах выборок (т. е. являются асимптотическими, см. § 8.4), так что при малых  с ними могут конкурировать (и даже превосходить их) другие оценки, например оценки метода моментов, метода наименьших квадратов и т. д. (см., ниже, п. 8.6.2-8.6.5). Во-вторых, и это, пожалуй, главное «узкое место» данного подхода, для построения оценок максимального правдоподобия и обеспечения их хороших свойств необходимо точное знание типа анализируемого закона распределения
с ними могут конкурировать (и даже превосходить их) другие оценки, например оценки метода моментов, метода наименьших квадратов и т. д. (см., ниже, п. 8.6.2-8.6.5). Во-вторых, и это, пожалуй, главное «узкое место» данного подхода, для построения оценок максимального правдоподобия и обеспечения их хороших свойств необходимо точное знание типа анализируемого закона распределения  что в большинстве случаев оказывается практически нереальным. В подобных ситуациях бывает выгоднее искать не оценку, являющуюся наилучшей в рамках данного конкретного общего вида
что в большинстве случаев оказывается практически нереальным. В подобных ситуациях бывает выгоднее искать не оценку, являющуюся наилучшей в рамках данного конкретного общего вида  (но, как часто бывает, резко теряющую свои хорошие свойства при отклонениях реального распределения от типа
(но, как часто бывает, резко теряющую свои хорошие свойства при отклонениях реального распределения от типа  ), а оценку, хотя и не наилучшую в рамках совокупности
), а оценку, хотя и не наилучшую в рамках совокупности  но обладающую достаточно устойчивыми свойствами в более широком классе распределений, включающем в себя
но обладающую достаточно устойчивыми свойствами в более широком классе распределений, включающем в себя  в качестве частного случая (см. ниже, п. 8.6.4). Подобные оценки принято называть устойчивыми или робастными (английский термин robust estimation означает грубое, или устойчивое, оценивание). И наконец, оценки максимального правдоподобия могут не быть даже состоятельными, если число k оцениваемых по выборке параметров
в качестве частного случая (см. ниже, п. 8.6.4). Подобные оценки принято называть устойчивыми или робастными (английский термин robust estimation означает грубое, или устойчивое, оценивание). И наконец, оценки максимального правдоподобия могут не быть даже состоятельными, если число k оцениваемых по выборке параметров  велико (имеет тот же порядок, что и объем выборки
велико (имеет тот же порядок, что и объем выборки  ) и растет вместе с увеличением числа наблюдений. Ниже приведен пример подобной ситуации (см. пример 8.7).
) и растет вместе с увеличением числа наблюдений. Ниже приведен пример подобной ситуации (см. пример 8.7).
Попытаемся ответить на вопрос, как конкретно находятся оценки максимального правдоподобия, т. е. как проводится решение оптимизационной задачи типа (8.19).
Если функция  удовлетворяет определенным условиям регулярности (дифференцируемость по
удовлетворяет определенным условиям регулярности (дифференцируемость по  и т. п., см. условия а)-в) § 8.3) и экстремум в (8.19) достигается
и т. п., см. условия а)-в) § 8.3) и экстремум в (8.19) достигается
во внутренней точке области допустимых значений неизвестного параметра  то в точке
то в точке  должны обращаться в нуль частные производные функции
должны обращаться в нуль частные производные функции  а следовательно, к логарифмической функции правдоподобия
а следовательно, к логарифмической функции правдоподобия

в силу монотонного характера этой зависимости: последняя удобнее для вычислений. Значит, в данном случае оценка максимального правдоподобия  должна удовлетворять уравнениям:
должна удовлетворять уравнениям:

и может определяться в качестве решения этой системы уравнений.
Однако могут быть ситуации (случай нерегулярных по 0 законов распределения), когда система (8.21) не определена или не имеет решений, в то время как решение (8.19) существует. В подобных ситуациях оценку  следует искать другими способами, в том числе с помощью непосредственного подбора решения (8.19) (см. ниже примеры 8.5 и 8.6).
следует искать другими способами, в том числе с помощью непосредственного подбора решения (8.19) (см. ниже примеры 8.5 и 8.6).
Пример 8.3. Исследуемая случайная величина  имеет нормальную плотность вероятности
имеет нормальную плотность вероятности

с неизвестным средним значением  и неизвестной дисперсией
и неизвестной дисперсией 
В соответствии с (8.5) функция правдоподобия в этом случае будет

Соответствующая логарифмическая функция правдоподобия

Дифференцируя  по
по  и последовательно приравнивая соответствующие частные производные к нулю, получаем конкретный вид системы (8.21):
и последовательно приравнивая соответствующие частные производные к нулю, получаем конкретный вид системы (8.21):

Решение этой системы относительно а и  дает оценки максимального правдоподобия этих параметров:
дает оценки максимального правдоподобия этих параметров:

Выше (см. § 8.3) установлено, что оценка  является эффективной оценкой параметра а (так как ее эффективность
является эффективной оценкой параметра а (так как ее эффективность  а оценка
а оценка  — асимптотически-эффекгивной оценкой параметра
— асимптотически-эффекгивной оценкой параметра  (так как ее эффективность
(так как ее эффективность  )
) 
Пример 8.4. Исследуемая случайная величина  подчинена закону распределения Пуассона, т. е.
подчинена закону распределения Пуассона, т. е.

с неизвестным значением параметра К.
В соответствии с (8.20) логарифмическая функция правдоподобия, построенная по выборке  имеет вид
имеет вид

Отсюда после дифференцирования по X получаем уравнение метода максимального правдоподобия

откуда

Легко видеть, что эта оценка несмещенная, так как

Вычислим эффективность оценки  Нижняя граница дисперсии по всем возможным оценкам параметра X может быть вычислена в соответствии с неравенством информации (8.12):
Нижняя граница дисперсии по всем возможным оценкам параметра X может быть вычислена в соответствии с неравенством информации (8.12):

Дисперсию оценки  вычислим, опираясь на следующий известный факт (см., например, [48, с. 229]): сумма независимых случайных величин
вычислим, опираясь на следующий известный факт (см., например, [48, с. 229]): сумма независимых случайных величин  подчиняющихся распределению Пуассона со средними значениями соответственно
подчиняющихся распределению Пуассона со средними значениями соответственно  ХПУ имеет распределение Пуассона со средним значением, равным Поэтому дисперсия
ХПУ имеет распределение Пуассона со средним значением, равным Поэтому дисперсия

Сравнивая  с
с  убеждаемся, что оценка максимального правдоподобия среднего значения пуассоновской случайной величины является эффективной.
убеждаемся, что оценка максимального правдоподобия среднего значения пуассоновской случайной величины является эффективной.
Пример 8.5. Исследуемая случайная величина  распределена по равномерному закону (см. п. 6.1.7), т. е.
распределена по равномерному закону (см. п. 6.1.7), т. е.

где параметры а и b неизвестны (подлежат оцениванию).
Легко проверить, что это — случай нерегулярный (в первую очередь потому, что область возможных значений исследуемого признака, в которой плотность положительна, зависит от оцениваемых по выборке параметров а и b). Поэтому обычная техника, использующая уравнения (8.21) метода максимального правдоподобия, здесь неприменима. Однако в этом случае экстремальная задача (8.19) может быть решена непосредственно.
Действительно,

причем область допустимых значений параметров a и b, где производится поиск тех значений  , при которых
, при которых  описывается соотношениями:
описывается соотношениями:

где  — имеющиеся в нашем распоряжении наблюдения исследуемой случайной величины. Очевидно, решение экстремальной задачи
— имеющиеся в нашем распоряжении наблюдения исследуемой случайной величины. Очевидно, решение экстремальной задачи

дается соотношениями:

Опираясь на результаты п. 5.6.4 (см. также п. 8.6.4), можно подсчитать:
 (8.22)
(8.22)
Использовать неравенство информации для вычисления нижней границы дисперсии этих оценок мы не можем, так как случай нерегулярный. Из (8.22) видно, что величины  характеризуют одновременно средний квадрат отклонения «подправленных на несмещенность» оценок
характеризуют одновременно средний квадрат отклонения «подправленных на несмещенность» оценок

от истинных значений параметров а и b.
Пример 8.6. Снова рассмотрим задачу оценивания параметра сдвига  в экспоненциальном распределении, задаваемом плотностью
в экспоненциальном распределении, задаваемом плотностью

Как и в предыдущем примере, имеем дело с нерегулярным случаем. Поэтому приходится непосредственно решать экстремальную задачу вида

Легко видеть, что  является решением этой задачи: при любом другом
является решением этой задачи: при любом другом  , удовлетворяющем условию (8.22), очевидно
, удовлетворяющем условию (8.22), очевидно

и, следовательно,

Опираясь на результаты п. 5.6.4 (см. также п. 8.6.4), можно подсчитать:
 (8.23)
(8.23)
Однако оценка  получающаяся из оценки
получающаяся из оценки  «подправлением на несмещенность», будет иметь средний квадрат отклонения
«подправлением на несмещенность», будет иметь средний квадрат отклонения

Пример 8.7 (заимствован из [22, с. 187]). Рассмотрим ситуацию, когда метод максимального правдоподобия не приводит к состоятельной оценке.
С целью оценки  концентраций некоторого элемента
концентраций некоторого элемента  в лаборатории производились двукратные измерения
в лаборатории производились двукратные измерения  каждой из концентраций
каждой из концентраций  . Предполагается, что все
. Предполагается, что все  результатов измерений
результатов измерений  имеют одинаковую точность и являются независимыми нормальными случайными величинами (см. п. 6.1.5), так что в качестве функции правдоподобия получаем
имеют одинаковую точность и являются независимыми нормальными случайными величинами (см. п. 6.1.5), так что в качестве функции правдоподобия получаем

Неизвестными параметрами являются  средних значений
средних значений  и дисперсия
и дисперсия  . Нетрудно получить оценки максимального правдоподобия параметров
. Нетрудно получить оценки максимального правдоподобия параметров 

Решая теперь уравнение максимального правдоподобия (8.21), в которое вместо  подставлены значения
подставлены значения  получаем
получаем

Нетрудно подсчитать, что  т. е. метод максимального правдоподобия дает в этом случае оценку параметра
т. е. метод максимального правдоподобия дает в этом случае оценку параметра  с постоянным (асимптотически-неустранимым) отрицательным смещением, равным
с постоянным (асимптотически-неустранимым) отрицательным смещением, равным  . В качестве наилучшей несмещенной оценки следовало бы выбрать в данном случае статистику
. В качестве наилучшей несмещенной оценки следовало бы выбрать в данном случае статистику

8.6.2. Метод моментов. Пусть, как и прежде,  — исследуемая
— исследуемая  -мерная случайная величина, подчиняющаяся закону распределения
-мерная случайная величина, подчиняющаяся закону распределения  , где функция
, где функция  — плотность вероятности, если
— плотность вероятности, если  непрерывна, и вероятность
непрерывна, и вероятность  если
если  дискретна, зависит от некоторого, вообще говоря, многомерного параметра
дискретна, зависит от некоторого, вообще говоря, многомерного параметра  . И пусть мы хотим оценить неизвестное значениехэтого параметра, т. е. построить оценку
. И пусть мы хотим оценить неизвестное значениехэтого параметра, т. е. построить оценку  по имеющейся в нашем распоряжении выборке, состоящей из независимых наблюдений
по имеющейся в нашем распоряжении выборке, состоящей из независимых наблюдений  где
где 
Метод моментов заключается в приравнивании определенного количества выборочных моментов к соответствующим теоретическим (т. е. вычисленным с использованием функции  ) моментам исследуемой случайной величины, причем последние, очевидно, являются функциями от неизвестных параметров
) моментам исследуемой случайной величины, причем последние, очевидно, являются функциями от неизвестных параметров  . Рассматривая количество моментов, равное числу k подлежащих оценке параметров, и решая полученные уравнения относительно этих параметров, мы получаем искомые оценки. Таким образом, оценки по методу моментов неизвестных параметров
. Рассматривая количество моментов, равное числу k подлежащих оценке параметров, и решая полученные уравнения относительно этих параметров, мы получаем искомые оценки. Таким образом, оценки по методу моментов неизвестных параметров  являются решениями системы уравнений:
являются решениями системы уравнений:

(очевидно, если анализируемая случайная величина  дискретна, интегралы в левых частях (8.25) следует заменить соответствующими суммами типа
дискретна, интегралы в левых частях (8.25) следует заменить соответствующими суммами типа 
Число уравнений в системе (8.25) должно быть равным числу k оцениваемых параметров. Вопрос о том, какие именно моменты включать в систему (8.25) (начальные, центральные или их некоторые модификации типа коэффициентов асимметрии или эксцесса), следует решать, руководствуясь конкретными целями исследования и сравнительной простотой формы зависимости альтернативных теоретических характеристик от оцениваемых параметров 
В статистической практике дело редко доходит даже до моментов четвертого порядка (исключение составляет, пожалуй, практика эксплуатации так называемой «системы кривых Пирсона», см., например, [16, с. 101], однако этот чисто формальный аппарат подгонки эмпирического распределения под одну из теоретических кривых практически не в состоянии, с нашей точки зрения, решать сколь-нибудь интересные задачи содержательного статистического анализа данных).
К достоинствам метода моментов следует отнести его сравнительно простую вычислительную реализацию, а также то, что оценки, полученные в качестве решений системы (8.25), являются функциями от выборочных моментов. Это упрощает исследование статистических свойств оценок метода моментов: можно показать (см. [48, гл. 27 и  ), что при довольно общих условиях распределение оценки такого рода при больших
), что при довольно общих условиях распределение оценки такого рода при больших  асимптотически-нормально, среднее значение такой оценки отличается от истинного значения параметра на величину порядка
асимптотически-нормально, среднее значение такой оценки отличается от истинного значения параметра на величину порядка  а стандартное
а стандартное  отклонение
отклонение  асимптотически имеет вид
асимптотически имеет вид  , где с — некоторая постоянная величина.
, где с — некоторая постоянная величина.
В то же время, как показал Р. Фишер (см. [48]), асимптотическая эффективность оценок, полученных методом моментов, оказывается, как правило, меньше единицы, и в этом отношении они уступают оценкам, полученным методом максимального правдоподобия. Тем не менее метод моментов часто очень удобен на практике. Иногда оценки, получаемые с помощью метода моментов, принимаются в качестве первого приближения, по которому можно определять другими методами оценки более высокой эффективности.
Вернемся к нашим примерам.
В примере 8.3 в качестве системы (8.25) имеем:

что дает уже знакомые нам по методу максимального правдоподобия оценки для параметров:

Нормальное распределение, так же как и распределение Пуассона (в чем легко убедиться, обратившись к примеру 8.4), относится к тем редким случаям, когда оценки по методу моментов совпадают с оценками по методу максимального правдоподобия.
Построение системы (8.25) в примере 8.5 дает:

Откуда легко получаем оценки:

Можно сравнить асимптотическую эффективность оценок, полученных методом максимального правдоподобия и методом моментов: учитывая, что дисперсия оценок (8.26) как дисперсия функций выборочных моментов  имеет порядок
имеет порядок  (см. [48, с. 388]), и принимая во внимание соотношение (8.22), в соответствии с которым дисперсии оценок по методу максимального правдоподобия
(см. [48, с. 388]), и принимая во внимание соотношение (8.22), в соответствии с которым дисперсии оценок по методу максимального правдоподобия
тех же параметров имеют порядок  получаем, что эффективность
получаем, что эффективность  в сравнении с эффективностью
в сравнении с эффективностью  и
и  стремится к нулю при
стремится к нулю при 
Реализация метода моментов в примере 8.6 дает

Следовательно, 
Для подсчета среднего значения и дисперсии оценки  воспользуемся следующими фактами: а) случайную величину
воспользуемся следующими фактами: а) случайную величину  распределенную экспоненциально с параметром
распределенную экспоненциально с параметром  и с параметром сдвига
и с параметром сдвига  (см. п. 6.1.8), можно интерпретировать как частный случай гамма-распределенной случайной величины с параметрами
(см. п. 6.1.8), можно интерпретировать как частный случай гамма-распределенной случайной величины с параметрами  и с параметром сдвига
и с параметром сдвига  (см. п. 6.2.5); б) сумма
(см. п. 6.2.5); б) сумма  независимых случайных величин
независимых случайных величин  каждая из которых распределена по закону гамма с параметрами
каждая из которых распределена по закону гамма с параметрами  и с параметром сдвига 0, подчиняется гамма-распределению с параметрами
и с параметром сдвига 0, подчиняется гамма-распределению с параметрами  и с тем же самым параметром сдвига
и с тем же самым параметром сдвига  (см. п. 6.2.5). Поэтому
(см. п. 6.2.5). Поэтому

Учитывая выражение (8.24) для среднего квадрата ошибки «подправленной» оценки по методу максимального правдоподобия  того же параметра
того же параметра  получаем
получаем

т. е. и в этом случае асимптотическая эффективность оценки по методу моментов стремится к нулю.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.1.2. Два варианта интерпретации исходных данных и два подхода к их статистической обработке.
- 1.1.3. Основные этапы статистической обработки исходных данных.
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1. Теория вероятностей и условия ее применимости
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1. Для чего нужны математические модели
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей»
- 3.5.4. Геометрические модели.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1. Дискретное вероятностное пространство
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
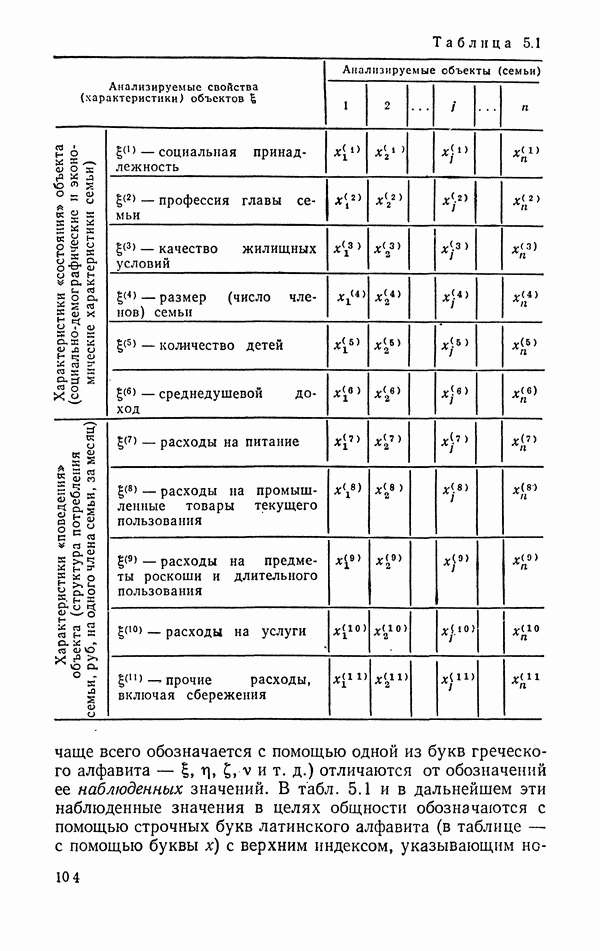
- 5.2. Возможные и наблюденные значения случайной величины
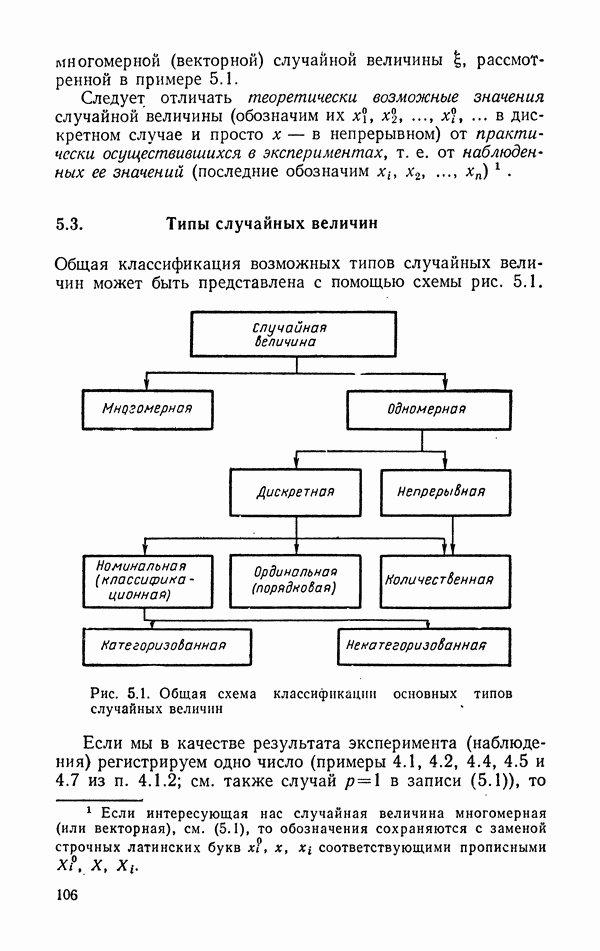
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.2. Характеристики центра группирования значений случайной величины.
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
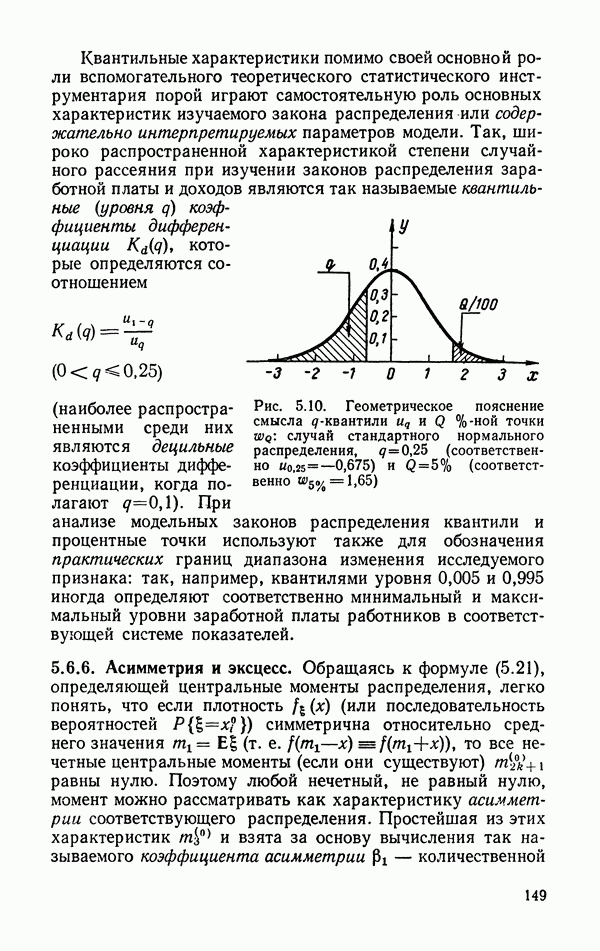
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
- 6.1.5. Нормальное (гауссовское) распределение.
- 6.1.6. Логарифмически-нормальное распределение.
- 6.1.7. Равномерное (прямоугольное) распределение.
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных распределениях.
- 6.2.5. Г-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.2. Моделирование дискретных случайных величин. Стандартный метод.
- 6.3.3. Моделирование непрерывных распределений.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.2. Многомерная центральная предельная теорема (см. [12, с. 105]).
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия.
- 8.3. Неравенство Рао — Крамера — Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4. Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1.1. Критерий «хи квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий w^2 (Крамера — Мнзеса — Смирнова).
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и w^2 для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- 11.1.7. Использование критериев согласия Колмогорова и w^2 в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.2. Критерий однородности «хи квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия.
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа w^2
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ