| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
12.2.6. Нецентральные распределения.
Функции распределения нецентральных  и
и  -распределений выражаются
-распределений выражаются
в виде бесконечных функциональных рядов:
 (12.32)
(12.32)
где 
Таким образом, нецентральные распределения (12.31) и (12.32) можно рассматривать как смеси со счетным числом компонент из соответствующих центральных распределений. Прямой путь для вычисления значений функций распределения (12.21) и (12.32) состоит в суммировании вычисленных с необходимой точностью членов рядов (12.31) и (12.32). При этом погрешность вычисления  складывается из двух компонент
складывается из двух компонент  , где
, где  — погрешность вычисления члена ряда и
— погрешность вычисления члена ряда и  — погрешность, возникающая из-за «обрезания» ряда на
— погрешность, возникающая из-за «обрезания» ряда на  члене.
члене.
Для величины  имеем следующую оценку сверху:
имеем следующую оценку сверху:

С помощью этого неравенства нетрудно оценить число  членов ряда (12.31) или (12.32), достаточное для выполнения неравенства
членов ряда (12.31) или (12.32), достаточное для выполнения неравенства  , где
, где  — заданная величина погрешности.
— заданная величина погрешности.
Для нецентральных распределений (12.31) и (12.32) известны аппроксимационные формулы, выражающие их через соответствующие центральные распределения
 (12.33)
(12.33)
где

и
 (12.34)
(12.34)
где

Эти аппроксимации можно использовать, в частности, для нахождения приближенных оценок обратных функций нецентральных распределений (см. формулы (12.18), (12.19)).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.1.2. Два варианта интерпретации исходных данных и два подхода к их статистической обработке.
- 1.1.3. Основные этапы статистической обработки исходных данных.
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1. Теория вероятностей и условия ее применимости
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1. Для чего нужны математические модели
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей»
- 3.5.4. Геометрические модели.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1. Дискретное вероятностное пространство
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
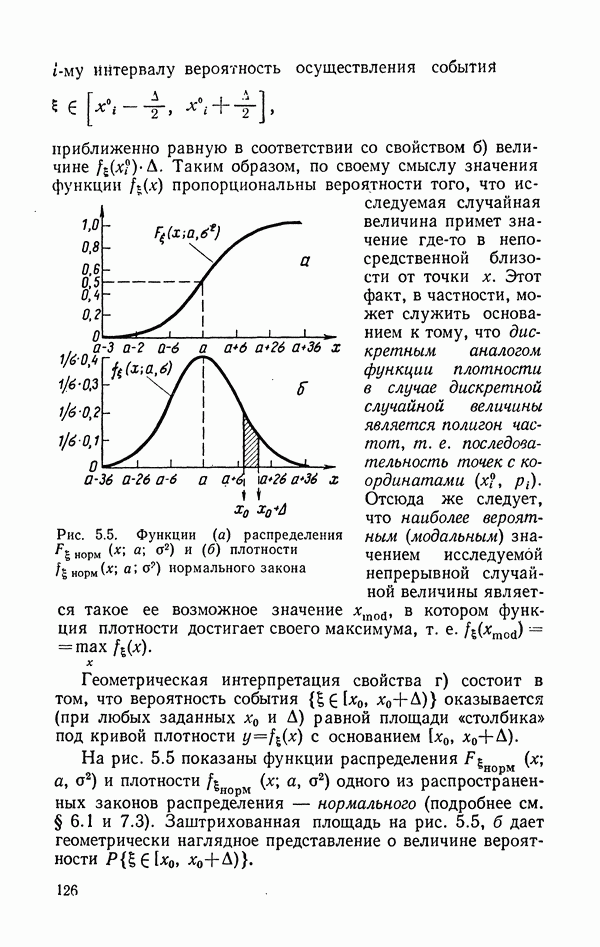
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
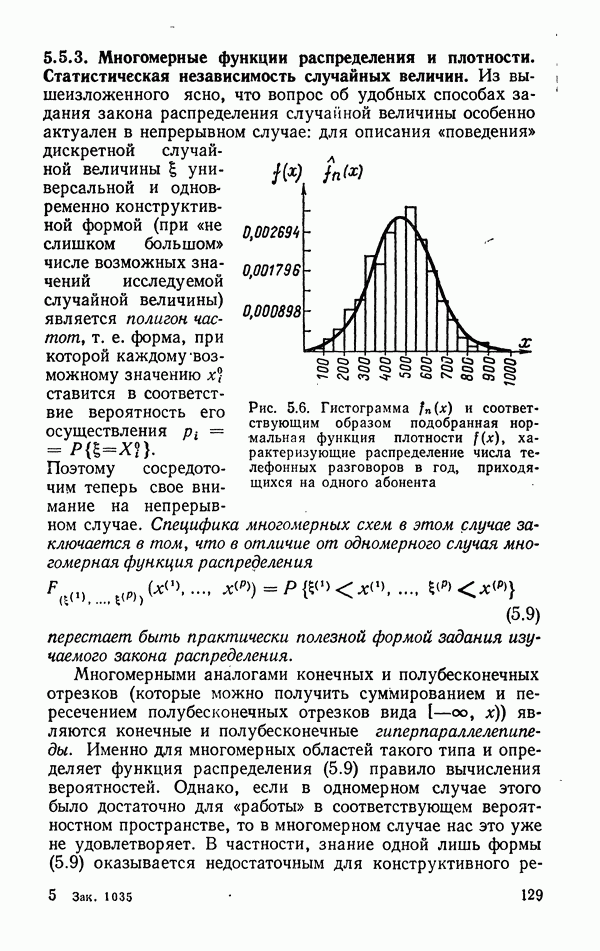
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
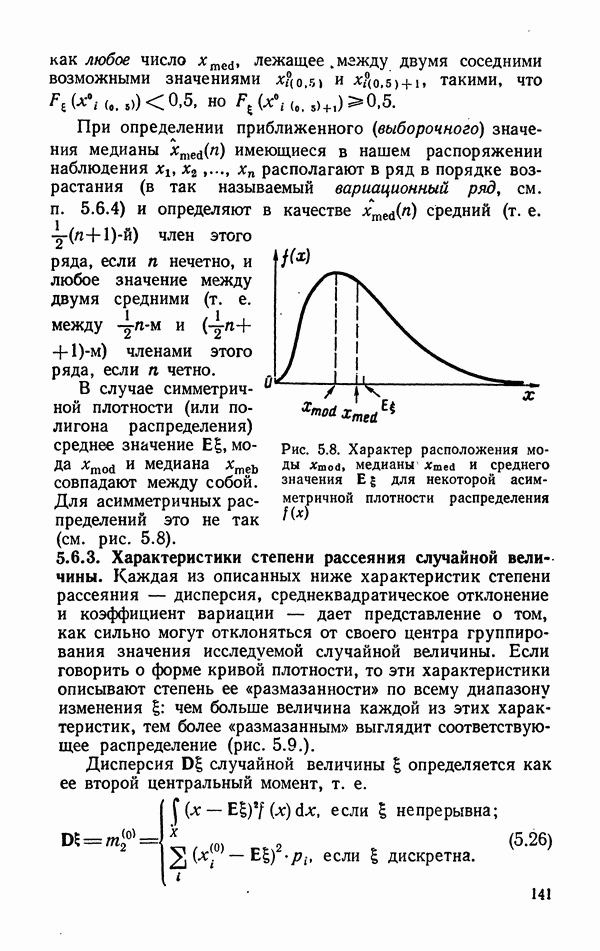
- 5.6.2. Характеристики центра группирования значений случайной величины.
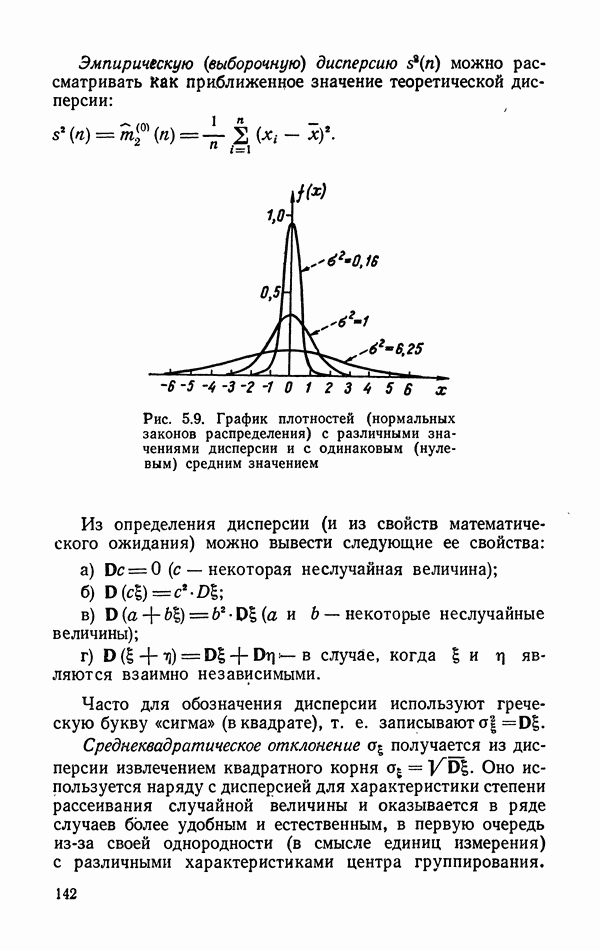
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
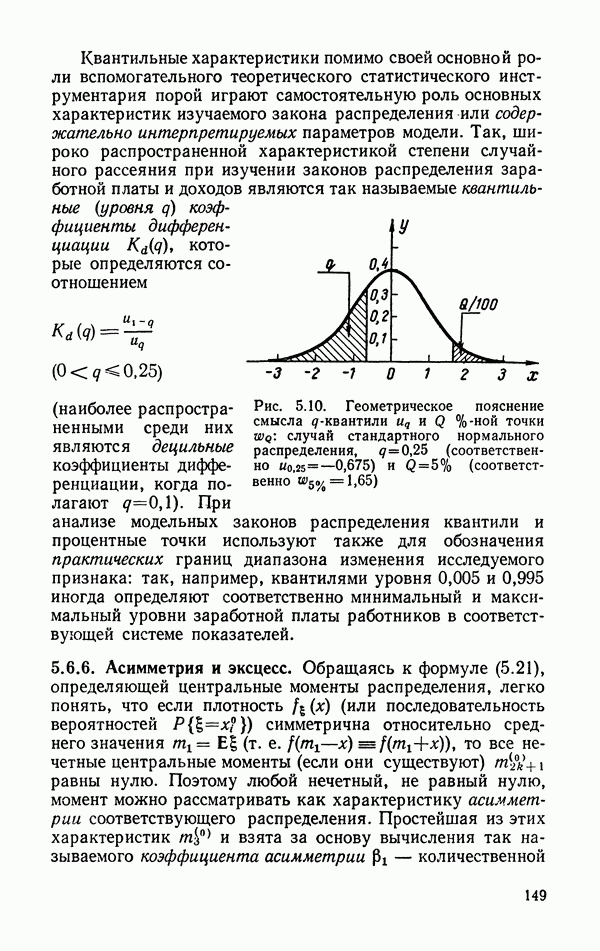
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
- 6.1.5. Нормальное (гауссовское) распределение.
- 6.1.6. Логарифмически-нормальное распределение.
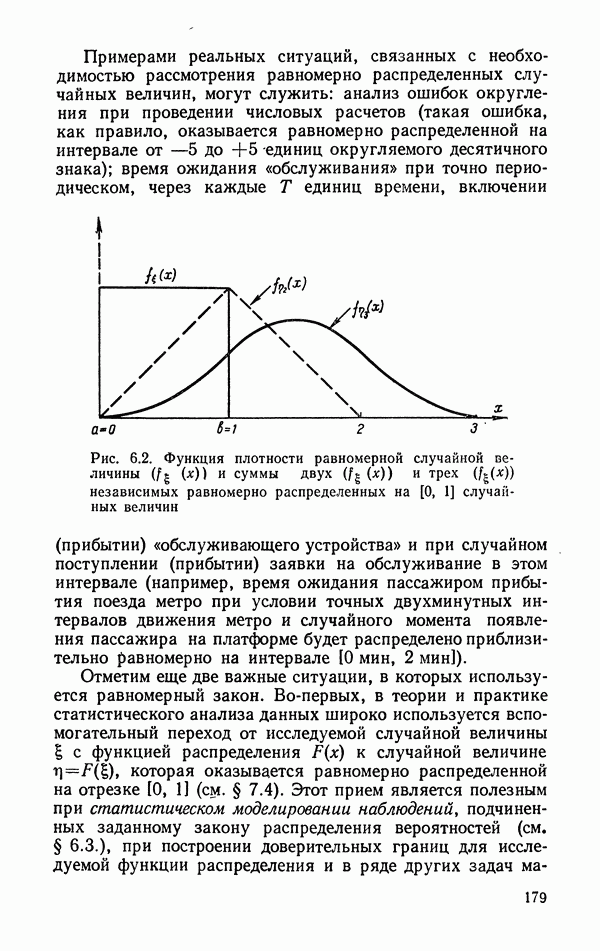
- 6.1.7. Равномерное (прямоугольное) распределение.
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
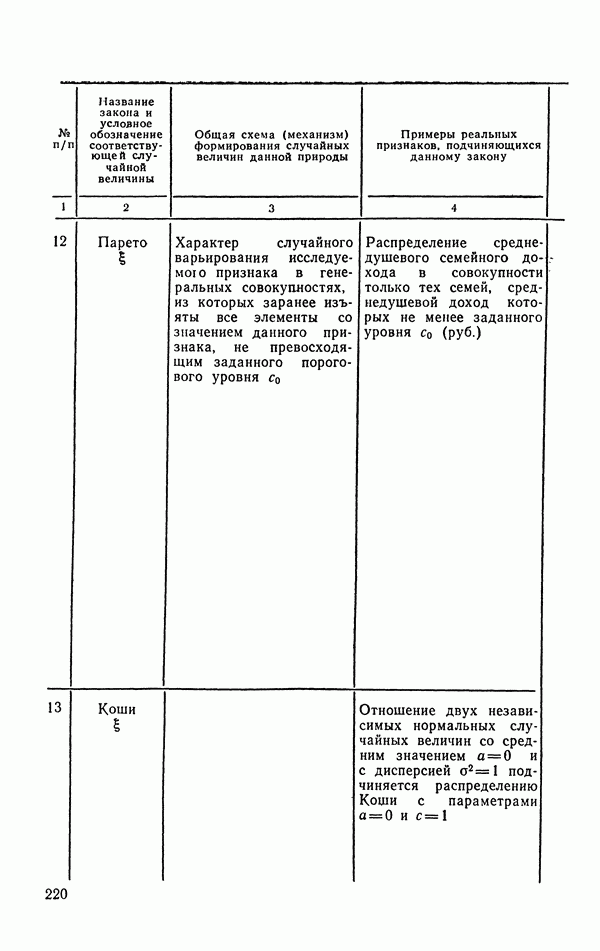
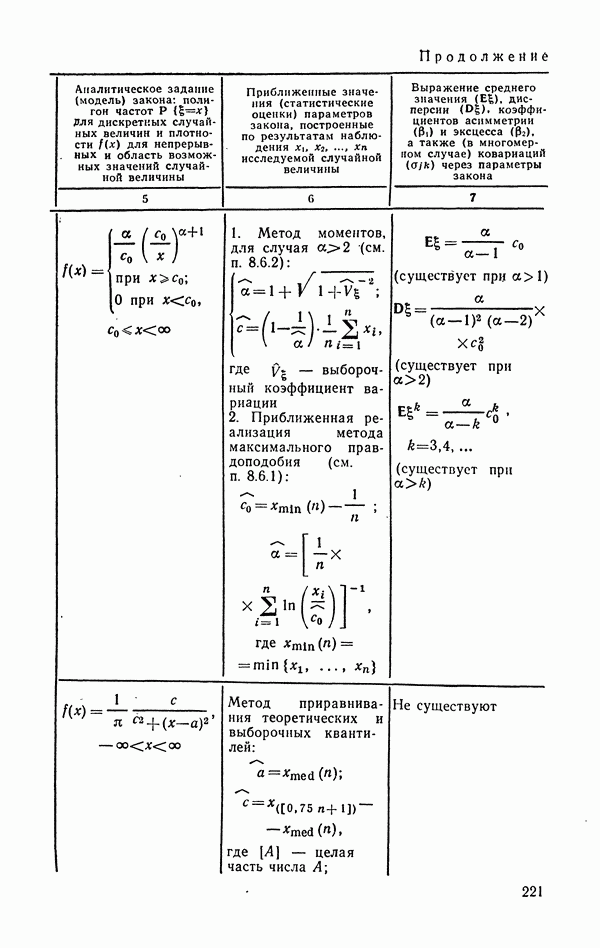
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных распределениях.
- 6.2.5. Г-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.2. Моделирование дискретных случайных величин. Стандартный метод.
- 6.3.3. Моделирование непрерывных распределений.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.2. Многомерная центральная предельная теорема (см. [12, с. 105]).
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия.
- 8.3. Неравенство Рао — Крамера — Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4. Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1.1. Критерий «хи квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий w^2 (Крамера — Мнзеса — Смирнова).
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и w^2 для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- 11.1.7. Использование критериев согласия Колмогорова и w^2 в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.2. Критерий однородности «хи квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия.
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.2. Вычисление функций распределения и обратных к ним
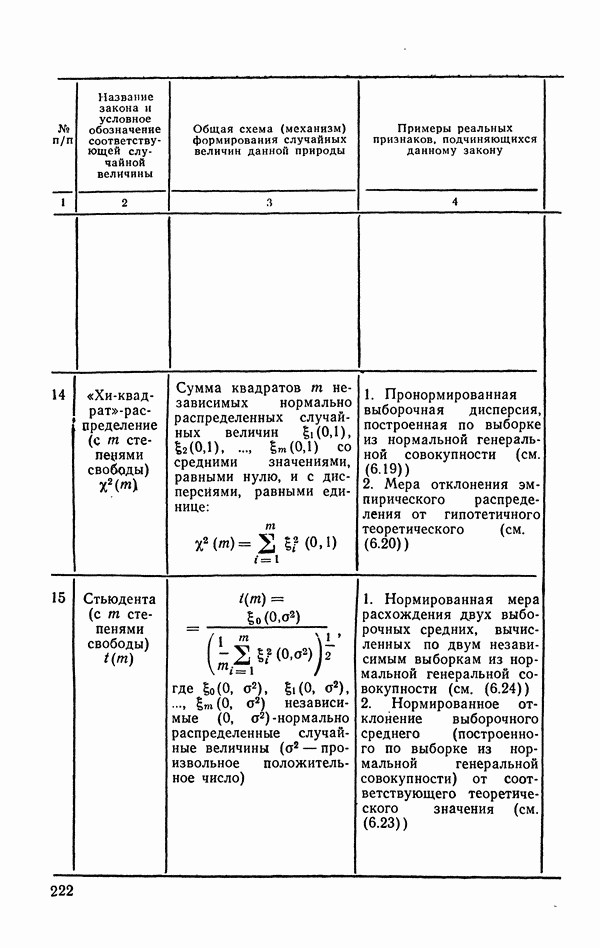
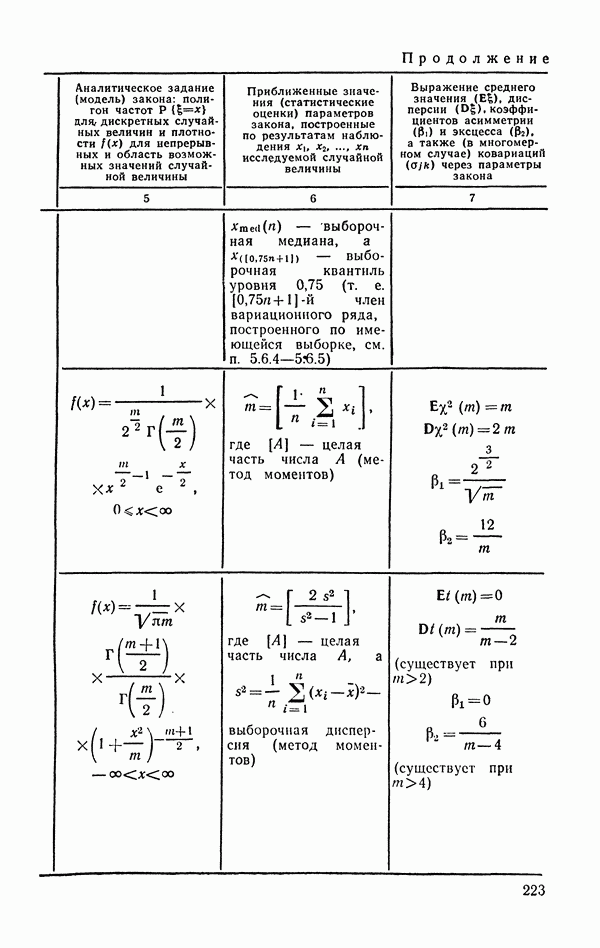
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа w^2
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ