| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
Определим ту часть подмножеств пространства элементарных событий  , которая содержит подмножества-события. Схема определения случайного события А в общем случае подобна той, которая была принята в дискретном случае. Но если в той ситуации нам достаточно было определить в качестве исходных понятий элементарные события
, которая содержит подмножества-события. Схема определения случайного события А в общем случае подобна той, которая была принята в дискретном случае. Но если в той ситуации нам достаточно было определить в качестве исходных понятий элементарные события  (и любое подмножество пространства элементарных событий объявлялось событием), то в общем случае мы в каждой конкретной реальной ситуации должны (из физических, содержательных соображений) определить дополнительно к
(и любое подмножество пространства элементарных событий объявлялось событием), то в общем случае мы в каждой конкретной реальной ситуации должны (из физических, содержательных соображений) определить дополнительно к  категорию подмножеств
категорию подмножеств  , которые, очевидно, являются событиями. А затем любое случайное событие А определяется как некоторое производное от «очевидно событийных» подмножеств введенной категории.
, которые, очевидно, являются событиями. А затем любое случайное событие А определяется как некоторое производное от «очевидно событийных» подмножеств введенной категории.
Определение случайного события.
Рассмотрим систему (конечную или счетную) подмножеств  пространства элементарных событий
пространства элементарных событий  , каждое из которых является событием. Тогда множество
, каждое из которых является событием. Тогда множество  , состоящее из всех элементарных событий, дополнения
, состоящее из всех элементарных событий, дополнения  и сумма
и сумма  также являются событиями (отсюда непосредственно следует, что и произведение
также являются событиями (отсюда непосредственно следует, что и произведение  является событием, так как его
является событием, так как его  дополнение
дополнение  в соответствии с данным определением является событием).
в соответствии с данным определением является событием).
Будем обозначать в дальнейшем систему тех подмножеств пространства элементарных исходов  , которые являются событиями, буквой С.
, которые являются событиями, буквой С.
Аксиома. Каждому подмножеству-событию А из системы С соответствует неотрицательное и не превосходящее единицы число  называемое вероятностью события А у причем задающая это соответствие числовая функция множеств
называемое вероятностью события А у причем задающая это соответствие числовая функция множеств  обладает следующими свойствами:
обладает следующими свойствами:

б) если события  несовместны, то
несовместны, то

Из этой аксиомы непосредственно следует, в частности, связь между вероятностями прямого (А) и противоположного (А) событий:

Аксиоматическое свойство б) вероятностей формулировалось и доказывалось в дискретном случае в виде теоремы сложения вероятностей.
Точно так же то, что называлось теоремой умножения вероятностей (и выводилось из определения и аксиомы в дискретном случае), в общем случае принимается по определению.
Определение условной вероятности.
Условная вероятность  события А при условии, что уже имеет место событие В, определяется с помощью формулы
события А при условии, что уже имеет место событие В, определяется с помощью формулы

Правила действий с событиями и их вероятностями
В частности, формула полной вероятности (4.14), формула Байеса (4.18), определение независимости для системы событий  и другие, доказанные в дискретном случае, имеют место (и могут быть доказаны) и в случае общего вероятностного пространства.
и другие, доказанные в дискретном случае, имеют место (и могут быть доказаны) и в случае общего вероятностного пространства.
Итак, для исчерпывающего описания механизма исследуемого случайного эксперимента в общем случае, т. е. для задания в этом случае вероятностного пространства, необходимо: 1) описать пространство элементарных событий Q; 2) описать систему С измеримых подмножеств этого пространства или таких подмножеств, которые должны быть принципиально наблюдаемыми (т. е. являются событиями); 3) каждому такому событию А из системы С поставить в соответствие неотрицательное число  , называемое вероятностью события А, причем это соответствие должно удовлетворять требованиям а) и б) аксиомы (очевидно, такое соответствие Р есть числовая функция множества, определенная на подмножествах системы С; функции такого типа принято называть вероятностными мерами, определенными на системе подмножеств С). Поэтому если в дискретном случае для краткого символического
, называемое вероятностью события А, причем это соответствие должно удовлетворять требованиям а) и б) аксиомы (очевидно, такое соответствие Р есть числовая функция множества, определенная на подмножествах системы С; функции такого типа принято называть вероятностными мерами, определенными на системе подмножеств С). Поэтому если в дискретном случае для краткого символического
описания вероятностного пространства достаточно было пары символов  то в общем случае для этой же цели требуется уже «тройка»
то в общем случае для этой же цели требуется уже «тройка»  .
.
Приведенный выше пример с астрономическими наблюдениями звездного неба как бы подкрепляет физическую естественность понятий измеримого («наблюдаемого») и неизмеримого («ненаблюдаемого») подмножества пространства элементарных событий  . Однако всякая модель, всякая теория, и в том числе современная аксиоматическая концепция теории вероятностей, есть лишь форма приближенного представления реальной действительности, форма, не свободная от недостатков. Чтобы предостеречь читателя от переоценки возможностей аксиоматической теоретико-вероятностной модели, рассмотрим несложный пример.
. Однако всякая модель, всякая теория, и в том числе современная аксиоматическая концепция теории вероятностей, есть лишь форма приближенного представления реальной действительности, форма, не свободная от недостатков. Чтобы предостеречь читателя от переоценки возможностей аксиоматической теоретико-вероятностной модели, рассмотрим несложный пример.
Практика долгосрочного социально-экономического и научно-технического прогнозирования широко использует различные формы экспертных опросов. Одной из таких форм является подход, при котором каждого из опрашиваемых экспертов просят субъективно оценить вероятность осуществления интересующего нас события в будущем  Подходя к моделированию этого процесса с позиций субъективистской школы вероятностей и соответственно интерпретируя каждого из опрашиваемых экспертов в качестве своеобразного «измерительного прибора», мы можем определить понятие случайного эксперимента как результат ответа эксперта на поставленный ему вопрос. В этом случае пространство элементарных исходов Q, очевидно, должно состоять из всех точек отрезка [0, 1]. При конструировании системы С «наблюдаемых» подмножеств пространства Q естественно было бы априори потребовать, чтобы любой отрезок
Подходя к моделированию этого процесса с позиций субъективистской школы вероятностей и соответственно интерпретируя каждого из опрашиваемых экспертов в качестве своеобразного «измерительного прибора», мы можем определить понятие случайного эксперимента как результат ответа эксперта на поставленный ему вопрос. В этом случае пространство элементарных исходов Q, очевидно, должно состоять из всех точек отрезка [0, 1]. При конструировании системы С «наблюдаемых» подмножеств пространства Q естественно было бы априори потребовать, чтобы любой отрезок  лежащий внутри отрезка
лежащий внутри отрезка  (т. е. принадлежал бы к категории событий (т. е. для любого отрезка
(т. е. принадлежал бы к категории событий (т. е. для любого отрезка  должна быть определена вероятность
должна быть определена вероятность  того, что численный ответ наугад выбранного эксперта будет принадлежать этому отрезку). Но тогда в соответствии с определением случайного события в общем случае событиями будут не только отрезки, но и все, что можно получить из них применением к ним (взятым в счетном числе) суммирования и перемножения, а также взятием дополнения (т. е. противоположного
того, что численный ответ наугад выбранного эксперта будет принадлежать этому отрезку). Но тогда в соответствии с определением случайного события в общем случае событиями будут не только отрезки, но и все, что можно получить из них применением к ним (взятым в счетном числе) суммирования и перемножения, а также взятием дополнения (т. е. противоположного
события). Поэтому, выбирая произвольную точку с на отрезке [0, 1] и рассматривая последовательность отрезков  вида
вида  мы обнаруживаем, что точка должна быть событием, так как она является, как легко видеть, счетным произведением отрезков
мы обнаруживаем, что точка должна быть событием, так как она является, как легко видеть, счетным произведением отрезков  Итак, любая точка отрезка [0, 1] — событие. Множество рациональных точек, как известно, складывается из счетного числа точек. Следовательно, это множество — тоже событие. Но множество иррациональных точек есть дополнение к множеству рациональных точек. Значит, и множество иррациональных точек — событие. Но вряд ли естественно, с физической точки зрения, считать наблюдаемыми (и, следовательно, физически различимыми) событиями факты принадлежности точки к множеству рациональных и к множеству иррациональных чисел. Как видно из этого примера, и использование общепринятой сейчас аксиоматической концепции теории вероятностей может приводить к плохо физически интерпретируемым выводам. В данном примере мы не провели до конца построение вероятностного пространства, так как не определили (аксиоматически) способ вычисления вероятностей на отрезках, т. е. величин
Итак, любая точка отрезка [0, 1] — событие. Множество рациональных точек, как известно, складывается из счетного числа точек. Следовательно, это множество — тоже событие. Но множество иррациональных точек есть дополнение к множеству рациональных точек. Значит, и множество иррациональных точек — событие. Но вряд ли естественно, с физической точки зрения, считать наблюдаемыми (и, следовательно, физически различимыми) событиями факты принадлежности точки к множеству рациональных и к множеству иррациональных чисел. Как видно из этого примера, и использование общепринятой сейчас аксиоматической концепции теории вероятностей может приводить к плохо физически интерпретируемым выводам. В данном примере мы не провели до конца построение вероятностного пространства, так как не определили (аксиоматически) способ вычисления вероятностей на отрезках, т. е. величин  Физически естественное аксиоматическое задание этих вероятностей также обусловлено спецификой реального комплекса условий, характеризующих наш случайный эксперимент. Так, если представить, что мы находимся в самой «неблагоприятной» для прогноза ситуации (интересующее нас событие настолько удалено во времени и неопределенно или опрашиваемые эксперты настолько некомпетентны, что ответы экспертов оказываются приблизительно равномерно «разбросанными» по всей длине отрезка
Физически естественное аксиоматическое задание этих вероятностей также обусловлено спецификой реального комплекса условий, характеризующих наш случайный эксперимент. Так, если представить, что мы находимся в самой «неблагоприятной» для прогноза ситуации (интересующее нас событие настолько удалено во времени и неопределенно или опрашиваемые эксперты настолько некомпетентны, что ответы экспертов оказываются приблизительно равномерно «разбросанными» по всей длине отрезка  ), то естественно предположить, что вероятности
), то естественно предположить, что вероятности  будут зависеть только от длины отрезка
будут зависеть только от длины отрезка  и не будут зависеть от того, в каком именно месте отрезок располагается, и определить их соответственно с помощью соотношений
и не будут зависеть от того, в каком именно месте отрезок располагается, и определить их соответственно с помощью соотношений

Легко проверить, что заданные этим соотношением вероятности удовлетворяют свойствам а) и б) аксиомы.
Подчеркнем, кстати, на этом примере одно из существенных отличий широкого класса непрерывных вероятностных пространств от дискретных: вероятность осуществления любого элементарного события (т. е. любого возможного исхода) со в данном примере равна нулю; однако для сколь угодно малого отрезка  вероятность
вероятность  всегда будет положительной (это непосредственно следует из (4.20)). Таким образом, в этом примере мы впервые встретились с, казалось бы, парадоксальной ситуацией, когда события со хотя и являются возможными, но обладают нулевой вероятностью. Соответственно события
всегда будет положительной (это непосредственно следует из (4.20)). Таким образом, в этом примере мы впервые встретились с, казалось бы, парадоксальной ситуацией, когда события со хотя и являются возможными, но обладают нулевой вероятностью. Соответственно события  являющиеся дополнением к событиям нулевой вероятности со, хотя и не могут быть названы достоверными, но имеют вероятность осуществления, равную единице. О событиях типа То часто говорят как о событиях, происходящих «почти всегда». При более глубоком рассмотрении можно понять, что подобные ситуации в непрерывном вероятностном пространстве на самом деле не являются парадоксальными. Для пояснения этой мысли можно привести аналогию с физическим телом, имеющим определенную массу, в то время как ни одна из точек, составляющих это тело, сама массой не обладает. Очевидно, тело в этой аналогии играет роль события, точка — роль элементарного исхода, а масса — роль вероятности.
являющиеся дополнением к событиям нулевой вероятности со, хотя и не могут быть названы достоверными, но имеют вероятность осуществления, равную единице. О событиях типа То часто говорят как о событиях, происходящих «почти всегда». При более глубоком рассмотрении можно понять, что подобные ситуации в непрерывном вероятностном пространстве на самом деле не являются парадоксальными. Для пояснения этой мысли можно привести аналогию с физическим телом, имеющим определенную массу, в то время как ни одна из точек, составляющих это тело, сама массой не обладает. Очевидно, тело в этой аналогии играет роль события, точка — роль элементарного исхода, а масса — роль вероятности.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.1.2. Два варианта интерпретации исходных данных и два подхода к их статистической обработке.
- 1.1.3. Основные этапы статистической обработки исходных данных.
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1. Теория вероятностей и условия ее применимости
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1. Для чего нужны математические модели
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей»
- 3.5.4. Геометрические модели.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1. Дискретное вероятностное пространство
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.2. Характеристики центра группирования значений случайной величины.
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
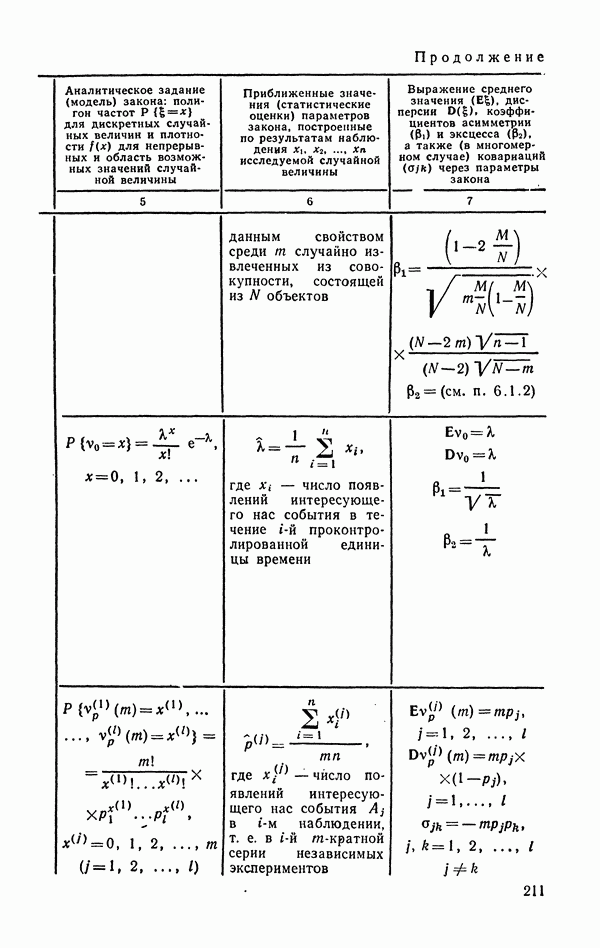
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
- 6.1.5. Нормальное (гауссовское) распределение.
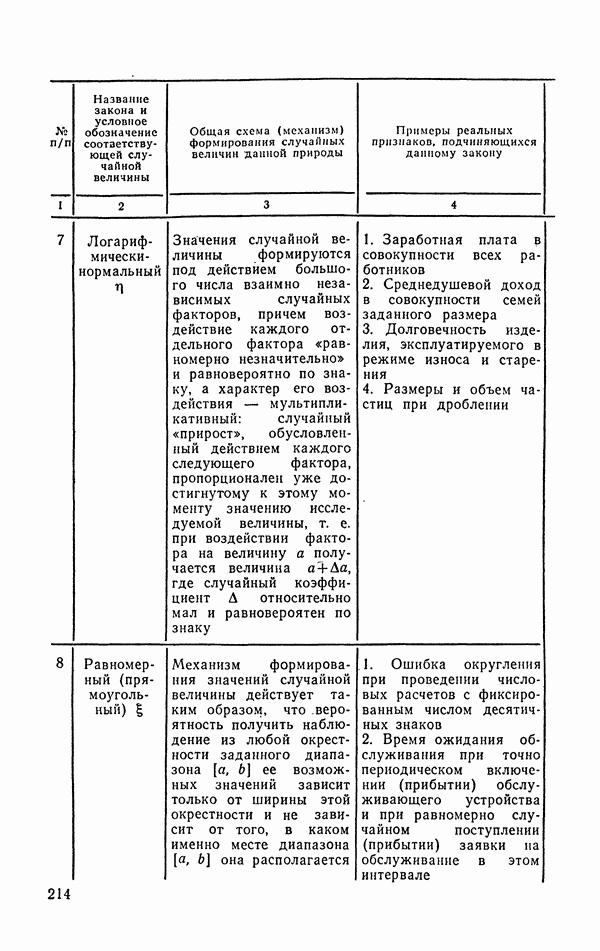
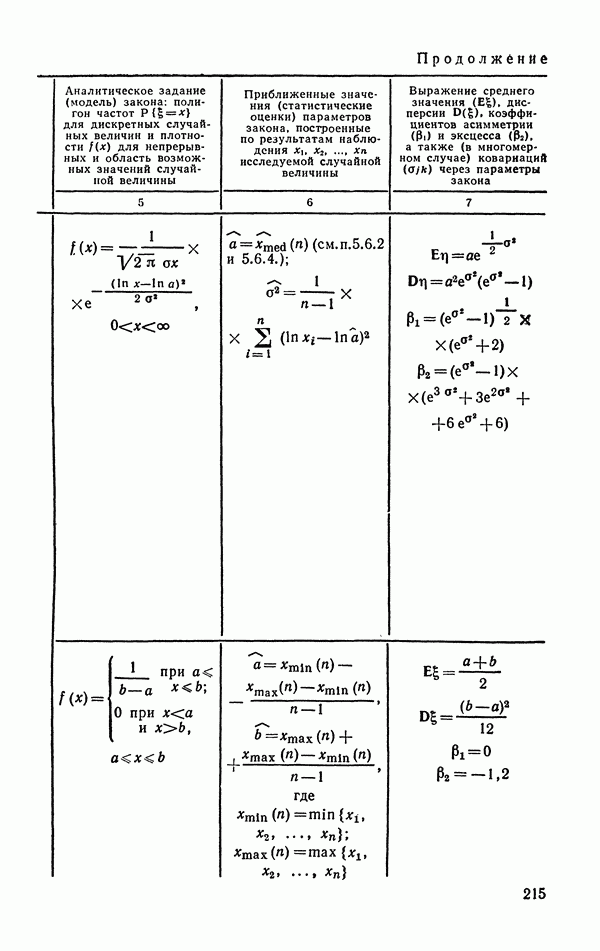
- 6.1.6. Логарифмически-нормальное распределение.
- 6.1.7. Равномерное (прямоугольное) распределение.
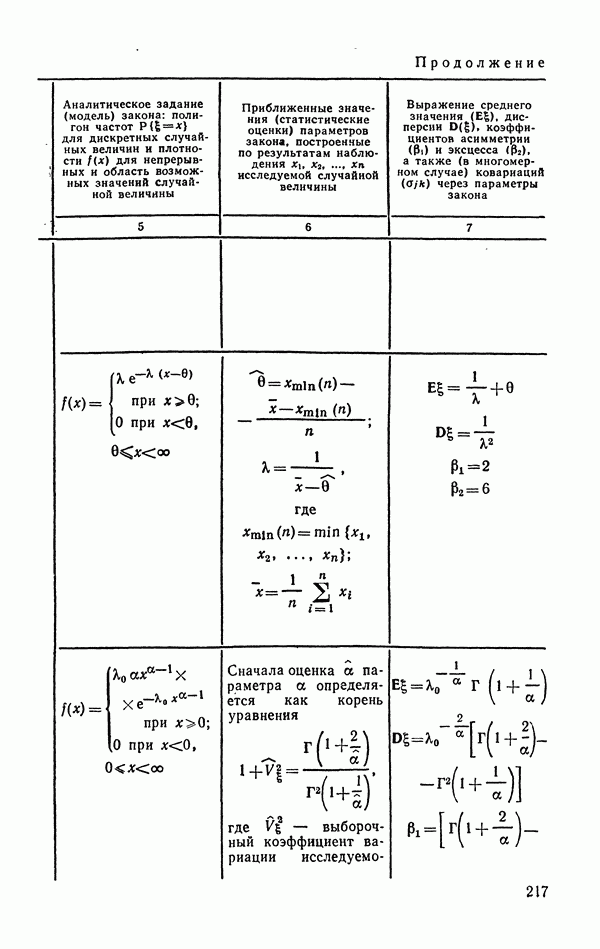
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
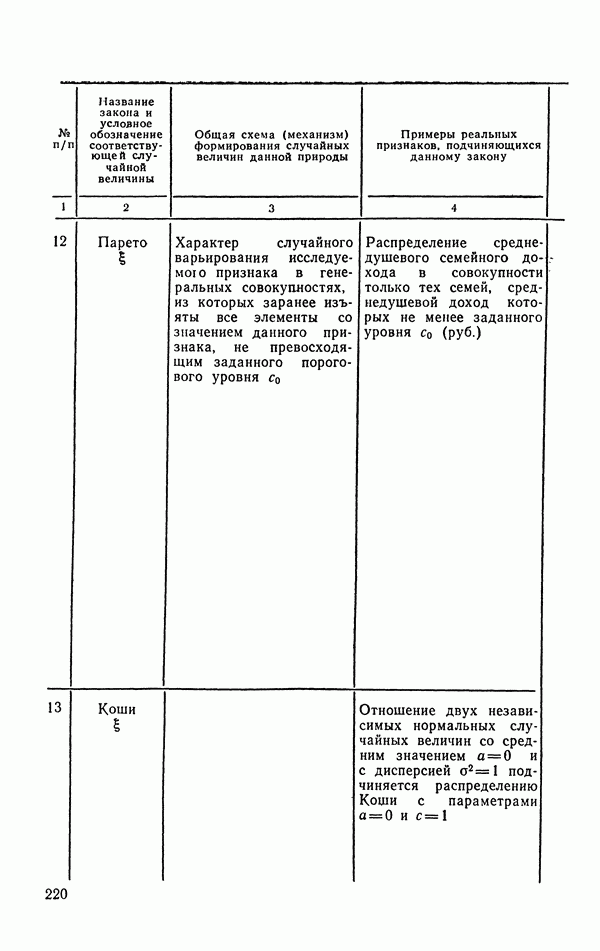
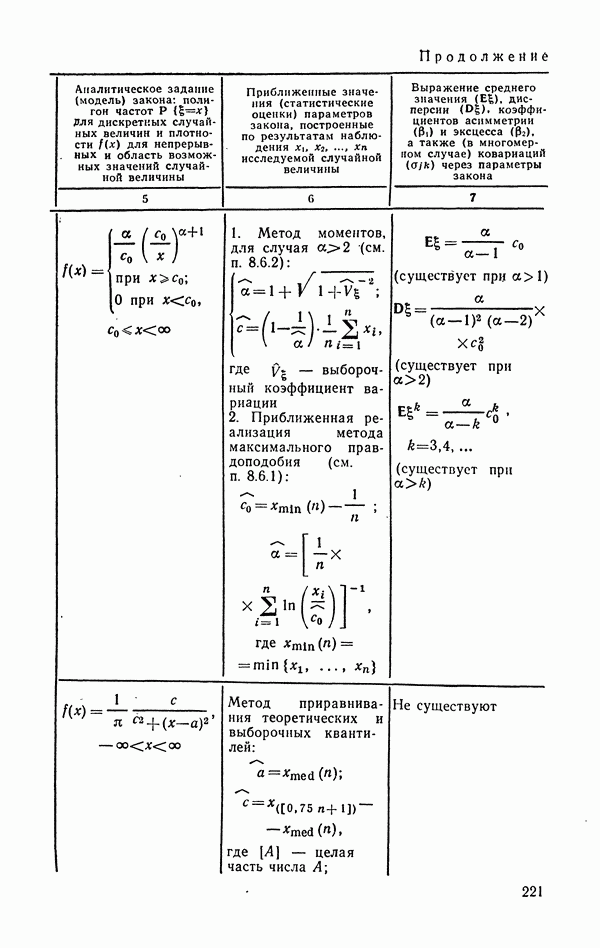
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
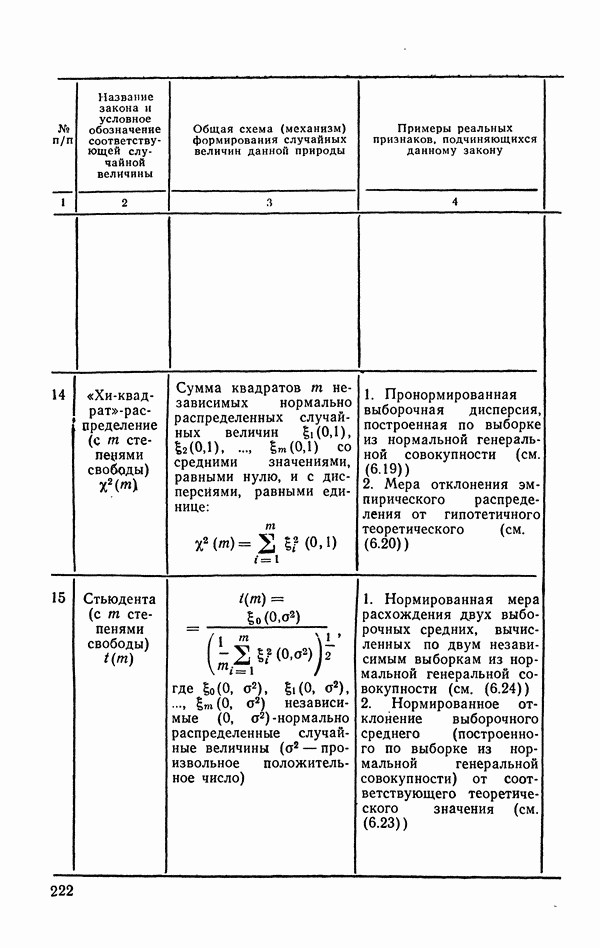
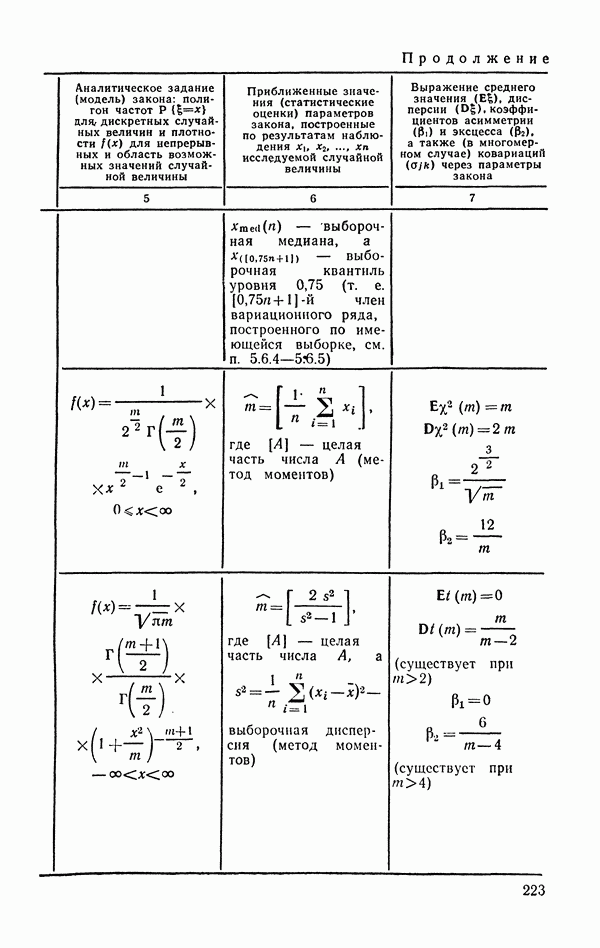
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных распределениях.
- 6.2.5. Г-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.2. Моделирование дискретных случайных величин. Стандартный метод.
- 6.3.3. Моделирование непрерывных распределений.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.2. Многомерная центральная предельная теорема (см. [12, с. 105]).
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия.
- 8.3. Неравенство Рао — Крамера — Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4. Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1.1. Критерий «хи квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
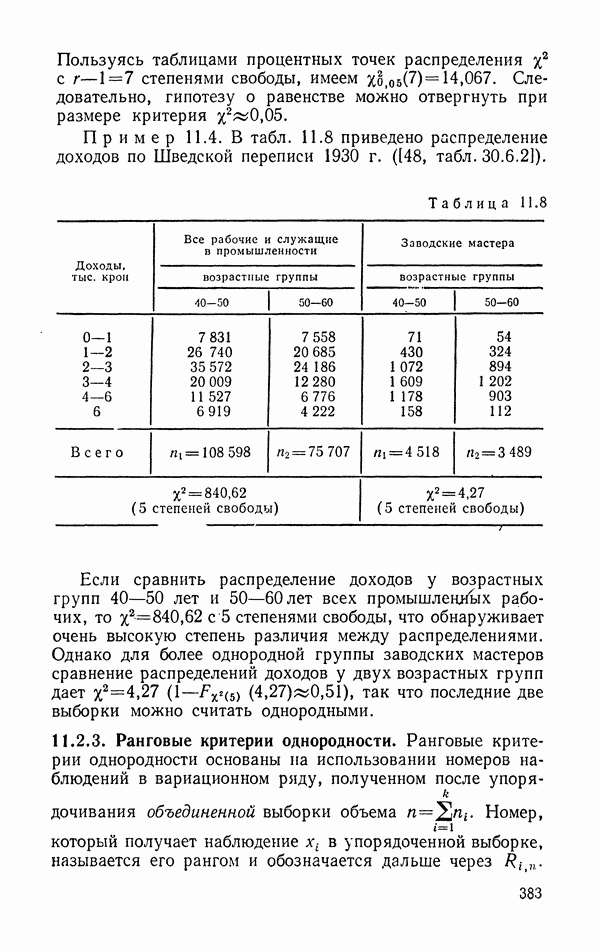
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий w^2 (Крамера — Мнзеса — Смирнова).
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и w^2 для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- 11.1.7. Использование критериев согласия Колмогорова и w^2 в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.2. Критерий однородности «хи квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия.
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
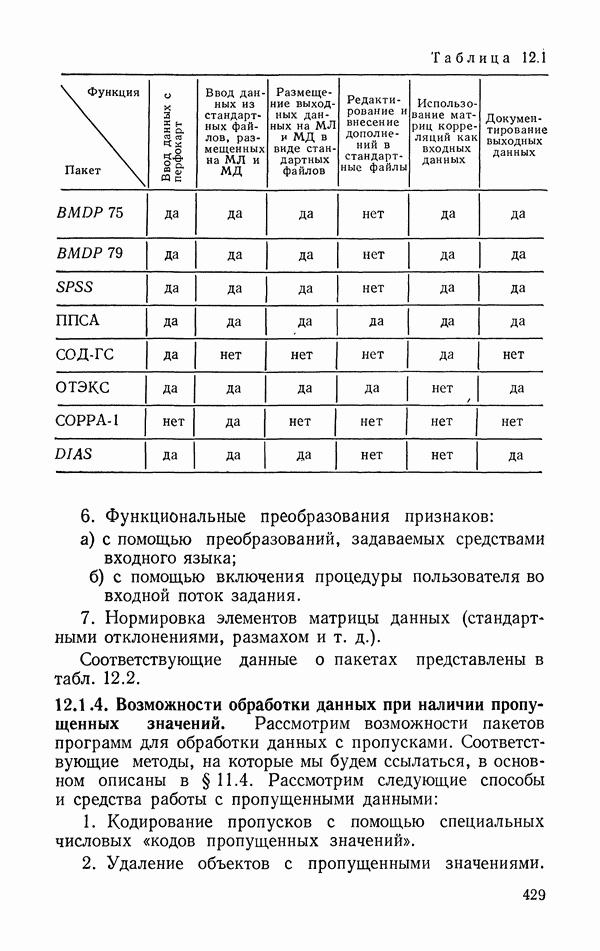
- 12.1. Программное обеспечение прикладной статистики
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
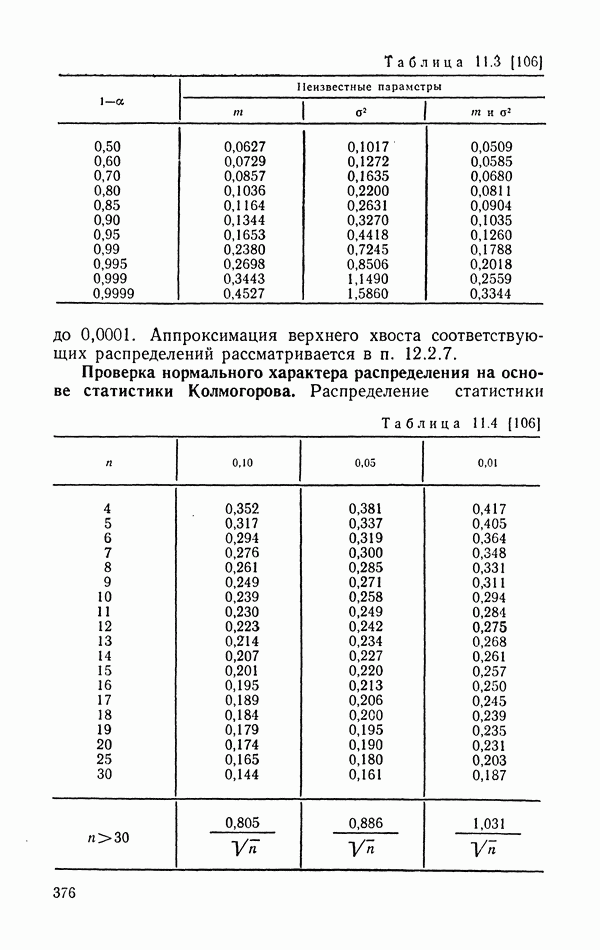
- 12.2.7. Аппроксимация «хвостов» распределений типа w^2
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ