| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
5.5.1. Функция распределения вероятностей одномерной случайной величины.
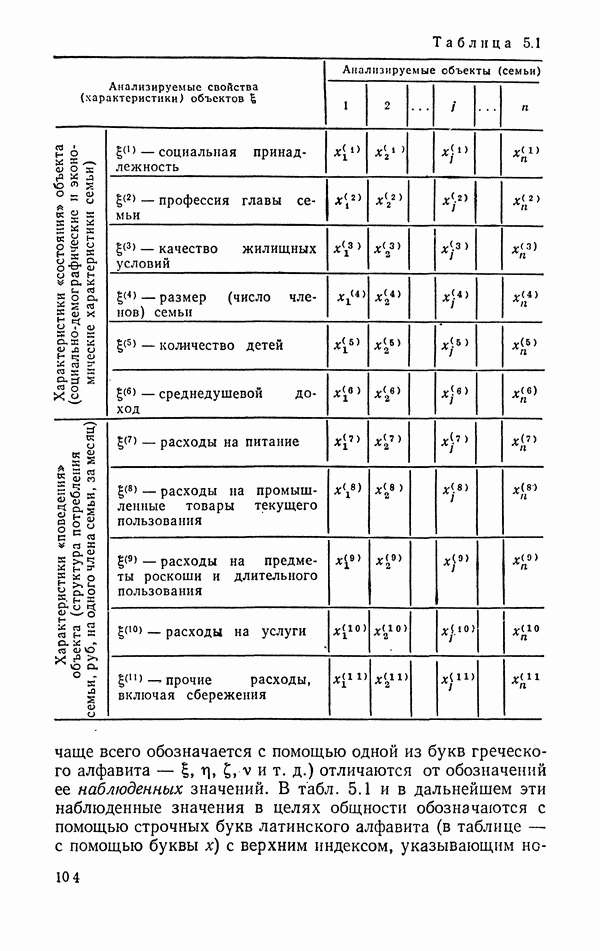
Как установлено выше (см. § 5.4), всякая генеральная совокупность (случайная величина) определяется своим законом распределения вероятностей  Поскольку интересующие нас области
Поскольку интересующие нас области  могут быть в общем случае подмножествами общей природы, то возникает вопрос: каковы те способы задания числовых функций
могут быть в общем случае подмножествами общей природы, то возникает вопрос: каковы те способы задания числовых функций  , определенных на подмножествах
, определенных на подмножествах  , которые были бы достаточно удобны в плане конструктивном, практическом?
, которые были бы достаточно удобны в плане конструктивном, практическом?
Оказывается, для описания распределений одномерных случайных величин  достаточно задать способ вычисления вероятностей
достаточно задать способ вычисления вероятностей  лишь для подмножеств
лишь для подмножеств  некоторого специального вида, а именно лишь для полузамкнутых слева интервалов вида
некоторого специального вида, а именно лишь для полузамкнутых слева интервалов вида

где  минимально возможное значение исследуемой случайной величины
минимально возможное значение исследуемой случайной величины  (оно может быть равно и
(оно может быть равно и  ), а х - любое «текущее» (т. е. задаваемое нами) возможное значение Вероятность же
), а х - любое «текущее» (т. е. задаваемое нами) возможное значение Вероятность же  однозначно определяется заданием правого конца интервала, т. е. числа
однозначно определяется заданием правого конца интервала, т. е. числа  а потому может интерпретироваться как обычная функция от одного числового аргумента
а потому может интерпретироваться как обычная функция от одного числового аргумента 
Функцией распределения вероятностей (накопленной частотой)  случайной величины
случайной величины  называют функцию, ставящую в соответствие любому заданному значению
называют функцию, ставящую в соответствие любому заданному значению  величину вероятности события
величину вероятности события  т. е.
т. е.

В дальнейшем, если это не будет вызывать недоразумении, будем опускать нижний индекс  у функции F и называть ее просто «функцией распределения».
у функции F и называть ее просто «функцией распределения».
Рассмотрим поведение функции распределения. Во-первых, отметим, что в дискретном случае событие  состоит из всех элементарных событий
состоит из всех элементарных событий  таких, что
таких, что  Поэтому в соответствии с определением вероятности составного события (см. п. 4.1.3) имеем
Поэтому в соответствии с определением вероятности составного события (см. п. 4.1.3) имеем

(суммирование в правых частях (5.5) проводится по всем тем i, для которых 
Из (5.5) видно, что значения функции  изменяются при увеличении аргумента
изменяются при увеличении аргумента  скачками, а именно при «переползании» величины
скачками, а именно при «переползании» величины  через очередное возможное значение
через очередное возможное значение  функция
функция  скачком увеличивает свое значение на величину
скачком увеличивает свое значение на величину 
Несколько иную картину мы будем наблюдать, анализируя поведение функции распределения  в случае непрерывного исследуемого признака
в случае непрерывного исследуемого признака  Подавляющее большинство представляющих практический интерес непрерывных случайных величин обладают тем свойством, что для любого отрезка
Подавляющее большинство представляющих практический интерес непрерывных случайных величин обладают тем свойством, что для любого отрезка  вероятности
вероятности  стремятся к нулю по мере стремления к нулю длины этого отрезка, и, следовательно, вероятности принятия отдельных возможных значений
стремятся к нулю по мере стремления к нулю длины этого отрезка, и, следовательно, вероятности принятия отдельных возможных значений  равны нулю (конкретный пример такого рода приведен в п. 4.2.2 в задаче с экспертным оцениванием вероятности интересующего нас события). Нетрудно понять, что для таких случайных величин их функции распределения
равны нулю (конкретный пример такого рода приведен в п. 4.2.2 в задаче с экспертным оцениванием вероятности интересующего нас события). Нетрудно понять, что для таких случайных величин их функции распределения
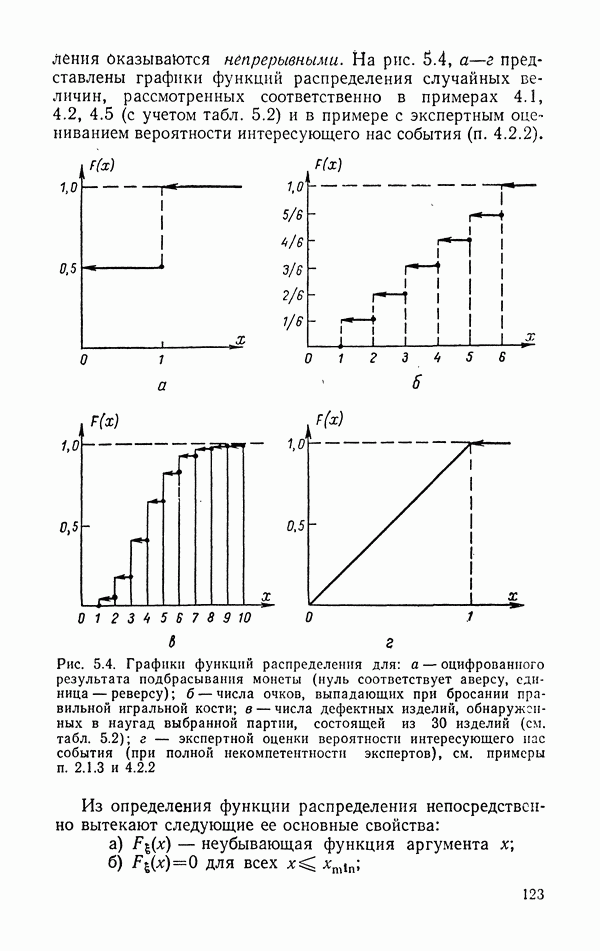
оказываются непрерывными. На рис. 5.4, а-г представлены графики функций распределения случайных величин, рассмотренных соответственно в примерах 4.1, 4.2, 4.5 (с учетом табл. 5.2) и в примере с экспертным оцениванием вероятности интересующего нас события (п. 4.2.2).

Рис. 5.4. Графики функций распределения для: а — оцифрованного результата подбрасывания монеты (нуль соответствует аверсу, единица — реверсу); б — числа очков, выпадающих при бросании правильной игральной кости; в — числа дефектных изделий, обнаруженных в наугад выбранной партии, состоящей из 30 изделий (см. табл. 5.2); г — экспертной оценки вероятности интересующего нас события (при полной некомпетентности экспертов), см. примеры п. 2.1.3 и 4.2.2
Из определения функции распределения непосредственно вытекают следующие ее основные свойства:
а)  — неубывающая функция аргумента х;
— неубывающая функция аргумента х;
б)  для всех
для всех 
в)  для всех
для всех  соответственно минимальное и максимальное возможные значения исследуемой случайной величины
соответственно минимальное и максимальное возможные значения исследуемой случайной величины  ;
;
г)  для любых заданных значений а и b (для доказательства последнего свойства следует воспользоваться теоремой сложения вероятностей (см. п. 4.1.3), а также тем обстоятельством, что события
для любых заданных значений а и b (для доказательства последнего свойства следует воспользоваться теоремой сложения вероятностей (см. п. 4.1.3), а также тем обстоятельством, что события  связаны между собой соотношением
связаны между собой соотношением 
В практике статистической обработки данных точный вид функции распределения, как правило, бывает неизвестен. Эмпирическим (или выборочным, т. е. построенным по выборке объема  ) аналогом теоретической функции распределения
) аналогом теоретической функции распределения  является функция
является функция  определяемая соотношениями:
определяемая соотношениями:

или, в случае группированных данных (см. п. 5.4.2),

где  — число наблюденных значений исследуемой случайной величины в выборке
— число наблюденных значений исследуемой случайной величины в выборке  меньших
меньших  — число наблюденных значений в выборке, попавших в
— число наблюденных значений в выборке, попавших в  интервал группирования,
интервал группирования,  — номер самого правого из интервалов группирования, правый конец которых не превосходит
— номер самого правого из интервалов группирования, правый конец которых не превосходит  Из определения эмпирической функции распределения непосредственно следует объяснение часто используемого ее другого названия — «накопленная частота». Свойство статистической устойчивости относительных частот (см. § 7.2) является основанием использования
Из определения эмпирической функции распределения непосредственно следует объяснение часто используемого ее другого названия — «накопленная частота». Свойство статистической устойчивости относительных частот (см. § 7.2) является основанием использования  в качестве приближенного значения неизвестной теоретической функции распределения
в качестве приближенного значения неизвестной теоретической функции распределения  и того факта, что по мере роста объема выборки (т. е. при
и того факта, что по мере роста объема выборки (т. е. при  ) ошибка этой аппроксимации неограниченно убывает. Такая оценка
) ошибка этой аппроксимации неограниченно убывает. Такая оценка  значений
значений  т. е. оценка, не связанная с предварительным выбором общего модельного вида этой функции, называется непараметрической. Более подробные сведения, относящиеся к статистическому изучению эмпирических функций распределения, даны в § 10.3 и 11.1.
т. е. оценка, не связанная с предварительным выбором общего модельного вида этой функции, называется непараметрической. Более подробные сведения, относящиеся к статистическому изучению эмпирических функций распределения, даны в § 10.3 и 11.1.
5.5.2. Функция плотности вероятности одномерной случайной величины. В классе таких непрерывных случайных величин, функции распределений которых всюду непрерывны и дифференцируемы  как уже отмечалось, этот класс охватывает подавляющее большинство представляющих практический интерес непрерывных случайных величин), другой удобной формой задания генеральной совокупности (исследуемой случайной величины
как уже отмечалось, этот класс охватывает подавляющее большинство представляющих практический интерес непрерывных случайных величин), другой удобной формой задания генеральной совокупности (исследуемой случайной величины  ) является функция плотности вероятности
) является функция плотности вероятности  определяемая как предел
определяемая как предел

или, что то же,

 — это производная функции распределения
— это производная функции распределения  в точке
в точке  Из эквивалентных соотношений (5.7) и (5.7), определяющих функцию плотности
Из эквивалентных соотношений (5.7) и (5.7), определяющих функцию плотности  вытекают непосредственно следующие ее свойства:
вытекают непосредственно следующие ее свойства:
а)  так как функция
так как функция  неубывающая;
неубывающая;
б)  Для малых отрезков А (следует из сравнения первых двух членов тождества
Для малых отрезков А (следует из сравнения первых двух членов тождества  );
);
в)  для любых х;
для любых х;
г)  для любых
для любых  ;
;

Прокомментируем некоторые из этих свойств функции плотности.
Свойство б) позволяет пояснить вероятностный смысл функции плотности. Так, предположив для определенности область возможных значений  исследуемой случайной величины
исследуемой случайной величины  конечной и разбив ее на одинаковые и достаточно мелкие интервалы группирования
конечной и разбив ее на одинаковые и достаточно мелкие интервалы группирования  с центрами
с центрами

и т. д., мы можем поставить в соответствие каждому
 интервалу вероятность осуществления событий
интервалу вероятность осуществления событий

приближенно равную в соответствии со свойством б) величине  . Таким образом, по своему смыслу значения функции
. Таким образом, по своему смыслу значения функции  пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки
пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки  Этот факт, в частности, может служить основанием к тому, что дискретным аналогом функции плотности в случае дискретной случайной величины является полигон частот, т. е. последовательность точек с координатами
Этот факт, в частности, может служить основанием к тому, что дискретным аналогом функции плотности в случае дискретной случайной величины является полигон частот, т. е. последовательность точек с координатами  . Отсюда же следует, что наиболее вероятным (модальным) значением исследуемой непрерывной случайной величины является такое ее возможное значение
. Отсюда же следует, что наиболее вероятным (модальным) значением исследуемой непрерывной случайной величины является такое ее возможное значение  , в котором функция плотности достигает своего максимума, т. е.
, в котором функция плотности достигает своего максимума, т. е. 

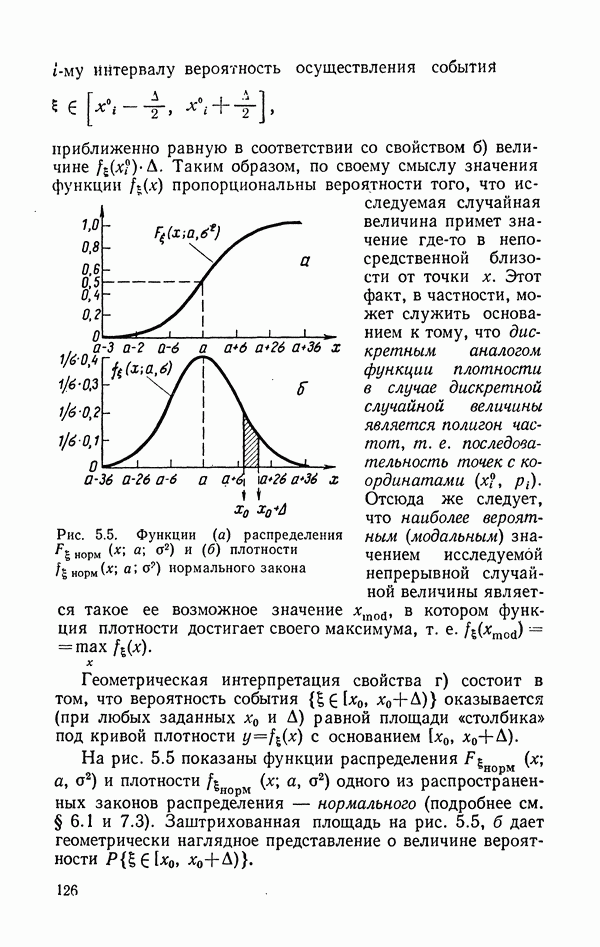
Рис. 5.5. Функции (а) распределения  норм
норм  и (б) плотности h норм
и (б) плотности h норм  нормального закона
нормального закона
Геометрическая интерпретация свойства г) состоит в том, что вероятность события  оказывается (при любых заданных
оказывается (при любых заданных  равной площади «столбика» под кривой плотности
равной площади «столбика» под кривой плотности  с основанием
с основанием 
На рис. 5.5 показаны функции распределения  и плотности
и плотности  одного из распространенных законов распределения — нормального (подробнее см. § 6.1 и 7.3). Заштрихованная площадь на рис. 5.5, б дает геометрически наглядное представление о величине вероятности
одного из распространенных законов распределения — нормального (подробнее см. § 6.1 и 7.3). Заштрихованная площадь на рис. 5.5, б дает геометрически наглядное представление о величине вероятности 
Располагая лишь выборочными данными (выборкой)  мы должны суметь составить по ним приближенное представление о неизвестной теоретической функции плотности
мы должны суметь составить по ним приближенное представление о неизвестной теоретической функции плотности  . Если нас интересует малый отрезок
. Если нас интересует малый отрезок  и мы подсчитали, что в этот отрезок попало
и мы подсчитали, что в этот отрезок попало  наблюдений нашей выборки, то, очевидно, выборочным аналогом величины
наблюдений нашей выборки, то, очевидно, выборочным аналогом величины

будет величина

Очевидно, значение  характеризует плотность наблюдений исследуемой случайной величины в окрестности точки
характеризует плотность наблюдений исследуемой случайной величины в окрестности точки  т. е. относительную частоту этих наблюдений, приходящуюся на единицу длины интервала ее возможных значений. Поэтому функцию
т. е. относительную частоту этих наблюдений, приходящуюся на единицу длины интервала ее возможных значений. Поэтому функцию  определенную соотношением (5.8), называют эмпирической (или выборочной) функцией плотности. Это же обстоятельство может служить основанием выбора такой терминологии и применительно к теоретической плотности
определенную соотношением (5.8), называют эмпирической (или выборочной) функцией плотности. Это же обстоятельство может служить основанием выбора такой терминологии и применительно к теоретической плотности  так как в соответствии со свойством статистической устойчивости частот (см. § 7.2) эти две характеристики неограниченно сближаются в процессе увеличения объема выборки
так как в соответствии со свойством статистической устойчивости частот (см. § 7.2) эти две характеристики неограниченно сближаются в процессе увеличения объема выборки  и сужения длины интервала
и сужения длины интервала 
Для построения эмпирической функции плотности  на всей области ее определения (т. е. для всех возможных значений исследуемой величины) используют предварительно сгруппированные данные (см. п. 5.4.2) и полагают
на всей области ее определения (т. е. для всех возможных значений исследуемой величины) используют предварительно сгруппированные данные (см. п. 5.4.2) и полагают

где  — порядковый номер того интервала группирования, который накрывает точку
— порядковый номер того интервала группирования, который накрывает точку  как и прежде, число наблюдений, попавших в этот интервал, и его длина соответственно. Геометрическое изображение таким образом определенной эмпирической функции плотности носит название гистограммы.
как и прежде, число наблюдений, попавших в этот интервал, и его длина соответственно. Геометрическое изображение таким образом определенной эмпирической функции плотности носит название гистограммы.
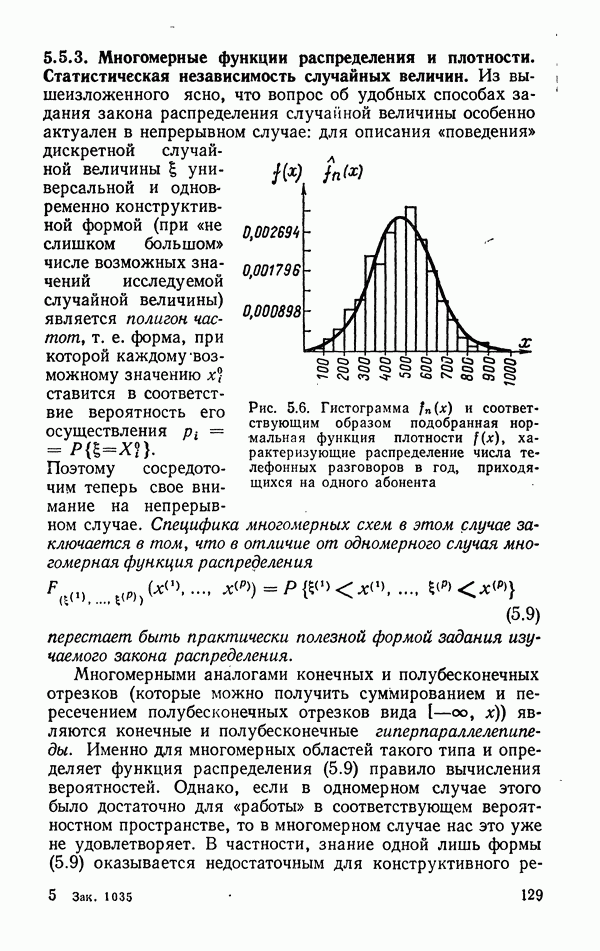
Пример 5.2. Объект (совокупность единиц) обследования — 995 телефонных абонентов города Буффало,
штат Нью-Йорк. Цель обследования — фиксация общего числа  телефонных разговоров за год на каждом абоненте. Таким образом, в данном случае
телефонных разговоров за год на каждом абоненте. Таким образом, в данном случае  число телефонных разговоров в году на
число телефонных разговоров в году на  обследованном абоненте. В табл. 5.4 приведены выборочные данные, сгруппированные методом, описанным в п. 5.4.2.
обследованном абоненте. В табл. 5.4 приведены выборочные данные, сгруппированные методом, описанным в п. 5.4.2.
Таблица 5.4

Были выбраны число интервалов группирования  и соответственно длина интервала группирования
и соответственно длина интервала группирования  Графики соответствующих эмпирической (гистограмма) и теоретической плотностей
Графики соответствующих эмпирической (гистограмма) и теоретической плотностей  приведены на рис. 5.6 (для построения теоретической кривой плотности в нормальную модель распределения, см. § 6.1, подставлялись вместо неизвестных параметров — среднего а и дисперсии
приведены на рис. 5.6 (для построения теоретической кривой плотности в нормальную модель распределения, см. § 6.1, подставлялись вместо неизвестных параметров — среднего а и дисперсии  значения соответствующих выборочных характеристик а и
значения соответствующих выборочных характеристик а и  см. § 10.4).
см. § 10.4).
Более подробные сведения о методах построения эмпирических функций плотности и их статистического анализа приводятся в § 10.3, 10.4, 11.1 и 11.2.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.1.2. Два варианта интерпретации исходных данных и два подхода к их статистической обработке.
- 1.1.3. Основные этапы статистической обработки исходных данных.
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1. Теория вероятностей и условия ее применимости
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1. Для чего нужны математические модели
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей»
- 3.5.4. Геометрические модели.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1. Дискретное вероятностное пространство
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
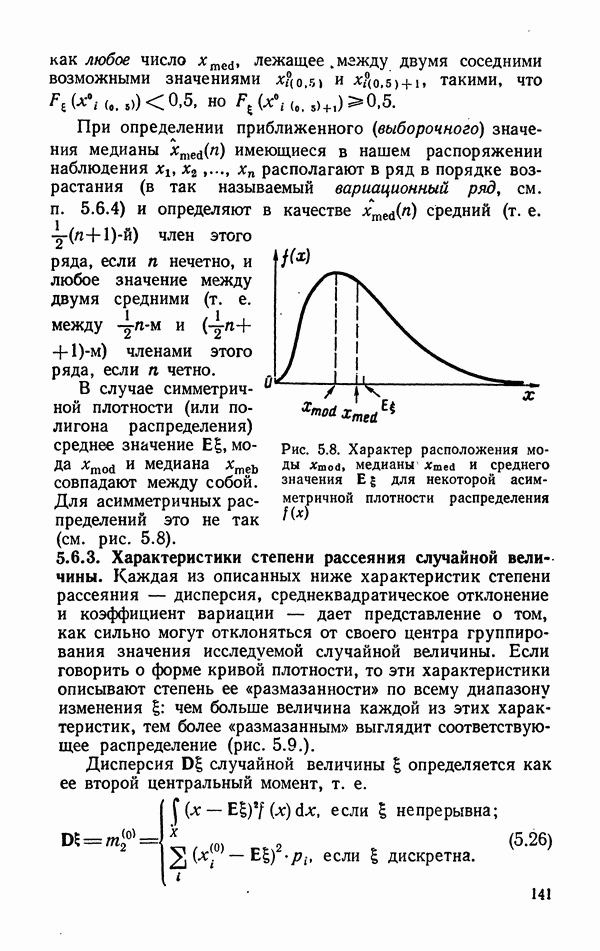
- 5.6.2. Характеристики центра группирования значений случайной величины.
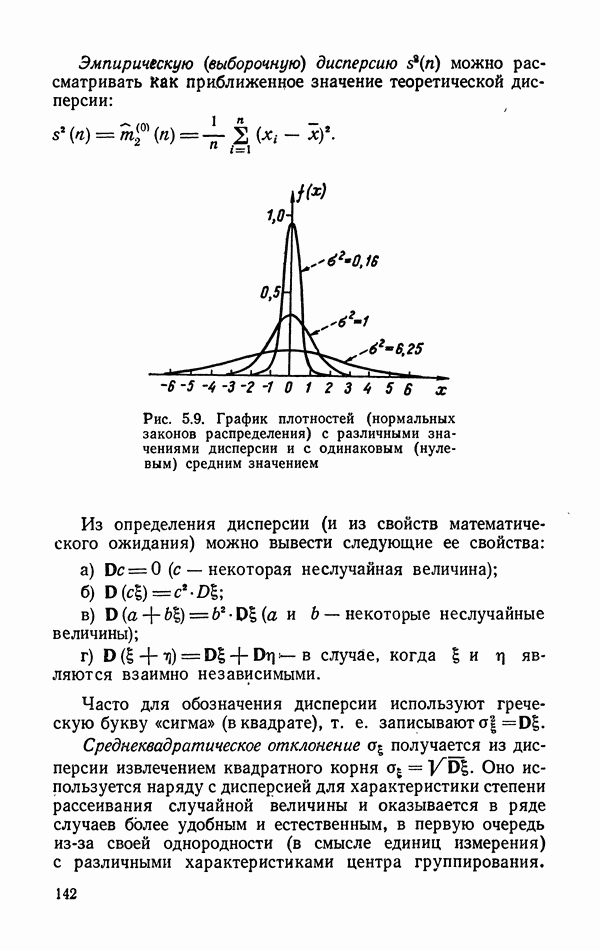
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
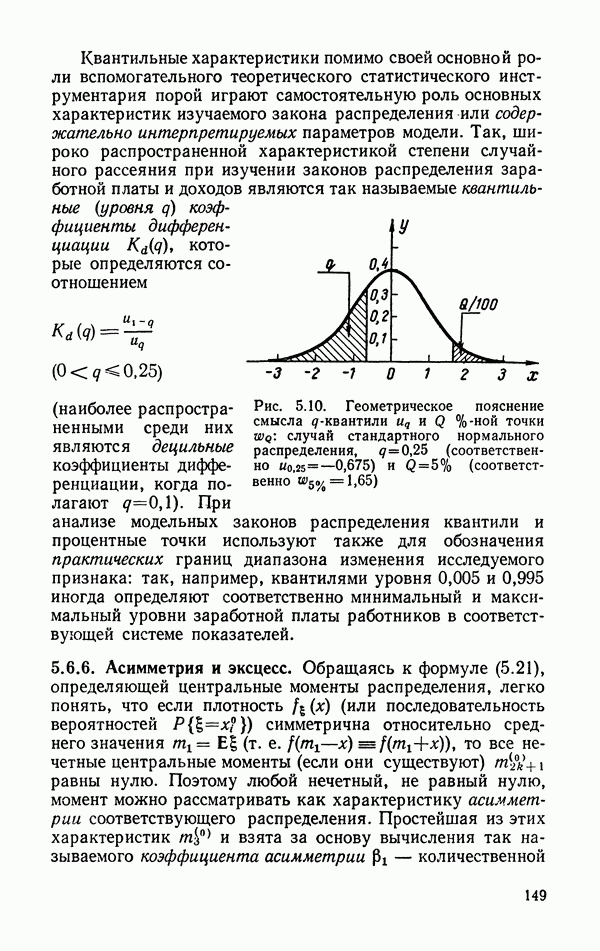
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
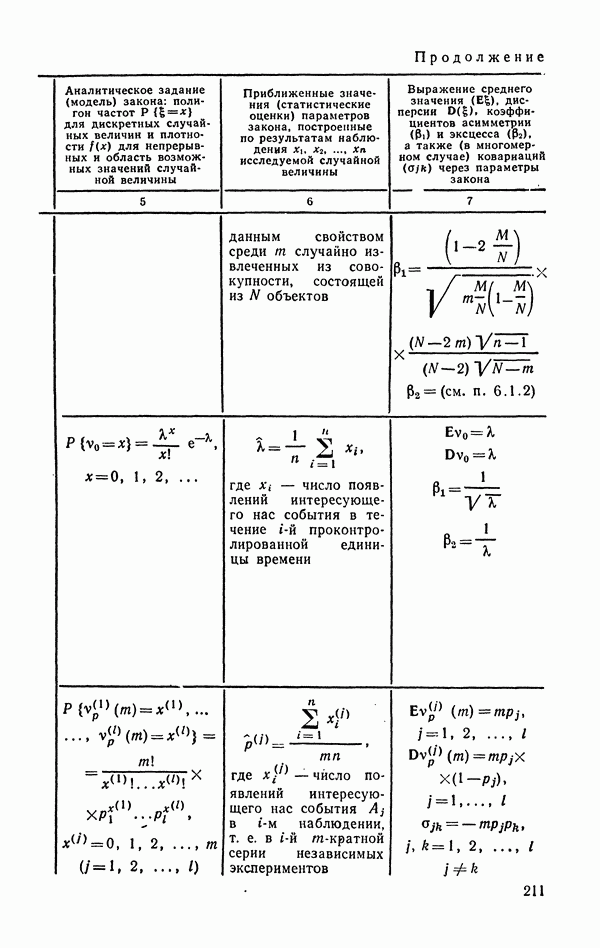
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
- 6.1.5. Нормальное (гауссовское) распределение.
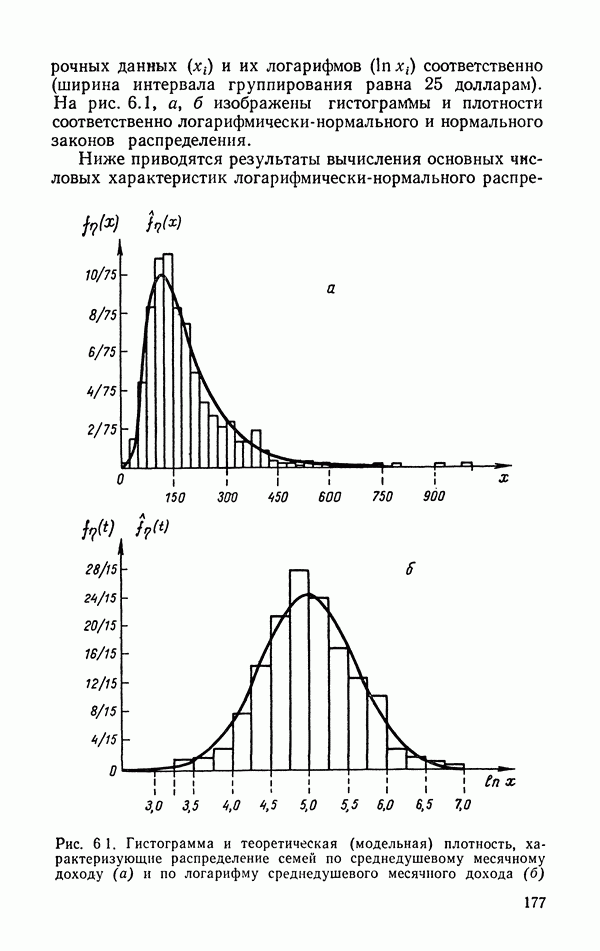
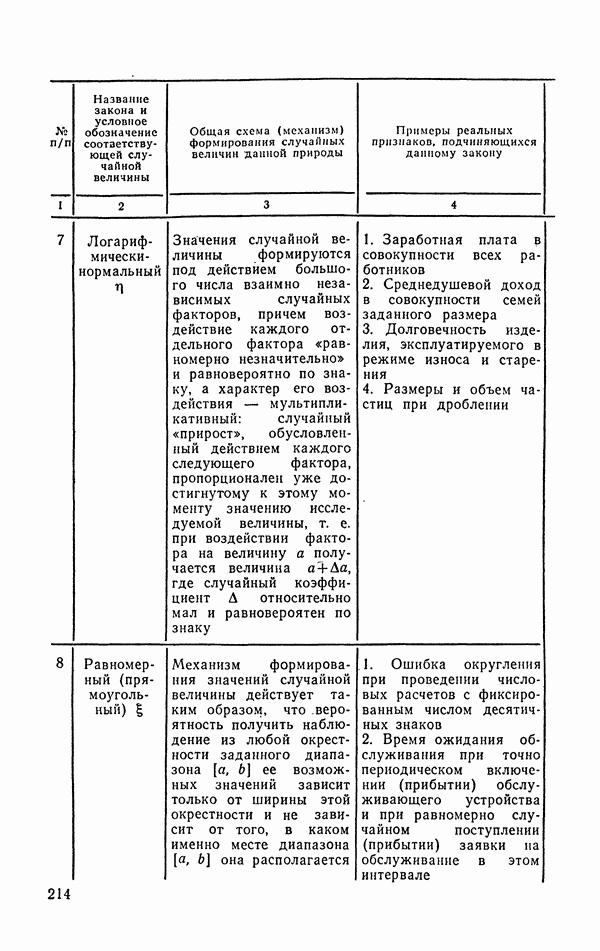
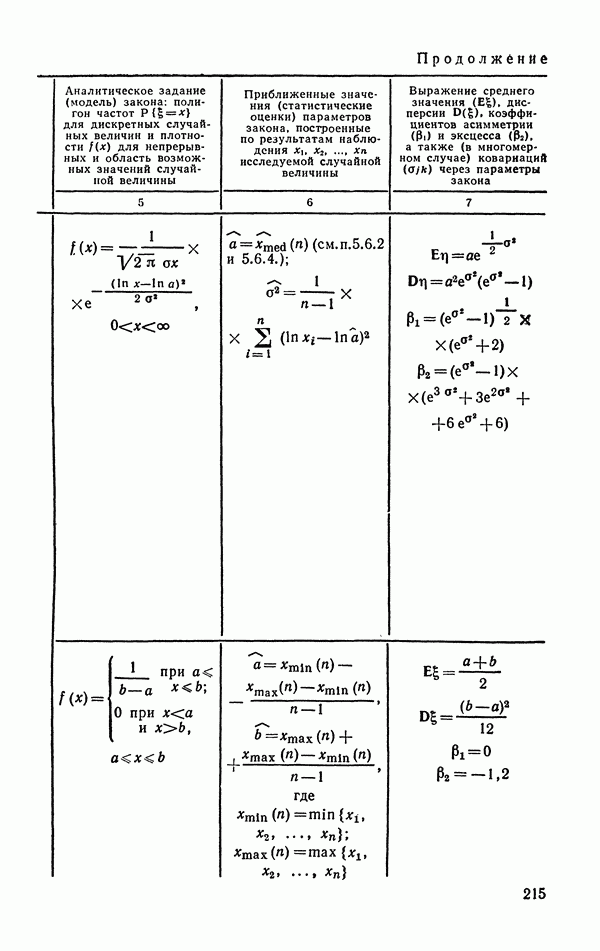
- 6.1.6. Логарифмически-нормальное распределение.
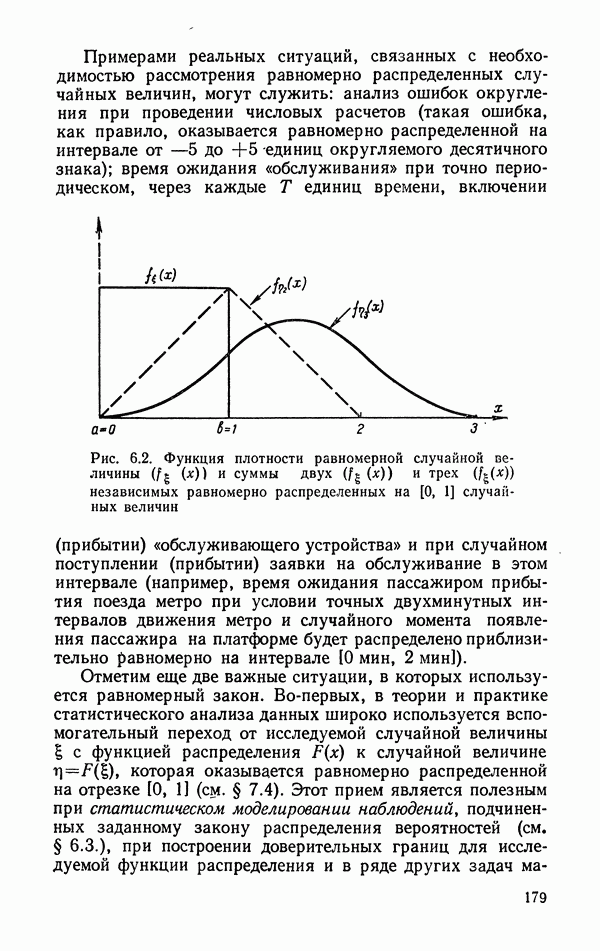
- 6.1.7. Равномерное (прямоугольное) распределение.
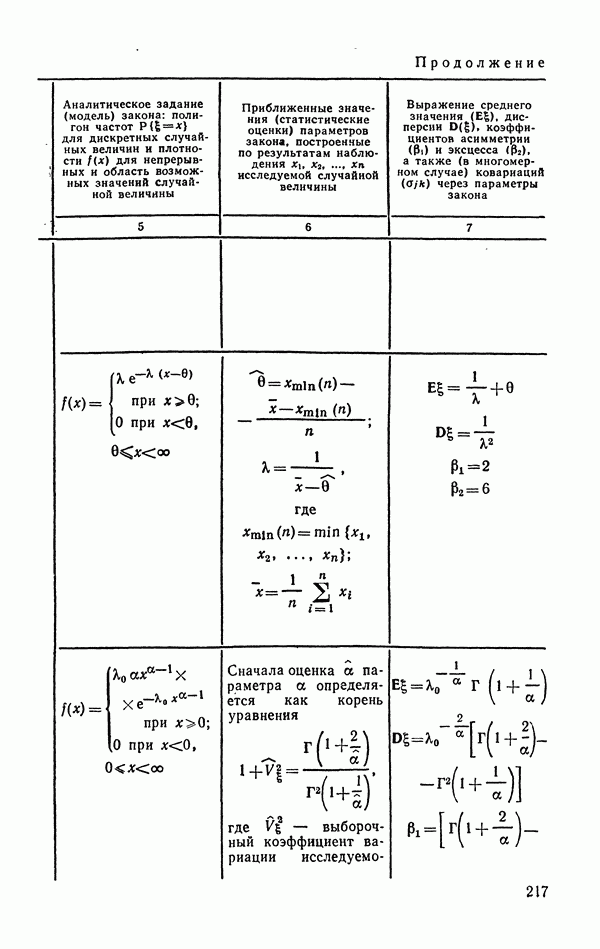
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
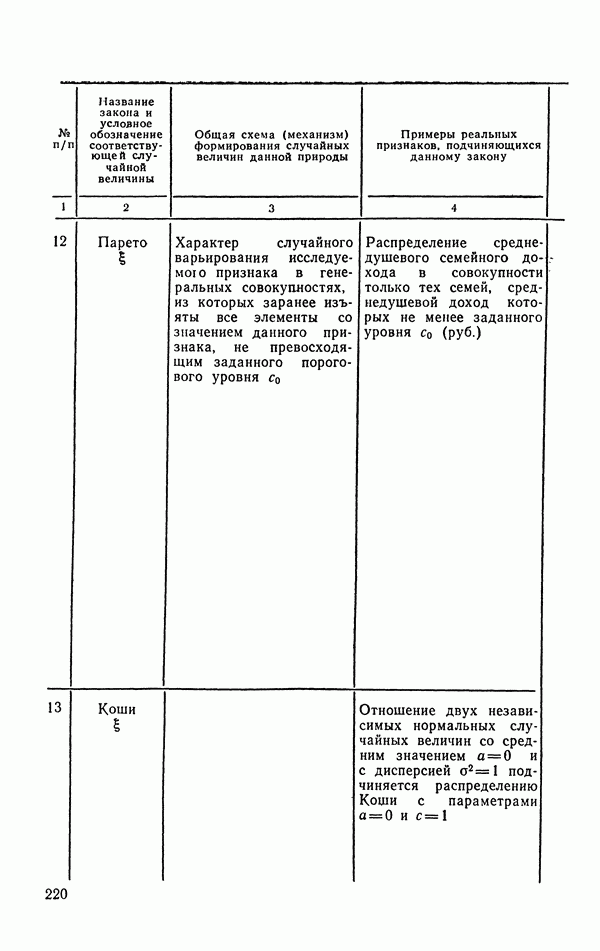
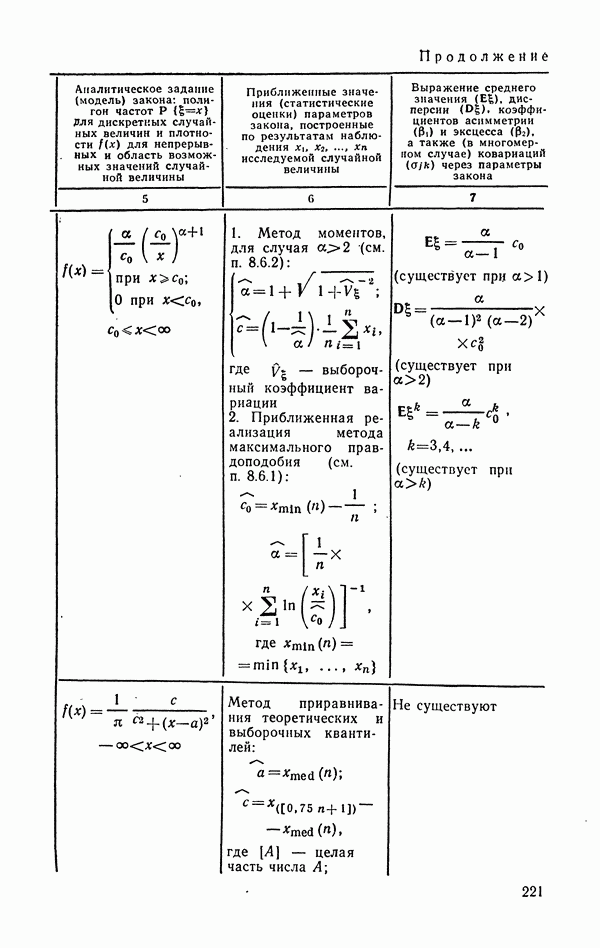
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
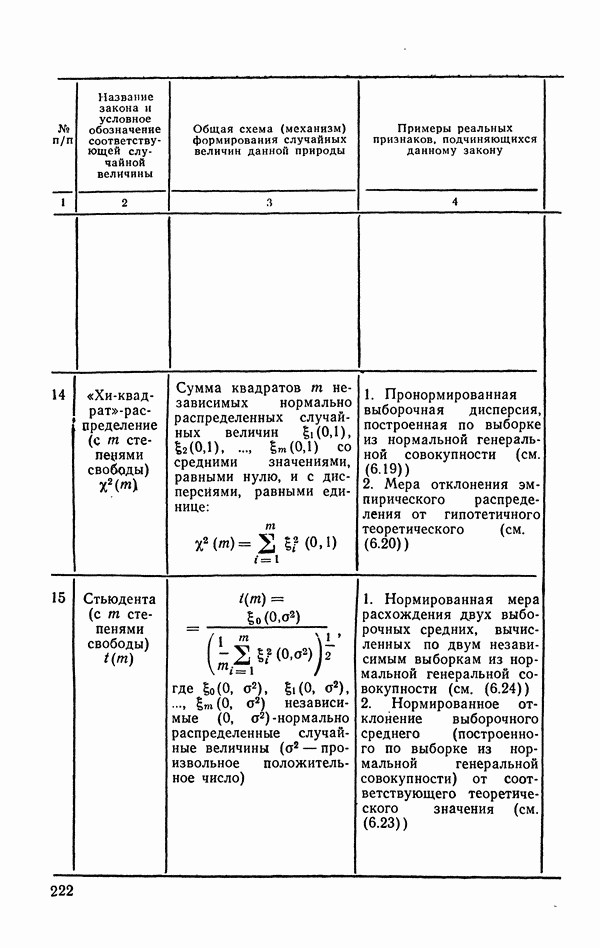
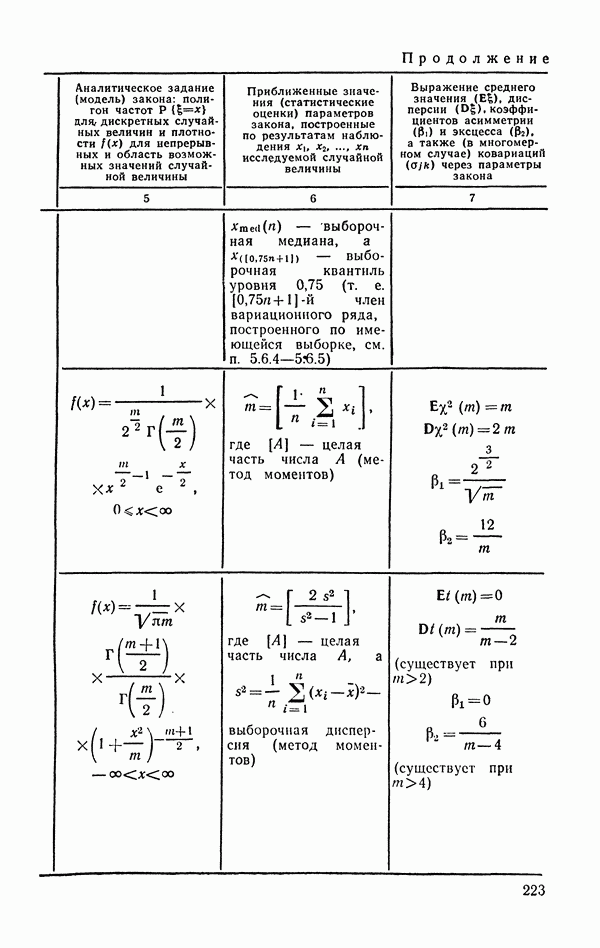
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных распределениях.
- 6.2.5. Г-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.2. Моделирование дискретных случайных величин. Стандартный метод.
- 6.3.3. Моделирование непрерывных распределений.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.2. Многомерная центральная предельная теорема (см. [12, с. 105]).
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия.
- 8.3. Неравенство Рао — Крамера — Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4. Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1.1. Критерий «хи квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий w^2 (Крамера — Мнзеса — Смирнова).
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и w^2 для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- 11.1.7. Использование критериев согласия Колмогорова и w^2 в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.2. Критерий однородности «хи квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия.
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа w^2
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ