| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.5. Анализ резко выделяющихся наблюдений
11.5.1. Постановка задачи.
В этом параграфе рассматриваются методы выделения наблюдений, которые сильно отклоняются от центра распределения. Иногда такие большие отклонения возникают в результате случайного просчета, неправильного чтения показаний измерительного прибора, случайного сдвига запятой в десятичной записи числа и т. д., т. е. в результате действительной ошибки. Иногда же они отражают более тонкие моменты, такие, как несоответствие в отдельных точках действительности используемой математической модели, незамеченное исследователем изменение
условий эксперимента и т. п. В любом случае с математической точки зрения речь идет о выделении наблюдений, величина которых не согласуется с распределением основной массы данных. Идентификация выделяющихся наблюдений позволяет обычно еще раз проверить условия их регистрации и процессирования и тем самым подчас выявить и устранить ошибку. Если же ошибку устранить не удается, то наблюдение обычно просто исключается из дальнейшей обработки как нетипичное.
Рассматриваемая задача разделяется на два этапа: выявление «подозрительных» наблюдений и проверка статистической значимости их отличия от основной массы данных.
Естественно, что оба этапа основываются на определенных предположениях о распределении как основной («незасоренной») части наблюдений, так и «выбросов» («засорений»). Обычно предполагается, что наблюдения незасоренной части имеют одномерное или многомерное нормальное распределение с неизвестными параметрами. При анализе отклонений наблюдений от математической модели иногда дополнительно предполагается, что среднее распределения отклонений равно нулю, т. е. что модель в среднем не вносит смещения. Относительно моделей для засорения единства предположений нет. Иногда предполагается, что выбросы имеют такую же дисперсию, что основная часть выборки, но заметно сдвинутое среднее. Иногда, что среднее не сильно отличается от среднего основной части, но зато дисперсия значительно больше. Для удобства дальнейших ссылок запишем эти предположения в более формальном виде. Пусть  — результаты наблюдения,
— результаты наблюдения,  — наборы индексов из множества
— наборы индексов из множества  соответствующие незасоренной и засоренной частям выборки. Предположение о незасоренной части выборки:
соответствующие незасоренной и засоренной частям выборки. Предположение о незасоренной части выборки:
 (11.77)
(11.77)
где  от — неизвестные параметры.
от — неизвестные параметры.
Предположения о засоренной части случай сдвига среднего:
 (11.78)
(11.78)
и случай большой дисперсии:
 (11.79)
(11.79)
В случае когда из априорных соображений можно считать, что среднее основной части выборки равно нулю, (11.77) переходит в
 (11.80)
(11.80)
а предположения относительно засоренной части — в

Прежде чем приступить к описанию конкретных методов выделения выбросов, отметим, что чисто статистический подход к проблеме идентификации и удаления нестандартных наблюдений, развиваемый в этом параграфе, требует определенной осторожности при интерпретации данных. Предположение однородности, лежащее в основе статистических процедур, в действительности может не иметь места, и выбросы могут оказаться наиболее важными наблюдениями, проливающими свет на то, как собирались данные.
11.5.2 Графические методы.
Назовем  -нормальной (half-normal) вероятностную бумагу, которая получается из нормальной вероятностной бумаги следующим образом: от нормальной бумаги отрезается нижняя полуплоскость, соответствующая значениям ординат, меньшим 0,5, и числовые значения ординат заменяются на
-нормальной (half-normal) вероятностную бумагу, которая получается из нормальной вероятностной бумаги следующим образом: от нормальной бумаги отрезается нижняя полуплоскость, соответствующая значениям ординат, меньшим 0,5, и числовые значения ординат заменяются на  . На
. На  -нормальной бумаге функция распределения
-нормальной бумаге функция распределения  , где
, где  изображается в виде прямой линии, выходящей из начала координат с угловым коэффициентом
изображается в виде прямой линии, выходящей из начала координат с угловым коэффициентом  , т. е. с тем же угловым коэффициентом, с каким на нормальной бумаге была бы изображена функция распределения
, т. е. с тем же угловым коэффициентом, с каким на нормальной бумаге была бы изображена функция распределения 
Рассмотрим теперь случай, когда имеют место предположения (11.80) для основной части выборки и (11.81) или (11.82) — для засоренной. Если построить на  -нормальной бумаге функцию распределения
-нормальной бумаге функцию распределения  то полученный график должен в своей левой части хорошо аппроксимироваться прямой линией, выходящей из начала координат. Правый конец графика будет отклоняться от прямой вправо и точка его отрыва даст возможность оценить долю засорения.
то полученный график должен в своей левой части хорошо аппроксимироваться прямой линией, выходящей из начала координат. Правый конец графика будет отклоняться от прямой вправо и точка его отрыва даст возможность оценить долю засорения.
В общем случае, когда имеют место модели (11.80), (11.81), (11.82), сначала любым устойчивым методом оценивают параметр  (см. § 10.4) и далее наносят на
(см. § 10.4) и далее наносят на  -нормальную бумагу разности
-нормальную бумагу разности  Свойства и интерпретация
Свойства и интерпретация
графика такие же, что и в рассмотренном только что частном случае.
В многомерном случае, когда предполагается, что основная часть выборки имеет приближенно нормальное распределение  , параметры этого закона оцениваются с помощью
, параметры этого закона оцениваются с помощью  -моментов (см. § 10.4) при таком значении X, чтобы влияние засорения на оценку было небольшим и вместе с тем оценки имели хорошие выборочные свойства. Далее строится гистограмма распределения
-моментов (см. § 10.4) при таком значении X, чтобы влияние засорения на оценку было небольшим и вместе с тем оценки имели хорошие выборочные свойства. Далее строится гистограмма распределения
 (11.83)
(11.83)
При сделанных предположениях эта величина должна приближенно иметь  -распределение с
-распределение с  степенями свободы. Заметное утяжеление правого конца гистограммы говорит о засорении выборки. Этот способ, хотя и носит приближенный характер, удобен на практике, так как при подсчете
степенями свободы. Заметное утяжеление правого конца гистограммы говорит о засорении выборки. Этот способ, хотя и носит приближенный характер, удобен на практике, так как при подсчете  -моментов для каждого параметра одновременно оценивается по (11.83) и вес, с которым наблюдение входит в оценка
-моментов для каждого параметра одновременно оценивается по (11.83) и вес, с которым наблюдение входит в оценка 
11.5.3. Аналитический метод исключения одного экстремального наблюдения.
Не нарушая общности, будем считать, что речь идет о максимальном наблюдении. Пусть  — вариационный ряд выборки. Решающее правило для исключения экстремального члена вариационного ряда основано на статистике
— вариационный ряд выборки. Решающее правило для исключения экстремального члена вариационного ряда основано на статистике  где
где  и s определяются обычным образом. Распределение и процентные точки
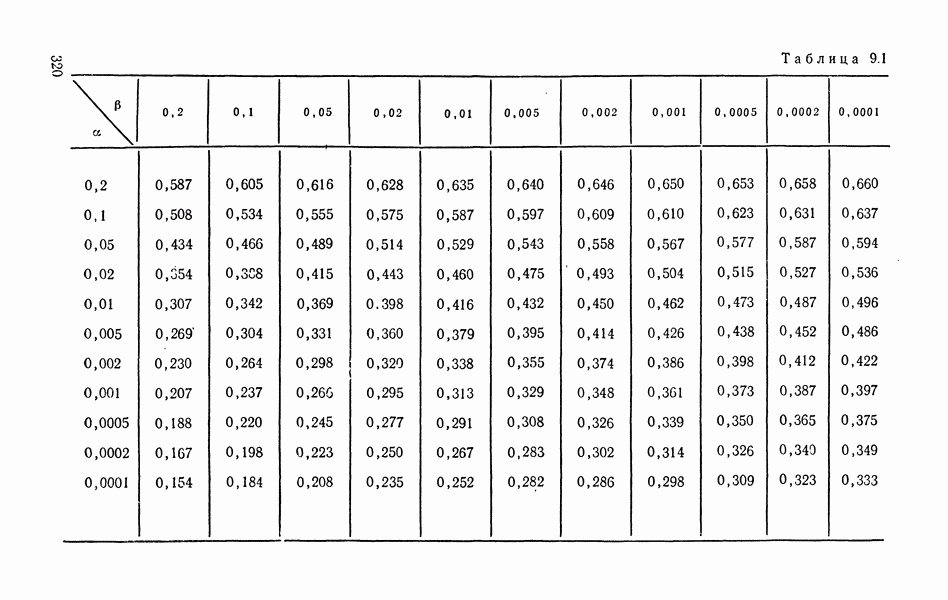
и s определяются обычным образом. Распределение и процентные точки  изучались К. Пирсоном [130], Н. В. Смирновым], Ф. Граббсом [113]. Таблица критических значений
изучались К. Пирсоном [130], Н. В. Смирновым], Ф. Граббсом [113]. Таблица критических значений  рассчитанная Граббсом, может быть найдена в [16]. Если
рассчитанная Граббсом, может быть найдена в [16]. Если  больше соответствующего критического значения, то гипотеза о наличии выброса принимается, если же
больше соответствующего критического значения, то гипотеза о наличии выброса принимается, если же  меньше критического значения, то со статистической точки зрения нет оснований говорить о наличии выброса.
меньше критического значения, то со статистической точки зрения нет оснований говорить о наличии выброса.
Отмеченная в § 10.4 неустойчивость оценок  и s к отклонениям распределения
и s к отклонениям распределения  от нормальности снижает практическую ценность изложенного критерия. Опираясь на устойчивые оценки параметров сдвига и масштаба, можно сконструировать более устойчивые критерии типа
от нормальности снижает практическую ценность изложенного критерия. Опираясь на устойчивые оценки параметров сдвига и масштаба, можно сконструировать более устойчивые критерии типа 
Если в выборке подозревают несколько экстремальных значений, то критерий сначала применяется к максимальному из них. Если оно признается выбросом, то его удаляют из выборки, и критерий, применяется к следующему по величине и т. д. до тех пор, пока не будет признано, что выбросов
больше нет. Одна из трудностей такого итерационного подхода состоит в том, что подозрительные наблюдения часто группируются близко друг к другу, образуя группу в стороне от основной массы наблюдений, что делает итерационную процедуру, основанную на использовании  и s, нечувствительной к ним. Так же, как и в п. 11.5.2, здесь можно рекомендовать заменить
и s, нечувствительной к ним. Так же, как и в п. 11.5.2, здесь можно рекомендовать заменить  и s на соответствующие моменты (см. § 10.4 и [56], [57]).
и s на соответствующие моменты (см. § 10.4 и [56], [57]).
11.5.4. Аналитический критерий одновременного исключения нескольких экстремальных наблюдений.
Излагаемый ниже критерий принадлежит Г. Титьену и Г. Муру [138]. Нулевая гипотеза, как обычно, состоит в том, что выборка извлечена из нормальной совокупности. Решающее правило для исключения k наибольших членов вариационного ряда основано на статистике
 (11.84)
(11.84)
где  — среднее первых
— среднее первых  членов вариационного ряда,
членов вариационного ряда,  среднее всей совокупности. При наличии выбросов статистика
среднее всей совокупности. При наличии выбросов статистика  должна быть меньше критического предела, рассчитанного для нормального распределения. Таблицы критических значений для
должна быть меньше критического предела, рассчитанного для нормального распределения. Таблицы критических значений для  можно найти в [76].
можно найти в [76].
Если в выборке возможны выбросы и влево, и вправо, то для оценки их значимости изложенное выше правило должно быть модифицировано. Модификация близка к приему, описанному в п. 11.5.2, и состоит в следующем. Сначала по выборке  вычисляется
вычисляется  затем абсолютные отклонения
затем абсолютные отклонения  . Построим вариационный ряд из абсолютных отклонений и обозначим его элементы
. Построим вариационный ряд из абсолютных отклонений и обозначим его элементы  Пусть
Пусть  — средняя арифметическая из
— средняя арифметическая из  первых членов вариационного ряда, тогда модифицированный критерий имеет вид:
первых членов вариационного ряда, тогда модифицированный критерий имеет вид:
 (11.85)
(11.85)
Недостатком изложенного критерия является то, что он опирается на статистики, сильно зависящие от предположений нормальности, а также и то, что в практической работе k никогда заранее не известно, а оценивается по тем же данным, к которым затем применяется статистика  и s. Последнее обстоятельство, как было показано Г. Титьеном и Г. Муром, существенно влияет на фактический критический уровень критерия, что лишний раз является аргументом в пользу «наивных» графических методов.
и s. Последнее обстоятельство, как было показано Г. Титьеном и Г. Муром, существенно влияет на фактический критический уровень критерия, что лишний раз является аргументом в пользу «наивных» графических методов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.1.2. Два варианта интерпретации исходных данных и два подхода к их статистической обработке.
- 1.1.3. Основные этапы статистической обработки исходных данных.
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1. Теория вероятностей и условия ее применимости
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1. Для чего нужны математические модели
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей»
- 3.5.4. Геометрические модели.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1. Дискретное вероятностное пространство
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.2. Характеристики центра группирования значений случайной величины.
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
- 6.1.5. Нормальное (гауссовское) распределение.
- 6.1.6. Логарифмически-нормальное распределение.
- 6.1.7. Равномерное (прямоугольное) распределение.
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
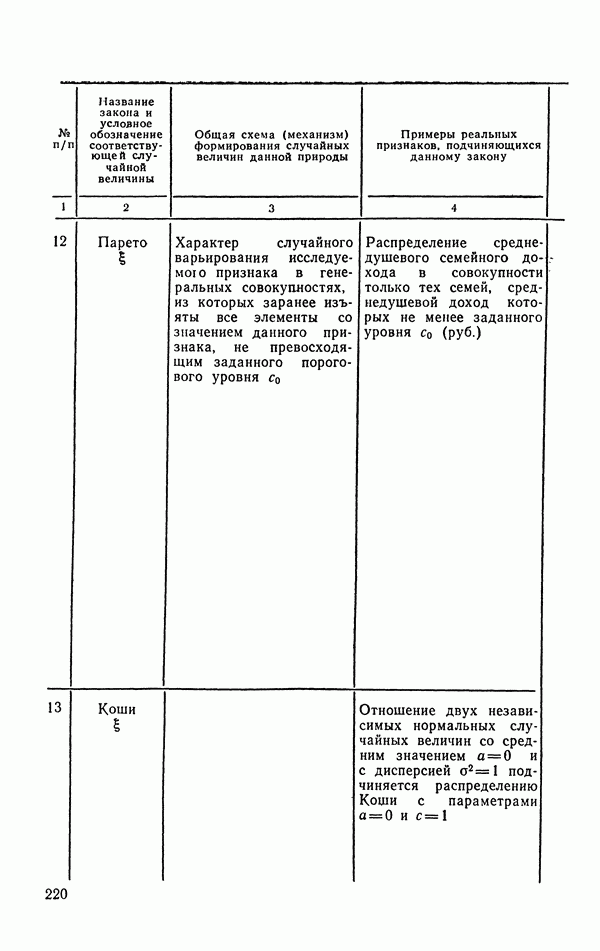
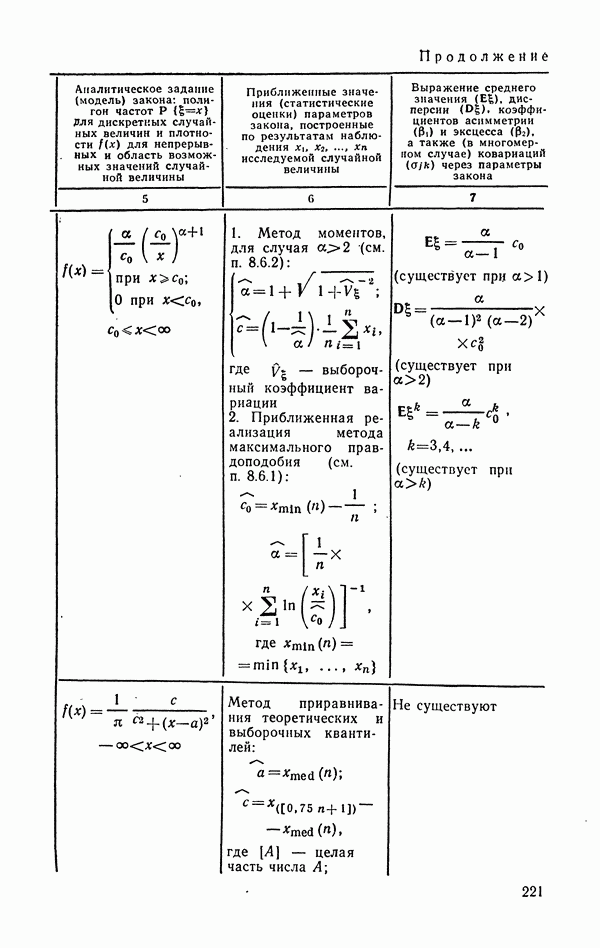
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
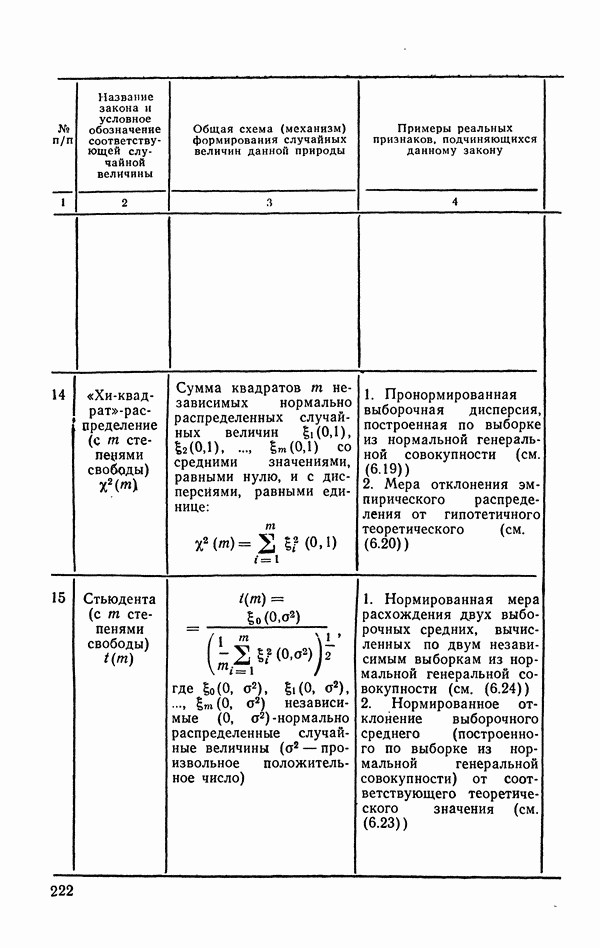
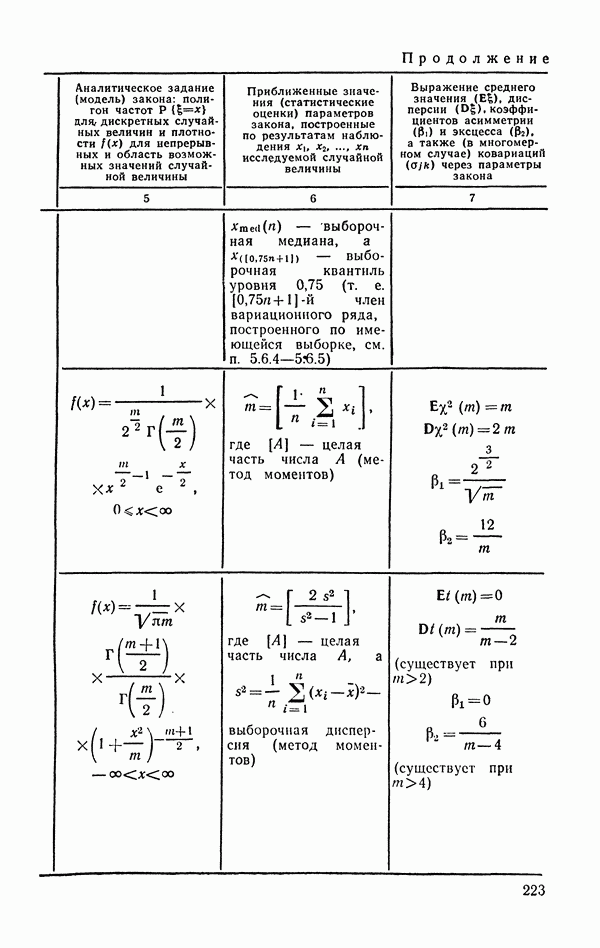
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных распределениях.
- 6.2.5. Г-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.2. Моделирование дискретных случайных величин. Стандартный метод.
- 6.3.3. Моделирование непрерывных распределений.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.2. Многомерная центральная предельная теорема (см. [12, с. 105]).
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия.
- 8.3. Неравенство Рао — Крамера — Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4. Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1.1. Критерий «хи квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий w^2 (Крамера — Мнзеса — Смирнова).
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и w^2 для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- 11.1.7. Использование критериев согласия Колмогорова и w^2 в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.2. Критерий однородности «хи квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия.
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа w^2
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ