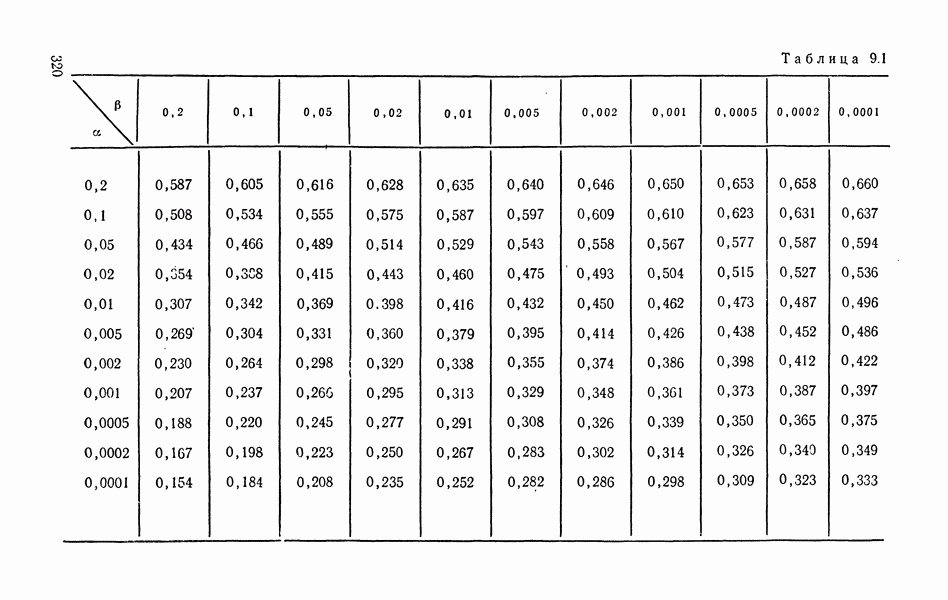
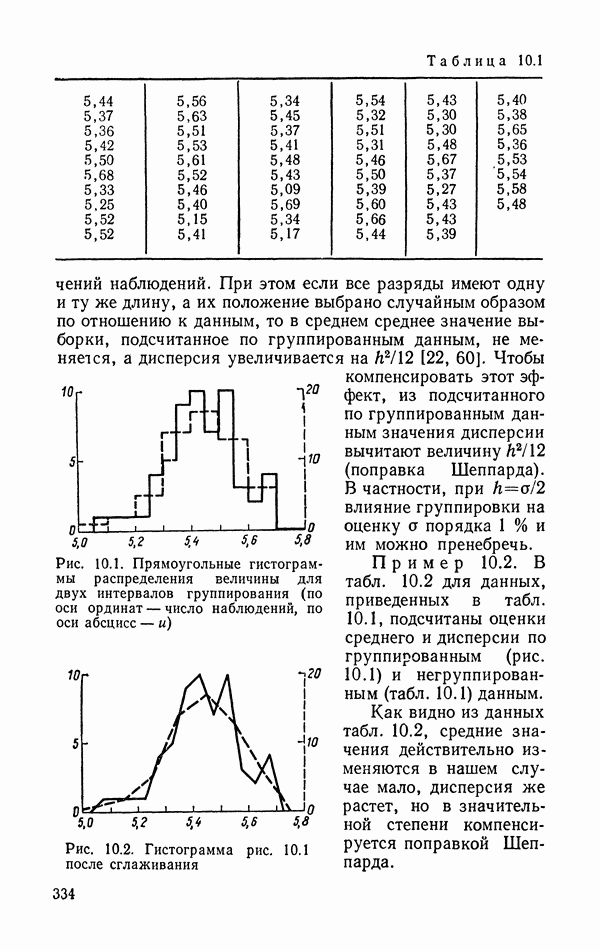
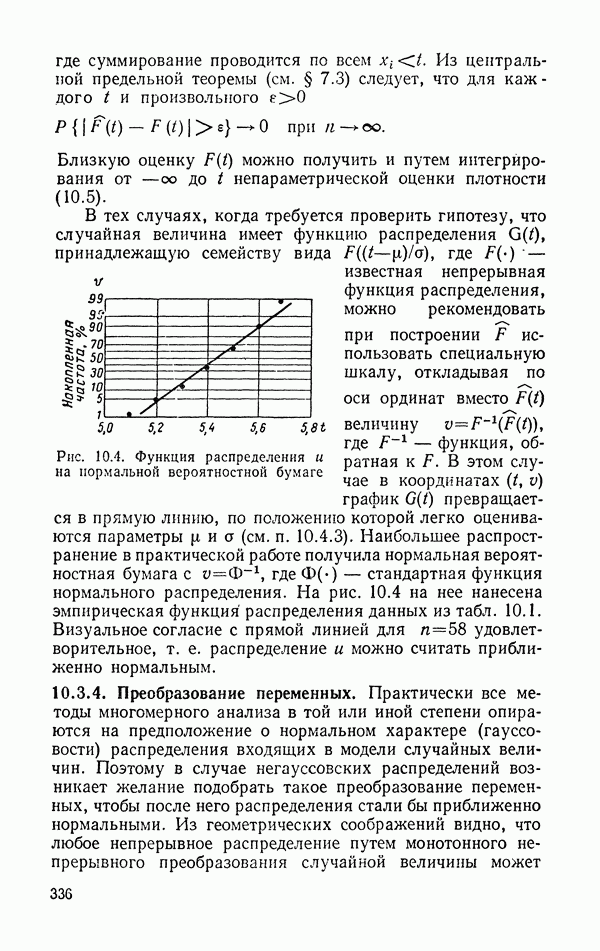
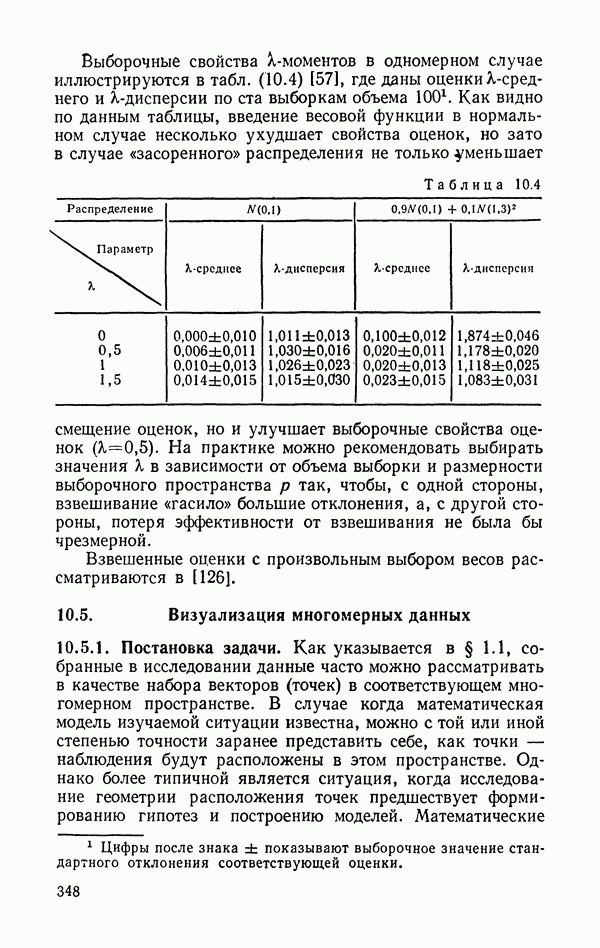
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
5.4.1. Закон распределения вероятностей.
Мы уже знаем (см. п. 4.1.3), что для полного описания механизма исследуемого случайного эксперимента, т. е. для полного описания вероятностного пространства (или, что то же, для исчерпывающего задания интересующей нас случайной величины), недостаточно задать лишь пространство элементарных событий  (и тем самым описать множество теоретически возможных значений анализируемой случайной величины). К этому необходимо добавить также: в дискретном случае — правило сопоставления с каждым возможным значением X? случайной величины
(и тем самым описать множество теоретически возможных значений анализируемой случайной величины). К этому необходимо добавить также: в дискретном случае — правило сопоставления с каждым возможным значением X? случайной величины  вероятности его появления
вероятности его появления  в непрерывном случае — правило сопоставления с каждой измеримой областью
в непрерывном случае — правило сопоставления с каждой измеримой областью  возможных значений случайной величины
возможных значений случайной величины  вероятности
вероятности  события, заключающегося в том, что в случайном эксперименте реализуется одно из возможных значений, принадлежащих заданной области
события, заключающегося в том, что в случайном эксперименте реализуется одно из возможных значений, принадлежащих заданной области  . Это правило, позволяющее устанавливать соответствия вида:
. Это правило, позволяющее устанавливать соответствия вида:

принято называть законом распределения вероятностей исследуемой случайной величины ?. Прозрачное пояснение такой терминологии мы получаем в рамках дискретного вероятностного пространства, поскольку в этом случае речь идет о правиле распределения суммарной единичной вероятности (т. е. вероятности достоверного события) между отдельными возможностями 
Очевидно, задание закона распределения вероятностей, т. е. соответствий типа (5.2), может осуществляться с помощью таблиц и графиков (только в дискретном случае), а также с помощью функций и алгоритмически (об основных формах задания законов распределения и примерах их модельной, т. е. аналитической, записи см. гл. 6).
Приведем примеры табличного и графического задания законов распределения вероятностей.
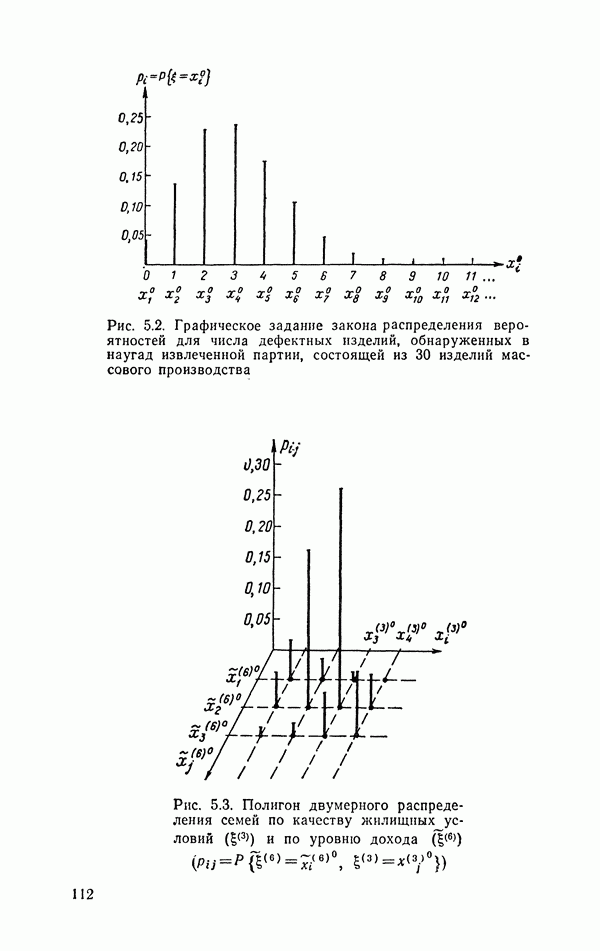
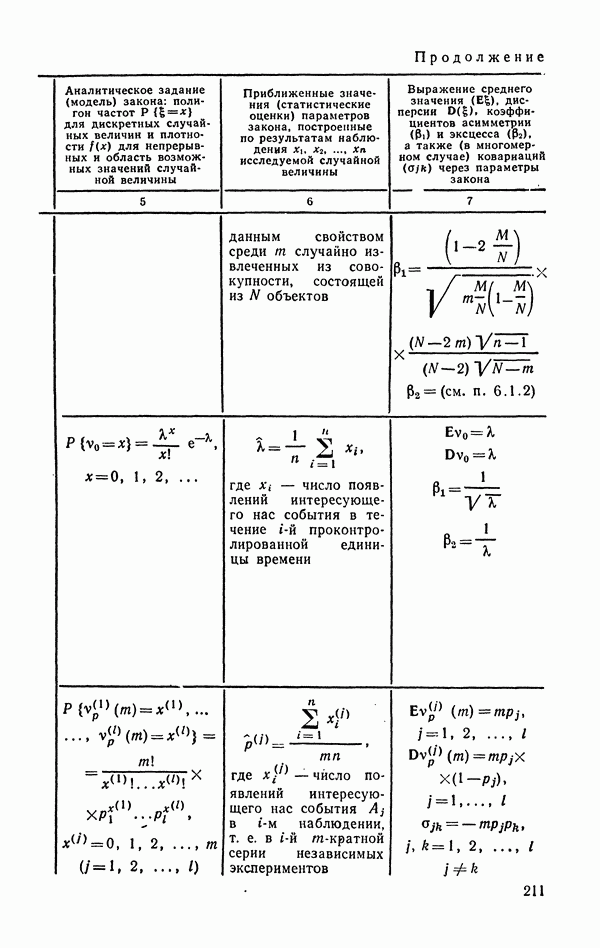
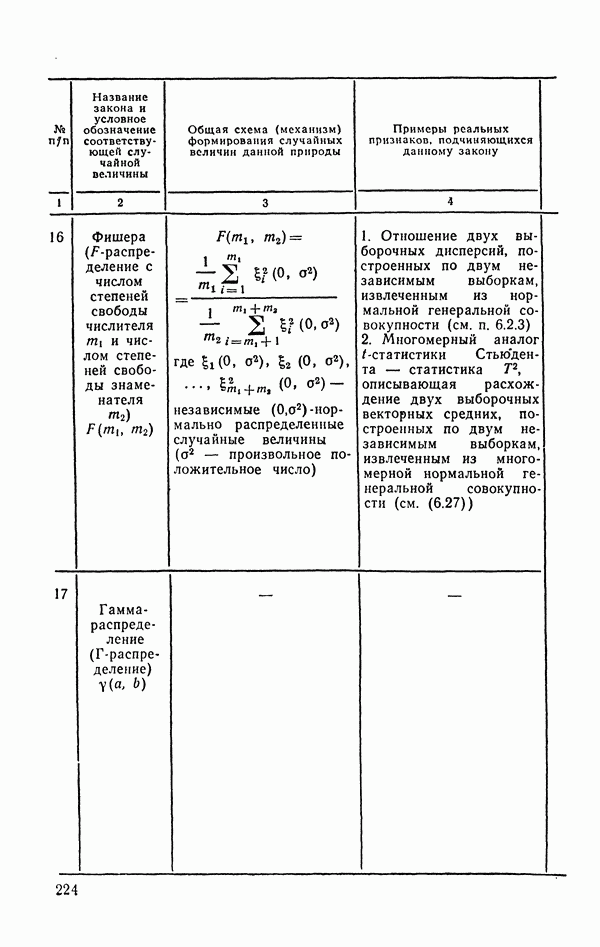
Тщательный статистический анализ засоренности партий дефектными изделиями (пример 4.5) позволил построить следующее распределение вероятностей для случайной величины выражающей число дефектных изделий, обнаруженных при контроле партии, состоящей из N=30 изделий, случайно отобранных из продукции массового производства (табл. 5.2):
Таблица 5.2

Значения вероятностей, приведенные в табл. 5.2, даны с точностью до третьего десятичного знака, поэтому то, что суммирование представленных в таблице вероятностей дает 0,998 (вместо единицы), легко объяснимо: недостающие 0,002 как-то «размазаны» между возможными значениями  но на каждое отдельное возможное значение приходится вероятность, меньшая 0,0005.
но на каждое отдельное возможное значение приходится вероятность, меньшая 0,0005.
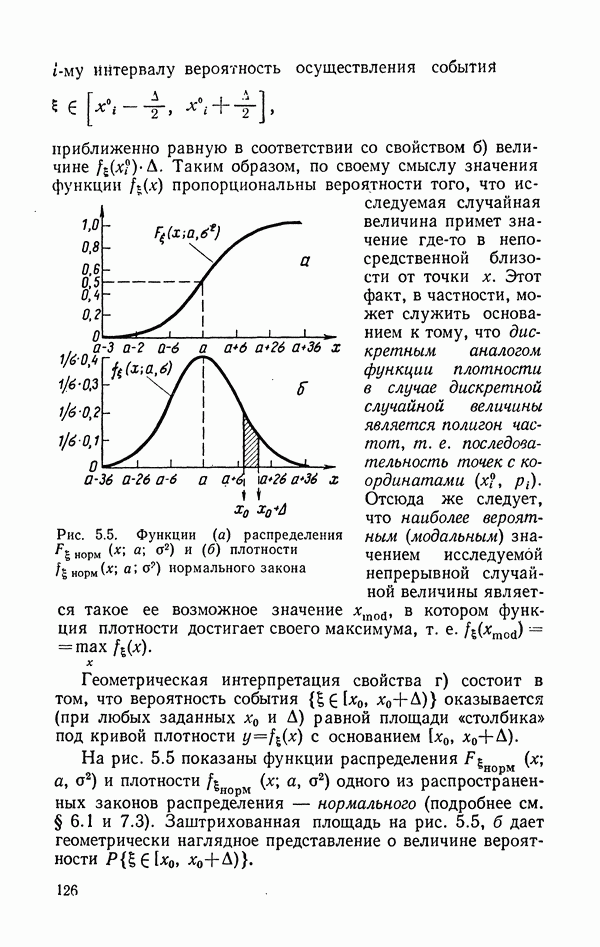
Тот же закон распределения может быть представлен графически (рис. 5.2).
Геометрическое изображение закона распределения вероятностей дискретной случайной величины часто называют полигоном распределения или полигоном частот
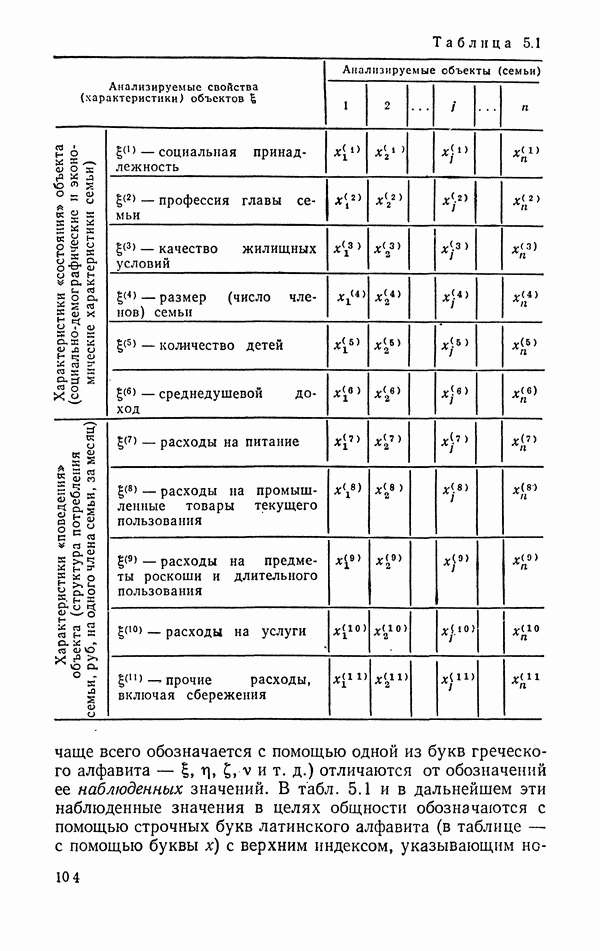
В качестве другого примера рассмотрим фрагмент табл. 5.1, выбрав из одиннадцати представленных в ней компонент только две: качество жилищных условий  и среднедушевой доход
и среднедушевой доход  Еще более упростим рассматриваемую схему, перейдя от по существу непрерывной случайной величины
Еще более упростим рассматриваемую схему, перейдя от по существу непрерывной случайной величины  к ее дискретному аналогу
к ее дискретному аналогу  отказываясь от точного знания среднедушевого дохода каждой семьи и ограничиваясь лишь тремя возможными градациями: семья имеет низкий доход (градация
отказываясь от точного знания среднедушевого дохода каждой семьи и ограничиваясь лишь тремя возможными градациями: семья имеет низкий доход (градация  ), средний доход (градация
), средний доход (градация  ) и высокий доход (градация
) и высокий доход (градация  ). С учетом четырех градаций качества жилищных условий:
). С учетом четырех градаций качества жилищных условий:  качество низкое;
качество низкое;  - качество удовлетворительное;
- качество удовлетворительное;  качество хорошее и
качество хорошее и  качество очень хорошее, и проведенного вероятностно-статистического анализа получаем следующий закон распределения вероятностей двумерной случайной величины
качество очень хорошее, и проведенного вероятностно-статистического анализа получаем следующий закон распределения вероятностей двумерной случайной величины  (данные условные):
(данные условные):
Таблица 5.3

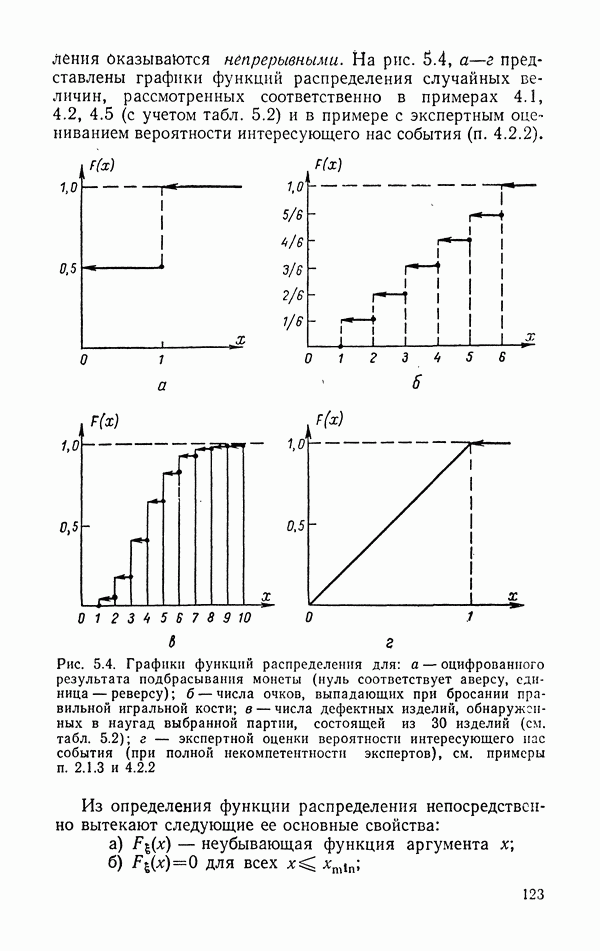
Соответствующий двумерный полигон распределения представлен на рис. 5.3.
Закон распределения вероятностей многомерной случайной величины называют многомерным или совместным. Если каждая из компонент  см.
см.  анализируемого многомерного признака
анализируемого многомерного признака  дискретна и имеет конечное число
дискретна и имеет конечное число  всех возможных значений, то, очевидно, общее число возможных «значений» случайного вектора
всех возможных значений, то, очевидно, общее число возможных «значений» случайного вектора  будет
будет  . В этом случае вместо общей индексации
. В этом случае вместо общей индексации

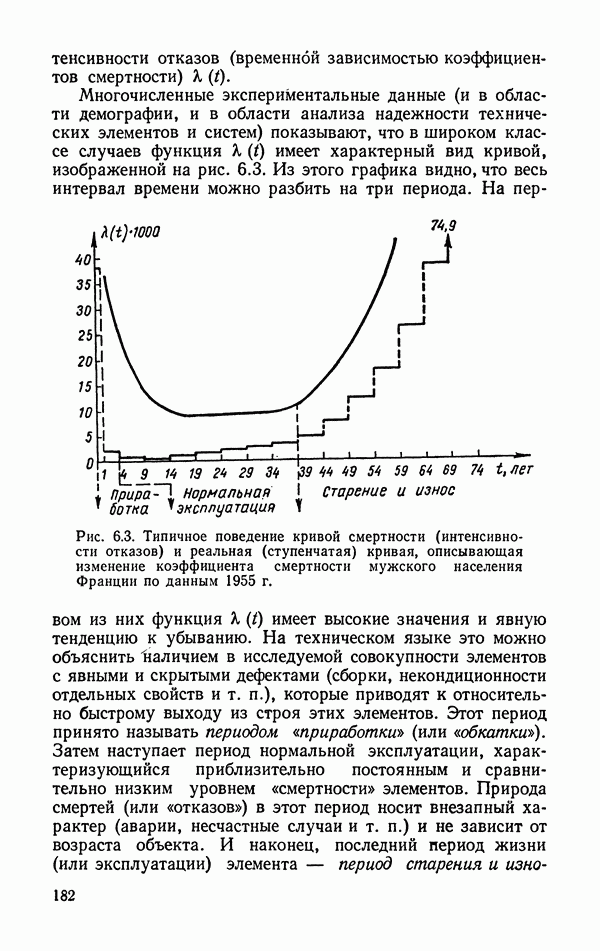
Рис. 5.2. Графическое задание закона распределения вероятностей для числа дефектных изделий, обнаруженных в наугад извлеченной партии, состоящей из 30 изделий массового производства

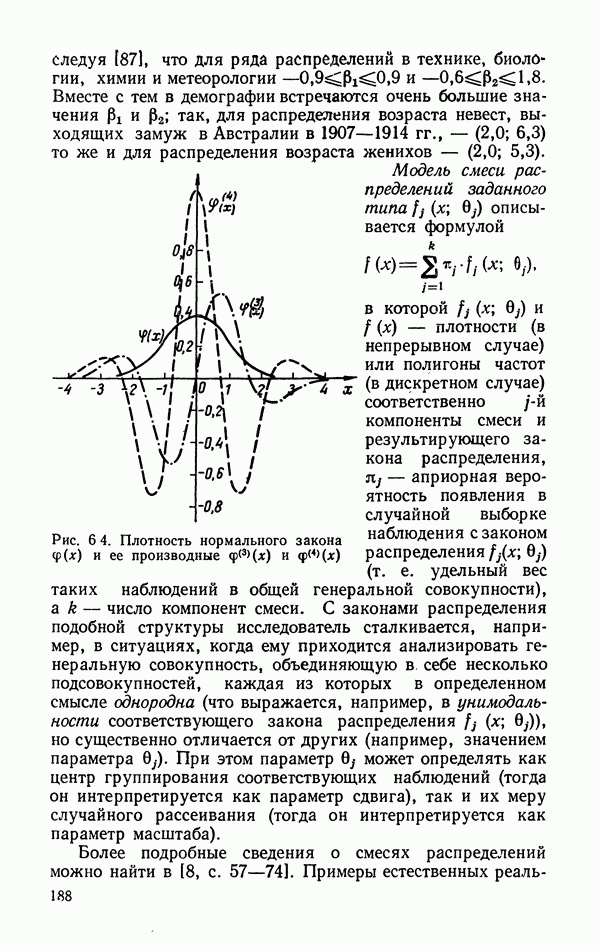
Рис. 5.3. Полигон двумерного распределения семей по качеству жилищных условий  и по уровню дохода
и по уровню дохода 
всех возможных многомерных значений  удобнее пользоваться
удобнее пользоваться  -мерной индексацией вида
-мерной индексацией вида  где первый индекс i определяет номер возможного значения по первой компоненте, второй индекс j — по второй компоненте и т. д. Тогда
где первый индекс i определяет номер возможного значения по первой компоненте, второй индекс j — по второй компоненте и т. д. Тогда  будет означать возможное значение
будет означать возможное значение  , полученное сочетанием i-го возможного значения компоненты
, полученное сочетанием i-го возможного значения компоненты  возможного значения компоненты
возможного значения компоненты  возможного значения компоненты
возможного значения компоненты  а вероятности
а вероятности  удобно обозначать
удобно обозначать  Таким образом, в табл. 5.3 представлены вероятности
Таким образом, в табл. 5.3 представлены вероятности 
При анализе многомерных (совместных) распределений часто бывает необходимо получить закон распределения лишь для какой-то части компонент анализируемого векторного признака. Так, многомерная случайная величина  , рассмотренная в табл. 5.1, естественно разбивается на два подвектора:
, рассмотренная в табл. 5.1, естественно разбивается на два подвектора:  описывающий социальнодемографические и экономическую характеристики семьи, и
описывающий социальнодемографические и экономическую характеристики семьи, и  описывающий структуру семейного потребления.
описывающий структуру семейного потребления.
Частный (маржинальный) закон распределения
Подвектора анализируемой многомерной случайной величины  описывает распределение вероятностей признака в ситуации, когда на значения другой части компонент
описывает распределение вероятностей признака в ситуации, когда на значения другой части компонент  не накладывается никаких условий. В дискретном случае соответствующие вероятности определяются по формулам:
не накладывается никаких условий. В дискретном случае соответствующие вероятности определяются по формулам:

где  возможные значения векторных признаков соответственно h и
возможные значения векторных признаков соответственно h и  .
.
Формулы (5.3) и (5.3) получаются как непосредственные следствия теоремы сложения вероятностей  если принять во внимание следующие очевидные связи между интересующими нас событиями:
если принять во внимание следующие очевидные связи между интересующими нас событиями:


В рассматриваемом примере (см. табл. 5.3) частные распределения  подсчитаны по формулам (5.3) и (5.3) и задают соответственно распределение семей отдельно по качеству жилищных условий и по уровню дохода (они приведены соответственно в последней строке и в последнем столбце табл. 5.3).
подсчитаны по формулам (5.3) и (5.3) и задают соответственно распределение семей отдельно по качеству жилищных условий и по уровню дохода (они приведены соответственно в последней строке и в последнем столбце табл. 5.3).
Условный закон распределения
подвектора h анализируемой многомерной случайной величины  ПРИ условии, что значение другого подвектора
ПРИ условии, что значение другого подвектора  зафиксировано на уровне вычисляется по формуле
зафиксировано на уровне вычисляется по формуле

Аналогично

Формулы (5.4) и (5.4) получаются как простые следствия теоремы умножения вероятностей (4.11).
Так, например, если нас интересует условное распределение группы семей с высоким доходом по качеству жилищных условий, т. е. распределение  то вычисления по (5.4) на основе данных табл. 5.3 дают:
то вычисления по (5.4) на основе данных табл. 5.3 дают:

что означает, в частности, что из всей совокупности семей с высоким доходом  проживает в плохих жилищных условиях, 10 % - в удовлетворительных, 35 % - в хороших и 50 % - в очень хороших.
проживает в плохих жилищных условиях, 10 % - в удовлетворительных, 35 % - в хороших и 50 % - в очень хороших.
5.4.2. Генеральная совокупность и выборка из нее.
Итак, закономерности, которым подчиняется исследуемая случайная величина, физически полностью обусловливаются реальным комплексом условий ее наблюдения (или эксперимента), а математически задаются соответствующим вероятностным пространством  или, что то же, соответствующим законом распределения вероятностей. Однако при проведении статистических исследований несколько более удобной оказывается другая терминология, связанная с понятием генеральной совокупности.
или, что то же, соответствующим законом распределения вероятностей. Однако при проведении статистических исследований несколько более удобной оказывается другая терминология, связанная с понятием генеральной совокупности.
Генеральной совокупностью называют совокупность всех мыслимых наблюдений (или всех мысленно возможных объектов интересующего нас типа, с которых «снимаются» наблюдения), которые могли бы быть произведены при данном реальном комплексе условий. Поскольку в определении речь идет о всех мысленно возможных наблюдениях (или объектах), то понятие генеральной совокупности есть понятие условно-математическое, абстрактное и его не следует смешивать с реальными совокупностями, подлежащими статистическому исследованию. Так, обследовав даже все предприятия подотрасли с точки зрения регистрации значений характеризующих их технико-экономических показателей, мы можем рассматривать обследованную совокупность лишь как представителя гипотетически возможной более широкой совокупности предприятий, которые могли бы функционировать в рамках того же самого реального комплекса условий.
В практической работе удобнее выбор связывать с объектами наблюдения, чем с характеристиками этих объектов. Мы отбираем для изучения машины, геологические пробы, людей, но не значения характеристик машин, проб, людей. С другой стороны, в математической теории объекты и совокупность их характеристик не различаются и двойственность введенного определения исчезает.
Как видим, математическое понятие «генеральная совокупность» физически полностью обусловливается, так же как и понятия «вероятностное пространство», «случайная величина» и «закон распределения вероятностей», соответствующим реальным комплексом условий, а потому все эти четыре математических понятия можно считать в определенном смысле синонимами. Генеральная совокупность называется конечной или бесконечной в зависимости от того, конечна или бесконечна совокупность всех мыслимых наблюдений.
Из определения следует, что непрерывные генеральные совокупности (состоящие из наблюдений признаков непрерывной природы) всегда бесконечны. Дискретные же генеральные совокупности могут быть как бесконечными, так и конечными. Скажем, если анализируется партия из N изделий на сортность (см. пример в п. 4.1.3), когда каждое изделие может быть отнесено к одному из четырех сортов, исследуемой случайной величиной  является номер сорта случайно извлеченного из партии изделия, а множество возможных значений случайной величины состоит соответственно из четырех точек (1, 2, 3 и 4) то, очевидно, генеральная совокупность будет конечной (всего N мыслимых наблюдений).
является номер сорта случайно извлеченного из партии изделия, а множество возможных значений случайной величины состоит соответственно из четырех точек (1, 2, 3 и 4) то, очевидно, генеральная совокупность будет конечной (всего N мыслимых наблюдений).
Понятие бесконечной генеральной совокупности есть математическая абстракция, как и представление о том, что измерение случайной величины можно повторить бесконечное число раз. Приближенно бесконечную генеральную совокупность можно истолковывать как предельный случай конечной, когда число объектов, порождаемых данным реальным комплексом условий, неограниченно возрастает. Так, если в только что приведенном примере вместо партий изделий рассматривать непрерывное массовое производство тех же изделий, то мы и придем к понятию бесконечной генеральной совокупности. Практически же такое видоизменение равносильно требованию 
Выборка из данной генеральной совокупности — это результаты ограниченного ряда наблюдений  случайной величины
случайной величины  . Выборку можно рассматривать как некий эмпирический аналог генеральной совокупности, то, с чем мы чаще всего на практике имеем дело, поскольку обследование всей генеральной совокупности бывает либо слишком трудоемко (в случае больших N), либо принципиально невозможно (в случае бесконечных генеральных
. Выборку можно рассматривать как некий эмпирический аналог генеральной совокупности, то, с чем мы чаще всего на практике имеем дело, поскольку обследование всей генеральной совокупности бывает либо слишком трудоемко (в случае больших N), либо принципиально невозможно (в случае бесконечных генеральных
совокупностей). Число  наблюдений, образующих выборку, называют объемом выборки.
наблюдений, образующих выборку, называют объемом выборки.
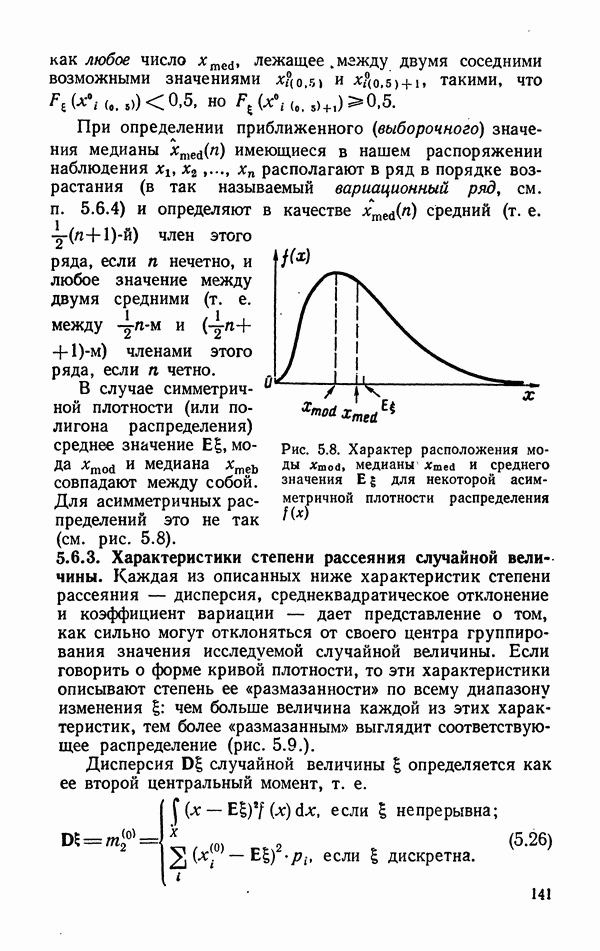
Если объем выборки  велик
велик  и при этом мы имеем дело с одномерной непрерывной величиной (или с одномерной дискретной, число возможных значений которой достаточно велико, скажем больше 10), то часто удобнее, с точки зрения упрощения дальнейшей статистической обработки результатов наблюдений, перейти к так называемым «группированным» выборочным данным. Этот переход осуществляется обычно следующим образом:
и при этом мы имеем дело с одномерной непрерывной величиной (или с одномерной дискретной, число возможных значений которой достаточно велико, скажем больше 10), то часто удобнее, с точки зрения упрощения дальнейшей статистической обработки результатов наблюдений, перейти к так называемым «группированным» выборочным данным. Этот переход осуществляется обычно следующим образом:
а) отмечаются наименьшее  и наибольшее
и наибольшее  значения в выборке;
значения в выборке;
б) весь обследованный диапазон  разбивается на определенное число 5 равных интервалов группирования; при этом количество интервалов s не должно быть меньше 8—10 и больше 20—25: выбор количества интервалов существенно зависит от объема выборки
разбивается на определенное число 5 равных интервалов группирования; при этом количество интервалов s не должно быть меньше 8—10 и больше 20—25: выбор количества интервалов существенно зависит от объема выборки  для примерной ориентации в выборе 5 можно пользоваться приближенной формулой
для примерной ориентации в выборе 5 можно пользоваться приближенной формулой

которую следует воспринимать скорее как оценку снизу для s (особенно при больших 
в) отмечаются крайние точки каждого из интервалов  в порядке возрастания, а также их середины
в порядке возрастания, а также их середины 
г) подсчитываются числа выборочных данных, попавших в каждый из интервалов:  (очевидно,
(очевидно,  ); выборочные данные, попавшие на границы интервалов, либо равномерно распределяются по двум соседним интервалам, либо условливаются относить их только к какому-либо одному из них, например к левому.
); выборочные данные, попавшие на границы интервалов, либо равномерно распределяются по двум соседним интервалам, либо условливаются относить их только к какому-либо одному из них, например к левому.
В зависимости от конкретного содержания задачи в данную схему группирования могут быть внесены некоторые видоизменения (например, в некоторых случаях целесообразно отказаться от требования равной длины интервалов группирования).
Во всех дальнейших рассуждениях, использующих выборочные данные, будем исходить из только что описанной системы обозначений.
Напомним, что сущность статистических методов состоит в том, чтобы по некоторой части генеральной совокупности (т.е. по выборке) выносить суждения о ее свойствах в целом.
Один из важнейших вопросов, от успешного решения которого зависит достоверность получаемых в результате статистической обработки данных выводов, является вопрос репрезентативности выборки, т. е. вопрос полноты и адекватности представления ею интересующих нас свойств анализируемой генеральной совокупности. В практической работе одна и та же группа объектов, взятых для изучения, может рассматриваться как выборка из разных генеральных совокупностей. Так, группу семей, наудачу отобранных из кооперативных домов одной из жилищноэксплуатационных контор (ЖЭК) одного из районов города для подробного социологического обследования, можно рассматривать и как выборку из генеральной совокупности семей (с кооперативной формой жилья) данной ЖЭК, и как выборку из генеральной совокупности семей данного района, и как выборку из генеральной совокупности всех семей города, и, наконец, как выборку из генеральной совокупности всех семей города, проживающих в кооперативных домах. Содержательная интерпретация результатов апробации существенно зависит от того, представителем какой генеральной совокупности мы рассматриваем отобранную группу семей, для какой генеральной совокупности эту выборку можно считать представительной (репрезентативной). Ответ на этот вопрос зависит от многих факторов. В приведенном выше примере, в частности, от наличия или отсутствия специального (быть может, скрытого) фактора, определяющего принадлежность семьи к данной ЖЭК или району в целом (таким фактором может быть, например, среднедушевой доход семьи, географическое расположение района в городе, «возраст» района и т. п.).
5.4.3. Основные способы организации выборки.
При оценке репрезентативности выборки учитывается и то, как выборка получена, и то, насколько распределение в выборке существенных для изучаемого вопроса показателей характерно для анализируемой генеральной совокупности в целом. Первый путь повышения степени репрезентативности — достижение полностью случайного отбора объектов из генеральной совокупности — часто бывает труден в организационном плане. Кроме того, сочетание регулярного и случайного выбора иногда оказывается более эффективным. В любом случае способ сбора исходных данных должен тщательно планироваться и его необходимо полностью описывать в отчетах о выполненной работе.
Использование для оценки репрезентативности распределений основных показателей в выборке и в генеральной совокупности также имеет свои трудности, одни из которых носят чисто статистический характер — недостаточный объем (число отобранных для использования объектов) выборки, неразработанность методов сравнения многомерных распределений и т.п., а другие — содержательный, ведь заранее неизвестно, распределение каких показателей следует сравнивать при доказательстве репрезентативности.
Опишем кратко основные способы организации выборки.
Простой случайный отбор — способ извлечения  объектов из конечной генеральной совокупности N объектов, при котором каждая из С" возможных выборок имеет равную вероятность быть отобранной. На практике часто нумеруют объекты в генеральной совокупности числами от 1 до N и затем, используя таблицы случайных чисел или какой-либо другой метод, обеспечивающий равную вероятность выбора объекта (например, урну с N шарами, занумерованными цифрами от 1 до N), отбирают один за другим
объектов из конечной генеральной совокупности N объектов, при котором каждая из С" возможных выборок имеет равную вероятность быть отобранной. На практике часто нумеруют объекты в генеральной совокупности числами от 1 до N и затем, используя таблицы случайных чисел или какой-либо другой метод, обеспечивающий равную вероятность выбора объекта (например, урну с N шарами, занумерованными цифрами от 1 до N), отбирают один за другим  объектов. Полученная таким способом выборка называется случайной.
объектов. Полученная таким способом выборка называется случайной.
Простой отбор с помощью регулярной, но несущественной для изучаемого вопроса процедуры часто применяется вместо случайного отбора. В медицинской практике отбор может проводиться по дню недели, что удобно с организационной точки зрения; в социологических обследованиях — по букве, с которой начинается фамилия индивидуума, проживающего в домах данной жилищно-эксплуатационной конторы, и т. п. Получаемые таким образом выборки часто называют механическими.
Стратифицированный (расслоенный) отбор заключается в том, что исходная генеральная совокупность объема N подразделяется на подсовокупности объема  При этом подсовокупности не содержат общих объектов и вместе исчерпывают всю генеральную совокупность, так что
При этом подсовокупности не содержат общих объектов и вместе исчерпывают всю генеральную совокупность, так что  Подсовокупности называют стратами или слоями. Когда слои определены, из каждого слоя извлекается простая случайная выборка объема соответственно
Подсовокупности называют стратами или слоями. Когда слои определены, из каждого слоя извлекается простая случайная выборка объема соответственно  Для того чтобы можно было полностью воспользоваться выгодами от расслоения, значения
Для того чтобы можно было полностью воспользоваться выгодами от расслоения, значения  должны быть известны. Стратифицированный отбор применяется, когда слои однородны в том смысле, что входящие в них объекты имеют близкие характеристики (средние значения которых могут быть оценены по малым
должны быть известны. Стратифицированный отбор применяется, когда слои однородны в том смысле, что входящие в них объекты имеют близкие характеристики (средние значения которых могут быть оценены по малым
выборкам); либо когда нецелесообразно изучать генеральную совокупность с равной тщательностью во всех слоях; либо по организационным причинам, когда методы проведения отбора в слоях должны быть разными. Выборки, полученные таким способом, называются стратифицированными или расслоенными (иногда — районированными).
Частным случаем стратифицированного отбора является способ организации выборки, при котором страты (слои) генеральной совокупности выделены по косвенному признаку, как-то связанному с изучаемым. Так, изучая средний душевой доход семей, для получения стратифицированных выборок можно предварительно разбить исследуемую совокупность семей на группы, однородные по какой-либо из социально-экономических характеристик главы семьи (например, по заработку). В подобных случаях говорят о типическом способе отбора и соответственно о типических выборках.
Методы серийного отбора (и соответственно серийные выборки) используются тогда, когда удобнее назначать к обследованию не отдельные элементы генеральной совокупности, а целые «блоки» или серии таких элементов. Так, при проведении выборочных обследований населения способ территориально-административного деления страны и характер ведения соответствующей документации обусловливают большее удобство сплошного способа обследования целых территориальных единиц (домов, кварталов), а не отдельных семей. Подобный способ отбора часто называют также гнездовым.
Комбинированный (ступенчатый) отбор сочетает в себе сразу несколько из вышеописанных способов отбора, образующих различные ступени (или фазы) выборочного обследования. Так, при выборочном обследовании условий жизни и структуры семей какого-либо города на первой ступени можно с помощью случайного отбора назначить городские районы, в которых будет производиться это обследование, затем способом механического отбора определить подлежащие обследованию жилищно-эксплуатационные конторы (ЖЭКи), а внутри ЖЭКов сделать серийную (гнездовую) выборку домов.
Подробное описание теории и методов выборочных обследований дано, например, в [43].
Последовательный (активный) выбор. При анализе физико-химических и технологических процессов часто исследуется зависимость некоторого результирующего показателя
(«отклика») у от набора управляющих показателей  которая описывается формулой вида
которая описывается формулой вида

где  — известная функция своих аргументов, 0 — неизвестная точка в пространстве параметров («состояние природы»),
— известная функция своих аргументов, 0 — неизвестная точка в пространстве параметров («состояние природы»),  — случайная ошибка со средним, равным нулю. Требуется по возможно меньшему числу опытов в точках
— случайная ошибка со средним, равным нулю. Требуется по возможно меньшему числу опытов в точках  принадлежащих «разрешенной» области значений
принадлежащих «разрешенной» области значений  оценить «состояние природы»
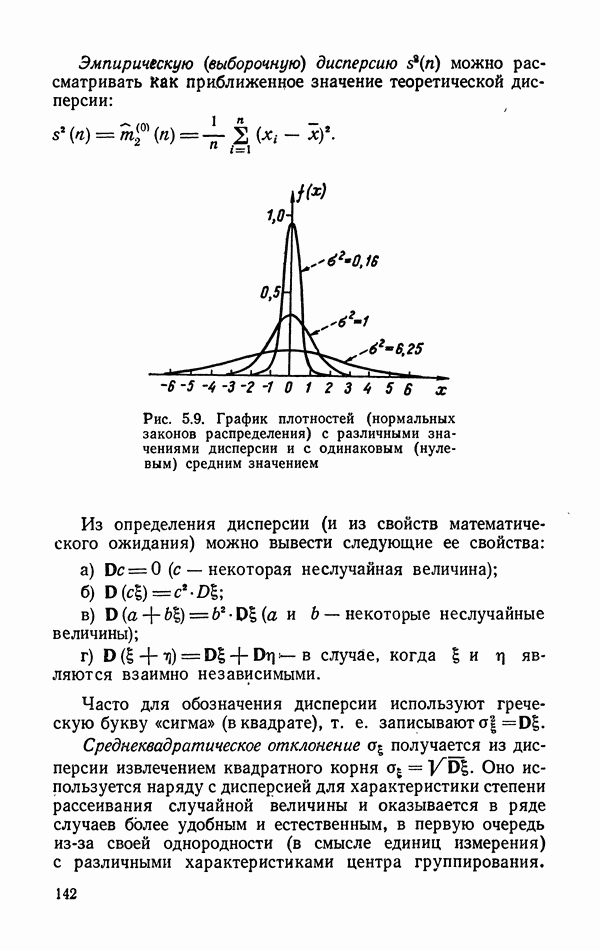
оценить «состояние природы»  . Опыты можно ставить в любой из точек X, принадлежащих «разрешенной» области
. Опыты можно ставить в любой из точек X, принадлежащих «разрешенной» области  значений управляющих показателей. В этих условиях после каждой серии опытов в результате обработки полученных данных рассчитывается следующая «наиболее информативная» относительно 0 серия точек X, в них проводятся новые опыты и отыскиваются новая оценка 0 и новая серия точек X, в которых целесообразно проводить опыты, и т. д. Чтобы подчеркнуть, что точки X отбираются не наудачу, такие эксперименты часто называют активными. О задачах такого типа см. подробнее, например, в [81].
значений управляющих показателей. В этих условиях после каждой серии опытов в результате обработки полученных данных рассчитывается следующая «наиболее информативная» относительно 0 серия точек X, в них проводятся новые опыты и отыскиваются новая оценка 0 и новая серия точек X, в которых целесообразно проводить опыты, и т. д. Чтобы подчеркнуть, что точки X отбираются не наудачу, такие эксперименты часто называют активными. О задачах такого типа см. подробнее, например, в [81].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.1.2. Два варианта интерпретации исходных данных и два подхода к их статистической обработке.
- 1.1.3. Основные этапы статистической обработки исходных данных.
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1. Теория вероятностей и условия ее применимости
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1. Для чего нужны математические модели
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей»
- 3.5.4. Геометрические модели.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1. Дискретное вероятностное пространство
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
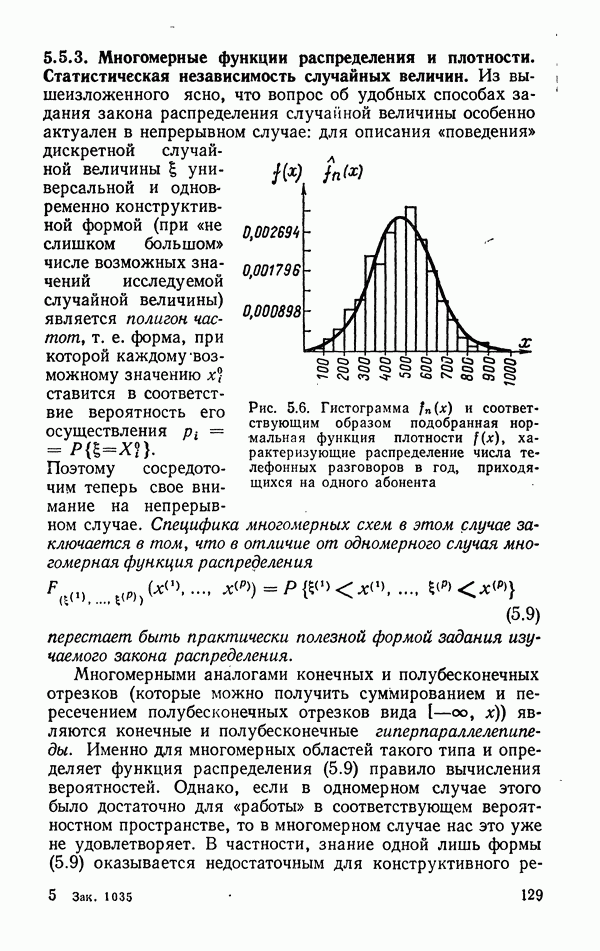
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.2. Характеристики центра группирования значений случайной величины.
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
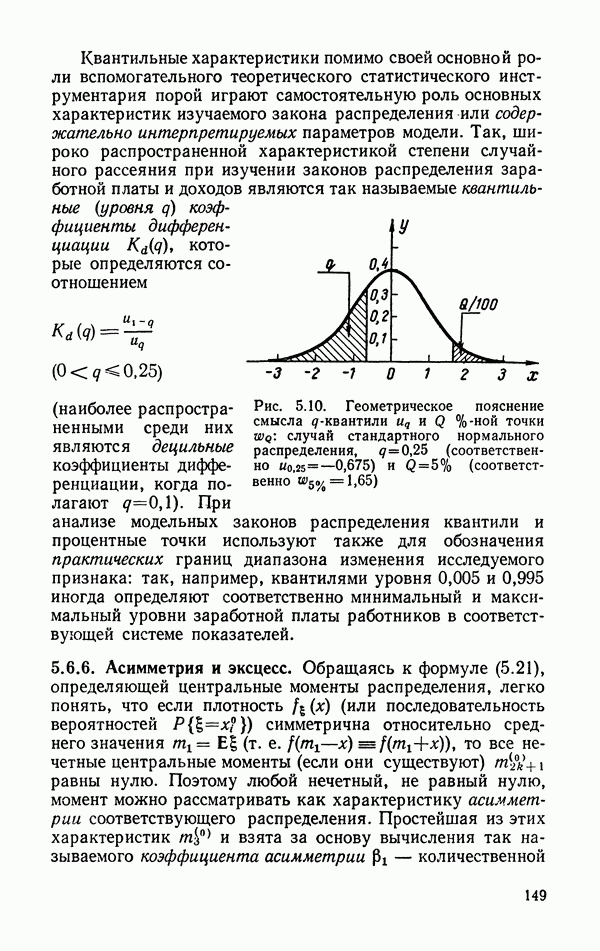
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
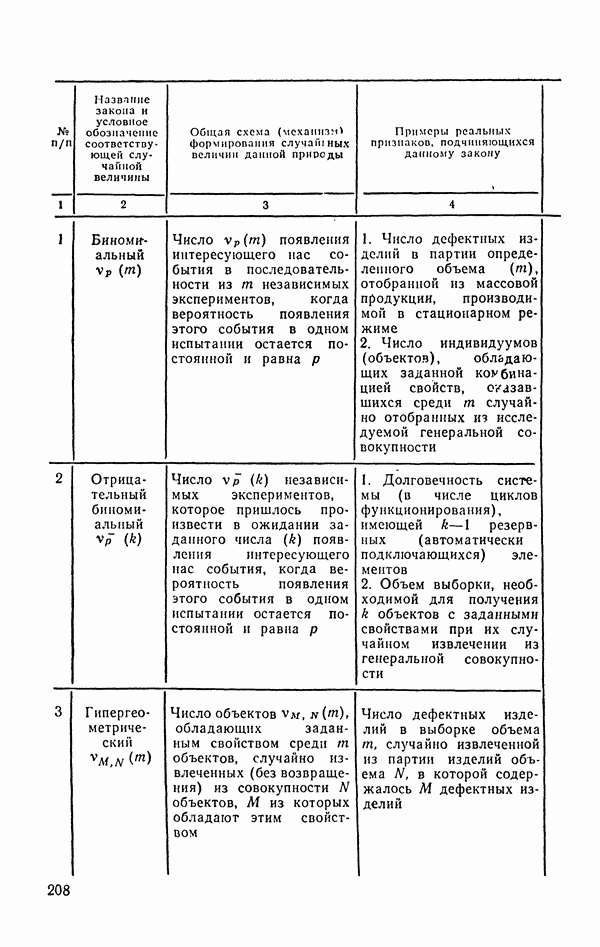
- 6.1.5. Нормальное (гауссовское) распределение.
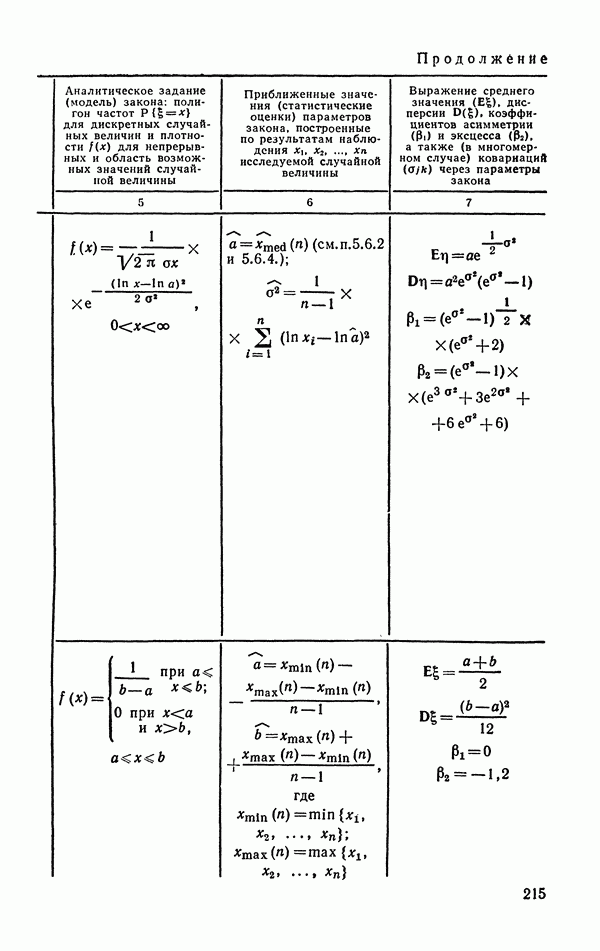
- 6.1.6. Логарифмически-нормальное распределение.
- 6.1.7. Равномерное (прямоугольное) распределение.
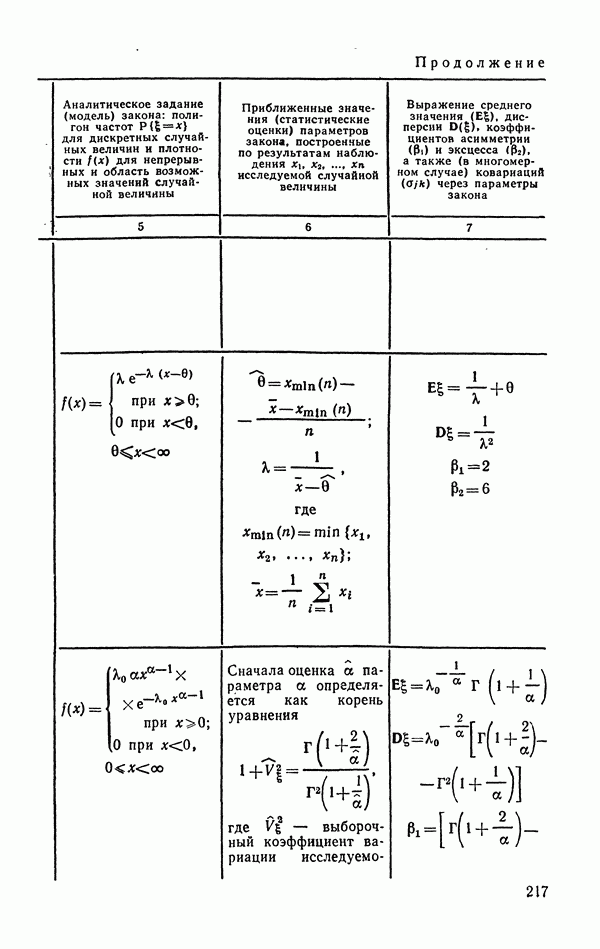
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
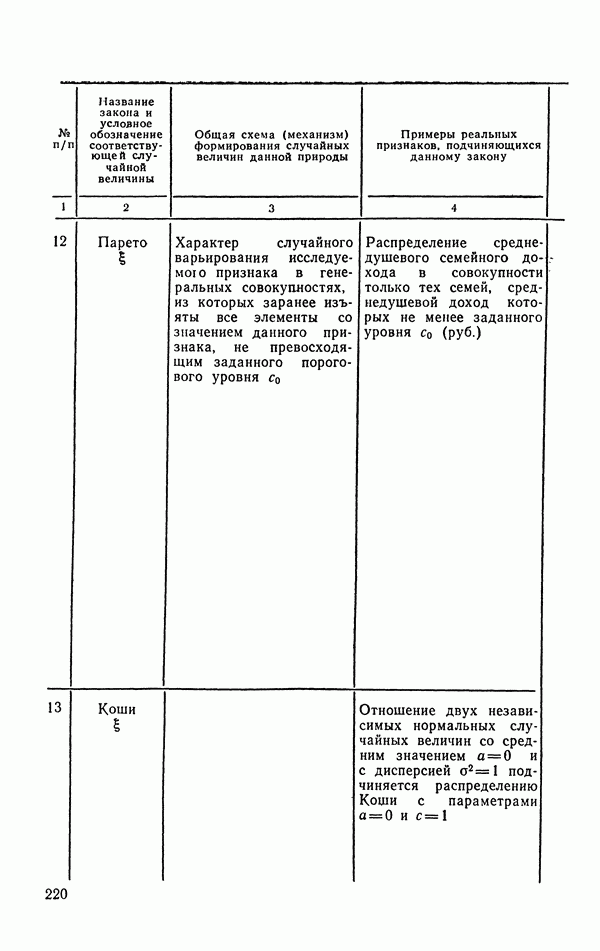
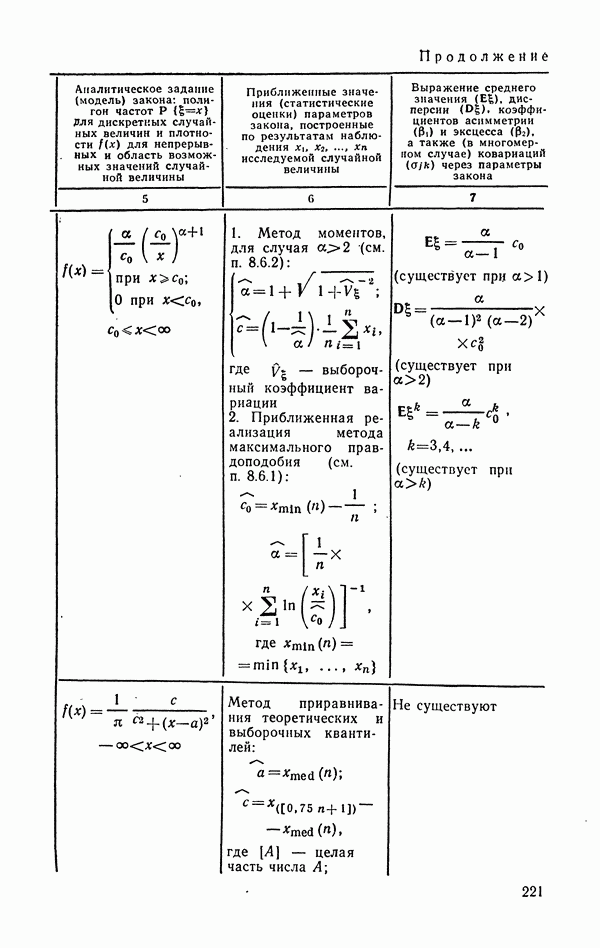
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
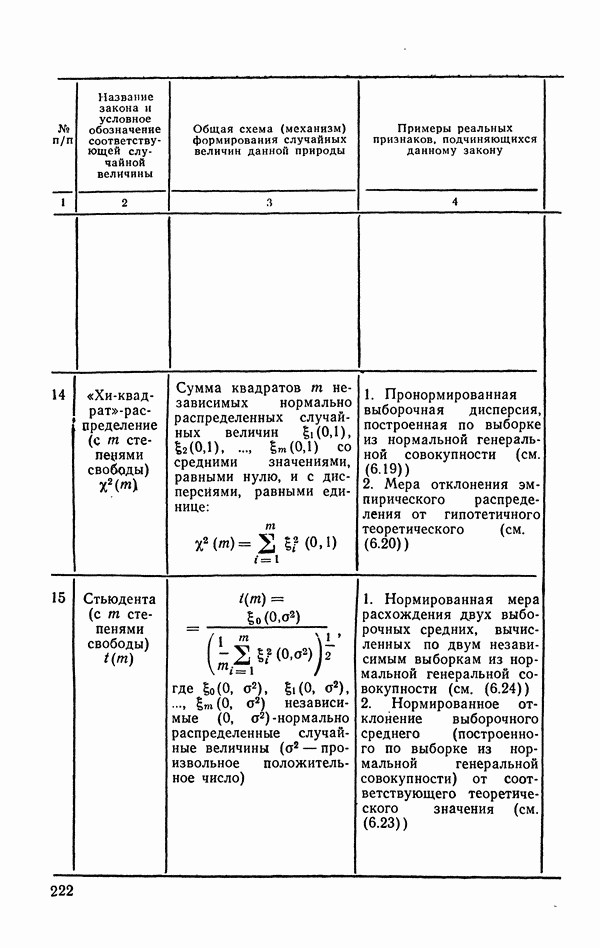
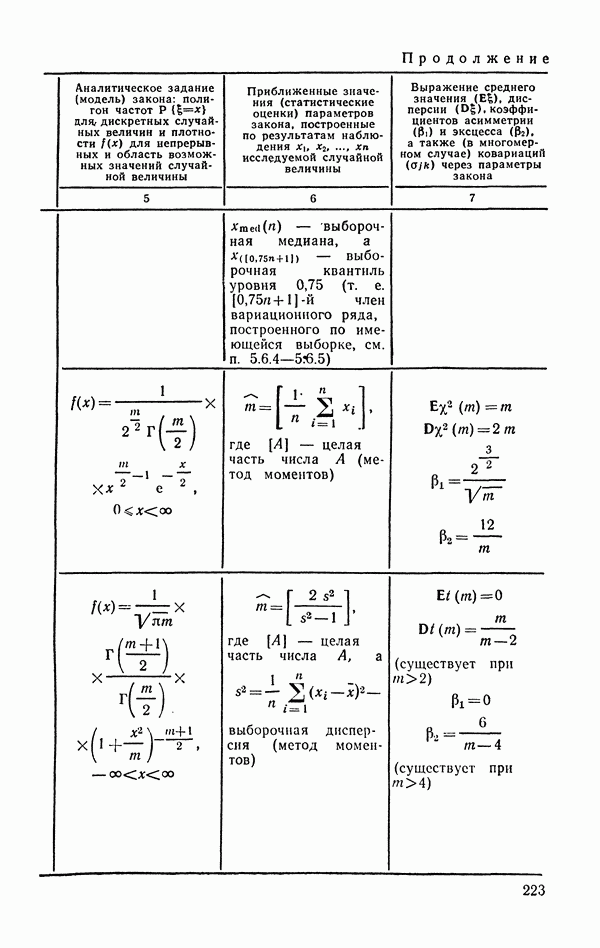
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных распределениях.
- 6.2.5. Г-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.2. Моделирование дискретных случайных величин. Стандартный метод.
- 6.3.3. Моделирование непрерывных распределений.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.2. Многомерная центральная предельная теорема (см. [12, с. 105]).
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
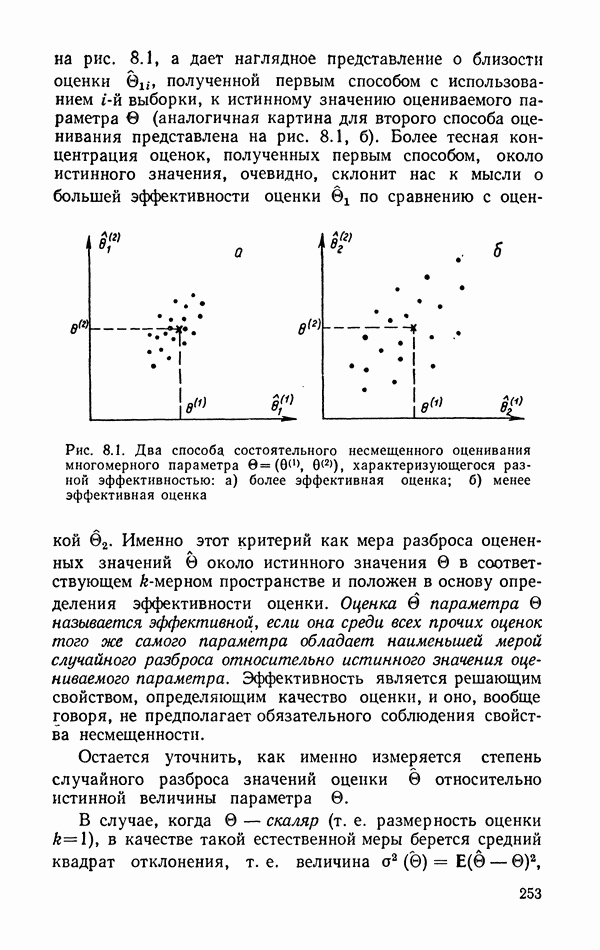
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
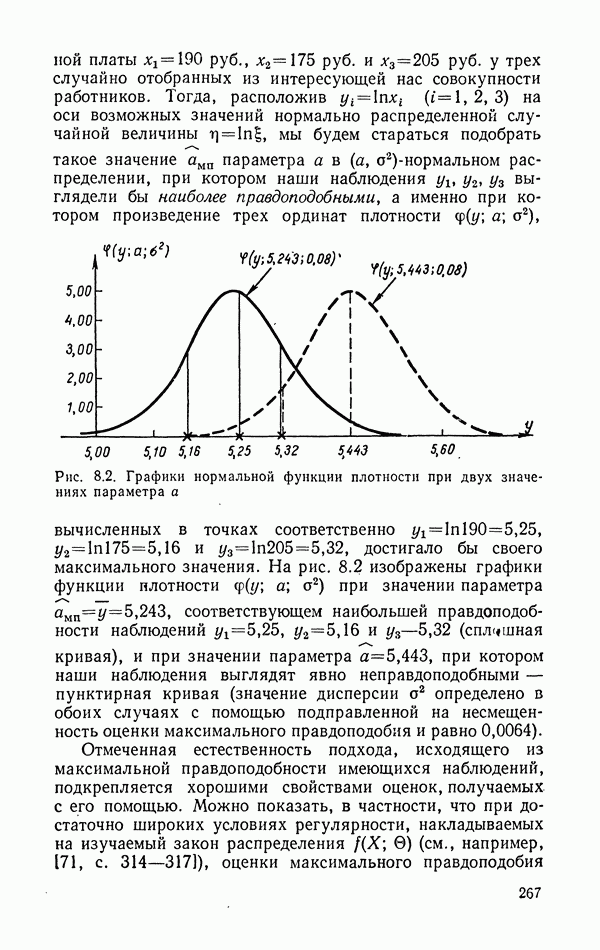
- 8.2. Функция правдоподобия.
- 8.3. Неравенство Рао — Крамера — Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
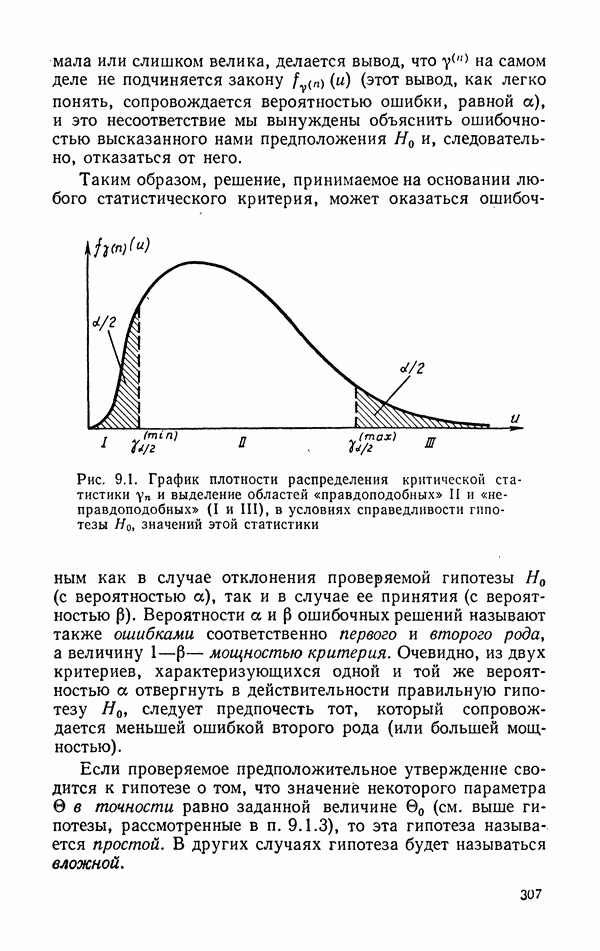
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4. Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1.1. Критерий «хи квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий w^2 (Крамера — Мнзеса — Смирнова).
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и w^2 для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- 11.1.7. Использование критериев согласия Колмогорова и w^2 в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.2. Критерий однородности «хи квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
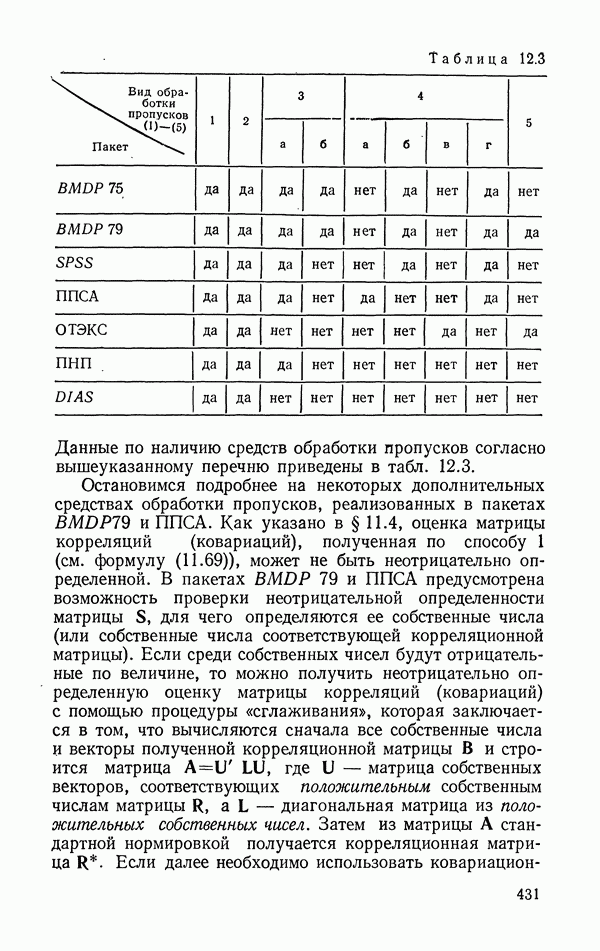
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия.
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа w^2
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ