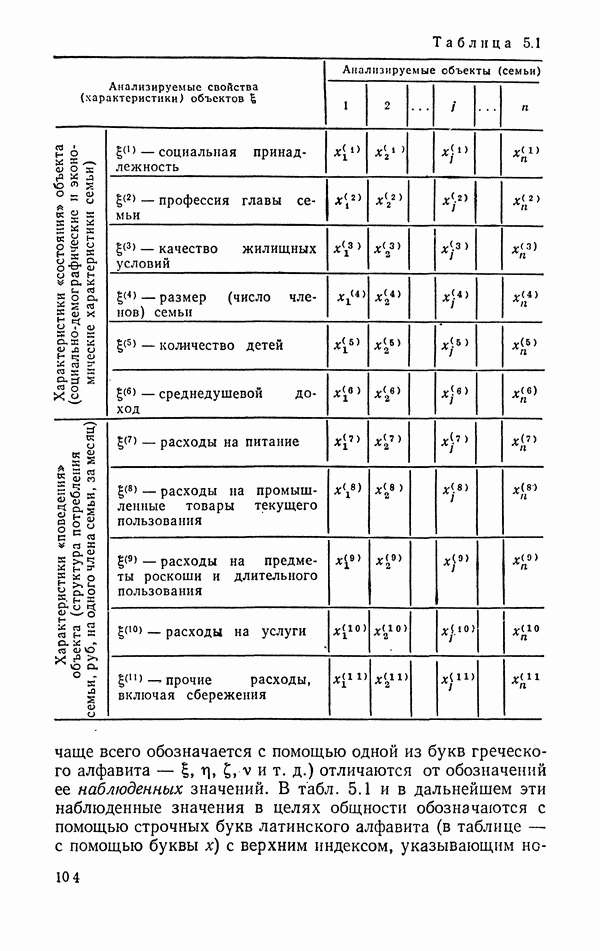
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
12.1. Программное обеспечение прикладной статистики
Программное обеспечение прикладной статистики (ПС) к настоящему времени хорошо развито и продолжает интенсивно развиваться у нас в стране и за рубежом. Развитие программного обеспечения ПС происходит как по линии
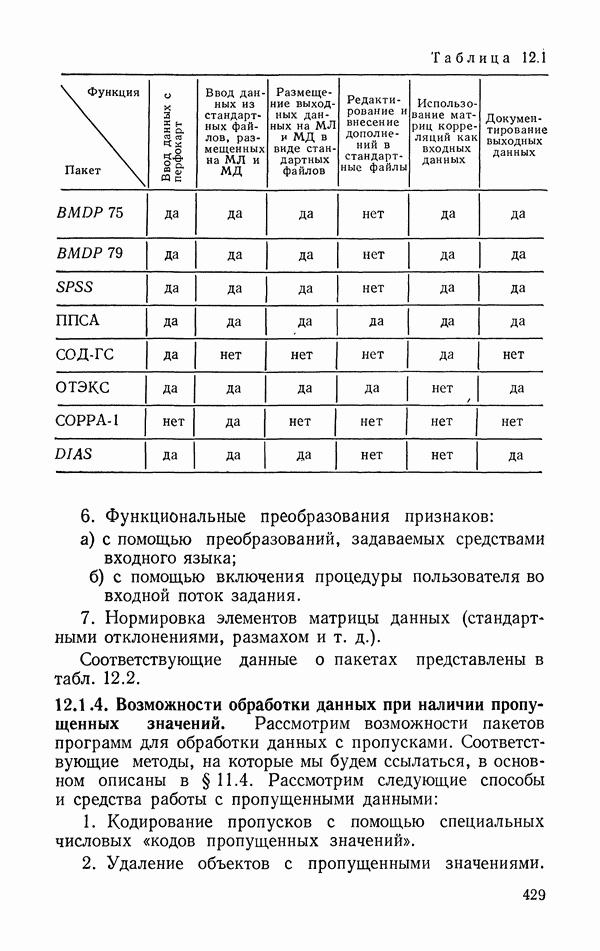
разработки новых методов обработки данных, так и по пути совершенствования организации и структуры программного обеспечения. Удобной современной формой организации программного обеспечения, позволяющей эффективно проводить обработку данных, являются пакеты программ. Перечислим основные характеристики, которые определяют качество пакета программ по ПС.
Первая группа характеристик определяет доступность и удобство управления работой пакета для пользователя. Сюда относятся:
1. Наличие подробной и хорошо оформленной документации на пакет. В первую очередь это «Руководство пользователя», которое предназначено для ознакомления пользователей с возможностями применения пакета и для обучения его использованию. Этот документ является одним из основных документов, необходимых для распространения пакета программ. Единая Система Конструкторской Документации (ЕСКД) на программную продукцию такого документа не предусматривает — наиболее близким к «Руководству пользователя» из предусмотренных в ЕСКД документов является, по-видимому, «Руководство программиста». Примерами хорошо оформленных «Руководств пользователя» являются соответствующие документы пакетов BMDP [99], [100] и SPSS [135].
2. Возможность формулировки задания пользователя и управления данными с помощью простого проблемно-ориентированного (на прикладную статистику) языка.
3. Наличие системы подробной индикации и комментария ошибок, возникающих при формулировке задания и в процессе обработки.
4. Возможность диалогового режима работы с пакетом.
Вторая группа характеристик связана с функциональными качествами пакета.
5. Наличие легкодоступных средств манипуляции с данными (сортировка, редактирование, преобразования, слияние и разделение наборов данных и т. д.) до обработки их методами ПС.
6. Наличие достаточно широкого спектра процедур ПС для обработки данных.
7. Возможность организации последовательных многошаговых процедур обработки данных.
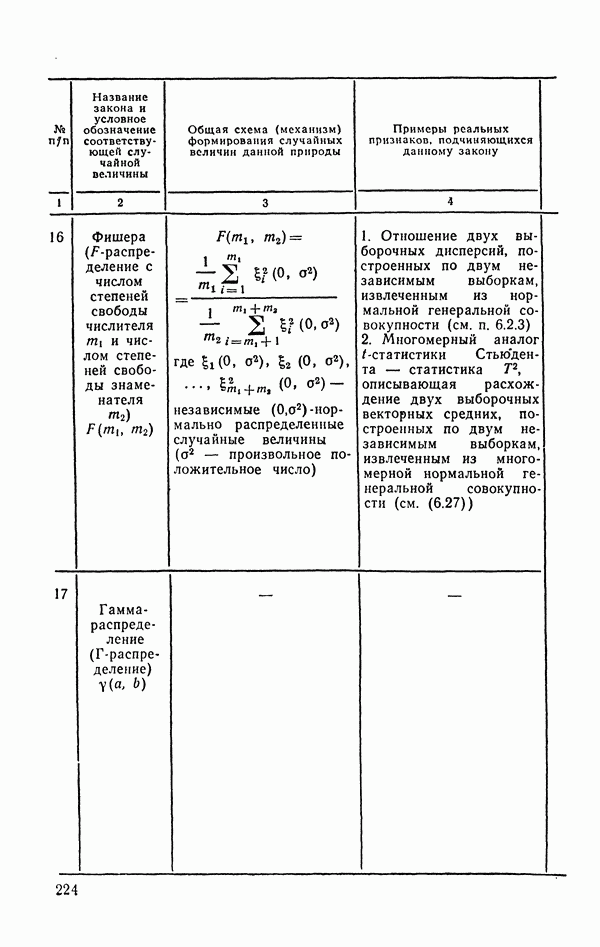
8. Возможность обработки данных большой размерности.
Третья группа характеристик важна при длительной работе с большими массивами данных.
9. Наличие средств ведения и документирования данных.
10. Возможность связи пакета с банками данных.
12.1.1. Организация пакетов программ.
Можно выделить следующие уровни в организации пакетов программ.
Первым уровнем организации пакета является пакет простой структуры, представляющий собой библиотеку модулей, под которыми здесь понимается процедура, подпрограмма или программа на языке программирования высокого уровня (ФОРТРАН, ПЛ/1), удовлетворяющие некоторым дополнительным ограничениям, наличие которых обеспечивает концептуальное единство пакета. Наиболее важными ограничениями такого рода являются ограничения на структуру размещения в памяти основных информационных единиц, необходимые для согласования входных и выходных данных различных модулей. Например, требуется, чтобы матрица данных на входе всех модулей, ее использующих, представлялась в виде двумерного массива с расположением объектов по строкам (или по столбцам). Другие ограничения связаны со способами передачи информации (например, допустимость или запрет переменных внешнего типа), с использованием операторов ввода-вывода, со способом аварийного завершения работы модуля. Подпрограммы в этих пакетах имеют также согласованную документацию. Пакет простой структуры может использоваться как в виде библиотеки исходных модулей (на программном языке высокого уровня), так и в виде библиотеки загрузочных модулей, полученных в результате компиляции и редактирования соответствующих исходных модулей. Примером пакета простой структуры является Пакет научных подпрограмм (ПНП) на Фортране для ЕС ЭВМ [55], поставляемый обычно именно в виде загрузочных модулей. Описания интересующих нас разделов ПНП содержатся в [вып. 2], [вып. 10]. Разработан и аналог ПНП на ПЛ/1 (см. [вып. 14]). Прообразом для версии ПНП на Фортране явился пакет SSP фирмы IBM, а для версии ПНП на ПЛ/1 — версия SSP на ПЛ/1. В настоящее время состав процедур по ПС в ПНП существенно расширен по сравнению с исходными пакетами SSP, особенно в области обработки многомерных данных. Помимо чисто статистических
программ, эти пакеты содержат еще подпрограммы из многих других разделов вычислительной математики — линейной алгебры, интерполяции и экстраполяции табличных функций и т. д.
Использование пакета простой структуры требует от пользователя достаточно хорошей программистской подготовки и состоит в отборе подходящих модулей и в ручном (т. е. осуществляемом самим пользователем) составлении головной программы на языке программирования высокого уровня, организующей вызов отобранных модулей в определенном порядке, размещение и ввод-вывод данных. Язык пользователя на этом уровне образует язык программирования высокого уровня (Фортран, ПЛ/1), язык обращения к операционной системе и языковые средства, введенные самим пользователем для управления созданной программой.
Существенно более высокий уровень организации представляют собой пакеты, состоящие из набора программ, готовых к выполнению, управляемых единым для всех программ входным проблемно-ориентированным языком и имеющих унифицированный ввод-вывод данных. На этом уровне организации появляется возможность создания сравнительно просто управляемых средств манипуляции с данными, их ведения и документирования.
Программы пакета составлены из модулей, которые, как правило, берутся из библиотеки модулей, организованной, как описано выше (пакет простой структуры). Для уменьшения требуемых ресурсов основной памяти программы обычно имеют оверлейную структуру.
Внесение изменений для пользователя в такие программы практически невозможно, за исключением предусмотренных заранее случаев изменения допустимого объема памяти, отводимой под данные, и включения по определенным правилам некоторых процедур пользователя на языке Фортран или ПЛ/1, например для преобразований признаков. Тем не менее благодаря наличию гибкого входного языка и возможности просто составлять многоэтапные процедуры обработки из последовательности программ пакета такие пакеты позволяют удовлетворить подавляющую часть потребностей пользователя по обработке данных. В то же
время сами эти пакеты влияют на ход статистического исследования, определяя составом допустимых процедур и требованиями на входные данные форму подготовки и, в значительной степени, сбора и накопления данных. Работа с таким пакетом доступна пользователю, не обладающему подготовкой в области программирования, хотя обычно необходимо знание некоторого минимального объема языковых средств для общения с операционной системой.
Одним из известных пакетов такого типа является BMDP, разработанный в США. Мы будем рассматривать далее две версии этого пакета — версию 1975 г. [99], адаптированную в СССР для ЕС ЭВМ, и версию 1979 г. [100], существенно расширенную по сравнению с версией 1975 г. Далее для обозначения соответствующих версий будем писать BMDP 75 и BMDP 79.
Другим пакетом такого рода является пакет Программ по прикладному статистическому анализу (ППСА) [67], разработанный в ЦЭМИ АН СССР. Пакет ППСА отличается от BMDP составом реализованных методов обработки, входным языком, организацией и документированием данных, а также организацией программ. Если в BMDP каждая программа реализует только один метод обработки, то ППСА использует тематически-ориентированные (ТО) программы [9]. Каждая из ТО-программ, по существу, является пакетом программ для решения некоторого подмножества задач ПС (оценивания, регрессионного, дискриминантного анализов и т. д.). Подмножества модулей, используемые различными ТО-программами, частично пересекаются. Так, все программы эксплуатируют одни и те же модули ввода и трансляции предложений входного языка, ввода данных, вывода данных в виде таблиц и графиков и т. д. Организация связей между модулями в ТО-программе позволяет создавать простую оверлейную структуру. Во многих случаях использование ТО-программ уменьшает затраты усилий пользователя по созданию многоэтапных процедур обработки,
Дальнейшим развитием концепции ТО-программ (в отношении способа организации пакета программ, но не исторически) являются пакеты программ, у которых последовательность необходимых процедур обработки создается на основе анализа предложений входного языка пакета, описывающего задание пользователя. Способы реализации этого подхода могут быть самыми различными. Из зарубежных пакетов к этому типу относятся, например, пакеты
P-STAT [132], SPSS [135], а из пакетов, разработанных в нашей стране, — СОД-ГС [68], ОТЭКС [66].
Внешне, для пользователя, работа с пакетами такого типа организации мало отличается от работы с пакетами типа BMDP или ППСА. Поэтому в дальнейшем эти способы организации пакетов мы различать не будем, именуя условно пакеты из обеих групп просто пакеты программ и отличая их от пакетов (библиотек) подпрограмм типа ПНП. Все упомянутые выше пакеты предназначены для ЕС ЭВМ или IBM-380/370. Исключение представляет версия ПНП на Фортране, которая может быть использована (в виде исходных модулей) на ЭВМ БЭСМ-6 и «Минск-32». Из пакетов программ, предназначенных для БЭСМ-6, отметим пакет СОРРА-12, направленный для решения задач многомерной классификации и регрессии, и пакет DIAS [82].
12.1.2. Вопросы организации и возможности ведения данных.
Основным видом входных данных, обрабатываемых пакетами программ по ПС, является матрица данных типа «объект-признак». Для всех рассматриваемых пакетов программ предполагается, что матрица данных на внешних носителях информации упорядочена по объектам, так что порядок следования ее элементов таков:

Ввод данных может осуществляться с перфокарт (или их образов на МЛ и МД), либо из стандартных файлов (для данного пакета) на МЛ или МД, представляющих информацию о матрице данных в виде двоичных кодов и имеющих последовательную организацию по записям (запись понимается согласно определению, принятому в ОС ЕС), так что каждая запись представляет собой один объект. Анализируемые признаки в матрице данных могут быть измерены в разных шкалах — количественной, качественной (ординальной) или номинальной (см. гл. 10). Некоторые значения могут быть вообще не определены. Однако для программ
пакетов все элементы матрицы данных считаются представленными в виде чисел. Для признаков, измеренных в шкалах, отличных от количественной, эти числа представляют собой, следовательно, некоторые условные коды. Для перекодировки исходной информации, заданной в символьной форме, в пакете ППСА предусмотрена специальная программа перекодировки такой информации в числовую форму, заданную пользователем.
Рассмотрим теперь, какие возможности ведения данных предоставляют пользователю средства, включенные в пакеты программ, для выполнения следующих функций:
1. Размещение выходных данных в виде стандартных файлов, например матриц данных после преобразования признаков, ковариационных матриц, матриц расстояний и т. д.
2. Документирование входных и выходных данных с помощью меток файлов или архивных файлов и т. п.
3. Редактирование, внесение дополнений и исправлений в стандартные файлы.
Соответствующие данные по этим вопросам относительно рассматриваемых пакетов программ представлены в табл. 12.1 совместно с некоторыми другими характеристиками организации данных.
12.1.3. Средства предварительной обработки (манипуляции) данных.
Рассмотрим возможности проведения некоторых важных видов обработки данных, предшествующих собственно статистической обработке:
1. Выделение подмножества признаков, заданного списком имен или номеров.
2. Выделение подмножества объектов, заданного списком имен или номеров.
3. Выделение подмножеств строк и столбцов других видов матриц (ковариаций, расстояний), заданных списками имен или номеров, если они используются в качестве входных объектов.
4. Выделение подмножества объектов, у которых значения признаков находятся внутри (или вне) заданных границ.
5. Группирование объектов:
а) в соответствии с попаданием значения заданного, признака, называемого обычно группирующим признаком, в тот или иной интервал;
б) другие способы группировки.
Таблица 12.1

6. Функциональные преобразования признаков:
а) с помощью преобразований, задаваемых средствами входного языка; б) с помощью включения процедуры пользователя во входной поток задания.
7. Нормировка элементов матрицы данных (стандартными отклонениями, размахом и т. д.).
Соответствующие данные о пакетах представлены в табл. 12.2.
12.1.4. Возможности обработки данных при наличии пропущенных значений.
Рассмотрим возможности пакетов программ для обработки данных с пропусками. Соответствующие методы, на которые мы будем ссылаться, в основном описаны в § 11.4. Рассмотрим следующие способы и средства работы с пропущенными данными:
1. Кодирование пропусков с помощью специальных числовых «кодов пропущенных значений».
2. Удаление объектов с пропущенными значениями.
Таблица 12.2

3. Оценивание матрицы ковариаций и вектора средних:
а) по формулам (11.69), т. е. с учетом всех измеренных значений пар признаков (для недиагональных элементов ковариационной матрицы) и всех измеренных значений признака для оценивания среднего и дисперсии;
б) другие способы оценивания матрицы ковариаций без предварительного заполнения пропусков в матрице данных.
4. Заполнение пропусков в матрице данных:
а) с помощью главных компонент;
б) с помощью линейной регрессии на измеренные переменные;
в) с помощью других алгоритмов (например, алгоритма ZET);
г) средними значениями.
5. Дополнительные возможности обработки пропусков.
Пакеты СОД-ГС, СОРРА-1 вообще не имеют средств обработки пропущенных данных. С другой стороны, для пакета ОТЭКС заполнение пропусков на основе алгоритма ZET в матрице данных является одной из основных задач.
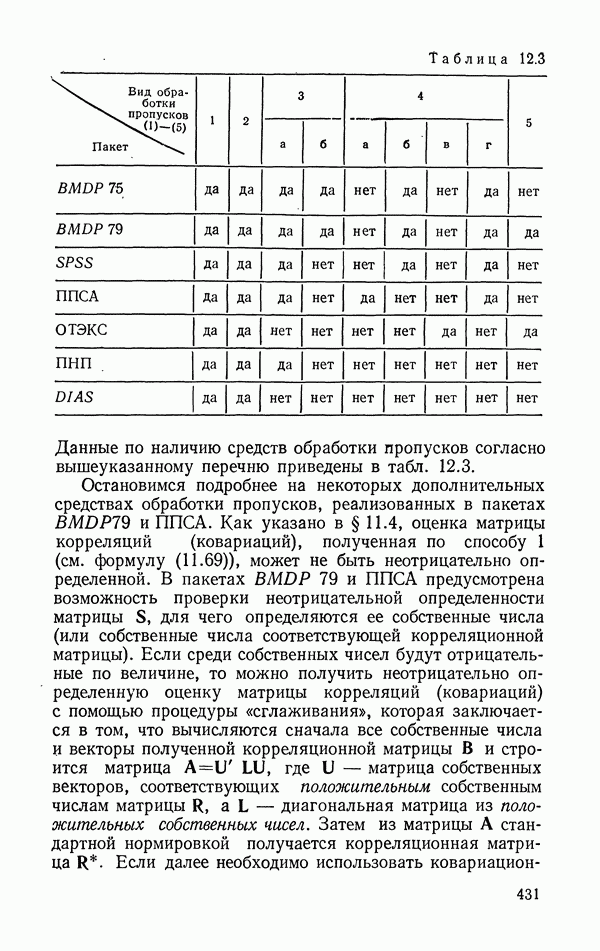
Таблица 12.3

Данные по наличию средств обработки пропусков согласно вышеуказанному перечню приведены в табл. 12.3.
Остановимся подробнее на некоторых дополнительных средствах обработки пропусков, реализованных в пакетах BMDP79 и ППСА. Как указано в § 11.4, оценка матрицы корреляций (ковариаций), полученная по способу 1 (см. формулу (11.69)), может не быть неотрицательно определенной. В пакетах BMDP 79 и ППСА предусмотрена возможность проверки неотрицательной определенности матрицы S, для чего определяются ее собственные числа (или собственные числа соответствующей корреляционной матрицы). Если среди собственных чисел будут отрицательные по величине, то можно получить неотрицательно определенную оценку матрицы корреляций (ковариаций) с помощью процедуры «сглаживания», которая заключается в том, что вычисляются сначала все собственные числа и векторы полученной корреляционной матрицы В и строится матрица  где U — матрица собственных векторов, соответствующих положительным собственным числам матрицы a L - диагональная матрица из положительных собственных чисел. Затем из матрицы А стандартной нормировкой получается корреляционная матрица R. Если далее необходимо использовать ковариационную
где U — матрица собственных векторов, соответствующих положительным собственным числам матрицы a L - диагональная матрица из положительных собственных чисел. Затем из матрицы А стандартной нормировкой получается корреляционная матрица R. Если далее необходимо использовать ковариационную
матрицу S, то она получается из R умножеййем столбцов и строк на оценки стандартных отклонений. Очевидно, как матрица R, так и матрица S будут неотрицательно определенными, но могут быть матрицами неполного ранга. Так как, однако, ранг этих матриц, а также собственные числа и векторы матрицы R известны, нетрудно получить, при необходимости, обобщенную обратную матрицу (см. [73]) для целей регрессионного и дискриминантного анализа.
12.1.5. Первичная обработка неколичественных данных.
Рассмотрим следующие методы обработки неколичественных данных:
1. Анализ таблиц сопряженности, включающий
1) оценку параметров и проверку гипотез независимости для различных моделей таблиц сопряженности;
2) оценку параметров логлинейной модели таблицы сопряженностей;
3) вычисление различных коэффициентов связи в двумерных таблицах сопряженности.
2. Приведение переменных к системе двоичных переменных (п. 10.2.4).
3. Оцифровка неколичественных переменных.
Анализ таблиц сопряженности (1.1 и 1.3) реализован в пакетах BMDP 75 и BMDP 79 (программы  ), по 1.3 — в ППСА. Оценка параметров логлинейной модели реализована в BMDP 79 (программа
), по 1.3 — в ППСА. Оценка параметров логлинейной модели реализована в BMDP 79 (программа  ).
).
Представление переменных в бинарной форме используется при решении задач классификации в пакете ОТЭКС. В пакетах BMDP 75, BMDP 79, ППСА переход к двоичному представлению легко осуществляется с помощью средств функционального преобразования признаков, хотя специальные программы для такого преобразования отсутствуют.
Дадим более подробное изложение подхода к оцифровке неколичественных переменных. Суть этого подхода состоит в присвоении категориям (градациям) неколичественных переменных «разумных», в рамках решаемой задачи, числовых меток. Далее с оцифрованными переменными обращаются как с дискретными числовыми переменными. Критерий, согласно которому присваиваются метки, зависит от последующей статистической обработки — анализа главных компонент, регрессионного анализа, дискриминантного анализа. Допустимость присвоения числовых меток градациям ординальных переменных представляется достаточно
естественной. Допустимость оцифровки номинальных переменных основывается на том, что в рамках конкретной задачи градациям номинальный переменной соответствует некоторая совокупность значений скрытых, непосредственно неизмеряемых, но реально существующих переменных. Так что число, присваиваемое какой-либо градации некоторой номинальной переменной, является обобщенным (результирующим) значением для совокупности значений неизмеряемых переменных, характерной для объектов, соответствующих данной градации рассматриваемой номинальной переменной.
Критерии, на основе которых производится оцифровка (см. [32]), зависят от используемого далее метода статистического анализа. Однако все они являются некоторыми функционалами матрицы ковариаций (корреляций) в пространстве оцифрованных признаков. Это связано прежде всего с тем, что матрица ковариаций (корреляций) является основным объектом, который используется перечисленными выше методами статистического анализа.
Сущность указанных методов состоит в выделении одной или нескольких линейных комбинаций исходных переменных, обладающих некоторыми экстремальными свойствами, а успешность их применения к реальным данным в первую очередь зависит от того, насколько сильно связаны переменные и насколько полно матрица ковариаций отражает эту зависимость, т. е. насколько точно эти зависимости можно считать линейными.
Например, в случае когда после оцифровки предлагается использовать методы сокращения размерности или регрессионного анализа в программе CODAGE пакета ППСА, категориям неколичественных признаков приписываются числовые метки, максимизирующие величину

где  — число признаков, подлежащих кодировке;
— число признаков, подлежащих кодировке;  — коэффициенты корреляции между
— коэффициенты корреляции между  признаками после кодировки, a — неотрицательные весовые коэффициенты. Вычислительная схема в этом случае такова.
признаками после кодировки, a — неотрицательные весовые коэффициенты. Вычислительная схема в этом случае такова.
Пусть  — вектор размерности
— вектор размерности  — число категорий для i-го признака), коэффициентами которого
— число категорий для i-го признака), коэффициентами которого
являются метки, приписанные соответствующим категориям  признака.
признака.
Оценим по исходной выборке матрицу (таблицу) сопряженности  размера
размера  , у которой значением элемента
, у которой значением элемента  является оценка вероятности для i-го признака принять
является оценка вероятности для i-го признака принять  категорию одновременно с принятием
категорию одновременно с принятием  категории для
категории для  признака. Пусть Р — диагональная матрица, элементами которой являются частоты категорий i-го признака,
признака. Пусть Р — диагональная матрица, элементами которой являются частоты категорий i-го признака,  — симметричная неотрицательно определенная матрица с элементами
— симметричная неотрицательно определенная матрица с элементами

где  меняются от 1 до числа градаций
меняются от 1 до числа градаций  признака;
признака;  — скалярное произведение
— скалярное произведение  строки матрицы
строки матрицы  на вектор
на вектор  координатами которого являются метки соответствующих категорий
координатами которого являются метки соответствующих категорий  признака.
признака.
Числовые метки, максимизирующие величину критерия (12.2), находятся в результате следующего итерационного процесса.
Напервом шаге задаются начальные значения для  (например, координатами каждого вектора
(например, координатами каждого вектора  являются натуральные числа, т. е. номера градаций
являются натуральные числа, т. е. номера градаций  признака). Эти метки нормируются и центрируются. Затем по формуле (12.3) вычисляется матрица
признака). Эти метки нормируются и центрируются. Затем по формуле (12.3) вычисляется матрица  и находится собственный вектор с максимальным собственным значением для уравнения
и находится собственный вектор с максимальным собственным значением для уравнения

Координаты этого вектора и будут новыми значениями меток для 
Теперь, зная  определим матрицу
определим матрицу  при фиксированных значениях
при фиксированных значениях  и находим новый вектор
и находим новый вектор  . Далее определяется
. Далее определяется  и т. д.
и т. д.
Вычислив все значения меток  переходим к определению
переходим к определению  при фиксированных
при фиксированных  и вычисления повторяются.
и вычисления повторяются.
Процесс останавливается, когда разница между значениями критерия (12.2) на соседних шагах итерации будет меньше заданной пороговой величины.
Замечание. В случае когда число признаков  в результате работы программы получаются так называемые метки Ланкастера [40].
в результате работы программы получаются так называемые метки Ланкастера [40].
12.1.6. Средства визуализации данных.
Рассмотрим программное обеспечение следующих методов визуализации данных (см. § 10.5):
1) стандартный метод главных компонент;
2) нелинейный метод главных компонент;
3) многомерное метрическое шкалирование.
Стандартный метод главных компонент реализован в пакетах BMDP 75, BMDP 79 (в программе факторного анализа  ), в ПНП [55, вып. 2,14], в ППСА (программа REDUCT). Нелинейный метод главных компонент и многомерное метрическое шкалирование реализованы из рассматриваемых пакетов в ППСА (программа REDUCT).
), в ПНП [55, вып. 2,14], в ППСА (программа REDUCT). Нелинейный метод главных компонент и многомерное метрическое шкалирование реализованы из рассматриваемых пакетов в ППСА (программа REDUCT).
Важным моментом сервиса, определяющим эффективность применения методов визуализации, является возможность вывода диаграммы рассеивания (см. гл. 10) с помощью различного рода терминальных устройств — АЦПУ, графопостроителя или дисплея. Обычным и достаточно удобным средством является использование АЦПУ.
Рассмотрим подробнее, как построена (например, в ППСА) диаграмма рассеивания. Координаты двумерных проекций точек нормируются. Пусть L и М — соответственно горизонтальный и вертикальный размер диаграммы. Эти величины либо задаются пользователем, либо принимают умалчиваемые значения. Позиция  объекта по горизонтали (оси ОХ) от левого края диаграммы вычисляется по формуле
объекта по горизонтали (оси ОХ) от левого края диаграммы вычисляется по формуле

где  означает целую часть числа,
означает целую часть числа,  — соответственно максимальное и минимальное значения координаты х. Аналогично вычисляется и положение объекта (номер строки) по вертикали. В точке с этими координатами печатается какой-либо символ, например буква А. Если в одну точку попадает не один, а
— соответственно максимальное и минимальное значения координаты х. Аналогично вычисляется и положение объекта (номер строки) по вертикали. В точке с этими координатами печатается какой-либо символ, например буква А. Если в одну точку попадает не один, а  объектов, то, если
объектов, то, если  печатается цифра, равная числу объектов, попавших в эту точку, а если
печатается цифра, равная числу объектов, попавших в эту точку, а если  , то символ
, то символ  Если имеется несколько групп объектов, для каждой из них может быть использован свой собственный символ. Значения координат X и Y в исходных шкалах печатаются соответственно по нижнему краю (через каждые пять позиций) и левому краю (через каждые пять строк) диаграммы.
Если имеется несколько групп объектов, для каждой из них может быть использован свой собственный символ. Значения координат X и Y в исходных шкалах печатаются соответственно по нижнему краю (через каждые пять позиций) и левому краю (через каждые пять строк) диаграммы.
12.1.7. Оценивание параметров и выделение аномальных наблюдений.
Рассмотрим программное обеспечение, связанное
с оцениванием параметров, для следующих видов оценок.
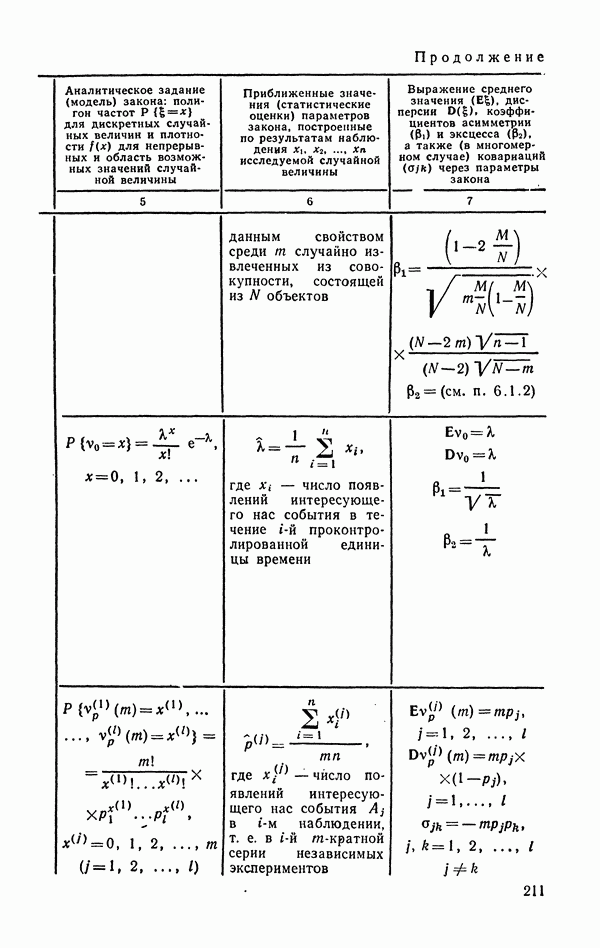
1. Стандартные оценки основных числовых характеристик случайных величин — среднего, медианы, дисперсии, размаха, асимметрии, эксцесса и др.
2. Оценки параметров для известного априори типа распределения — гамма-распределение, бета-распределение, распределение Пуассона, биномиальное распределение и др.
3. Стандартные оценки параметров многомерных случайных величин — вектора средних значений и матрицы ковариаций.
4. Устойчивое оценивание параметров сдвига (см. п. 10.4.5):
1) урезанное среднее и медиана;
2) среднее по Винзору;
3) оценки Хампеля, Тьюки, Эндрюса;
4)  -моменты.
-моменты.
5. Устойчивое оценивание параметров масштаба.
Вычисление стандартных оценок 1 и 3 с небольшими вариациями по составу реализованы в любом из рассматриваемых пакетов программ. Оценки параметров при известной модели распределения реализованы в пакете СОД и в ПНП [55, вып. 10, разд. 4]. Менее развито программное обеспечение устойчивого оценивания. Оценки 4.1-4.3 реализованы в пакетах BMDP 75 и BMDP 79 (программы  ) и ППСА (программа ESTM), а также в ПНП [55, вып. 2, 10].
) и ППСА (программа ESTM), а также в ПНП [55, вып. 2, 10].
Остановимся подробнее на методе реализации устойчивых оценок вектора средних и матрицы ковариаций, реализованном в ППСА [67]. Недостаток взвешенных оценок (10.23), (10.24), в том числе и  состоит в том, что их дисперсии растут с ростом размерности пространства признаков
состоит в том, что их дисперсии растут с ростом размерности пространства признаков  [89]. Чтобы избежать этого, в программе ESTM ППСА используется следующий подход. Сначала для каждого из
[89]. Чтобы избежать этого, в программе ESTM ППСА используется следующий подход. Сначала для каждого из  признаков находятся
признаков находятся  одномерных устойчивых оценок среднего и дисперсии, а затем решается
одномерных устойчивых оценок среднего и дисперсии, а затем решается  двумерных задач по определению устойчивых оценок ковариаций, например, с помощью
двумерных задач по определению устойчивых оценок ковариаций, например, с помощью  -моментов. Трудности здесь такие же, как и при оценке ковариационной матрицы в случае пропущенных наблюдений — иногда матрица ковариаций может не быть неотрицательноопределенной. Асимптотические свойства этих оценок, названных редуцированными, приведены в работе [90].
-моментов. Трудности здесь такие же, как и при оценке ковариационной матрицы в случае пропущенных наблюдений — иногда матрица ковариаций может не быть неотрицательноопределенной. Асимптотические свойства этих оценок, названных редуцированными, приведены в работе [90].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.1.2. Два варианта интерпретации исходных данных и два подхода к их статистической обработке.
- 1.1.3. Основные этапы статистической обработки исходных данных.
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1. Теория вероятностей и условия ее применимости
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1. Для чего нужны математические модели
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей»
- 3.5.4. Геометрические модели.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1. Дискретное вероятностное пространство
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
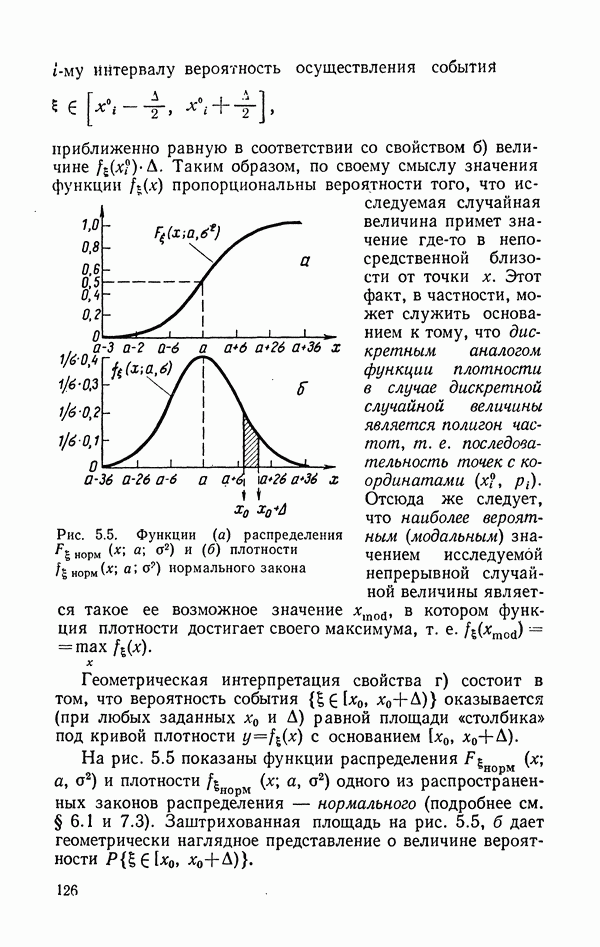
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
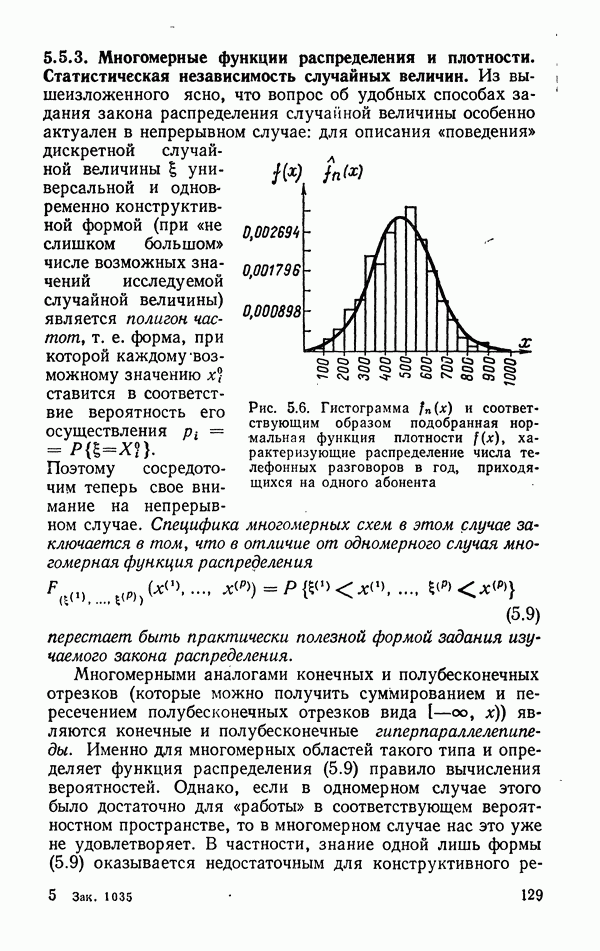
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
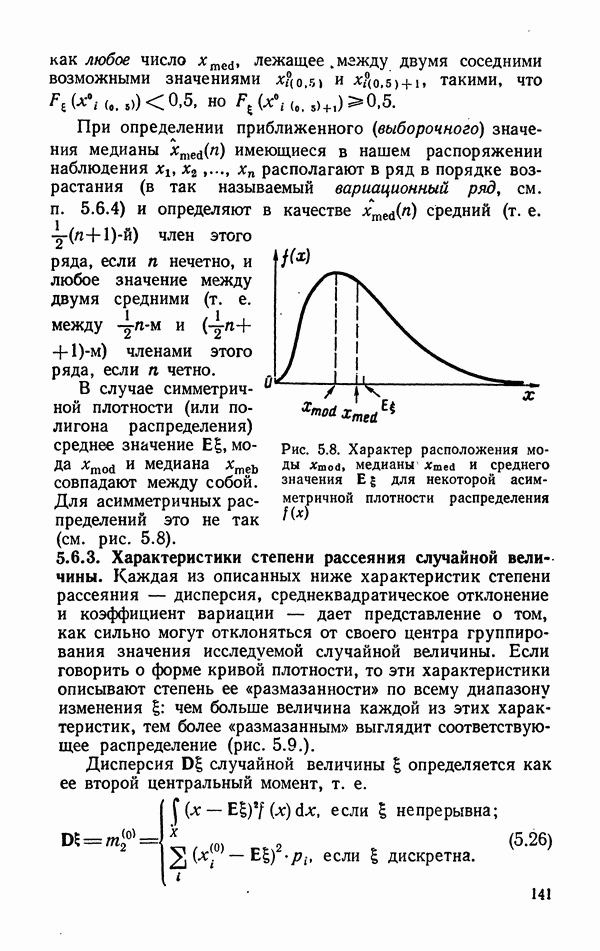
- 5.6.2. Характеристики центра группирования значений случайной величины.
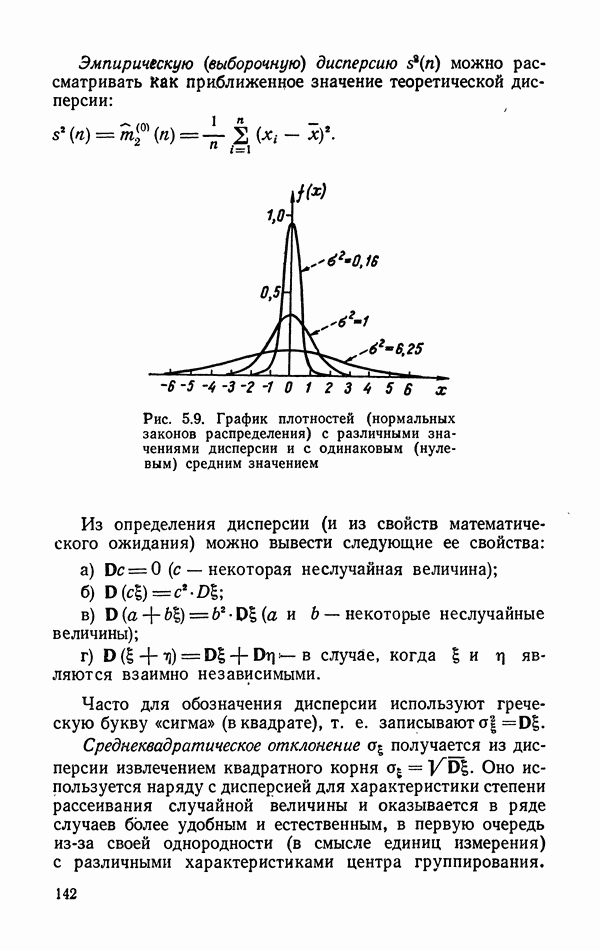
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
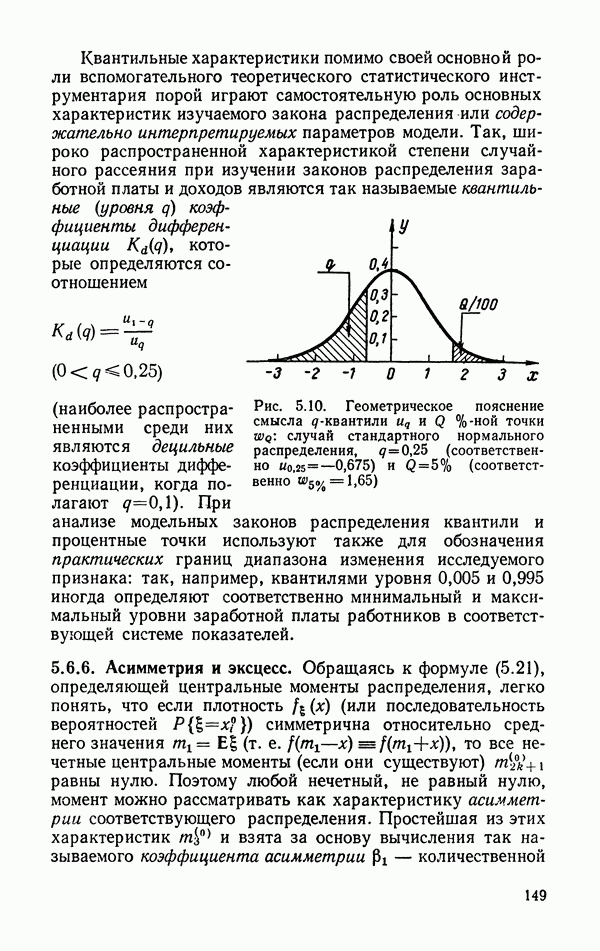
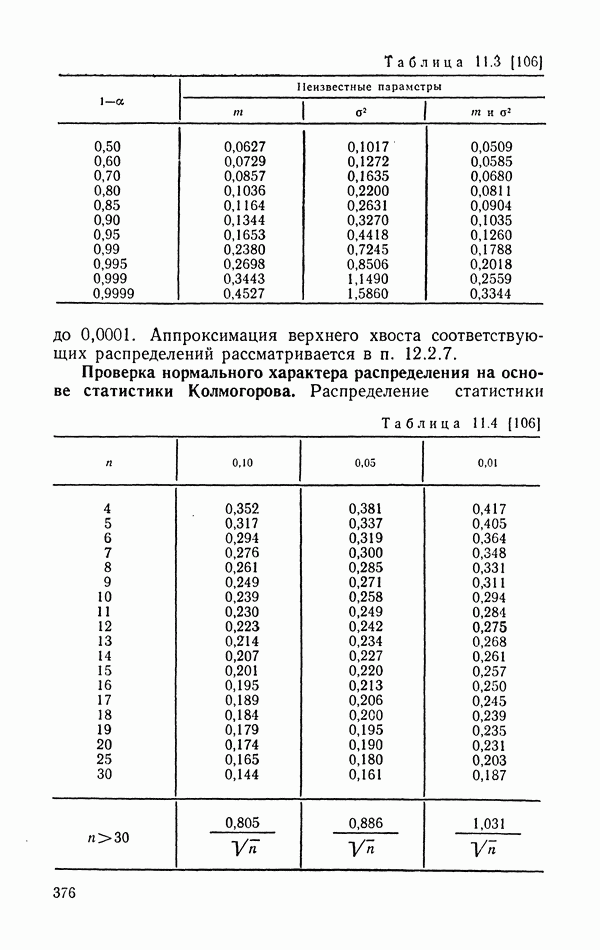
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
- 6.1.5. Нормальное (гауссовское) распределение.
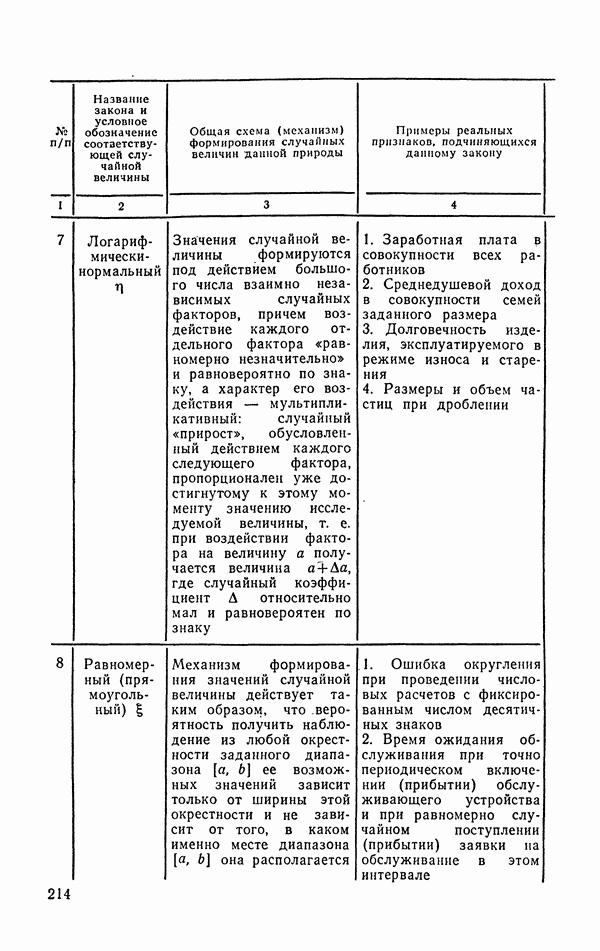
- 6.1.6. Логарифмически-нормальное распределение.
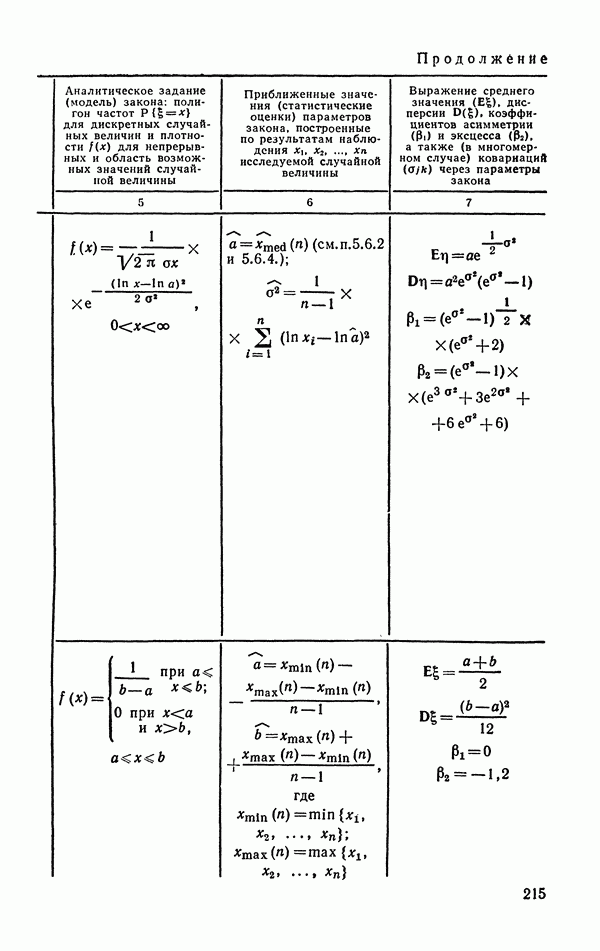
- 6.1.7. Равномерное (прямоугольное) распределение.
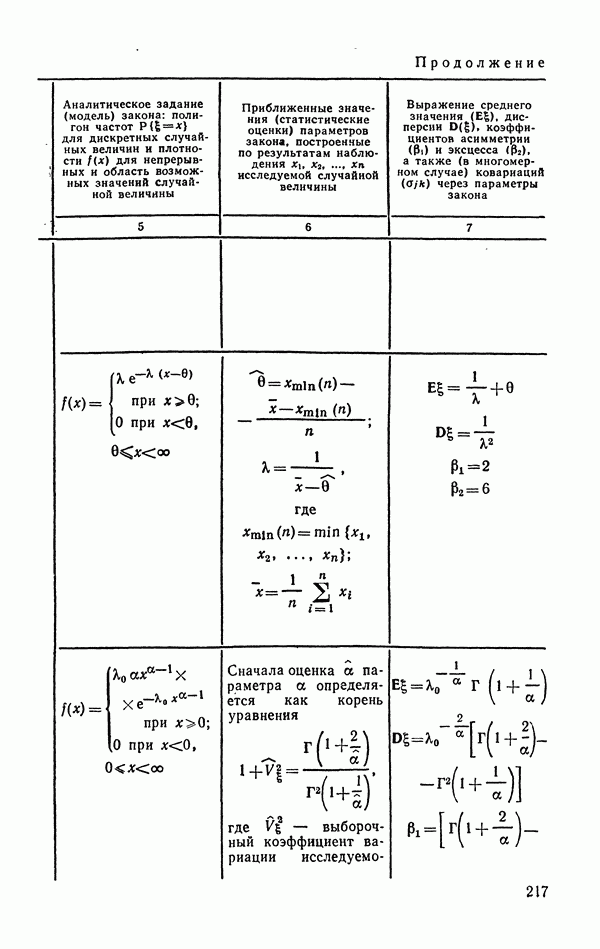
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
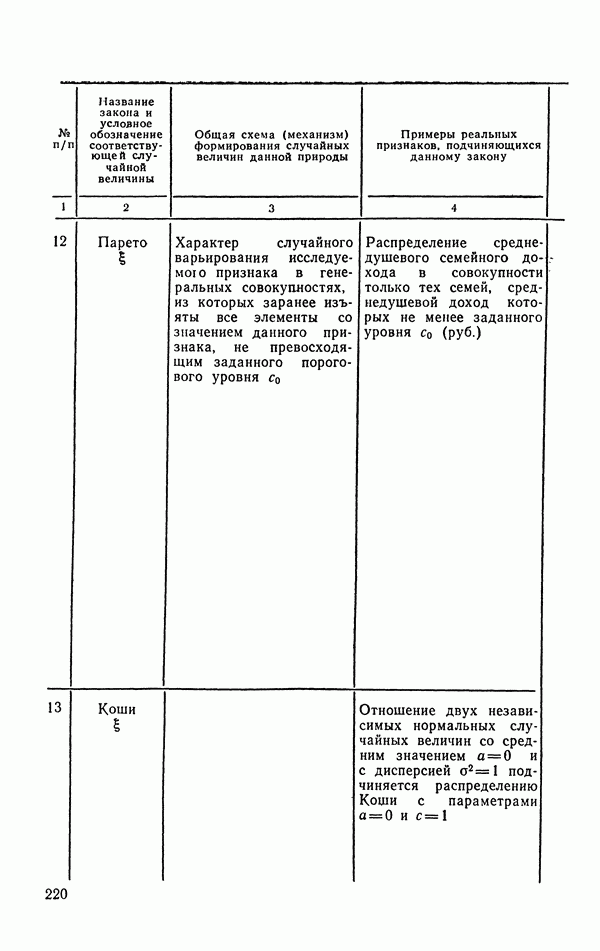
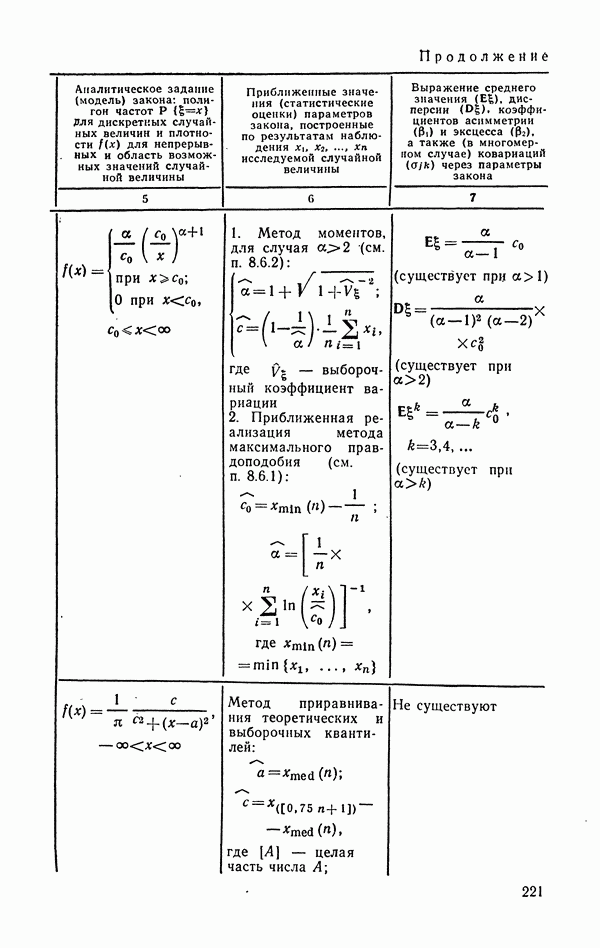
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
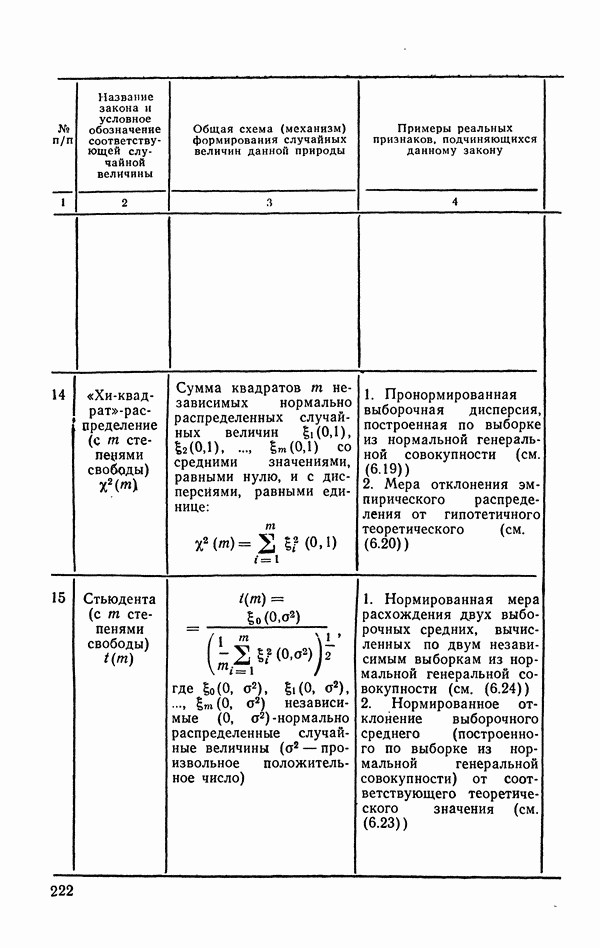
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
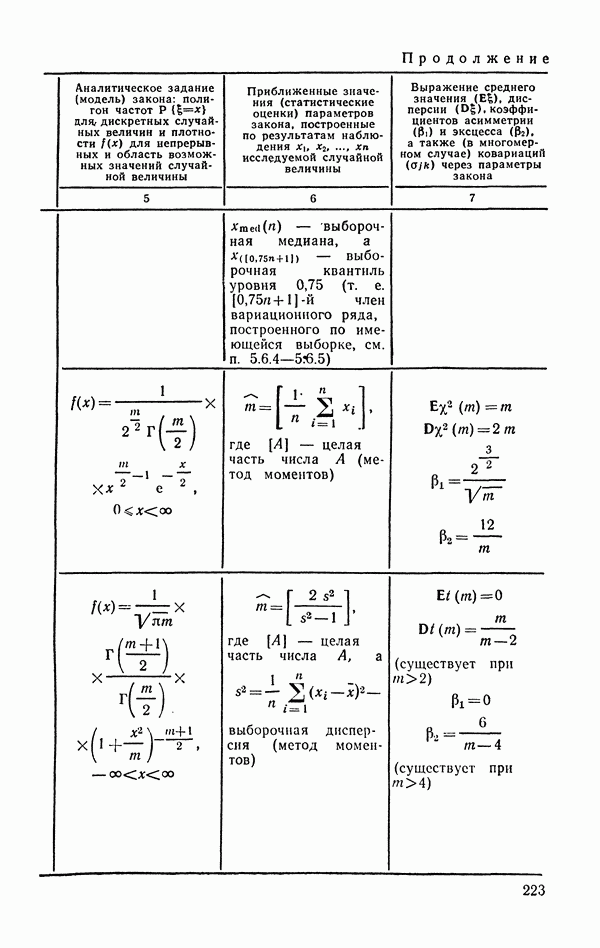
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных распределениях.
- 6.2.5. Г-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.2. Моделирование дискретных случайных величин. Стандартный метод.
- 6.3.3. Моделирование непрерывных распределений.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.2. Многомерная центральная предельная теорема (см. [12, с. 105]).
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
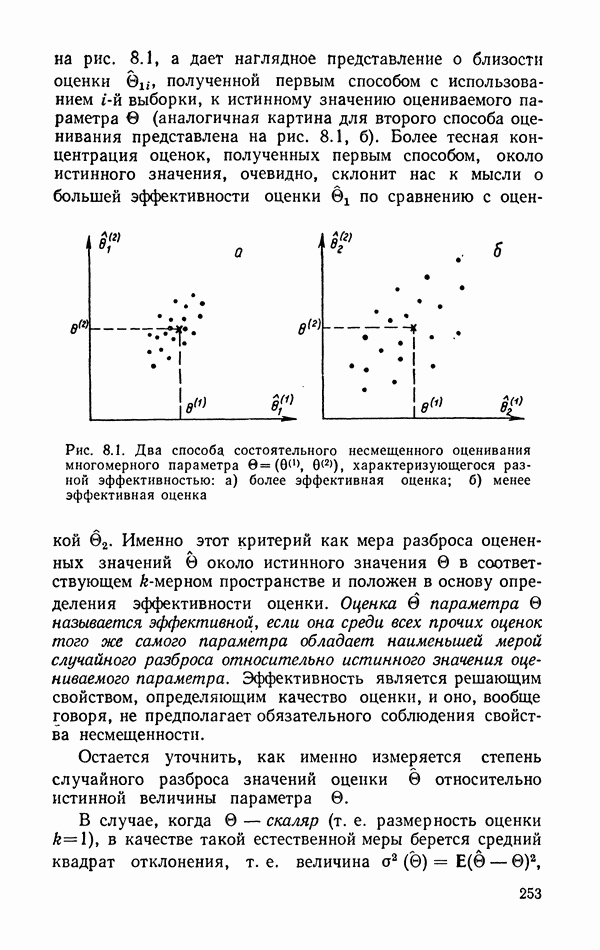
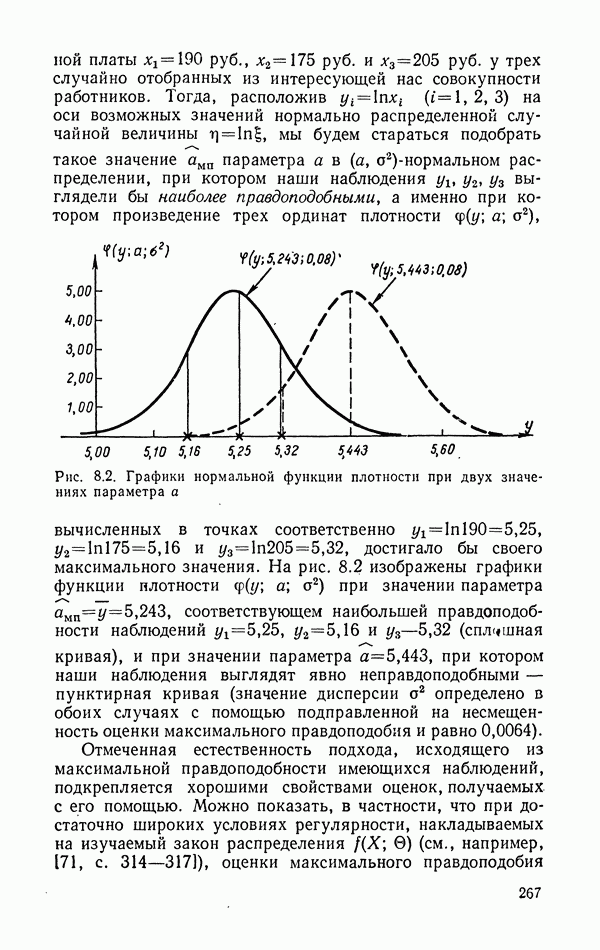
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия.
- 8.3. Неравенство Рао — Крамера — Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4. Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
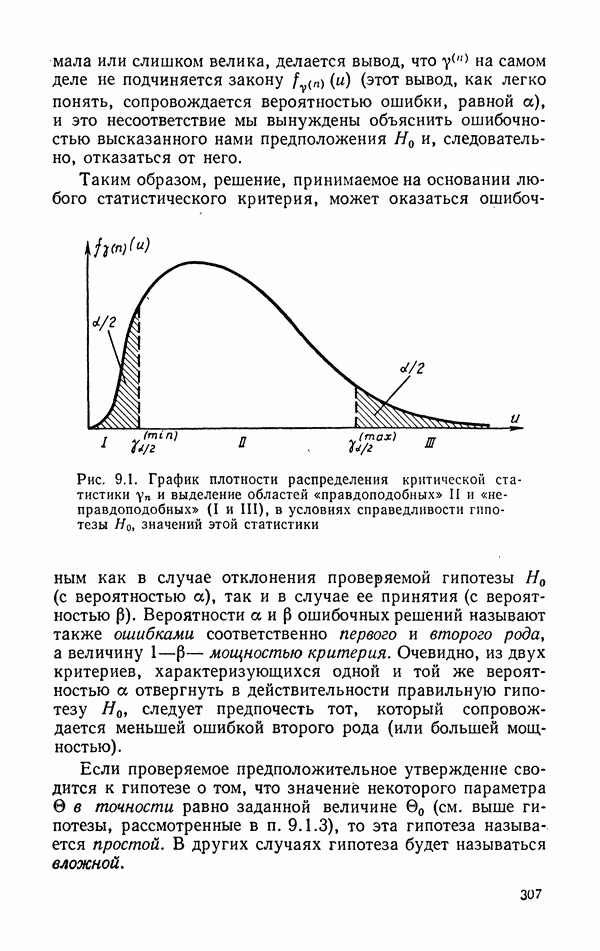
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1.1. Критерий «хи квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий w^2 (Крамера — Мнзеса — Смирнова).
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и w^2 для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- 11.1.7. Использование критериев согласия Колмогорова и w^2 в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.2. Критерий однородности «хи квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
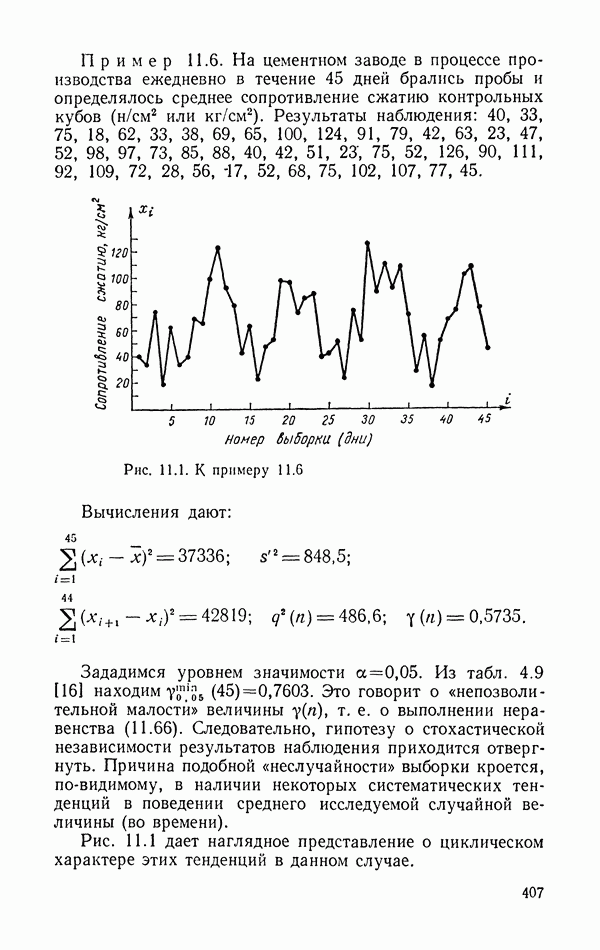
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия.
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа w^2
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ