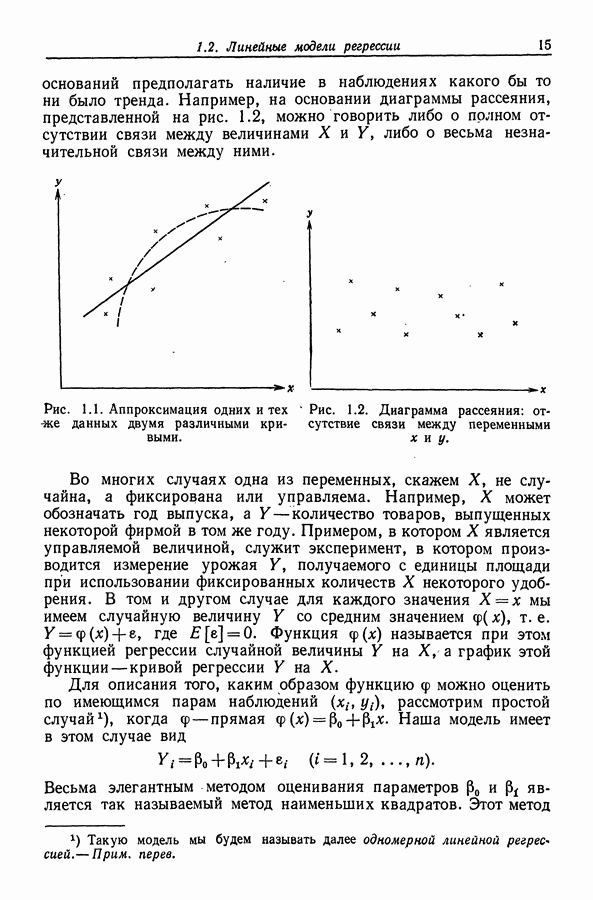
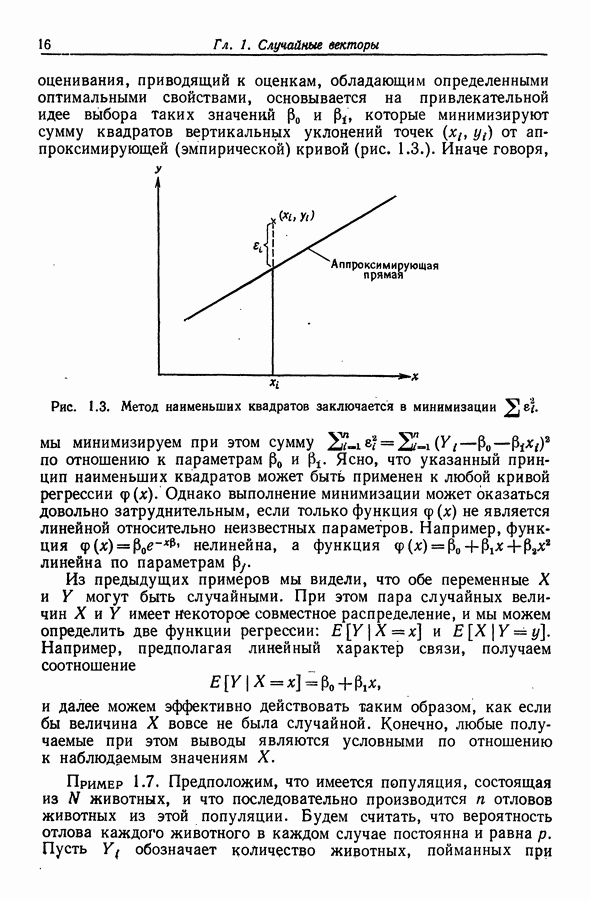
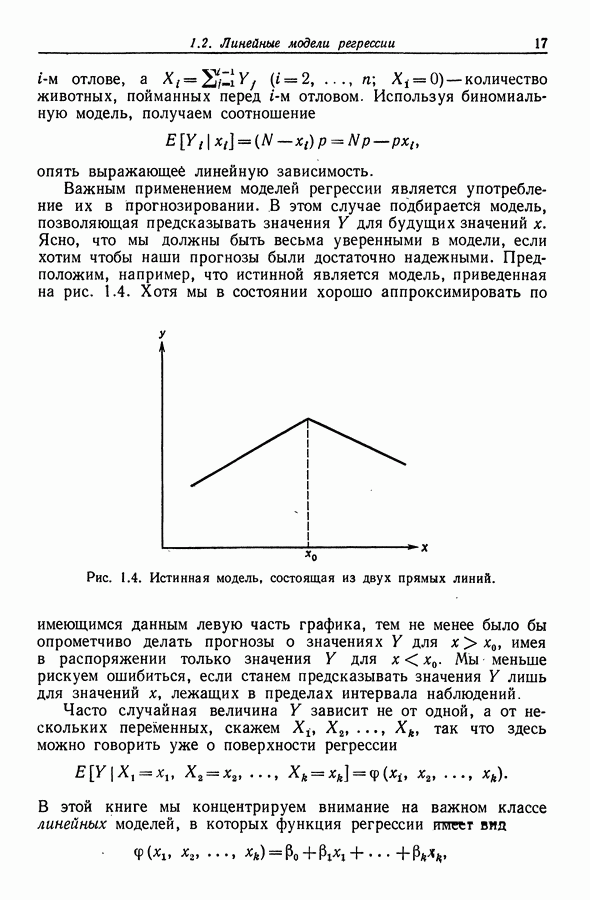
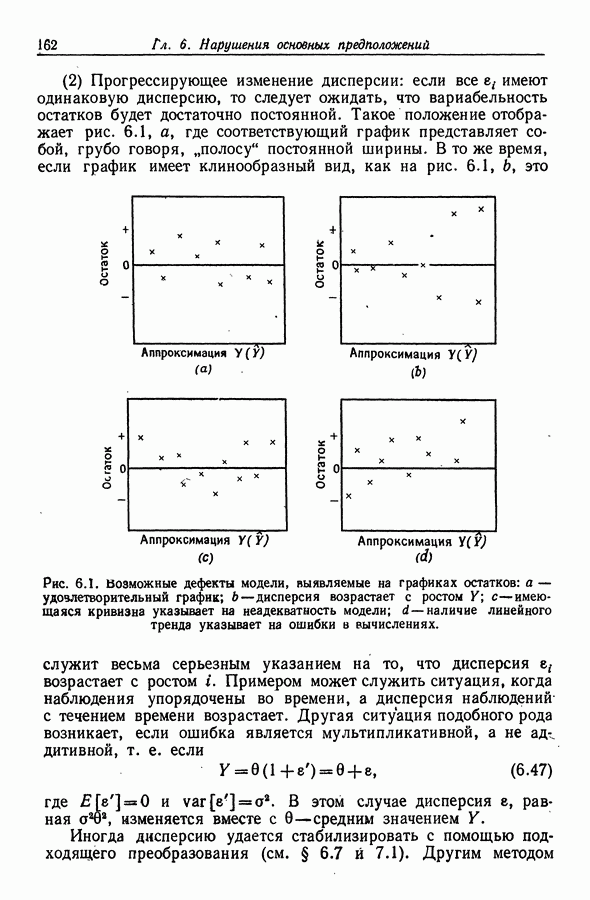
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
10.1. Ковариационный анализ
10.1.1 Оценивание методом наименьших квадратов
В экспериментальных ситуациях некоторые "факторы" могут быть количественными, а другие — качественными. Предположим, например, что мы исследуем влияние температуры  и концентрации с некоторого реактива на выход
и концентрации с некоторого реактива на выход  процесса и подбираем модель регрессии
процесса и подбираем модель регрессии

Температура и концентрация представлены здесь количественно, и наша модель имеет вид  , где
, где  - матрица данных размера
- матрица данных размера  . В то же время в планах экспериментов мы часто имеем факторы, являющиеся чисто качественными. К таким факторам относятся, например, географическое положение, тип удобрения, сорт зерна, способ обработки, тип лекарства и др. Мы, скажем, можем пожелать сравнить действие на людей трех различных лекарств, измеряя некоторую реакцию
. В то же время в планах экспериментов мы часто имеем факторы, являющиеся чисто качественными. К таким факторам относятся, например, географическое положение, тип удобрения, сорт зерна, способ обработки, тип лекарства и др. Мы, скажем, можем пожелать сравнить действие на людей трех различных лекарств, измеряя некоторую реакцию  Если
Если  обозначает реакцию
обозначает реакцию  пациента, принявшего лекарство
пациента, принявшего лекарство  -го типа, то можно произвести однофакторный анализ (один фактор на трех уровнях), используя модель
-го типа, то можно произвести однофакторный анализ (один фактор на трех уровнях), используя модель  или
или  Качественный характер фактора проявляется здесь в том, что элементы матрицы плана могут быть равны только единице или нулю (уравнение
Качественный характер фактора проявляется здесь в том, что элементы матрицы плана могут быть равны только единице или нулю (уравнение  Конечно, количественные факторы, подобные температуре и концентрации, можно трактовать и как качественные. Так, в приведенной однофакторной модели можно говорить, скажем, о трех различных температурах или группах температур.
Конечно, количественные факторы, подобные температуре и концентрации, можно трактовать и как качественные. Так, в приведенной однофакторной модели можно говорить, скажем, о трех различных температурах или группах температур.
Вообще говоря, мы используем термин дисперсионный анализ, когда все факторы трактуются как качественные, и говорим о регрессионном анализе, если все факторы трактуются как количественные. Если же мы имеем смешанную модель, скажем  в котороц одни факторы являются количественными, а другие — качественными, то мы используем термин «ковариационный ацализ» [Scheffe (1959)]. Например, мы можем
в котороц одни факторы являются количественными, а другие — качественными, то мы используем термин «ковариационный ацализ» [Scheffe (1959)]. Например, мы можем
обнаружить, что действие некоторого лекарства зависит от возраста пациента, так что одной из возможных моделей может быть модель

где  возраст
возраст  пациента, принимающего лекарство и
пациента, принимающего лекарство и  типа. Эту модель можно представить в виде
типа. Эту модель можно представить в виде

где

Если взаимодействие между возрастом больного и типом лекарства отсутствует, т. е. влияние возраста оказывается одинаковым для каждого из типов лекарств, то модель можно привести к более простому виду:

или

Действие лекарства может зависеть, кроме возраста, и от веса пациента, также не взаимодействующего с типом лекарства. При этом подходящей может быть модель

где  вес
вес  пациента, принимающего
пациента, принимающего  лекарство. Если лекарства изменяют вес пациентов, то
лекарство. Если лекарства изменяют вес пациентов, то  можно трактовать как рачальщлй вес. Входящие в модель (10.1) три величины — возраст,
можно трактовать как рачальщлй вес. Входящие в модель (10.1) три величины — возраст,
(возраст) и вес — обычно называют сопутствующими переменными. Они часто бывают случайными величинами и не управляются экспериментатором. Это означает, что методы, рассмотренные в настоящей главе, относятся непосредственно к условным моделям. Например, левая часть (10.1) должна иметь вид  а предположения об обычной составляющей
а предположения об обычной составляющей  характеризующей ошибку, будут условными относительно наблюдающихся значений
характеризующей ошибку, будут условными относительно наблюдающихся значений 
Если в упомянутом выше эксперименте возраст и вес, по всей вероятности, существенно влияют на действие лекарства и нас особенно интересует как раз это влияние, то более подходящим может оказаться трехфакторный план с тремя факторами, трактуемыми как качественные: лекарство, возраст и вес. Поскольку модели ковариационного анализа обычно не имеют тех свойств устойчивости, которыми обладают модели дисперсионного анализа (разд. 10.1.3), то их следует использовать с осторожностью. Некоторые полезные замечания по поводу выбора подходящих моделей имеются в работах Cochran (1957, 1969).
Рассмотрим общую модель ковариационного анализа

где  -матрица размера
-матрица размера  -матрица размера
-матрица размера  и столбцы матрицы
и столбцы матрицы  не зависят линейно от столбцов матрицы
не зависят линейно от столбцов матрицы  Хотя эту модель можно исследовать и как одну большую модель регрессии, тем не менее общий метод состоит здесь в том, чтобы использовать наши знания о модели дисперсионного анализа
Хотя эту модель можно исследовать и как одну большую модель регрессии, тем не менее общий метод состоит здесь в том, чтобы использовать наши знания о модели дисперсионного анализа  и использовать двухшаговый метод наименьших квадратов, описанный в разд. 3.7.3. Этот метод применим даже тогда, когда матрица X имеет неполный ранг или когда имеются ограничения на вектор
и использовать двухшаговый метод наименьших квадратов, описанный в разд. 3.7.3. Этот метод применим даже тогда, когда матрица X имеет неполный ранг или когда имеются ограничения на вектор  (разд. 3.8.3). Прежде чем привести два примера, мы хотим выделить предположение об отсутствии влияния на
(разд. 3.8.3). Прежде чем привести два примера, мы хотим выделить предположение об отсутствии влияния на  "способов обработки" в
"способов обработки" в  Например, как было указано выше, если некоторое лекарство вызывает изменение веса, то о
Например, как было указано выше, если некоторое лекарство вызывает изменение веса, то о  следует говорить как об исходном весе, на который данное лекарство, конеччо, не влияет.
следует говорить как об исходном весе, на который данное лекарство, конеччо, не влияет.
Пример 10.1 (план с рандомизированными блоками). Рассмотрим модель

где  Такой моделью может описываться, например, сельскохозяйственный эксперимент, проводимый на песчаной почве, в котором
Такой моделью может описываться, например, сельскохозяйственный эксперимент, проводимый на песчаной почве, в котором  способов обработки могут соответствовать различным удобрениям,
способов обработки могут соответствовать различным удобрениям,  блоков — различным полоскам земли, а гц может быть мерой содержания песка на
блоков — различным полоскам земли, а гц может быть мерой содержания песка на  участке.
участке.
Даже хотя модель дисперсионного анализа  и не имеет полного ранга, с помощью двухшаговой процедуры наименьших квадратов все же можно найти оценки наименьших квадратов неизвестных параметров и остаточную сумму квадратов для
и не имеет полного ранга, с помощью двухшаговой процедуры наименьших квадратов все же можно найти оценки наименьших квадратов неизвестных параметров и остаточную сумму квадратов для  Шаги этой процедуры состоят в следующем (ср. с разд. 3.7.3).
Шаги этой процедуры состоят в следующем (ср. с разд. 3.7.3).
(1) Находим оценки наименьших квадратов  и остаточную сумму квадратов
и остаточную сумму квадратов

для модели 
(2) Заменяем  на
на  в RSS и минимизируем полученное выражение относительно у. После замены имеем
в RSS и минимизируем полученное выражение относительно у. После замены имеем

где

и т. п. Уравнение  дает
дает

откуда и получаем оценку наименьших квадратов для у в модели 
(3) Остаточная сумма квадратов для модели  равна
равна

или

(4) Заменяя  на
на  и т. д., получаем
и т. д., получаем

(5) Коэффициент при  в (10.3) равен
в (10.3) равен  так что
так что

Последний результат можно получить и непосредственно (ср. с упр. 1 в конце главы).
Пример 10.2 (классификация по одному признаку). Для анализа модели

мы применим двухшаговый метод наименьших квадратов к модели  Для последней модели и
Для последней модели и  причем эта процедура, как оказывается, совпадает с процедурой, приведенной в примере 10.1, с той лишь разницей, что
причем эта процедура, как оказывается, совпадает с процедурой, приведенной в примере 10.1, с той лишь разницей, что 
10.1.2. Проверка гипотез
Теперь мы на нескольких примерах продемонстрируем основные идеи проверки гипотез в моделях ковариационного анализа.
Пример  (проверка гипотезы о параллельности линий регрессии). Пусть модель
(проверка гипотезы о параллельности линий регрессии). Пусть модель

в которой случайные величины  независимы и имеют одно и то же распределение
независимы и имеют одно и то же распределение  описывает
описывает  линий регрессии с У наблюдениями на каждую линию, и пусть мы хотим проверить гипотезу
линий регрессии с У наблюдениями на каждую линию, и пусть мы хотим проверить гипотезу  Для модели
Для модели  остаточная сумма квадратов равна
остаточная сумма квадратов равна  Заменяя в этом выражении
Заменяя в этом выражении  на
на  получаем
получаем

где

и т. д. Уравнение  приводит к оценке
приводит к оценке

При этом

Число степеней свободы, соответствующее  равно
равно  поскольку матрица
поскольку матрица  лежащая в основе модели
лежащая в основе модели  является, очевидно, матрицей размера
является, очевидно, матрицей размера  ранга
ранга 
Если гипотеза Я верна, то модель  редуцируется к модели, рассмотренной в примере 10.2, так что из соотношения (10.5) имеем
редуцируется к модели, рассмотренной в примере 10.2, так что из соотношения (10.5) имеем

Поскольку гипотеза  имеет вид
имеет вид

или  где А — матрица размера
где А — матрица размера  ранга
ранга  -статистика для проверки гипотезы
-статистика для проверки гипотезы  имеет вид
имеет вид 

Несмотря на различия в обозначениях, этот результат совпадает с результатом, приведенным в разд. 7.5.2.
Пример  (план с рандомизированными блоками). Сейчас мы рассмотрим проверку двух различных гипотез для модели с рандомизированными блоками из примера 10.1. (i) Проверка гипотезы
(план с рандомизированными блоками). Сейчас мы рассмотрим проверку двух различных гипотез для модели с рандомизированными блоками из примера 10.1. (i) Проверка гипотезы  Из примера 10.1 (выражение (10.5)) имеем
Из примера 10.1 (выражение (10.5)) имеем

 степенями свободы (поскольку мы добавили еще один параметр у к обычной модели; разд. 9.4.1). Если
степенями свободы (поскольку мы добавили еще один параметр у к обычной модели; разд. 9.4.1). Если  то возвращаемся к обычной модели без сопутствующих переменных, так что
то возвращаемся к обычной модели без сопутствующих переменных, так что  Те же рассуждения, что и в примере 10.3, показывают, что гипотезе
Те же рассуждения, что и в примере 10.3, показывают, что гипотезе  соответствует одна степень свободы, так что
соответствует одна степень свободы, так что  -статистика для проверки этой гипотезы имеет вид
-статистика для проверки этой гипотезы имеет вид

Если это отношение оказывается значимым, т. е. сопутствующей переменной  пренебрегать нельзя, то может возникнуть желание построить для
пренебрегать нельзя, то может возникнуть желание построить для  доверительный интервал. Применяя к модели (10.2) общую теорию регрессии, находим, что
доверительный интервал. Применяя к модели (10.2) общую теорию регрессии, находим, что  и 6 не зависит от
и 6 не зависит от  (равной
(равной  ). Поскольку в рассмотренном примере
). Поскольку в рассмотренном примере 
 то
то  (будучи элементом вектора
(будучи элементом вектора  и
и

имеет  -распределение с
-распределение с  степенями свободы,
степенями свободы,
(ii) Проверка гипотезы  для всех
для всех 
Для отыскания  где
где

опять применим двухшаговый метод наименьших квадратов к модели  Мы отправляемся от суммы
Мы отправляемся от суммы

производим замену  на
на  и получаем выражение
и получаем выражение

где

и т. д. Из уравнения  получаем
получаем 

Окончательно  -статистика для проверки гипотезы Н имеет вид
-статистика для проверки гипотезы Н имеет вид

Число степеней свободы для числителя можно получить из соображений, аналогичных приведенным в разд. 9.2.2.
Если отношение  оказывается значимым, то можно проверить все сравнения
оказывается значимым, то можно проверить все сравнения  параметров
параметров  используя метод множественного сравнения Шеффе (разд. 9.2.4). При этом следует применить оценку (ср. с (10.6))
используя метод множественного сравнения Шеффе (разд. 9.2.4). При этом следует применить оценку (ср. с (10.6))

Действительно, из того, что для всех 

вытекает (см. также (3.34))

и

Поэтому совокупность совместных доверительных интервалов дается соотношением

Требующиеся в ковариационном анализе суммы квадратов и попарных произведений обычно размещают в виде таблицы, подобной табл. 10.1. Здесь

и

Таблица 10.1. (см. скан) Суммы квадратов и смешанных произведений для ковариационного анализа плана с рандомизированными блоками
Отметим также, что определенная выше сумма  дается формулой
дается формулой

Правила, аналогичные тем, которые использовались для разложения сумм квадратов, можно легко получить и для разложения сумм попарных произведений. Например,

и

10.1.3. Основные предположения
Общие замечания гл. 6 применимы и к моделям ковариационного анализа, поскольку они являются частными случаями модели регрессии. Например, в свете разд. 6.3.1 можно ожидать, что в моделях со сбалансированными планами (которые в отсутствие сопутствующих переменных устойчивы к отклонениям от нормальности) именно степень "ненормальности" сопутствующих переменных определяет чувствительность произвольного  -критерия к ненормальности наблюдений
-критерия к ненормальности наблюдений  Этот факт иллюстрирует, например, Atiqullah (1964), который исследует влияние ненормальности на
Этот факт иллюстрирует, например, Atiqullah (1964), который исследует влияние ненормальности на  -статистику для проверки гипотезы
-статистику для проверки гипотезы  в следующем однофакторном плане с
в следующем однофакторном плане с  сопутствующими переменными:
сопутствующими переменными:

где  Используя метод разд. 6.3.2, он находит приближенные выражения для среднего и дисперсии статистики
Используя метод разд. 6.3.2, он находит приближенные выражения для среднего и дисперсии статистики  Эти выражения выписаны подробно для частного случая
Эти выражения выписаны подробно для частного случая 

Atiqullah (1964), кроме того, выяснял также, что будет со статистикой  для указанной модели, когда случайные величины
для указанной модели, когда случайные величины  независимы и нормально распределены с одной и той же дисперсией
независимы и нормально распределены с одной и той же дисперсией  но действительная модель имеет вид
но действительная модель имеет вид

или

Он показал, что в случае  при больших
при больших  влияние переменной
влияние переменной  по-видимому, не слишком существенно, если
по-видимому, не слишком существенно, если

где

В то же время влияние квадратичной составляющей в (10.11). уже значительно более существенно, хотя оно и ослабляется при 
Адекватность каждой конкретной модели можно проверить, используя общие методы графиков остатков, указанные в § 6.6. В то же время имеются и другие графики, позволяющие проверять предположения, относящиеся к сопутствующим переменным. Например, в модели (10.9) предположение о том, что регрессия  на
на  линейная и не зависит от "способов обработки" (т. е. от
линейная и не зависит от "способов обработки" (т. е. от  можно проверить, вычерчивая для каждого
можно проверить, вычерчивая для каждого  график зависимости
график зависимости  от
от  Если все эти графики линейны и имеют почти одинаковый наклон, то такое предположение разумно. Можно применить также критерий для проверки равенства углов наклона (разд. 10.1.2, пример 10.3). Однако указанный метод не применим, если
Если все эти графики линейны и имеют почти одинаковый наклон, то такое предположение разумно. Можно применить также критерий для проверки равенства углов наклона (разд. 10.1.2, пример 10.3). Однако указанный метод не применим, если  что как раз и свойственно планам эксперимента без повторений, таким, как планы с рандомизированными блоками и латинские квадраты. В этом случае Snee (1971) рекомендует для каждого способа обработки строить обычный график зависимости остатков
что как раз и свойственно планам эксперимента без повторений, таким, как планы с рандомизированными блоками и латинские квадраты. В этом случае Snee (1971) рекомендует для каждого способа обработки строить обычный график зависимости остатков  от остатков
от остатков  (вычисляемых точно таким же образом) для проверки равенства наклонов. Комбинированный график зависимости К-остатков от
(вычисляемых точно таким же образом) для проверки равенства наклонов. Комбинированный график зависимости К-остатков от  -остатков дает возможность проверки линейности. Например, в плане с рандомизированными блоками
-остатков дает возможность проверки линейности. Например, в плане с рандомизированными блоками  упомянутые К-остатки
упомянутые К-остатки  -остатки равны
-остатки равны  соответственно. Этот метод иллюстрируется в работе Snee (1971) на примере греко-латинского квадрата.
соответственно. Этот метод иллюстрируется в работе Snee (1971) на примере греко-латинского квадрата.
В моделях ковариационного анализа более трудно определить значения сопутствующих переменных заранее, поскольку более важными обычно являются другие черты плана (например, сбалансированность плана, равные числа наблюдений на каждое среднее). Это означает, что сопутствующими переменными обычно служат случайные величины, так что любой анализ является условным относительно принимаемых ими значений. Если вдобавок сопутствующие переменные измерены с ошибкой, следует использовать метод DeGracie, Fuller (1972).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
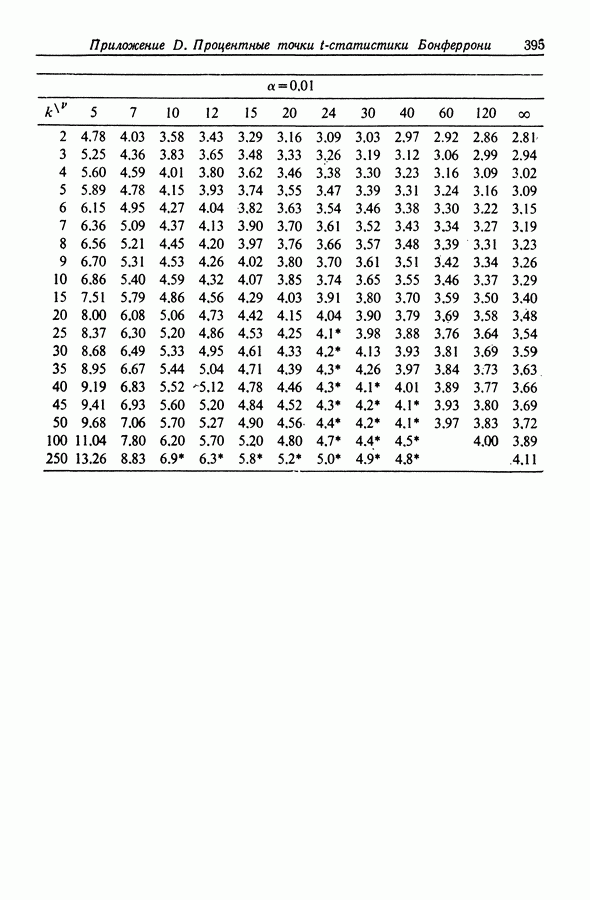
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
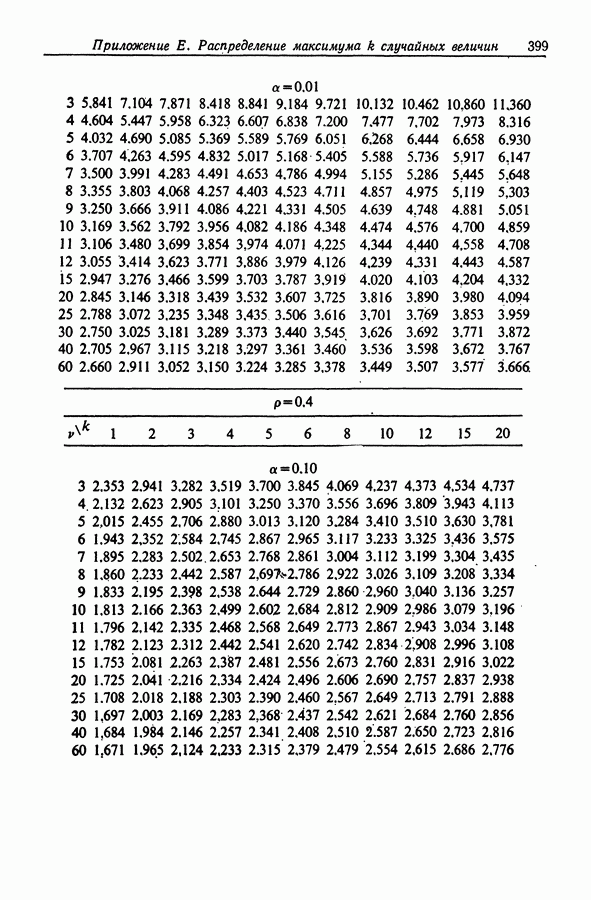
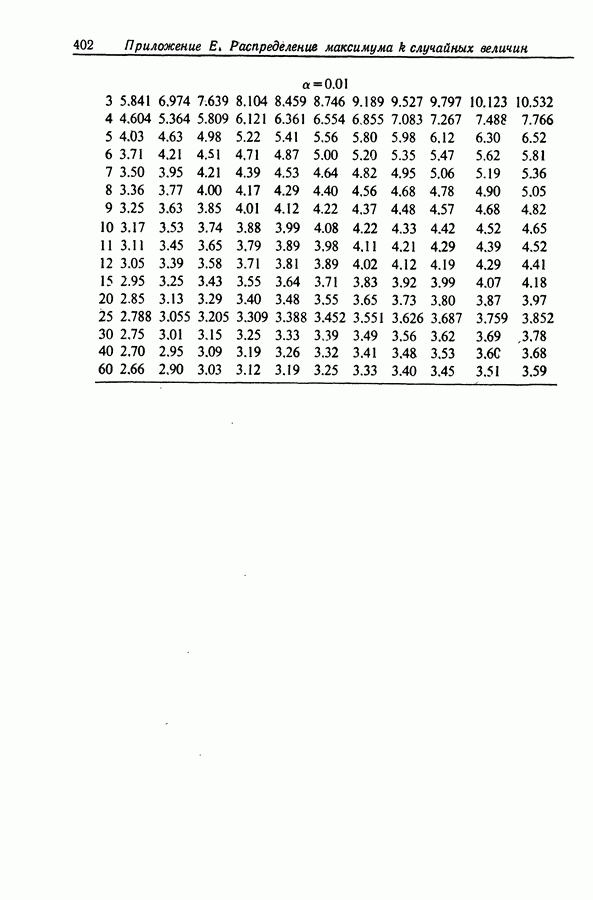
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
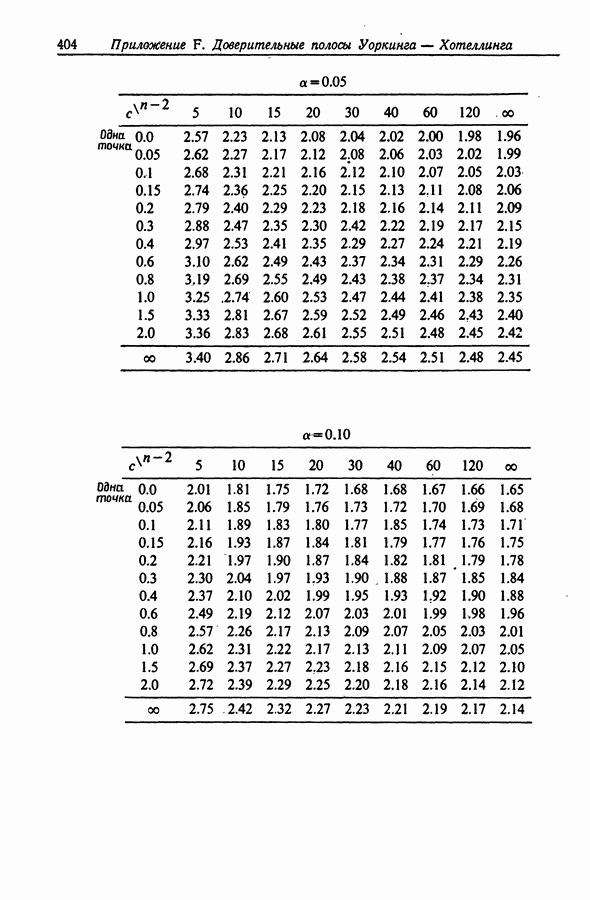
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ