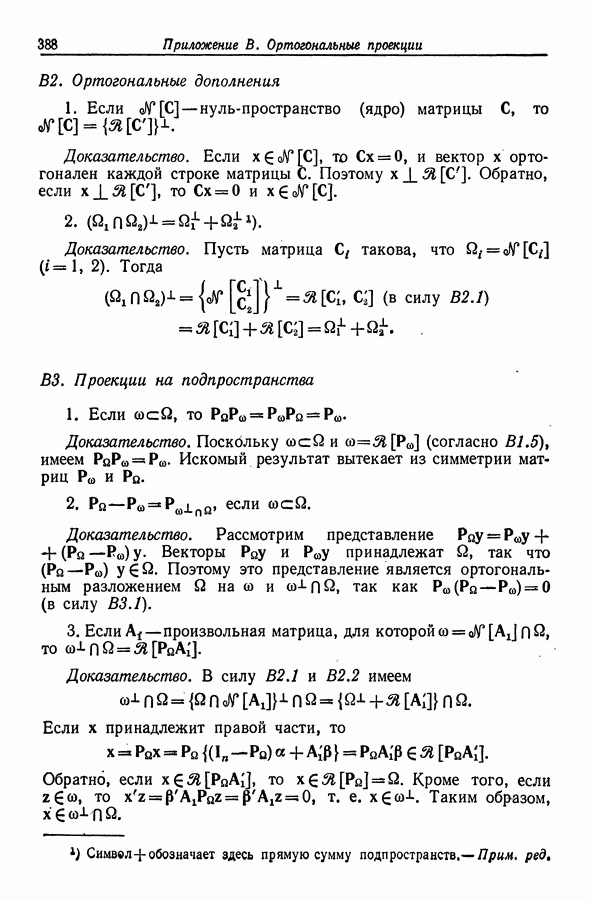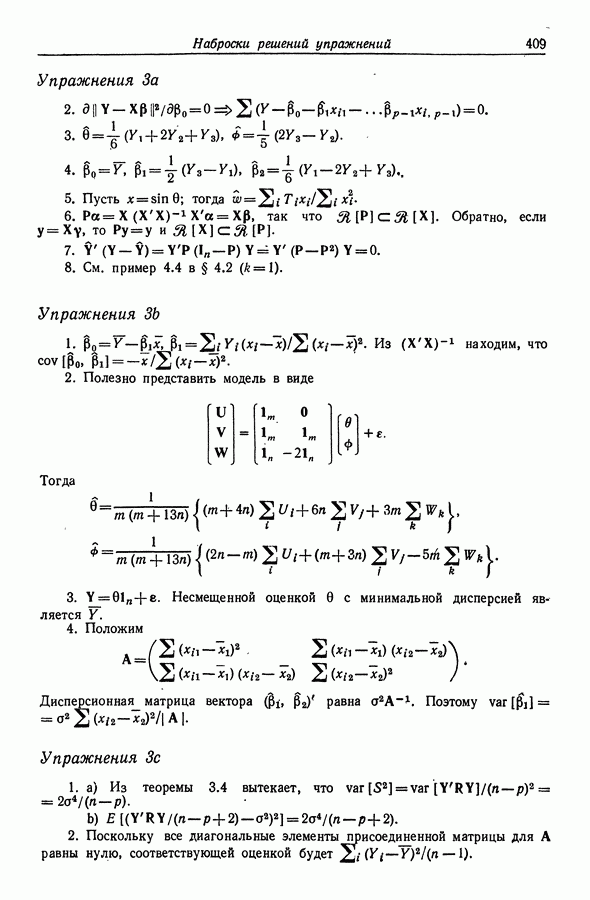| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.6. Анализ остатков
6.6.1. Определение и свойства
Электронные вычислительные машины дают нам прекрасную возможность вычисления отклонений каждого из наблюдавшихся значений  от аппроксимирующей регрессии
от аппроксимирующей регрессии  Эти разности называются остатками и обозначаются символами
Эти разности называются остатками и обозначаются символами

или

где  (Если матрица X имеет неполный ранг, то мы можем использовать в определении
(Если матрица X имеет неполный ранг, то мы можем использовать в определении  обобщенную обратную матрицу
обобщенную обратную матрицу  Остатки, связаны математической зависимостью, определяемой соотношением (4.29) из § 4.2, а именно
Остатки, связаны математической зависимостью, определяемой соотношением (4.29) из § 4.2, а именно

Если  то
то  Напомним, что
Напомним, что  - несмещенная оценка для
- несмещенная оценка для  и поскольку
и поскольку  то
то 
Если  то вектор
то вектор  имеет вырожденное многомерное нормальное распределение (вырожденность возникает из-за того, что матрица
имеет вырожденное многомерное нормальное распределение (вырожденность возникает из-за того, что матрица  положительно полуопределена), и маргинальным распределением
положительно полуопределена), и маргинальным распределением  является
является  Поскольку
Поскольку  то
то  и/поэтому
и/поэтому  Равенство достигается здесь (это соответствует
Равенство достигается здесь (это соответствует  только для некоторых специально подобранных планов [Behnken, Draper (1972, с. 102)]. Заметим, наконец, что (теорема 3.5(iii) из § 3.4)
только для некоторых специально подобранных планов [Behnken, Draper (1972, с. 102)]. Заметим, наконец, что (теорема 3.5(iii) из § 3.4)

и для 

Второе равенство здесь — следствие соотношения (6.41). Последнее равенство в (6.43) вытекает из нормальных уравнений, что можно увидеть, дифференцируя  а также из соотношения
а также из соотношения 
Рассмотрим теперь некоторые графические методы, основанные на остатках и дающие возможность исследовать отклонения от основной модели и от сделанных предположений относительно распределений. Смысл использования этих графиков состоит в том, что всякое отклонение от сделанных предположений относительно распределения 8 отражается на векторе  При этом различные графики отражают разные типы отклонении.
При этом различные графики отражают разные типы отклонении.
6.6.2. Графики остатков
Первый шаг состоит в таком выборе масштаба остатков, при котором они будут иметь дисперсии, приблизительно равные единице. Достичь этого можно, используя, например, понятие средней дисперсии

Оценивая  с помощью
с помощью  мы приходим к шкалированным остаткам
мы приходим к шкалированным остаткам

(см. Daniel, Wood (1971, с. 28), Behnken, Draper (1972, с. 102)). В то же время, поскольку  естественнее использовать "стьюдентизированные" остатки
естественнее использовать "стьюдентизированные" остатки

Хотя сами остатки и их шкалированные варианты  и коррелированы, эта корреляция, по-видимому, мало влияет на характер графиков, описанных ниже. Поэтому мы можем обращаться с
и коррелированы, эта корреляция, по-видимому, мало влияет на характер графиков, описанных ниже. Поэтому мы можем обращаться с  и (до некоторой степени) с
и (до некоторой степени) с  как с приблизительно независимыми и одинаково распределенными случайными величинами, имеющими распределение
как с приблизительно независимыми и одинаково распределенными случайными величинами, имеющими распределение 
Практика показывает, что во многих случаях, величины  можно не учитывать, и при этом можно использовать либо
можно не учитывать, и при этом можно использовать либо  либо, если
либо, если  не мало,
не мало,  [Behnken, Draper (1972, 1.3 и 2.5)].
[Behnken, Draper (1972, 1.3 и 2.5)].
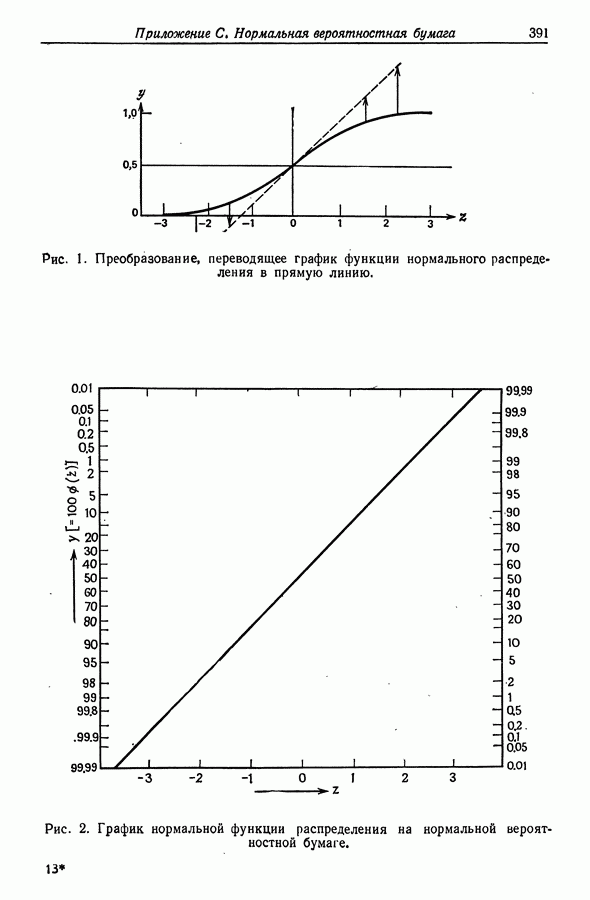
(а) Нормальная вероятностная бумага
Пусть  стьюдентизированные остатки, расположенные в порядке возрастания. Для умеренно больших значений
стьюдентизированные остатки, расположенные в порядке возрастания. Для умеренно больших значений  (см. приложение С) построенный на вероятностной бумаге график зависимости
(см. приложение С) построенный на вероятностной бумаге график зависимости  от
от  будет выявлять
будет выявлять
любые заметные отклонения от нормальности, поскольку при наличии нормальности точки графика должны располагаться приблизительно вдоль прямой  Такой график полезен также для обнаружения "выделяющихся", или "сомнительных", наблюдений. Они выглядят на графике как точки, значительно удаленные от прямой, соответствующей линейному тренду, на который указывают остальные точки. Однако к таким точкам надо относиться с достаточной осторожностью. Считается, что отбрасывать их как выделяющиеся наблюдения следует только в случае, когда их аномалия достаточно очевидна из каких-то соображений нестатистического характера. Так, возможны поломка измерительного устройства при проведении отдельного измерения, неправильная запись наблюдения или неправильное занесение его на перфокарту. Иногда наличие "странной" точки может иметь даже большее значение, чем весь остальной график, поскольку оно может указывать на серьезные недостатки в модели. Например, если такая точка соответствует экстремальному значению одного из это может означать такое изменение в модели, которое приводит к выходу за обычные рамки эксперимента. Следует отметить, что при малых
Такой график полезен также для обнаружения "выделяющихся", или "сомнительных", наблюдений. Они выглядят на графике как точки, значительно удаленные от прямой, соответствующей линейному тренду, на который указывают остальные точки. Однако к таким точкам надо относиться с достаточной осторожностью. Считается, что отбрасывать их как выделяющиеся наблюдения следует только в случае, когда их аномалия достаточно очевидна из каких-то соображений нестатистического характера. Так, возможны поломка измерительного устройства при проведении отдельного измерения, неправильная запись наблюдения или неправильное занесение его на перфокарту. Иногда наличие "странной" точки может иметь даже большее значение, чем весь остальной график, поскольку оно может указывать на серьезные недостатки в модели. Например, если такая точка соответствует экстремальному значению одного из это может означать такое изменение в модели, которое приводит к выходу за обычные рамки эксперимента. Следует отметить, что при малых  практически невозможно определить, является данное наблюдение выделяющимся или нет.
практически невозможно определить, является данное наблюдение выделяющимся или нет.
(b) График зависимости остатков от подобранных значений
Построение графика зависимости  от
от  помогает выявлять три довольно распространенных дефекта.
помогает выявлять три довольно распространенных дефекта.
(1) Выделяющиеся наблюдения: некоторые из остатков могут по абсолютной величине существенно превосходить все остальные остатки. Одна из возможных процедур проверки такова: остаток, имеющий экстремальное значение, скажем  исключается из рассмотрения, если
исключается из рассмотрения, если  где С — некоторое заранее выбранное число. Если
где С — некоторое заранее выбранное число. Если  то можно использовать простое приближенное правило, согласно которому из рассмотрения исключаются все те остатки
то можно использовать простое приближенное правило, согласно которому из рассмотрения исключаются все те остатки  для которых
для которых  Совместное распределение остатков известно (Ellenberg (1973)), так что, по крайней мере теоретически, можно найти распределение
Совместное распределение остатков известно (Ellenberg (1973)), так что, по крайней мере теоретически, можно найти распределение  и определить соответствующее значение С. Эмпирическое решение этой задачи для случая одномерной линейной регрессии приведено в работе
и определить соответствующее значение С. Эмпирическое решение этой задачи для случая одномерной линейной регрессии приведено в работе  и др. (1973). Маргинальное распределение величины
и др. (1973). Маргинальное распределение величины  также известно (Beckman, Trussell (1974)). В то же время имеется и приближенный критерий, основанный на максимуме нормированных остатков
также известно (Beckman, Trussell (1974)). В то же время имеется и приближенный критерий, основанный на максимуме нормированных остатков  [см. Stefansky (1971. 1972), Goldsmith, Boddy (1973), а также Williams (1973)].
[см. Stefansky (1971. 1972), Goldsmith, Boddy (1973), а также Williams (1973)].
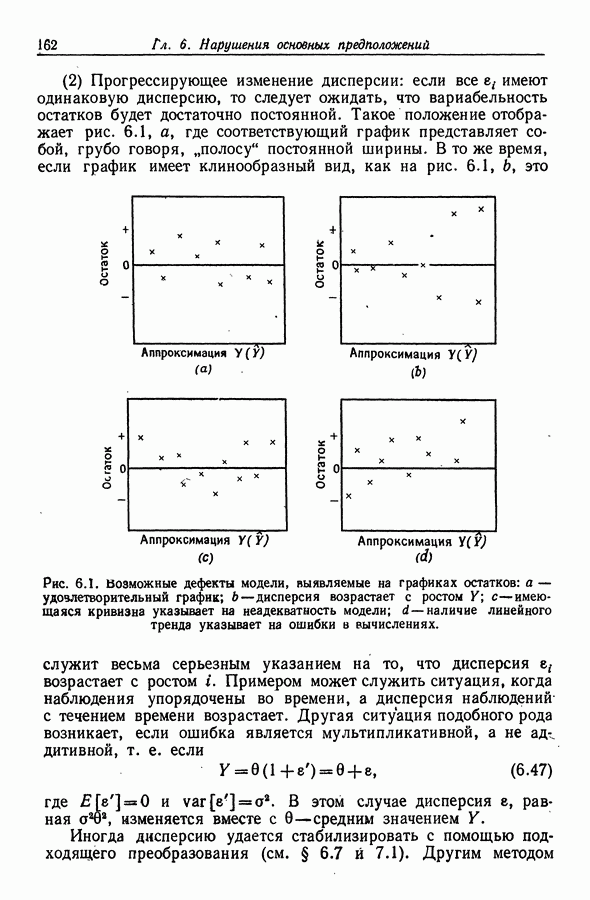
(2) Прогрессирующее изменение дисперсии: если все имеют одинаковую дисперсию, то следует ожидать, что вариабельность остатков будет достаточно постоянной. Такое положение отображает рис. 6.1, а, где соответствующий график представляет собой, грубо говоря, "полосу" постоянной ширины. В то же время, если график имеет клинообразный вид, как на рис. 6.1, 6, это служит весьма серьезным указанием на то, что дисперсия  возрастает с ростом
возрастает с ростом 

Рис. 6.1. Возможные дефекты модели, выявляемые на графиках остатков: а — удовлетворительный график; Ь—дисперсия возрастает с ростом  с — имеющаяся кривизна указывает на неадекватность модели;
с — имеющаяся кривизна указывает на неадекватность модели;  наличие линейного тренда указывает на ошибки в вычислениях.
наличие линейного тренда указывает на ошибки в вычислениях.
Примером может служить ситуация, когда наблюдения упорядочены во времени, а дисперсия наблюдений с течением времени возрастает. Другая ситуация подобного рода возникает, если ошибка является мультипликативной, а не  дитивной, т. е. если
дитивной, т. е. если

где  В этом случае дисперсия
В этом случае дисперсия  равная
равная  изменяется вместе с
изменяется вместе с  -средним значением
-средним значением 
Иногда дисперсию удается стабилизировать с помощью подходящего преобразования (см. § 6.7 и 7.1). Другим методом
может являться использование взвешенной процедуры наименьших квадратов. Итерационную процедуру оценивания весов в случае, когда  является функцией от
является функцией от  приводят Box, Hill (1974). Устойчивый метод взвешивания, основанный на использовании остатков, описан в работе Beaton, Tukey (1974).
приводят Box, Hill (1974). Устойчивый метод взвешивания, основанный на использовании остатков, описан в работе Beaton, Tukey (1974).
(3) Неадекватность модели: криволинейный характер графика, подобный характеру графика, приведенного на рис. 6.1, с, указывает на неадекватность модели. Пусть, например, подобрана модель  а истинная модель имеет вид
а истинная модель имеет вид 
Тогда нетрудно показать, что

где  и
и  -функции от
-функции от  Поскольку и
Поскольку и  систематически изменяются с/изменением
систематически изменяются с/изменением  то систематическое изменение наблюдается и в графике зависимости
то систематическое изменение наблюдается и в графике зависимости  или
или  от
от 
Заметим, наконец, что наличие в графике линейного тренда, подобного изображенному на рис.  указывает на ошибки, имеющиеся в вычислениях, поскольку, как показали Draper, Smith (1966),
указывает на ошибки, имеющиеся в вычислениях, поскольку, как показали Draper, Smith (1966),  (см. (6.42)).
(см. (6.42)).
(с) График зависимости остатков от пропущенных факторов
На практике любой фактор, который может влиять на отклик следует включать в регрессионную модель в качестве регрессора. Однако если какой-либо из вероятных факторов был пропущен, то это может быть выявлено по графику зависимости остатков от этого фактора (такой график, конечно, можно построить, только если известны уровни этого фактора). Например, график зависимости  от времени, который часто является и графиком зависимости
от времени, который часто является и графиком зависимости  от
от  может показывать наличие корреляции между последовательными (по времени) значениями
может показывать наличие корреляции между последовательными (по времени) значениями  (на рис. 6.2 показаны соответственно случаи положительной и
(на рис. 6.2 показаны соответственно случаи положительной и

Рис. 6.2. Графики остатков, указывающие на. наличие корреляции между последовательными по времени значениями  : а - положительная корреляция; б - отрицательная корреляция.
: а - положительная корреляция; б - отрицательная корреляция.
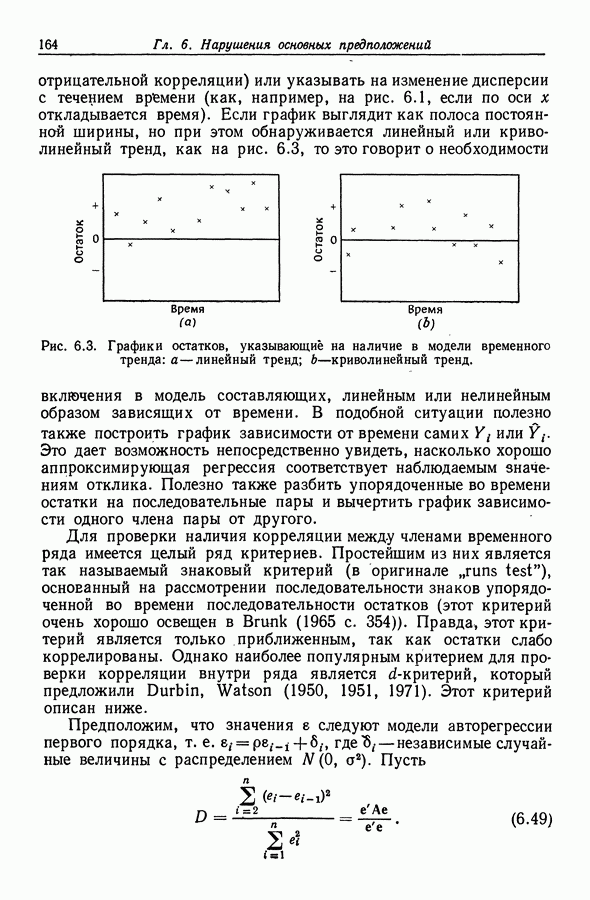
отрицательной корреляции) или указывать на изменение дисперсии с течением времени (как, например, на рис. 6.1, если по оси х откладывается время). Если график выглядит как полоса постоянной ширины, но при этом обнаруживается линейный или криволинейный тренд, как на рис. 6.3, то это говорит о необходимости включения в модель составляющих, линейным или нелинейным образом зависящих от времени.

Рис. 6.3. Графики остатков, указывающие на наличие в модели временного тренда: а — линейный тренд; b — криволинейный тренд.
В подобной ситуации полезно также построить график зависимости от времени самих  или
или  Это дает возможность непосредственно увидеть, насколько хорошо аппроксимирующая регрессия соответствует наблюдаемым значениям отклика. Полезно также разбить упорядоченные во времени остатки на последовательные пары и вычертить график зависимости одного члена пары от другого.
Это дает возможность непосредственно увидеть, насколько хорошо аппроксимирующая регрессия соответствует наблюдаемым значениям отклика. Полезно также разбить упорядоченные во времени остатки на последовательные пары и вычертить график зависимости одного члена пары от другого.
Для проверки наличия корреляции между членами временного ряда имеется целый ряд критериев. Простейшим из них является так называемый знаковый критерий (в оригинале "runs test"), основанный на рассмотрении последовательности знаков упорядоченной во времени последовательности остатков (этот критерий очень хорошо освещен в Brunk (1965 с. 354)). Правда, этот критерий является только приближенным, так как остатки слабо коррелированы. Однако наиболее популярным критерием для проверки корреляции внутри ряда является  -критерий, который предложили Durbin, Watson (1950, 1951, 1971). Этот критерий описан ниже.
-критерий, который предложили Durbin, Watson (1950, 1951, 1971). Этот критерий описан ниже.
Предположим, что значения  следуют модели авторегрессии первого порядка, т. е.
следуют модели авторегрессии первого порядка, т. е.  где
где  — независимые случайные величины с распределением
— независимые случайные величины с распределением  Пусть
Пусть

Тогда, как показали Durbin, Watson (1971), критическая область  для проверки нулевой гипотезы
для проверки нулевой гипотезы  против односторонней альтернативы
против односторонней альтернативы  обладает определенными свойствами оптимальности. Например, она является локально наиболее мощной инвариантной критической областью. К сожалению, распределение статистики
обладает определенными свойствами оптимальности. Например, она является локально наиболее мощной инвариантной критической областью. К сожалению, распределение статистики  при гипотезе
при гипотезе  зависит от матрицы данных X, так что
зависит от матрицы данных X, так что  надо вычислять для каждой матрицы X отдельно. Тем не менее Durbin, Watson предложили несколько приближенных методов, которые как будто весьма хорошо работают на практике. Прежде всего они доказали [Durbin, Watson (1950)], что
надо вычислять для каждой матрицы X отдельно. Тем не менее Durbin, Watson предложили несколько приближенных методов, которые как будто весьма хорошо работают на практике. Прежде всего они доказали [Durbin, Watson (1950)], что  где
где  и
и  - случайные величины, распределения которых уже не зависят от
- случайные величины, распределения которых уже не зависят от  Процентные точки для распределений
Процентные точки для распределений  и
и  табулированы для различных
табулированы для различных  в их статье за 1951 г., а также в работе Koerts, Abrahamse (1969, с. 176—178). Они также показали, что распределение статистики
в их статье за 1951 г., а также в работе Koerts, Abrahamse (1969, с. 176—178). Они также показали, что распределение статистики  при гипотезе
при гипотезе  можно удовлетворительно аппроксимировать бета-распределением, имеющим такие же среднее и дисперсию. Иначе говоря, плотность распределения статистики
можно удовлетворительно аппроксимировать бета-распределением, имеющим такие же среднее и дисперсию. Иначе говоря, плотность распределения статистики  при нулевой гипотезе аппроксимируется плотностью
при нулевой гипотезе аппроксимируется плотностью

а выражения для  приведены в статье Durbin, Watson (1971, соотношения (3.1) — (3.4)). На основе такой аппроксимации они предлагают следующую процедуру. Пусть А — наблюдаемое значение статистики
приведены в статье Durbin, Watson (1971, соотношения (3.1) — (3.4)). На основе такой аппроксимации они предлагают следующую процедуру. Пусть А — наблюдаемое значение статистики  -размер критерия,
-размер критерия,  нижние
нижние  -процентные точки распределений
-процентные точки распределений  соответственно. Если
соответственно. Если  то гипотеза
то гипотеза  отвергается; если
отвергается; если  то гипотеза
то гипотеза  принимается; если
принимается; если  то вычисляется (численными методами) интеграл
то вычисляется (численными методами) интеграл

и гипотеза  принимается или отвергается в зависимости от того, будет ли этот интеграл больше или меньше а. (Здесь можно воспользоваться имеющимися пакетами программ для вычисления функции бета-распределения.)
принимается или отвергается в зависимости от того, будет ли этот интеграл больше или меньше а. (Здесь можно воспользоваться имеющимися пакетами программ для вычисления функции бета-распределения.)
Если в качестве альтернативы выступает гипотеза о наличии отрицательной корреляции, т. е.  то надо попросту использовать статистику
то надо попросту использовать статистику  При этом с релчицой
При этом с релчицой  можно
можно
обращаться так, как если бы она была наблюдаемым значением статистики  используемой для проверки наличия положительной корреляции. Двусторонние критерии для альтернативы
используемой для проверки наличия положительной корреляции. Двусторонние критерии для альтернативы  получаются путем комбинации пары указанных выше односторонних критериев, для каждого из которых берется уровень значимости
получаются путем комбинации пары указанных выше односторонних критериев, для каждого из которых берется уровень значимости  .
.
Durbin, Watson (1971, с. 18) предложили и другой приближенный критерий, основанный на критическом значении  где а и
где а и  подбираются таким образом, чтобы статистики
подбираются таким образом, чтобы статистики  имели одинаковые средние и одинаковые дисперсии. В этой же статье кратко описаны и другие тестовые статистики, распределения которых при нулевой гипотезе не зависят функциойально от матрицы
имели одинаковые средние и одинаковые дисперсии. В этой же статье кратко описаны и другие тестовые статистики, распределения которых при нулевой гипотезе не зависят функциойально от матрицы  . К этой категории принадлежит и так называемый НЛНШ-критерий [см. Koerts, Abrahamse 1969)]. Он является точным критерием и основывается на другом типе остатков — так называемых НЛНШ-остатках. К сожалению, последние требуют проведения большого количества вычислений.
. К этой категории принадлежит и так называемый НЛНШ-критерий [см. Koerts, Abrahamse 1969)]. Он является точным критерием и основывается на другом типе остатков — так называемых НЛНШ-остатках. К сожалению, последние требуют проведения большого количества вычислений.
Другой точный критерий, основанный на остатках рекуррентного типа, предложили Phillips, Harvey (1974). Этот критерий, по-видимому, лучше НЛНШ-критерия, хотя оба эти критерия являются менее мощными, чем взятая в целом процедура Durbin, Watson (1971), описанная выше.
Полезный графический метод обнаружения корреляции членов ряда, использующий накопленную периодограмму, построенную по остаткам  предложил Durbin (1969). Предлагаем обратиться читателю к его работе, в которой можно найти детали этой и других процедур, использующих периодограммы.
предложил Durbin (1969). Предлагаем обратиться читателю к его работе, в которой можно найти детали этой и других процедур, использующих периодограммы.
(d) Графики зависимостей остатков от каждого из регрессоров
Эти графики полезны для обнаружения нелинейной зависимости от переменной  При этом может оказаться уместным включить в исходную модель слагаемое
При этом может оказаться уместным включить в исходную модель слагаемое  (или перейти, например, от
(или перейти, например, от  к
к  Для иллюстрации предположим, что в
Для иллюстрации предположим, что в  Тогда
Тогда  Отсюда видно, что в обычной ситуации, когда
Отсюда видно, что в обычной ситуации, когда  остатки
остатки  от модели, выражаемой прямой линией, будут располагаться на графике вокруг параболы
от модели, выражаемой прямой линией, будут располагаться на графике вокруг параболы  При
При  соответствующий график зависимости
соответствующий график зависимости  от
от  будет иметь вид, подобный указанному на рис. 6.1, с Отметим, что линейный тренд здесь наблюдаться не должен, так как выборочная ковариация пар
будет иметь вид, подобный указанному на рис. 6.1, с Отметим, что линейный тренд здесь наблюдаться не должен, так как выборочная ковариация пар  равна нулю (соотношение
равна нулю (соотношение 
Наша линейная модель предполагает, что сами регрессоры не взаимодействуют друг с другом, так что изменение значений одного из них не оказывает никакого влияния на то, какими будут значения других регрессоров. Чтобы убедиться в том, что это предположение правильно, можно построить график зависимости  от произведения
от произведения  Если такое произведение необходимо в модели по существу, то будет наблюдаться тенденция к коррелированности остатков с этим произведением, выражающаяся в виде тренда, наблюдаемого на графике.
Если такое произведение необходимо в модели по существу, то будет наблюдаться тенденция к коррелированности остатков с этим произведением, выражающаяся в виде тренда, наблюдаемого на графике.
Указанные графики дают возможность обнаруживать также и любые заметные изменения дисперсии.
В заключение сделаем одно предостережение. Графики зависимости  от каждого из
от каждого из  редко оказываются полезными и, более того, могут даже вводить в заблуждение (см., например, Daniel Wood (1971, с. 53)).
редко оказываются полезными и, более того, могут даже вводить в заблуждение (см., например, Daniel Wood (1971, с. 53)).
(е) Графики зависимости ... от ...
Если какие-нибудь два регрессора  сильно коррелировать между собой, то, вообще говоря, нет никакой необходимости включать в исходную модель регрессии обе эти переменные. В этом случае включение в модель одной из этих переменных означает в то же самое время, что в расчет, по существу, принимается и вторая неременная.
сильно коррелировать между собой, то, вообще говоря, нет никакой необходимости включать в исходную модель регрессии обе эти переменные. В этом случае включение в модель одной из этих переменных означает в то же самое время, что в расчет, по существу, принимается и вторая неременная.
Другие типы графиков зависимостей между регрессорами вместе с некоторыми полезными ссылками можно найти в Anscombe (1973).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
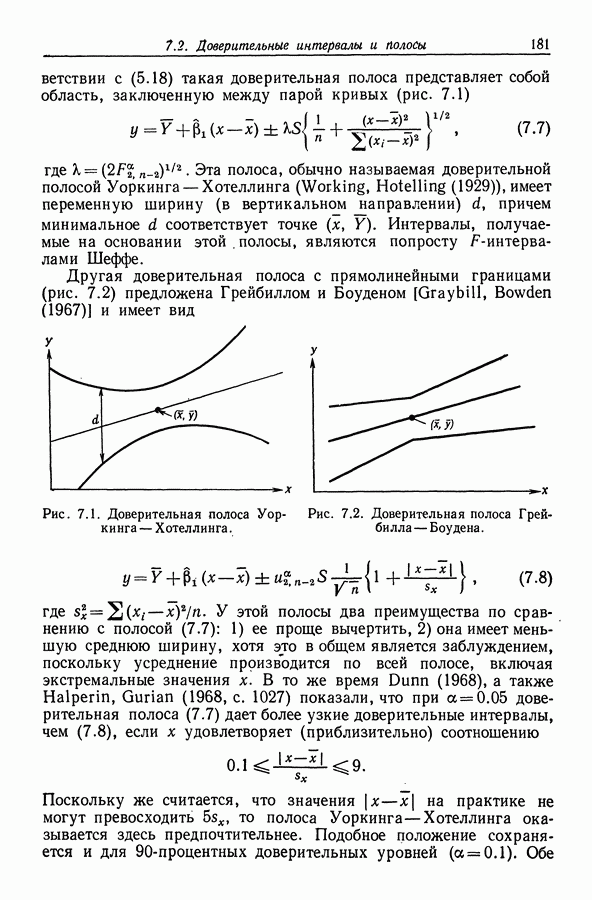
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
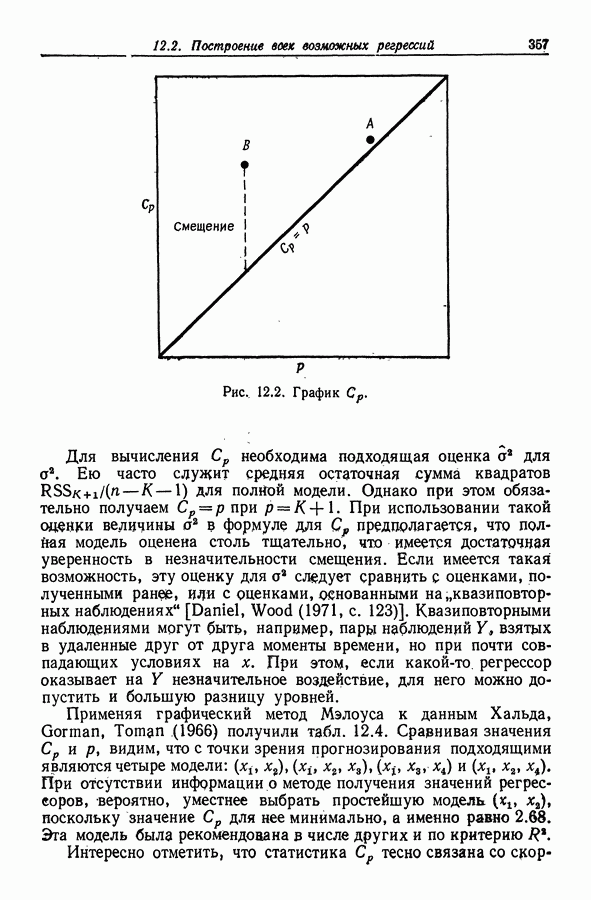
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
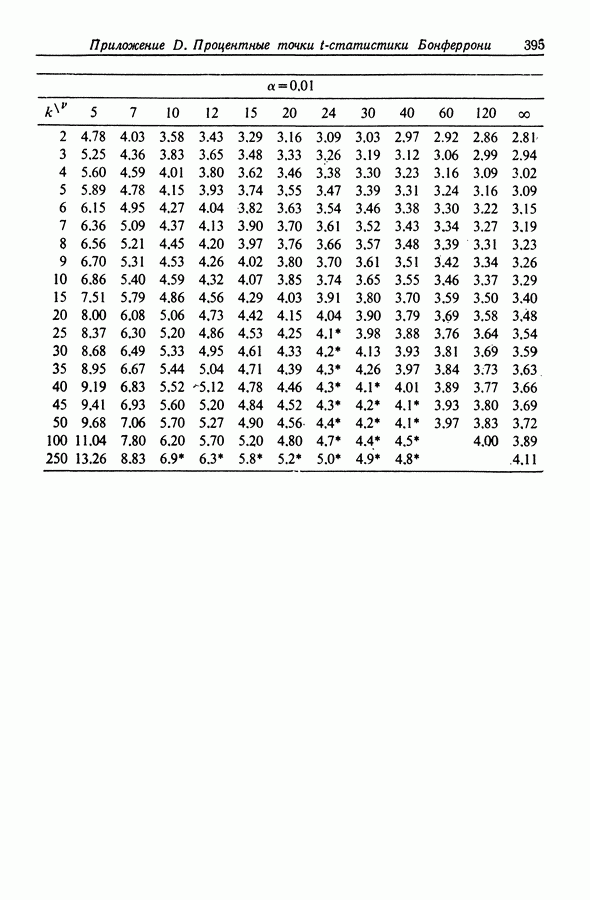
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
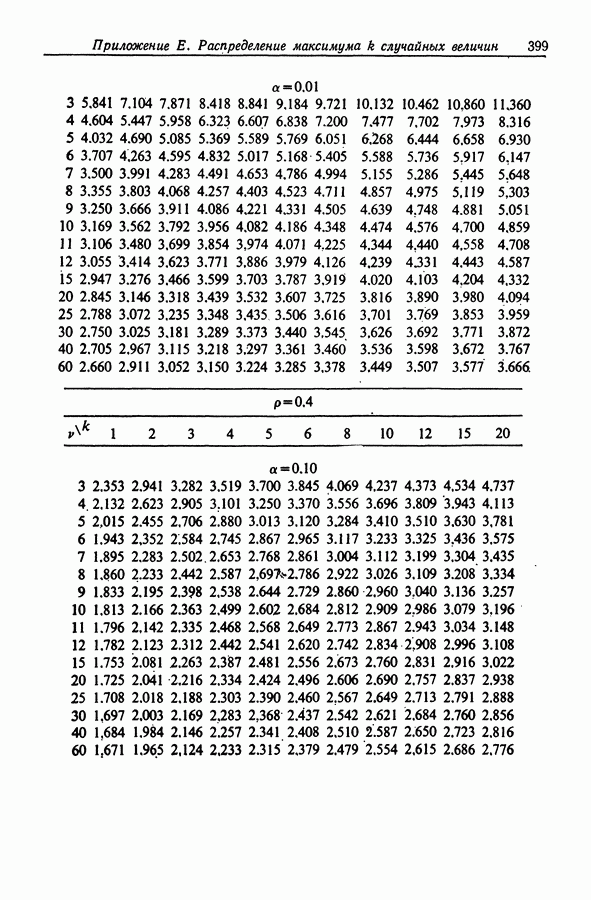
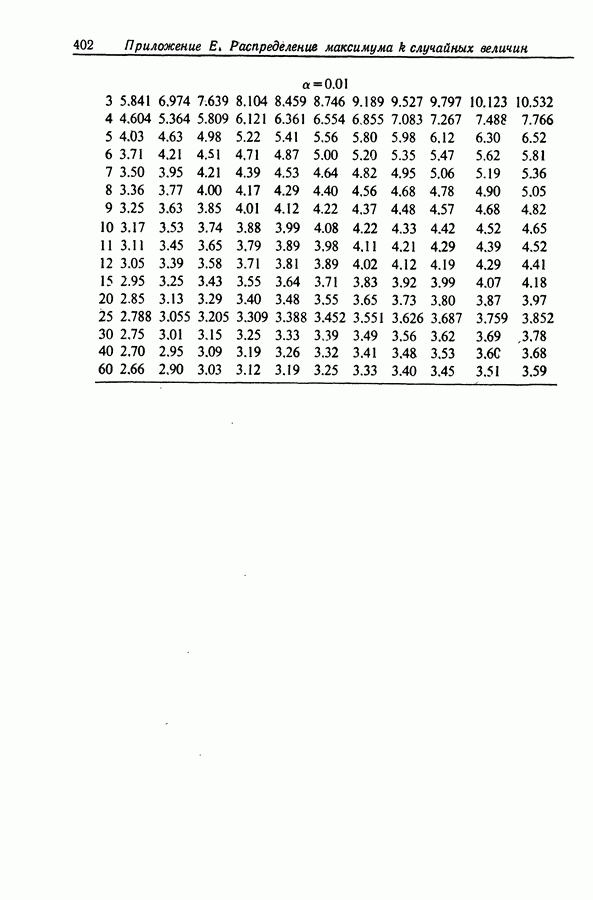
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
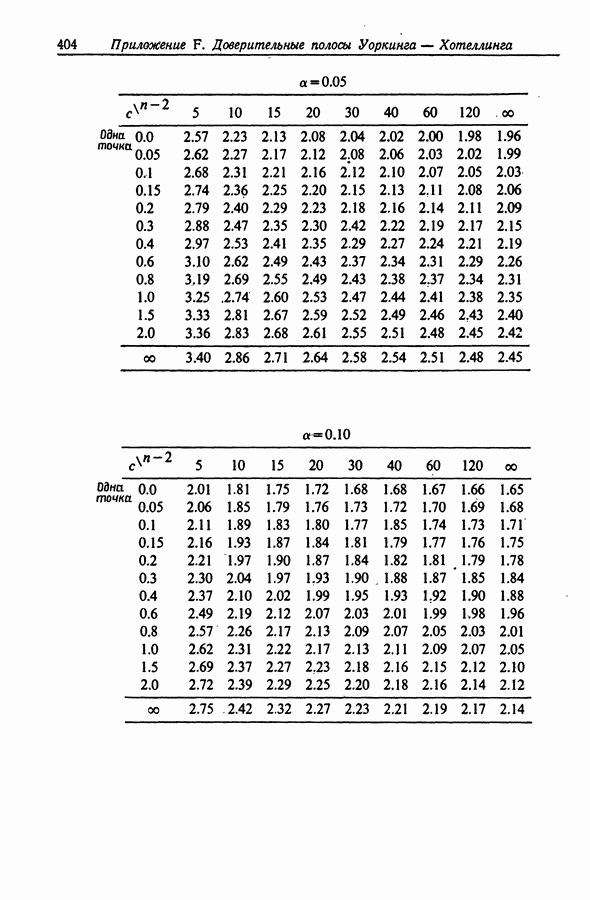
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ