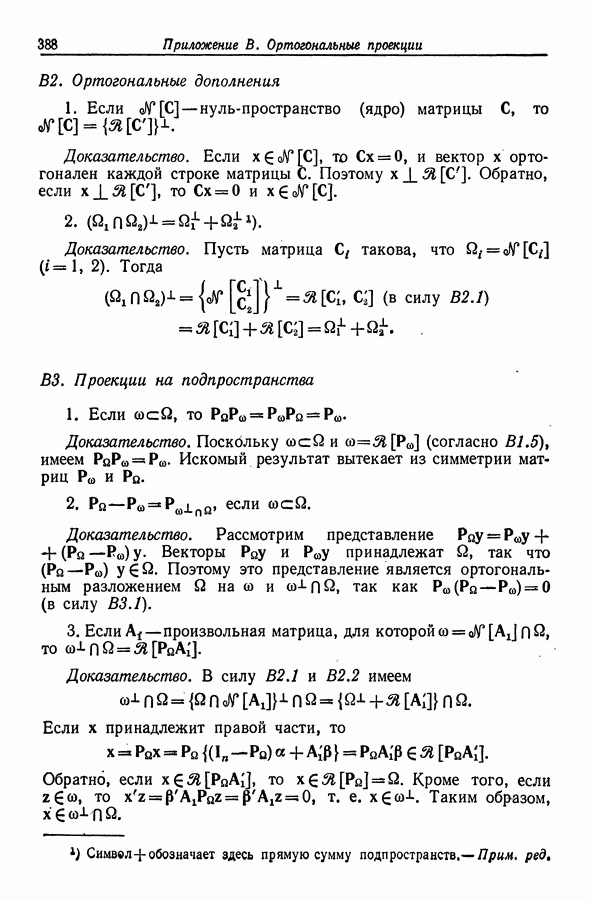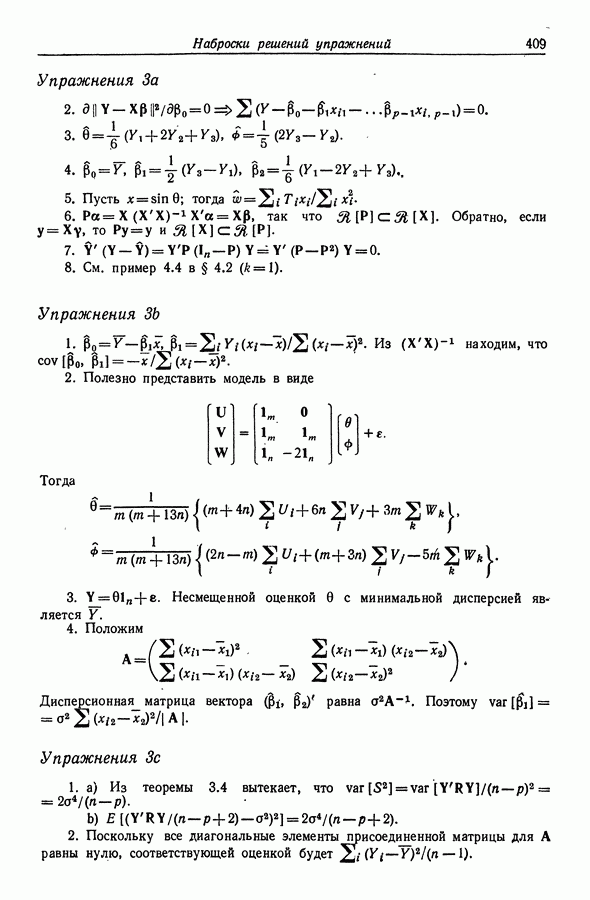| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.2.6. Предсказание для обратной задачи (дискриминация)
Пусть мы хотим произвести калибровку какого-либо прибора, скажем манометра (датчика давления), и при этом нам известно, что показания манометра являются линейной функцией от давления, а именно

или

Для калибровки манометра мы подаем на него два или более (скажем,  ) контролируемых давления
) контролируемых давления  и считываем соответствующие показания манометра
и считываем соответствующие показания манометра  По этим данным мы подбираем уравнение
По этим данным мы подбираем уравнение  которое можно использовать для оценивания (предсказания) неизвестного давления при заданном показании манометра
которое можно использовать для оценивания (предсказания) неизвестного давления при заданном показании манометра  Эта задача обратна рассмотренной в разд. 7.2.4 задаче предсказания значения
Эта задача обратна рассмотренной в разд. 7.2.4 задаче предсказания значения  при заданном значении
при заданном значении 
Естественной оценкой для  (являющейся также оценкой максимального правдоподобия) является оценка, получаемая как решение подобранного уравнения
(являющейся также оценкой максимального правдоподобия) является оценка, получаемая как решение подобранного уравнения  а именно
а именно

Правда, эта оценка оказывается смещенной, поскольку в общем случае

В то же время для х, можно построить доверительный интервал, используя метод разд. 7.2.2. Из (5.21) имеем

так что

Поскольку

то совокупность всех значений x, удовлетворяющих неравенству

где  образует 100
образует 100  -процентную доверительную область для х. Это множество, обычно называемое интервалом дискриминации, может образовывать конечный интервал, пару полупрямых и даже всю действительную прямую (см. Miller (1966, с. 118—119, рис. 2,3 и 4), Hoadley (1970)). Конечный интервал получается тогда и только тогда, когда
-процентную доверительную область для х. Это множество, обычно называемое интервалом дискриминации, может образовывать конечный интервал, пару полупрямых и даже всю действительную прямую (см. Miller (1966, с. 118—119, рис. 2,3 и 4), Hoadley (1970)). Конечный интервал получается тогда и только тогда, когда  когда
когда  -критерий для
-критерий для  оказывается значимым). При этом указанный интервал содержит оценку
оказывается значимым). При этом указанный интервал содержит оценку  и имеет вид
и имеет вид  где
где  (действительные, несовпадающие) корни уравнения
(действительные, несовпадающие) корни уравнения

(Это уравнение получается из (7.11), если положить  Если
Если  не попадает в интервал
не попадает в интервал  то доверительная область для состоит из двух полупрямых. В то же время, если уравнение (7.12) не имеет действительных корней, то доверительная область совпадает со всей действительной прямой.
то доверительная область для состоит из двух полупрямых. В то же время, если уравнение (7.12) не имеет действительных корней, то доверительная область совпадает со всей действительной прямой.
Указанная теория легко ббобщается на случай отыскания  совместных интервалов дискриминации, соответствующих
совместных интервалов дискриминации, соответствующих  различным значениям К, скажем
различным значениям К, скажем  При этом следует просто подставить
При этом следует просто подставить  в (7.12) и взять А, равным
в (7.12) и взять А, равным  или
или  в зависимости от того, используем ли мы соответственно интервалы Бонферрони, Шеффе или интервалы максимального модуля.
в зависимости от того, используем ли мы соответственно интервалы Бонферрони, Шеффе или интервалы максимального модуля.
К сожалению, этот метод не применим, если значение  не известно. Так получается, например, в случае задачи калибровки, в которой подобранная калибровочная линия используется для коррекции неограниченного числа считываемых затем показаний прибора. Так, при проведении биологических испытаний строится стандартная кривая, используемая при последующих испытаниях (дискриминациях). Если
не известно. Так получается, например, в случае задачи калибровки, в которой подобранная калибровочная линия используется для коррекции неограниченного числа считываемых затем показаний прибора. Так, при проведении биологических испытаний строится стандартная кривая, используемая при последующих испытаниях (дискриминациях). Если  велико, то к может оказаться столь большим, что пользоваться указанными интервалами дискриминации будет бессмысленно. Однако если
велико, то к может оказаться столь большим, что пользоваться указанными интервалами дискриминации будет бессмысленно. Однако если  велико или просто не известно, то можно воспользоваться двумя методами, описанными Lieberman и др. (1967). Первый метод, предложенный, по-видимому, в Miller (1966, с. 125—128), использует неравенство Бонферрони (5.5) (при
велико или просто не известно, то можно воспользоваться двумя методами, описанными Lieberman и др. (1967). Первый метод, предложенный, по-видимому, в Miller (1966, с. 125—128), использует неравенство Бонферрони (5.5) (при  ) и сочетает при заданном
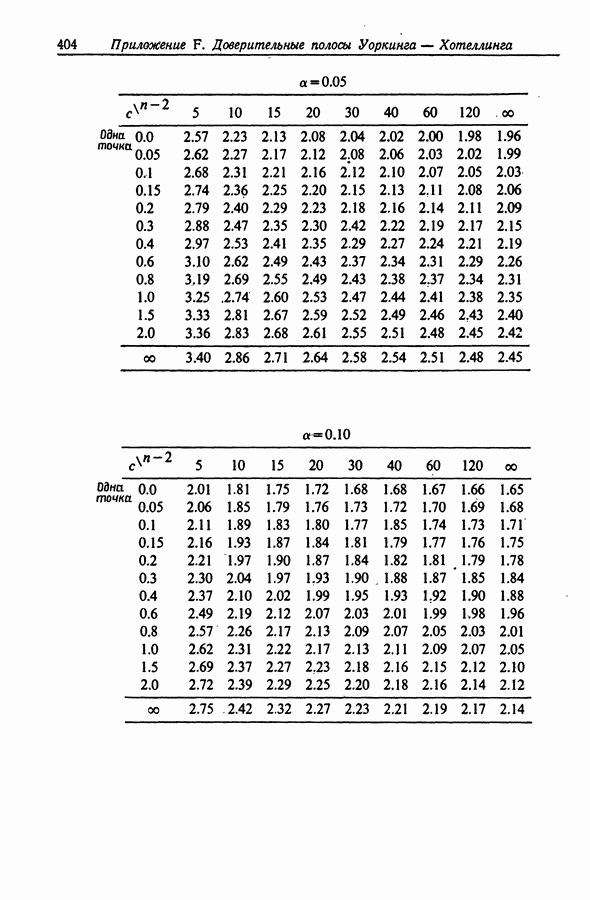
) и сочетает при заданном  доверительный интервал для с доверительной полосой Уоркинга-Хотеллинга для прямой
доверительный интервал для с доверительной полосой Уоркинга-Хотеллинга для прямой  Второй метод, по существу, использует соображения, аналогичные использованным Шеффе, и называется усиленным
Второй метод, по существу, использует соображения, аналогичные использованным Шеффе, и называется усиленным  -методом. Оба метода приводят к завышению ширины интервалов дискриминации. Lieberman и др. (1967) считают, что
-методом. Оба метода приводят к завышению ширины интервалов дискриминации. Lieberman и др. (1967) считают, что
в большинстве задач, в которых эти методы могут оказаться полезными, метод Бонферрони дает более короткие интервалы, особенно если ожидается, что последующие значения  не будут значительно отличаться от
не будут значительно отличаться от  Модификация метода Бонферрони принадлежит Oden (1973), который уточнил одно из использованных Миллером неравенств и получил более короткие интервалы.
Модификация метода Бонферрони принадлежит Oden (1973), который уточнил одно из использованных Миллером неравенств и получил более короткие интервалы.
(а) Альтернативные оценки
Мы видели уже, что оценка указанная в (7.10), является смещенной. Кроме того, она имеет неограниченную среднеквадратичную ошибку  В то же время Williams (1969) показал, что несмещенной оценки с конечной дисперсией для не существует, и поэтому он рекомендует все-таки использовать оценку
В то же время Williams (1969) показал, что несмещенной оценки с конечной дисперсией для не существует, и поэтому он рекомендует все-таки использовать оценку  учитывая, что она строится по совокупности достаточных статистик для неизвестных параметров. Альтернативный метод, основанный на использовании регрессии х на У (даже если величина х не случайна), был возрожден в работах Krutchoff (1967, 1969). При этом было произведено сравнение обычного прогноза для х, получаемого по этой "обратной" модели (обозначим его
учитывая, что она строится по совокупности достаточных статистик для неизвестных параметров. Альтернативный метод, основанный на использовании регрессии х на У (даже если величина х не случайна), был возрожден в работах Krutchoff (1967, 1969). При этом было произведено сравнение обычного прогноза для х, получаемого по этой "обратной" модели (обозначим его  ), со значением х, получаемым с использованием статистического моделирования. Однако Williams (1969) и Halperin (1970) показали, что критерий, использованный Krutchoff для сравнения указанных оценок, был неудовлетворительным. Halperin (1970) провел теоретический анализ, показывающий предпочтительность использования
), со значением х, получаемым с использованием статистического моделирования. Однако Williams (1969) и Halperin (1970) показали, что критерий, использованный Krutchoff для сравнения указанных оценок, был неудовлетворительным. Halperin (1970) провел теоретический анализ, показывающий предпочтительность использования  вместо Hoadley (1970) также рассмотрел эту задачу, но с точки зрения байесовского подхода. Он отметил следующее неудовлетворительное свойство оценку Коэффициент при
вместо Hoadley (1970) также рассмотрел эту задачу, но с точки зрения байесовского подхода. Он отметил следующее неудовлетворительное свойство оценку Коэффициент при  в (7.12) равен
в (7.12) равен

где уменьшаемое в квадратных скобках есть просто обычное F-отношение для проверки гипотезы  Поэтому, если значение
Поэтому, если значение  много больше, чем
много больше, чем  то интервал дискриминации узок, и х оценивается довольно точно. Если же F-отношение оказывается лишь едва значимым (соответствующая прямая почти горизонтальна), то оценивание становится неточным. Другими словами, информация о точности
то интервал дискриминации узок, и х оценивается довольно точно. Если же F-отношение оказывается лишь едва значимым (соответствующая прямая почти горизонтальна), то оценивание становится неточным. Другими словами, информация о точности  содержится в самих данных, так что представляется разумным придавать оценке
содержится в самих данных, так что представляется разумным придавать оценке  меньший вес, если известно, что она ненадежна. А это именно то, что
меньший вес, если известно, что она ненадежна. А это именно то, что
делает байесовская оценка. Hoadley (1970, с. 365) доказал, что

и что х является байесовской оценкой по отношению к некоторому априорному распределению  Им указан также доверительный интервал, основанный на для случая, когда это частное априорное предположение может быть подтверждено.
Им указан также доверительный интервал, основанный на для случая, когда это частное априорное предположение может быть подтверждено.
Если данные близки к некоторой прямой, то особенной разницы в оценках  при этом мало,
при этом мало,  в (7.13) велико (см. упр. 4 в конце главы).
в (7.13) велико (см. упр. 4 в конце главы).
(b) Повторные наблюдения
Пусть мы имеем  повторных наблюдений
повторных наблюдений  с выборочным средним
с выборочным средним  произведенных при неизвестном значении
произведенных при неизвестном значении  такой ситуации мы располагаем двумя оценками для
такой ситуации мы располагаем двумя оценками для  , а именно
, а именно  которые можно использовать в сочетании для построения доверительного интервала для
которые можно использовать в сочетании для построения доверительного интервала для  .
.
Следуя Graybill (1961, с. 125—127), положим 

и

то случайные величины  и взаимно независимы и
и взаимно независимы и

Поэтому

и уравнение (7.12) принимает вид

где  Заметим, что оценка
Заметим, что оценка  основанная на
основанная на  степенях свободы, имеет меньшую выборочную дисперсию по сравнению с оценкой
степенях свободы, имеет меньшую выборочную дисперсию по сравнению с оценкой  степенями свободы; кроме того,
степенями свободы; кроме того,  Эти два факта приводят к тому, что [Сох (1971)] (1) интервалы, даваемые (7.13), будут в среднем уже интервалов, даваемых (7.12), (2) коэффициент при
Эти два факта приводят к тому, что [Сох (1971)] (1) интервалы, даваемые (7.13), будут в среднем уже интервалов, даваемых (7.12), (2) коэффициент при  в (7.14) будет обычно большим, чем соответствующий коэффициент в (7.12), так что вероятность получения конечного доверительного интервала для х увеличивается, если используются повторные наблюдения
в (7.14) будет обычно большим, чем соответствующий коэффициент в (7.12), так что вероятность получения конечного доверительного интервала для х увеличивается, если используются повторные наблюдения 
В заключение упомянем еще о двух методах. Kalotay (1971) предложил структурное решение рассмотренной задачи, a Perng, Tong (1974) привели последовательную процедуру, в которой  случайная величина. Эта процедура дает правило остановки при построении для х доверительного интервала фиксированной ширины.
случайная величина. Эта процедура дает правило остановки при построении для х доверительного интервала фиксированной ширины.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
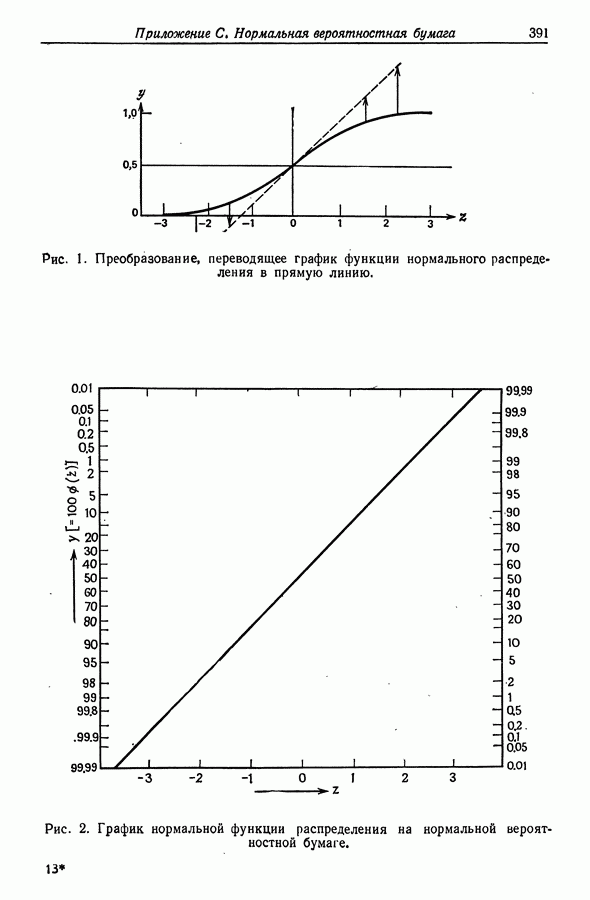
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
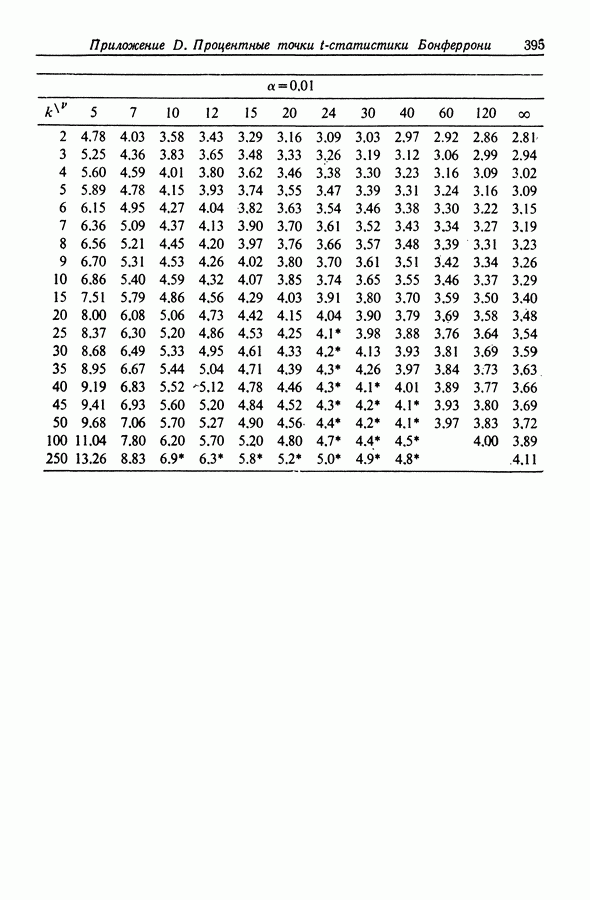
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
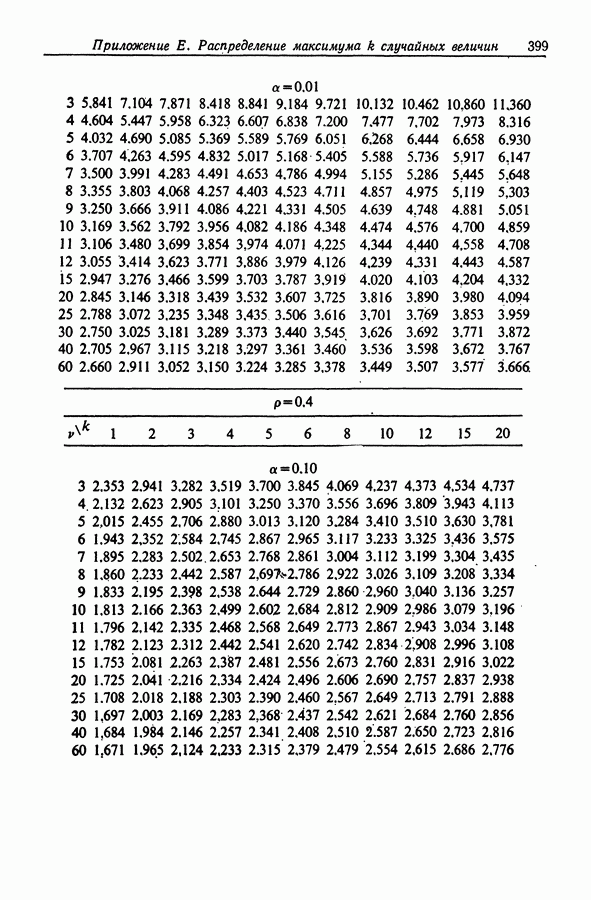
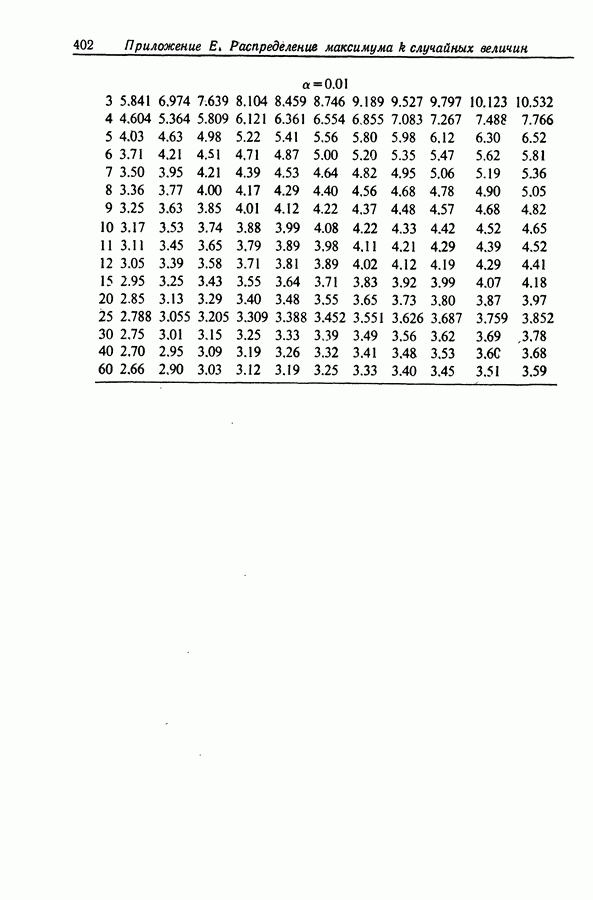
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ