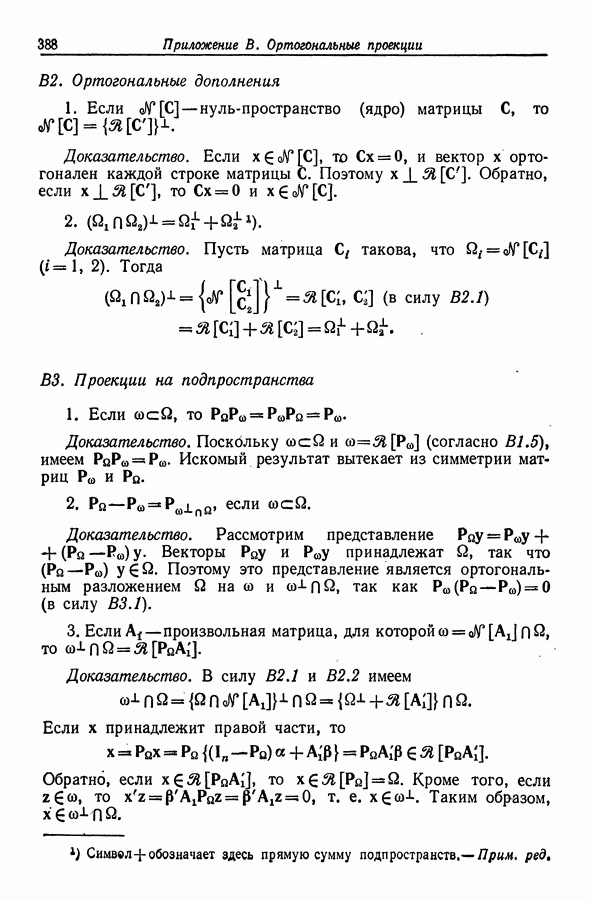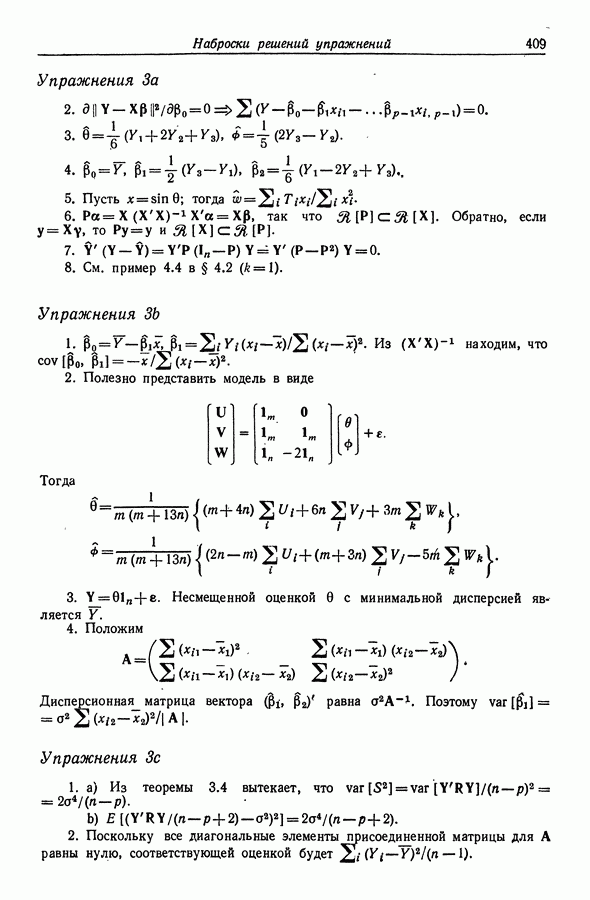| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. Линейные модели регрессии
Одна из наиболее общих задач Статистики состоит в  -вании степени связи между двумя случайными величинами (если такая связь существует). Такими парами случайных величин Могут быть, например, рост и вес, зарплата и уровень интеллекта, возраст мужа и жены в момент вступления в брак, длина и ширина листьев, температура и давление некоторого объема газа, длина металлического стержня и его температура. Если имеется
-вании степени связи между двумя случайными величинами (если такая связь существует). Такими парами случайных величин Могут быть, например, рост и вес, зарплата и уровень интеллекта, возраст мужа и жены в момент вступления в брак, длина и ширина листьев, температура и давление некоторого объема газа, длина металлического стержня и его температура. Если имеется  пар наблюдений
пар наблюдений  над такими
над такими
случайными величинами, то наблюдения можно представить точками на плоскости, получая так называемую диаграмму рассеяния. Затем можно попытаться подобрать по этим точкам некоторую гладкую кривую таким образом, чтобы они располагались как можно "ближе" к этой кривой. Ясно, что нам не следует ожидать того, что все точки диаграммы лягут на соответствующую кривую, поскольку каждая из случайных величин в рассмотренных выше примерах подвержена случайным флуктуациям в результате воздействия факторов, которыми мы не в состоянии управлять. Даже если между какими-то двумя величинами, как, например, между температурой и давлением, существует совершенно определенная связь, то на диаграмме рассеяния все же будут наблюдаться флуктуации, вызванные ошибками измерений.
Весьма часто тип эмпирической кривой определяется экспериментальными или теоретическими соображениями, как в приводимых ниже примерах.
Пример 1.1. Закон Ома утверждает, что если  -ток (в амперах), протекающий через сопротивление
-ток (в амперах), протекающий через сопротивление  (в омах),
(в омах),  напряжение (в вольтах) на этом сопротивлении, то три эти величины связаны соотношением
напряжение (в вольтах) на этом сопротивлении, то три эти величины связаны соотношением  . В прямоугольных координатах
. В прямоугольных координатах  закон Ома выражается прямой линией, проходящей через начало координат, так что подтверждением закона будет линейный характер диаграммы рассеяния. Величину
закон Ома выражается прямой линией, проходящей через начало координат, так что подтверждением закона будет линейный характер диаграммы рассеяния. Величину  можно оценить по наклону эмпирической прямой.
можно оценить по наклону эмпирической прямой.
Пример 1-2. Согласно законам механики, для удержания от соскальзывания по наклонной плоскости с углом наклона 0 тела, имеющего вес  необходимо приложить силу
необходимо приложить силу  Полагая
Полагая  мы опять получаем прямую линию, проходящую через начало координат. В этом случае наблюдаемые значения
мы опять получаем прямую линию, проходящую через начало координат. В этом случае наблюдаемые значения  будут несколько отклоняться от прямой линии из-за ошибок в измерении
будут несколько отклоняться от прямой линии из-за ошибок в измерении  и из-за наличия трения между рассматриваемым телом и плоскостью.
и из-за наличия трения между рассматриваемым телом и плоскостью.
Пример 1.3. Теоретическая  химия предсказывает, что при сохранении постоянной температуры данного количества газа его объем V и давление
химия предсказывает, что при сохранении постоянной температуры данного количества газа его объем V и давление  приблизительно удовлетворяют соотношению
приблизительно удовлетворяют соотношению  Обозначая
Обозначая  получаем
получаем 
Пример 1-4. При более тщательном проведении экспериментов оказывается, что уравнение, связывающее давление и объем, имеет вид  где
где  Однако и здесь можно добиться
Однако и здесь можно добиться
линейности уравнения связи, переходя к логарифмам в обеих частях указанного равенства:

или в соответствующих обозначениях

Поэтому значения  можно оценить по положению эмпирической прямой, выравнивающей экспериментальные данные.
можно оценить по положению эмпирической прямой, выравнивающей экспериментальные данные.
Пример 1.5. Закон обратного квадрата утверждает, что сила, с которой притягиваются друг к другу два тела, расстояние между которыми равно  задается формулой
задается формулой

где  Переходя к логарифмам, получаем соотношение
Переходя к логарифмам, получаем соотношение

По экспериментальным данным можно оценить значение  и проверить гипотезу о том, что
и проверить гипотезу о том, что 
Пример 1.6. Эксперименты показывают, что металлический стержень при нагревании удлиняется и это удлинение пропорционально повышению температуры. Если взять пару идентичных стержней и приложить их концами друг к другу, то приращение их суммарной длины ровно в два раза превысит приращение длины одного стержня, так что удлинение стержня пропорционально его исходной длине: Мы приходим к рассмотрению модели прямой линии  где
где  -длина стержня при температуре
-длина стержня при температуре  (измеренной от соответствующего начала координат), а
(измеренной от соответствующего начала координат), а  -так называемый коэффициент линейного температурного расширения. Для более точных расчетов предлагается квадратичная модель
-так называемый коэффициент линейного температурного расширения. Для более точных расчетов предлагается квадратичная модель

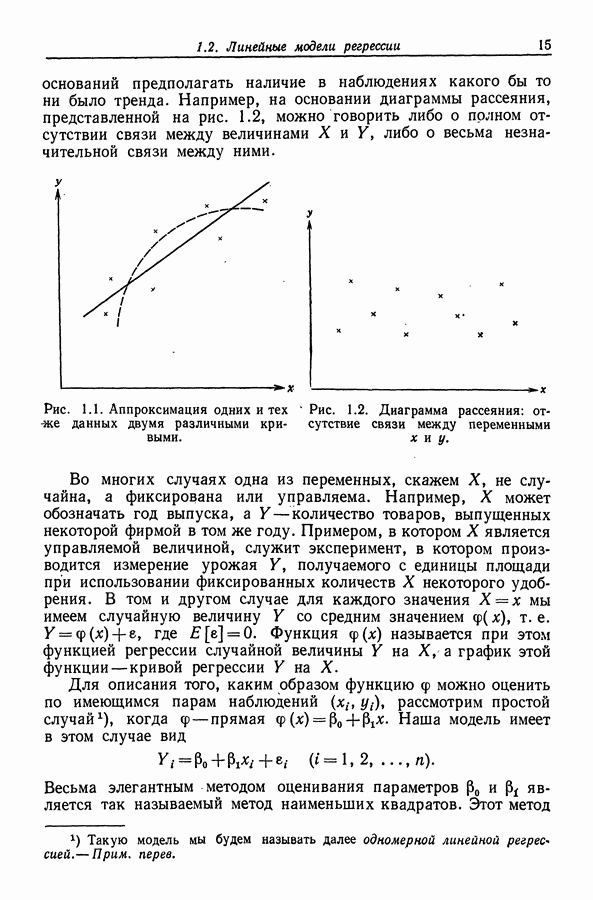
Если в нашем распоряжении нет никаких теоретических или экспериментальных соображений, которые могли бы помочь в выборе типа эмпирической кривой, то такой выбор иногда бывает осуществить довольно трудно, как это показывает рис. 1.1. Здесь прямая линия представляется не, менее удобной для использования, чем любая другая, поскольку она описывается малым числом параметров, хотя очевидна необходимость иметь какую-то. меру, характеризующую качество подбора кривой, чтобы можно было сравнивать различные эмпирические кривые. Иногда точки на диаграмме рассеяния располагаются таким образом, что не наблюдается никакого их группирования, и соответственно нет никаких
оснований предполагать наличие в наблюдениях какого бы то ни было тренда. Например, на основании диаграммы рассеяния, представленной на рис. 1.2, можно говорить либо о полном отсутствии связи между величинами  либо о весьма незначительной связи между ними.
либо о весьма незначительной связи между ними.

Рис. 1.1. Аппроксимация одних и тех же данных двумя различными кривыми.

Рис. 1.2. Диаграмма рассеяния: отсутствие связи между переменными X и у.
Во многих случаях одна из переменных, скажем X, не случайна, а фиксирована или управляема. Например, X может обозначать год выпуска,  - количество товаров, выпущенных некоторой фирмой в том же году. Примером, в котором X является управляемой величиной, служит эксперимент, в котором производится измерение урожая
- количество товаров, выпущенных некоторой фирмой в том же году. Примером, в котором X является управляемой величиной, служит эксперимент, в котором производится измерение урожая  получаемого с единицы площади при использовании фиксированных количеств X некоторого удобрения. В том и другом случае для каждого значения
получаемого с единицы площади при использовании фиксированных количеств X некоторого удобрения. В том и другом случае для каждого значения  мы имеем случайную величину
мы имеем случайную величину  со средним значением
со средним значением  т.е.
т.е.  где
где  Функция
Функция  называется при этом функцией регрессии случайной величины
называется при этом функцией регрессии случайной величины  на X, а график этой функции — кривой регрессии
на X, а график этой функции — кривой регрессии  на
на 
Для описания того, каким образом функцию  можно оценить по имеющимся парам наблюдений
можно оценить по имеющимся парам наблюдений  рассмотрим простой случай, когда
рассмотрим простой случай, когда  прямая
прямая  Наша модель имеет в этом случае вид
Наша модель имеет в этом случае вид

Весьма элегантным методом оценивания параметров  и является так называемый метод наименьших квадратов. Этот метод
и является так называемый метод наименьших квадратов. Этот метод
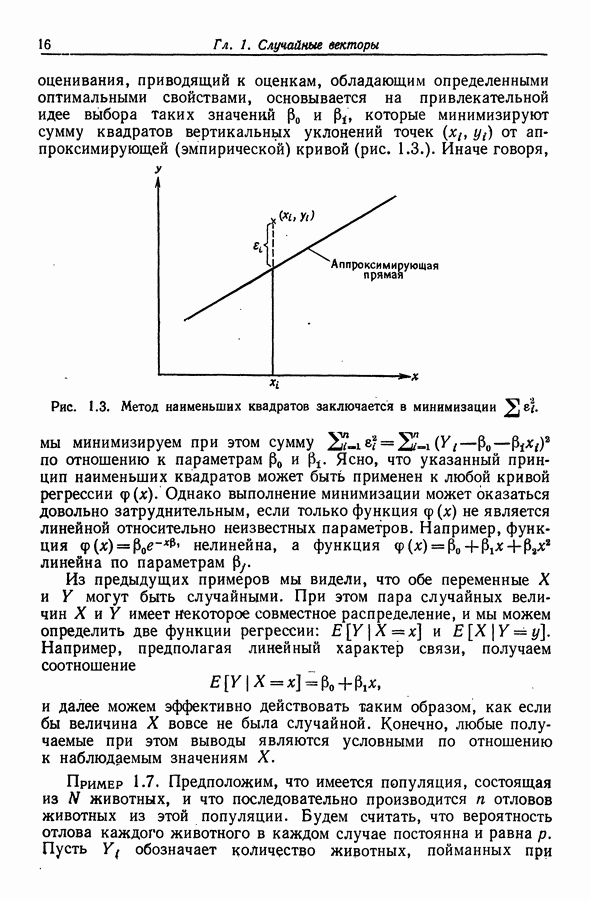
оценивания, приводящий к оценкам, обладающим определенными оптимальными свойствами, основывается на привлекательной идее выбора таких значений  и которые минимизируют сумму квадратов вертикальных уклонений точек
и которые минимизируют сумму квадратов вертикальных уклонений точек  от аппроксимирующей (эмпирической) кривой
от аппроксимирующей (эмпирической) кривой  Иначе говоря, мы минимизируем при этом сумму
Иначе говоря, мы минимизируем при этом сумму  по отношению к параметрам
по отношению к параметрам 

Рис. 1.3. Метод наименьших квадратов заключается в минимизации 
Ясно, что указанный принцип наименьших квадратов может быть применен к любой кривой регрессии  Однако выполнение минимизации может оказаться довольно затруднительным, если только функция
Однако выполнение минимизации может оказаться довольно затруднительным, если только функция  не является линейной относительно неизвестных параметров. Например, функция
не является линейной относительно неизвестных параметров. Например, функция  нелинейна, а функция
нелинейна, а функция  линейна по параметрам
линейна по параметрам 
Из предыдущих примеров мы видели, что обе переменные  могут быть случайными. При этом пара случайных величин
могут быть случайными. При этом пара случайных величин  имеет некоторое совместное распределение, и мы можем определить две функции регрессии:
имеет некоторое совместное распределение, и мы можем определить две функции регрессии:  Например, предполагая линейный характер связи, получаем соотношение
Например, предполагая линейный характер связи, получаем соотношение

и далее можем эффективно действовать таким образом, как если бы величина X вовсе не была случайной. Конечно, любые получаемые при этом выводы являются условными по отношению к наблюдаемым значениям 
Пример 1.7. Предположим, что имеется популяция, состоящая из  животных, и что последовательно производится
животных, и что последовательно производится  отловов животных из этой популяции. Будем считать, что вероятность отлова каждого животного в каждом случае постоянна и равна
отловов животных из этой популяции. Будем считать, что вероятность отлова каждого животного в каждом случае постоянна и равна  Пусть
Пусть  обозначает количество животных, пойманных при
обозначает количество животных, пойманных при
 отлове,
отлове,  количество животных, пойманных перед
количество животных, пойманных перед  отловом. Используя биномиальную модель, получаем соотношение
отловом. Используя биномиальную модель, получаем соотношение

опять выражающее линейную зависимость.
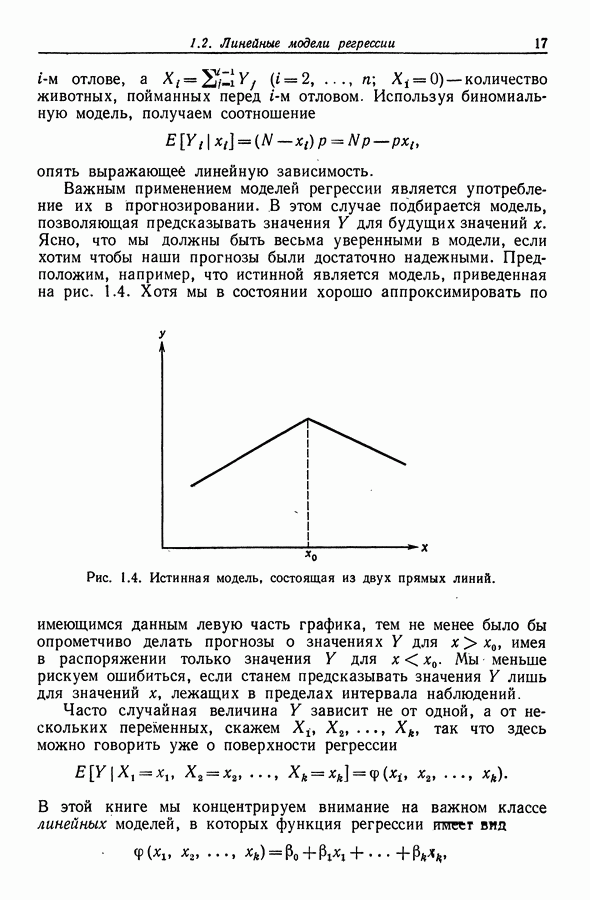
Важным применением моделей регрессии является употребление их в прогнозировании. В этом случае подбирается модель, позволяющая предсказывать значения  для будущих значений х. Ясно, что мы должны быть весьма уверенными в модели, если хотим чтобы наши прогнозы были достаточно надежными. Предположим, например, что истинной является модель, приведенная на рис. 1.4.
для будущих значений х. Ясно, что мы должны быть весьма уверенными в модели, если хотим чтобы наши прогнозы были достаточно надежными. Предположим, например, что истинной является модель, приведенная на рис. 1.4.

Рис. 1.4. Истинная модель, состоящая из двух прямых линий.
Хотя мы в состоянии хорошо аппроксимировать по имеющимся данным левую часть графика, тем не менее было бы опрометчиво делать прогнозы о значениях  для
для  имея в распоряжении только значения
имея в распоряжении только значения  для
для  Мы меньше рискуем ошибиться, если станем предсказывать значения У лишь для значений лежащих в пределах интервала наблюдений.
Мы меньше рискуем ошибиться, если станем предсказывать значения У лишь для значений лежащих в пределах интервала наблюдений.
Часто случайная величина  зависит не от одной, а от нескольких переменных, скажем
зависит не от одной, а от нескольких переменных, скажем  так что здесь можно говорить уже о поверхности регрессии
так что здесь можно говорить уже о поверхности регрессии

В этой книге мы концентрируем внимание на важном классе линейных моделей, в которых функция регрессии имеет вид

т. е. линейна по параметрам  Выбор для рассмотрения только линейных моделей вовсе не столь ограничителен, как это может показаться. Например, многие функции нескольких переменных являются приблизительно линейными в достаточно малых областях или могут быть приведены к линейным с помощью надлежащего преобразования, как мы уже видели выше. Кроме того, сами
Выбор для рассмотрения только линейных моделей вовсе не столь ограничителен, как это может показаться. Например, многие функции нескольких переменных являются приблизительно линейными в достаточно малых областях или могут быть приведены к линейным с помощью надлежащего преобразования, как мы уже видели выше. Кроме того, сами  могут быть функциями от каких-то других переменных
могут быть функциями от каких-то других переменных  например
например  или
или  соотношение приводит к полиномиальной регрессии). Можно включить в наше рассмотрение также и "категоризованные" модели, используя фиктивные переменные
соотношение приводит к полиномиальной регрессии). Можно включить в наше рассмотрение также и "категоризованные" модели, используя фиктивные переменные  . Предположим, например, что мы хотим сравнить средние двух популяций, скажем
. Предположим, например, что мы хотим сравнить средние двух популяций, скажем  Можно объединить при этом данные в одну модель
Можно объединить при этом данные в одну модель

где  если
если  является наблюдением переменной
является наблюдением переменной  в противном случае
в противном случае  Приблизительно описав природу линейных моделей, приведем теперь краткую сводку вопросов, рассмотренных в этой книге.
Приблизительно описав природу линейных моделей, приведем теперь краткую сводку вопросов, рассмотренных в этой книге.
После того как произведен выбор модели, ее неизвестные параметры  можно оценить, используя метод наименьших квадратов. Этот метод лучше всего описывается геометрически, с использованием теории матриц. Теоретические аспекты метода приведены в гл. 3, а вычислительные алгоритмы описаны в гл. И. Имея совместное распределение величин
можно оценить, используя метод наименьших квадратов. Этот метод лучше всего описывается геометрически, с использованием теории матриц. Теоретические аспекты метода приведены в гл. 3, а вычислительные алгоритмы описаны в гл. И. Имея совместное распределение величин  можно исследовать статистические свойства соответствующих оценок наименьших квадратов.
можно исследовать статистические свойства соответствующих оценок наименьших квадратов.
Следующей задачей, рассмотренной в книге, является задача проверки гипотез. Например, нас могли бы заинтересовать задачи проверки гипотез в примере  в примере 1.6 или
в примере 1.6 или  в (1.1). Все эти задачи являются частными случаями задачи проверки гипотезы
в (1.1). Все эти задачи являются частными случаями задачи проверки гипотезы  где
где  некоторая линейная комбинация параметров
некоторая линейная комбинация параметров  . В общем случае нас интересует проверка значений целой совокупности линейнцх комбинаций, а именно проверка гипотезы
. В общем случае нас интересует проверка значений целой совокупности линейнцх комбинаций, а именно проверка гипотезы  Эта задача обсуждается в гл. 4, а приложения ее к моделям типа (1.1) описаны в гл. 9 и 10.
Эта задача обсуждается в гл. 4, а приложения ее к моделям типа (1.1) описаны в гл. 9 и 10.
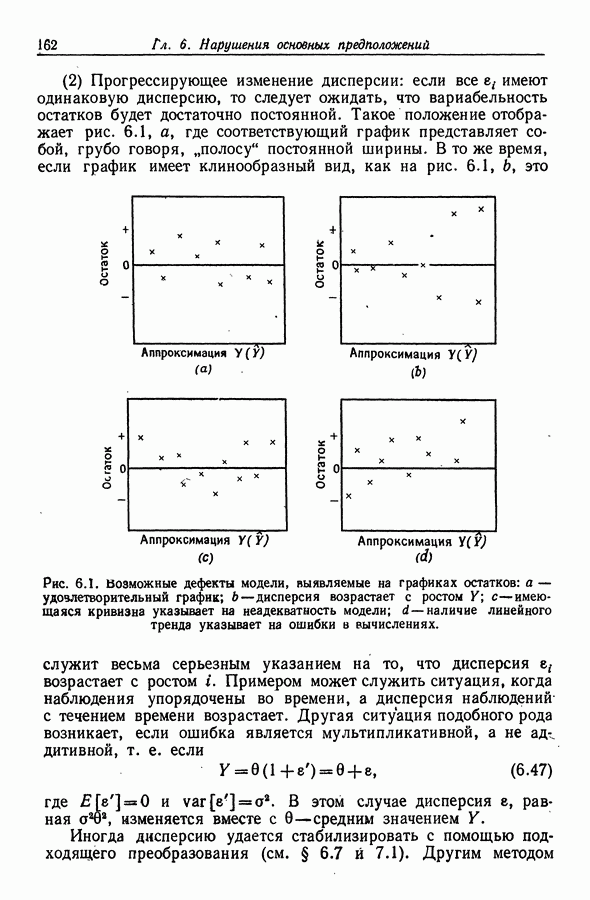
Помимо проверки гипотез, мы можем пожелать построить доверительные интервалы для тех или иных параметров или для линейных комбинаций параметров либо получить доверительные интервалы для значений будущих наблюдений. Такие построения проводятся в гл. 5. В весьма важной гл. 6 рассматриваются предположения о характере распределений случайных составляющих  лежащие в основе развитой к этому моменту теории. Описаны критерии и графики, позволяющие проверять выполнение соответствующих предположений.
лежащие в основе развитой к этому моменту теории. Описаны критерии и графики, позволяющие проверять выполнение соответствующих предположений.
В связи с важностью одномерной линейной регрессии, она подробно обсуждается в гл. 7. В гл. 8 рассмотрена полиномиальная регрессия, в которой возникают свои собственные проблемы.
До сих пор мы обычно предполагали, что подлежащая изучению модель уже выбрана. Однако во многих практических ситуациях возникает необходимость решить, какие из возможных переменных  следует включать в модель.. Этому важному вопросу посвящена гл. 12.
следует включать в модель.. Этому важному вопросу посвящена гл. 12.
Остаток настоящей главы и гл. 2, в которой рассматривается многомерное нормальное распределение, призваны снабдить читателя некоторыми теоретическими сведениями, необходимыми для чтения остального материала.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
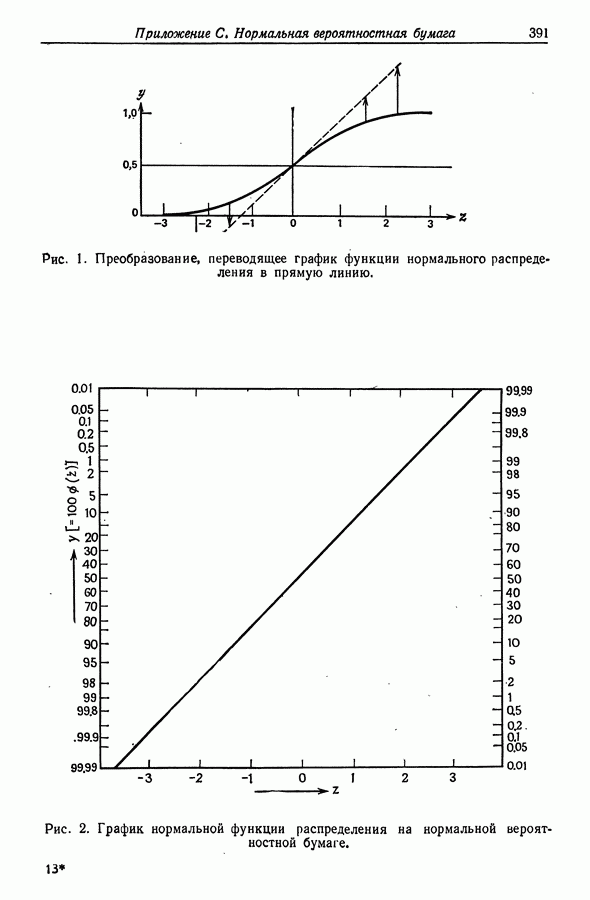
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
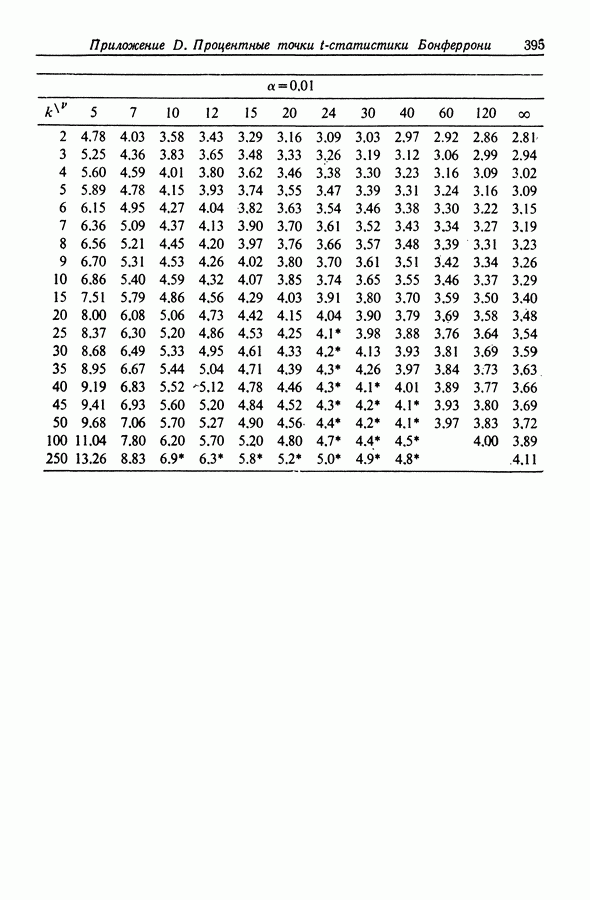
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
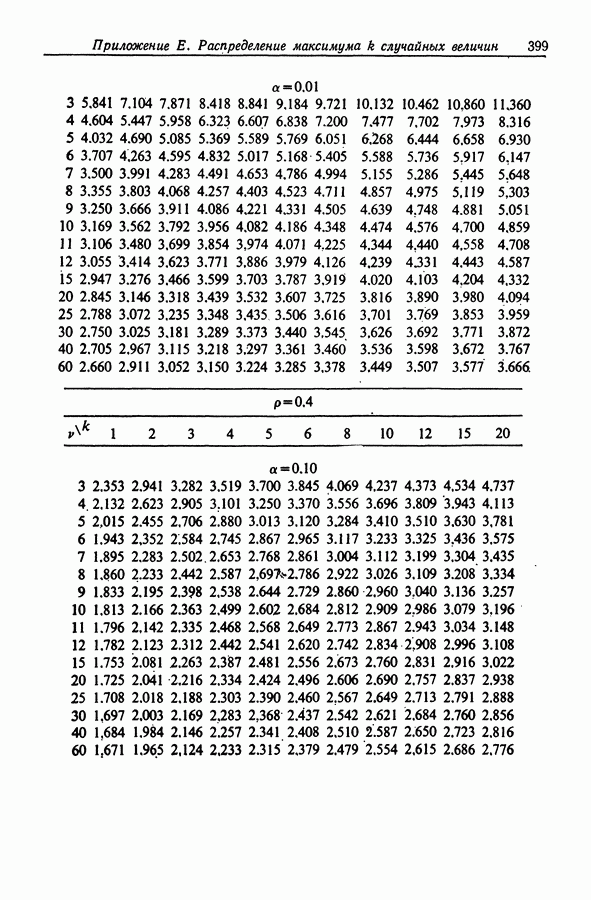
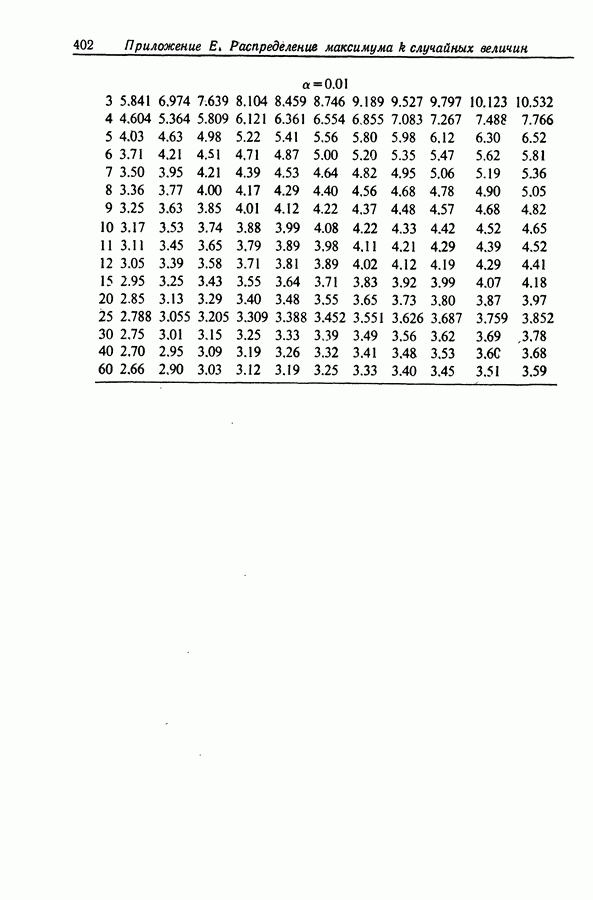
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
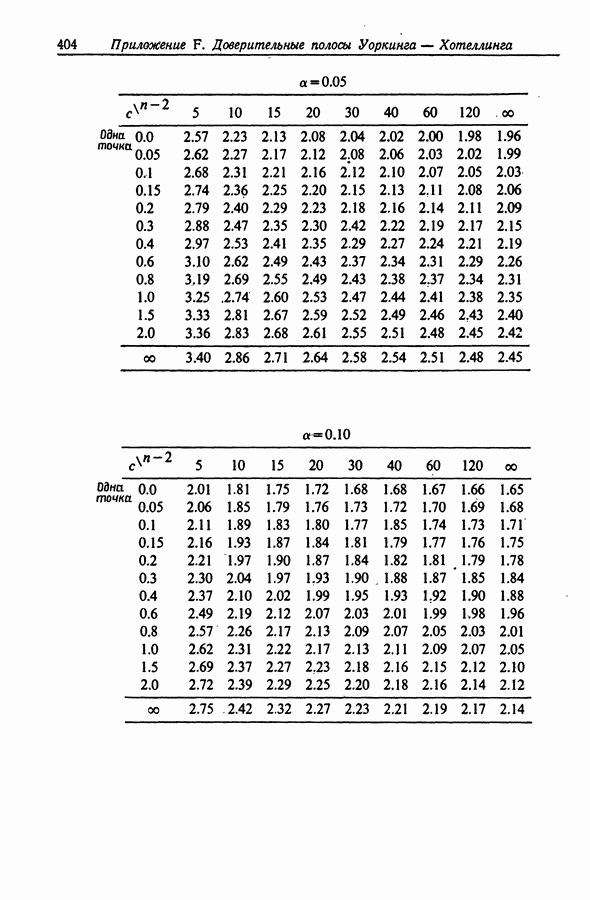
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ