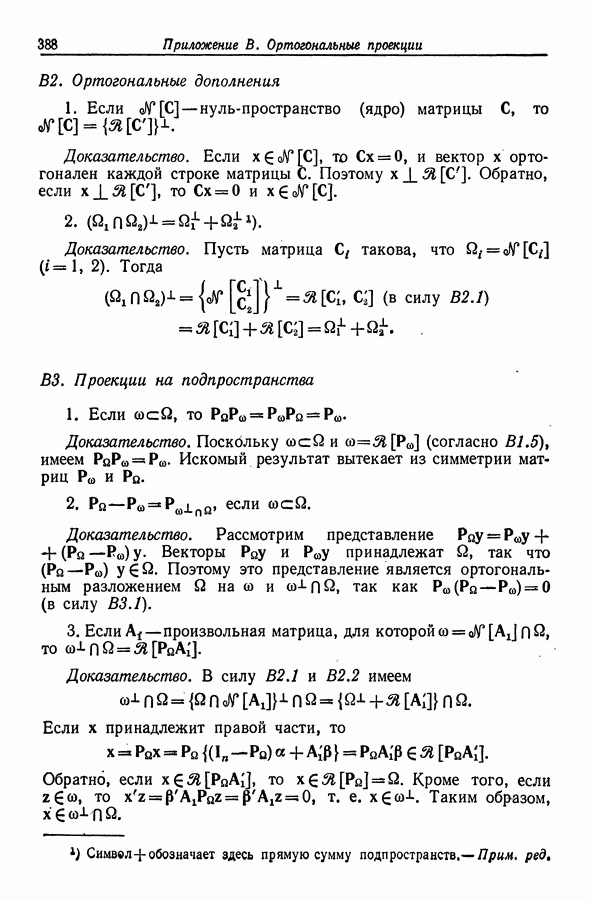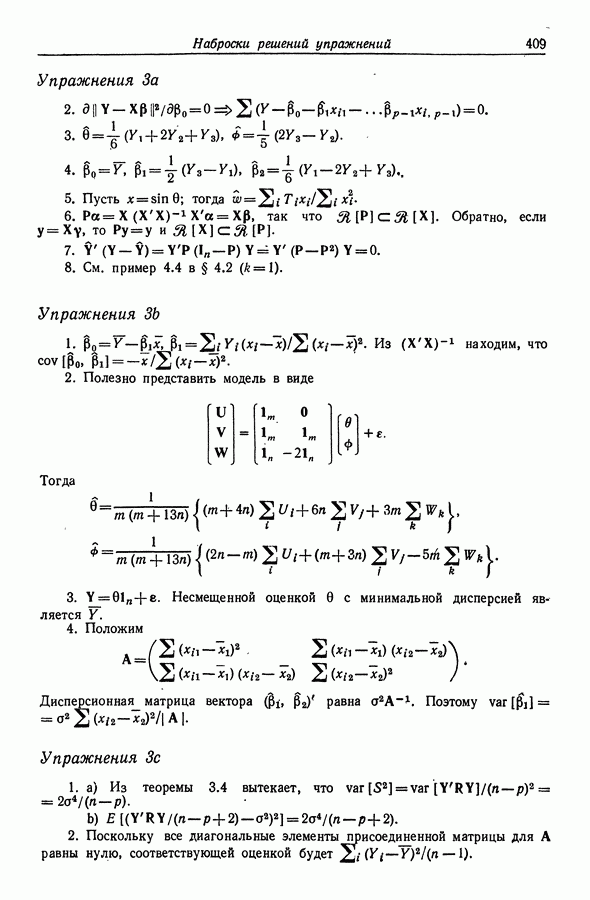| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
12.4. Пошаговая регрессия
12.4.1. Описание метода
Метод пошаговой регрессии состоит в том, что на каждом шаге производится либо включение в модель, либо исключение из модели какого-то одного регрессора. В этой процедуре [Efroymson (1960)] мы имеем два F-уровня - назовем  На каждом шаге один из регрессоров, скажем
На каждом шаге один из регрессоров, скажем  исключается, если при его удалении RSS увеличивается на величину, не большую, чем умноженное на
исключается, если при его удалении RSS увеличивается на величину, не большую, чем умноженное на  значение средней остаточной суммы квадратов
значение средней остаточной суммы квадратов  Другими словами,
Другими словами,  -регрессор
-регрессор  -исключается на данном шаге, если
-исключается на данном шаге, если  -отношение для проверки гипотезы
-отношение для проверки гипотезы  в используемой в этот момент модели регрессии не превышает значения
в используемой в этот момент модели регрессии не превышает значения  Если такому условию удовлетворяет несколько регрессоров, то выбирается тот из них, для которого увеличение RSS оказывается наименьшим (это равносильно наименьшему
Если такому условию удовлетворяет несколько регрессоров, то выбирается тот из них, для которого увеличение RSS оказывается наименьшим (это равносильно наименьшему  -отношению). Если указанному условию не удовлетворяет ни один из регрессоров, то в модель включают регрессор, скажем
-отношению). Если указанному условию не удовлетворяет ни один из регрессоров, то в модель включают регрессор, скажем  введение которого
введение которого
уменьшает. RSS на величину, не меньшую, чем умноженное на  значение средней остаточной суммы квадратов, подсчитанной после включения
значение средней остаточной суммы квадратов, подсчитанной после включения  в модель. Иначе говоря, регрессор
в модель. Иначе говоря, регрессор  включается на данном шаге в модель, если
включается на данном шаге в модель, если  -отношение для проверки гипотезы
-отношение для проверки гипотезы  в модели, полученной добавлением этого регрессора к модели, рассматриваемой на данном шаге, оказывается не меньшим, чем
в модели, полученной добавлением этого регрессора к модели, рассматриваемой на данном шаге, оказывается не меньшим, чем  И опять, если такому условию удовлетворяет несколько регрессоров, то в модель включается тот из них, который обеспечивает наибольшее уменьшение RSS (или, что равносильно, наибольшее
И опять, если такому условию удовлетворяет несколько регрессоров, то в модель включается тот из них, который обеспечивает наибольшее уменьшение RSS (или, что равносильно, наибольшее  -отношение). Процедура начинается с того, что мы подбираем
-отношение). Процедура начинается с того, что мы подбираем  а затем пытаемся ввести в модель какой-нибудь регрессор.
а затем пытаемся ввести в модель какой-нибудь регрессор.
К сожалению, эта процедура приводит к единственному подмножеству и не предлагает альтернативных хороших подмножеств.
12.4.2. Использование выметания
Для введения в модель или выведения из нее какого-либо регрессора можно использовать метод выметания, описанный в разд. 12.4.2. Здесь выметание применяется к расширенной матрице

где  корреляционная матрица для всех К регрессоров. Если вымести
корреляционная матрица для всех К регрессоров. Если вымести  по произвольному подмножеству ее первых К ведущих элементов, то мы получим новую матрицу
по произвольному подмножеству ее первых К ведущих элементов, то мы получим новую матрицу

где матрица В, вектор с и число  суть не что иное, как матрица, обратная корреляционной матрице, шкалированный вектор коэффициентов регрессии а и значение
суть не что иное, как матрица, обратная корреляционной матрице, шкалированный вектор коэффициентов регрессии а и значение  соответствующие регрессорам, входящим теперь в уравнение. После каждого шага мы вычисляем
соответствующие регрессорам, входящим теперь в уравнение. После каждого шага мы вычисляем  для каждого
для каждого  большего нижнего допустимого значения. Контролируя величину
большего нижнего допустимого значения. Контролируя величину  мы тем самым избегаем включения в модель регрессора, почти линейно зависящего от регрессоров, уже включенных в модель. Элементы вектора
мы тем самым избегаем включения в модель регрессора, почти линейно зависящего от регрессоров, уже включенных в модель. Элементы вектора  соответствующие регрессорам, не содержащимся в уравнении, равны соответствующим элементам вектора с, а остальные элементы векторов
соответствующие регрессорам, не содержащимся в уравнении, равны соответствующим элементам вектора с, а остальные элементы векторов  и с суть соответственно —а и а. Таким образом, если регрессор
и с суть соответственно —а и а. Таким образом, если регрессор  входит в уравнение регрессии, то величина
входит в уравнение регрессии, то величина  равна
равна  (или в обозначениях соотношения
(или в обозначениях соотношения
(11.51) из разд.  и отрицательна, а если регрессор
и отрицательна, а если регрессор  не входит в уравнение, то величина
не входит в уравнение, то величина  равна
равна  и положительна. Для определения того, нужно ли исключать из уравнения какой-нибудь из регрессоров, и если да, то какой именно, мы находим минимальное значение
и положительна. Для определения того, нужно ли исключать из уравнения какой-нибудь из регрессоров, и если да, то какой именно, мы находим минимальное значение  по всем скажем
по всем скажем  и исключаем регрессор, соответствующий
и исключаем регрессор, соответствующий  если (ср. с (11.51) при
если (ср. с (11.51) при 

где

Подобным же образом мы определяем, какой из регрессоров следует включить в модель и нужно ли вообще это делать. Для этого мы находим максимальное значение  по всем
по всем  скажем
скажем  и если
и если

то вводим в модель регрессор, соответствующий  На каждом шаге мы стараемся не исключать переменную, которая была только что введена в модель, и не включать переменную, которая только что была отброшена. Это будет обеспечиваться автоматически, если выбрать
На каждом шаге мы стараемся не исключать переменную, которая была только что введена в модель, и не включать переменную, которая только что была отброшена. Это будет обеспечиваться автоматически, если выбрать 
В оригинальном описании приведенного метода Efroymson (1960) рассматривает выметание матрицы

где  есть
есть  -матрица, состоящая из нулей. На каждом этапе выметания преобразованную матрицу
-матрица, состоящая из нулей. На каждом этапе выметания преобразованную матрицу  можно разбить точно таким же образом, а именно
можно разбить точно таким же образом, а именно

где с точностью до ошибок округления  . В его методе ведущие элементы матриц
. В его методе ведущие элементы матриц  выметаются только по одному разу. Выметание
выметаются только по одному разу. Выметание  ведущего элемента матрицы В включает в модель переменную
ведущего элемента матрицы В включает в модель переменную  а выметание ненулевого ведущего элемента матрицы
а выметание ненулевого ведущего элемента матрицы  скажем
скажем  исключает из модели переменную
исключает из модели переменную  На каждом шаге вектор
На каждом шаге вектор  содержит шкалированные коэффициенты регрессии а модели, оцененной к этому моменту, а
содержит шкалированные коэффициенты регрессии а модели, оцененной к этому моменту, а
остальные его элементы равны нулю. Матрица  также состоит из нулей и из матрицы, обратной к блоку матрицы
также состоит из нулей и из матрицы, обратной к блоку матрицы  соответствующему регрессорам, находящимся в рассматриваемой в этот момент модели. Таким образом,
соответствующему регрессорам, находящимся в рассматриваемой в этот момент модели. Таким образом,  и
и  содержат просто "полезные" части вектора с и матрицы В, незашумленные другими ненулевыми элементами.
содержат просто "полезные" части вектора с и матрицы В, незашумленные другими ненулевыми элементами.
Поскольку с точностью до знака матрица  симметрична, нам достаточно работать только с верхней треугольной матрицей, что сокращает объем вычислений и требуемую память. Вгеаих (1968) приводит соответствующий алгоритм, использующий метод симметричного выметания, описанный в разд. 12.2.2. По его утверждению, для этой модификации можно составить программу, которая в состоянии работать примерно с
симметрична, нам достаточно работать только с верхней треугольной матрицей, что сокращает объем вычислений и требуемую память. Вгеаих (1968) приводит соответствующий алгоритм, использующий метод симметричного выметания, описанный в разд. 12.2.2. По его утверждению, для этой модификации можно составить программу, которая в состоянии работать примерно с  переменными и требует менее
переменными и требует менее  слов памяти, тогда как обычная процедура, использующая матрицу
слов памяти, тогда как обычная процедура, использующая матрицу  требовала бы при этом более
требовала бы при этом более  слов памяти.
слов памяти.
12.4.3. Метод исключения Гаусса-Жордана
Вместо чвыметания можно использовать метод исключения Жордана, описанный ближе к концу разд. 11.2.1, в котором ведущий элемент нормируется (приводится шкалированием к единице), а остальные элементы этого столбца обращаются в нуль. Этот метод можно применить к матрице  в (12.12), так что при этом некоторая заданная подматрица матрицы
в (12.12), так что при этом некоторая заданная подматрица матрицы  приведется к единичной в матрице В (соотношение (12.13)), а обратная к ней матрица появится в
приведется к единичной в матрице В (соотношение (12.13)), а обратная к ней матрица появится в  (и в
(и в  . В отличие от метода выметания, который обращает подматрицу на своем месте, матрица В уже не содержит ненулевой части матрицы
. В отличие от метода выметания, который обращает подматрицу на своем месте, матрица В уже не содержит ненулевой части матрицы  Вектор
Вектор  также не содержит уже вектора —а шкалированных коэффициентов регрессии. Это означает, что
также не содержит уже вектора —а шкалированных коэффициентов регрессии. Это означает, что  представляет теперь максимальное значение отношения
представляет теперь максимальное значение отношения  по всем
по всем  не включенным в модель, в то время как
не включенным в модель, в то время как  является минимальным значением отношения
является минимальным значением отношения  по всем
по всем  (т. е. по всем
(т. е. по всем  содержащимся в модели). Для включения в модель, скажем, регрессора
содержащимся в модели). Для включения в модель, скажем, регрессора  в качестве ведущего используют элемент
в качестве ведущего используют элемент  который делают равным единице. Для исключения же из Модели, например, регрессора
который делают равным единице. Для исключения же из Модели, например, регрессора  в качестве ведущего берется элемент
в качестве ведущего берется элемент  (а не
(а не  поскольку мы в действительности хотим обратить процедуру Жордана для этой переменной.
поскольку мы в действительности хотим обратить процедуру Жордана для этой переменной.
Указанная выше модификация метода Efroymson (1960) довольно подробно описана в работе Draper, Smith (1966, разд. 6.8). Используя данные Хальда  они приходят в результате к модели
они приходят в результате к модели  которая совпадает с моделью, полученной различными методами в разд. 12.2.3. Основные шаги их вычислений таковы:
которая совпадает с моделью, полученной различными методами в разд. 12.2.3. Основные шаги их вычислений таковы:
(1) Проверка на исключение: исключать здесь нечего.
Проверка на включение новой переменной: 
3, 4) равен  и значение
и значение  превышено, так что в модель включается переменная
превышено, так что в модель включается переменная 
(2) Проверка на исключение: исключать нечего, так как текущая модель содержит только одну переменную, а она только что была введена в модель.
Проверка на включение новой переменной:  3) равен
3) равен  и значение превышено, так что в модель включается переменная
и значение превышено, так что в модель включается переменная 
(3) Проверка на исключение: текущая модель  ; исключать можно только переменную
; исключать можно только переменную  так как
так как  только что включена в модель, однако значение
только что включена в модель, однако значение  превышено, так что
превышено, так что  остается в модели.
остается в модели.
Проверка на включение:  равен
равен  значение
значение  превышено, и переменная
превышено, и переменная  вводится в модель.
вводится в модель.
(4) Проверка на исключение: текущий набор  равен
равен  значение
значение  не будет превышено, и
не будет превышено, и  исключается из набора.
исключается из набора.
Проверка на включение: текущий набор  поскольку
поскольку  только что исключили из модели, то единственной кандидатурой на включение в модель является переменная
только что исключили из модели, то единственной кандидатурой на включение в модель является переменная  однако значение
однако значение  здесь не превышено, и
здесь не превышено, и  не включается в модель. Поскольку добавить к модели нечего, процесс останавливается. Результирующим набором является
не включается в модель. Поскольку добавить к модели нечего, процесс останавливается. Результирующим набором является 
12.4.4. Выбор значений F
При использовании метода пошаговой регрессии мы сталкиваемся с задачей выбора значений  и
и  Обычно полагают
Обычно полагают  где
где  некоторая произвольная постоянная. Например, Efroymson (1960) использует
некоторая произвольная постоянная. Например, Efroymson (1960) использует  для той же самой совокупности данных (Хальда) берут
для той же самой совокупности данных (Хальда) берут  Мы можем действовать и иначе, полагая и
Мы можем действовать и иначе, полагая и  где
где  число степеней свободы, соответствующее текущей RSS. Однако такой выбор значений
число степеней свободы, соответствующее текущей RSS. Однако такой выбор значений  не является, строго говоря, корректным, поскольку на каждом шаге мы ищем максимум или минимум совокупности коррелированных
не является, строго говоря, корректным, поскольку на каждом шаге мы ищем максимум или минимум совокупности коррелированных  -переменных. Например, чем больше число переменных, из которых производится отбор, тем больше Умах» и, следовательно, тем большим следует ожидать значение
-переменных. Например, чем больше число переменных, из которых производится отбор, тем больше Умах» и, следовательно, тем большим следует ожидать значение  при котором производится включение регрессора в модель. Ряд авторов [например, Draper и др. (1971), Pope, Webster (1972)] рассматривали этот вопрос об упорядоченных зависимых
при котором производится включение регрессора в модель. Ряд авторов [например, Draper и др. (1971), Pope, Webster (1972)] рассматривали этот вопрос об упорядоченных зависимых  -переменных, и кое-что здесь удалось сделать. Forsythe
-переменных, и кое-что здесь удалось сделать. Forsythe
и др. (1973) рассматривали эту задачу, допуская только включение переменных, и получили критерий перестановок для замены 
12.4.5. Другие пошаговые методы
Имеются две, по-видимому, довольно распространенные разновидности пошаговой процедуры. Одна из них — это так называемый метод включения, в котором переменные не исключаются, а только поочередно вводятся в модель с использованием, скажем,  -критерия. Вторая — это метод исключения, в котором сначала подбирается полная модель с
-критерия. Вторая — это метод исключения, в котором сначала подбирается полная модель с  регрессорами, а затем производится поочередное исключение регрессоров с использованием, скажем,
регрессорами, а затем производится поочередное исключение регрессоров с использованием, скажем,  -критерия; в этой процедуре проверка возможности включения регрессоров не производится. К сожалению, эти два метода не обязательно приводят к одной и той же модели. Например, Hamaker (1962), используя данные Хальда, по методу включения получил подмножество
-критерия; в этой процедуре проверка возможности включения регрессоров не производится. К сожалению, эти два метода не обязательно приводят к одной и той же модели. Например, Hamaker (1962), используя данные Хальда, по методу включения получил подмножество  а по методу исключения
а по методу исключения  .
.
Некоторые аргументы за и против этих двух методов подробно рассматривают Mantel (1970) и Beale (1970). Большинство авторов, по-видимому, предпочитает метод исключения (см., например, Draper, Smith (1966, с. 187)), и такое предпочтение подкрепляется анализом, произведенным Kennedy, Bancroft (1971), хотя в их сравнении порядок выбора регрессоров предопределен заранее (как в полиномиальной регрессии). Метод исключения, кроме того, подходит тем статистикам, которые предпочитают видеть в уравнении все регрессоры сразу, дабы "чего-нибудь не пропустить"!
Другие вариаций на  тему описаны в Mantel (1970) и Draper, Smith (1966). Однако предпочитать следует, по-видимому, все же пошаговую процедуру с одним очевидным исключением — полиномиальной регрессией.
тему описаны в Mantel (1970) и Draper, Smith (1966). Однако предпочитать следует, по-видимому, все же пошаговую процедуру с одним очевидным исключением — полиномиальной регрессией.
В заключение стоит отметить, что использовать пошаговую регрессию уместно, когда значение К очень велико (приблизительно когда  хотя это зависит от ЭВМ). В противном случае следует использовать методы § 12.2 и 12.3.
хотя это зависит от ЭВМ). В противном случае следует использовать методы § 12.2 и 12.3.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
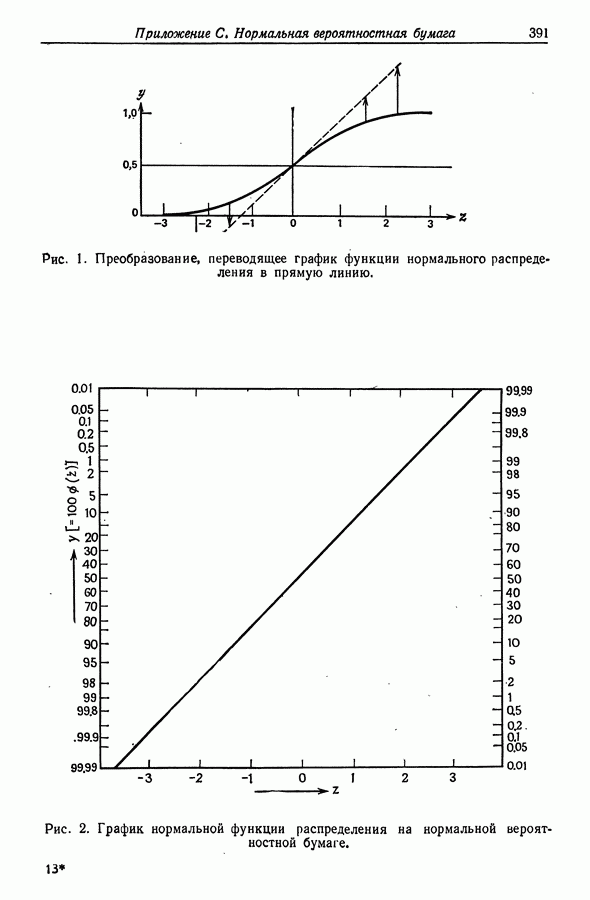
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
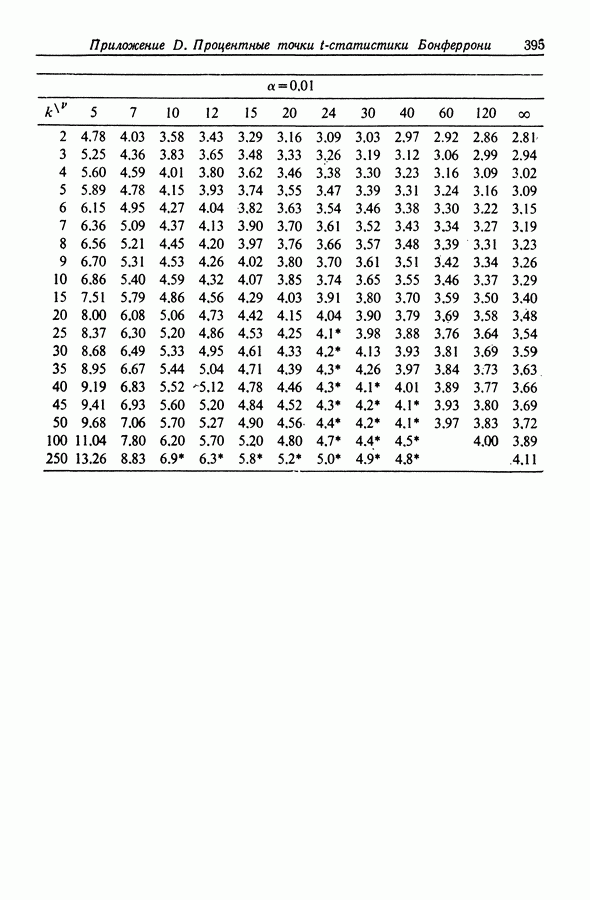
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
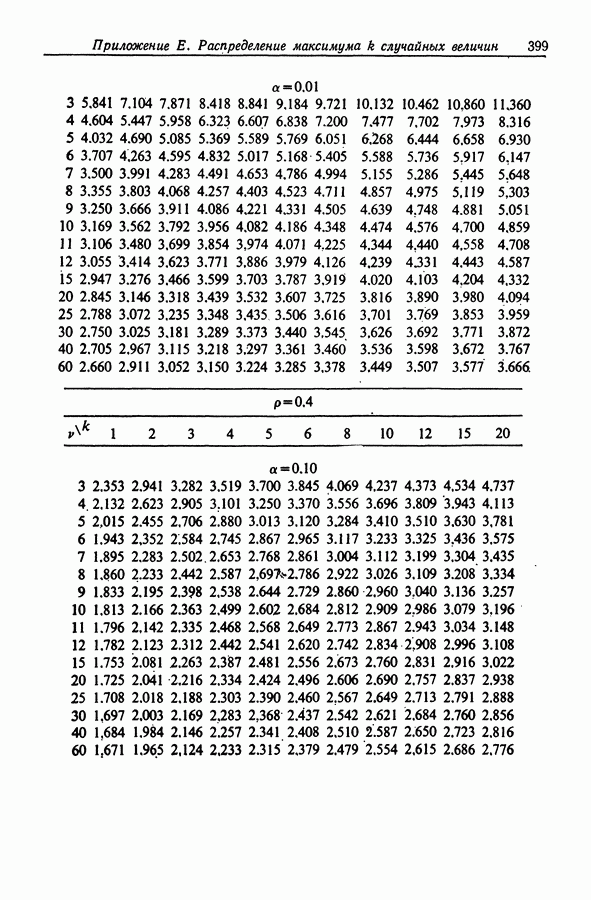
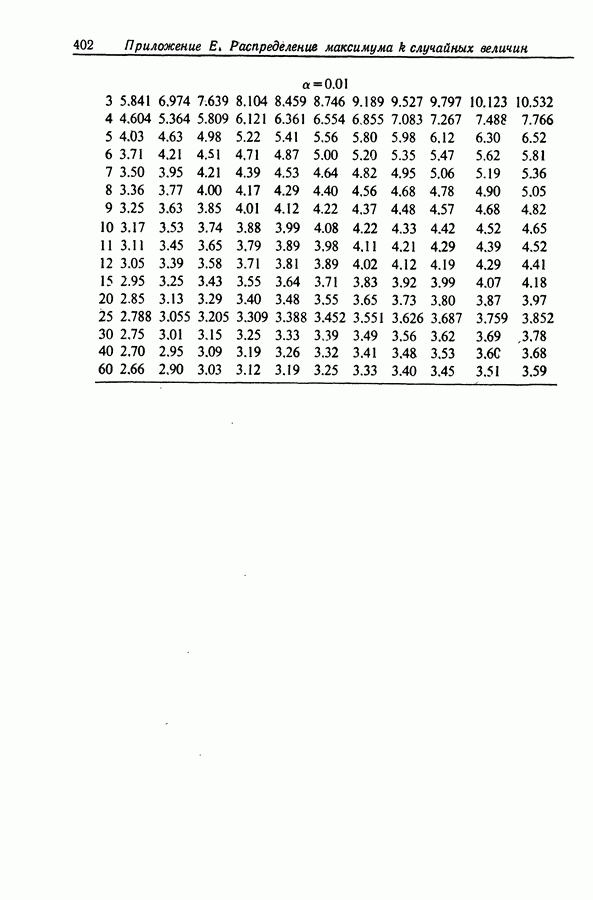
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
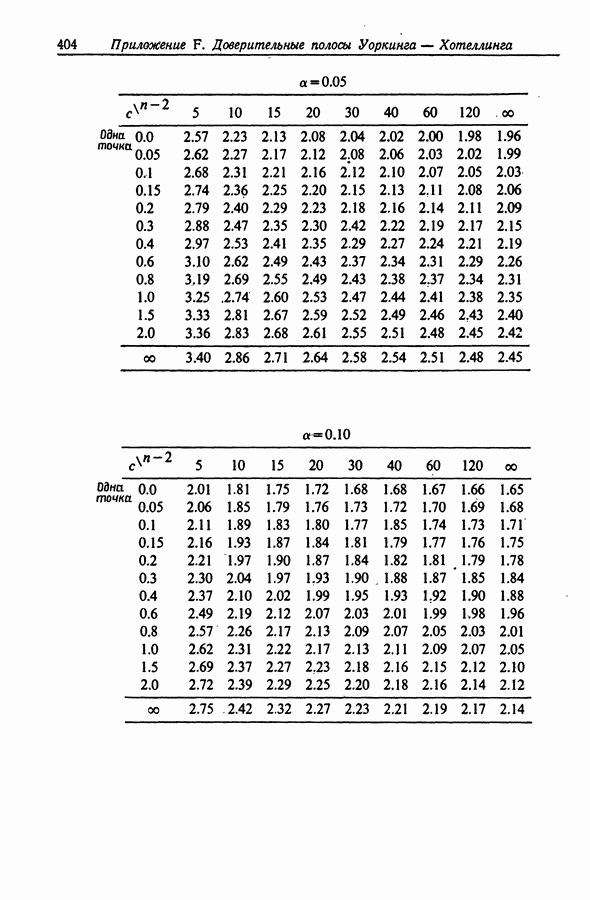
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ