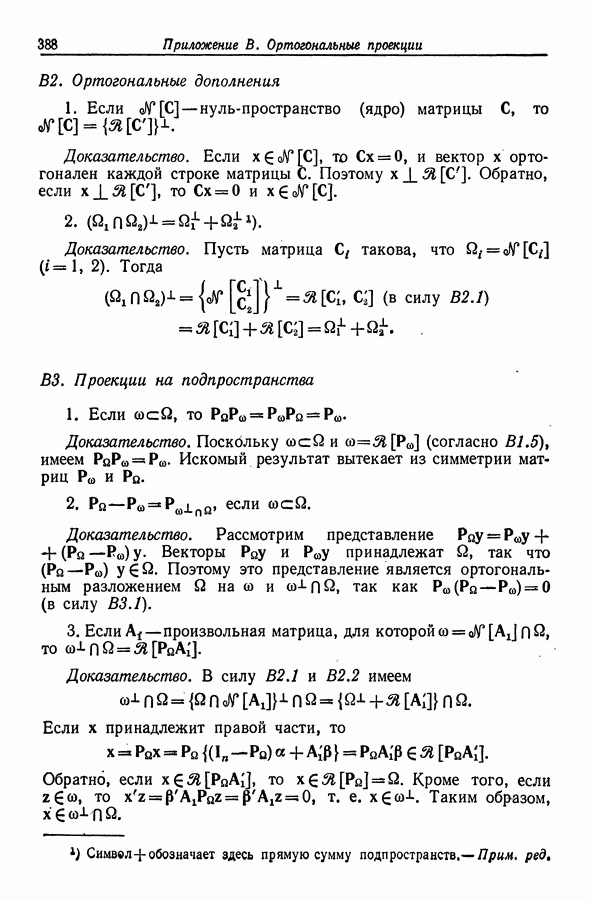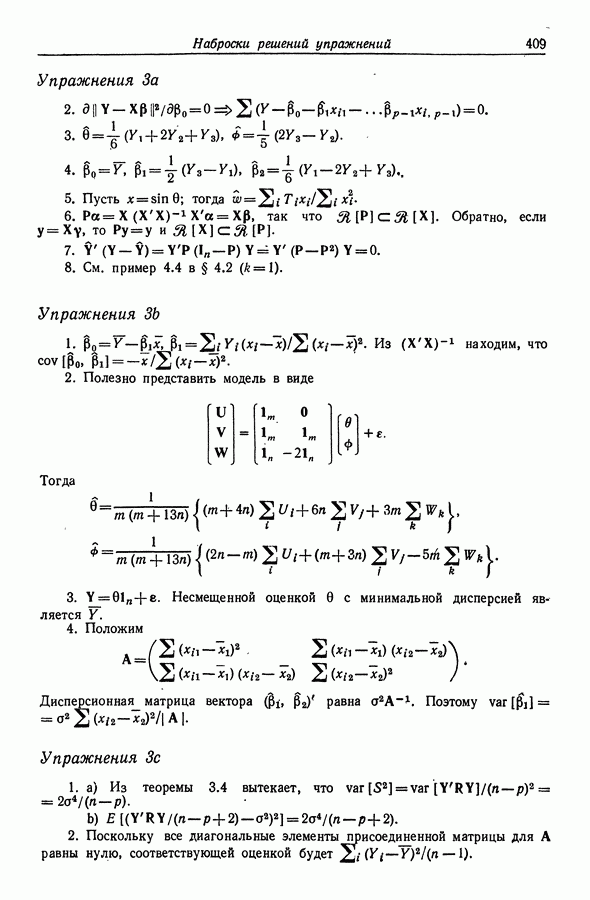| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
9.1. Классификация по одному признаку
9.1.1. Представление в виде регрессионной модели
В примере 4.2 из разд. 4.1.3 мы показали, как общую теорию регрессии можно применить к задаче сравнения средних двух нормальных совокупностей, когда дисперсии этих совокупностей равны. Теперь мы распространим эту теорию на случай сравнения I нормальных совокупностей  .
.
Пусть  — значение
— значение  наблюдения
наблюдения  над I-й нормальной совокупностью
над I-й нормальной совокупностью  При этом имеем следующий массив данных:
При этом имеем следующий массив данных:

Для того чтобы использовать общую теорию регрессии, объединим имеющуюся информацию в модель

 независимые и одинаково распределенные случайные величины, имеющие распределение
независимые и одинаково распределенные случайные величины, имеющие распределение  Используя векторную запись, эту модель можно представить в виде
Используя векторную запись, эту модель можно представить в виде

или

где  Поскольку столбцы матрицы X линейно независимы, то (9.2) представляет собой частный случай линейной модели регрессии (полного ранга) из § 3.1 с
Поскольку столбцы матрицы X линейно независимы, то (9.2) представляет собой частный случай линейной модели регрессии (полного ранга) из § 3.1 с  сюда не включается).
сюда не включается).
Интересующая нас нулевая гипотеза имеет вид  (обозначим это общее значение символом
(обозначим это общее значение символом  или
или  . В матричной форме она записывается так:
. В матричной форме она записывается так:

или  Строки входящей сюда матрицы А очевидным образом линейно независимы. Поэтому матрица А имеет размер
Строки входящей сюда матрицы А очевидным образом линейно независимы. Поэтому матрица А имеет размер  и ранг
и ранг  где
где  Таким образом,
Таким образом,  — линейная гипотеза, и применима теория гл. 4;
— линейная гипотеза, и применима теория гл. 4;  -критерий для гипотезы Я задается с помощью статистики
-критерий для гипотезы Я задается с помощью статистики

Для отыскания RSS надо минимизировать  по отношению к Переходя к частным производным по переменным
по отношению к Переходя к частным производным по переменным  получаем
получаем

и

Для отыскания RSS минимизация  производится при ограничениях, задаваемых гипотезой
производится при ограничениях, задаваемых гипотезой  . Простейший путь состоит здесь в использовании гипотезы
. Простейший путь состоит здесь в использовании гипотезы  для уменьшения числа свободных параметров до одного, скажем
для уменьшения числа свободных параметров до одного, скажем  Минимизируя сумму
Минимизируя сумму  по отношению к
по отношению к  получаем
получаем  где
где  общее среднее"), и
общее среднее"), и

Последнее выражение легко преобразуется к виду

(сумма со смешанными произведениями равна нулю), и поэтому

Таким образом, (9.4) принимает вид

Если гипотеза Я верна, то эта статистика имеет распределение 
Заметим, наконец, что модель (9.1) можно представить также в виде

где  является
является  наблюдением над
наблюдением над  фиктивным категоризованным регрессором
фиктивным категоризованным регрессором  Здесь
Здесь  если
если  -наблюдение, соответствующее 1-й совокупности, и
-наблюдение, соответствующее 1-й совокупности, и  в противном случае.
в противном случае.
9.1.2. Вычисления
На практике различные суммы квадратов принято располагать в виде таблицы (табл. 9.1).
Таблица 9.1 (см. скан) Таблица дисперсионного анализа для классификации по одному признаку
При этом строки, расположенные ниже строки "скорректированная полная" (имеется в виду "полная сумма квадратов, скорректированная относительно среднего"), часто опускаются. Терминология для сумм, используемых
в столбце "источник" (т. е. источник дисперсии, изменчивости. Перев.), в различных работах бывает разной. Так, вместо термина "между совокупностями" употребляется термин "между группами", а также термин "между способами обработки". Сумма квадратов, расположенная в строке "ошибки", иногда называется суммой квадратов "внутри групп", "внутри совокупностей" или "остаточной" суммой квадратов. Эта сумма дает оценку для  построенную по всем наблюдениям.
построенную по всем наблюдениям.
Если вычисления производятся на настольном калькуляторе, то полезно использовать соотношения

где

Формулы (9.6) и (9.7) требуют вычисления только полных сумм и их квадратов. При этом ошибки округления, связанные с делением, сводятся к минимуму. В то же время необходимо проявлять достаточную осторожность, вычисляя разность двух величин (особенно приблизительно равных). Если при подобных вычислениях использовать слишком мало десятичных знаков, то полученное значение разности может оказаться весьма далеким (в смысле относительной погрешности. Перев.) от действительного. По этой причине в программах для ЭВМ предпочтительнее непосредственно использовать разности  (или использовать методы Youngs, Cramer (1971) и Ling (1974)), а не пользоваться соотношениями (9.6) и (9.7).
(или использовать методы Youngs, Cramer (1971) и Ling (1974)), а не пользоваться соотношениями (9.6) и (9.7).
Стоит, наверное, отметить простой способ запоминания приведенных двух формул. Рассмотрим первую из них. Вид суммируемых квадратов  указывает на то, что сумма
указывает на то, что сумма  составляется из элементов
составляется из элементов  Перед первым надо поставить знак суммы
Перед первым надо поставить знак суммы  (на это "указывает" индекс
(на это "указывает" индекс  Перев.), а перед вторым — знак минус. Кроме того, первую из этих составляющих надо разделить на число наблюдений У, участвующих в построении элемента
Перев.), а перед вторым — знак минус. Кроме того, первую из этих составляющих надо разделить на число наблюдений У, участвующих в построении элемента  , а вторую - на число наблюдений
, а вторую - на число наблюдений  участвующих в построении элемента
участвующих в построении элемента  С помощью подобных "правил" можно легко выписывать выражения типа (9.6) и (9.7) и для других
С помощью подобных "правил" можно легко выписывать выражения типа (9.6) и (9.7) и для других
сумм. Например, сумму  можно сразу записать в виде
можно сразу записать в виде

Эксперименты, используемые для проведения классификации по одному признаку, обычно называются однофакторными экспериментами. Так, например, может возникнуть задача сравнения эффективности шести различных лекарств или эффективности одного и того же лекарства, но даваемого в шести различных дозах. При этом данное лекарство является фактором, и имеется шесть различных уровней этого фактора.
9.1.3. Математические ожидания
Из общей теории (теорема 4.1) нам известно, что

и

При выводе этих выражений мы воспользовались тем, что необходимые нам степени свободы известны из анализа рангов матриц, связанных с исходной моделью регрессии из разд. 9.1.1. С другой стороны, в ряде планов эксперимента найти степени свободы непосредственно на основании рангов довольно трудно. В таких случаях эти степени свободы можно найти, используя общую формулу

в которой  а
а  - сумма коэффициентов при квадратах составляющих вектора
- сумма коэффициентов при квадратах составляющих вектора  Эти коэффициенты можно определить из соотношений (9.6) и (9.7). Например, из (9.6) имеем
Эти коэффициенты можно определить из соотношений (9.6) и (9.7). Например, из (9.6) имеем

9.1.4. Перепараметризация модели
Установив возможность использования для проверки интересующей нас линейной гипотезы общей теории регрессии, мы затем отыскиваем выражения для RSS и  Рассмотрим теперь отличный от предыдущего метод отыскания этих сумм, использующий перепараметризацию модели. Пусть
Рассмотрим теперь отличный от предыдущего метод отыскания этих сумм, использующий перепараметризацию модели. Пусть

где  Тогда гипотеза Я принимает вида
Тогда гипотеза Я принимает вида  (ограничение а.
(ограничение а.  влечет за собой и равенство
влечет за собой и равенство  . Рассмотрим далее аналогичное разложение для
. Рассмотрим далее аналогичное разложение для  а именно
а именно

так что

Возведем обе части последнего равенства в квадрат и просуммируем полученные выражения по  и по
и по  При этом
При этом

и

Учитывая теперь, что  получаем
получаем

Из этого разложения для  мы и находим
мы и находим  и
и  Например, при условии а.
Например, при условии а.  правая часть (9.13) достигает минимума, если
правая часть (9.13) достигает минимума, если  равны
равны  соответственно. При этом
соответственно. При этом

Если верна гипотеза Я, то (9.13) принимает вид

 и его правая часть достигает минимума при
и его правая часть достигает минимума при  Поэтому
Поэтому

и

Хотя указанная перепараметризация и не приводит здесь к реальному упрощению вычисления  -статистики, используемой для проверки гипотезы
-статистики, используемой для проверки гипотезы  , мы увидим в дальнейшем, что она приводит к значительным упрощениям в задачах классификации по двум и большему числу признаков.
, мы увидим в дальнейшем, что она приводит к значительным упрощениям в задачах классификации по двум и большему числу признаков.
9.1.5. Геометрический анализ
Представляется интересным более внимательно рассмотреть геометрическую сущность разложения (9.12). Соответственно структуре вектора 8, образованного элементами  (см.
(см.  Перев.), введем векторы
Перев.), введем векторы  у которых
у которых  Тогда, учитывая (9.10), имеем
Тогда, учитывая (9.10), имеем

Векторы  взаимно ортогональны. Например, из (9.11) вытекает, что
взаимно ортогональны. Например, из (9.11) вытекает, что  Поэтому
Поэтому

а это и есть соотношение (9.12). Если  то можно показать, что матрицы
то можно показать, что матрицы  будут при этом симметричны и идемпотентны, причем
будут при этом симметричны и идемпотентны, причем  Поэтому в силу теорем 2.7 (следствие 1) и 2.8 случайные величины
Поэтому в силу теорем 2.7 (следствие 1) и 2.8 случайные величины  взаимно независимы и имеют
взаимно независимы и имеют  -распределения с числами степеней свободы, задаваемыми следами матриц
-распределения с числами степеней свободы, задаваемыми следами матриц  соответственно. Таким образом, если гипотеза
соответственно. Таким образом, если гипотеза  верна, то
верна, то

и

Это показывает, что при справедливости гипотезы Я статистика (9.5) имеет  -распределение.
-распределение.
Интересно отметить, что взаимную независимость указанных квадратичных форм можно доказать и непосредственно следующим образом. Повторным применением теоремы 1.5 (для одномерных векторов, т. е. для скалярных величин) находим

так что  Подобным же образом показываем, что
Подобным же образом показываем, что  а тогда по следствию 1 из теоремы 2.7 (§ 2.3) случайные величины
а тогда по следствию 1 из теоремы 2.7 (§ 2.3) случайные величины  и
и  взаимно независимы.
взаимно независимы.
9.1.6. Идентифицирующие ограничения
Заметим, что перепараметризованная модель

имеет неполный ранг, поскольку. первый столбец  соответствующей матрицы плана X равен сумме остальных ее столбцов (ср. с (3.40) из разд. 3.8.1). Ограничение
соответствующей матрицы плана X равен сумме остальных ее столбцов (ср. с (3.40) из разд. 3.8.1). Ограничение  участвовавшее в определении
участвовавшее в определении  (соотношение (9.9)), являете необходимым и достаточным для идентификации
(соотношение (9.9)), являете необходимым и достаточным для идентификации  В то же время мы могли бы отправляться непосредственно от модели (9.17) и ввести идентифицирующее ограничение вида
В то же время мы могли бы отправляться непосредственно от модели (9.17) и ввести идентифицирующее ограничение вида  Дополним матрицу X в (9.1) строкой (
Дополним матрицу X в (9.1) строкой ( не зависящей линейно от остальных строк этой матрицы. Если
не зависящей линейно от остальных строк этой матрицы. Если  то столбцы расширенной матрицы также линейно независимы. Поэтому для идентификации можно использовать любую линейную комбинацию
то столбцы расширенной матрицы также линейно независимы. Поэтому для идентификации можно использовать любую линейную комбинацию  параметров
параметров  для которой (см. теорему 3.9 из разд. 3.8.1). При выбранных значениях дооценки наименьших квадратов для
для которой (см. теорему 3.9 из разд. 3.8.1). При выбранных значениях дооценки наименьших квадратов для  можно найти непосредственно из соотношения
можно найти непосредственно из соотношения  Так, мы получаем
Так, мы получаем  д. В то же время, как мы уже видели, выбор значений
д. В то же время, как мы уже видели, выбор значений  приводит к более простому анализу.
приводит к более простому анализу.
9.1.7. Доверительные интервалы
Если в результате применения  -критерия гипотеза
-критерия гипотеза  отвергается, то следующий шаг состоит в выяснении того, в какой степени параметры
отвергается, то следующий шаг состоит в выяснении того, в какой степени параметры  отличаются друг от друга. В частности, нас обычно интересуют также разности, как
отличаются друг от друга. В частности, нас обычно интересуют также разности, как  и т. п. Эти линейные комбинации называются сравнениями (contrasts) параметров
и т. п. Эти линейные комбинации называются сравнениями (contrasts) параметров  так как все они имеют вид
так как все они имеют вид  где
где  Поскольку линейная комбинация
Поскольку линейная комбинация  имеет дисперсию
имеет дисперсию  то, используя рассуждения из разд. 4.1.5, можно легко показать, что интервал
то, используя рассуждения из разд. 4.1.5, можно легко показать, что интервал

где  является
является  -процентным двусторонним доверительным интервалом для
-процентным двусторонним доверительным интервалом для  Заметим, что
Заметим, что  значимо отличается от нуля, если этот интервал не содержит нуля.
значимо отличается от нуля, если этот интервал не содержит нуля.
Если нас интересуют сразу несколько сравнений, выбранных априори, до обращения к данным, мы сталкиваемся с задачей одновременного (совместного) интервального оценивания, обсуждавшейся в гл. 5. Там были описаны три метода построения доверительных интервалов, причем наиболее узкими оказываются  -интервалы максимального модуля. Если, однако, нас интересуют все возможные сравнения, то следует использовать метод Шеффе. Положим,
-интервалы максимального модуля. Если, однако, нас интересуют все возможные сравнения, то следует использовать метод Шеффе. Положим,  — матрица, указанная в (9.3). Тогда множество всех линейных комбинаций
— матрица, указанная в (9.3). Тогда множество всех линейных комбинаций  совпадает с множеством всех сравнений
совпадает с множеством всех сравнений  (см. (5.16)). Поэтому, как явствует из последнего пункта разд.
(см. (5.16)). Поэтому, как явствует из последнего пункта разд.  -статистика для гипотезы
-статистика для гипотезы  будет значимой в том и только том случае, когда хотя бы один из интервалов Шеффе
будет значимой в том и только том случае, когда хотя бы один из интервалов Шеффе

не содержит нуля (т. е. ненулевым оказывается хотя бы одно из сравнений Таким образом, если  -статистика оказывается значимой, можно попытаться найти те сравнения, которые являются тому причиной (хотя такой поиск может быть и непростым ввиду потенциально бесконечного числа сравнений).
-статистика оказывается значимой, можно попытаться найти те сравнения, которые являются тому причиной (хотя такой поиск может быть и непростым ввиду потенциально бесконечного числа сравнений).
Если интерес для нас представляют только разности вида  то для этих разностей можно построить совокупность доверительных интервалов с вероятностью одновременного накрытия, в точности равной
то для этих разностей можно построить совокупность доверительных интервалов с вероятностью одновременного накрытия, в точности равной  Эти интервалы имеют вид
Эти интервалы имеют вид

или

где  верхняя
верхняя  -процентная точка распределения стьюдентизированного размаха с параметрами
-процентная точка распределения стьюдентизированного размаха с параметрами  (т. е. распределения размаха
(т. е. распределения размаха  независимых
независимых  -случайных величин, деленного на
-случайных величин, деленного на  где V — независимая от них случайная величина, имеющая распределение
где V — независимая от них случайная величина, имеющая распределение  Данный метод, предложенный Тьюки, подробно описан в работах Scheffe (1959, с. 111 — 112) и Miller (1966, с. 37). Соответствующие таблицы можно найти, например, в работе Pearson, Hartley (1970, с. 191 — 193). Поскольку во всяком отклонении разности
Данный метод, предложенный Тьюки, подробно описан в работах Scheffe (1959, с. 111 — 112) и Miller (1966, с. 37). Соответствующие таблицы можно найти, например, в работе Pearson, Hartley (1970, с. 191 — 193). Поскольку во всяком отклонении разности  от нуля более, чем на
от нуля более, чем на  усматривают связь с тем, что
усматривают связь с тем, что  то можно рассортировать средние по группам, внутри которых
то можно рассортировать средние по группам, внутри которых
средние не будут значимо отличаться друг от друга. Например, если  и упорядоченные (по возрастанию) значения выборочных средних равны
и упорядоченные (по возрастанию) значения выборочных средних равны

то  и соответствующими группами средних будут
и соответствующими группами средних будут  (обычно принято подчеркивать выделенные группы, как это сделано в нашей табличке).
(обычно принято подчеркивать выделенные группы, как это сделано в нашей табличке).
Другим методом разбиения средних по группам является критерий множественного ранжирования Дункана [Miller (1966, с. 81)]. Хотя эта процедура весьма популярна среди исследователей, тем не менее она не стала общепринятой среди статистиков. Особенно много споров вызвал непостоянный уровень значимости этой процедуры [ONeill, Wetherill (J971, с. 226- 227)].
Имеются еще два подхода к задаче сортировки средних, представляющихся весьма многообещающими. Поскольку мы, по существу, имеем дело с вопросом принятия решений, то естественно поставить задачу именно в контексте теории принятия решений. Подобную формулировку задачи дали Waller, Duncan (1969). С другой стороны, задачу сортировки средних можно рассматривать как задачу отнесения точек выборки (представляющих выборочные средние) к одному из нескольких кластеров. Относительно техники кластер-анализа, которая может оказаться полезной в этом смысле, см. Scott, Knott (1974).
Различные процедуры попарных сравнений, подобные упомянутым выше, сопоставляются в статье Carmer, Swanson (1973) с помощью численного моделирования. При этом наилучшими для выполненных экспериментов оказались так называемый метод минимальной значимой разности, основанный на простых попарных -сравнениях

(которые производятся только в случае, когда величина Л-статистики оказывается значимой), и байесовская процедура Waller, Duncan (1969).
9.1.8. Исходные предположения
В разд. 6.3.2 мы видели, что квадратично сбалансированные  -критерии устойчивы к отклонениям от предположения нормальности. Теперь мы в состоянии, получив
-критерии устойчивы к отклонениям от предположения нормальности. Теперь мы в состоянии, получив  -статистику, сразу
-статистику, сразу
проверить ее на квадратичную сбалансированность. Надо просто, взяв числитель и знаменатель этой статистики, посмотреть, будет ли в каждом случае коэффициент при  одним и тем же для всех
одним и тем же для всех  Поскольку для статистики (9.5) это так, то классификация по одному признаку с равными числами наблюдений на каждое среднее, обладает указанной устойчивостью.
Поскольку для статистики (9.5) это так, то классификация по одному признаку с равными числами наблюдений на каждое среднее, обладает указанной устойчивостью.
Вопрос устойчивости рассмотрен довольно подробно также в книге Scheffe (1959, гл. 10). Там показано, что  -статистика устойчива и по отношению к возможному неравенству дисперсий. совокупностей, но не является устойчивой по отношению к наличию корреляций между членами совокупностей. Bhargava, Srivastava (1973) показали, как в последнем случае следует модифицировать совместные доверительные интервалы Шеффе, чтобы допустить возможность наличия постоянной корреляции. Их метод, по существу, сводится к замене
-статистика устойчива и по отношению к возможному неравенству дисперсий. совокупностей, но не является устойчивой по отношению к наличию корреляций между членами совокупностей. Bhargava, Srivastava (1973) показали, как в последнем случае следует модифицировать совместные доверительные интервалы Шеффе, чтобы допустить возможность наличия постоянной корреляции. Их метод, по существу, сводится к замене  на
на

и соответствующему изменению числа степеней свободы.
Для проверки равенства дисперсий совокупностей имеется целый ряд процедур. Среди них можно отметить, в частности, приближенный  -критерий [Box (1953)], описанный Scheffe (1959, с. 128), служащий хорошим примером использования метода наименьших квадратов; приближенный
-критерий [Box (1953)], описанный Scheffe (1959, с. 128), служащий хорошим примером использования метода наименьших квадратов; приближенный  -критерий, основанный на абсолютных уклонениях [Levene (1960), Draper, Hunter (1969)], а также два других критерия [Layard (1973)], носящих названия хи-квадрат критерия и критерия "складного ножа" (эти критерии незначительно модифицировали Brown, Forsythe (1974)). Используя моделирование, Layard (1973) показал, что оба его критерия вполне удовлетворительны, когда упор делается на устойчивость и на мощность критерия. С другой стороны, критерий Бокса является не столь мощным, зато он более, устойчив в отношении уровня значимости. При наличии корреляции полезными могут оказаться процедуры, предложенные Han (1968).
-критерий, основанный на абсолютных уклонениях [Levene (1960), Draper, Hunter (1969)], а также два других критерия [Layard (1973)], носящих названия хи-квадрат критерия и критерия "складного ножа" (эти критерии незначительно модифицировали Brown, Forsythe (1974)). Используя моделирование, Layard (1973) показал, что оба его критерия вполне удовлетворительны, когда упор делается на устойчивость и на мощность критерия. С другой стороны, критерий Бокса является не столь мощным, зато он более, устойчив в отношении уровня значимости. При наличии корреляции полезными могут оказаться процедуры, предложенные Han (1968).
При неравенстве дисперсий совокупностей можно использовать модификацию совместных доверительных интервалов Шеффе [Spjotvoll (1972b)]. Если нас интересует лишь один доверительный интервал, скажем для  можно применить устойчивую процедуру Scott, Smith (1971) (см. конец разд. 9.1.9).
можно применить устойчивую процедуру Scott, Smith (1971) (см. конец разд. 9.1.9).
9.1.9. Неравные числа наблюдений на каждое среднее
Если мы имеем  наблюдений над
наблюдений над  нормальной совокуп ностью, то единственное изменение в теории разд. 9.1.1 состоит в том, что здесь
нормальной совокуп ностью, то единственное изменение в теории разд. 9.1.1 состоит в том, что здесь  Соответствующей
Соответствующей  -статистикой для
-статистикой для
гипотезы  будет
будет

В разд. 9.1.2 в соотношениях (9.6) и (9.7) величины  заменяются соответственно на
заменяются соответственно на  Лравила" Для запоминания этих соотношений остаются в силе. В то же время при использовании предложенной в разд. 9.1.4 перепараметризации возникают некоторые трудности. Разложение (9.10) остается ортогональным, если положить
Лравила" Для запоминания этих соотношений остаются в силе. В то же время при использовании предложенной в разд. 9.1.4 перепараметризации возникают некоторые трудности. Разложение (9.10) остается ортогональным, если положить  поскольку например, (9.11) все еще выполняется, и
поскольку например, (9.11) все еще выполняется, и

так что имеет место (9.12). Однако соотношение (9.13) уже не будет справедливым, потому, например, что

Однако последнее можно обойти. Для этого надо просто выбрать другое идентифицирующее ограничение, а именно  -Тогда (9.13) сохраняет силу. (Напомним, что в соответствии с разд. 9.1.6 для идентификации можно использовать любое ограничение
-Тогда (9.13) сохраняет силу. (Напомним, что в соответствии с разд. 9.1.6 для идентификации можно использовать любое ограничение  в котором левая часть не является сравнением.)
в котором левая часть не является сравнением.)
Хотя при классификации по одному признаку перепараметризация модели имеет в основном лишь теоретический интерес, она, как мы увидим позднее, дает по крайней мере подходящую процедуру для проведения классификации по большому числу признаков. Трудности, с которыми мы встретились в случае неравных чисел наблюдений, оказываются на практике типичными и при классификации по двум и более признакам при неравных числах наблюдений на каждое среднее.
Заметим, что и здесь можно использовать совместные доверительные интервалы Шеффе и Тьюки [Spjotvoll, Stoline (1973)]. Последние рекомендуются, если основной интерес заключается в попарном сравнении средних и если значения  не слишком отличаются друг от друга. Однако
не слишком отличаются друг от друга. Однако  -статистика для проверки
-статистика для проверки
гипотезы  более не является устойчивой относительно отклонений от нормальности (так как она уже не является квадратично сбалансированной) и относительно возможного неравенства дисперсии совокупностей. Если дисперсии совокупностей различны, то можно использовать модификацию Spjotvoll (1972b) совместных доверительных интервалов Шеффе. Если нас интересует только один доверительный интервал, скажем для
более не является устойчивой относительно отклонений от нормальности (так как она уже не является квадратично сбалансированной) и относительно возможного неравенства дисперсии совокупностей. Если дисперсии совокупностей различны, то можно использовать модификацию Spjotvoll (1972b) совместных доверительных интервалов Шеффе. Если нас интересует только один доверительный интервал, скажем для  то можно использовать приблизительно распределенную по
то можно использовать приблизительно распределенную по  статистику [Scott, Smith (1971)]
статистику [Scott, Smith (1971)]

где 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
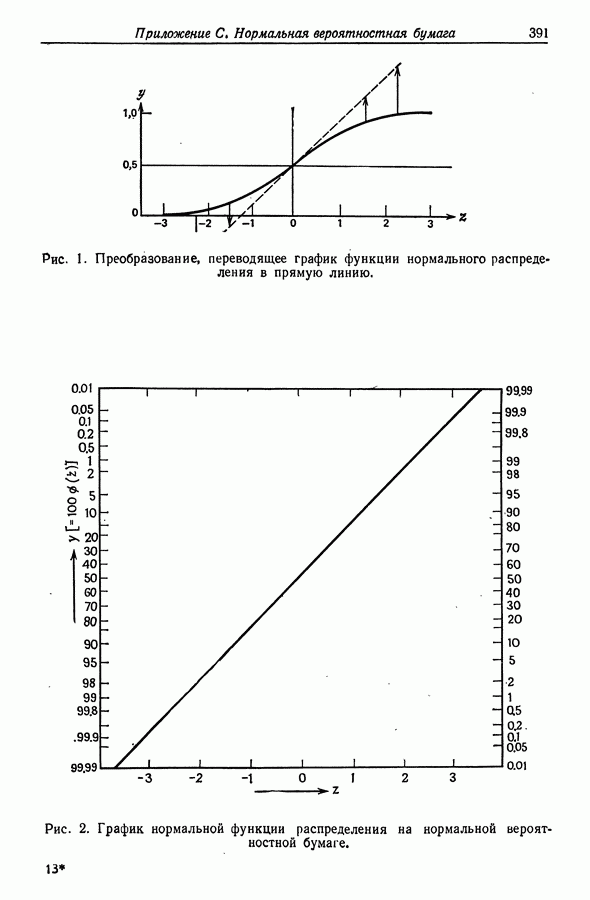
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
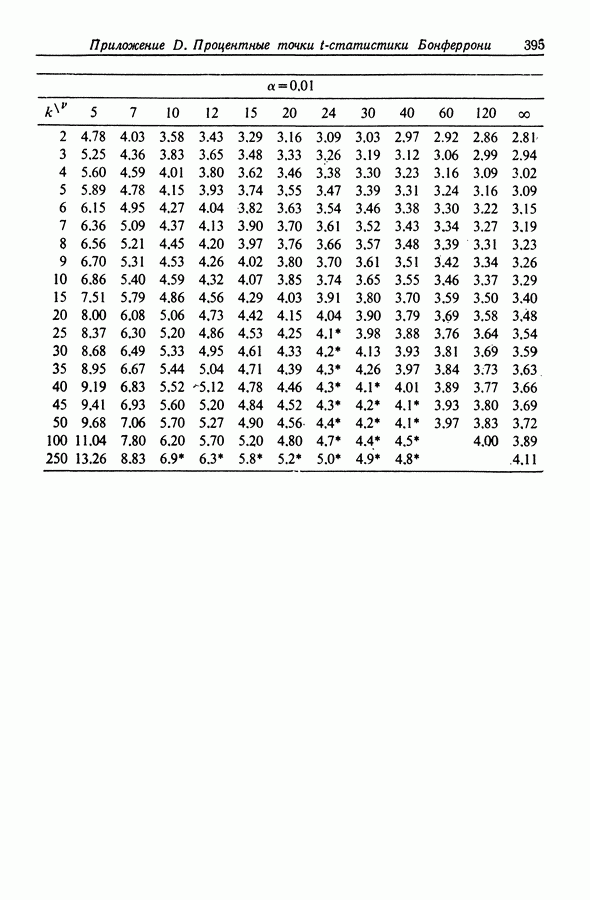
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
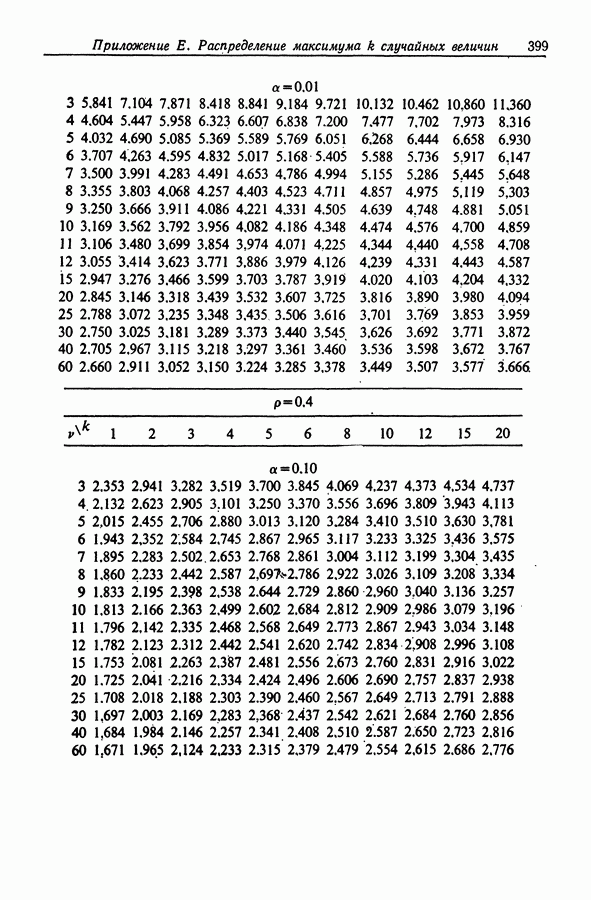
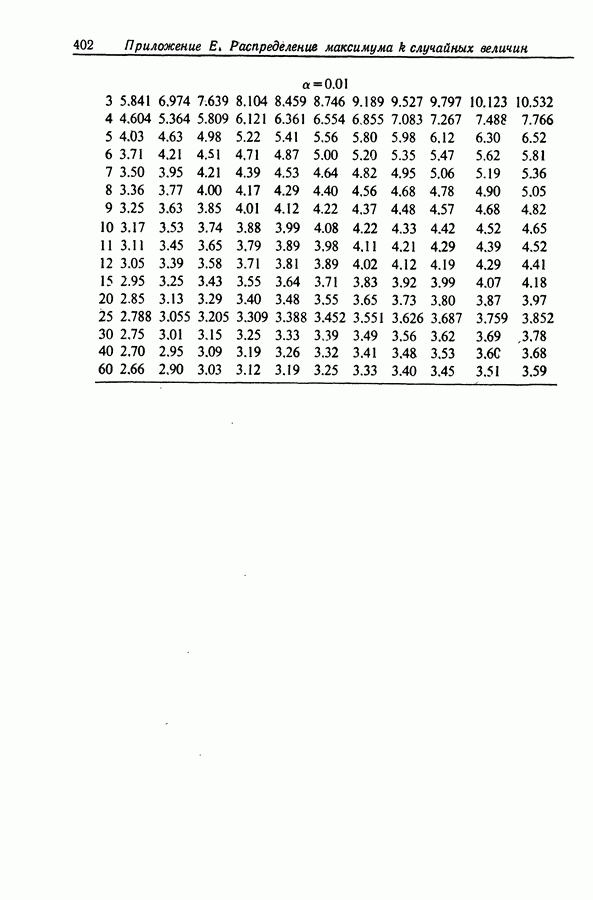
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
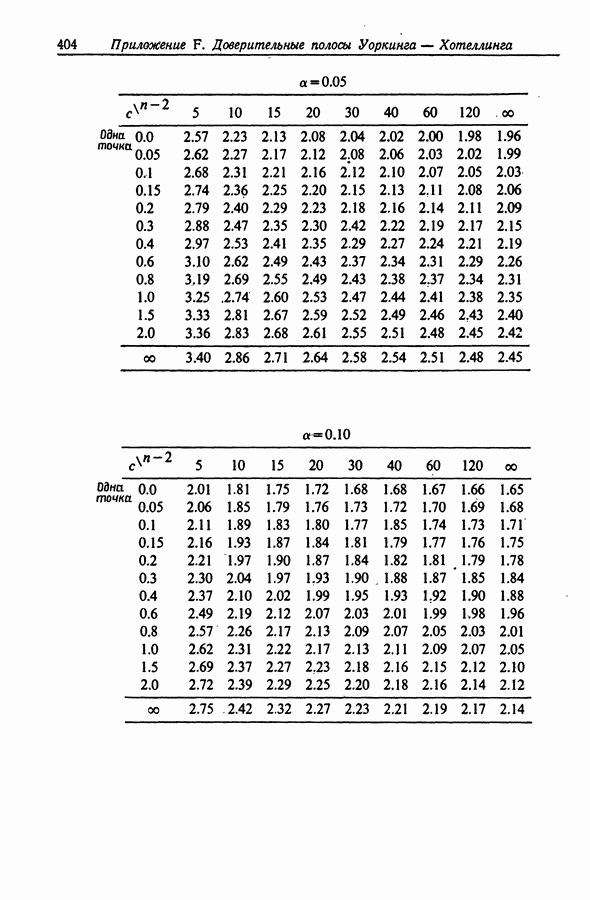
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ