| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.2. Доверительные интервалы и полосы
7.2.1. Доверительные интервалы для углового коэффициента и свободного члена
В соответствии с разд. 4.1.4 имеем

и

Применяя метод максимального модуля из разд. 5.1.1 (соотношение  , мы достигаем вероятности одновременного накрытия, в точности равной
, мы достигаем вероятности одновременного накрытия, в точности равной  , используя для
, используя для  доверительные интервалы
доверительные интервалы

и

где

Более широкие, чем следует, интервалы получаются, если положить 
Указанные интервалы можно также использовать для проверки гипотез, касающихся значений обоих параметров  Если же нас интересует гипотеза о значении только одного из этих параметров, скажем гипотеза
Если же нас интересует гипотеза о значении только одного из этих параметров, скажем гипотеза  то в этом случае мы используем обычную
то в этом случае мы используем обычную  -статистику
-статистику

и отвергаем гипотезу  с уровнем значимости а при
с уровнем значимости а при  Эту статистику можно получить непосредственно из того факта, что
Эту статистику можно получить непосредственно из того факта, что  не зависит от
не зависит от 
7.2.2. Доверительный интервал для ...
Построим доверительный интервал для отношения  используя метод, восходящий к Fieller (1940). Пусть
используя метод, восходящий к Fieller (1940). Пусть

Тогда  Кроме того,
Кроме того,

так, что

Разность  имеет вид
имеет вид  Поэтому она имеет нормальное распределение, а именно
Поэтому она имеет нормальное распределение, а именно  Статистика
Статистика  не зависит от
не зависит от  (теорема 3.5) (iii) из § 3.4), а следовательно, и от
(теорема 3.5) (iii) из § 3.4), а следовательно, и от  Поэтому, используя обычные рассуждения, приводящие к
Поэтому, используя обычные рассуждения, приводящие к  -статистикам (разд. 4.1.5), получаем:
-статистикам (разд. 4.1.5), получаем:

и  -процентное доверительное множество для 6 задается неравенством
-процентное доверительное множество для 6 задается неравенством

Оказывается, это множество сводится к интервалу  где
где  и
и  -корни квадратного уравнения
-корни квадратного уравнения

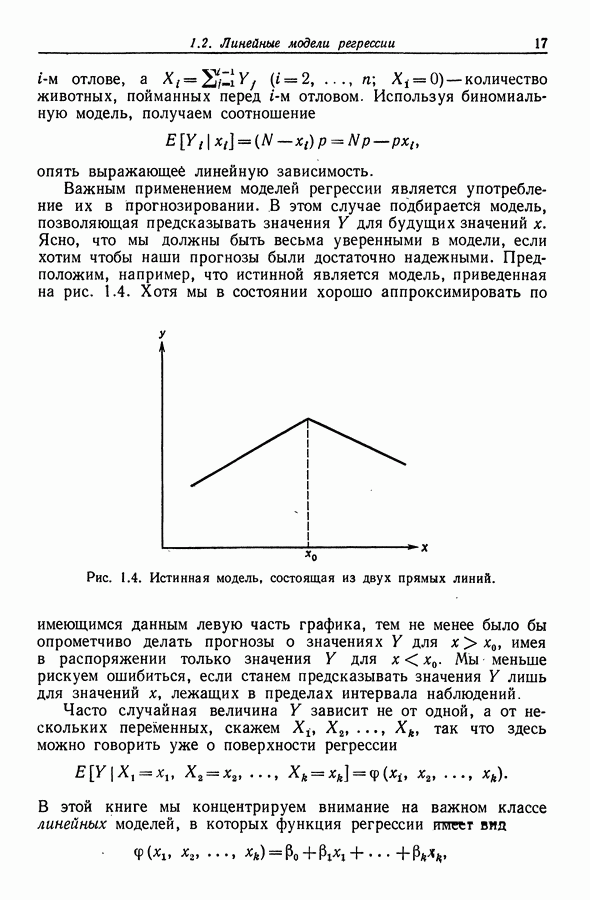
тогда и только тогда, когда коэффициент при  в уравнении (7.4) положителен (т. е. линия не слишком уплощена). В этом случае, как следует из уравнения (7.3), соответствующим интервалом для
в уравнении (7.4) положителен (т. е. линия не слишком уплощена). В этом случае, как следует из уравнения (7.3), соответствующим интервалом для  будет
будет  и оценка
и оценка  лежит в этом интервале.
лежит в этом интервале.
Если  то
то  и указанный метод приводит к доверительному интервалу для длины отрезка
и указанный метод приводит к доверительному интервалу для длины отрезка  отсекаемого линией регрессии
отсекаемого линией регрессии  оси абсцисс. Это частный случай обратного предсказания, рассматриваемого в разд. 7.2.6
оси абсцисс. Это частный случай обратного предсказания, рассматриваемого в разд. 7.2.6  ,
,
При изучении популяций животных часто возникает модель

(см. Seber (1973, с. И, 128, 145—148, 150, 298—299, 325)). В подобных приложениях нас интересуют доверительные интервалы именно для отношения  так что приведенная выше теория оказывается здесь полезной.
так что приведенная выше теория оказывается здесь полезной.
Отметим, что  является отношением двух коррелированных нормальных случайных величин. Точное распределение такого отношения указано Hinkley (1969 а).
является отношением двух коррелированных нормальных случайных величин. Точное распределение такого отношения указано Hinkley (1969 а).
7.2.3. Интервалы и полосы предсказания
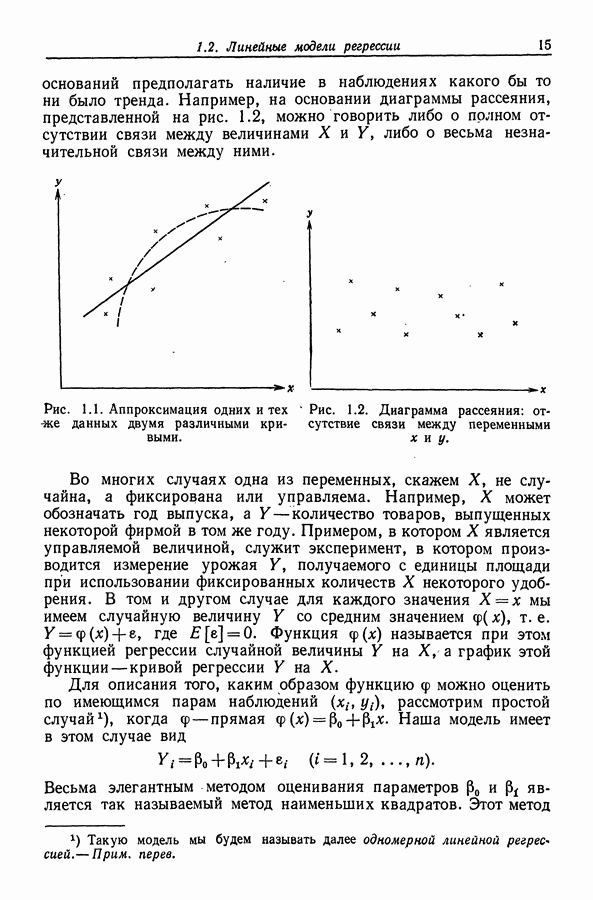
Аппроксимирующая прямая регрессии имеет вид

и, следовательно, проходит через точку  Из общей теории § 5.2 видно, что с помощью прогноза
Из общей теории § 5.2 видно, что с помощью прогноза  можно получить
можно получить  -процентный доверительный интервал для
-процентный доверительный интервал для  —математического ожидания значения наблюдения в точке
—математического ожидания значения наблюдения в точке  интервал имеет вид
интервал имеет вид

где

(Выражение для можно получить и непосредственно — см. упр. 1 в конце главы). Заметим, что  минимально при
минимально при  Чем дальше мы удаляемся от
Чем дальше мы удаляемся от  тем шире становится доверительный интервал.
тем шире становится доверительный интервал.
Когда нам нужны  доверительных интервалов, критическое значение
доверительных интервалов, критическое значение  в (7.5) следует заменить на
в (7.5) следует заменить на  или
или  если мы используем соответственно метод Бонферрони, метод Шеффе или метод максимального модуля. Если, однако, значение
если мы используем соответственно метод Бонферрони, метод Шеффе или метод максимального модуля. Если, однако, значение  не известно или настолько велико, что интервалы получаются слишком широкими, то можно построить доверительную полосу для всей линии регрессии и тем самым получить неограниченное число доверительных интервалов, для которых вероятность одновременного накрытия будет не меньше
не известно или настолько велико, что интервалы получаются слишком широкими, то можно построить доверительную полосу для всей линии регрессии и тем самым получить неограниченное число доверительных интервалов, для которых вероятность одновременного накрытия будет не меньше  В
В
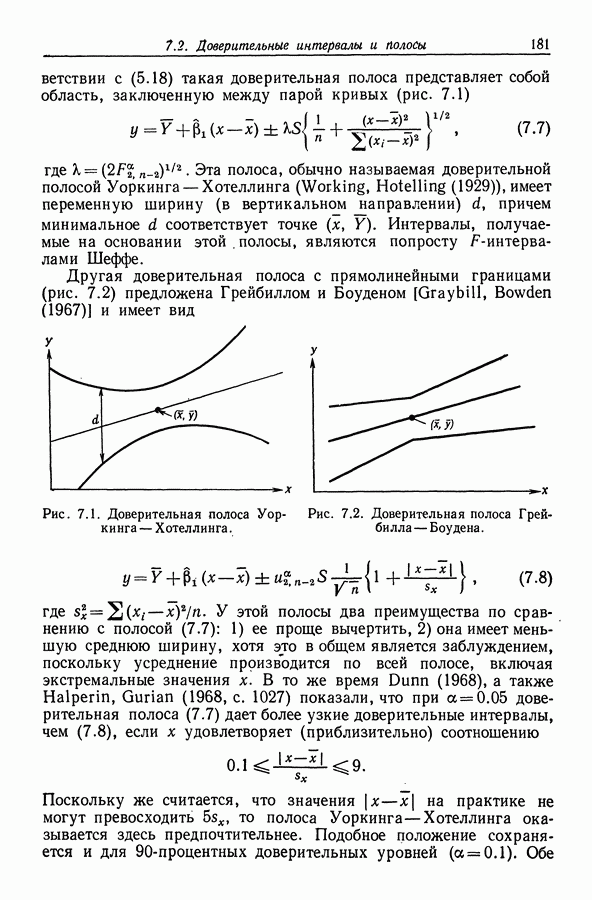
соответствии с (5.18) такая доверительная полоса представляет собой область, заключенную между парой кривых (рис. 7.1)

где  Эта полоса, обычно называемая доверительной полосой Уоркинга — Хотеллинга (Working, Hotelling (1929)), имеет переменную ширину (в вертикальном направлении)
Эта полоса, обычно называемая доверительной полосой Уоркинга — Хотеллинга (Working, Hotelling (1929)), имеет переменную ширину (в вертикальном направлении)  причем минимальное
причем минимальное  соответствует точке
соответствует точке  Интервалы, получаемые на основании этой
Интервалы, получаемые на основании этой  полосы, являются попросту
полосы, являются попросту  -интервалами Шеффе.
-интервалами Шеффе.
Другая доверительная полоса с прямолинейными границами (рис. 7.2) предложена Грейбиллом и Боуденом [Graybill, Bowden (1967)] и имеет вид

где 

Рис. 7.1. Доверительная полоса Уоркинга-Хотеллинга.

Рис. 7.2. Доверительная полоса Грейбилла — Боудена.
У этой полосы два преимущества по сравнению с полосой (7.7): 1) ее проще вычертить, 2) она имеет меньшую среднюю ширину, хотя это в общем является заблуждением, поскольку усреднение производится по всей полосе, включая экстремальные значения х. В то же время Dunn (1968), а также Halperin, Gurian (1968, с. 1027) показали, что при  доверительная полоса (7.7) дает более узкие доверительные интервалы, чем (7.8), если х удовлетворяет (приблизительно) соотношению
доверительная полоса (7.7) дает более узкие доверительные интервалы, чем (7.8), если х удовлетворяет (приблизительно) соотношению

Поскольку же считается, что значения  на практике не могут превосходить
на практике не могут превосходить  то полоса Уоркинга-Хотеллинга оказывается здесь предпочтительнее. Подобное положение сохраняется и для
то полоса Уоркинга-Хотеллинга оказывается здесь предпочтительнее. Подобное положение сохраняется и для  -процентных доверительных уровней
-процентных доверительных уровней  . Обе
. Обе
рассмотренные полосы можно получить как частные случаи процедуры, предложенной в Bowden (1970) (ср. с формулой (5.19) и последующим обсуждением).
Задачу построения точной доверительной полосы для линии регрессии в случае, когда значения  сосредоточены на конечном отрезке
сосредоточены на конечном отрезке  впервые решил Gafarian (1964). Он показал, как можно построить полосу, имеющую постоянную ширину
впервые решил Gafarian (1964). Он показал, как можно построить полосу, имеющую постоянную ширину  , и привел соответствующие таблицы для случая
, и привел соответствующие таблицы для случая  и четных
и четных  .
.
Miller (1966, с. 121) провел полезное обсуждение этого метода и указал, что сделанные afarian (1964) ограничения при построении таблиц несущественны. Дело в том, что интервал  на котором сосредоточены значения хобычно плохо определен, так что его границы можно скорректировать и считать, что х — средняя точка этого интервала. Кроме того, путем интерполяции табличных значений можно получить приближенные значения и для нечетных
на котором сосредоточены значения хобычно плохо определен, так что его границы можно скорректировать и считать, что х — средняя точка этого интервала. Кроме того, путем интерполяции табличных значений можно получить приближенные значения и для нечетных  Однако Bowden, Graybill (1966) позже получили таблицы для любого конечного интервала
Однако Bowden, Graybill (1966) позже получили таблицы для любого конечного интервала  и четных
и четных  Эти таблицы можно использовать и для построения точных доверительных полос трапецеидальной формы, которые могут оказаться более пригодными, чем полосы постоянной ширины, если х лежит вне интервала
Эти таблицы можно использовать и для построения точных доверительных полос трапецеидальной формы, которые могут оказаться более пригодными, чем полосы постоянной ширины, если х лежит вне интервала 
Dunn (1968) предложила урезанную модификацию полосы (7.8), которая приводит к более широким доверительным интервалам. Halperin и др. (1967), а также Halperin, Gurian (1968) получили точную полосу, имеющую вид (7.7), но с другим X и урезанную при  Однако их таблицы можно использовать только при
Однако их таблицы можно использовать только при  Значения X табулированы в работе Halperin и др. (1967) для различных значений
Значения X табулированы в работе Halperin и др. (1967) для различных значений  где
где

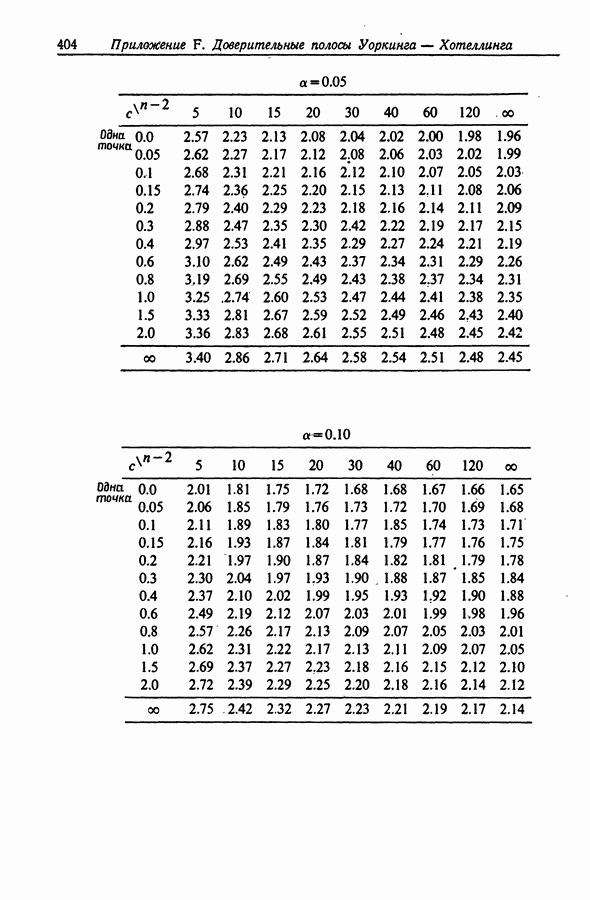
Wynn, Bloomfield (1971) подошли к этой задаче с другой стороны и получили таблицы (воспроизведенные в приложении  для произвольного интервала
для произвольного интервала  При этом просто вычисляется "стандартизированный" вариант ширины интервала
При этом просто вычисляется "стандартизированный" вариант ширины интервала

и по таблицам в приложении  отыскивается соответствующее ему значение
отыскивается соответствующее ему значение  Если к то
Если к то 
Последнее соотношение связывает таблицы, приведенные в при ложении  с таблицами, имеющимися в Halperin и др. (1967). При
с таблицами, имеющимися в Halperin и др. (1967). При  и
и  получаем
получаем  как
как
и следовало ожидать. Вычисления, проведенные Halperin, Gurian (1968), показывают, что эта модификация полосы Уоркинга-Хотеллинга, по-видимому, вообще приводит к доверительным интервалам более узким, чем интервалы, получаемые из полос постоянной ширины и трапецеидальной формы. Поэтому мы рекомендуем как итог использовать полосу (7.7), но значение X в случае  определять по таблицам, приведенным в приложении
определять по таблицам, приведенным в приложении 
Наконец, следует упомянуть об односторонних доверительных интервалах. Bohrer, Francis (1972) приводят (верхний) односторонний аналог полосы (7.7). Он имеет следующий вид (мы несколько видоизменили их модель, так чтобы  а не
а не 

Величина  в их обозначениях) табулирована для различных значений
в их обозначениях) табулирована для различных значений  в их обозначениях). Нижние односторонние интервалы получаются заменой знаков неравенств на противоположные и заменой X на
в их обозначениях). Нижние односторонние интервалы получаются заменой знаков неравенств на противоположные и заменой X на 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
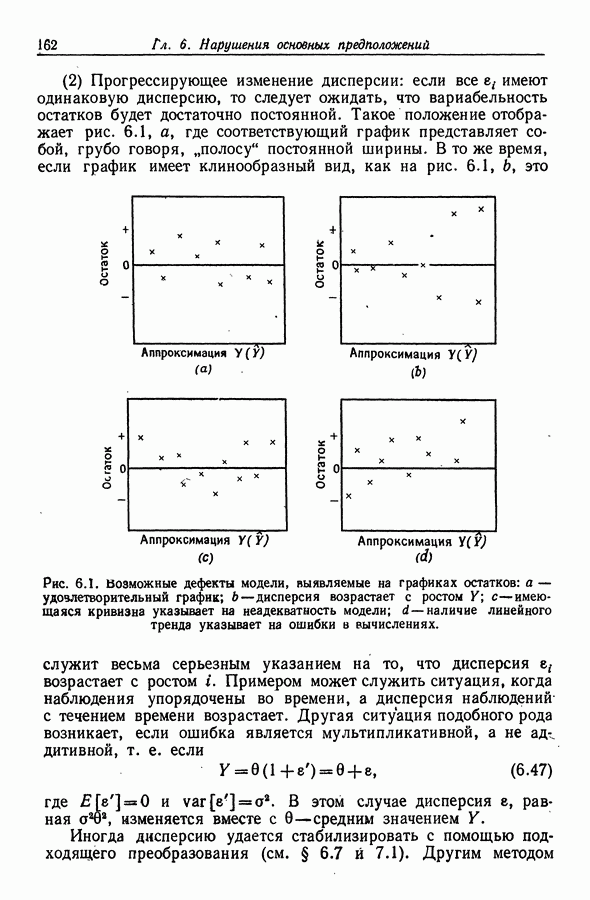
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
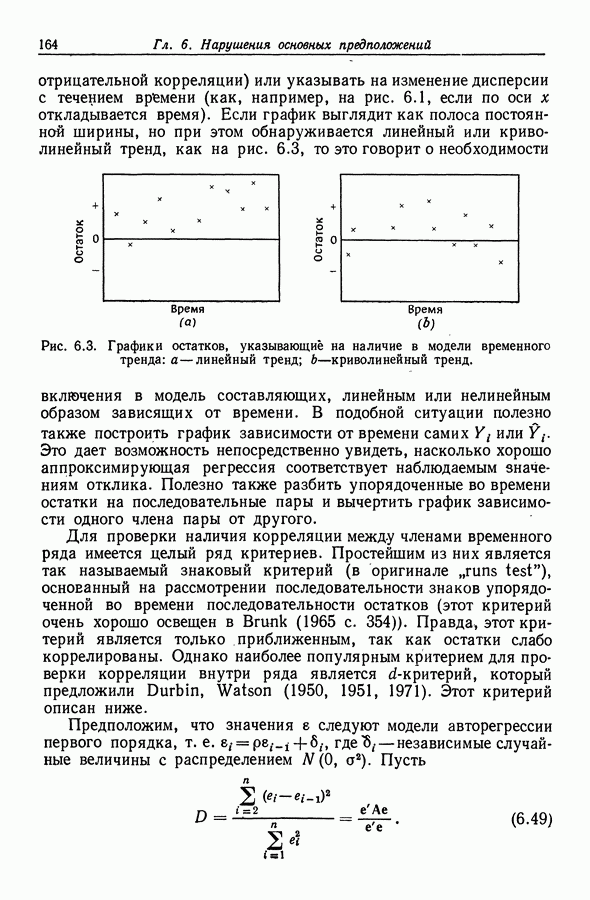
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
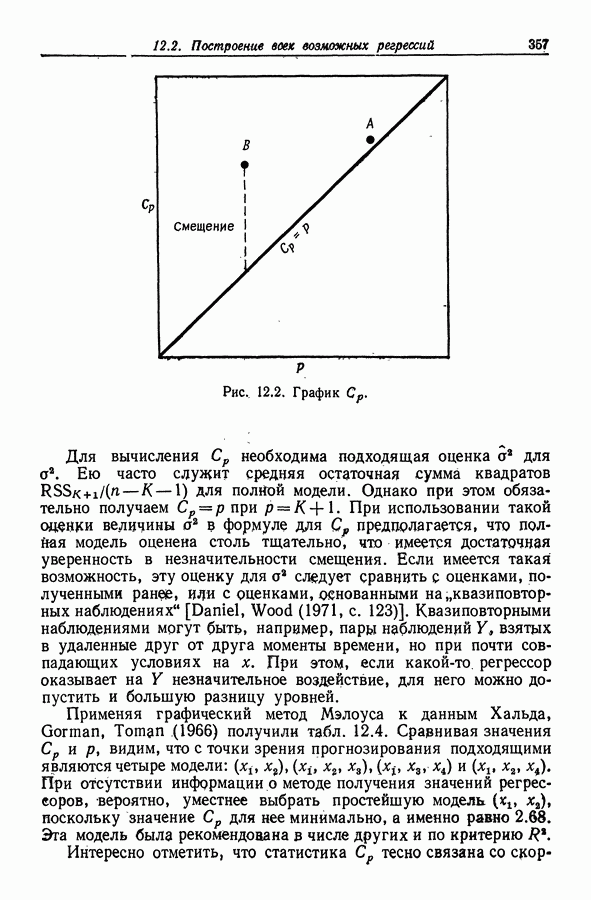
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
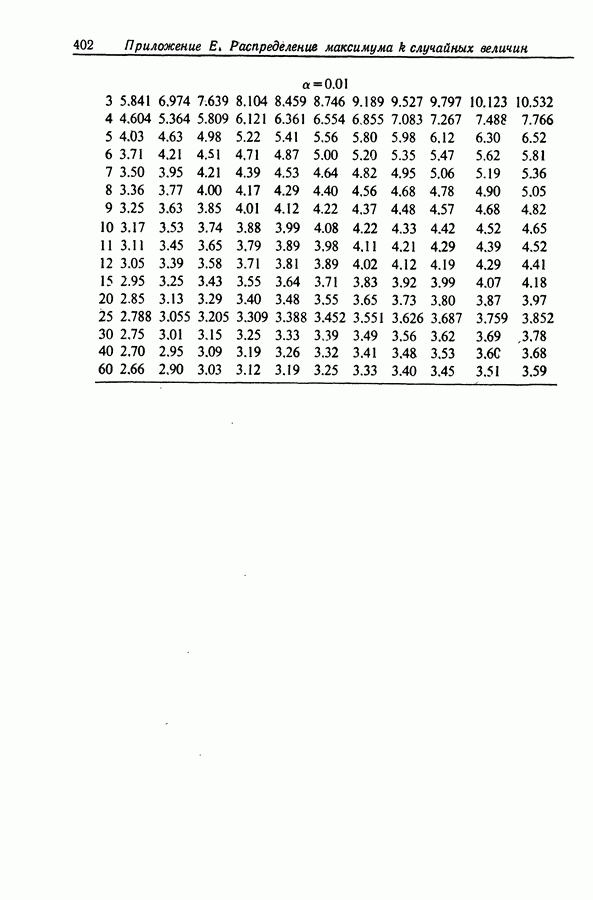
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ