| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.4. Сравнение методов
Система линейных уравнений  называется плохо обусловленной, если небольшие ошибки или изменения элементов матрицы В и вектора с очень сильно изменяют точное решение х этой системы. Разность
называется плохо обусловленной, если небольшие ошибки или изменения элементов матрицы В и вектора с очень сильно изменяют точное решение х этой системы. Разность  между решением уравнения
между решением уравнения  и решением уравнения
и решением уравнения

можно представить в виде

так что ее величина существенно зависит от входящей сюда обратной матрицы. Если матрица В близка к вырожденной, т. е. небольшие изменения элементов этой матрицы могут привести к ее вырождению, то разность  может оказаться очень большой.
может оказаться очень большой.
При составлении нормальных уравнений метода наименьших квадратов матрицы  и вектор
и вектор  содержат ошибки округления, поскольку они получаются путем выполнения определенных операций над
содержат ошибки округления, поскольку они получаются путем выполнения определенных операций над  Но даже если бы матрицу В можно было вычислить совершенно точно, при ее запоминании в вычислительной машине эта точность может быть утеряна. Дело в том, что все числа должны быть представлены в ЭВМ в двоичной системе, и такое десятичное число, как, скажем, 0.1, образует бесконечную двоичную дробь точно так же, как обыкновенная дробь 1/7 является бесконечной десятичной дробью. Это означает, что если матрица X плохо обусловлена (т. е. "небольшие" изменения ее элементов могут приводить к "большим" изменениям матрицы
Но даже если бы матрицу В можно было вычислить совершенно точно, при ее запоминании в вычислительной машине эта точность может быть утеряна. Дело в том, что все числа должны быть представлены в ЭВМ в двоичной системе, и такое десятичное число, как, скажем, 0.1, образует бесконечную двоичную дробь точно так же, как обыкновенная дробь 1/7 является бесконечной десятичной дробью. Это означает, что если матрица X плохо обусловлена (т. е. "небольшие" изменения ее элементов могут приводить к "большим" изменениям матрицы  и вектора
и вектора  то любые ошибки при формировании матрицы
то любые ошибки при формировании матрицы  могут серьезно повлиять на устойчивость и точность решения. В действительности описанное положение усугубляется еще и тем, что само, решение системы нормальных уравнений нельзя получить в точном виде. В процессе решения происходит накопление ошибок округления, и они в конце концов могут нарушить равновесие и сделать задачу неустойчивой, если матрица
могут серьезно повлиять на устойчивость и точность решения. В действительности описанное положение усугубляется еще и тем, что само, решение системы нормальных уравнений нельзя получить в точном виде. В процессе решения происходит накопление ошибок округления, и они в конце концов могут нарушить равновесие и сделать задачу неустойчивой, если матрица  близка к вырожденной. Проблема плохой обусловленности оказывается особенно серьезной в полиномиальной регрессии (см. разд. 8.1.1),
близка к вырожденной. Проблема плохой обусловленности оказывается особенно серьезной в полиномиальной регрессии (см. разд. 8.1.1),
Степень плохой обусловленности матрицы X измеряется числом обусловленности  которое мы определяем как отношение наибольшего сингулярного значения матрицы X к ее наименьшему ненулевому сингулярному значению (используются и другие определения). Сингулярные значения матрицы X — это положительные квадратные корни из собственных значений матрицы
которое мы определяем как отношение наибольшего сингулярного значения матрицы X к ее наименьшему ненулевому сингулярному значению (используются и другие определения). Сингулярные значения матрицы X — это положительные квадратные корни из собственных значений матрицы  Отметим следующие факты, относящиеся к числам
Отметим следующие факты, относящиеся к числам 

(2) Поскольку  имеем
имеем  .
.
Так как  то из свойства (1) вытекает, что матрица
то из свойства (1) вытекает, что матрица  обусловлена еще хуже, чем матрица X, поэтому, за исключением тех случаев, когда
обусловлена еще хуже, чем матрица X, поэтому, за исключением тех случаев, когда  имеет умеренное значение и матрица
имеет умеренное значение и матрица  может быть построена точно, лучше вообще не строить матрицу
может быть построена точно, лучше вообще не строить матрицу  Учитывая свойство (2) и тот факт, что число
Учитывая свойство (2) и тот факт, что число  до начала вычислений не известно, безопаснее работать с самой матрицей X и получать матрицу
до начала вычислений не известно, безопаснее работать с самой матрицей X и получать матрицу  непосредственно, используя методы ортогонального разложения из разд. 11.2.4. Однако все же и это не столь просто, поскольку влияние
непосредственно, используя методы ортогонального разложения из разд. 11.2.4. Однако все же и это не столь просто, поскольку влияние  полностью исключить невозможно [Golub (1969, с. 385), Wilkinson (1974)]. Из рассмотренных трех методов метод Хаусхольдера является в настоящее время (
полностью исключить невозможно [Golub (1969, с. 385), Wilkinson (1974)]. Из рассмотренных трех методов метод Хаусхольдера является в настоящее время ( по-видимому, наиболее Популярным среди специалистов в области численных методов. Он работает, несколько более быстро, чем
по-видимому, наиболее Популярным среди специалистов в области численных методов. Он работает, несколько более быстро, чем  приблизительно вдвое быстрее, чем метод Гивенса, и обладает примерно такой же точностью, как и каждый из этих двух методов. Однако модификация метода Гивенса, в которой отсутствует извлечение квадратных корней, успешно конкурирует с методом Хаусхольдера, поскольку она требует примерно таких, же вычислительных затрат, легко приспосабливается к взвешенному методу наименьших квадратов и обладает всеми преимуществами, описанными в разд. 11.2.4с. Ее легко приспособить также к случаю неполного ранга (разд. 11.5.4). Анализ ошибок для всех этих методов см. в работах Wilkinson (1967, 1974), Golub (1969, с. 382—385) и Gentleman (1973).
приблизительно вдвое быстрее, чем метод Гивенса, и обладает примерно такой же точностью, как и каждый из этих двух методов. Однако модификация метода Гивенса, в которой отсутствует извлечение квадратных корней, успешно конкурирует с методом Хаусхольдера, поскольку она требует примерно таких, же вычислительных затрат, легко приспосабливается к взвешенному методу наименьших квадратов и обладает всеми преимуществами, описанными в разд. 11.2.4с. Ее легко приспособить также к случаю неполного ранга (разд. 11.5.4). Анализ ошибок для всех этих методов см. в работах Wilkinson (1967, 1974), Golub (1969, с. 382—385) и Gentleman (1973).
В § 11.5 приведен ряд модификаций, допускающих вырожденность матрицы  Например, используя метод выбора главных элементов, т. е. допуская перестановку столбцов матрицы X, при которой на каждом шаге максимизируется следующий диагональный элемент матрицы
Например, используя метод выбора главных элементов, т. е. допуская перестановку столбцов матрицы X, при которой на каждом шаге максимизируется следующий диагональный элемент матрицы  можно все указанные в § 11.2 методы (за исключением метода Гивенса) обобщить таким образом, чтобы они допускали вырожденность матрицы
можно все указанные в § 11.2 методы (за исключением метода Гивенса) обобщить таким образом, чтобы они допускали вырожденность матрицы  В то же время при введении идентифицирующих ограничений можно использовать и метод Гивенса, не производя выбора главных элементов (разд. 11.5.4). Приведенное в разд. 11.5.4 разложение по сингулярным значениям, которое, по-видимому, является не менее точным, чем другие методы, оказывается особенно полезным, когда
В то же время при введении идентифицирующих ограничений можно использовать и метод Гивенса, не производя выбора главных элементов (разд. 11.5.4). Приведенное в разд. 11.5.4 разложение по сингулярным значениям, которое, по-видимому, является не менее точным, чем другие методы, оказывается особенно полезным, когда
ранг матрицы X неизвестен или когда матрица имеет полный ранг, но плохо обусловлена, причем непредсказуемым образом, как, например, в гребневой регрессии [Chambers (1971)]. Однако оно требует в два—четыре раза больших затрат, чем алгоритм Хаусхольдера, и не обладает присущей ему приспособляемостью.
Метод Хаусхольдера легко обобщить для использования его в задаче вычисления  -статистики для проверки общей линейной гипотезы (§ 11.10). К тому же его можно без труда видоизменить таким образом, чтобы допустить возможность добавления строки к матрице
-статистики для проверки общей линейной гипотезы (§ 11.10). К тому же его можно без труда видоизменить таким образом, чтобы допустить возможность добавления строки к матрице  (§ 11.8) или добавления столбца к матрице X (§ 11.9). Удалять строки и столбцы матрицы X лучше всего, используя преобразования Гивенса. Метод
(§ 11.8) или добавления столбца к матрице X (§ 11.9). Удалять строки и столбцы матрицы X лучше всего, используя преобразования Гивенса. Метод  также позволяет простым способом добавлять столбцы к матрице X, однако добавлять строки при этом труднее. Что касается метода Гивенса, то этим методом хорошо добавлять как раз строки, а не столбцы. Ясно, что подходящей процедурой является комбинация методов Хаусхольдера и Гивенса.
также позволяет простым способом добавлять столбцы к матрице X, однако добавлять строки при этом труднее. Что касается метода Гивенса, то этим методом хорошо добавлять как раз строки, а не столбцы. Ясно, что подходящей процедурой является комбинация методов Хаусхольдера и Гивенса.
На практике не так уже редко бывает, что один из регрессоров весьма сильно коррелирован с линейной комбинацией других регрессоров, так что столбцы матрицы X оказываются близкими к линейно зависимым. Это означает, что матрица  близка к вырожденной, наименьшее ее собственное значение мало, а
близка к вырожденной, наименьшее ее собственное значение мало, а  велико. Так, для тестовых данных Longley (1967)
велико. Так, для тестовых данных Longley (1967)  а для полиномиальных моделей Wampler (1970) соответствующее значение имеет порядок
а для полиномиальных моделей Wampler (1970) соответствующее значение имеет порядок  : На самом деле полиномиальные модели регрессии заведомо плохо обусловлены, если степень полинома больше 5 или 6, особенно если значения х являются равноотстоящими (разд. 8.1.1). Поэтому следует исходить из того что всякая разумная программа должна либо приводить к правильно округленному решению
: На самом деле полиномиальные модели регрессии заведомо плохо обусловлены, если степень полинома больше 5 или 6, особенно если значения х являются равноотстоящими (разд. 8.1.1). Поэтому следует исходить из того что всякая разумная программа должна либо приводить к правильно округленному решению  либо указывать на то, что матрица
либо указывать на то, что матрица  слишком плохо обусловлена и не позволяет достичь этого без увеличения точности вычислений (или может быть даже вырождена). При выборе главных элементов, когда на каждом шаге производится максимизация
слишком плохо обусловлена и не позволяет достичь этого без увеличения точности вычислений (или может быть даже вырождена). При выборе главных элементов, когда на каждом шаге производится максимизация  неполнота ранга матрицы X, искаженной ошибками округления, проявляется в том, что на некотором шаге значение
неполнота ранга матрицы X, искаженной ошибками округления, проявляется в том, что на некотором шаге значение  оказывается меньшим некоторого допустимого предела. Более высокую точность при вычислении
оказывается меньшим некоторого допустимого предела. Более высокую точность при вычислении  можно получить, используя итерационное уточнение решения (§ 11.6). Правда, этот метод не, пригоден, когда модель обусловлена слишком плохо. Если после одной итерации заметного улучшения
можно получить, используя итерационное уточнение решения (§ 11.6). Правда, этот метод не, пригоден, когда модель обусловлена слишком плохо. Если после одной итерации заметного улучшения  не наблюдается, это означает, что модель обусловлена в высшей
не наблюдается, это означает, что модель обусловлена в высшей  пени плохо. В таком случае, если производить вычисления с более высокой точностью невозможно, следует попробовать применить более точный метод разложения по сингулярным значениям (разд. 11.5.5) или обращаться с моделью так, как если бы она
пени плохо. В таком случае, если производить вычисления с более высокой точностью невозможно, следует попробовать применить более точный метод разложения по сингулярным значениям (разд. 11.5.5) или обращаться с моделью так, как если бы она
была вырождена. Указанным требованиям удовлетворяет программа [Bjorck, Golub (1967)], использующая преобразования Хаусхольдера. В ней предусмотрен специальный выход "отказ", соответствующий тем ситуациям, когда в результате ошибок округления ранг матрицы X оказывается неполным или когда процедура итерационного уточнения не дает существенного улучшения.
Чтобы по возможности избежать трудностей с вычислениями, рекомендуется перед расчетом регрессий производить, как в разд. 11.7.1, вычитание средних из  Такое "центрирование" данных может приводить к уменьшению числа обусловленности матрицы X [Golub, Styan (1974)]. Некоторые авторы рекомендуют также нормировать столбцы матриц
Такое "центрирование" данных может приводить к уменьшению числа обусловленности матрицы X [Golub, Styan (1974)]. Некоторые авторы рекомендуют также нормировать столбцы матриц  как в разд. 11.7.2, особенно при использовании метода разложения по сингулярным значениям.
как в разд. 11.7.2, особенно при использовании метода разложения по сингулярным значениям.
В заключение этого сравнения алгоритмов, реализующих метод наименьших квадратов, следует упомянуть еще об одном алгоритме [Bauer (1965)]. В этом алгоритме, использующем разложение матрицы X, подобное разложению (11.23) из разд. 11.2.4, применяется схема исключения Гаусса, но только для исключения используется не отдельная строка, а линейная комбинация строк с надлежащим образом выбранными весами. Прекрасные программы на языке АЛГОЛ для этого алгоритма и для большинства других методов, описанных в § 11.2, приводят Wilkinson, Reinsch (1971). Численное сравнение программ, использующих алгоритмы из § 11.2, дает Wampler (1970). Относительно общей библиографии по вопросу применения ЭВМ для анализа данных можно рекомендовать работу Muller (1970).
11.5. Случай неполного ранга
Если матрица X имеет ранг  то матрица
то матрица  вырождена (положительно полуопределена) и нормальные уравнения
вырождена (положительно полуопределена) и нормальные уравнения  уже не именэт единственного решения. Ниже приводится пять численных методов обработки данных в такой ситуации.
уже не именэт единственного решения. Ниже приводится пять численных методов обработки данных в такой ситуации.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
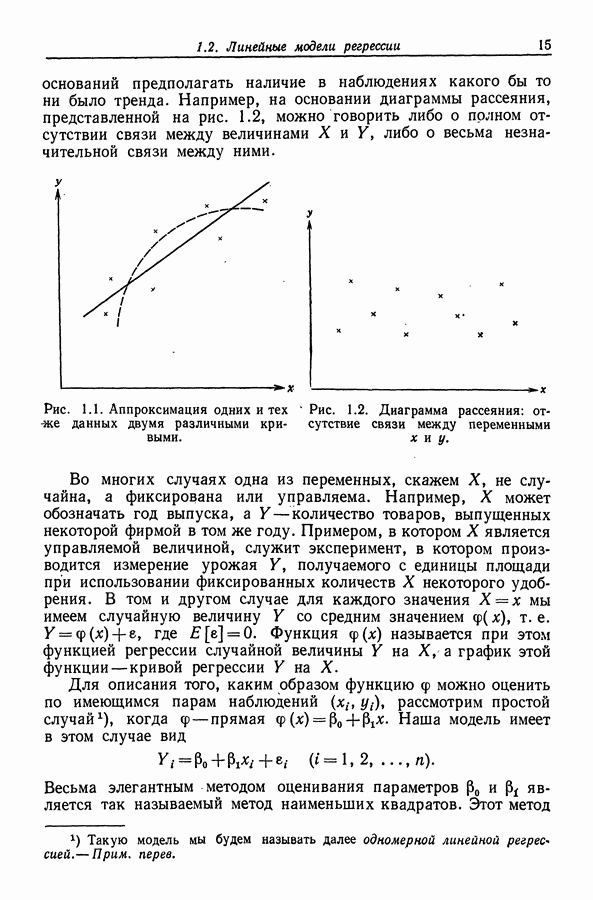
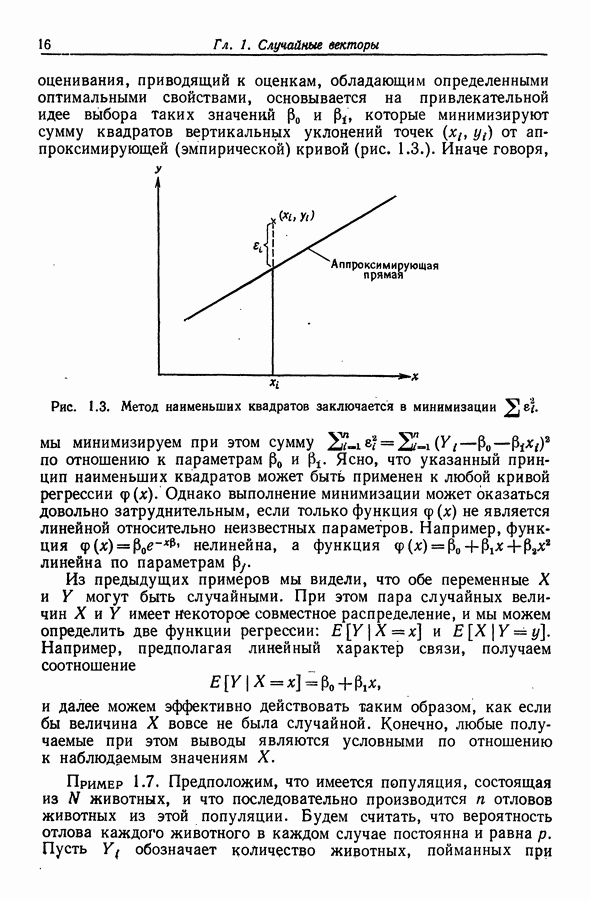
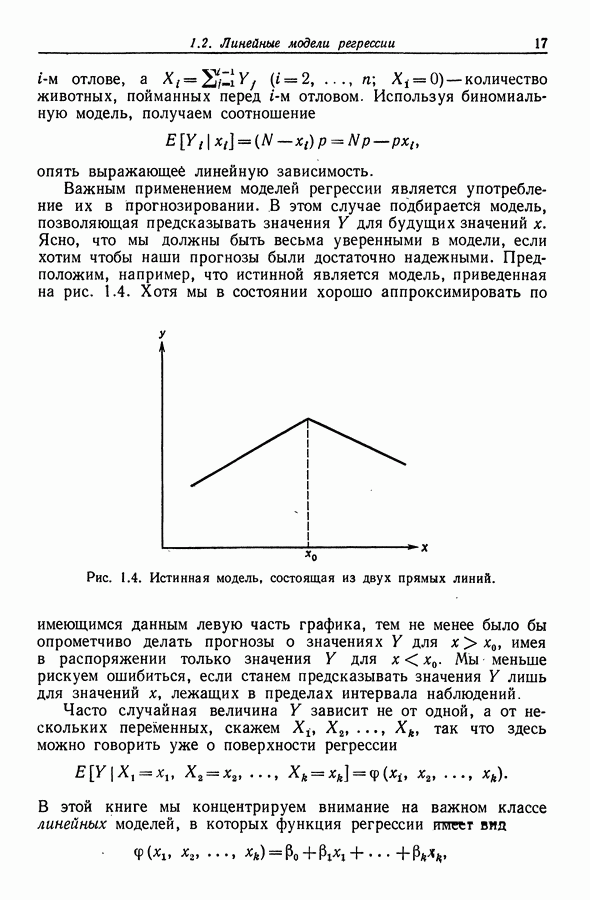
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
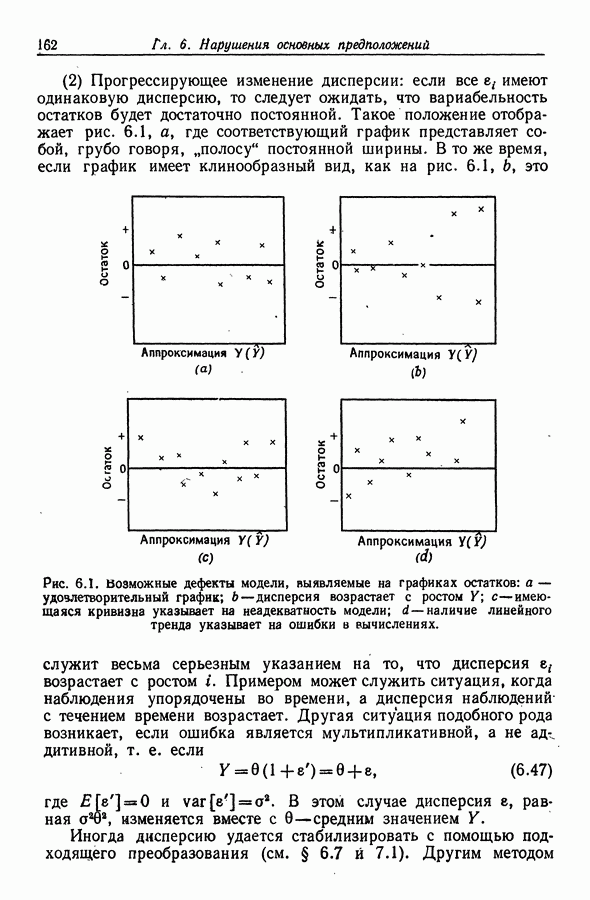
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
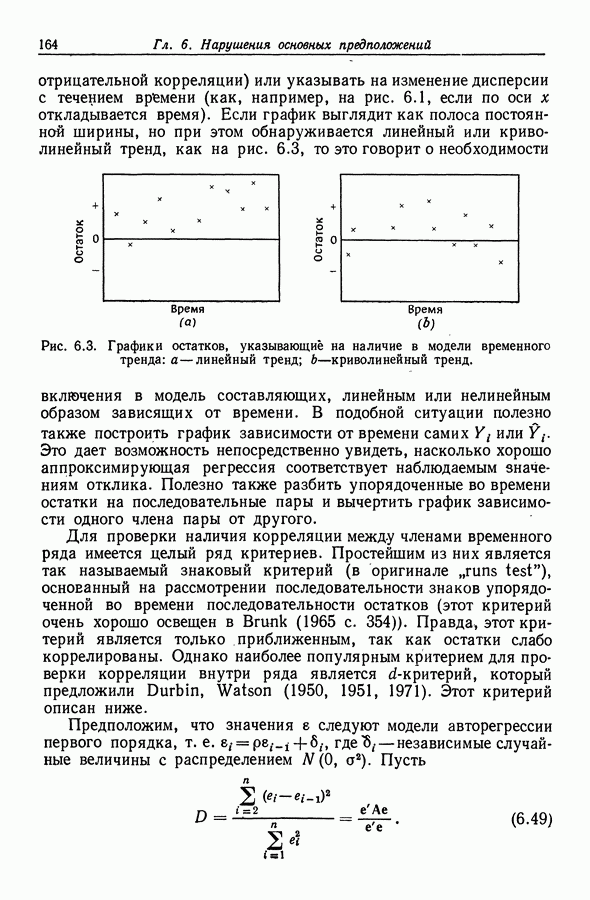
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
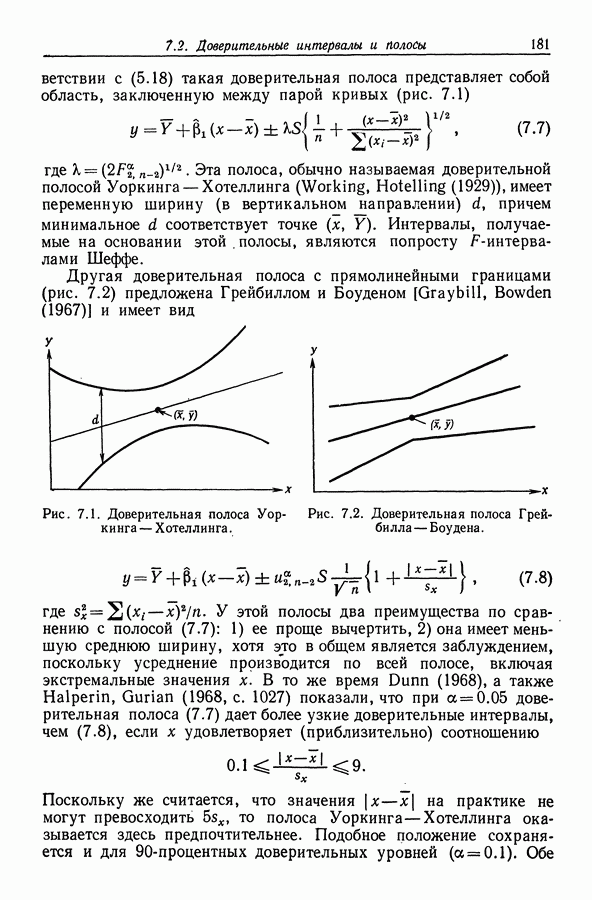
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
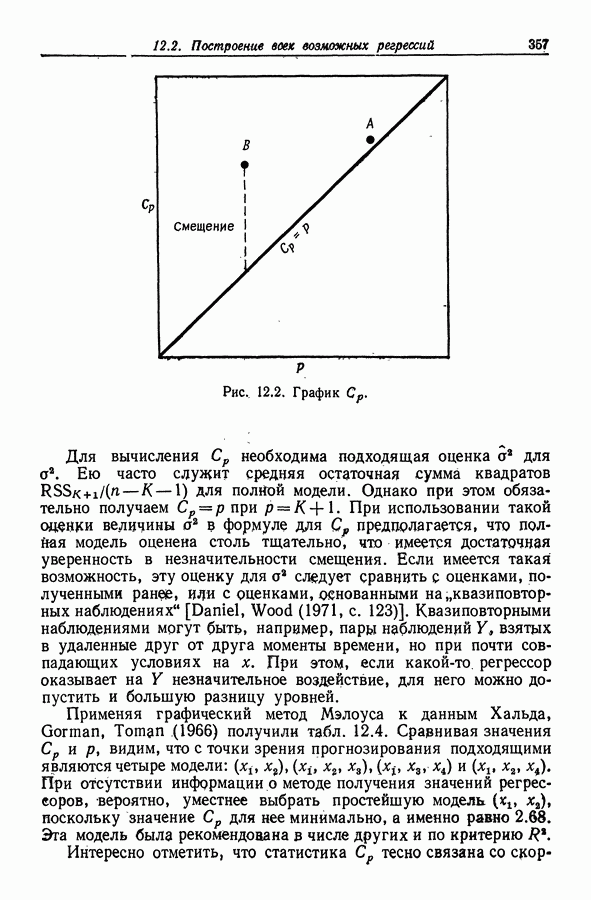
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
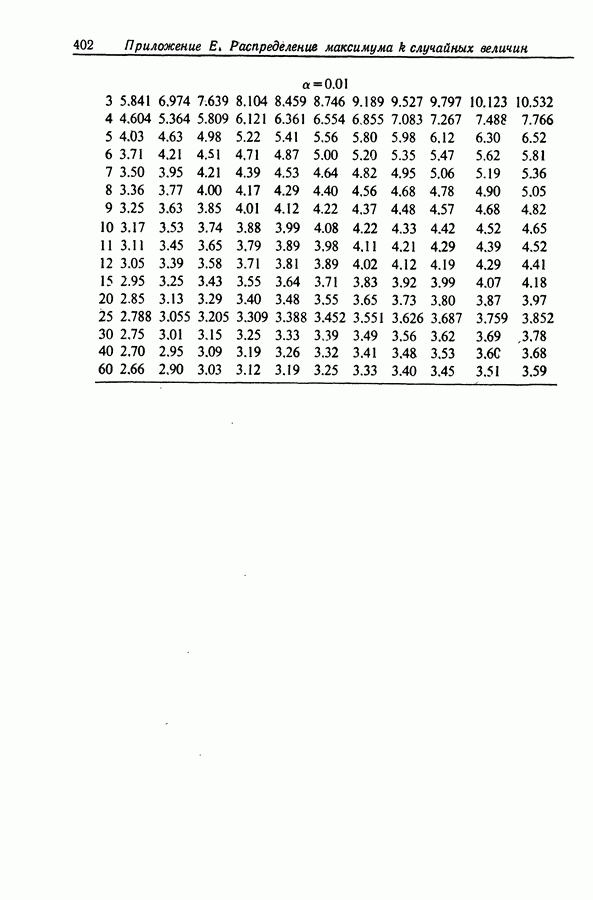
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
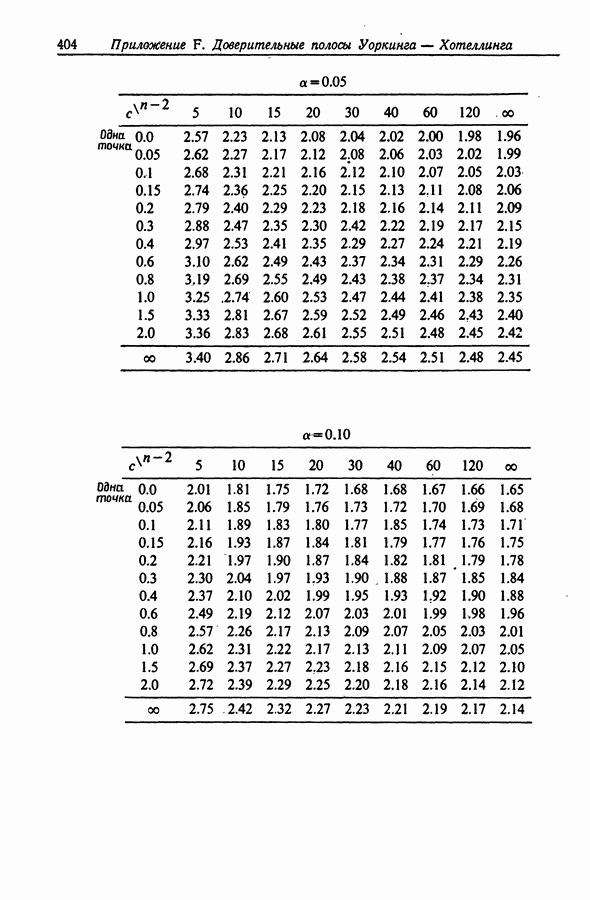
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ