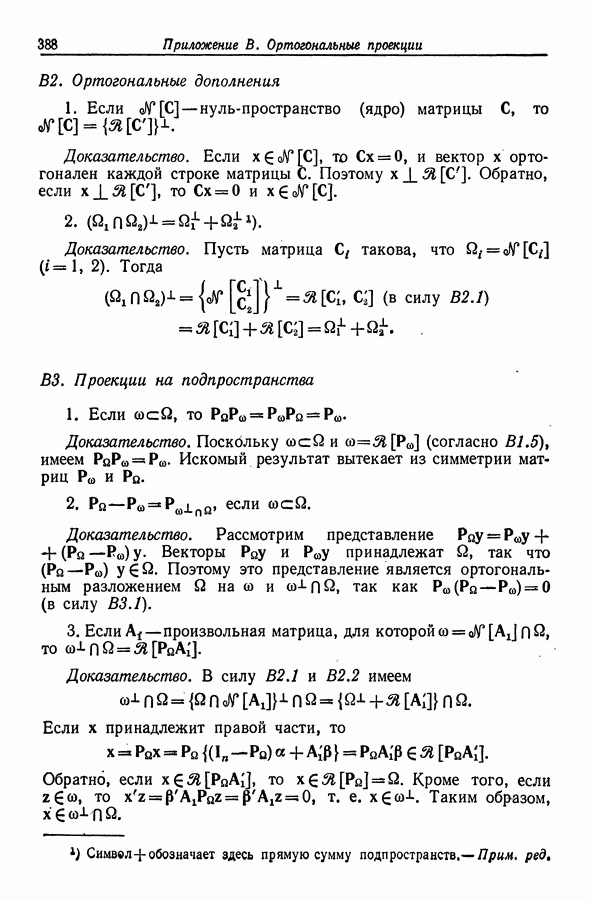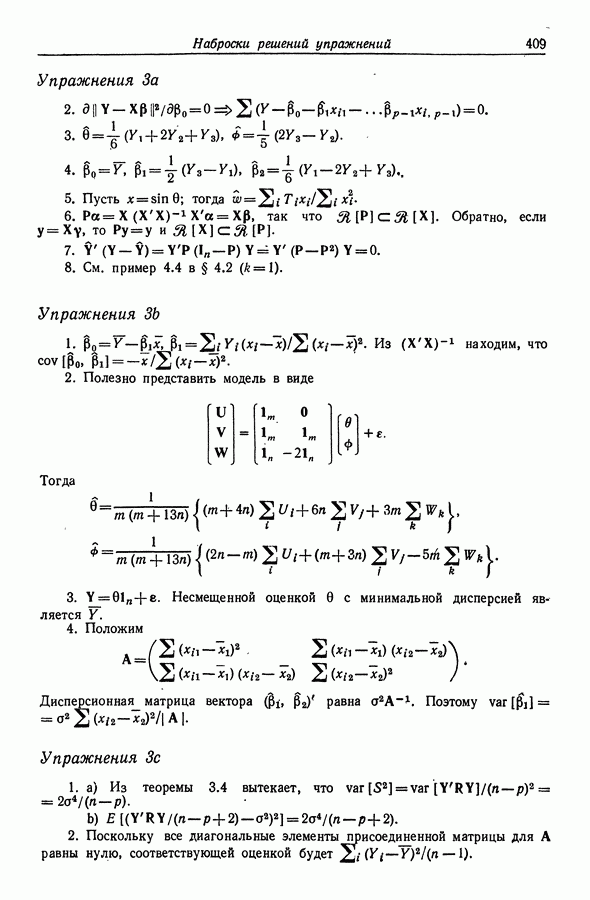| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.5. Многомерная полиномиальная регрессия
8.5.1. Подбор аппроксимирующей поверхности
Значительное внимание в литературе уделено задаче подбора полинома второй степени от нескольких переменных

Как оказывается, вся теория ортогональных полиномов может быть обобщена и для использования ее в двумерном случае. И здесь фундаментальную роль играют полиномы Чебышева. За подробностями мы отсылаем читателя к работе Hayes (1974).
8.5.2. Поверхности отклика
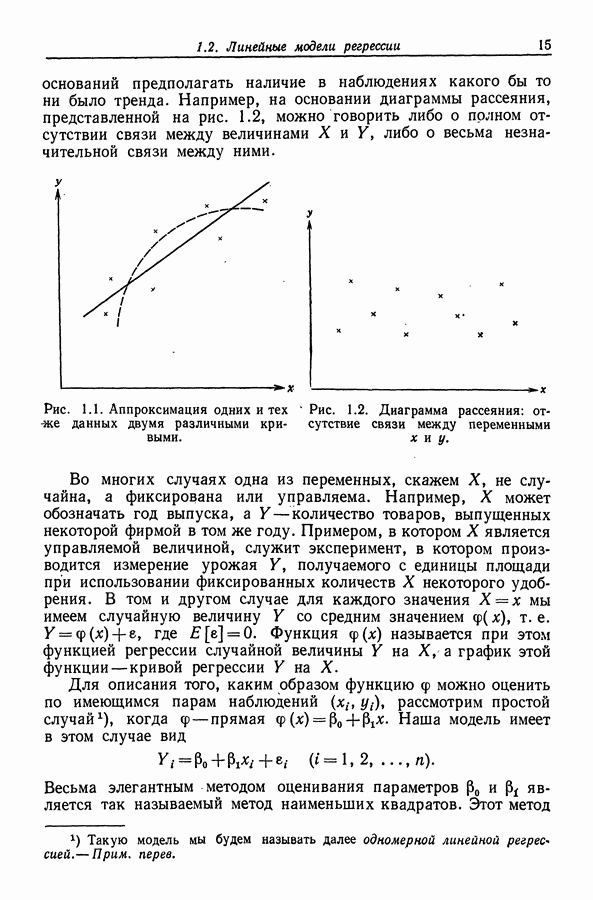
Одним из наиболее важных применений полиномиальной регрессии от нескольких переменных является изучение поверхностей отклика. Мы проиллюстрируем некоторые основные черты этой методологии, рассматривая случай, когда имеются только два регрессора.
Предположим, что "отклик" (выход)  в заданном эксперименте является неизвестной функцией
в заданном эксперименте является неизвестной функцией  от двух переменных:
от двух переменных:  (температуры) и
(температуры) и  (концентрации). Предположим также, что поверхность в трехмерном пространстве, реализующая эту функцию, "ведет себя достаточно хорошо". В частности, пусть
(концентрации). Предположим также, что поверхность в трехмерном пространстве, реализующая эту функцию, "ведет себя достаточно хорошо". В частности, пусть
она является гладкой и имеет единственный хорошо выраженный пик. Значение  отклика измеряется с ошибкой, так что в действительности мы наблюдаем величину
отклика измеряется с ошибкой, так что в действительности мы наблюдаем величину  где
где  Основная задача теории откликов состоит в оценке координат
Основная задача теории откликов состоит в оценке координат  вершины указанного пика.
вершины указанного пика.
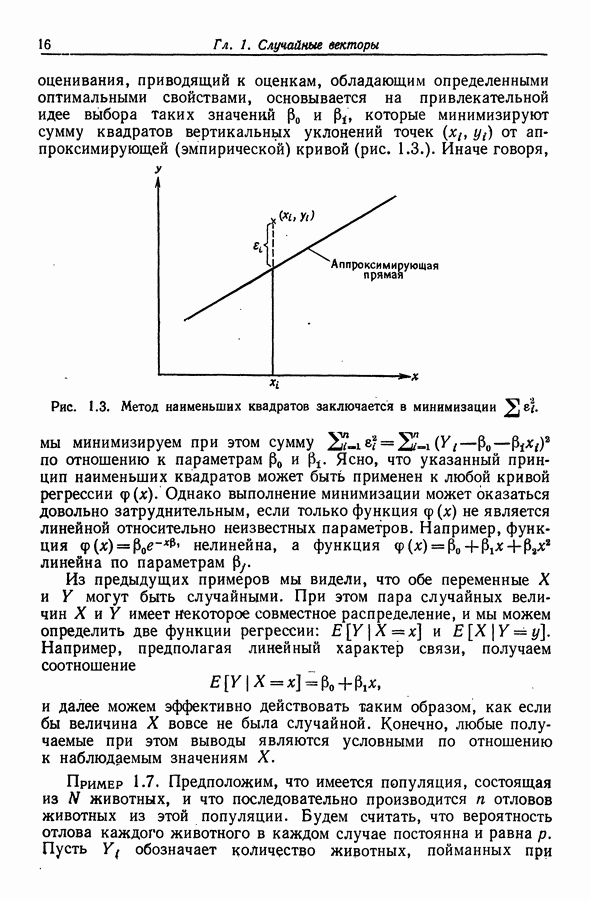
Один из способов решения этой задачи заключается в использовании последовательности экспериментов и метода быстрейшего восхождения для "подъема на вершину" поверхности. Для точек, удаленных от точки максимума, поверхность является относительно линейной, так что ее можно приблизить в окрестности такой точки некоторой плоскостью

Для оценки коэффициентов  можно использовать, например, так называемый
можно использовать, например, так называемый  -план, в котором наблюдаются значения
-план, в котором наблюдаются значения  в четырех вершинах малого прямоугольника с центром
в четырех вершинах малого прямоугольника с центром  на плоскости
на плоскости  (рис. 8.1).
(рис. 8.1).

Рис. 8.1. Поверхность отклика..
Предположим, что мы наблюдаем при этом значения  величины
величины  в точках
в точках  где
где  два выбранных значения переменной
два выбранных значения переменной  два выбранных значения переменной
два выбранных значения переменной  Тогда мы можем подбирать к этим данным модель
Тогда мы можем подбирать к этим данным модель

где  и получить аппроксимирующую плоскость в виде
и получить аппроксимирующую плоскость в виде

Если  — точка этой плоскости, расположенная по вертикали над точкой
— точка этой плоскости, расположенная по вертикали над точкой  то плоскость, аппроксимирующая поверхность
то плоскость, аппроксимирующая поверхность
в окрестности точки  может помочь нам переместиться в сторону более высокой точки
может помочь нам переместиться в сторону более высокой точки  поверхности и соответственно получить большее значение К. Например, если в
поверхности и соответственно получить большее значение К. Например, если в  положительны, то следует увеличить
положительны, то следует увеличить  Однако наиболее эффективный способ подъема состоит в перемещении по направлению наибольшей крутизны. Для отыскания этого так называемого пути быстрейшего подъема рассмотрим следующую задачу. Предположим, что нам нужно максимизировать разность
Однако наиболее эффективный способ подъема состоит в перемещении по направлению наибольшей крутизны. Для отыскания этого так называемого пути быстрейшего подъема рассмотрим следующую задачу. Предположим, что нам нужно максимизировать разность  при условии
при условии  Используя множитель Лагранжа
Используя множитель Лагранжа  имеем
имеем

Приравнивая  правой части (8.28), находим, что значения
правой части (8.28), находим, что значения  соответствующие максимальному значению указанной разности, должны быть пропорциональны значениям
соответствующие максимальному значению указанной разности, должны быть пропорциональны значениям  Поэтому, рассматривая
Поэтому, рассматривая  как начало координат, следует выбрать координаты
как начало координат, следует выбрать координаты  точки следующего наблюдения в виде
точки следующего наблюдения в виде  где
где  какое-нибудь положительное число. Постепенно увеличивая значения
какое-нибудь положительное число. Постепенно увеличивая значения  мы можем проводить измерения соответствующих значений К до тех пор, пока не достигнем такой точки
мы можем проводить измерения соответствующих значений К до тех пор, пока не достигнем такой точки  на плоскости
на плоскости  в которой изменение
в которой изменение  при изменении
при изменении  становится или очень малым, или даже отрицательным. После этого мы реализуем новый
становится или очень малым, или даже отрицательным. После этого мы реализуем новый  -план на малом прямоугольнике с центром в точке
-план на малом прямоугольнике с центром в точке  и подбираем новую плоскость (8.28). Затем опять определяем направление быстрейшего подъема и движемся в этом направлении, пока не достигнем малых изменений в значениях
и подбираем новую плоскость (8.28). Затем опять определяем направление быстрейшего подъема и движемся в этом направлении, пока не достигнем малых изменений в значениях  скажем в точке
скажем в точке  На этом пути мы продвигаемся в сторону вершины поверхности.
На этом пути мы продвигаемся в сторону вершины поверхности.
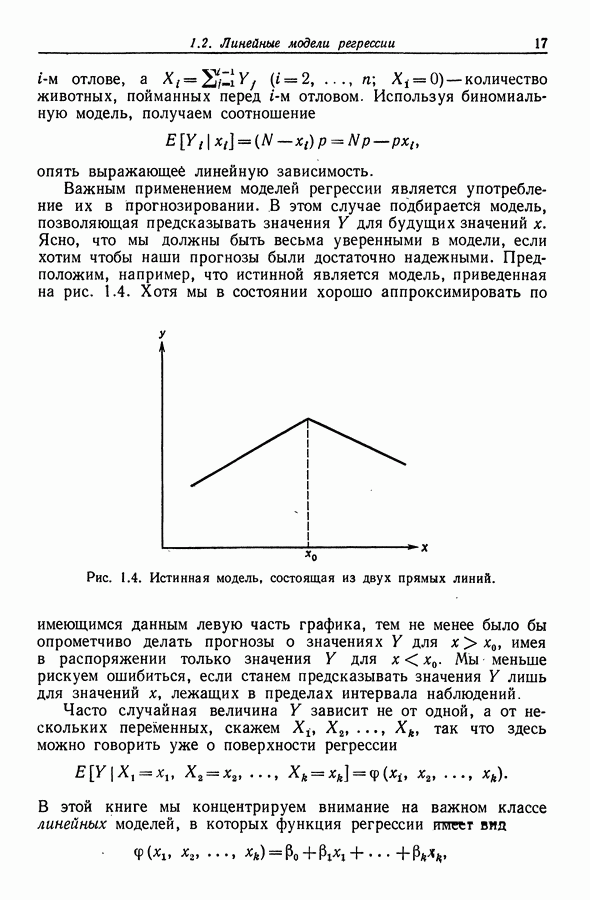
При приближении к вершине значения  становятся все более малыми и продвигаться, используя метод быстрейшего подъема, становится все труднее. Здесь уже существенное влияние на значения
становятся все более малыми и продвигаться, используя метод быстрейшего подъема, становится все труднее. Здесь уже существенное влияние на значения  оказывает кривизна поверхности. Поэтому в непосредственной близости к вершине можно подбирать не плоскость, а квадратичный полином вида (8.25), используя для этой цели, скажем,
оказывает кривизна поверхности. Поэтому в непосредственной близости к вершине можно подбирать не плоскость, а квадратичный полином вида (8.25), используя для этой цели, скажем,  -план. Этот план состоит в использовании трех значений
-план. Этот план состоит в использовании трех значений  и трех значений
и трех значений  и в наблюдении значений
и в наблюдении значений  в соответствующих 9 точках. Посредством переноса начала и поворота осей аппроксимирующую поверхность
в соответствующих 9 точках. Посредством переноса начала и поворота осей аппроксимирующую поверхность

можно представить в каноническом виде

здесь  — оценки координат вершины
— оценки координат вершины  поверхности. Тройку чисел
поверхности. Тройку чисел  проще всего найти, беря частные
проще всего найти, беря частные
производные (8.29) по  и решая получающуюся пару уравнений относительно
и решая получающуюся пару уравнений относительно  При этом мы получаем значения
При этом мы получаем значения  а значение
а значение  есть просто значение у в (8.29) при
есть просто значение у в (8.29) при 
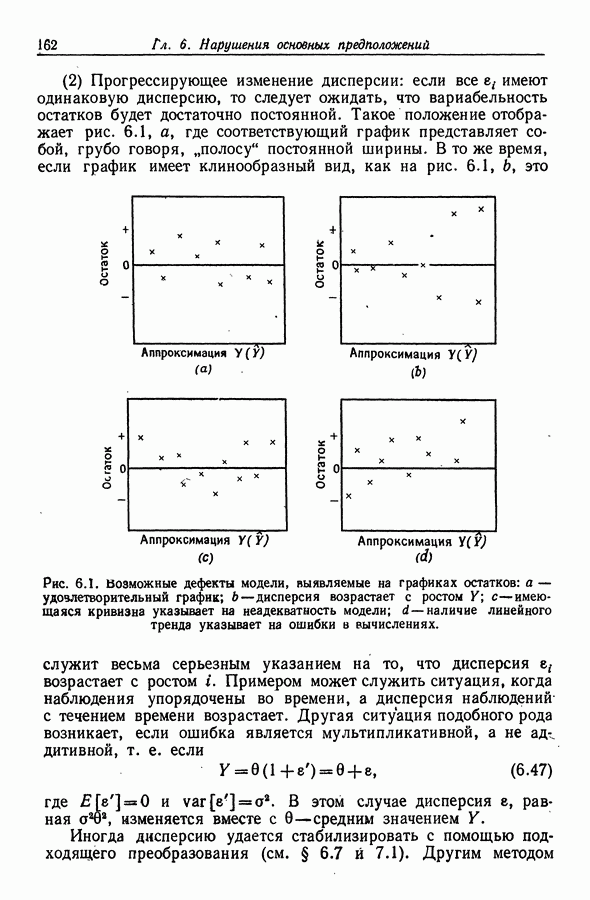
Приведенное нами довольно беглое описание методологии, связанной с поверхностями отклика, оставляет открытыми целый ряд вопросов. Укажем, например, такие из них:
(1) В указанном рассмотрении мы использовали для подбора плоскости в качестве плана первого порядка  -план, а для подбора квадратичного полинома (в качестве плана второго порядка) -
-план, а для подбора квадратичного полинома (в качестве плана второго порядка) -  -план (план второго порядка). При этом возникает вопрос: какие планы лучше использовать в каждом из этих случаев?
-план (план второго порядка). При этом возникает вопрос: какие планы лучше использовать в каждом из этих случаев?
(2) Как мы можем узнать, когда надо переходить от плана первого порядка к плану второго порядка?
(3) Как следует выбирать значения 
(4) Что будет, если в процессе подъема мы попадем в стационарную точку, не являющуюся максимумом, или на медленно повышающийся гребень? (Подобная ситуация соответствует случаю, когда в (8.30) то или иное значение к; оказывается отрицательным.)
Хотя у нас и нет возможности рассматривать здесь эти и другие важные в практическом отношении вопросы, некоторые комментарии относительно планов первого порядка все же уместно сделать. Мы видели в § 3.5 (лемма), что планы с ортогональной структурой обладают некоторыми свойствами оптимальности. В частности,  -план относится к этой категории и является
-план относится к этой категории и является  -оптимальным
-оптимальным  если шкалировать значения
если шкалировать значения  так, чтобы они принимали значения ±1. Для изучения этой ортогональной структуры удобно представить символически два уровня значений переменной
так, чтобы они принимали значения ±1. Для изучения этой ортогональной структуры удобно представить символически два уровня значений переменной  в виде 1 и а, а два уровня значений переменной
в виде 1 и а, а два уровня значений переменной  виде
виде  Тогда все четыре возможных комбинации
Тогда все четыре возможных комбинации  можно представить символически (перемножая значения уровней в каждой паре) как
можно представить символически (перемножая значения уровней в каждой паре) как  а значения
а значения  в этих точках — как
в этих точках — как  соответственно. В такой записи модель (8.27) принимает вид
соответственно. В такой записи модель (8.27) принимает вид

или  где столбцы матрицы X взаимно ортогональны и удовлетворяют условиям леммы из § 3.5. Поэтому
где столбцы матрицы X взаимно ортогональны и удовлетворяют условиям леммы из § 3.5. Поэтому

так что

и

Если использовать терминологию факторного анализа и именовать  "факторами"
"факторами"  то
то  и
и  — суть оценки величин, которые можно было бы назвать главными эффектами факторов
— суть оценки величин, которые можно было бы назвать главными эффектами факторов  соответственно.
соответственно.
Дальнейшее рассмотрение общей теории выбора оптимальных планов для анализа поверхностей отклика можно найти в работах Box, Draper (1971, 1975), Atkinson (1972), Thompson (1973) и Mitchel (1974b). Описание методов анализа поверхности отклика имеется в работах Davies (1960), Hill, Hunter (1966, обзорная статья), John (1971, гл. 10), Guttman и др. (1971, с. 435 и далее), а также в работах Myers (1971), Налимов, Чернова (1965, В дополнение к методу быстрейшего подъема Box (1957) и Box, Draper (1969) предложили другой метод, известный под названием эволюционного планирования, который можно рекомендовать для использования в промышленности. Этот метод, однако, не используется столь широко, как это могло бы быть, и мы отсылаем читателя за полезными комментариями по этому поводу к работам Hahn, Dershowitz (1974) и Lowe (1974).
Упражнения к гл. 8
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
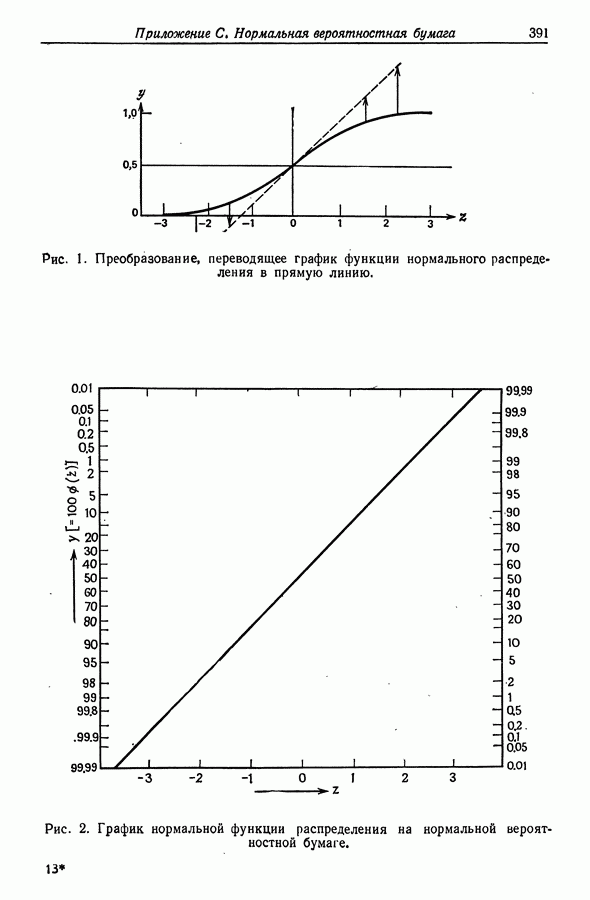
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
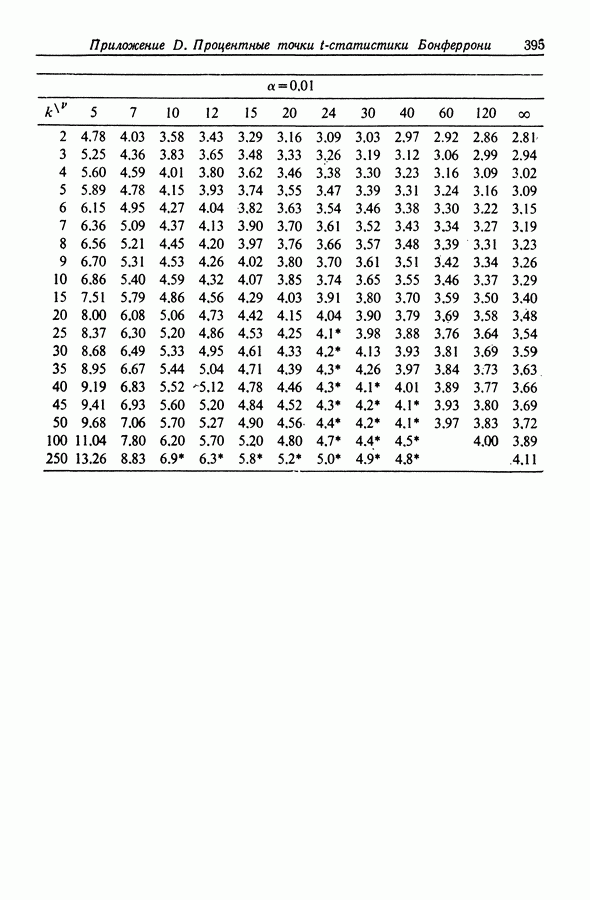
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
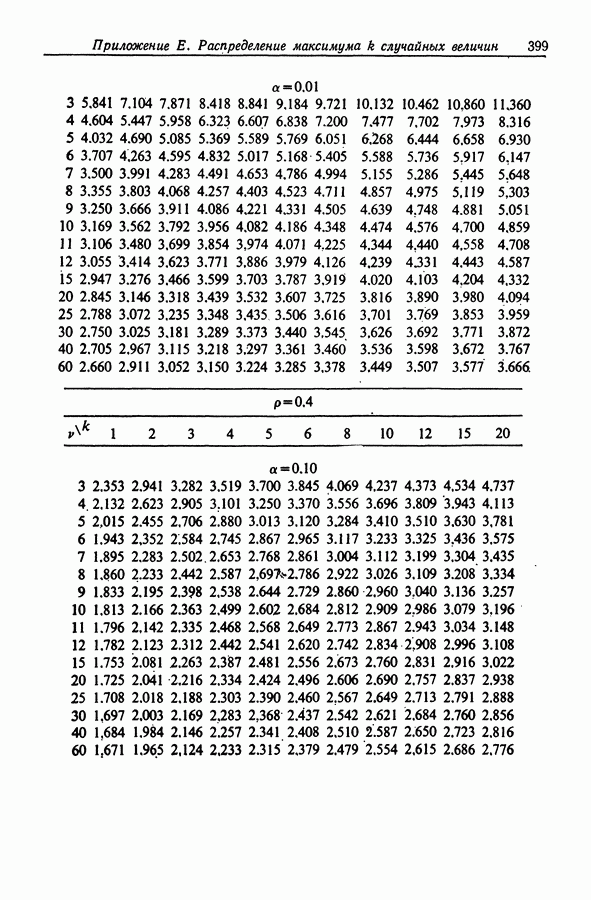
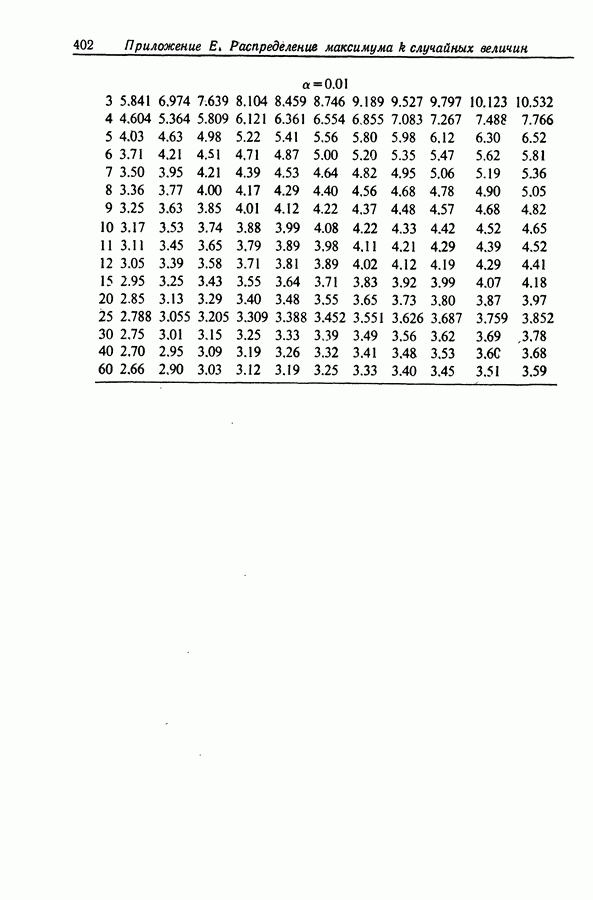
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
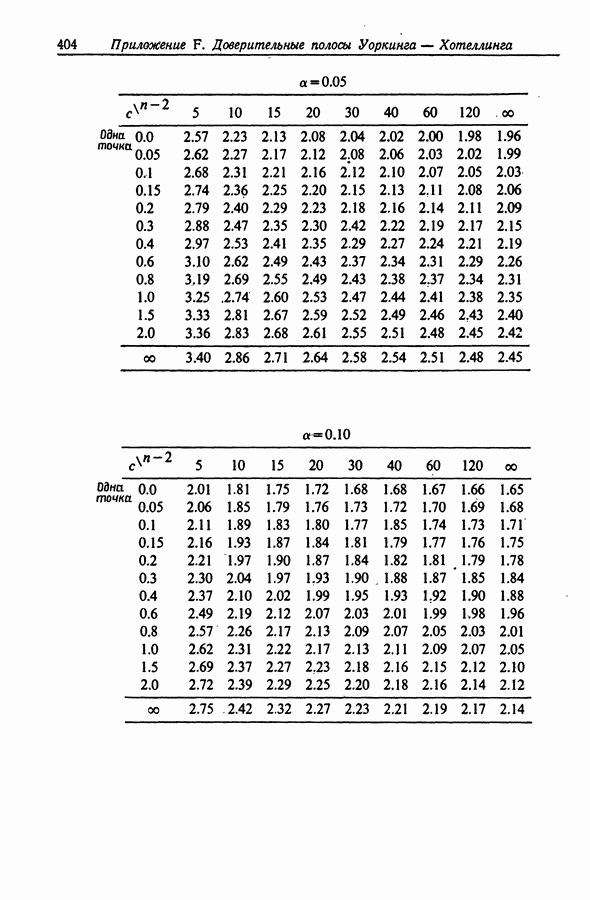
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ