| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
12.3. Построение только наилучших регрессий
12.3.1. Поиск вдоль перспективных ветвей
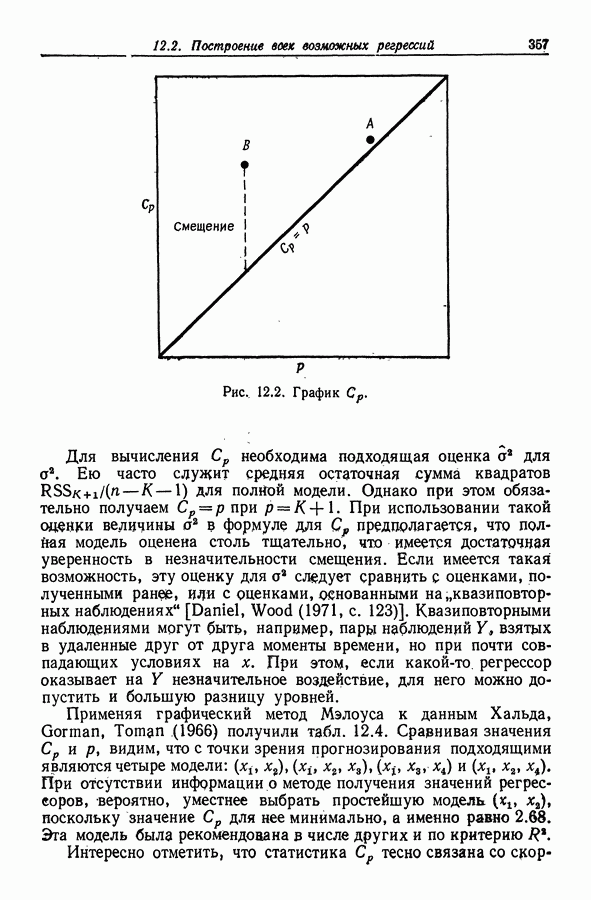
При наличии современных ЭВМ исследование всех  регрессий для
регрессий для  оказывается не столь уж бессмысленным. Daniel, Wood (1971, с. 85) утверждают, например, что при эффективном
оказывается не столь уж бессмысленным. Daniel, Wood (1971, с. 85) утверждают, например, что при эффективном
программировании  остаточных сумм квадраюв могут быть вычислены (что равносильно подбору 4096 уравнений) на машине типа IBM 360-65 менее чем за 10 с. Поэтому здесь лимитирующим фактором является, по существу, не время, а объем памяти, В то же время с ростом К количество вычислений растет экспоненциальным образом, и, поскольку использование регрессий с 20 и более переменными не является чем-то необычным, мы нуждаемся в таком методе, который ограничивал бы процедуру поиска только наиболее "полезными" регрессиями. Можно показать, что всякий такой метод поиска по крайней мере должен для каждого значения
остаточных сумм квадраюв могут быть вычислены (что равносильно подбору 4096 уравнений) на машине типа IBM 360-65 менее чем за 10 с. Поэтому здесь лимитирующим фактором является, по существу, не время, а объем памяти, В то же время с ростом К количество вычислений растет экспоненциальным образом, и, поскольку использование регрессий с 20 и более переменными не является чем-то необычным, мы нуждаемся в таком методе, который ограничивал бы процедуру поиска только наиболее "полезными" регрессиями. Можно показать, что всякий такой метод поиска по крайней мере должен для каждого значения  отыскивать среди всех возможных моделей с
отыскивать среди всех возможных моделей с  переменными
переменными  включается в модель) тот набор
включается в модель) тот набор  регрессоров, который имеет минимальное значение
регрессоров, который имеет минимальное значение  что равносильно, минимальное значение
что равносильно, минимальное значение  Поскольку можно ожидать, что лишь некоторые из остальных -наборов будут иметь значения
Поскольку можно ожидать, что лишь некоторые из остальных -наборов будут иметь значения  близкие к этому минимальному, то следует надеяться, что поиск минимума попутно приведет и к получению конкурирующих моделей,
близкие к этому минимальному, то следует надеяться, что поиск минимума попутно приведет и к получению конкурирующих моделей,
Два подобных метода приводящие к большинству наиболее полезных моделей и не требующие перебора всех подмножеств, указаны в работе Beale и др. (1967) и в статье Hocking, Leslie (1967). Они, по существу, используют метод поиска по деревьям, избегающий поиска вдоль бесперспективных ветвей. В приводимом ниже рассмотрении, взятом из статьи Hocking, Leslie, удобнее иметь дело с  переменными не включаемыми в модель, т. е. с переменными, исключенными из полной модели с К регрессорами.
переменными не включаемыми в модель, т. е. с переменными, исключенными из полной модели с К регрессорами.
Пусть  остаточная сумма квадратов, полученная при включении в модель всех К регрессоров, кроме регрессора
остаточная сумма квадратов, полученная при включении в модель всех К регрессоров, кроме регрессора  Предположим, что регрессоры перенумерованы в соответствии с величиной
Предположим, что регрессоры перенумерованы в соответствии с величиной  т. е.
т. е.

После подсчета всех  для
для  выполняются следующие этапы вычислений:
выполняются следующие этапы вычислений:
Этап 1. Вычисляется RSS для модели, в которой отсутствуют регрессоры с номерами  Если полученная
Если полученная  не превосходит
не превосходит  то процесс останавливается. При этом регрессия, образованная
то процесс останавливается. При этом регрессия, образованная  регрессорами
регрессорами  будет соответствовать "наилучшему" набору
будет соответствовать "наилучшему" набору  регрессоров в смысле минимума RSS. Если же полученная RSS оказывается большей, чем
регрессоров в смысле минимума RSS. Если же полученная RSS оказывается большей, чем  то никакого решения не принимается, и мы переходим к
то никакого решения не принимается, и мы переходим к 
Этап 2. Регрессор  включается теперь в число кандидатур на исключение из модели, и подсчитываются значений RSS, получаемых исключением из набора первых
включается теперь в число кандидатур на исключение из модели, и подсчитываются значений RSS, получаемых исключением из набора первых  регрессоров любого набора
регрессоров любого набора  регрессоров, обязательно содержащего
регрессоров, обязательно содержащего  регрессор. Если после этого наименьшая из
регрессор. Если после этого наименьшая из  подсчитанных к этому моменту остаточных сумм квадратов не превосходит
подсчитанных к этому моменту остаточных сумм квадратов не превосходит  то процедура заканчивается, а соответствующая подобранная регрессия является "наилучшей". В противном случае мы переходим к этапу 3.
то процедура заканчивается, а соответствующая подобранная регрессия является "наилучшей". В противном случае мы переходим к этапу 3.
Этап 3. Теперь в число кандидатур на исключение из модели вводится регрессор  и подсчитываются значений RSS, полученных при исключении из набора первых
и подсчитываются значений RSS, полученных при исключении из набора первых  регрессоров любого набора
регрессоров любого набора  регрессоров, содержащего
регрессоров, содержащего  После этого минимальное из
После этого минимальное из  значений RSS, подсчитанных на первых трех этапах, сравнивается с
значений RSS, подсчитанных на первых трех этапах, сравнивается с  и процедура либо заканчивается, если это минимальное значение меньше, чем
и процедура либо заканчивается, если это минимальное значение меньше, чем  либо происходит переход к следующему этапу. Вообще
либо происходит переход к следующему этапу. Вообще  этап выглядит следующим образом:
этап выглядит следующим образом:
Этап  Подсчитывается значений RSS, получаемых при исключении из набора первых
Подсчитывается значений RSS, получаемых при исключении из набора первых  переменных любого набора
переменных любого набора  регрессоров, содержащего
регрессоров, содержащего  Если после этого минимальное из подсчитанных
Если после этого минимальное из подсчитанных  значений RSS не превосходит
значений RSS не превосходит  то соответствующее подмножество является "наилучшим". В противном случае мы переходим к этапу
то соответствующее подмножество является "наилучшим". В противном случае мы переходим к этапу  на котором перебираются наборы по
на котором перебираются наборы по  регрессоров, содержащие
регрессоров, содержащие 
Может получиться так, что придется реализовать все  этапов, а следовательно, вычислить все
этапов, а следовательно, вычислить все  регрессий. Однако, как было замечено, это случается редко, если только
регрессий. Однако, как было замечено, это случается редко, если только  не слишком мало. Последний же случай не требует большого объема вычислений. Обычно для определения подмножества размера
не слишком мало. Последний же случай не требует большого объема вычислений. Обычно для определения подмножества размера  с минимальной RSS требуется рассмотреть лишь небольшую часть всех
с минимальной RSS требуется рассмотреть лишь небольшую часть всех  регрессий.
регрессий.
В пределах каждого этапа вычислений подмножества размера  удобно образовывать в таком порядке, чтобы каждое следующее отличалось от предыдущего только одним элементом. Это можно сделать, используя последовательность, построенную в разд. 12.2.1. При этом о подмножествах, получаемых методом Гарсайда (Garside), мы будем теперь говорить как
удобно образовывать в таком порядке, чтобы каждое следующее отличалось от предыдущего только одним элементом. Это можно сделать, используя последовательность, построенную в разд. 12.2.1. При этом о подмножествах, получаемых методом Гарсайда (Garside), мы будем теперь говорить как  исключаемых наборах,
исключаемых наборах,
Например, для  соответствующая последовательность исключаемых наборов представлена в табл. 12.4. Ее можно представить также в виде ряда подпоследовательностей, как это сделано в табл. 12.5.
соответствующая последовательность исключаемых наборов представлена в табл. 12.4. Ее можно представить также в виде ряда подпоследовательностей, как это сделано в табл. 12.5.
Таблица 12.5 (см. скан) Порядок получения подмножеств регрессий с  регрессорами, определяемый методом Гарсайда, в котором при переходе от одного подмножества к другому изменяется только один регрессор
регрессорами, определяемый методом Гарсайда, в котором при переходе от одного подмножества к другому изменяется только один регрессор
Чтобы показать, что этот метод действительно приводит к минимальной RSS для заданного значения  заметим прежде всего, что при исключении регрессора из модели остаточная сумма квадратов может только возрасти или остаться без изменения. Это означает, что всякая оцененная подмодель регрессии, не содержащая
заметим прежде всего, что при исключении регрессора из модели остаточная сумма квадратов может только возрасти или остаться без изменения. Это означает, что всякая оцененная подмодель регрессии, не содержащая  не может иметь
не может иметь  меньшую
меньшую  Предположим теперь, что RSS, получаемая исключением любого набора
Предположим теперь, что RSS, получаемая исключением любого набора  регрессоров, в котором максимальный индекс регрессора равен
регрессоров, в котором максимальный индекс регрессора равен  не превосходит
не превосходит  Тогда, поскольку значение RSS для этой частной модели не превосходит
Тогда, поскольку значение RSS для этой частной модели не превосходит  мы не можем уменьшить значение RSS, исключая
мы не можем уменьшить значение RSS, исключая  и заменяя его каким-либо из регрессоров
и заменяя его каким-либо из регрессоров  уже не содержащихся в модели. В противном случае мы смогли бы найти модель с исключенным
уже не содержащихся в модели. В противном случае мы смогли бы найти модель с исключенным  для которой RSS была бы меньшей дозволенного минимума
для которой RSS была бы меньшей дозволенного минимума  Мы знаем, что при остановке
Мы знаем, что при остановке
процесса, скажем, на  этапе в наилучшую регрессию должны включаться переменные
этапе в наилучшую регрессию должны включаться переменные  В таком случае вопрос состоит в отыскании наилучшего подмножества размера
В таком случае вопрос состоит в отыскании наилучшего подмножества размера  содержащего эти переменные, путем перебора всех подсчитанных к этому времени значений RSS.
содержащего эти переменные, путем перебора всех подсчитанных к этому времени значений RSS.
Описывая указанную процедуру, Hocking, Leslie (1967) предпочитают при исключений регрессоров следить за уменьшением регрессионной суммы квадратов. Соответствующее уменьшение подсчитывается непосредственно, путем обращения главного  -минора матрицы
-минора матрицы  если или главного
если или главного  -минора матрицы
-минора матрицы  если
если  В пределах каждого этапа последовательность этих обратных величий можно эффективно вычислять, используя упорядочение, указанное в табл. 12.5. Поскольку переменные вводятся в модель и выводятся из нее поодиночке, то всякие две расположенные друг за другом подматрицы различаются только одной строкой (и в силу симметрии одним столбцом). Эти авторы замечают также, что через уменьшение регрессионной суммы квадратов легко выразить
В пределах каждого этапа последовательность этих обратных величий можно эффективно вычислять, используя упорядочение, указанное в табл. 12.5. Поскольку переменные вводятся в модель и выводятся из нее поодиночке, то всякие две расположенные друг за другом подматрицы различаются только одной строкой (и в силу симметрии одним столбцом). Эти авторы замечают также, что через уменьшение регрессионной суммы квадратов легко выразить  В связи с этим они предлагают несколько методов сокращения длины поиска, основанных на подсчитанных значениях
В связи с этим они предлагают несколько методов сокращения длины поиска, основанных на подсчитанных значениях  В более поздней статье La Motte, Hocking (1970) приводят модификацию указанного метода, позволяющую значительно сократить объем вычислений. При этом они считают, что их метод достаточно эффективен для значений К вплоть до 30, а возможно, даже и до 50. Аналогичный изложенному метод Beale и др. (1967) удовлетворителен по-видимому, для значений К, не слишком превышающих 20 [Beale (1970, с. 913)].
В более поздней статье La Motte, Hocking (1970) приводят модификацию указанного метода, позволяющую значительно сократить объем вычислений. При этом они считают, что их метод достаточно эффективен для значений К вплоть до 30, а возможно, даже и до 50. Аналогичный изложенному метод Beale и др. (1967) удовлетворителен по-видимому, для значений К, не слишком превышающих 20 [Beale (1970, с. 913)].
При поочередном введении и выведении регрессоров можно использовать эффективный метод Хаусхольдера-Гивенса (разд. 12.2.2), с помощью которого одну переменную можно ввести, а другую вывести из уравнения.
Совсем недавно Furnival, Wilson (1974) предложили другой метода который является, по-видимому, еще значительно более быстрым, чем упомянутые,
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
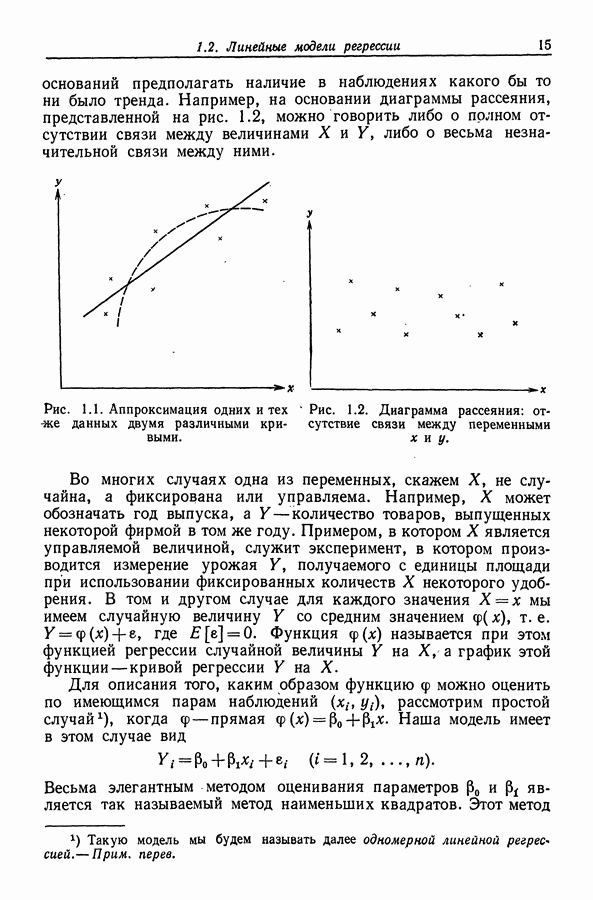
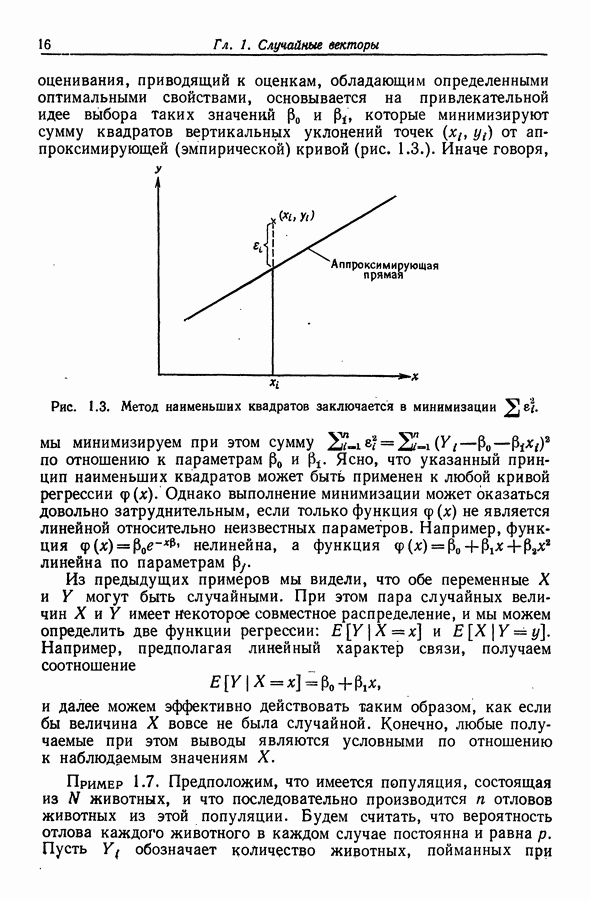
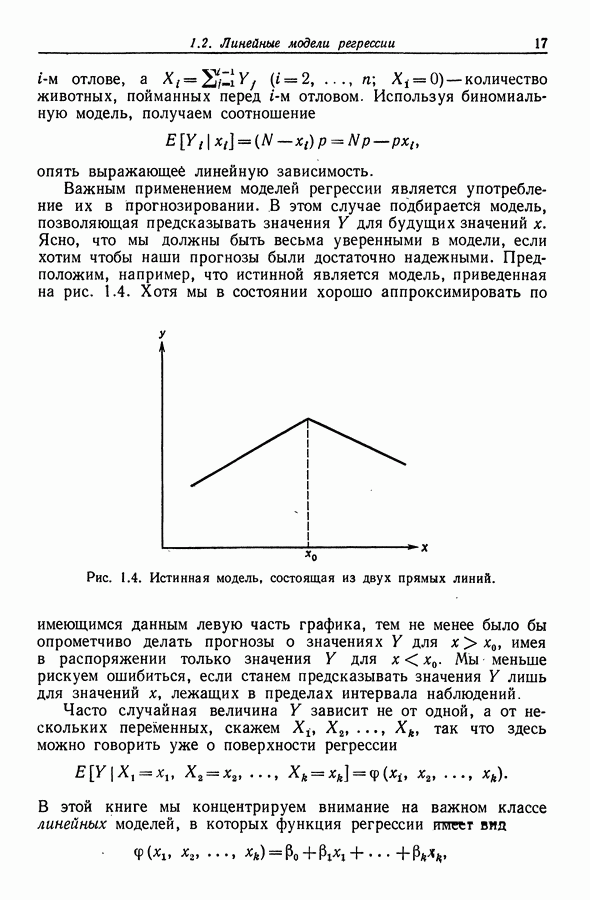
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
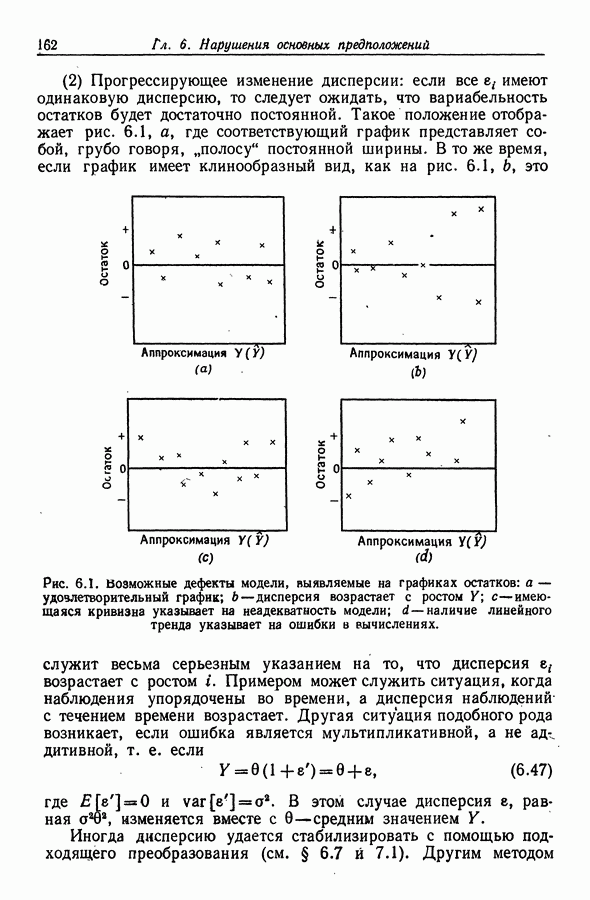
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
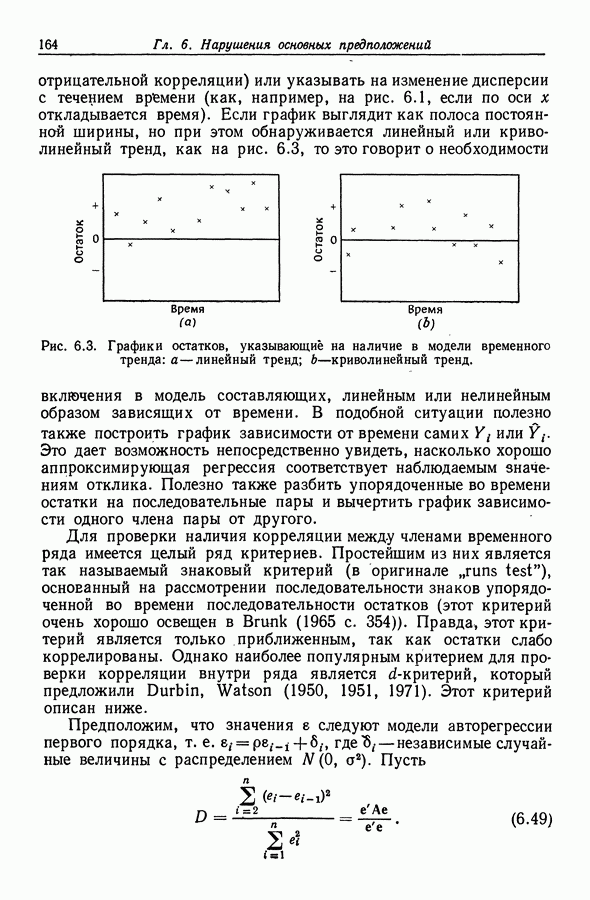
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
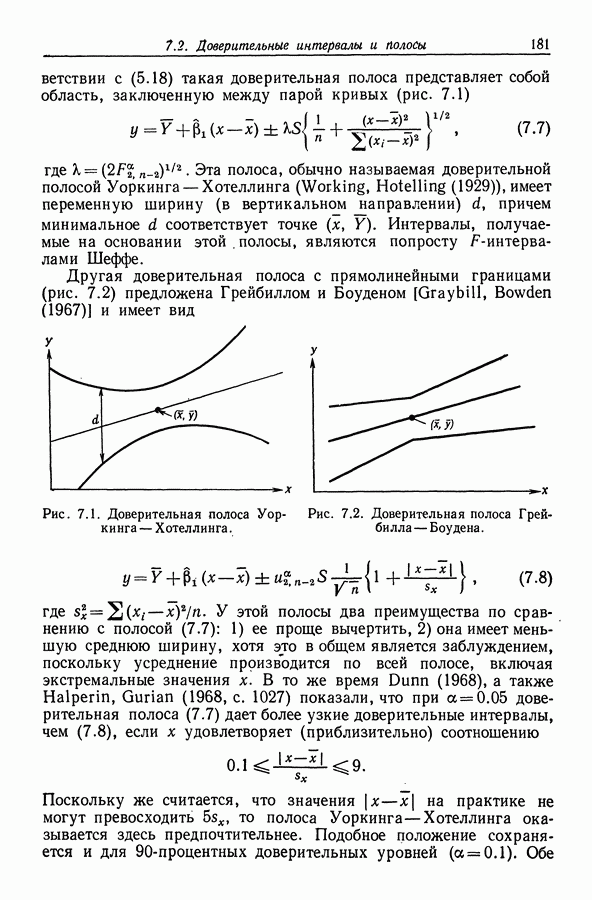
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
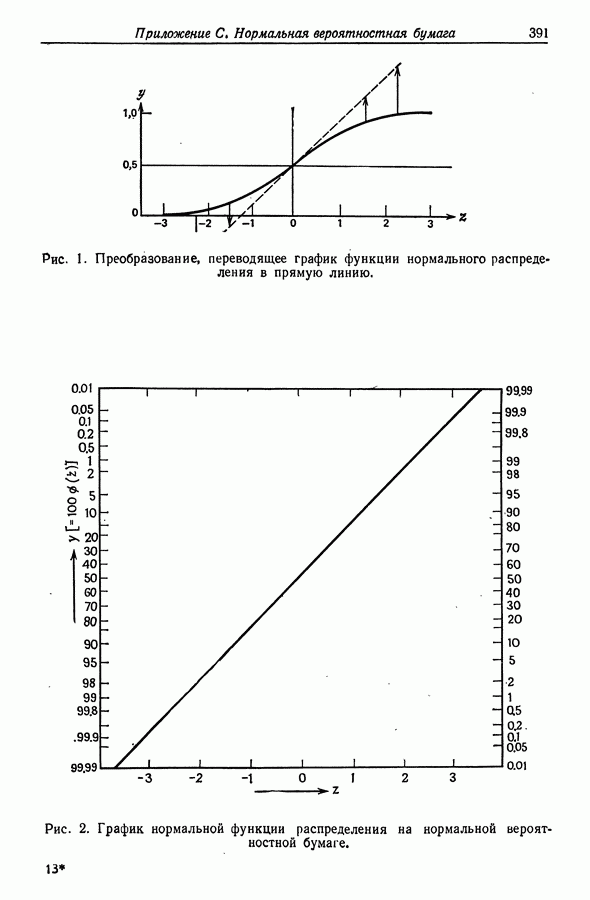
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
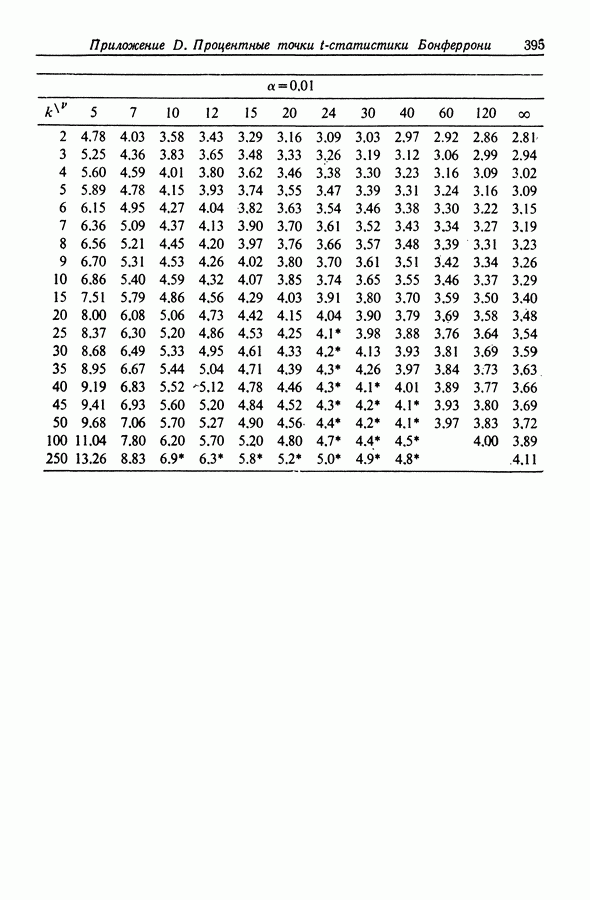
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
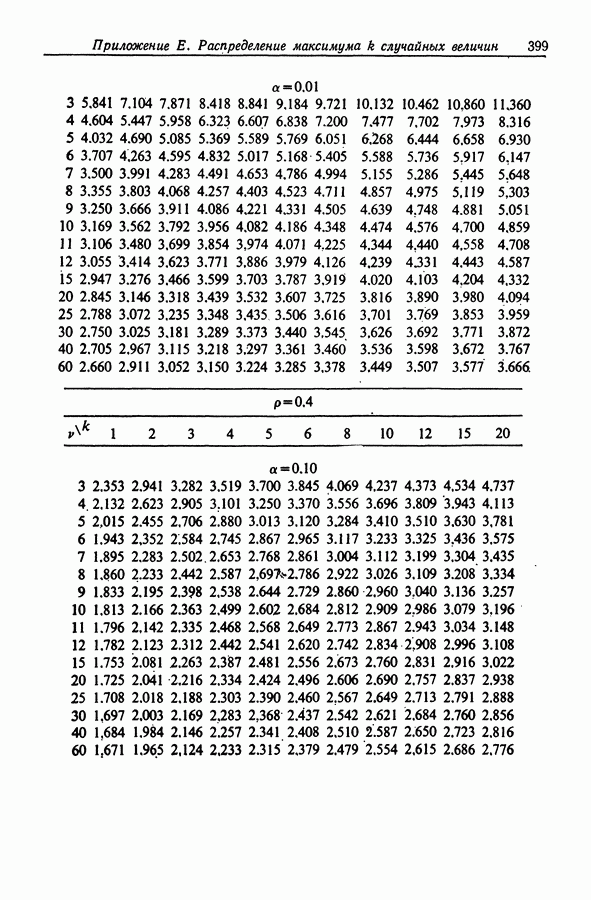
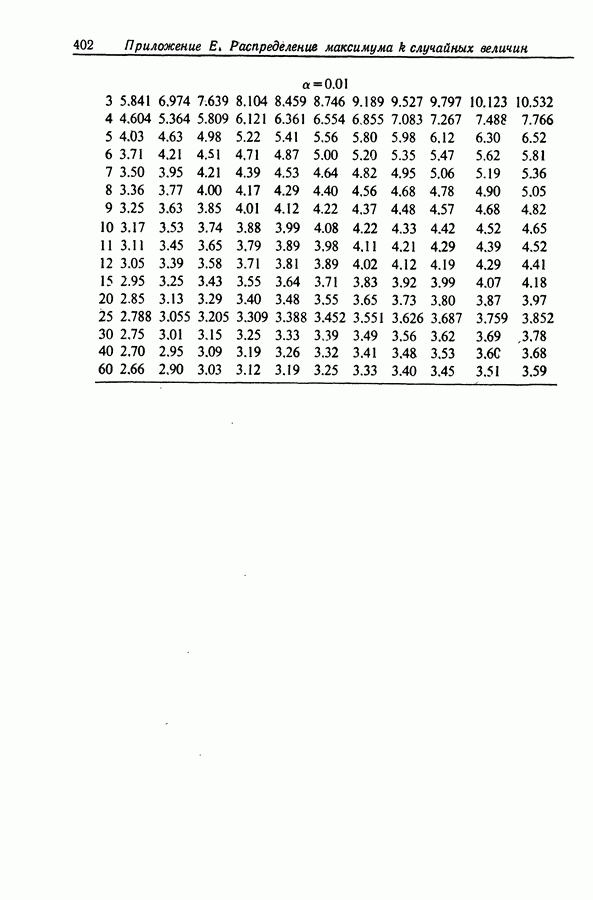
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
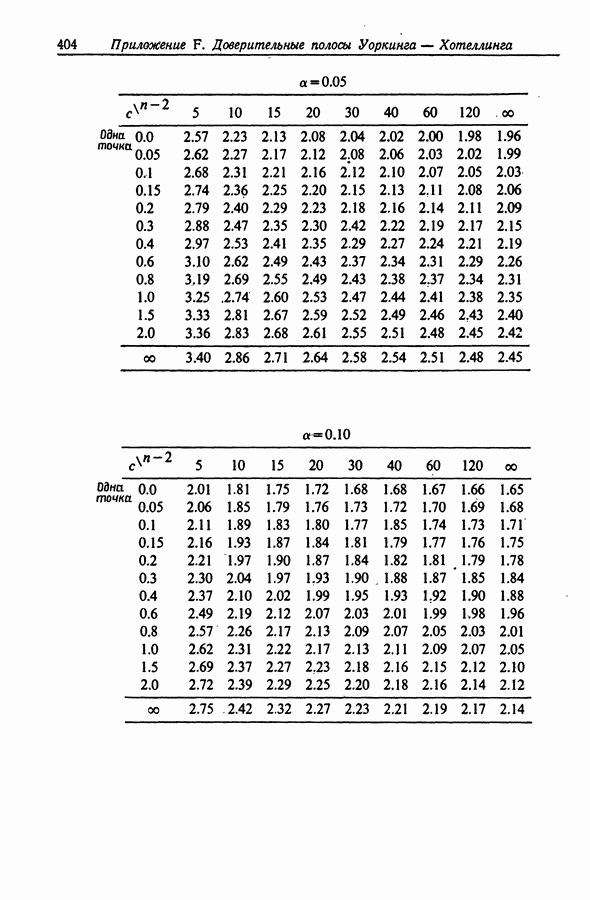
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ