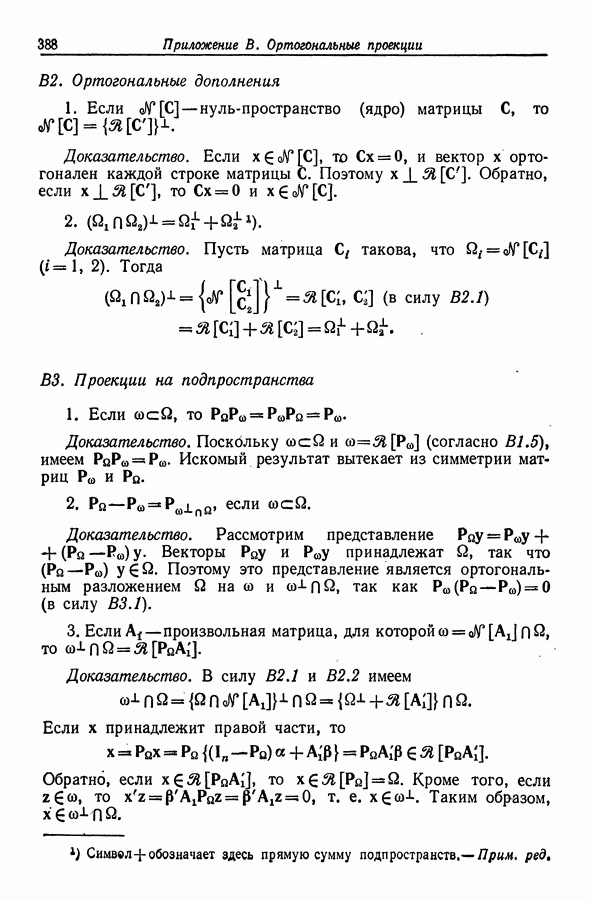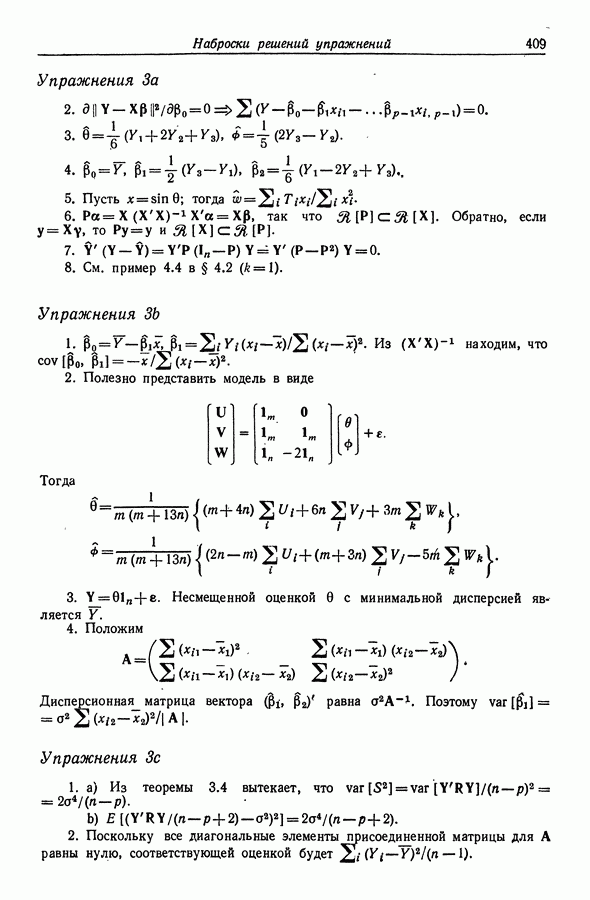| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.2. Пропущенные наблюдения
10.2.1. Теория оценивания
При реализации планов эксперимента иногда возникает такое положение, когда одно или большее число наблюдений оказывается пропущенным. Например, в ходе эксперимента какое-то растение может погибнуть, пробирка — разбиться, а пациент — отказаться от обследования. В таких случаях нарушается симметрия (сбалансированность) плана, и обычные вычисления дисперсионного анализа к оставшимся данным непосредственно не применимы. Один общий способ действий в подобной ситуации состоит в отыскании таких оценок пропущенных наблюдений, чтобы дисперсионный анализ полученного таким образом "полного" множества данных был равносилен анализу данных, действительно имеющихся в наличии. Матрица плана при работе с этим полным множеством данных определяется без труда, и при вычислениях можно уже полностью использовать симметрию плана.
Предположим, что в общей модели  в которой матрица X имеет размер
в которой матрица X имеет размер  пропущено
пропущено  из
из  наблюдений. Тогда, переобозначая, если требуется, переменные
наблюдений. Тогда, переобозначая, если требуется, переменные  модель можно записать в виде
модель можно записать в виде

где только  наблюдений
наблюдений  из
из  имеются в распоряжении, т. е.. получены. Пусть
имеются в распоряжении, т. е.. получены. Пусть

и р — оценка наименьших квадратов для  т.е.
т.е.  достигает минимума при
достигает минимума при  где
где  решение нормальных уравнений
решение нормальных уравнений  Тогда величина
Тогда величина  достигает минимума относительно пары
достигает минимума относительно пары  если
если  (т.е.
(т.е.  Из равенства
Из равенства  получаем полезное соотношение
получаем полезное соотношение

Определенное выше  называют оценкой наименьших квадратов для
называют оценкой наименьших квадратов для 
Заметим, что приведенные соображения, представленные в различном виде многими авторами (см., например, Wilkinson (1958а, b, 1960) и "Letters to the Editor" в журнале. The American Statistican (1972 (4))), сохраняют силу независимо от того, имеет
матрица X полный ранг  или нет. Более общие, "бескоординатные" соображения, допускающие другие представления для
или нет. Более общие, "бескоординатные" соображения, допускающие другие представления для  (например,
(например,  вместо
вместо  приводят Kruskal (1960) и Seber (1966, гл. 8).
приводят Kruskal (1960) и Seber (1966, гл. 8).
Предположим теперь, что матрица  размера
размера  имеет ранг
имеет ранг  Тогда
Тогда

и это есть просто то значение, которое мы могли бы "предсказать" для  основываясь на совокупности значений х, заданной матрицей
основываясь на совокупности значений х, заданной матрицей  В то же время можно получить и более удобную формулу, использующую полноту ранга матрицы X (которая также имеет ранг
В то же время можно получить и более удобную формулу, использующую полноту ранга матрицы X (которая также имеет ранг  поскольку она содержит
поскольку она содержит  линейно независимых строк матрицы
линейно независимых строк матрицы  Для этой цели сложим уравнения
Для этой цели сложим уравнения  Получим уравнение
Получим уравнение

Умножая обе его части на  получаем
получаем

или

Соотношения (10.14) и  показывают, что
показывают, что

так что для отыскания  можно сначала минимизировать
можно сначала минимизировать  относительно
относительно  а затем минимизировать остаточную сумму квадратов относительно пропущенных наблюдений
а затем минимизировать остаточную сумму квадратов относительно пропущенных наблюдений  Этот результат принадлежит Yates (1933). Польза уравнения (10.14) станет ясна из следующего примера.
Этот результат принадлежит Yates (1933). Польза уравнения (10.14) станет ясна из следующего примера.
Пример 10.5 (план с рандомизированными блоками). Пусть модель

представляет собой план с рандомизированными блоками. Предположим, что последнее наблюдение  пропущено. Тогда из соотношений
пропущено. Тогда из соотношений  вытекает, что
вытекает, что

где

Разрешая это уравнение относительно  получаем
получаем

В соответствии с (10.17) остаточная сумма квадратов для имеющихся в наличии данных равна  и заменяется на
и заменяется на  Заметим, что остаток
Заметим, что остаток  (равный
(равный  равен нулю.
равен нулю.
Пример  (классификация по одному признаку). Пусть
(классификация по одному признаку). Пусть

и предположим, что наблюдение  пропущено. Тогда
пропущено. Тогда

и

т. е. равно среднему из оставшихся  наблюдений, соответствующих
наблюдений, соответствующих 
Приложение указанной техники к латинским квадратам и квадратам Юдена можно найти в работе Jaech (1966). Другие формулы оценивания единственного наблюдения приведены для большинства стандартных планов в книге Cochran, Сох (1957),
10.2.2. Проверка гипотез
Пусть задана общая модель  где матрица X имеет размер
где матрица X имеет размер  и ранг Предположим, что мы хотим проверить (допускающую проверку) гипотезу
и ранг Предположим, что мы хотим проверить (допускающую проверку) гипотезу  где матрица А имеет размер
где матрица А имеет размер  и ранг
и ранг  Если бы пропущенных наблюдений не было, то
Если бы пропущенных наблюдений не было, то  -статистика для проверки гипотезы Я имела бы вид
-статистика для проверки гипотезы Я имела бы вид

Однако если пропущен вектор  то в качестве его оценки можно взять
то в качестве его оценки можно взять  где и получается минимизацией RSS относительно
где и получается минимизацией RSS относительно  (или, что равносильно, решением уравнения
(или, что равносильно, решением уравнения  как в приведенных выше примерах 10.5 и 10.6). Минимальное значение RSS, обозначаемое здесь символом
как в приведенных выше примерах 10.5 и 10.6). Минимальное значение RSS, обозначаемое здесь символом  является в точности остаточной суммой квадратов для исходной модели. С другой стороны, значение RSS суммы RSS при
является в точности остаточной суммой квадратов для исходной модели. С другой стороны, значение RSS суммы RSS при  уже не является остаточной суммой квадратов при гипотезе Я, так что разность
уже не является остаточной суммой квадратов при гипотезе Я, так что разность  не будет соответствующей гипотезе суммой квадратов, используемой при проверке гипотезы Я. Нам нужна здесь такая оценка вектора
не будет соответствующей гипотезе суммой квадратов, используемой при проверке гипотезы Я. Нам нужна здесь такая оценка вектора  которая была бы совместима с моделью Н. Решая уравнение
которая была бы совместима с моделью Н. Решая уравнение  относительно
относительно  получим значение
получим значение  которое уже можно использовать для построения
которое уже можно использовать для построения  -статистики для проверки гипотезы Н:
-статистики для проверки гипотезы Н:

Здесь  степеней свободы оказываются "потерянными" в знаменателе
степеней свободы оказываются "потерянными" в знаменателе  -статистики из-за того, что приходится оценивать
-статистики из-за того, что приходится оценивать  пропущенных наблюдений
пропущенных наблюдений  (предполагается, что матрица X размера
(предполагается, что матрица X размера  имеет тот же ранг, что и матрица X, т.е.
имеет тот же ранг, что и матрица X, т.е.  ).
).
Поскольку  можно также получить минимизацией
можно также получить минимизацией  относительно
относительно  мы должны иметь
мы должны иметь

причем вероятность равенства (т.е.  равна здесь нулю. Поэтому, если мы используем статистику
равна здесь нулю. Поэтому, если мы используем статистику

и обращаемся с ней как со случайной величиной, имеющей  -распределение с
-распределение с  степенями свободы, то получаем слишком осторожный критерий, так как числитель оказывается чересчур большим [Yates (1933)].
степенями свободы, то получаем слишком осторожный критерий, так как числитель оказывается чересчур большим [Yates (1933)].
Вместо вычисления  обычно просто корректируют числитель статистики
обычно просто корректируют числитель статистики  вычитая поправку
вычитая поправку

и используя следующую лемму. (Заметим, что значение  надо вычислять, только если
надо вычислять, только если  значимо.)
значимо.)
Лемма. Записывая  имеем
имеем

(Этот результат доказал Wilkinson (1958b); более общее доказательство дал Seber (1966, стр. 70).)
Доказательство. Если  то из (4.5) имеем
то из (4.5) имеем

и

Пусть  и матрица
и матрица  разбита следующим образом:
разбита следующим образом:

Из соотношения

вытекает, что  Кроме того,
Кроме того,

(последнее верно в силу (10.19)), так что

Пример 10.7. Предположим, что мы хотим проверить гипотезу  (для всех
(для всех  для плана с рандомизированными блоками из примера 10.5. Применяя технику, которую мы там использовали, к гипотезе
для плана с рандомизированными блоками из примера 10.5. Применяя технику, которую мы там использовали, к гипотезе  получаем
получаем

так что

или

Применяя теперь доказанную лемму (уравнение (10.19)) к (10.20), имеем  так что
так что

и

Таким образом,  -статистика для проверки гипотезы
-статистика для проверки гипотезы  имеет вид
имеет вид

Другой, несколько более сложный способ отыскания значения  в указанном примере предложил Kshirsagar (1971).
в указанном примере предложил Kshirsagar (1971).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
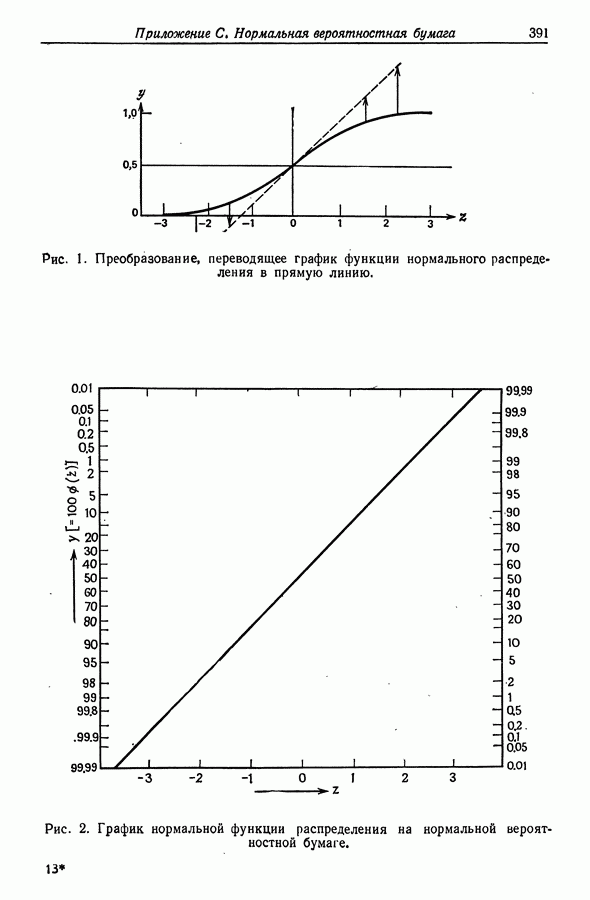
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
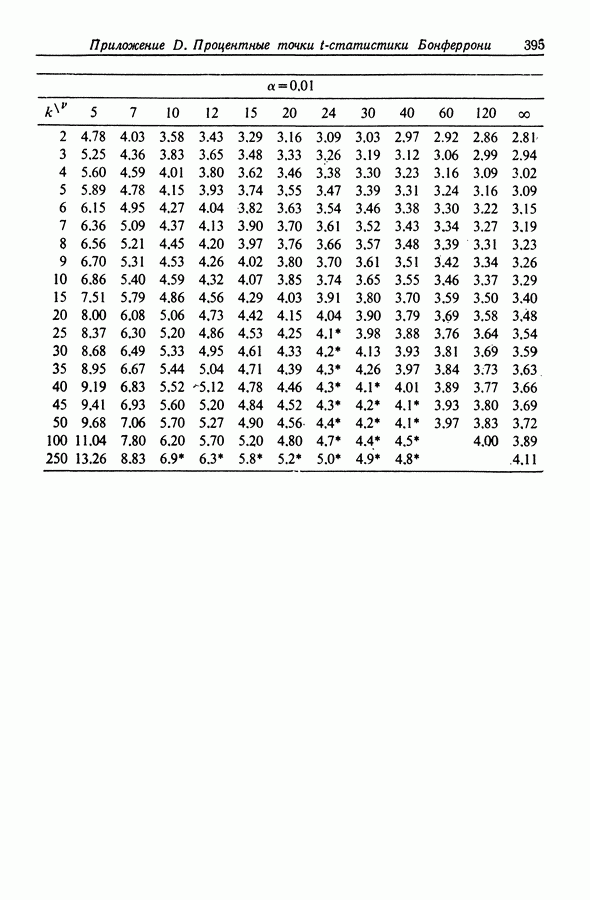
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
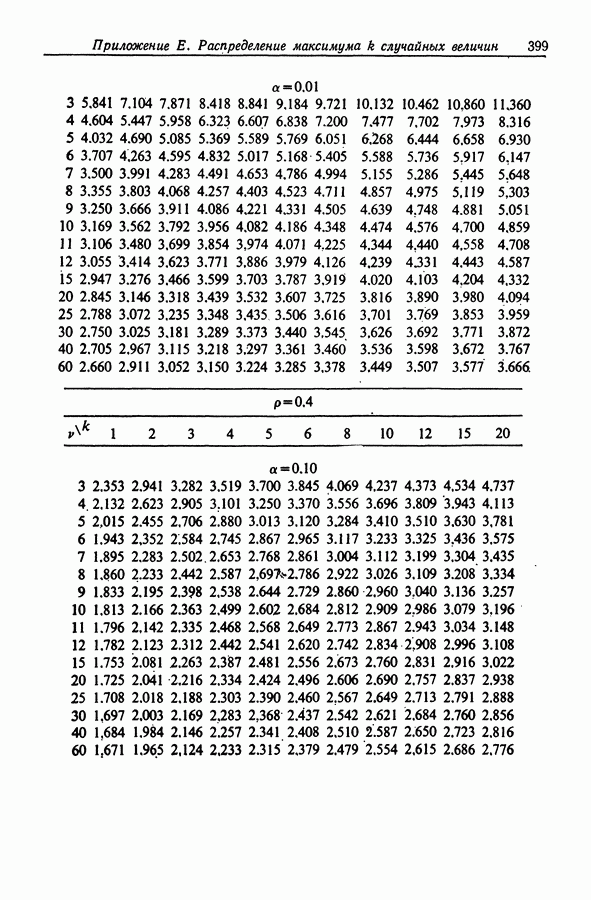
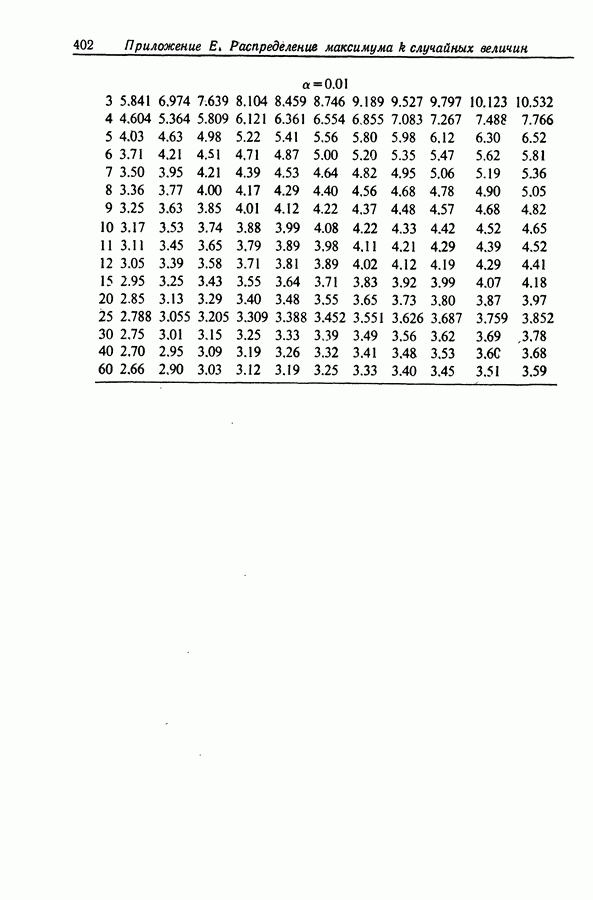
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
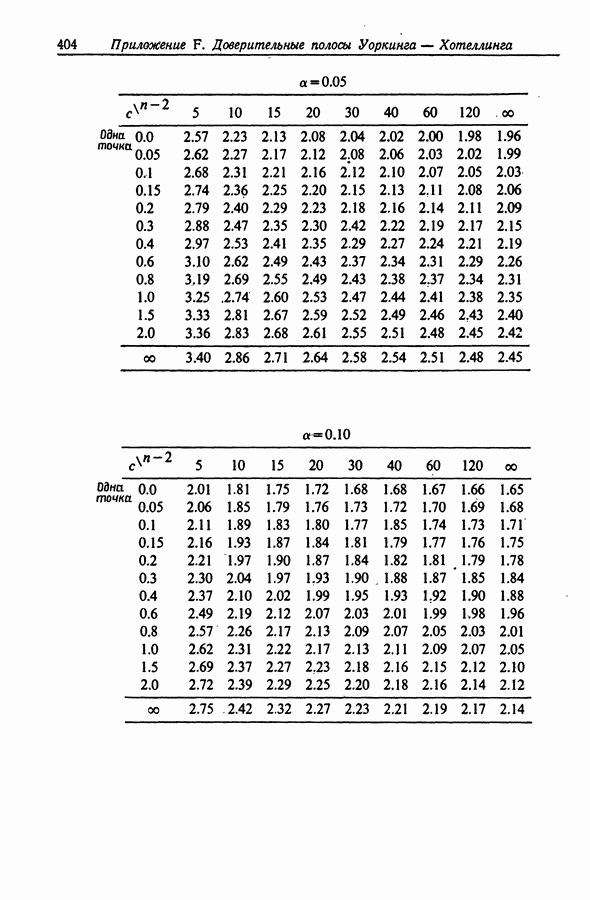
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ