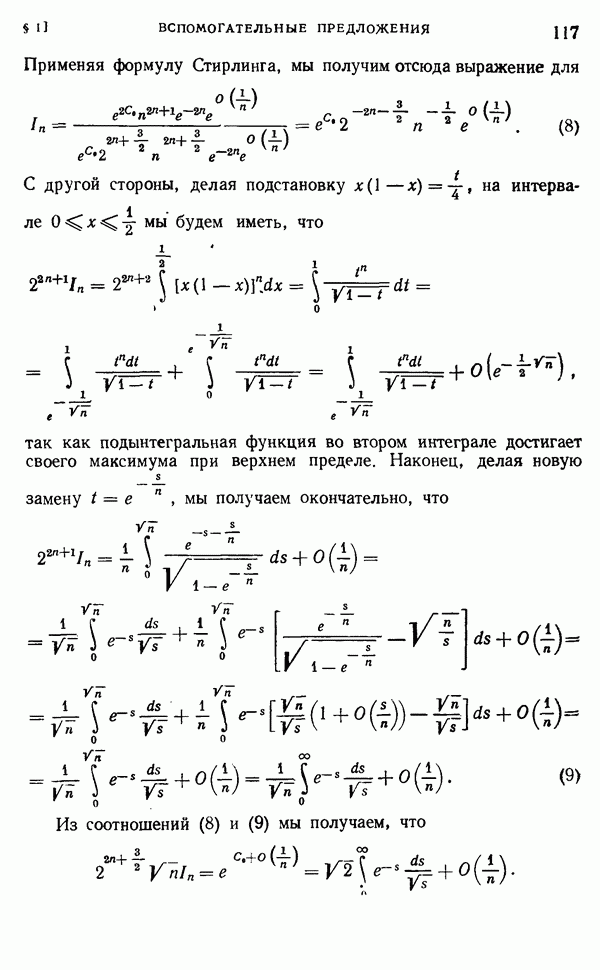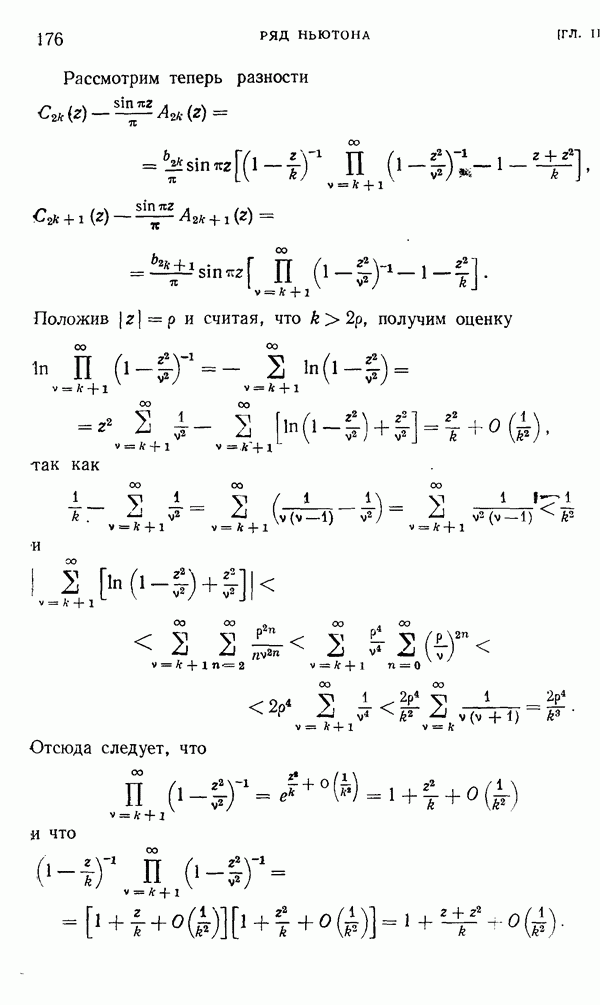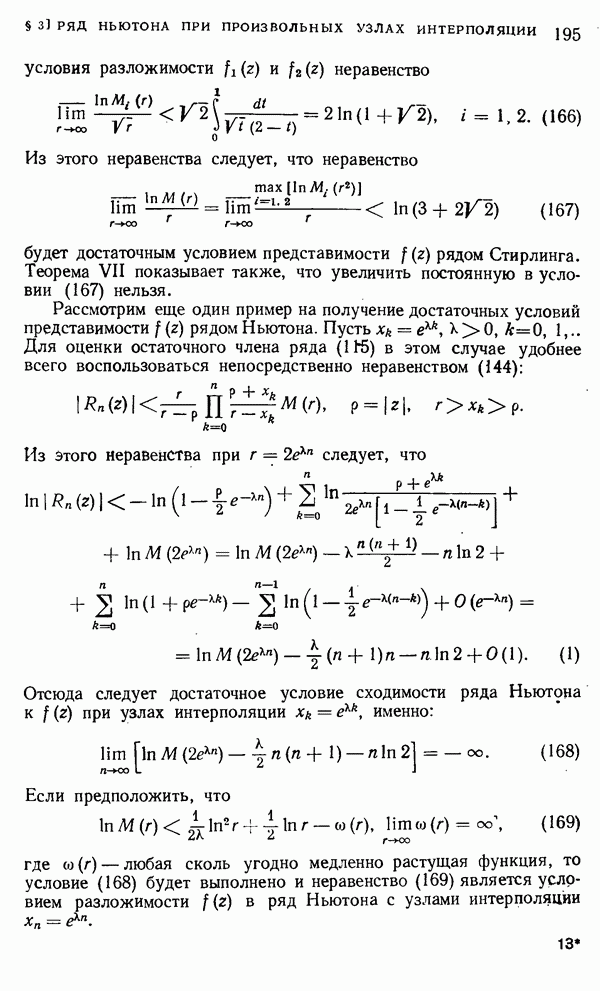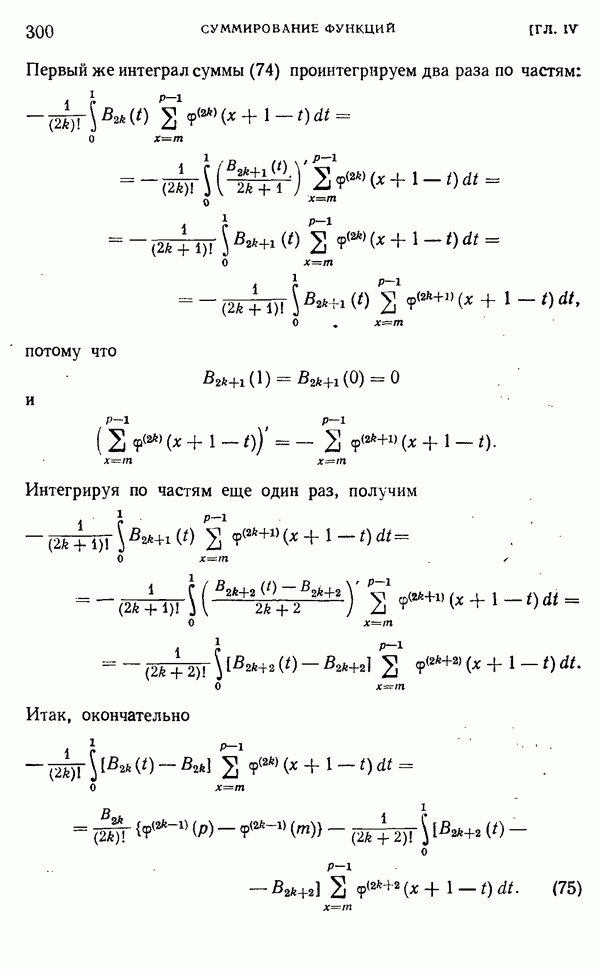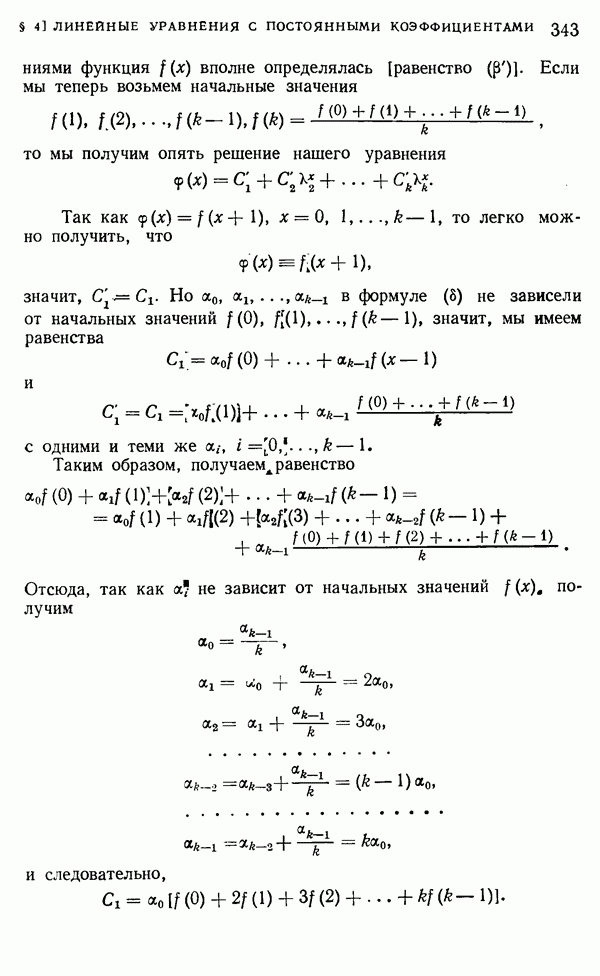| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Многочлены С. Н. Бернштейна и их обобщение.
Весьма существенный в различных вопросах анализа процесс приближения многочленами произвольной, непрерывной на [0, 1] функции был найден С. Н. Бернштейном. Как показал С. Н, Бернштейн, многочлены

равномерно сходятся к  если
если  на отрезке
на отрезке  непрерывна. Оценка приближения дается неравенствами
непрерывна. Оценка приближения дается неравенствами

где  — модуль непрерывности f(x) на [0, 1], причем эта оценка, вообще говоря, не может быть улучшена. Хотя из-за этого обстоятельства многочлены С. Н. Бернштейна нельзя использовать в тех вопросах, где нужны многочлены наилучшего приближения, или другие достаточно хорошо приближающие функцию многочлены, многочлены Бернштейна играют большую роль в проблемах, где необходимо иметь простую связь приближающих многочленов с функцией. Особенно эффектно эти многочлены используются для решения задачи моментов на конечном интервале. Заметим, что многочлены Бернштейна были найдены благодаря некоторым проблемам теории вероятностей.
— модуль непрерывности f(x) на [0, 1], причем эта оценка, вообще говоря, не может быть улучшена. Хотя из-за этого обстоятельства многочлены С. Н. Бернштейна нельзя использовать в тех вопросах, где нужны многочлены наилучшего приближения, или другие достаточно хорошо приближающие функцию многочлены, многочлены Бернштейна играют большую роль в проблемах, где необходимо иметь простую связь приближающих многочленов с функцией. Особенно эффектно эти многочлены используются для решения задачи моментов на конечном интервале. Заметим, что многочлены Бернштейна были найдены благодаря некоторым проблемам теории вероятностей.
Мы рассмотрим обобщенные многочлены Бернштейна, с помощью которых непосредственно устанавливается полнота системы функций

в классе всех непрерывных на отрезке [0, 1] функцийпри условии, что

Пусть  Пусть также
Пусть также  Число повторений одного и того же а в ряде мы будем называть кратностью а. Для функции
Число повторений одного и того же а в ряде мы будем называть кратностью а. Для функции  мы
мы
построим разделенную разность с узлами  По формуле (57) настоящей главы
По формуле (57) настоящей главы

если  — не равные между собой числа последовательности
— не равные между собой числа последовательности  не превосходит кратности точки в нашей основной последовательности.
не превосходит кратности точки в нашей основной последовательности.
В силу неравенства (44) настоящей главы, которое остается в силе для нашей последовательности  так как
так как  -любое число раз дифференцируемая функция,
-любое число раз дифференцируемая функция,

Многочлен  как мы уже знаем,
как мы уже знаем,

будет интерполяционным многочленом, удовлетворяющим условиям

где  — частота точки
— частота точки  в ряду
в ряду 
Вводя обозначения

и полагая  в (164), мы получим тождество
в (164), мы получим тождество

Ьткуда следует, так как  вследствие неравенства (163), что
вследствие неравенства (163), что

Полагая в тождестве  мы получаем тождество
мы получаем тождество

Положим

Тогда

Построим разделенные разности с узлами  для функции
для функции  и рассмотрим интерполяционный многочлен
и рассмотрим интерполяционный многочлен

 Положив
Положив  мы получаем, что
мы получаем, что

где

к  применимы те же рассуждения, что и к
применимы те же рассуждения, что и к  поэтому
поэтому  Положив
Положив

мы из (172) получаем тождество

Рассмотрим функцию

Заметим прежде всего, что 
Далее, в силу (167), (170) и (174)

Выбирая  при условии, что
при условии, что  полагая
полагая

и замечая, что

мы из соотношения (176) получаем неравенство

где  — постоянная, не зависящая от
— постоянная, не зависящая от  При условиях
При условиях  величина
величина  стремится к нулю с ростом
стремится к нулю с ростом  Мы ниже это докажем, а пока будем ссылаться, как на известный факт.
Мы ниже это докажем, а пока будем ссылаться, как на известный факт.
Рассмотрим теперь сумму 

Пользуясь неравенством Буняковского

и полагая

мы непосредственно получаем неравенство

Рассмотрим, наконец, сумму 

Дадим две оценки величины этой суммы в зависимости от того, будет ли  . Пусть
. Пусть  . Тогда при
. Тогда при 

Поэтому

Пусть теперь  Так как при
Так как при 

то при любом 

Значит,

Полагая  мы получаем окончательно неравенство
мы получаем окончательно неравенство

Считая, что  , и принимая во внимание (182), мыполучаем, что при любом
, и принимая во внимание (182), мыполучаем, что при любом  имеет место неравенство
имеет место неравенство

Определим обобщенный многочлен С. Н. Бернштейна для любой ограниченной на [0. 1] функции  положив
положив

Этот многочлен связан с последовательностью 
Если положить  то простой подсчет показывает, что этот многочлен переходит в обыкновенный многочлен С. Н. Бернштейна (159).
то простой подсчет показывает, что этот многочлен переходит в обыкновенный многочлен С. Н. Бернштейна (159).
Теорема V. Если задана последовательность 

и  ограничена на [0, 1], то в каждой точке непрерывности
ограничена на [0, 1], то в каждой точке непрерывности  многочлены
многочлены  сходятся к
сходятся к  Если же
Если же  непрерывна на [0, 1] и ее модуль непрерывности со (8), то при условии
непрерывна на [0, 1] и ее модуль непрерывности со (8), то при условии  имеет место неравенство
имеет место неравенство

Наконец, если  на [0, 1] имеет производную, удовлетворяющую условию Липшица с константой
на [0, 1] имеет производную, удовлетворяющую условию Липшица с константой  , то
, то

Доказательство. Докажем первую часть теоремы. Рассмотрим неравенство

имеющее место в силу соотношения (167) и неотрицательности  Если
Если  точка непрерывности
точка непрерывности  максимум
максимум  на [0, 1], то для любого
на [0, 1], то для любого  найдется такое
найдется такое  , что
, что

Действительно, если  то это неравенство следует из непрерывности
то это неравенство следует из непрерывности  в точке х, а если
в точке х, а если  то оно тривиально следует из ограниченности
то оно тривиально следует из ограниченности  Пользуясь этим неравенством, мы из (188) получаем неравенство
Пользуясь этим неравенством, мы из (188) получаем неравенство

откуда в силу (167) и (183) мы будем иметь

при  так как
так как  стремится к нулю с ростом
стремится к нулю с ростом  Это и доказывает первую часть теоремы. Если же
Это и доказывает первую часть теоремы. Если же  имеет на [0, 1] модуль непрерывности
имеет на [0, 1] модуль непрерывности  , то, построив при произвольном
, то, построив при произвольном  ломаную линию, состоящую из отрезков, соединяющих точки
ломаную линию, состоящую из отрезков, соединяющих точки
кривой  при
при  уравнение которой будет
уравнение которой будет  мы будем иметь благодаря неравенствам (117) и (118), что
мы будем иметь благодаря неравенствам (117) и (118), что

Воспользовавшись этим неравенством, мы из неравенства (188) получаем неравенство

Отсюда, беря  из интервала
из интервала  мы получаем, что
мы получаем, что

другими словами, неравенство (186). При  из (169) и (166)
из (169) и (166)

 непосредственно вычисляется. Действительно,
непосредственно вычисляется. Действительно,

Поэтому для обыкновенных многочленов С. Н. Бернштейна неравенство (186) имеет вид

Докажем вторую часть теоремы. Если  удовлетворяет условию Липшица с константой К, то
удовлетворяет условию Липшица с константой К, то

и

так как 
Из соотношения

так как при 

следует последнее утверждение нашей теоремы. Для обыкновенных многочленов С. Н. Бернштейна тогда, так как К — будет иметь место неравенство

Теперь докажем, что  Из неравенства (178) следует, что
Из неравенства (178) следует, что 

Прежде всего можно утверждать, что

в силу расходимости ряда 
Положим

Но тогда

Поэтому, если максимальное из чисел  будет одним из крайних, то действительно
будет одним из крайних, то действительно

и значит,

в силу условий  Допустим, что максимальное число в ряду
Допустим, что максимальное число в ряду  будет
будет  Тогда из тождества
Тогда из тождества

в силу максимальности  следует неравенство
следует неравенство

или неравенство

Итак, максимальная из величин  не превышает макси-, мального из чисел
не превышает макси-, мального из чисел

Одно из двух неравенств при любом 

должно быть неверным в силу условий, наложенных на
Поэтому

при  . Итак,
. Итак,

Рассмотрим пример. Пусть  Тогда
Тогда  и
и

Далее,

и

Поэтому

где  — постоянная.
— постоянная.
Из теоремы V следует теорема V.
Теорема V. Система функций

 — целые рациональные чист, полна в классе непрерывных функций на отрезке [0, 1], если
— целые рациональные чист, полна в классе непрерывных функций на отрезке [0, 1], если  и
и

Когда  то мы получаем теорему Мюнца. Для полноты этой системы условие В необходимо. (Условие А, вообще говоря, необходимым не является.)
то мы получаем теорему Мюнца. Для полноты этой системы условие В необходимо. (Условие А, вообще говоря, необходимым не является.)
Действительно, пусть  Тогда, если только теорема V верна без условия В, то для любого
Тогда, если только теорема V верна без условия В, то для любого  будет существовать квазиполином
будет существовать квазиполином  такой, что
такой, что

Но тогда

и значит,

где минимум берется по всем квазиполиномам степени не выше  . Решим точно эту задачу о минимуме при
. Решим точно эту задачу о минимуме при  для функции
для функции  Выберем числа
Выберем числа  так, чтобы интеграл
так, чтобы интеграл

достигал своего минимума. Для этого продифференцируем  по
по  и найдем а, удовлетворяющие условиям
и найдем а, удовлетворяющие условиям

Положив

мы будем иметь, что

где С — постоянная, так как степень  не выше
не выше  и выполнены условия (200). Для определения С достаточно умножить обе части тождества (201) на
и выполнены условия (200). Для определения С достаточно умножить обе части тождества (201) на  и положить
и положить  Мы получим тогда, что
Мы получим тогда, что

Из (199) и (201) находим

другими словами,

откуда

в силу сходимости ряда  Это противоречит предельному соотношению (198), что и показывает необходимость условия В.
Это противоречит предельному соотношению (198), что и показывает необходимость условия В.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧ ТЕОРИИ КОНЕЧНЫХ РАЗНОСТЕЙ
- 2. Суммирование функций и уравнения в конечных разностях.
- 3. Постановка задач теории конечных разностей для аналитических функций комплексного переменного.
- ГЛАВА I. ЗАДАЧА ИНТЕРПОЛЯЦИИ
- § 1. Общая постановка проблемы интерполяции
- 2. Формула Лагранжа.
- 3. Формула Ньютона.
- § 2. Многочлены Чебышева
- § 3. Формула Ньютона для равноотстоящих значений независимого переменного
- 2. Второй вывод формулы Ньютона.
- 3. Понятие обобщенной степени.
- 4. Примеры.
- § 4. Различные представления разделенной разности в общем случае расположения узлов интерполяции
- 2. Второе представление разделенной разности и формула Ньютона при произвольных узлах интерполяции.
- 3. Третье представление разделенной разности и формула Эрмита.
- § 5. Интерполяционный процесс при треугольной таблице
- 2. Оценки остаточного члена в общей интерполяционной формуле и основные теоремы о представлении функций интерполяционным рядом.
- 3. Основные теоремы о представлении функций общим интерполяционным рядом.
- § 6. Приближение функций
- 2. Приближение функций многочленами.
- 3. Сходимость интерполяционного процесса Лагранжа и теорема С. Н. Бернштейна.
- 4. Многочлены С. Н. Бернштейна и их обобщение.
- 5. Приближение функций многочленами в комплексной плоскости. Многочлены Фабера.
- § 7. Интерполяционная задача и проблема моментов в комплексной плоскости
- ГЛАВА II. РЯД НЬЮТОНА
- 2. Гамма-функция, ее определение и основные свойства.
- 3. Асимптотическое представление Г(z).
- 4. Некоторые общие характеристики поведения целых аналитических функций.
- 5. Некоторые свойства выпуклых областей. Опорная функция выпуклой области.
- 6. Связь между индикатрисой роста целой аналитической функции первого порядка нормального типа и расположением особенностей ассоциированной с ней функции.
- 7. Плотность последовательности и показатель сходимости.
- § 2. Ряд Ньютона с узлами интерполяции 1, 2, 3,…
- 2. Свойства функций, представляемых рядом Ньютона.
- 3. Разложение аналитических функций в ряд Ньютона.
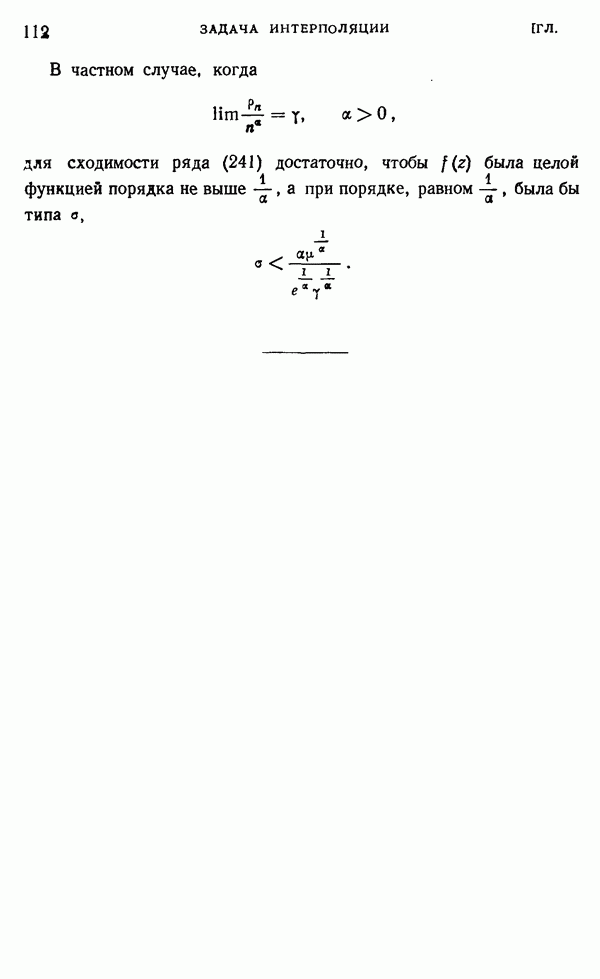
- § 3. Ряд Ньютона при произвольных узлах интерполяции
- 2. Случай конечного числа предельных точек последовательности узлов интерполяции на конечной части плоскости.
- 3. Интерполяционный процесс Ньютона в случае, когда узлы интерполяции имеют точку накопления только в бесконечности.
- 4. Приложение интерполяционных процессов к решению некоторых вопросов теории чисел.
- ГЛАВА III. ПОСТРОЕНИЕ ЦЕЛОЙ ФУНКЦИИ С ЗАДАННЫМИ ЭЛЕМЕНТАМИ
- § 1. Постановка задач и построение целой функции по ее значениям
- 2. Интерполяция рациональными дробями и одна теорема а целых функциях.
- 3. Определение целой функции по значениям последовательных производных.
- 4. Постановка общей задачи определения целой функции по заданным элементам.
- § 2. Проблема моментов в комплексной области для целых функций не выше первого порядка нормального типа
- § 3. Частные случаи общей интерполяционной задачи
- § 4. Линейные дифференциальные уравнения бесконечного порядка с постоянными коэффициентами и некоторые интерполяционные задачи, приводящиеся к решению подобных уравнений
- ГЛАВА IV. СУММИРОВАНИЕ ФУНКЦИЙ. ЧИСЛА И МНОГОЧЛЕНЫ БЕРНУЛЛИ
- § 2. Числа и многочлены Бернулли
- 2. Дальнейшие свойства чисел Бернулли.
- 3. О малой теореме Ферма.
- 4. Другой вид производящей функции бернуллиевых чисел.
- 5. Теорема Штаудта.
- 6. Аналитические свойства многочленов Бернулли.
- 7. Теорема умножения бернуллиевых многочленов.
- 8. Геометрические свойства многочленов Бернулли.
- § 3. Формула Эйлера
- 2. Строгий вывод формулы Эйлера с остаточным членом.
- 3. Остаточный член формулы Эйлера.
- 4. Другая форма остаточного члена формулы Эйлера.
- 5. Формула Стирлинга.
- ГЛАВА V. УРАВНЕНИЯ В КОНЕЧНЫХ РАЗНОСТЯХ
- § 2. Линейные уравнения первсго порядка
- 2. Неоднородное линейное уравнение.
- § 3. Линейные уравнения. Обшая теория
- 2. Основные теоремы о решениях линейного уравнения.
- 3. Линейная зависимость и независимость функций.
- 4. Свойства частных решений линейного однородного уравнения.
- 5. Неоднородное линейное уравнение. Метод вариации постоянных.
- 6. Выражение многократной суммы через однократную.
- § 4. Линейные уравнения с постоянными коэффициентами
- 2. Случай кратных корней.
- 3. Общее решение и линейная независимость частных решений.
- 4. Решение неоднородного линейного уравнения.
- 5. Примеры.
- § 5. Теорема Пуанкаре
- 3. Теорема Перрона.
- 4. Пример к теореме Пуанкаре.
- § 6. Теорема Гёльдера
- § 7. Линейные дифференциальные уравнения с постоянными коэффициентами бесконечного порядка
- 2. Линейные однородные дифференциальные уравнения бесконечного порядка с постоянными коэффициентами.
- 3. Обобщенные функции Бернулли, порождаемые оператором L(F).
- 4. Линейные неоднородные уравнения.
- 5. Обобщения понятия периода функции.
- ЛИТЕРАТУРА