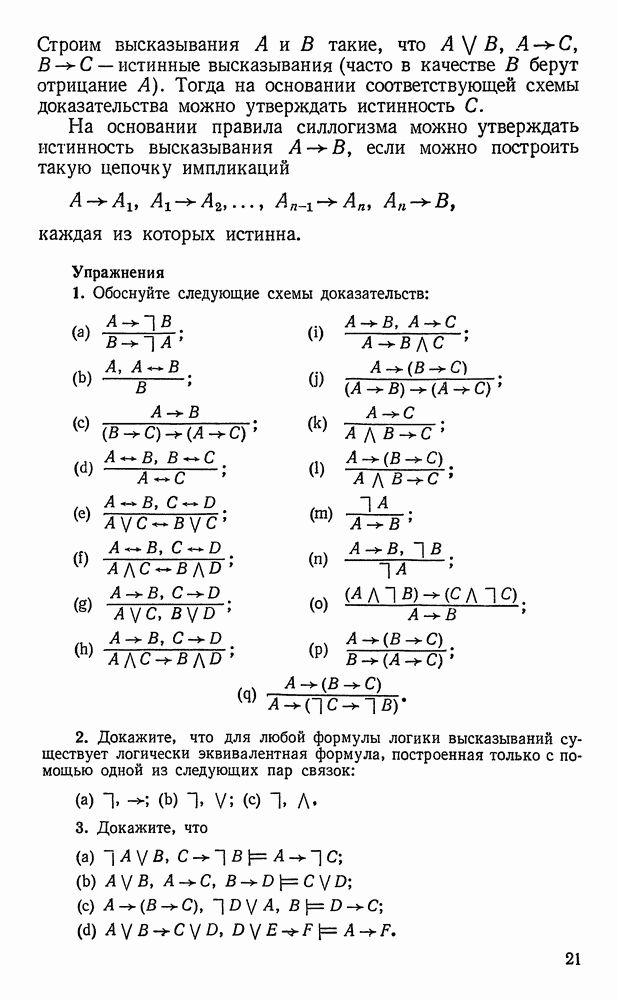| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2. ПРОСТОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ
Простое расширение поля.
Пусть  — кольцо полиномов от
— кольцо полиномов от  над полем где
над полем где  — подполе поля
— подполе поля  . Напомним,, что элемент а поля
. Напомним,, что элемент а поля  называется алгебраическим над полем
называется алгебраическим над полем  , если а является корнем какого-нибудь полинома положительной степени из
, если а является корнем какого-нибудь полинома положительной степени из 
ОПРЕДЕЛЕНИЕ. Пусть в  Простым расширением поля с помощью элемента а называется наименьшее подполе поля
Простым расширением поля с помощью элемента а называется наименьшее подполе поля  содержащее множество Р и элемент а. Простое расширение с помощью а обозначается через
содержащее множество Р и элемент а. Простое расширение с помощью а обозначается через  основное множество поля
основное множество поля  обозначается через Р (а).
обозначается через Р (а).
Пусть  — кольцо полиномов от
— кольцо полиномов от  и
и

 есть множество всех выражений вида
есть множество всех выражений вида  где
где  и
и  — любое натуральное число.
— любое натуральное число.
Легко видеть, что алгебра  - подкольцо поля
- подкольцо поля  — является кольцом; это кольцо обозначается символом
— является кольцом; это кольцо обозначается символом 
ТЕОРЕМА 2.1. Пусть  — кольцо полиномов от
— кольцо полиномов от  над
над  (а) — простое расширение поля
(а) — простое расширение поля  Пусть
Пусть  — отображение
— отображение  на
на  такое, что а) для любого f из
такое, что а) для любого f из  Тогда:
Тогда:

Доказательство. Утверждения (а) и  непосредственно следуют из определения
непосредственно следуют из определения  Отображение
Отображение  сохраняет главные операции кольца
сохраняет главные операции кольца  так как для любых f и g из
так как для любых f и g из 

Далее, по условию,  есть отображение
есть отображение  на
на  Следовательно,
Следовательно,  является гомоморфизмом кольца
является гомоморфизмом кольца  на кольцо
на кольцо 
Утверждение  непосредственно следует из определения отображения
непосредственно следует из определения отображения 
Поскольку  — гомоморфизм кольца
— гомоморфизм кольца  на
на  то, по теореме 13.1.6, фактор-кольцо
то, по теореме 13.1.6, фактор-кольцо  изоморфно кольцу
изоморфно кольцу 
СЛЕДСТВИЕ 2.2. Пусть а — трансцендентный элемент над полем Тогда кольцо полиномов  изоморфно кольцу
изоморфно кольцу 
Доказательство. В силу трансцендентности а над  Поэтому, согласно теореме
Поэтому, согласно теореме  Кроме того, фактор-кольцо кольца
Кроме того, фактор-кольцо кольца  по нулевому идеалу изоморфно
по нулевому идеалу изоморфно  Следовательно,
Следовательно, 
Минимальный полином алгебраического элемента.
Пусть  — кольцо полиномов над полем
— кольцо полиномов над полем
ОПРЕДЕЛЕНИЕ. Пусть a — алгебраический элемент над полем  Минимальным полиномом элемента а над Ф называется нормированный полином из
Минимальным полиномом элемента а над Ф называется нормированный полином из  наименьшей степени, корнем которого является а. Степень минимального полинома называется степенью элемента а над
наименьшей степени, корнем которого является а. Степень минимального полинома называется степенью элемента а над
Легко видеть, что для всякого элемента а, алгебраического над  существует минимальный полином.
существует минимальный полином.
ПРЕДЛОЖЕНИЕ 2.3. Если а — алгебраический элемент над полем a g и  — его минимальные полиномы над
— его минимальные полиномы над  то
то 
Доказательство. Степени минимальных полиномов g и  совпадают. Если
совпадают. Если  то элемент а (степени
то элемент а (степени  над
над  ) будет корнем полинома
) будет корнем полинома  степень которого меньше степени полинома
степень которого меньше степени полинома  (меньше
(меньше  ), что невозможно. Следовательно,
), что невозможно. Следовательно, 
ТЕОРЕМА 2.4. Пусть а — алгебраический элемент степени  над полем
над полем  и g — его минимальный полином над Тогда.
и g — его минимальный полином над Тогда.

Доказательство. Допустим, что полином g приводим в кольце  т. е. существуют в
т. е. существуют в  такие полиномы
такие полиномы  и h, что
и h, что

Тогда  Так как
Так как  — поле, то
— поле, то  или
или  что невозможно, поскольку, по условию, степень элемента а над
что невозможно, поскольку, по условию, степень элемента а над  равна
равна  .
.
Предположим, что  По условию,
По условию,  Следовательно, f и g не могут быть взаимно простыми. Поскольку полином g неприводим, то g делит
Следовательно, f и g не могут быть взаимно простыми. Поскольку полином g неприводим, то g делит 
Пусть  — гомоморфизм кольца
— гомоморфизм кольца  на кольцо
на кольцо  для всякого f из
для всякого f из  рассмотренный в теореме 2.1. В силу
рассмотренный в теореме 2.1. В силу  ядро гомоморфизма
ядро гомоморфизма  состоит из кратных полинома g, т. е.
состоит из кратных полинома g, т. е.  Следовательно, по теореме 13.1.6, фактор-кольцо
Следовательно, по теореме 13.1.6, фактор-кольцо  изоморфно кольцу
изоморфно кольцу 
Поскольку  , то
, то  есть область целостности. Так как то фактор-кольцо
есть область целостности. Так как то фактор-кольцо  также есть область целостности. Нам надо показать, что любой ненулевой элемент f из
также есть область целостности. Нам надо показать, что любой ненулевой элемент f из  обратим в
обратим в  . Пусть f — элемент смежного класса
. Пусть f — элемент смежного класса  Так как
Так как  то
то  ; поэтому полином g не делит полином f.
; поэтому полином g не делит полином f.
Поскольку полином g неприводим, отсюда следует, что полиномы  — взаимно простые. Следовательно, в
— взаимно простые. Следовательно, в  существуют такие полиномы и и а, что
существуют такие полиномы и и а, что  Отсюда вытекает равенство
Отсюда вытекает равенство  , показывающее, что элемент f обратим в кольце. Итак, установлено, что фактор-кольцо
, показывающее, что элемент f обратим в кольце. Итак, установлено, что фактор-кольцо  является полем.
является полем.
В силу  является полем и поэтому
является полем и поэтому  Кроме того, очевидно,
Кроме того, очевидно,  . Значит,
. Значит,  Следовательно, кольцо
Следовательно, кольцо  совпадает с полем
совпадает с полем 
Строение простого алгебраического расширения поля.
ТЕОРЕМА 2.5. Пусть а — алгебраический над полем элемент положительной степени  . Тогда любой элемент поля
. Тогда любой элемент поля  однозначно представим в виде линейной комбинации
однозначно представим в виде линейной комбинации  элементов
элементов  с коэффициентами из Р.
с коэффициентами из Р.
Доказательство. Пусть Р — любой элемент поля  По теореме
По теореме  следовательно, существует в
следовательно, существует в  полином f такой, что
полином f такой, что

Пусть g — минимальный полином для а над в силу условия теоремы его степень равна  . По теореме о делении с остатком, существуют в
. По теореме о делении с остатком, существуют в  полиномы
полиномы  такие, что
такие, что

Полагая в  и учитывая равенство (1), имеем
и учитывая равенство (1), имеем

Покажем, что элемент Р однозначно представим в виде линейной комбинации элементов  Пусть
Пусть

— любое такое представление. Рассмотрим полином 

Случай, когда степень  меньше
меньше  , невозможен, так как в силу (3) и
, невозможен, так как в силу (3) и  и степень
и степень  меньше степени g. Возможен лишь случай, когда
меньше степени g. Возможен лишь случай, когда  Следовательно, элемент
Следовательно, элемент  однозначно представим в виде линейной комбинации элементов
однозначно представим в виде линейной комбинации элементов 
Освобождение от алгебраической иррациональности в знаменателе дроби.
Задача об освобождении от алгебраической иррациональности в знаменателе дроби состоит в следующем. Пусть  — алгебраический элемент степени
— алгебраический элемент степени  над полем f и h — полиномы из кольца полиномов
над полем f и h — полиномы из кольца полиномов  Требуется представить элемент
Требуется представить элемент  в виде линейной комбинации степеней элемента а, т. е. в виде
в виде линейной комбинации степеней элемента а, т. е. в виде  где
где 
Эта задача решается следующим образом. Пусть g — минимальный полином для а над  . Так как, по теореме 2.4, полином неприводим над
. Так как, по теореме 2.4, полином неприводим над  то g не делит h и, значит, полиномы h и g — взаимно простые. Поэтому существуют в
то g не делит h и, значит, полиномы h и g — взаимно простые. Поэтому существуют в  такие полиномы
такие полиномы  и
и  , что
, что

Поскольку  из (1) следует, что
из (1) следует, что

Следовательно,  причем
причем  . Итак, мы освободились от иррациональности в знаменателе дроби
. Итак, мы освободились от иррациональности в знаменателе дроби 
Упражнения
1. Найдите минимальный полином для а над полем  если:
если:

2. Освободитесь от алгебраической иррациональности в знаменателе дроби 
3. Освободитесь от иррациональности в знаменателе дроби 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава первая. ЭЛЕМЕНТЫ ЛОГИКИ
- § 1. ЛОГИКА ВЫСКАЗЫВАНИЙ
- Формулы логики высказываний.
- Законы логики.
- Упражнения
- § 2. ЛОГИЧЕСКОЕ СЛЕДСТВИЕ
- Схемы доказательств.
- § 3. ПРЕДИКАТЫ
- Предикаты.
- Операции над предикатами.
- Упражнения
- § 4. КВАНТОРЫ
- Запись высказываний на языке логики предикатов.
- Упражнения
- § 5. ПРЕДИКАТНЫЕ ФОРМУЛЫ. ЗАКОНЫ ЛОГИКИ
- Предикатные формулы.
- Законы логики предикатов.
- Упражнения
- Глава вторая. МНОЖЕСТВА И ОТНОШЕНИЯ
- § 1. МНОЖЕСТВА
- Подмножества.
- Пустое множество.
- Операции над множествами.
- Основные свойства операций над множествами.
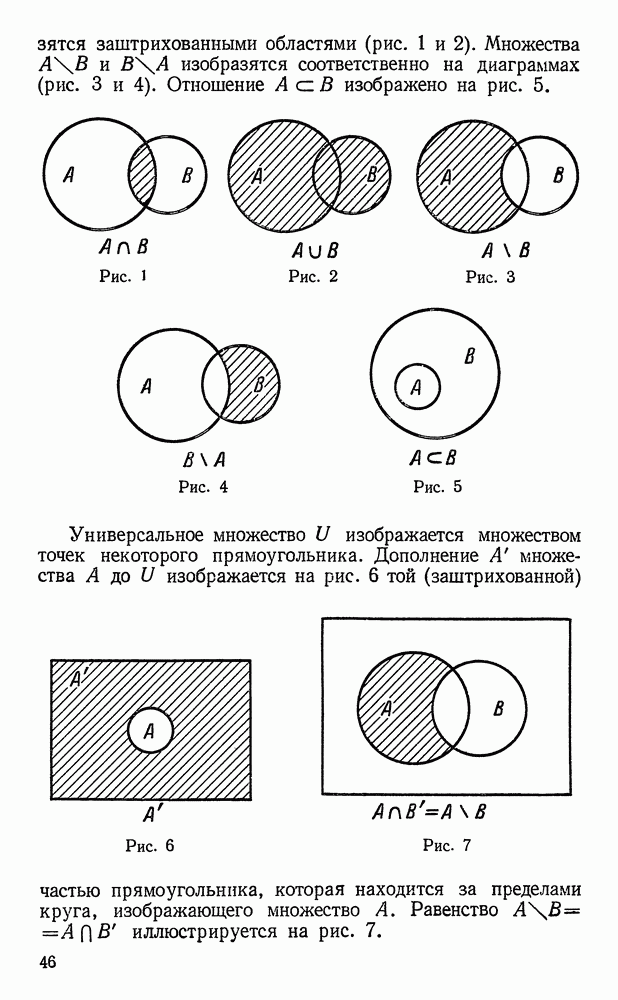
- Универсальное множество. Дополнение множества.
- Диаграммы Эйлера — Венна.
- Упражнения
- § 2. БИНАРНЫЕ ОТНОШЕНИЯ
- Упражнения
- § 3. ФУНКЦИИ
- Композиция функций.
- Инъективные функции.
- Обратимые функции.
- Ограничение функции.
- Упражнения
- § 4. ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ
- Отношение эквивалентности.
- Фактор-множество.
- Отношение равнообразности отображения.
- Упражнения
- § 5. ОТНОШЕНИЯ ПОРЯДКА
- Упорядоченное множество.
- Упражнения
- Глава третья. АЛГЕБРЫ И АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
- § 1. БИНАРНЫЕ ОПЕРАЦИИ
- Виды бинарных операций.
- Нейтральные элементы.
- Симметричные элементы.
- Подмножества, замкнутые относительно операций.
- Аддитивная и мультипликативная формы записи.
- Конгруэнция.
- Упражнения.
- § 2. АЛГЕБРЫ
- Гомоморфизмы алгебр.
- Подалгебры.
- Фактор-алгебра.
- Упражнения
- § 3. ГРУППЫ
- Примеры групп.
- Простейшие свойства группы.
- Гомоморфизмы групп.
- Подгруппы.
- Упражнения
- § 4. КОЛЬЦА
- Простейшие свойства кольца.
- Гомоморфизмы колец.
- Подкольца.
- Упражнения
- § 5. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
- Изоморфизмы алгебраических систем.
- Подсистемы.
- Упражнения
- Глава четвертая. ОСНОВНЫЕ ЧИСЛОВЫЕ СИСТЕМЫ
- § 1. СИСТЕМА НАТУРАЛЬНЫХ ЧИСЕЛ
- Слова в однобуквенном алфавите.
- Система натуральных чисел.
- Принцип математической индукции.
- Упражнения
- § 2. СВОЙСТВА СЛОЖЕНИЯ И УМНОЖЕНИЯ НАТУРАЛЬНЫХ ЧИСЕЛ
- Свойства умножения.
- § 3. ОТНОШЕНИЕ ПОРЯДКА НА МНОЖЕСТВЕ НАТУРАЛЬНЫХ ЧИСЕЛ
- Полная упорядоченность множества натуральных чисел.
- Упражнения
- § 4. КОЛЬЦО ЦЕЛЫХ ЧИСЕЛ
- Естественное умножение в аддитивной группе целых чисел.
- Кольцо целых чисел.
- Отношение делимости в кольце целых чисел.
- Упражнения
- § 5. ПОЛЯ. ПОЛЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- Поле рациональных чисел.
- Упражнения
- § 6. СИСТЕМА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- Система действительных чисел.
- Упражнения
- § 7. ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ
- Поле комплексных чисел.
- Модуль комплексного числа.
- Геометрическое представление комплексных чисел.
- Упражнения
- § 8. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА. ИЗВЛЕЧЕНИЕ КОРНЕЙ ИЗ КОМПЛЕКСНЫХ ЧИСЕЛ
- Корни n-й степени из единицы.
- Корни n-й степени из произвольного комплексного числа.
- Упражнения
- Глава пятая. АРИФМЕТИЧЕСКИЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. АРИФМЕТИЧЕСКИЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Линейная зависимость и независимость системы векторов.
- Эквивалентные системы векторов.
- Базис конечной системы векторов.
- Ранг конечной системы векторов.
- Упражнения
- § 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- Равносильные системы линейных уравнений и элементарные преобразования системы.
- Равенство строчечного и столбцового рангов матрицы.
- Связь между решениями неоднородной линейной системы и решениями ассоциированной с ней однородной системы.
- Теоремы о следствиях системы линейных уравнений.
- Упражнения.
- § 3. СТУПЕНЧАТЫЕ МАТРИЦЫ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- Приведенные ступенчатые матрицы.
- Однородные системы линейных уравнений.
- Фундаментальная система решений.
- Решение системы линейных уравнений методом последовательного исключения переменных.
- Упражнения
- Глава шестая. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- § 1. ОПЕРАЦИИ НАД МАТРИЦАМИ И ИХ СВОЙСТВА
- Транспонирование произведения матриц.
- Упражнения
- § 2. ОБРАТИМЫЕ МАТРИЦЫ
- Элементарные матрицы.
- Вычисление обратной матрицы.
- Запись и решение системы n линейных уравнений с n переменными в матричной форме.
- Упражнения
- § 3. ПОДСТАНОВКИ
- Четные и нечетные подстановки.
- Знак подстановки.
- Упражнения
- § 4. ОПРЕДЕЛИТЕЛИ
- Основные свойства определителей.
- Упражнения
- § 5. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ. ТЕОРЕМЫ ОБ ОПРЕДЕЛИТЕЛЯХ
- Разложение определителя по строке или столбцу.
- Определитель произведения матриц.
- Необходимые и достаточные условия равенства нулю определителя.
- § 6. ТЕОРЕМЫ О МАТРИЦАХ. ПРАВИЛО КРАМЕРА
- Правило Крамера.
- Условия, при которых система n линейных однородных уравнений с n переменными имеет ненулевые решения.
- Упражнения
- Глава седьмая. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- § 1. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Простейшие свойства векторных пространств.
- Линейная зависимость и независимость системы векторов.
- Упражнения
- § 2. ПОДПРОСТРАНСТВА ВЕКТОРНОГО ПРОСТРАНСТВА
- Линейная оболочка множества векторов.
- Сумма подпространств.
- Линейные многообразия.
- Упражнения
- § 3. БАЗИС И РАЗМЕРНОСТЬ ВЕКТОРНОГО ПРОСТРАНСТВА
- Дополнение независимой системы векторов до базиса.
- Размерность векторного пространства.
- Упражнения.
- § 4. ИЗОМОРФИЗМЫ ВЕКТОРНЫХ ПРОСТРАНСТВ
- Изоморфизм векторных пространств.
- Упражнения
- § 5. ВЕКТОРНЫЕ ПРОСТРАНСТВА СО СКАЛЯРНЫМ УМНОЖЕНИЕМ
- Ортогональная система векторов.
- Процесс ортогонализации.
- Упражнения.
- § 6. ЕВКЛИДОВЫ ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Норма вектора.
- Ортонормированный базис евклидова пространства.
- Изоморфизмы евклидовых пространств.
- Упражнения.
- Глава восьмая. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- § 1. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
- Ядро и образ линейного оператора.
- Операции над линейными отображениями.
- Упражнения
- § 2. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ОПЕРАТОРОВ МАТРИЦАМИ
- Связь между координатными столбцами векторов х и ф(x).
- Ранг линейного оператора.
- Связь между координатными столбцами вектора относительно различных базисов.
- Связь между матрицами линейного оператора относительно различных базисов.
- Упражнения
- § 3. ЛИНЕЙНЫЕ АЛГЕБРЫ
- Алгебра линейных операторов векторного пространства
- Изоморфизм алгебры линейных операторов и полной матричной алгебры.
- Упражнения
- § 4. ОБРАТИМЫЕ ОПЕРАТОРЫ
- Полная линейная группа.
- Упражнения
- § 5. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ. ХАРАКТЕРИСТИЧЕСКИЕ УРАВНЕНИЯ
- Нахождение собственных векторов линейного оператора.
- Характеристическое уравнение.
- Линейные операторы с простым спектром.
- Условия, при которых матрица подобна диагональной матрице.
- Упражнения
- Глава девятая. СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
- § 1. СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
- Однородные системы линейных неравенств и выпуклые конусы.
- Следствия однородной системы линейных неравенств.
- Теорема Минковского.
- Критерий несовместности системы линейных неравенств.
- Неотрицательные решения системы линейных уравнений и системы линейных неравенств.
- Упражнения
- § 2. СТАНДАРТНЫЕ И КАНОНИЧЕСКИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. ТЕОРЕМЫ ДВОЙСТВЕННОСТИ
- Допустимые и оптимальные векторы.
- Теорема двойственности для стандартных задач.
- Теорема двойственности для канонических задач.
- Теорема равновесия.
- Упражнения
- § 3. СИМПЛЕКС-МЕТОД
- Упражнения
- Глава десятая. ГРУППЫ
- § 1. ПОЛУГРУППЫ И МОНОИДЫ
- Моноиды.
- Обобщенный закон ассоциативности.
- Упражнения
- § 2. ПОДГРУППЫ И СМЕЖНЫЕ КЛАССЫ
- Смежные классы.
- Теорема Лагранжа.
- Упражнения
- § 3. ЦИКЛИЧЕСКИЕ ГРУППЫ
- Циклические группы.
- Подгруппы циклической группы.
- Упражнения
- § 4. НОРМАЛЬНЫЕ ДЕЛИТЕЛИ И ФАКТОР-ГРУППЫ
- Фактор-группа.
- Ядро гомоморфизма.
- Упражнения
- Глава одиннадцатая. ТЕОРИЯ ДЕЛИМОСТИ В КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
- § 1. РАЗЛОЖЕНИЕ ЦЕЛЫХ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ
- Простые числа.
- Разложение целых чисел на простые множители.
- Делители целого числа.
- Число и сумма натуральных делителей числа.
- Бесконечность множества простых чисел.
- Решето Эратосфена.
- Упражнения
- § 2. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ И НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Взаимно простые числа.
- Наименьшее общее кратное.
- Упражнения
- § 3. АЛГОРИТМ ЕВКЛИДА И КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
- Конечные цепные дроби.
- Подходящие дроби.
- Упражнения.
- § 4. ЦЕЛЫЕ СИСТЕМАТИЧЕСКИЕ ЧИСЛА
- Арифметические операции над целыми систематическими числами
- Перевод чисел из одной системы счисления в другую.
- Упражнения
- § 5. РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ
- Функции T(х) и Л(х).
- Неравенства для функции Т(х).
- Неравенства Чебышева.
- Простые числа в арифметических прогрессиях.
- Упражнения
- Глава двенадцатая. ТЕОРИЯ СРАВНЕНИЙ С АРИФМЕТИЧЕСКИМИ ПРИЛОЖЕНИЯМИ
- § 1. СРАВНЕНИЯ И ИХ СВОЙСТВА
- Упражнения
- § 2. ПОЛНАЯ СИСТЕМА ВЫЧЕТОВ
- Упражнения
- § 3. ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ
- Мультипликативная группа классов вычетов, взаимно простых с модулем.
- Функция Эйлера.
- Теоремы Эйлера и Ферма.
- Упражнения
- § 4. СРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ. СРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ ПО ПРОСТОМУ МОДУЛЮ
- Сравнения первой степени.
- Сравнения высших степеней по простому модулю.
- Упражнения
- § 5. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
- Первообразные корни по простому модулю.
- Индексы по простому модулю.
- Двучленные сравнения.
- Упражнения
- § 6. ОБРАЩЕНИЕ ОБЫКНОВЕННОЙ ДРОБИ В СИСТЕМАТИЧЕСКУЮ И ОПРЕДЕЛЕНИЕ ДЛИНЫ ПЕРИОДА СИСТЕМАТИЧЕСКОЙ ДРОБИ
- Упражнения
- Глава тринадцатая. КОЛЬЦА
- § 1. ИДЕАЛЫ КОЛЬЦА. ФАКТОР-КОЛЬЦО
- Сравнения и классы вычетов по идеалу.
- Фактор-кольцо.
- Теорема об эпиморфизмах колец.
- Характеристика кольца.
- Наименьшее подкольцо кольца.
- Упражнения
- § 2. ПОЛЕ ЧАСТНЫХ ОБЛАСТИ ЦЕЛОСТНОСТИ
- Изоморфизм полей частных.
- Упражнения
- § 3. КОЛЬЦА ГЛАВНЫХ ИДЕАЛОВ
- Простые и составные элементы области целостности.
- Кольца главных идеалов.
- Факториальность кольца главных идеалов.
- Евклидовы кольца.
- Упражнения
- § 4. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Наименьшее общее кратное.
- Упражнения
- Глава четырнадцатая. ПОЛИНОМЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. КОЛЬЦО ПОЛИНОМОВ
- Теорема о существовании простого трансцендентного расширения коммутативного кольца.
- Степень полинома.
- Деление полинома на двучлен и корни полинома.
- Теорема о наибольшем возможном числе корней полинома в области целостности.
- Алгебраическое и функциональное равенства полиномов.
- Упражнения
- § 2. ПОЛИНОМЫ НАД ПОЛЕМ
- Алгоритм Евклида.
- Неприводимые над данным полем полиномы.
- Разложение полинома в произведение нормированных неприводимых множителей.
- Упражнения
- § 3. ФАКТОРИАЛЬНОСТЬ КОЛЬЦА ПОЛИНОМОВ НАД ФАКТОРИАЛЬНЫМ КОЛЬЦОМ
- Факториальность кольца полиномов.
- § 4. ФОРМАЛЬНАЯ ПРОИЗВОДНАЯ ПОЛИНОМА. НЕПРИВОДИМЫЕ КРАТНЫЕ МНОЖИТЕЛИ
- Разложение полинома по степеням разности х — с.
- Неприводимые кратные множители полинома.
- Кратные корни полинома.
- Упражнения
- Глава пятнадцатая. ПОЛИНОМЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. КОЛЬЦО ПОЛИНОМОВ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- Кольцо полиномов от нескольких переменных.
- Изоморфизм колец полиномов.
- Нормальное представление полинома и степень полинома.
- Факториалыюсть кольца полиномов.
- § 2. СИММЕТРИЧЕСКИЕ ПОЛИНОМЫ
- Лемма о высшем члене произведения двух полиномов.
- Симметрические полиномы.
- Леммы о симметрических полиномах.
- Основная теорема о симметрических полиномах.
- Упражнения
- 3. РЕЗУЛЬТАНТ ПОЛИНОМОВ И ИСКЛЮЧЕНИЕ ПЕРЕМЕННЫХ
- Исключение переменных.
- Глава шестнадцатая. ПОЛИНОМЫ НАД ПОЛЕМ КОМПЛЕКСНЫХ ЧИСЕЛ И НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 1. АЛГЕБРАИЧЕСКАЯ ЗАМКНУТОСТЬ ПОЛЯ КОМПЛЕКСНЫХ ЧИСЕЛ
- Непрерывность модуля полинома.
- Наименьшее значение модуля полинома.
- Лемма Даламбера.
- Алгебраическая замкнутость поля комплексных чисел.
- Формулы Виета.
- Упражнения
- § 2. ПОЛИНОМЫ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 3. УРАВНЕНИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ СТЕПЕНИ
- Исследование корней уравнения третьей степени с действительными коэффициентами.
- Уравнения четвертой степени.
- § 4. ОТДЕЛЕНИЕ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ ПОЛИНОМА
- Теорема Штурма.
- Глава семнадцатая. ПОЛИНОМЫ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ЧИСЕЛ И АЛГЕБРАИЧЕСКИЕ ЧИСЛА
- § 1. ЦЕЛЫЕ И РАЦИОНАЛЬНЫЕ КОРНИ ПОЛИНОМА. КРИТЕРИЙ НЕПРИВОДИМОСТИ
- § 2. ПРОСТОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ
- § 3. СОСТАВНОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ
- § 4. УСЛОВИЯ РАЗРЕШИМОСТИ УРАВНЕНИЯ ТРЕТЬЕЙ СТЕПЕНИ В КВАДРАТНЫХ РАДИКАЛАХ
- ЛИТЕРАТУРА