| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ОСНОВНЫЕ ИДЕИ ОБЩЕЙ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
А. Вальд
1. Введение.
Математическая статистика чрезвычайно сильно развилась за последние 30 лет. Математическая статистика развивалась главным образом двумя школами: школой Р. А. Фишера и школой Неймана и Пирсона. Вопросы,
разрабатываемые этими школами, касались в основном различных критериев наилучшего использования наблюдений для проверки статистических гипотез и оценок параметров распределений. В этой связи нам хотелось бы упомянуть об основных понятиях эффективности и достаточности, введенных Фишером, и о понятии мощности критериев, введенном Нейманом и Пирсоном. Нет необходимости подробно останавливаться на важности этих понятий, так как это хорошо известно статистикам.
Около 10 лет назад статистические теории, за исключением небольшого числа отдельных результатов, были недостаточны в двух важных пунктах: 1) эксперимент состоял из одной стадии, т. е. число наблюдений фиксировалось до эксперимента, 2) рассматривались лишь два типа задач статистических решений, известные в литературе под именем проверки гипотез и оценки точек и интервалов. В течение нескольких последующих лет развилась общая теория статистических решений свободная от этих недостатков. В этой теории рассматриваются эксперименты, состоящие из многих стадий, и изучаются общие статистические проблемы, в которых статистик должен принять одно из многих решений.
Мне хочется описать принципы этой общей теории и некоторые ее результаты.
Любая задача статистического решения формулируется относительно некоторой последовательности  случайных величин. Для произвольной последовательности действительных чисел
случайных величин. Для произвольной последовательности действительных чисел  через
через  обозначим вероятность того, что
обозначим вероятность того, что  для всех целых положительных значений
для всех целых положительных значений  Функция
Функция  называется функцией распределения вероятностей
называется функцией распределения вероятностей  Типичная черта любой задачи статистического решения заключается в том, что
Типичная черта любой задачи статистического решения заключается в том, что  неизвестна. Известно лишь, что
неизвестна. Известно лишь, что  принадлежит некоторому классу 2 функций распределения. Класс 2 должен рассматриваться как данное задачи. Другим данным этой задачи является пространство
принадлежит некоторому классу 2 функций распределения. Класс 2 должен рассматриваться как данное задачи. Другим данным этой задачи является пространство  называемое пространством решений, элементы которого
называемое пространством решений, элементы которого  представляют собой возможные решения, которые может сделать статистик в этой задаче.
представляют собой возможные решения, которые может сделать статистик в этой задаче.
В этой работе для простоты будем полагать, что 1) каждая функция  класса 2 абсолютно непрерывна, т. е. существует
класса 2 абсолютно непрерывна, т. е. существует
плотность вероятности, 2) пространство  содержит конечное число элементов
содержит конечное число элементов  эксперимент производится последовательно. На первой стадии эксперимента наблюдается величина
эксперимент производится последовательно. На первой стадии эксперимента наблюдается величина  После того как была наблюдена величина
После того как была наблюдена величина  статистик решает, закончить ли эксперимент и принять некоторое решение
статистик решает, закончить ли эксперимент и принять некоторое решение  или наблюдать величину
или наблюдать величину  В последнем случае после наблюдения величин
В последнем случае после наблюдения величин  статистик снова решает, закончить ли эксперимент, приняв решение
статистик снова решает, закончить ли эксперимент, приняв решение  или наблюдать величину
или наблюдать величину 
В общей теории, изложенной в цитированной выше работе (см. сноску на стр. 309), условия, которым должны удовлетворять пространства  значительно более слабые. Приведенные выше условия вводятся здесь лишь для простоты изложения.
значительно более слабые. Приведенные выше условия вводятся здесь лишь для простоты изложения.
Решающее правило 8, т. е. правило выполнения эксперимента и принятия окончательного решения, определим при помощи последовательности действительных измеримых по Борелю функций  где
где  действительные переменные, а функции
действительные переменные, а функции  удовлетворяют условиям
удовлетворяют условиям 

Решающее правило определим следующим образом. Пусть  обозначают наблюденные значения величин
обозначают наблюденные значения величин  На каждой стадии эксперимента (после
На каждой стадии эксперимента (после  наблюдений, где
наблюдений, где  любое целое число) рассматриваем функции
любое целое число) рассматриваем функции  и затем производим вспомогательный случайный эксперимент с исходами
и затем производим вспомогательный случайный эксперимент с исходами  причем вероятность исхода
причем вероятность исхода  равна
равна  Если исходом явится
Если исходом явится  прекращаем эксперименты и принимаем решение
прекращаем эксперименты и принимаем решение  Если исходом явится 0, делаем дополнительное наблюдение (наблюдаем величину
Если исходом явится 0, делаем дополнительное наблюдение (наблюдаем величину  и повторяем такую же процедуру, используя на этот раз функции
и повторяем такую же процедуру, используя на этот раз функции 
Описанное решающее правило может быть названо рандомизированным правилом, так как на каждой стадии эксперимента используется случайный механизм для решения вопроса о прекращении испытаний и принятии решения или о проведении дополнительных наблюдений.
Специальный случай, когда функции  принимают только значения
принимают только значения  и 1, особенно интересен, так как в этом случае
и 1, особенно интересен, так как в этом случае
на каждой стадии эксперимента решение принимается исключительно на основе наблюденных величин и не связано ни с каким случайным механизмом.
Мы назовем правило решения  нерандомизированным, если функции
нерандомизированным, если функции  принимают лишь значения
принимают лишь значения  и 1. Вопрос о достаточности одних нерандомизированных правил для целей статистических решений важен и интересен. Мы возвратимся к этому вопросу позже.
и 1. Вопрос о достаточности одних нерандомизированных правил для целей статистических решений важен и интересен. Мы возвратимся к этому вопросу позже.
2. Функции потерь, стоимости и риска.
Основная проблема теории статистических решений заключается в выборе решающего правила 8. Чтобы судить о сравнительной ценности различных решающих правил, необходимо установить стоимость эксперимента, а также сравнительную характеристику различных решений, которые могут быть приняты, если функция  из 2 является истинным распределением. В качестве такой характеристики можно выбрать неотрицательную функцию
из 2 является истинным распределением. В качестве такой характеристики можно выбрать неотрицательную функцию  называемую функцией потерь, которая характеризует «убыток», понесенный статистиком, принявшим решение
называемую функцией потерь, которая характеризует «убыток», понесенный статистиком, принявшим решение  если
если  является истинным распределением
является истинным распределением  В большинстве задач статистических решений каждый элемент
В большинстве задач статистических решений каждый элемент  из
из  можно интерпретировать как решение принять гипотезу о том, что неизвестное распределение
можно интерпретировать как решение принять гипотезу о том, что неизвестное распределение  является элементом некоторого данного подкласса о в
является элементом некоторого данного подкласса о в  В таких случаях полагаем
В таких случаях полагаем  если
если  если
если  Стоимость эксперимента может быть представлена последовательностью
Стоимость эксперимента может быть представлена последовательностью  неотрицательных функций, где
неотрицательных функций, где  есть стоимость эксперимента, если он состоял из
есть стоимость эксперимента, если он состоял из  наблюдений, а
наблюдений, а  были наблюденными значениями
были наблюденными значениями  Функции потерь и стоимости эксперимента должны рассматриваться как данные задачи статистического решения. Функция стоимости
Функции потерь и стоимости эксперимента должны рассматриваться как данные задачи статистического решения. Функция стоимости  предполагается, конечно, измеримой по Борелю.
предполагается, конечно, измеримой по Борелю.
Пусть  обозначает условную вероятность того, что после
обозначает условную вероятность того, что после  наблюдений будет принято решение
наблюдений будет принято решение  если 8 принятое решающее правило,
если 8 принятое решающее правило,  наблюденные значения
наблюденные значения  Очевидно
Очевидно

Для любого целого положительного числа  через
через  обозначим совместную плотность
обозначим совместную плотность
распределения вероятностей величин  если
если  является истинной функцией распределения вероятностей
является истинной функцией распределения вероятностей  Среднее значение потерь, т. е. среднее значение величины
Среднее значение потерь, т. е. среднее значение величины  зависит только от распределения
зависит только от распределения  и принятого решающего правила
и принятого решающего правила  . Оно дается выражением
. Оно дается выражением

где  обозначает пространство всех
обозначает пространство всех  -мерных векторов
-мерных векторов 
Средняя стоимость эксперимента зависит только от истинного распределения  и принятого решающего правила о. Она дается формулой
и принятого решающего правила о. Она дается формулой

Пусть

Величина  называется риском при условии, что
называется риском при условии, что  истинное распределение,
истинное распределение,  принятое решающее правило. Для любого фиксированного решающего правила 8° риск является функцией лишь
принятое решающее правило. Для любого фиксированного решающего правила 8° риск является функцией лишь  Будем также называть
Будем также называть  функцией риска при заданном правиле решения 8°.
функцией риска при заданном правиле решения 8°.
Интересно сравнить различные правила решений, основываясь только на связанных с ними функциях риска. Мы скажем, что решающее правило  равномерно лучше решающего правила 82, если
равномерно лучше решающего правила 82, если  для всех
для всех  хотя бы для одного элемента
хотя бы для одного элемента  из 2. Решающее правило
из 2. Решающее правило  называется допустимым, если не существует равномерно лучших решающих правил. Два решающие правила
называется допустимым, если не существует равномерно лучших решающих правил. Два решающие правила  и
и  назовем эквивалентными, если они имеют одинаковые функции риска, т. е.
назовем эквивалентными, если они имеют одинаковые функции риска, т. е.  для всех
для всех  из 2. Для любого
из 2. Для любого  назовем решающие правила 81 и
назовем решающие правила 81 и  -эквивалентными, если
-эквивалентными, если  для всех
для всех  из 2.
из 2.
3. Устранение рандомизации при конечных 2.
Дворецким, Вольфовицем и автором было доказано, что при конечном 2 для каждого решающего правила  существует эквивалентное решающее нерандомизированное правило
существует эквивалентное решающее нерандомизированное правило  . Таким образом, в этих случаях можно избавиться от рандомизации и достаточно рассматривать только нерандомизированные решающие правила. Подобный результат для несколько более специального класса рандомизированных решающих правил был получен независимо Блэквеллом.
. Таким образом, в этих случаях можно избавиться от рандомизации и достаточно рассматривать только нерандомизированные решающие правила. Подобный результат для несколько более специального класса рандомизированных решающих правил был получен независимо Блэквеллом.
Доказательство основано на обобщении теоремы Ляпунова 3) о пространстве векторных мер. Непрерывность распределения  (вытекающая из нашего допущения об абсолютной непрерывности
(вытекающая из нашего допущения об абсолютной непрерывности  существенна для сформулированных выше результатов. В случае разрывных распределений могут существовать рандомизированные решающие правила с функциями риска, имеющими некоторые предписанные свойства, которые нельзя получить при помощи какого-либо нерандомизированного решающего правила.
существенна для сформулированных выше результатов. В случае разрывных распределений могут существовать рандомизированные решающие правила с функциями риска, имеющими некоторые предписанные свойства, которые нельзя получить при помощи какого-либо нерандомизированного решающего правила.
Конечность пространства 2 является очень стеснительным предположением, которое редко выполнено в задачах статистических решений. Однако при более общих условиях, которые обычно выполнены в задачах статистических решений, возникающих в приложениях, было показано, что для любого решающего правила 8 и для любого  существует е-эквивалентное нерандомизированное решающее правило 8.
существует е-эквивалентное нерандомизированное решающее правило 8.
Интересный результат о возможности устранения рандомизации, в несколько иной постановке задачи, был недавно найден Ходжесом и Леманом. Они доказали, что в случае, когда задача статистического решения есть задача оценки точки,  евклидово пространство и функция потерь
евклидово пространство и функция потерь  есть выпуклая функция
есть выпуклая функция  при любом
при любом  для любого рандомизированного решающего правила 8 (с ограниченной функцией риска) существует нерандомизированное решающее
для любого рандомизированного решающего правила 8 (с ограниченной функцией риска) существует нерандомизированное решающее
правило 8 такое, что  для всех
для всех  из 2. Заметим, что ни конечность 2, ни непрерывность его элементов
из 2. Заметим, что ни конечность 2, ни непрерывность его элементов  не необходимы для получения этого результата.
не необходимы для получения этого результата.
4. Определение сходимости в пространстве решающих правил и некоторые теоремы непрерывности.
Естественное определение сходимости в пространстве решающих правил, казалось бы, должно быть таким:  если
если

для всех  всех
всех  и всех
и всех  Это определение сходимости, однако, слишком сильно для наших целей. Вместо него примем следующее определение; мы скажем, что
Это определение сходимости, однако, слишком сильно для наших целей. Вместо него примем следующее определение; мы скажем, что

если

и

для каждого измеримого множества  в пространстве всех
в пространстве всех  -мерных векторов
-мерных векторов 
Было показано, что при таком определении сходимости справедлива следующая теорема.
Теорема 4.1. Пространство всех решающих правил компактно, т. е. всякая последовательность  решающих правил имеет предел.
решающих правил имеет предел.
Эта теорема есть простое следствие известных теорем о слабой компактности множества функции
Прежде чем перейти к теоремам о непрерывности, сформулируем два условия, налагаемые на функции потерь и стоимости.
Условие  есть ограниченная функция
есть ограниченная функция  для
для 
Условие II. Функция стоимости имеет следующие свойства: 1)  есть ограниченная функция переменных
есть ограниченная функция переменных  для каждого фиксированного
для каждого фиксированного  равномерно по всем
равномерно по всем 
Следующая теорема о непрерывности была доказана ранее.
Теорема 4.2. Пусть  есть такая последовательность решающих правил, что
есть такая последовательность решающих правил, что  и
и

для всех  при некотором целом положительном
при некотором целом положительном  Тогда, если условия I и II выполнены, имеем
Тогда, если условия I и II выполнены, имеем  для всех
для всех 
Теорема 4.3. Если  условия I и II выполнены,
условия I и II выполнены,  для всех
для всех 
5. Байесовские и минимаксные решения в задачах статистических решений.
В этом пункте рассмотрим байесовские и минимаксные решения и некоторые их свойства. Эти решения представляют не только самостоятельный интерес, но играют также важную роль в построении различных классов решающих правил в следующих разделях статьи. Начнем с некоторых определений.
Под априорным распределением вероятностей  на
на  будем понимать неотрицательную и счетно-аддитивную функцию множеств заданную на соответствующем образом выбранном борелевском поле подмножеств 2, причем
будем понимать неотрицательную и счетно-аддитивную функцию множеств заданную на соответствующем образом выбранном борелевском поле подмножеств 2, причем  Борелевское поле выбирается таким образом, чтобы
Борелевское поле выбирается таким образом, чтобы  была измеримой функцией
была измеримой функцией  для каждого фиксированного
для каждого фиксированного  .
.
Для любого априорного распределения вероятностей  положим
положим

Говорят, что решающее правило  является байесовским решением относительно априорного распределения если
является байесовским решением относительно априорного распределения если

Говорят, что решающее правило  есть байесовское решение в строгом смысле, если существует такое априорное распределение
есть байесовское решение в строгом смысле, если существует такое априорное распределение  что
что  есть байесовское решение относительно
есть байесовское решение относительно 
Говорят, что правило  есть байесовское решение относительно последовательности
есть байесовское решение относительно последовательности  априорных распределений, если
априорных распределений, если

где символ  обозначает нижнюю грань относительно
обозначает нижнюю грань относительно  .
.
Мы скажем, что решающее правило  есть байесовское решение в широком смысле, если существует последовательность априорных распределений, так что
есть байесовское решение в широком смысле, если существует последовательность априорных распределений, так что  есть байесовское решение относительно
есть байесовское решение относительно
Решающее правило  называется минимаксным решением, если
называется минимаксным решением, если

для всех  , где символ
, где символ  означает верхнюю грань относительно
означает верхнюю грань относительно 
Априорное распределение  называется наименее благоприятным, если удовлетворяется соотношение
называется наименее благоприятным, если удовлетворяется соотношение

Причина того, что априорное распределение  удовлетворяющее этому соотношению, называется наименее благоприятным. такова: если априорное распределение
удовлетворяющее этому соотношению, называется наименее благоприятным. такова: если априорное распределение  действительно существует и известно статистику, то байесовское решение 8, соответствующее
действительно существует и известно статистику, то байесовское решение 8, соответствующее  представляет собой удовлетворительное решение задачи статистического решения, так как 8 минимализирует средний риск (усредненный в соответствии с априорным распределением
представляет собой удовлетворительное решение задачи статистического решения, так как 8 минимализирует средний риск (усредненный в соответствии с априорным распределением  Минимум среднего риска, который может быть получен, будет, вообще говоря, различным при различных априорных распределениях, и априорное распределение
Минимум среднего риска, который может быть получен, будет, вообще говоря, различным при различных априорных распределениях, и априорное распределение  может рассматриваться тем менее благоприятным с точки зрения статистика, чем больше средний риск, связанный с распределением Таким образом, априорное распределение, удовлетворяющее (5.5), будет наименее благоприятным с точки зрения статистика.
может рассматриваться тем менее благоприятным с точки зрения статистика, чем больше средний риск, связанный с распределением Таким образом, априорное распределение, удовлетворяющее (5.5), будет наименее благоприятным с точки зрения статистика.
Приведем некоторые результаты, полученные для байесовских и минимаксных решений.
Теорема 5.1. Если выполнены условия I и II, то для любого априорного распределения  существует решающее правило 8, являющееся байесовским решением относительно
существует решающее правило 8, являющееся байесовским решением относительно
Теорема 5.2. Если выполнены условия I и II, то существует минимаксное решение.
Эти теоремы существования могут легко быть получены из теорем п. 4. При помощи этих теорем можем также доказать более сильный результат о том, что существует допустимое байесовское и допустимое минимаксное решение.
Теорема 5.3. Если выполнены условия I и II, то минимаксное решение всегда является байесовским в широком смысле.
Теорема 5.4. Пусть 8° есть минимаксное решение и — наименее благоприятное априорное распределение; тогда, если условия I и II выполнены, то 8° есть байесовское решение относительно  а множество
а множество  функций из 2, для которых
функций из 2, для которых  имеет вероятностную меру 1 относительно
имеет вероятностную меру 1 относительно 
Из последней части теоремы 5.4 вытекает, что функция риска минимаксного решения имеет постоянную величину на множестве  из 2, вероятностная мера которого относительно каждого наименее благоприятного априорного
из 2, вероятностная мера которого относительно каждого наименее благоприятного априорного
распределения  равна 1. Во многих задачах статистических решений функция риска минимаксного решения постоянна на всем пространстве 2.
равна 1. Во многих задачах статистических решений функция риска минимаксного решения постоянна на всем пространстве 2.
Несколько дополнительных результатов могут быть установлены, если выполняется следующее добавочное условие.
Условие III. Пространство 2 является компактным, а функция потерь  непрерывна по
непрерывна по  в смысле следующего определения сходимости в 2: скажем, что
в смысле следующего определения сходимости в 2: скажем, что  если для любого положительного
если для любого положительного  имеет место соотношение
имеет место соотношение

равномерно для всех измеримых подмножеств  в пространстве всех
в пространстве всех  -мерных векторов
-мерных векторов 
Теорема 5.5. Если выполнены условия I, II и III, то существует наименее благоприятное априорное распределение.
Доказательство этой теоремы основано на том факте, что множество всех вероятностных мер на компактном пространстве 2 компактно в смысле следующего определения сходимости:  если
если  для любого открытого подмножества
для любого открытого подмножества  пространства 2, граница которого имеет относительно
пространства 2, граница которого имеет относительно  вероятностную меру нуль. Этот результат был доказан автором. Близкий к этому результат был получен Крыловым и Боголюбовым. Их определение сходимости в пространстве вероятностных мер несколько отличается от используемого здесь.
вероятностную меру нуль. Этот результат был доказан автором. Близкий к этому результат был получен Крыловым и Боголюбовым. Их определение сходимости в пространстве вероятностных мер несколько отличается от используемого здесь.
Теорема 5.6. Если выполнены условия I, II, и III, то минимаксное решение всегда является байесовским решением в строгом смысле.
Эта теорема является прямым следствием теорем 5.4 и 5.5.
6. Полные классы решающих правил.
Класс С решающих правил 8 называется полным, если для любого не принадлежащего С правила 8 в С найдется равномерно лучшее правило 8. Мы будем говорить, что класс С решающих правил является существенно полным, если для любого не принадлежащего С правила 8 в С найдется такое правило 8. что  для всех
для всех  из 2.
из 2.
Очевидно, что если С — полный или, по меньшей мере, существенно полный класс решающих правил, то мы можем не рассматривать правил, не принадлежащих С, и задача выбора решающего правила сводится к задаче выбора определенного элемента из С. Таким образом, построение полных или существенно полных классов решающих правил имеет важное значение для любой задачи статистического решения.
Первый результат, касающийся полных классов решаюших правил, получен Леманом, который построил такой класс для одного специального случая. Вскоре после появления работы Лемана был получен ряд весьма общих результатов. Чтобы сформулировать некоторые из этих результатов, обозначим через А множество всех решающих правил 8 с ограниченными функциями риска. Будем говорить, что класс С решающих правил является полным или существенно полным относительно А, если соответствующие условия выполнены для каждого 8 из А. Автором был доказан следующий результат.
Теорема 6.1. Вели выполнены условия  то класс байесовских решений в широком смысле является полным относительно А.
то класс байесовских решений в широком смысле является полным относительно А.
Теорема 6.2. Если выполнены условия I и II, тогда замыкание класса всех байесовских решений в строгом смысле является существенно полным относительно 
Теорема 6.3. Если выполнены условия I, II и III, то класс всех байесовских решений в строгом смысле является полным относительно А.
Во избежание неясностей заметим, что понятие байесовского решения и априорного распределения используется здесь просто как математический инструмент для выражения некоторых результатов, касающихся полных классов решающих правил; действительное существование рассматриваемых здесь априорных распределений совершенно необязательно.
7. Применение к теории игр Неймана.
Теория статистических решений в том виде, в котором она была изложена здесь, тесно свазана с неймановской теорией игр двух игроков с нулевой суммой. Нормальная форма игры двух игроков с нулевой суммой была дана Нейманом в следующем виде. Имеется два игрока и задана ограниченная действительная функция  двух переменных и к
двух переменных и к  где и может быть любой точкой пространства
где и может быть любой точкой пространства  любой точкой пространства
любой точкой пространства  Игрок 1 выбирает точку и из
Игрок 1 выбирает точку и из  а игрок 2 выбирает точку
а игрок 2 выбирает точку  из V, причем точки выбираются независимо. Игрок 1 при этом выигрывает сумму
из V, причем точки выбираются независимо. Игрок 1 при этом выигрывает сумму  а игрок 2 — сумму —
а игрок 2 — сумму — 
Любая задача статистического решения может рассматриваться как игра двух игроков с нулевой суммой. Игрок 1 представляет собой некоторую внешнюю силу, например природу, которая выбирает элемент  из 2 и делает его истинным распределением X, а игрок 2, являющийся статистиком, выбирает решающее правило 8. Выигрыш дается функцией риска
из 2 и делает его истинным распределением X, а игрок 2, являющийся статистиком, выбирает решающее правило 8. Выигрыш дается функцией риска  которая зависит от выбора природы
которая зависит от выбора природы  и выбора статистика 8. Теория игр с двумя игроками и нулевой суммой была развита Нейманом для конечных пространств
и выбора статистика 8. Теория игр с двумя игроками и нулевой суммой была развита Нейманом для конечных пространств  В задачах статистических решений, однако, число стратегий природы (число элементов 2) и число стратегий статистика (число решающих правил) обычно бесконечны. Многие результаты теории статистических решений могут быть получены обобщением неймановской теории на случай бесконечных пространств стратегий. В частности, автором было показано, что если выполнены условия I и II, то задача статистического решения, рассматриваемая как игра двух игроков с нулевой суммой, является строго определенной в смысле неймановской теории, т. е.
В задачах статистических решений, однако, число стратегий природы (число элементов 2) и число стратегий статистика (число решающих правил) обычно бесконечны. Многие результаты теории статистических решений могут быть получены обобщением неймановской теории на случай бесконечных пространств стратегий. В частности, автором было показано, что если выполнены условия I и II, то задача статистического решения, рассматриваемая как игра двух игроков с нулевой суммой, является строго определенной в смысле неймановской теории, т. е.

Это соотношение играет фундаментальную роль в теории игр с двумя игроками и нулевой суммой. В теории статистических решений это соотношение является основным при
установлении результатов, касающихся полных классов решающих правил, но особого самостоятельного интереса не представляет.
8. Некоторые специальные случаи.
Мне хочется кратко остановиться на применении общей теории к некоторым специальным случаям.
Предположим, что 2 состоит из двух элементов:  Пусть случайные величины
Пусть случайные величины  независимы и их совместному распределению
независимы и их совместному распределению  соответствует плотность распределения каждой из них
соответствует плотность распределения каждой из них  Пространство решений
Пространство решений  содержит два элемента:
содержит два элемента:  где
где  означает решение принять гипотезу о том, что
означает решение принять гипотезу о том, что  является истинным распределением
является истинным распределением  . Пусть функция потерь
. Пусть функция потерь  если
если  если
если  Стоимость эксперимента установим пропорциональной числу наблюдений, т. е.
Стоимость эксперимента установим пропорциональной числу наблюдений, т. е.  где с — стоимость единичного наблюдения.
где с — стоимость единичного наблюдения.
Априорное распределение дается парой неотрицательных чисел  где
где  Величина
Величина  определяет априорную вероятность того, что
определяет априорную вероятность того, что  истинное распределение. Вольфовицем и автором было показано, что любое байесовское решение должно быть решающим правилом следующего типа. Пусть
истинное распределение. Вольфовицем и автором было показано, что любое байесовское решение должно быть решающим правилом следующего типа. Пусть  наблюденное значение величины
наблюденное значение величины  пусть
пусть

Выберем две константы  и на каждой стадии эксперимента (после
и на каждой стадии эксперимента (после  наблюдения, где
наблюдения, где  любое целое число) подсчитываем накопленную сумму
любое целое число) подсчитываем накопленную сумму  Как только нарушится соотношение
Как только нарушится соотношение  прекращаем эксперимент. Если при этом то принимаем решение
прекращаем эксперимент. Если при этом то принимаем решение  (принимаем гипотезу о том, что истинным распределением является
(принимаем гипотезу о том, что истинным распределением является  если же будет
если же будет  принимаем решение
принимаем решение  (т. е. гипотезу о том, что истинным распределением является
(т. е. гипотезу о том, что истинным распределением является  Решающее правило этого типа называется последовательным критерием отношений вероятностей.
Решающее правило этого типа называется последовательным критерием отношений вероятностей.
Применяя теоремы о полных классах к этому случаю, можно получить следующий результат. Класс всех последовательных критериев отношений вероятностей, соответствующий всем возможным значениям постоянных  является полным классом. Это означает, что если
является полным классом. Это означает, что если  — произвольное решающее правило, не являющееся последовательным критерием отношений вероятностей, то существует такая пара чисел
— произвольное решающее правило, не являющееся последовательным критерием отношений вероятностей, то существует такая пара чисел  что последовательный критерий отношений вероятностей с константами
что последовательный критерий отношений вероятностей с константами  равномерно лучше
равномерно лучше  .
.
Вследствие полноты класса всех последовательных критериев отношений вероятностей задача выбора решающего правила сводится к задаче выбора значений констант  Метод определения констант
Метод определения констант  при которых последовательный критерий отношений вероятностей является минимаксным или байесовским решением относительно данного априорного распределения, рассматривался Арроу, Блэкуэллом и Гиршиком.
при которых последовательный критерий отношений вероятностей является минимаксным или байесовским решением относительно данного априорного распределения, рассматривался Арроу, Блэкуэллом и Гиршиком.
Свойства последовательных критериев отношений вероятностей изучены довольно широко. Недавно возникший последовательный анализ основывается на последовательном критерии отношений вероятностей. Интересно заметить, что стохастический процесс, возникающий в последовательном критерии отношений вероятностей, тождественен с процессом одномерных случайных блуждений, играющем важную роль в молекулярной физике.
Теперь рассмотрим случай, когда  содержит конечное число элементов большее двух. Достаточно рассмотреть случай, когда 2 содержит 3 элемента
содержит конечное число элементов большее двух. Достаточно рассмотреть случай, когда 2 содержит 3 элемента  так как обобщение на случай любого числа элементов
так как обобщение на случай любого числа элементов  трудностей не представляет. Как и выше, случайные величины
трудностей не представляет. Как и выше, случайные величины  независимы, причем плотность распределения каждой из них равна
независимы, причем плотность распределения каждой из них равна  если
если  является истинным распределением
является истинным распределением  ). Пространство решений содержит
). Пространство решений содержит
также три элемента  где
где  означает решение принять гипотезу о том, что истинным распределением является
означает решение принять гипотезу о том, что истинным распределением является  Пусть
Пусть  если
если  если
если  Стоимость эксперимента опять установим пропорциональной числу наблюдений, положив стоимость единичного наблюдения равной с. Любое априорное распределение
Стоимость эксперимента опять установим пропорциональной числу наблюдений, положив стоимость единичного наблюдения равной с. Любое априорное распределение  может быть представлено точкой с координатами
может быть представлено точкой с координатами  . Множество всех априорных распределений при этом заполняет треугольную область
. Множество всех априорных распределений при этом заполняет треугольную область  с вершинами
с вершинами  и
и  где
где  представляет априорное распределение с
представляет априорное распределение с  компонентой равной 1 (рис. 17).
компонентой равной 1 (рис. 17).

Рис. 17.
Чтобы построить полный класс решающих правил для этой задачи, необходимо определить байесовское решение, соответствующее любому данному априорному распределению  Пусть
Пусть  обозначает наблюденное значение величины
обозначает наблюденное значение величины  После
После  наблюдений можем построить апостериорное распределение
наблюдений можем построить апостериорное распределение  имеющее вид
имеющее вид

На любой стадии эксперимента апостериорное распределение представляется точкой треугольной области 
Вольфовицем и автором было показано, что в области  можно выбрать три таких замкнутых и выпуклых множества
можно выбрать три таких замкнутых и выпуклых множества  (не зависящих от априорного распределения
(не зависящих от априорного распределения  что байесовское решение, соответствующее будет представлять собой следующее решающее правило. На каждой стадии эксперимента (после
что байесовское решение, соответствующее будет представлять собой следующее решающее правило. На каждой стадии эксперимента (после  наблюдений, где
наблюдений, где  определяется точка в области
определяется точка в области  Новые наблюдения производятся до тех пор, пока не попадает в одно
Новые наблюдения производятся до тех пор, пока не попадает в одно
из множеств  Если
Если  попадает внутрь области
попадает внутрь области  эксперимент прекращается и принимается решение
эксперимент прекращается и принимается решение  Если попадает на границу области
Если попадает на границу области  вопрос о прекращении эксперимента и принятии окончательного решения или о продолжении дальнейших наблюдений решается при помощи независимого случайного механизма.
вопрос о прекращении эксперимента и принятии окончательного решения или о продолжении дальнейших наблюдений решается при помощи независимого случайного механизма.
Выпуклые множества  зависят только от констант
зависят только от констант  Пока не существует метода для точного построения множеств
Пока не существует метода для точного построения множеств  и
и  по заданным величинам
по заданным величинам  Развитие метода для точного построения множеств
Развитие метода для точного построения множеств  имело бы чрезвычайно большую ценность, так как оно, вероятно, указало бы пути преодоления подобных трудностей в большом числе других задач последовательных статистических решений.
имело бы чрезвычайно большую ценность, так как оно, вероятно, указало бы пути преодоления подобных трудностей в большом числе других задач последовательных статистических решений.
Более общие результаты о байесовских решениях при допущении также нелинейных функций стоимости были получены Арроу, Блэкуэллом и Гиршиком.
В качестве последнего примера рассмотрим следующую задачу статистического решения. Известно, что  независимые и одинаково распределенные величины. Распределение каждой из них прямоугольное. Средняя точка
независимые и одинаково распределенные величины. Распределение каждой из них прямоугольное. Средняя точка  распределения является единственным неизвестным параметром, т. е. плотность распределения каждой из величин
распределения является единственным неизвестным параметром, т. е. плотность распределения каждой из величин  имеет вид
имеет вид

Для любой действительной величины  обозначим через
обозначим через  решение принять
решение принять  в качестве оценки для 0. Пространство решений состоит из элементов
в качестве оценки для 0. Пространство решений состоит из элементов  соответствующих всем действительным числам 0. Пусть функция потерь равна
соответствующих всем действительным числам 0. Пусть функция потерь равна  где
где  истинная величина средней точки распределения, а принято решение Стоимость эксперимента установим пропорциональной числу сделанных наблюдений. Стоимость единичного наблюдения обозначим через с.
истинная величина средней точки распределения, а принято решение Стоимость эксперимента установим пропорциональной числу сделанных наблюдений. Стоимость единичного наблюдения обозначим через с.
Ранее было показано, что минимаксное решение этой задачи дается следующим решающим правилом. Проводится
по меньшей мере одно наблюдение. На каждой стадии эксперимента  наблюдений, где
наблюдений, где  любое целое положительное число) подсчитывается величина
любое целое положительное число) подсчитывается величина

Эксперимент продолжается до тех пор, пока 
Как только окажется, что  эксперимент прекращается, и для 6 принимается оценка
эксперимент прекращается, и для 6 принимается оценка

Функция риска, связанная с минимаксным решением, постоянна на всем пространстве Допустимость этого минимаксного решения была доказана С. Блифом,
9. Заключительные замечания
В то время как общая теория получила значительное развитие в рассмотренных здесь направлениях и привела ко многим общим результатам, точные решения были разработаны для сравнительно небольшого числа специальных случаев. Математические трудности, с которыми приходится сталкиваться при получении точных решений, особенно в последовательном анализе, очень велики. Однако есть надежда, что в будущих исследованиях эти трудности будут преодолены и будут получены точные решения для большого числа различных проблем.
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ЧАСТЬ 1. ОБЩАЯ ТЕОРИЯ
- 1.1.1. Понятие случайной величины.
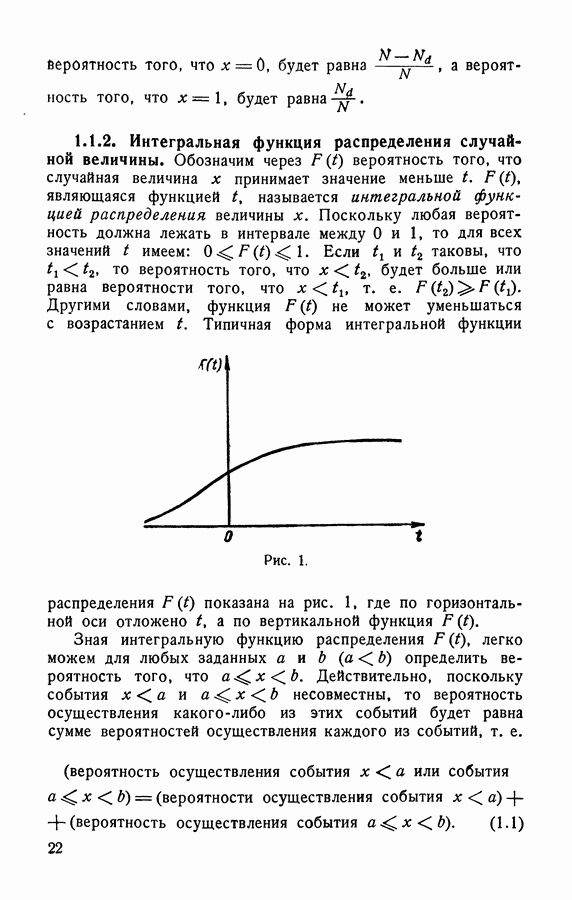
- 1.1.2. Интегральная функция распределения случайной величины.
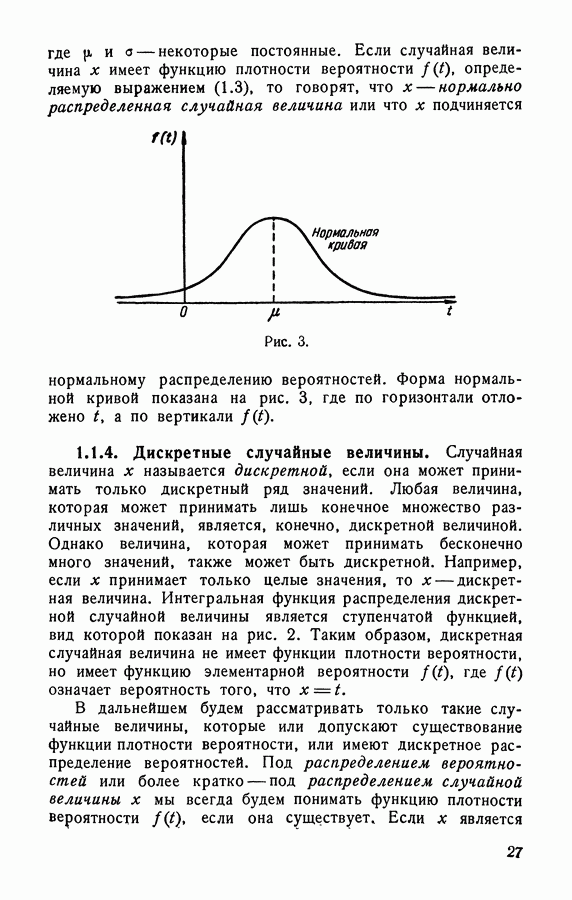
- 1.1.3. Функция плотности вероятности.
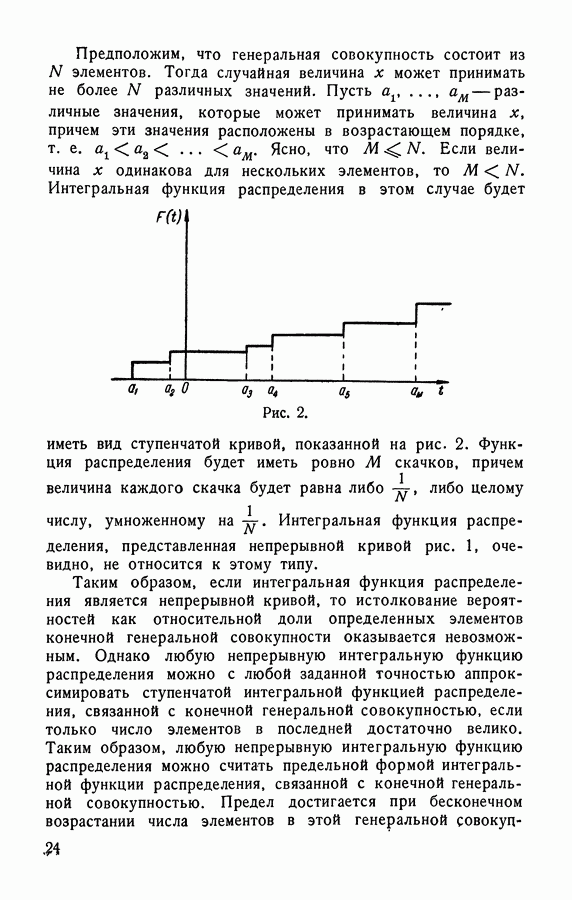
- 1.1.4. Дискретные случайные величины.
- 1.1.5. Математическое ожидание и высшие моменты случайной величины.
- § 1.2. Понятие статистической гипотезы
- 1.2.2. Простые и сложные гипотезы.
- § 1.3. Основные черты существующей методики проверки статистических гипотез
- 1.3.2. Общая методика проверки статистических гипотез.
- 1.3.3. Принципы выбора критической области.
- 1.3.4. Количество наблюдений, необходимых при заданных вероятностях a и b.
- 1.3.5. Проверка гипотезы как выбор между двумя возможными действиями.
- ГЛАВА 2. ПОСЛЕДОВАТЕЛЬНАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ОБЩИЕ ВОПРОСЫ
- § 2.2. Последствия выбора конкретной методики последовательной проверки
- 2.2.2. Функция среднего числа наблюдений последовательного критерия.
- § 2.3. Принципы, на которых основывается выбор последовательного критерия
- 2.3.2. Требования, предъявляемые к оперативной характеристике.
- 2.3.3. Функция среднего числа наблюдений как основа для выбора последовательного критерия.
- § 2.4. Проверка простой гипотезы Н0 при единственной конкурирующей гипотезе Н1
- 2.4.2. Эффективность существующей методики проверки гипотез, рассматриваемой как частный случай последовательного критерия.
- ГЛАВА 3. ПОСЛЕДОВАТЕЛЬНЫЙ КРИТЕРИЙ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ ДЛЯ ПРОВЕРКИ ПРОСТОЙ ГИПОТЕЗЫ Н0 ПРОТИВ ЕДИНСТВЕННОЙ КОНКУРИРУЮЩЕЙ ГИПОТЕЗЫ Н1
- § 3.1. Определение последовательного критерия отношений вероятностей
- § 3.2. Основные соотношения между величинами a, b, A и B
- § 3.3. Определение постоянных A и B на практике
- § 3.4. Оперативная характеристика последовательного критерия отношений вероятностей
- § 3.5. Среднее число наблюдений последовательного критерия отношений вероятностей
- § 3.6. Выигрыш в числе наблюдений при использовании последовательного критерия отношений вероятностей вместо обычной процедуры проверки
- § 3.7. Нижняя граница вероятности того, что последовательный критерий окончится при числе наблюдений, меньшем или равном заданному числу
- § 3.8. Усечение процедуры последовательного анализа
- § 3.9. Увеличение среднего числа наблюдений, обусловленное заменой точных значений A(a,b) и B(a,b) на …
- ГЛАВА 4. ОСНОВЫ ТЕОРИИ ПОСЛЕДОВАТЕЛЬНЫХ КРИТЕРИЕВ ДЛЯ ПРОСТЫХ И СЛОЖНЫХ ГИПОТЕЗ ОТНОСИТЕЛЬНО МНОЖЕСТВА КОНКУРИРУЮЩИХ ГИПОТЕЗ
- 4.1.2. Проверка простой гипотезы при односторонних конкурирующих гипотезах.
- 4.1.3. Проверка простой гипотезы в случае, когда на конкурирующие величины неизвестных параметров не накладывается никаких ограничений.
- 4.1.4. Применение общей методики к проверке среднего значения нормального распределения с известной дисперсией.
- § 4.2. Проверка сложных гипотез
- 4.2.2. Описание методики проверки в общем случае.
- 4.2.3. Применение общей методики к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий).
- 4.2.4. Частный класс задач, рассмотренный Гиршиком.
- ЧАСТЬ II. ПРИЛОЖЕНИЕ ОБЩЕЙ ТЕОРИИ К ЧАСТНЫМ СЛУЧАЯМ
- ГЛАВА 5. КРИТЕРИЙ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ (ПРИЕМОЧНАЯ ПРОВЕРКА ПАРТИИ ИЗДЕЛИЙ, В КОТОРОЙ КАЖДОЕ ИЗДЕЛИЕ ОТНЕСЕНО К ОДНОЙ ИЗ ДВУХ КАТЕГОРИЙ)
- § 5.2. Допускаемый риск, связанный с принятием неправильных решений
- § 5.3. Последовательный критерий отношения вероятностей, соответствующий величинам …
- 5.3.2. Табличный метод проведения контроля.
- 5.3.3. Графический метод проведения контроля.
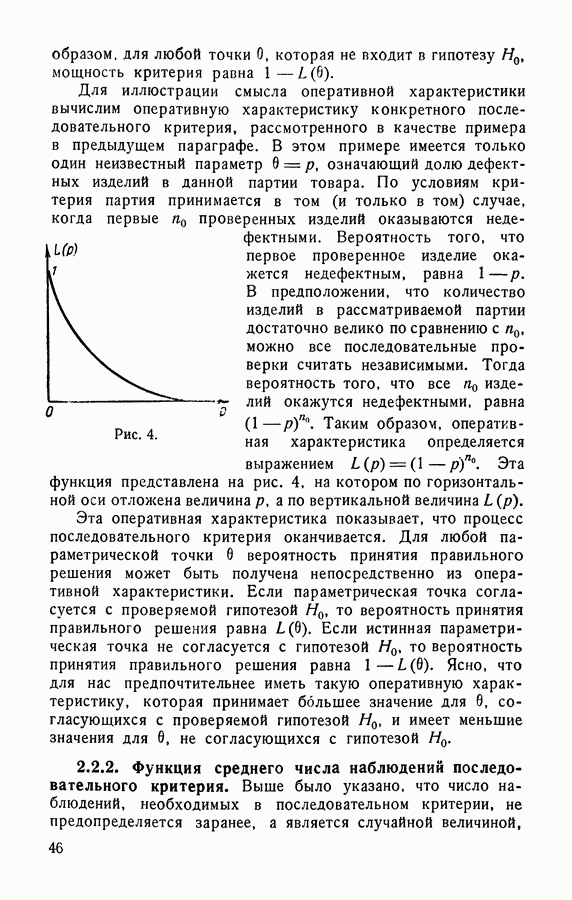
- § 5.4. Оперативная характеристика критерия L(p)
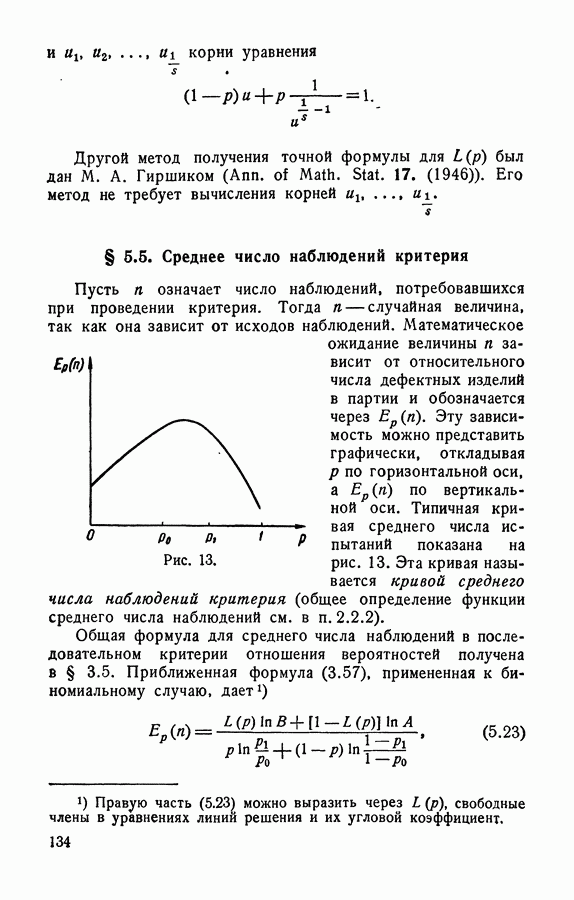
- § 5.5. Среднее число наблюдений критерия
- § 5.6. Группировка наблюдений
- 5.6.2. Влияние группировки на оперативную характеристику и среднее число наблюдений; верхние и нижние границы для них.
- § 5.7. Усеченный критерий
- ГЛАВА 6. КРИТЕРИЙ ДЛЯ РАЗНОСТИ МЕЖДУ СРЕДНИМИ ЗНАЧЕНИЯМИ ДВУХ БИНОМИАЛЬНЫХ РАСПРЕДЕЛЕНИЙ (ДВОЙНАЯ ДИХОТОМИЯ)
- § 6.4. Последовательный критерий для гипотезы …
- 6.4.1. Допускаемый риск, связанный с принятием неверных решений.
- 6.4.2. Последовательный критерий отношения вероятностей, соответствующий величинам u0, u1, a и b.
- 6.4.3. Кривая оперативной характеристики критерия.
- 6.4.4. Среднее число наблюдений, требуемых в критерии.
- 6.4.6. Наблюдения, осуществляемые группами.
- ГЛАВА 7. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНЫМ СРЕДНИМ КВАДРАТИЧЕСКИМ ОТКЛОНЕНИЕМ НЕ ПРЕВЫШАЕТ ЗАДАННОЙ ВЕЛИЧИНЫ
- § 7.2. Допускаемый риск, связанный с неправильным решением
- § 7.3. Последовательный критерий отношений вероятностей, соответствующий величинам …
- § 7.4. Кривая оперативной характеристики критерия
- § 7.6. Среднее число необходимых наблюдений в критерии
- ГЛАВА 8. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НЕ ПРЕВЫШАЕТ ЗАДАННОГО ЗНАЧЕНИЯ
- § 8.2. Допускаемый риск принятия неверного решения
- § 8.3. Последовательный критерий отношений вероятностей, соответствующий величинам …
- § 8.4. Оперативная характеристика критерия
- § 8.5. Среднее число наблюдений в критерии
- § 8.6. Модификация методики проверки, когда среднее значение генеральной совокупности неизвестно
- ГЛАВА 9. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНОЙ ДИСПЕРСИЕЙ РАВНО ОПРЕДЕЛЕННОЙ ВЕЛИЧИНЕ
- § 9.2. План последовательной проверки, удовлетворяющий заданным требованиям
- ЧАСТЬ III. ПРОБЛЕМА МНОГОЗНАЧНЫХ РЕШЕНИЙ И ОЦЕНКИ
- ГЛАВА 10. ВЫБОР ГИПОТЕЗЫ ИЗ МНОЖЕСТВА ВЗАИМНО ИСКЛЮЧАЮЩИХ ДРУГ ДРУГА ГИПОТЕЗ (МНОГОЗНАЧНОЕ РЕШЕНИЕ)
- § 10.2. Основные черты последовательного критерия для выбора гипотезы из множества взаимно исключающих друг друга гипотез
- § 10.3. Последствия выбора любого частного способа последовательной выборочной проверки
- § 10.4. Принципы выбора плана последовательной выборки
- 10.4.2. Функция риска, связанная с данным способом проверки.
- 10.4.3. Функция риска и среднее число наблюдений как основа для выбора плана последовательной выборки.
- 10.4.4. Использование некоторых простых весовых функций.
- § 10.5. Обсуждение специального класса планов последовательной выборки
- ГЛАВА 11. ПРОБЛЕМА ПОСЛЕДОВАТЕЛЬНОЙ ОЦЕНКИ
- § 11.1. Принципы современной теории оценок интервалами или множествами
- § 11.2. Постановка задачи о последовательной оценке посредством интервалов или множеств
- § 11.3. Специальный класс способов последовательной оценки
- ПРИЛОЖЕНИЯ
- П.1. Доказательство того, что с вероятностью, равной единице, последовательный критерий отношений вероятностей рано или поздно закончится
- П.2. Верхняя и нижняя границы оперативной характеристики последовательного критерия
- П.2.3. Определение верхней и нижней границ для оперативной характеристики.
- П.2.4. Расчет … для биномиального распределения
- П.2.5. Вычисление … для нормального распределения.
- П.3. Верхняя и нижняя границы для функции среднего числа наблюдений последовательного критерия отношений вероятностей
- П.3.2. Расчет величин … для биномиального и нормального распределений.
- П.4. Вывод точных формул для оперативной характеристики и функции среднего числа наблюдений в случае, когда z может принимать только конечное число значений, кратных постоянному числу
- П. 5. Характеристическая функция и высшие моменты величины n
- П.5.2. Вывод точной формулы для случая, когда z может принимать только конечное число значений, кратных некоторому постоянному числу.
- П.6. Приближенное распределение величины n для случая, когда z распределена по нормальному закону
- П.7. Эффективность последовательного критерия отношений вероятностей
- П.8. Определение оптимальной весовой функции w(O) в некоторых специальных случаях проверки простых гипотез без ограничения возможных конкурирующих значений параметров
- П.8.2. Приложение к проверке средних значений независимых нормально распределенных случайных величин с известными дисперсиями.
- П.9. Определение оптимальных весовых функций … в некоторых специальных случаях проверки сложных гипотез
- П.9.2. Применение к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий).
- ДОПОЛНЕНИЯ. АСИМПТОТИЧЕСКИЕ МИНИМАКСНЫЕ РЕШЕНИЯ ЗАДАЧ ПОСЛЕДОВАТЕЛЬНЫХ ТОЧЕЧНЫХ ОЦЕНОК
- ДИФФЕРЕНЦИРОВАНИЕ ПОД ЗНАКОМ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ В ОСНОВНОМ ТОЖДЕСТВЕ ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА
- НЕКОТОРЫЕ УТОЧНЕНИЯ ГРАНИЦ ДЛЯ СРЕДНЕГО ЧИСЛА НАБЛЮДЕНИЙ В ПОСЛЕДОВАТЕЛЬНОМ КРИТЕРИИ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
- ОПТИМАЛЬНЫЙ ХАРАКТЕР ПОСЛЕДОВАТЕЛЬНОГО КРИТЕРИЯ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
- ОСНОВНЫЕ ИДЕИ ОБЩЕЙ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ