| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ОПТИМАЛЬНЫЙ ХАРАКТЕР ПОСЛЕДОВАТЕЛЬНОГО КРИТЕРИЯ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
А. Вальд и Дж. Вольфовиц
1. Краткое содержание.
Пусть  есть какой-либо последовательный критерий отношений вероятностей для выбора между двумя простыми, альтернативами
есть какой-либо последовательный критерий отношений вероятностей для выбора между двумя простыми, альтернативами  другой критерий для этой же самой цели.
другой критерий для этой же самой цели.
Введем обозначения  вероятность в критерии
вероятность в критерии  отвергнуть верную гипотезу
отвергнуть верную гипотезу  среднее число наблюдений, необходимых для принятия решения в критерии
среднее число наблюдений, необходимых для принятия решения в критерии  если гипотеза
если гипотеза  истинна (предполагается, что
истинна (предполагается, что  существует).
существует).
В этой статье будет доказано, что если

то

Это значит, что из всех критериев одной и той же мощности последовательный критерий отношений вероятностей
требует в среднем наименьшее число наблюдений. Этот результат предвиделся ранее.
2. Введение.
Пусть  две различные функции плотности вероятности или (в дискретном случае) две вероятностные функции (в этой статье индекс
две различные функции плотности вероятности или (в дискретном случае) две вероятностные функции (в этой статье индекс  всегда будет принимать значения
всегда будет принимать значения  или 1). Пусть Лесть случайная величина, распределение вероятностей которой есть
или 1). Пусть Лесть случайная величина, распределение вероятностей которой есть  или
или  но какое именно — неизвестно. Необходимо выбрать одну из гипотез
но какое именно — неизвестно. Необходимо выбрать одну из гипотез  или
или  обозначает гипотезу, что
обозначает гипотезу, что  есть распределение вероятностей X) на основе
есть распределение вероятностей X) на основе  независимых наблюдений
независимых наблюдений  величины X, где
величины X, где  есть конечная случайная величина, определенная для почти каждой бесконечной последовательности
есть конечная случайная величина, определенная для почти каждой бесконечной последовательности

т. е.  конечна с вероятностью единица при
конечна с вероятностью единица при  Определение
Определение  одновременно с правилом выбора
одновременно с правилом выбора  или
или  и составляет последовательный анализ.
и составляет последовательный анализ.
Последовательный критерий отношений вероятностей определяется при помощи двух положительных чисел  следующим образом. Положим для краткости
следующим образом. Положим для краткости

Тогда  если
если

и

Если  то принимается гипотеза Ни если же
то принимается гипотеза Ни если же 
В, то принимается гипотеза 
В этой статье ограничимся рассмотрением таких последовательных критериев, для которых  существует, где
существует, где  математическое ожидание числа
математическое ожидание числа  когда верна
когда верна  (т. е. когда
(т. е. когда  есть распределение вероятностей
есть распределение вероятностей 
Стейном было доказано, что все последовательные критерий отношений вероятностей относятся к этому классу. Целью настоящей работы является доказательство результата, сформулированного в первом пункте. В процессе доказательства сделаем предположение, что априорная вероятность того, что верна гипотеза  равна
равна  будем в дальнейшем записывать
будем в дальнейшем записывать 
Многие статистики считают, что в большинстве практически важных задач не существует никакого априорного распределения вероятностей; если же оно существует, то оно часто неизвестно, и статистические выводы все равно приходится делать без него. Мы разделяем эту точку зрения. Введение в этой работе априорного распределения есть чисто технический прием, который не имеет отношения к методологии статистики, и читатель убедится, что это так. Также будем полагать, что  Пусть
Пусть  с — заданные положительные числа. Положим
с — заданные положительные числа. Положим

и назовем  средним риском, связанным с критерием S и заданным
средним риском, связанным с критерием S и заданным  (очевидно,
(очевидно,  есть функция
есть функция  Будем говорить, что принимается
Будем говорить, что принимается  если принимается решение, что
если принимается решение, что  есть распределение вероятностей
есть распределение вероятностей  Мы скажем, что
Мы скажем, что  отвергается, если принимается
отвергается, если принимается  и наоборот. Заметим, что
и наоборот. Заметим, что  можно рассматривать как величину потерь, понесенных статистиком, отвергнувшим гипотезу
можно рассматривать как величину потерь, понесенных статистиком, отвергнувшим гипотезу  когда она истинна,
когда она истинна,  — как стоимость единичного наблюдения,
— как стоимость единичного наблюдения,  как средние потери, связанные с заданным априорным распределением и критерием S. Формально это просто некоторые величины, с которыми будем оперировать в процессе доказательства.
как средние потери, связанные с заданным априорным распределением и критерием S. Формально это просто некоторые величины, с которыми будем оперировать в процессе доказательства.
3. Роль отношения вероятностей.
Пусть  и с фиксированы. Пусть S есть заданный последовательный критерий с риском
и с фиксированы. Пусть S есть заданный последовательный критерий с риском  и «функцией объема выборки»
и «функцией объема выборки»  Пусть
Пусть  есть «решающая» функция. Эта функция принимает лишь значения
есть «решающая» функция. Эта функция принимает лишь значения  и 1 и используется следующим образом: если
и 1 и используется следующим образом: если  есть выборочная точка, то гипотеза с индексом
есть выборочная точка, то гипотеза с индексом  отвергается. Определим следующую решающую функцию
отвергается. Определим следующую решающую функцию 
когда  и когда
и когда  Когда
Когда  можно по желанию брать равным
можно по желанию брать равным  или 1.
или 1.
Необходимо помнить, что всякая решающая функция есть однозначная функция от  При этом заметим, что:
При этом заметим, что:
а) Интересующие нас свойства критерия не зависят от изменения критерия на множестве  точек
точек  вероятности нуль при обеих гипотезах
вероятности нуль при обеих гипотезах  т. е. изменение определения на
т. е. изменение определения на  решающей функции (или
решающей функции (или  не изменяет
не изменяет  В частности, это относится к среднему риску
В частности, это относится к среднему риску 
б) Множество точек, для которых  и X неопределена, имеет вероятность нуль при обеих гипотезах
и X неопределена, имеет вероятность нуль при обеих гипотезах 
Во всех последовательных критериях, которые мы будем в дальнейшем рассматривать, условимся полагать  всякий раз, когда
всякий раз, когда 
В силу вышенаписанного это произвольное условие не может изменить 
Пусть

Имеем

где  обозначает математическое ожидание совместного распределения
обозначает математическое ожидание совместного распределения  т. е.
т. е.  есть оператор
есть оператор 
Если событие  имеет положительную вероятность при
имеет положительную вероятность при  или при
или при  то для
то для  будем иметь
будем иметь 
Следовательно, если решающая функция  связанная с критерием
связанная с критерием  будет заменена решающей функцией
будет заменена решающей функцией  то
то  уменьшится. Поскольку нашей целью является сделать
уменьшится. Поскольку нашей целью является сделать  возможно меньше, в дальнейшем будем рассматривать только критерии, для которых
возможно меньше, в дальнейшем будем рассматривать только критерии, для которых  является решающей функцией, если не оговорено противное.
является решающей функцией, если не оговорено противное.
Функция  пока еще не определена при
пока еще не определена при  Удобное для наших целей определение будет дано в следующем
Удобное для наших целей определение будет дано в следующем  разделе.
разделе.  остается одним и тем же для всех определений.
остается одним и тем же для всех определений.
Таким образом,  является функцией лишь X или, что при фиксированном
является функцией лишь X или, что при фиксированном  то же самое, лишь
то же самое, лишь  Определим
Определим

Сейчас будет доказана
Лемма 1. Пусть заданы  Существует последовательный критерий
Существует последовательный критерий  для которого средний риск минимален. Функция объема выборки
для которого средний риск минимален. Функция объема выборки  для этого критерия может быть определена при помощи соответствующим образом выбранного подмножества К неотрицательных чисел. Именно для каждого со рассмотрим связанную с ним последовательность
для этого критерия может быть определена при помощи соответствующим образом выбранного подмножества К неотрицательных чисел. Именно для каждого со рассмотрим связанную с ним последовательность

и обозначим через  наименьшее целое число, для которого
наименьшее целое число, для которого  Тогда
Тогда  Функция
Функция  может быть не определена на множестве точек
может быть не определена на множестве точек  вероятности нуль при
вероятности нуль при 
Пусть  произвольная точка некоторого
произвольная точка некоторого  -мерного евклидова пространства
-мерного евклидова пространства  конечно), обладающая лишь тем свойством, что
конечно), обладающая лишь тем свойством, что  отличны от нуля. Пусть
отличны от нуля. Пусть  Пусть, далее,
Пусть, далее,  есть любой последовательный критерий, для которого
есть любой последовательный критерий, для которого  при любой
при любой  , первые
, первые  координат которой такие же, что и у а, и для которого
координат которой такие же, что и у а, и для которого  здесь
здесь  условное математическое ожидание величины
условное математическое ожидание величины  соответствующей критерию А при условии, что первые
соответствующей критерию А при условии, что первые  координат
координат  такие же, как и у а. Для краткости, обозначим через О множество точек
такие же, как и у а. Для краткости, обозначим через О множество точек  для которых выполняется вышеприведенное условие, т. е.
для которых выполняется вышеприведенное условие, т. е.  первых координат которых такие же, как и у а. Наконец, пусть
первых координат которых такие же, как и у а. Наконец, пусть  есть условное математическое ожидание величины
есть условное математическое ожидание величины  соответствующей критерию
соответствующей критерию  при условии, что
при условии, что  принадлежит множеству О. Мы знаем, что
принадлежит множеству О. Мы знаем, что  зависит только от
зависит только от  Запишем
Запишем

Пусть  есть произвольная точка, для которой
есть произвольная точка, для которой 

Пусть  есть последовательный критерий, в котором
есть последовательный критерий, в котором  для любой
для любой  первые
первые  координат которой такие же, что и
координат которой такие же, что и  причем
причем  Пусть
Пусть

Докажем, что  Таким образом, мы можем писать
Таким образом, мы можем писать

Предположим, что  Пусть есть такой критерий типа
Пусть есть такой критерий типа  что
что

Определим теперь другой последовательный критерий  типа
типа  следующим образом. Пусть
следующим образом. Пусть

есть любая последовательность, для которой  Тогда для последовательности
Тогда для последовательности

положим  Решающая функция
Решающая функция  соответствующая
соответствующая  может быть определена следующим образом:
может быть определена следующим образом:

Так как  то
то

а это противоречит определению  Подобное же противоречие получается, если
Подобное же противоречие получается, если  Следовательно,
Следовательно,  что и требовалось доказать.
что и требовалось доказать.
Определим К таким образом, чтобы оно содержало все числа  для которых существуют точки а, обладающие свойством
для которых существуют точки а, обладающие свойством  Сейчас докажем, что критерий
Сейчас докажем, что критерий  определенный в соответствии с леммой, обладает наименьшей величиной
определенный в соответствии с леммой, обладает наименьшей величиной  Напомним, что средний риск есть математическое ожидание величины
Напомним, что средний риск есть математическое ожидание величины  Пусть 5 есть некоторый другой критерий. Пусть
Пусть 5 есть некоторый другой критерий. Пусть  произвольная последовательность, для которой или
произвольная последовательность, для которой или
 или
или  но
но  Мы исключаем тривиальный случай, когда вероятность появления этого события при обеих гипотезах
Мы исключаем тривиальный случай, когда вероятность появления этого события при обеих гипотезах  равна нулю. Пусть
равна нулю. Пусть  Последовательность а может принадлежать к одному из трех типов:
Последовательность а может принадлежать к одному из трех типов:
1)  . Следовательно,
. Следовательно,  С точки зрения уменьшения среднего риска выгодно прекратить проверку, так как
С точки зрения уменьшения среднего риска выгодно прекратить проверку, так как

2)  . Следовательно,
. Следовательно,  Если
Если  т. е. верхняя грань действительно достигается при критерии 5, то все равно, прекратить ли проверку с или продолжать ее в соответствии с 5. Если, однако,
т. е. верхняя грань действительно достигается при критерии 5, то все равно, прекратить ли проверку с или продолжать ее в соответствии с 5. Если, однако,  то ясно, что невыгодно продолжать проверку, согласно критерию
то ясно, что невыгодно продолжать проверку, согласно критерию  . Случай
. Случай  невозможен, так как
невозможен, так как 
3) Следовательно,  Очевидно, с точки зрения уменьшения среднего риска, не следует обрывать процесс последовательного критерия, и необходимо Продолжить его по крайней мере на одно наблюдение. После одного дополнительного наблюдения попадаем либо в случай 1, либо 2, когда выгодно прекратить проверку, либо опять в случай 3, когда выгодно проделать еще одно наблюдение.
Очевидно, с точки зрения уменьшения среднего риска, не следует обрывать процесс последовательного критерия, и необходимо Продолжить его по крайней мере на одно наблюдение. После одного дополнительного наблюдения попадаем либо в случай 1, либо 2, когда выгодно прекратить проверку, либо опять в случай 3, когда выгодно проделать еще одно наблюдение.
Таким образом,  минимально, что и требовалось доказать.
минимально, что и требовалось доказать.
4. Основная лемма.
Рассмотрим дополнение множества К на положительной полуоси и вычеркнем из него все точки V% для которых не существует точек а в  -мерном евклидовом пространстве, обладающих свойством
-мерном евклидовом пространстве, обладающих свойством  Точки 1 никогда не должны рассматриваться, как точки типа
Точки 1 никогда не должны рассматриваться, как точки типа  т. е. точки 1 никогда не должны вычеркиваться. Полученное множество обозначим К.
т. е. точки 1 никогда не должны вычеркиваться. Полученное множество обозначим К.
Доказательство теоремы, которой посвящена настоящая работа, будет основываться на следующей лемме.
Лемма 2. Пусть заданы  а множество К определено выше. Тогда существуют два положительных числа
а множество К определено выше. Тогда существуют два положительных числа  такие, что
такие, что

Прежде чем приступить к доказательству, сделаем два замечания.
1) Мы сейчас можем дополнить определение  для критериев типа
для критериев типа  Читатель помнит, что
Читатель помнит, что  определяется неоднозначно для
определяется неоднозначно для  т. е. когда
т. е. когда  Лемма 2 показывает, что
Лемма 2 показывает, что  нужно определить только для
нужно определить только для  поэтому X есть А или Определим
поэтому X есть А или Определим  как
как  или 1, смотря по тому, равняется ли А или В. Это просто удобное определение, которое устраняет неоднозначность. Когда
или 1, смотря по тому, равняется ли А или В. Это просто удобное определение, которое устраняет неоднозначность. Когда  ситуация тривиальна и можем положить, например,
ситуация тривиальна и можем положить, например, 
2) Если  то в силу последней леммы средний риск будет минимальным (для заданных
то в силу последней леммы средний риск будет минимальным (для заданных  конечно), если не производить ни одного наблюдения. Полагаем
конечно), если не производить ни одного наблюдения. Полагаем  или 1, соответственно при
или 1, соответственно при  или
или  .
.
Доказательство леммы. Пусть  есть некоторая точка из К. Докажем, что любая точка
есть некоторая точка из К. Докажем, что любая точка  для которой существует точка а в некотором
для которой существует точка а в некотором  -мерном евклидовом пространстве, такая, что
-мерном евклидовом пространстве, такая, что  также принадлежит К. Подобным же образом можно доказать, что если
также принадлежит К. Подобным же образом можно доказать, что если  есть некоторая точка из К, то любая точка
есть некоторая точка из К, то любая точка  для которой существует точка
для которой существует точка  в некотором
в некотором  -мерном евклидовом пространстве, такая, что
-мерном евклидовом пространстве, такая, что  также принадлежит
также принадлежит  Этим лемма и будет доказана.
Этим лемма и будет доказана.
Итак, пусть  выбраны, как указано выше. Пусть
выбраны, как указано выше. Пусть  есть последовательный критерий, основанный на К, с решающей функцией
есть последовательный критерий, основанный на К, с решающей функцией  Пусть а есть точка в
Пусть а есть точка в  -мерном пространстве, для которой
-мерном пространстве, для которой  Так как
Так как  то
то 
Сейчас введем несколько отличный от S последовательный критерий S с решающей функцией, которая может отличаться от  следующим образом. Возьмем а, определенное
следующим образом. Возьмем а, определенное
выше; запишем

Пусть

есть некоторая последовательность, для которой  Для последовательности
Для последовательности

положим  Решающую функцию
Решающую функцию  связанную с 5, определим равенством
связанную с 5, определим равенством

Очевидно,

и

Кроме того, имеем 

Так как 

то мы должны иметь

Из  следует, что
следует, что

Соотношения (4.1), (4.2), (4.4), (4.5) и (4.6) показывают что величина правой части (4.3) увеличивается, если там заменить  на
на  и
и  соответственно. Это и доказывает лемму.
соответственно. Это и доказывает лемму.
Если существуют значения, которые  не может принимать, то пара чисел В, А может оказаться не единственной.
не может принимать, то пара чисел В, А может оказаться не единственной.
Для удобства определим Ли В единственным образом так. как указано ниже. В дальнейшем будем придерживаться этого определения.
Для этого сначала определим  для всех положительных А, причем это определение должно согласовываться с предыдущим определением, по которому
для всех положительных А, причем это определение должно согласовываться с предыдущим определением, по которому  была определена только для тех значений А, которые может принимать
была определена только для тех значений А, которые может принимать  Пусть А есть произвольное положительное число и
Пусть А есть произвольное положительное число и  есть произвольный последовательный критерий, обладающий следующими свойствами.
есть произвольный последовательный критерий, обладающий следующими свойствами.

Для  положим
положим 

Для  сохраним прежнее определение. Таким образом,
сохраним прежнее определение. Таким образом,  определена для всех положительных А. Это определение совпадает с прежним определением в случае, когда оно применимо. Заметим, что операция взятия верхней грани в (4.10) производится лишь по критериям, зависящим только от отношения вероятностей, как это следует из (4.7); но выводы леммы 1 показывают, что это ограничение не уменьшает верхней грани. Может показаться, что для
определена для всех положительных А. Это определение совпадает с прежним определением в случае, когда оно применимо. Заметим, что операция взятия верхней грани в (4.10) производится лишь по критериям, зависящим только от отношения вероятностей, как это следует из (4.7); но выводы леммы 1 показывают, что это ограничение не уменьшает верхней грани. Может показаться, что для  определена неоднозначно, однако, как мы скоро увидим, это не так.)
определена неоднозначно, однако, как мы скоро увидим, это не так.)
Величина  зависит, конечно, от
зависит, конечно, от  Чтобы подчеркнуть это, будем писать
Чтобы подчеркнуть это, будем писать  Легко убедиться, что
Легко убедиться, что

Вообще для любых положительных величин  имеем
имеем  и — некоторые функции
и — некоторые функции  Таким образом, если
Таким образом, если  имеет значение, которое не может принимать отношение вероятностей,
имеет значение, которое не может принимать отношение вероятностей,  любое допустимое значение, мы можем интерпретировать величину
любое допустимое значение, мы можем интерпретировать величину  как величину у, соответствующую
как величину у, соответствующую  некоторым, подходящим образом подобранным, априорным вероятностям
некоторым, подходящим образом подобранным, априорным вероятностям 
Теперь определим А как нижнюю грань всех точек  для которых
для которых  как верхнюю грань всех точек
как верхнюю грань всех точек  для которых
для которых  Если
Если  для всех А, то это определение дает
для всех А, то это определение дает 
Выводы леммы 2 показывают, что  есть монотонно возрастающая функция в интервале
есть монотонно возрастающая функция в интервале  и монотонно убывающая функция в интервале
и монотонно убывающая функция в интервале 
Теперь определим последовательный критерий  для всех положительных А. Решающей функцией
для всех положительных А. Решающей функцией  будет
будет  тогда (и только тогда), когда
тогда (и только тогда), когда  член последовательности
член последовательности

является первым элементом 0. Мы видим, что

для всех А. Между прочим, этим доказано, что  однозначно определена при
однозначно определена при 
Докажем следующую лемму.
Лемма 3. Функция  обладает следующими свойствами:
обладает следующими свойствами:
a) она непрерывна для всех А,

Доказательства требуют только свойства а) и с), так как свойство  является тривиальным следствием утверждения а) и определения
является тривиальным следствием утверждения а) и определения 
Пусть  любая точка, неравная
любая точка, неравная  и пусть
и пусть  любая точка в окрестности
любая точка в окрестности  В окрестности
В окрестности  оба
оба  и
и  ограничены. Пусть
ограничены. Пусть  две произвольные точки из достаточно малой окрестности
две произвольные точки из достаточно малой окрестности  которая будет определена ниже. Будем рассуждать так же, как при доказательстве леммы 2, полагая, что
которая будет определена ниже. Будем рассуждать так же, как при доказательстве леммы 2, полагая, что  соответствует
соответствует  леммы
леммы  соответствует
соответствует  леммы
леммы  соответствует
соответствует  леммы 2. Поскольку
леммы 2. Поскольку  и
и  непрерывные функции
непрерывные функции  ограниченные функции
ограниченные функции  то для достаточно малой окрестности
то для достаточно малой окрестности 

Меняя ролями  получаем, что в этой же окрестности
получаем, что в этой же окрестности

и, следовательно,

Так как А произвольно, то отсюда вытекает непрерывность  везде, за исключением, быть может,
везде, за исключением, быть может, 
Чтобы рассмотреть точку  будем рассуждать следующим образом. Используя вышеприведенное доказательство и определения (4.9), (4.10), можно доказать, что
будем рассуждать следующим образом. Используя вышеприведенное доказательство и определения (4.9), (4.10), можно доказать, что  непрерывна справа в точке
непрерывна справа в точке  Используя в точке
Используя в точке  определение
определение  при
при  т. е.
т. е.

а также (4.10) и (4.11), можно доказать, что  непрерывна слева от
непрерывна слева от  Это доказывает утверждение
Это доказывает утверждение 
Докажем с). Предположим, что для  имеет место
имеет место  Так как
Так как

то будем иметь

Тогда при помощи рассуждений, подобных тем, которые были использованы при доказательстве леммы 2, можно показать, что  для
для  Это, однако, невозможно, так как противоречит определению А.
Это, однако, невозможно, так как противоречит определению А.
Подобным же образом можно доказать, что если  то
то  Это доказывает утверждение с). Лзмма доказана.
Это доказывает утверждение с). Лзмма доказана.
5. Поведение A и B.
Лемма 4. Пусть заданы  Тогда
Тогда  непрерывные функции
непрерывные функции 
Доказательство. Достаточно доказать непрерывность А. Непрерывность В доказывается аналогично.
Предположим, что  Пусть
Пусть  выбраны так, что
выбраны так, что

b)  , где А — некоторое произвольное положительное число. Будем вместо
, где А — некоторое произвольное положительное число. Будем вместо  временно писать
временно писать  чтобы подчеркнуть ее зависимость от
чтобы подчеркнуть ее зависимость от  Тогда
Тогда

следует, что  непрерывна по равномерно относительно
непрерывна по равномерно относительно  Следовательно,
Следовательно,  также непрерывна по
также непрерывна по  т. е. для достаточно малых
т. е. для достаточно малых 

Таким образом,

что и доказывает непрерывность, так как А было произвольным.
Если  то возьмем
то возьмем  путем аналогичных рассуждений можно показать, что
путем аналогичных рассуждений можно показать, что

Таким образом,

Лемма доказана.
Лемма 5. Пусть  фиксированы. А зависит от
фиксированы. А зависит от  строго монотонно. Когда
строго монотонно. Когда  стремится к
стремится к  также стремится к 0; когда
также стремится к 0; когда  стремится к
стремится к  А также стремится
А также стремится
Доказательство. Поскольку  то
то  когда
когда  Если
Если  то взятие хотя бы одного наблюдения никак не уменьшит средний риск, какова бы ни была величина А. Следовательно, при
то взятие хотя бы одного наблюдения никак не уменьшит средний риск, какова бы ни была величина А. Следовательно, при  имеем
имеем  для всех А, так что
для всех А, так что  Поскольку
Поскольку  то
то  при
при  Таким образом,
Таким образом,  при
при  Из (4.9) видно, что
Из (4.9) видно, что  не убывает с ростом
не убывает с ростом  (все остальное фиксировано). Поэтому функция
(все остальное фиксировано). Поэтому функция

также не убывает при возрастании  и фиксированных
и фиксированных  Для достаточно малого положительного А и для любого
Для достаточно малого положительного А и для любого  такого, что
такого, что  имеем
имеем

Следовательно, для таких  строго возрастает с ростом
строго возрастает с ростом  Таким образом,
Таким образом,  (строго) монотонно возрастает с ростом
(строго) монотонно возрастает с ростом 
Теперь определим функцию  двух положительных аргументов
двух положительных аргументов  В так, что
В так, что

Из леммы 5 следует, что такая функция существует и однозначна.
6. Свойства функции ...
Докажем лемму. Лемма  непрерывна по
непрерывна по  Доказательство. Пусть
Доказательство. Пусть

и предположим, что последовательность  не сходится. Предположим, что
не сходится. Предположим, что  две различные предельные
две различные предельные
точки этой последовательности. Из непрерывности А (лемма 4) следует, что

Это, однако, противоречит лемме 5. Единственная возможность, которая должна быть рассмотрена, такова:

Если это имеет место, то из  будет следовать
будет следовать  что противоречит тому факту, что
что противоречит тому факту, что 
Лемма 7. Для фиксированного 8 имеем

Доказательство. Если при малых  функция
функция  ограничена снизу положительным числом, то в силу можем сделать А произвольно большим, выбрав
ограничена снизу положительным числом, то в силу можем сделать А произвольно большим, выбрав  достаточно малым, а это противоречит тому, что
достаточно малым, а это противоречит тому, что  Для доказательства второй части леммы допустим, что
Для доказательства второй части леммы допустим, что  ограничена сверху при
ограничена сверху при  Тогда будет стремиться к нулю при
Тогда будет стремиться к нулю при  Пусть
Пусть  фиксировано таким образом, что
фиксировано таким образом, что  Рассмотрим множество точек
Рассмотрим множество точек  для которых существует целое число
для которых существует целое число  такое, что
такое, что

Условное математическое ожидание величины  по этому множеству при гипотезе
по этому множеству при гипотезе  можно сделать как угодно большим, если взять В достаточно малым. Таким образом, при достаточно большом
можно сделать как угодно большим, если взять В достаточно малым. Таким образом, при достаточно большом  и при фиксированном произвольном
и при фиксированном произвольном  оптимальная процедура с точки зрения минимума среднего риска состоит в том, что сразу же без дополнительных наблюдений отвергается
оптимальная процедура с точки зрения минимума среднего риска состоит в том, что сразу же без дополнительных наблюдений отвергается  Это, однако, противоречит тому, что
Это, однако, противоречит тому, что  лемма доказана.
лемма доказана.
Лемма 8. Для фиксированного  имеют место
имеют место

Доказательство. По лемме 7

Если при фиксированном с оба  достаточно малы, то, независимо от величины
достаточно малы, то, независимо от величины  Отсюда
Отсюда  что и доказывает первую половину леммы.
что и доказывает первую половину леммы.
Пусть теперь есть такая последовательность, для которой  Пусть
Пусть  Для краткости будем, писать
Для краткости будем, писать  вместо
вместо

Предположим, что для достаточно большого  ограничена снизу положительным числом. Тогда для достаточно большого
ограничена снизу положительным числом. Тогда для достаточно большого  вероятность отвергнуть
вероятность отвергнуть  когда она верна, ограничена снизу положительным числом. Более того, поскольку В то Для достаточно большого
когда она верна, ограничена снизу положительным числом. Более того, поскольку В то Для достаточно большого  отношение
отношение  ограничено снизу и сверху положительными константами. Таким образом, для достаточно большого
ограничено снизу и сверху положительными константами. Таким образом, для достаточно большого  средний риск критерия, определенного при помощи
средний риск критерия, определенного при помощи  больше, чем где а — положительная константа, не зависящая от
больше, чем где а — положительная константа, не зависящая от  Более того, по определению
Более того, по определению  этот риск минимален.
этот риск минимален.
Пусть  такое произвольное положительное число, что
такое произвольное положительное число, что  Для всех достаточно больших
Для всех достаточно больших  Пусть
Пусть  причем
причем  такие константы, что определенный при их помощи последовательный критерий отношений вероятностей имеет
такие константы, что определенный при их помощи последовательный критерий отношений вероятностей имеет  меньшие
меньшие  Величины
Величины  конечны и определены этим критерием. Для этого критерия средний риск меньше, чем
конечны и определены этим критерием. Для этого критерия средний риск меньше, чем

для достаточно больших Это противоречит тому факту; что минимальный риск  лемма доказана.
лемма доказана.
7. Доказательство теоремы.
Пусть заданный последовательный критерий отношений вероятностей определен при, помощи  Пусть
Пусть  есть
есть
соответствующая  вероятность браковки
вероятность браковки  , когда
, когда  верна. Пусть с фиксировано. По лемме 4 В есть непрерывная функция
верна. Пусть с фиксировано. По лемме 4 В есть непрерывная функция  и
и  Пусть в лемме
Пусть в лемме  Тогда существует такая пара
Тогда существует такая пара  что
что

Таким образом, средний риск

соответствующий последовательному критерию 50, минимален. Пусть теперь  есть другой критерий для выбора между
есть другой критерий для выбора между  причем
причем

Тогда

Так как 

Здесь  были выбраны произвольно (при очевидных, конечно, ограничениях). Таким образом,
были выбраны произвольно (при очевидных, конечно, ограничениях). Таким образом,

Это и есть доказываемый результат.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ЧАСТЬ 1. ОБЩАЯ ТЕОРИЯ
- 1.1.1. Понятие случайной величины.
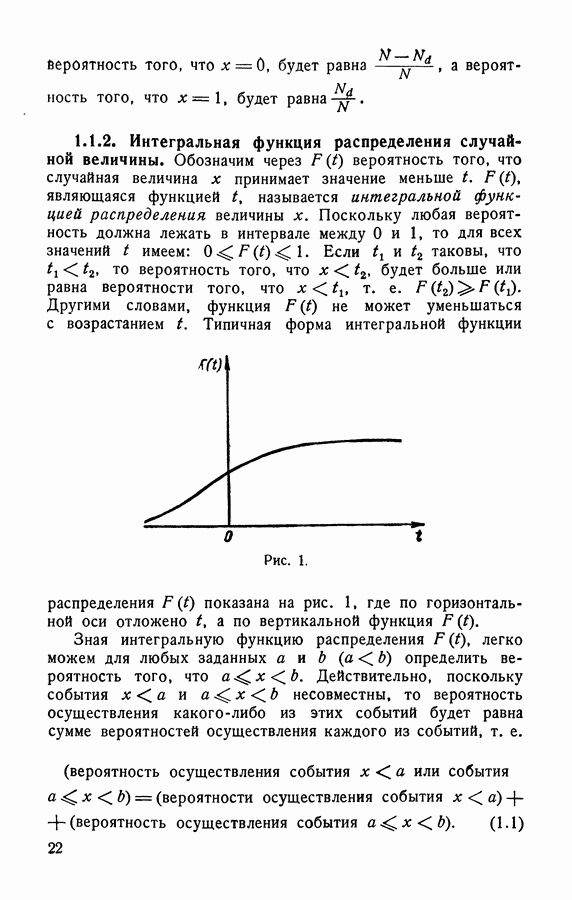
- 1.1.2. Интегральная функция распределения случайной величины.
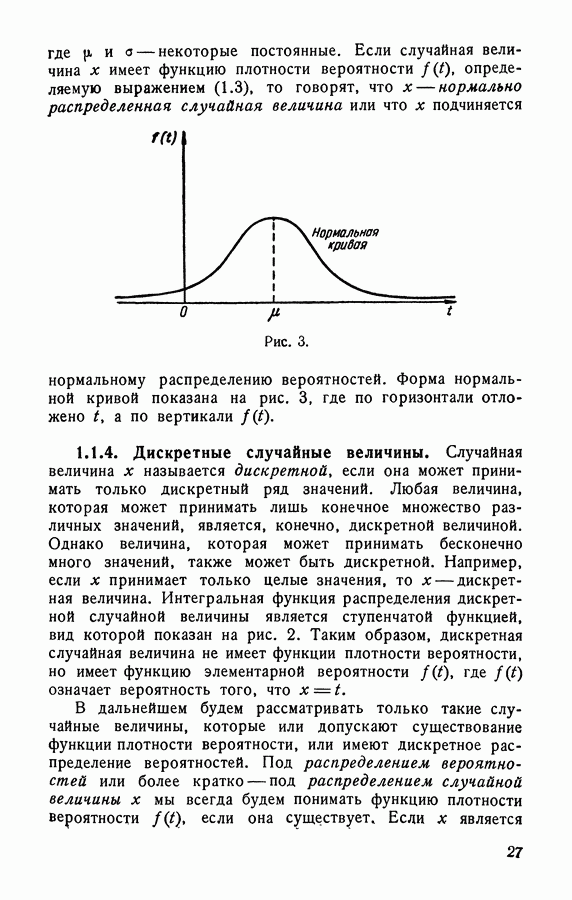
- 1.1.3. Функция плотности вероятности.
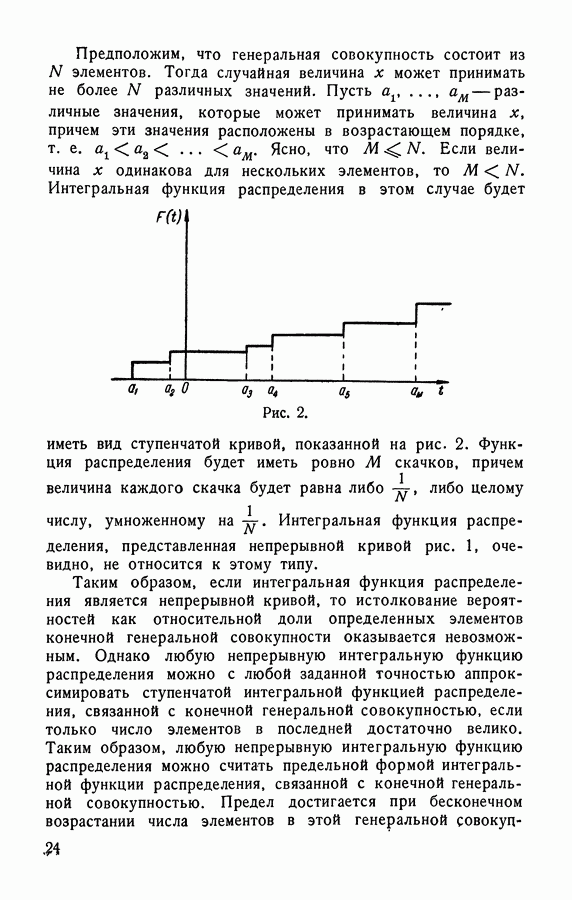
- 1.1.4. Дискретные случайные величины.
- 1.1.5. Математическое ожидание и высшие моменты случайной величины.
- § 1.2. Понятие статистической гипотезы
- 1.2.2. Простые и сложные гипотезы.
- § 1.3. Основные черты существующей методики проверки статистических гипотез
- 1.3.2. Общая методика проверки статистических гипотез.
- 1.3.3. Принципы выбора критической области.
- 1.3.4. Количество наблюдений, необходимых при заданных вероятностях a и b.
- 1.3.5. Проверка гипотезы как выбор между двумя возможными действиями.
- ГЛАВА 2. ПОСЛЕДОВАТЕЛЬНАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ОБЩИЕ ВОПРОСЫ
- § 2.2. Последствия выбора конкретной методики последовательной проверки
- 2.2.2. Функция среднего числа наблюдений последовательного критерия.
- § 2.3. Принципы, на которых основывается выбор последовательного критерия
- 2.3.2. Требования, предъявляемые к оперативной характеристике.
- 2.3.3. Функция среднего числа наблюдений как основа для выбора последовательного критерия.
- § 2.4. Проверка простой гипотезы Н0 при единственной конкурирующей гипотезе Н1
- 2.4.2. Эффективность существующей методики проверки гипотез, рассматриваемой как частный случай последовательного критерия.
- ГЛАВА 3. ПОСЛЕДОВАТЕЛЬНЫЙ КРИТЕРИЙ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ ДЛЯ ПРОВЕРКИ ПРОСТОЙ ГИПОТЕЗЫ Н0 ПРОТИВ ЕДИНСТВЕННОЙ КОНКУРИРУЮЩЕЙ ГИПОТЕЗЫ Н1
- § 3.1. Определение последовательного критерия отношений вероятностей
- § 3.2. Основные соотношения между величинами a, b, A и B
- § 3.3. Определение постоянных A и B на практике
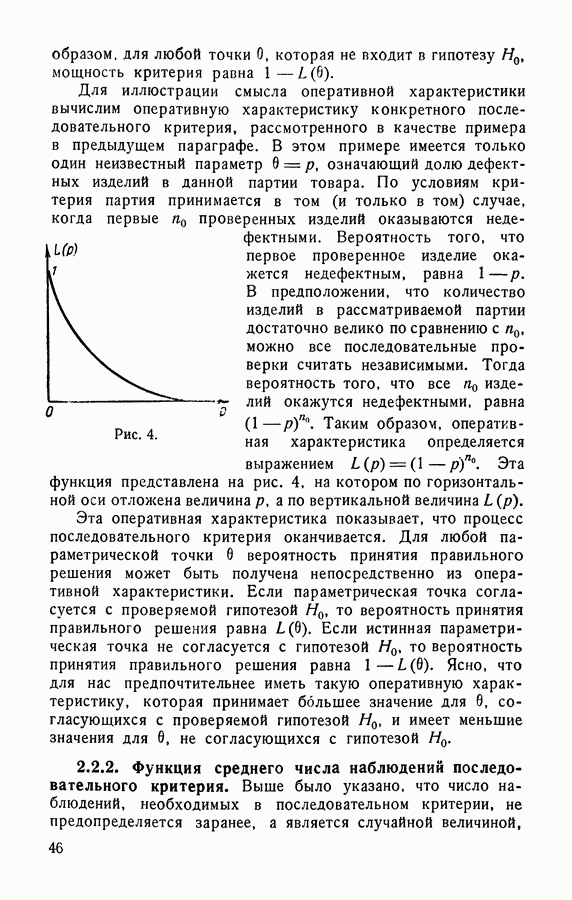
- § 3.4. Оперативная характеристика последовательного критерия отношений вероятностей
- § 3.5. Среднее число наблюдений последовательного критерия отношений вероятностей
- § 3.6. Выигрыш в числе наблюдений при использовании последовательного критерия отношений вероятностей вместо обычной процедуры проверки
- § 3.7. Нижняя граница вероятности того, что последовательный критерий окончится при числе наблюдений, меньшем или равном заданному числу
- § 3.8. Усечение процедуры последовательного анализа
- § 3.9. Увеличение среднего числа наблюдений, обусловленное заменой точных значений A(a,b) и B(a,b) на …
- ГЛАВА 4. ОСНОВЫ ТЕОРИИ ПОСЛЕДОВАТЕЛЬНЫХ КРИТЕРИЕВ ДЛЯ ПРОСТЫХ И СЛОЖНЫХ ГИПОТЕЗ ОТНОСИТЕЛЬНО МНОЖЕСТВА КОНКУРИРУЮЩИХ ГИПОТЕЗ
- 4.1.2. Проверка простой гипотезы при односторонних конкурирующих гипотезах.
- 4.1.3. Проверка простой гипотезы в случае, когда на конкурирующие величины неизвестных параметров не накладывается никаких ограничений.
- 4.1.4. Применение общей методики к проверке среднего значения нормального распределения с известной дисперсией.
- § 4.2. Проверка сложных гипотез
- 4.2.2. Описание методики проверки в общем случае.
- 4.2.3. Применение общей методики к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий).
- 4.2.4. Частный класс задач, рассмотренный Гиршиком.
- ЧАСТЬ II. ПРИЛОЖЕНИЕ ОБЩЕЙ ТЕОРИИ К ЧАСТНЫМ СЛУЧАЯМ
- ГЛАВА 5. КРИТЕРИЙ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ (ПРИЕМОЧНАЯ ПРОВЕРКА ПАРТИИ ИЗДЕЛИЙ, В КОТОРОЙ КАЖДОЕ ИЗДЕЛИЕ ОТНЕСЕНО К ОДНОЙ ИЗ ДВУХ КАТЕГОРИЙ)
- § 5.2. Допускаемый риск, связанный с принятием неправильных решений
- § 5.3. Последовательный критерий отношения вероятностей, соответствующий величинам …
- 5.3.2. Табличный метод проведения контроля.
- 5.3.3. Графический метод проведения контроля.
- § 5.4. Оперативная характеристика критерия L(p)
- § 5.5. Среднее число наблюдений критерия
- § 5.6. Группировка наблюдений
- 5.6.2. Влияние группировки на оперативную характеристику и среднее число наблюдений; верхние и нижние границы для них.
- § 5.7. Усеченный критерий
- ГЛАВА 6. КРИТЕРИЙ ДЛЯ РАЗНОСТИ МЕЖДУ СРЕДНИМИ ЗНАЧЕНИЯМИ ДВУХ БИНОМИАЛЬНЫХ РАСПРЕДЕЛЕНИЙ (ДВОЙНАЯ ДИХОТОМИЯ)
- § 6.4. Последовательный критерий для гипотезы …
- 6.4.1. Допускаемый риск, связанный с принятием неверных решений.
- 6.4.2. Последовательный критерий отношения вероятностей, соответствующий величинам u0, u1, a и b.
- 6.4.3. Кривая оперативной характеристики критерия.
- 6.4.4. Среднее число наблюдений, требуемых в критерии.
- 6.4.6. Наблюдения, осуществляемые группами.
- ГЛАВА 7. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНЫМ СРЕДНИМ КВАДРАТИЧЕСКИМ ОТКЛОНЕНИЕМ НЕ ПРЕВЫШАЕТ ЗАДАННОЙ ВЕЛИЧИНЫ
- § 7.2. Допускаемый риск, связанный с неправильным решением
- § 7.3. Последовательный критерий отношений вероятностей, соответствующий величинам …
- § 7.4. Кривая оперативной характеристики критерия
- § 7.6. Среднее число необходимых наблюдений в критерии
- ГЛАВА 8. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НЕ ПРЕВЫШАЕТ ЗАДАННОГО ЗНАЧЕНИЯ
- § 8.2. Допускаемый риск принятия неверного решения
- § 8.3. Последовательный критерий отношений вероятностей, соответствующий величинам …
- § 8.4. Оперативная характеристика критерия
- § 8.5. Среднее число наблюдений в критерии
- § 8.6. Модификация методики проверки, когда среднее значение генеральной совокупности неизвестно
- ГЛАВА 9. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНОЙ ДИСПЕРСИЕЙ РАВНО ОПРЕДЕЛЕННОЙ ВЕЛИЧИНЕ
- § 9.2. План последовательной проверки, удовлетворяющий заданным требованиям
- ЧАСТЬ III. ПРОБЛЕМА МНОГОЗНАЧНЫХ РЕШЕНИЙ И ОЦЕНКИ
- ГЛАВА 10. ВЫБОР ГИПОТЕЗЫ ИЗ МНОЖЕСТВА ВЗАИМНО ИСКЛЮЧАЮЩИХ ДРУГ ДРУГА ГИПОТЕЗ (МНОГОЗНАЧНОЕ РЕШЕНИЕ)
- § 10.2. Основные черты последовательного критерия для выбора гипотезы из множества взаимно исключающих друг друга гипотез
- § 10.3. Последствия выбора любого частного способа последовательной выборочной проверки
- § 10.4. Принципы выбора плана последовательной выборки
- 10.4.2. Функция риска, связанная с данным способом проверки.
- 10.4.3. Функция риска и среднее число наблюдений как основа для выбора плана последовательной выборки.
- 10.4.4. Использование некоторых простых весовых функций.
- § 10.5. Обсуждение специального класса планов последовательной выборки
- ГЛАВА 11. ПРОБЛЕМА ПОСЛЕДОВАТЕЛЬНОЙ ОЦЕНКИ
- § 11.1. Принципы современной теории оценок интервалами или множествами
- § 11.2. Постановка задачи о последовательной оценке посредством интервалов или множеств
- § 11.3. Специальный класс способов последовательной оценки
- ПРИЛОЖЕНИЯ
- П.1. Доказательство того, что с вероятностью, равной единице, последовательный критерий отношений вероятностей рано или поздно закончится
- П.2. Верхняя и нижняя границы оперативной характеристики последовательного критерия
- П.2.3. Определение верхней и нижней границ для оперативной характеристики.
- П.2.4. Расчет … для биномиального распределения
- П.2.5. Вычисление … для нормального распределения.
- П.3. Верхняя и нижняя границы для функции среднего числа наблюдений последовательного критерия отношений вероятностей
- П.3.2. Расчет величин … для биномиального и нормального распределений.
- П.4. Вывод точных формул для оперативной характеристики и функции среднего числа наблюдений в случае, когда z может принимать только конечное число значений, кратных постоянному числу
- П. 5. Характеристическая функция и высшие моменты величины n
- П.5.2. Вывод точной формулы для случая, когда z может принимать только конечное число значений, кратных некоторому постоянному числу.
- П.6. Приближенное распределение величины n для случая, когда z распределена по нормальному закону
- П.7. Эффективность последовательного критерия отношений вероятностей
- П.8. Определение оптимальной весовой функции w(O) в некоторых специальных случаях проверки простых гипотез без ограничения возможных конкурирующих значений параметров
- П.8.2. Приложение к проверке средних значений независимых нормально распределенных случайных величин с известными дисперсиями.
- П.9. Определение оптимальных весовых функций … в некоторых специальных случаях проверки сложных гипотез
- П.9.2. Применение к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий).
- ДОПОЛНЕНИЯ. АСИМПТОТИЧЕСКИЕ МИНИМАКСНЫЕ РЕШЕНИЯ ЗАДАЧ ПОСЛЕДОВАТЕЛЬНЫХ ТОЧЕЧНЫХ ОЦЕНОК
- ДИФФЕРЕНЦИРОВАНИЕ ПОД ЗНАКОМ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ В ОСНОВНОМ ТОЖДЕСТВЕ ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА
- НЕКОТОРЫЕ УТОЧНЕНИЯ ГРАНИЦ ДЛЯ СРЕДНЕГО ЧИСЛА НАБЛЮДЕНИЙ В ПОСЛЕДОВАТЕЛЬНОМ КРИТЕРИИ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
- ОПТИМАЛЬНЫЙ ХАРАКТЕР ПОСЛЕДОВАТЕЛЬНОГО КРИТЕРИЯ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
- ОСНОВНЫЕ ИДЕИ ОБЩЕЙ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ