| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.3.5. Проверка гипотезы как выбор между двумя возможными действиями.
На практике часто появляется необходимость выбора между двумя возможными действиями, скажем действием 1 и действием 2, причем предпочтительность того или иного действия зависит от величины неизвестного параметра  в распределении случайной величины х. Обозначим через
в распределении случайной величины х. Обозначим через  множество всех величин 0, для которых действие 1 предпочтительнее. Следовательно, для любой величины
множество всех величин 0, для которых действие 1 предпочтительнее. Следовательно, для любой величины  не входящей в
не входящей в  действие 2 предпочтительнее действия 1. Проблему выбора между этими двумя действиями в случае, когда выбор проводится на основе
действие 2 предпочтительнее действия 1. Проблему выбора между этими двумя действиями в случае, когда выбор проводится на основе  независимых наблюдений величины
независимых наблюдений величины  можно толковать как проблему проверки гипотезы
можно толковать как проблему проверки гипотезы  о том, что истинная величина
о том, что истинная величина  принадлежит множеству а). Если наша проверка приводит К принятию гипотезы И, мы совершаем действие 1; если проверка приводит к отклонению гипотезы
принадлежит множеству а). Если наша проверка приводит К принятию гипотезы И, мы совершаем действие 1; если проверка приводит к отклонению гипотезы  мы совершаем действие 2.
мы совершаем действие 2.
Рассмотрим в качестве примера следующую задачу. Предположим, что приемочной проверке подвергается партия товара, состоящая из большого количества промышленных изделий. Доля  дефектных изделий для данной партии неизвестна. Тогда возможны два действия: принять данную партию или забраковать ее. Вообще говоря, существует такая величина
дефектных изделий для данной партии неизвестна. Тогда возможны два действия: принять данную партию или забраковать ее. Вообще говоря, существует такая величина  что если истинная доля дефектных изде
что если истинная доля дефектных изде  меньше
меньше  то мы предпочитаем принять всю партию товара, а если
то мы предпочитаем принять всю партию товара, а если  то мы предпочитаем забраковать ее.
то мы предпочитаем забраковать ее.
Если  то для нас безразлично, принять партию или забраковать ее. Предположим, что решение о принятии партии принимается на основе выборки из
то для нас безразлично, принять партию или забраковать ее. Предположим, что решение о принятии партии принимается на основе выборки из  изделий, выбранных случайным образом из проверяемой партии. Тогда наша задача эквивалентна задаче проверки гипотезы И о том, что
изделий, выбранных случайным образом из проверяемой партии. Тогда наша задача эквивалентна задаче проверки гипотезы И о том, что  по Данной выборке, взятой из проверяемой партии. Вся партия принимается или бракуется в зависимости от того, принимается или отклоняется гипотеза И.
по Данной выборке, взятой из проверяемой партии. Вся партия принимается или бракуется в зависимости от того, принимается или отклоняется гипотеза И.
Как уже упоминалось в п. 1.3.3, выбор величины а, т. е. выбор уровня критической области, сильно зависит от относительной важности ошибок первого и второго рода. Если задача проверки той или иной гипотезы связана с проблемой выбора одного из двух возможных действий, то относительная важность ошибок первого и второго рода вытекает из рассмотрения практических последствий от принятия того или иного решения в тех случаях, когда величина интересующего нас параметра делает предпочтительным решение, как раз обратное принятому.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ЧАСТЬ 1. ОБЩАЯ ТЕОРИЯ
- 1.1.1. Понятие случайной величины.
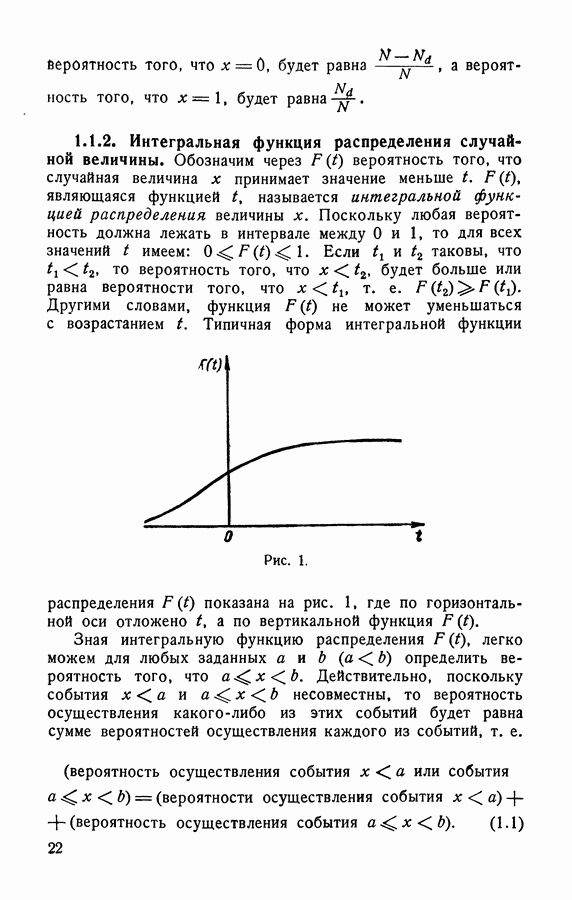
- 1.1.2. Интегральная функция распределения случайной величины.
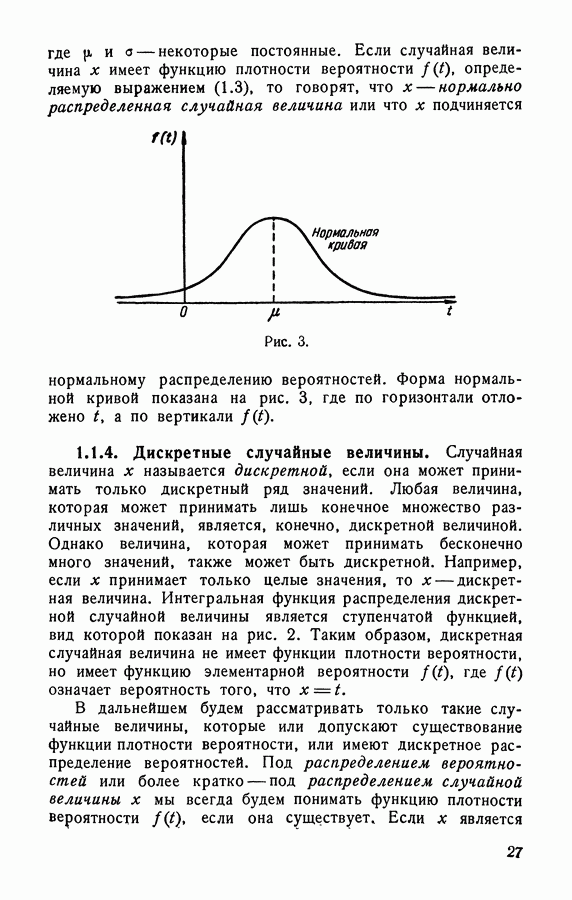
- 1.1.3. Функция плотности вероятности.
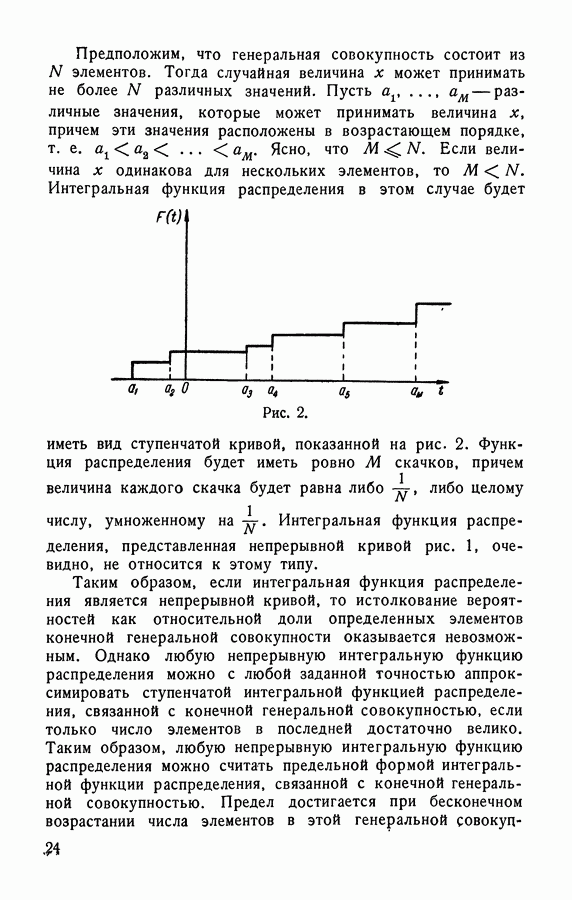
- 1.1.4. Дискретные случайные величины.
- 1.1.5. Математическое ожидание и высшие моменты случайной величины.
- § 1.2. Понятие статистической гипотезы
- 1.2.2. Простые и сложные гипотезы.
- § 1.3. Основные черты существующей методики проверки статистических гипотез
- 1.3.2. Общая методика проверки статистических гипотез.
- 1.3.3. Принципы выбора критической области.
- 1.3.4. Количество наблюдений, необходимых при заданных вероятностях a и b.
- 1.3.5. Проверка гипотезы как выбор между двумя возможными действиями.
- ГЛАВА 2. ПОСЛЕДОВАТЕЛЬНАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ОБЩИЕ ВОПРОСЫ
- § 2.2. Последствия выбора конкретной методики последовательной проверки
- 2.2.2. Функция среднего числа наблюдений последовательного критерия.
- § 2.3. Принципы, на которых основывается выбор последовательного критерия
- 2.3.2. Требования, предъявляемые к оперативной характеристике.
- 2.3.3. Функция среднего числа наблюдений как основа для выбора последовательного критерия.
- § 2.4. Проверка простой гипотезы Н0 при единственной конкурирующей гипотезе Н1
- 2.4.2. Эффективность существующей методики проверки гипотез, рассматриваемой как частный случай последовательного критерия.
- ГЛАВА 3. ПОСЛЕДОВАТЕЛЬНЫЙ КРИТЕРИЙ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ ДЛЯ ПРОВЕРКИ ПРОСТОЙ ГИПОТЕЗЫ Н0 ПРОТИВ ЕДИНСТВЕННОЙ КОНКУРИРУЮЩЕЙ ГИПОТЕЗЫ Н1
- § 3.1. Определение последовательного критерия отношений вероятностей
- § 3.2. Основные соотношения между величинами a, b, A и B
- § 3.3. Определение постоянных A и B на практике
- § 3.4. Оперативная характеристика последовательного критерия отношений вероятностей
- § 3.5. Среднее число наблюдений последовательного критерия отношений вероятностей
- § 3.6. Выигрыш в числе наблюдений при использовании последовательного критерия отношений вероятностей вместо обычной процедуры проверки
- § 3.7. Нижняя граница вероятности того, что последовательный критерий окончится при числе наблюдений, меньшем или равном заданному числу
- § 3.8. Усечение процедуры последовательного анализа
- § 3.9. Увеличение среднего числа наблюдений, обусловленное заменой точных значений A(a,b) и B(a,b) на …
- ГЛАВА 4. ОСНОВЫ ТЕОРИИ ПОСЛЕДОВАТЕЛЬНЫХ КРИТЕРИЕВ ДЛЯ ПРОСТЫХ И СЛОЖНЫХ ГИПОТЕЗ ОТНОСИТЕЛЬНО МНОЖЕСТВА КОНКУРИРУЮЩИХ ГИПОТЕЗ
- 4.1.2. Проверка простой гипотезы при односторонних конкурирующих гипотезах.
- 4.1.3. Проверка простой гипотезы в случае, когда на конкурирующие величины неизвестных параметров не накладывается никаких ограничений.
- 4.1.4. Применение общей методики к проверке среднего значения нормального распределения с известной дисперсией.
- § 4.2. Проверка сложных гипотез
- 4.2.2. Описание методики проверки в общем случае.
- 4.2.3. Применение общей методики к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий).
- 4.2.4. Частный класс задач, рассмотренный Гиршиком.
- ЧАСТЬ II. ПРИЛОЖЕНИЕ ОБЩЕЙ ТЕОРИИ К ЧАСТНЫМ СЛУЧАЯМ
- ГЛАВА 5. КРИТЕРИЙ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ (ПРИЕМОЧНАЯ ПРОВЕРКА ПАРТИИ ИЗДЕЛИЙ, В КОТОРОЙ КАЖДОЕ ИЗДЕЛИЕ ОТНЕСЕНО К ОДНОЙ ИЗ ДВУХ КАТЕГОРИЙ)
- § 5.2. Допускаемый риск, связанный с принятием неправильных решений
- § 5.3. Последовательный критерий отношения вероятностей, соответствующий величинам …
- 5.3.2. Табличный метод проведения контроля.
- 5.3.3. Графический метод проведения контроля.
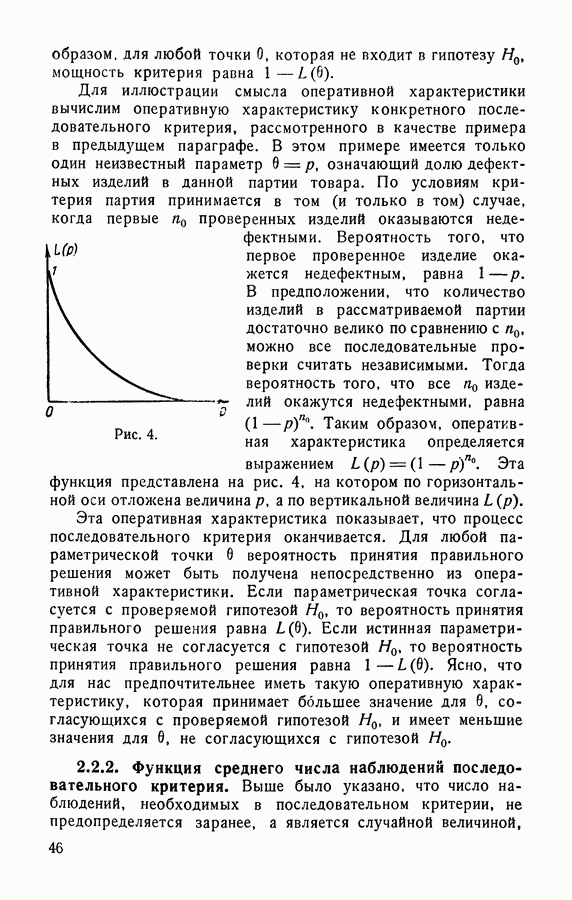
- § 5.4. Оперативная характеристика критерия L(p)
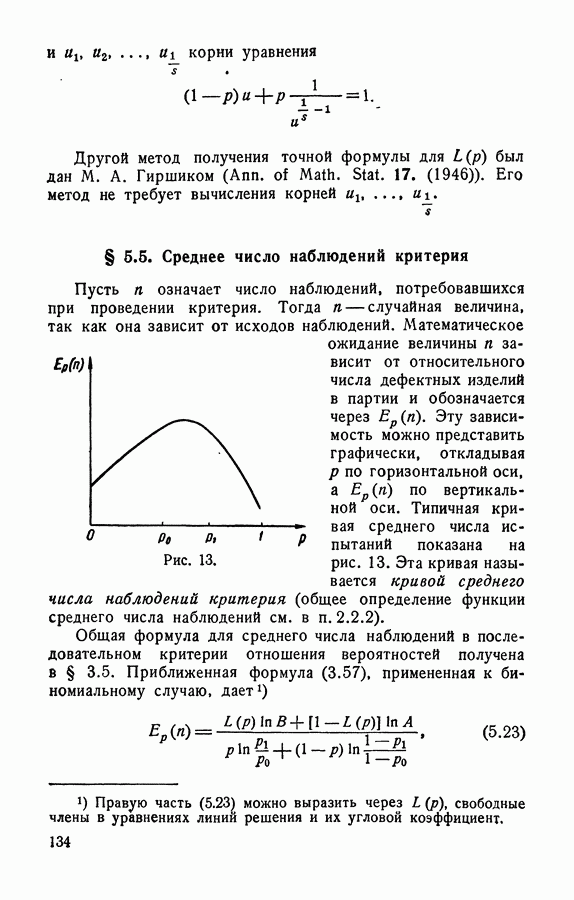
- § 5.5. Среднее число наблюдений критерия
- § 5.6. Группировка наблюдений
- 5.6.2. Влияние группировки на оперативную характеристику и среднее число наблюдений; верхние и нижние границы для них.
- § 5.7. Усеченный критерий
- ГЛАВА 6. КРИТЕРИЙ ДЛЯ РАЗНОСТИ МЕЖДУ СРЕДНИМИ ЗНАЧЕНИЯМИ ДВУХ БИНОМИАЛЬНЫХ РАСПРЕДЕЛЕНИЙ (ДВОЙНАЯ ДИХОТОМИЯ)
- § 6.4. Последовательный критерий для гипотезы …
- 6.4.1. Допускаемый риск, связанный с принятием неверных решений.
- 6.4.2. Последовательный критерий отношения вероятностей, соответствующий величинам u0, u1, a и b.
- 6.4.3. Кривая оперативной характеристики критерия.
- 6.4.4. Среднее число наблюдений, требуемых в критерии.
- 6.4.6. Наблюдения, осуществляемые группами.
- ГЛАВА 7. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНЫМ СРЕДНИМ КВАДРАТИЧЕСКИМ ОТКЛОНЕНИЕМ НЕ ПРЕВЫШАЕТ ЗАДАННОЙ ВЕЛИЧИНЫ
- § 7.2. Допускаемый риск, связанный с неправильным решением
- § 7.3. Последовательный критерий отношений вероятностей, соответствующий величинам …
- § 7.4. Кривая оперативной характеристики критерия
- § 7.6. Среднее число необходимых наблюдений в критерии
- ГЛАВА 8. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НЕ ПРЕВЫШАЕТ ЗАДАННОГО ЗНАЧЕНИЯ
- § 8.2. Допускаемый риск принятия неверного решения
- § 8.3. Последовательный критерий отношений вероятностей, соответствующий величинам …
- § 8.4. Оперативная характеристика критерия
- § 8.5. Среднее число наблюдений в критерии
- § 8.6. Модификация методики проверки, когда среднее значение генеральной совокупности неизвестно
- ГЛАВА 9. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНОЙ ДИСПЕРСИЕЙ РАВНО ОПРЕДЕЛЕННОЙ ВЕЛИЧИНЕ
- § 9.2. План последовательной проверки, удовлетворяющий заданным требованиям
- ЧАСТЬ III. ПРОБЛЕМА МНОГОЗНАЧНЫХ РЕШЕНИЙ И ОЦЕНКИ
- ГЛАВА 10. ВЫБОР ГИПОТЕЗЫ ИЗ МНОЖЕСТВА ВЗАИМНО ИСКЛЮЧАЮЩИХ ДРУГ ДРУГА ГИПОТЕЗ (МНОГОЗНАЧНОЕ РЕШЕНИЕ)
- § 10.2. Основные черты последовательного критерия для выбора гипотезы из множества взаимно исключающих друг друга гипотез
- § 10.3. Последствия выбора любого частного способа последовательной выборочной проверки
- § 10.4. Принципы выбора плана последовательной выборки
- 10.4.2. Функция риска, связанная с данным способом проверки.
- 10.4.3. Функция риска и среднее число наблюдений как основа для выбора плана последовательной выборки.
- 10.4.4. Использование некоторых простых весовых функций.
- § 10.5. Обсуждение специального класса планов последовательной выборки
- ГЛАВА 11. ПРОБЛЕМА ПОСЛЕДОВАТЕЛЬНОЙ ОЦЕНКИ
- § 11.1. Принципы современной теории оценок интервалами или множествами
- § 11.2. Постановка задачи о последовательной оценке посредством интервалов или множеств
- § 11.3. Специальный класс способов последовательной оценки
- ПРИЛОЖЕНИЯ
- П.1. Доказательство того, что с вероятностью, равной единице, последовательный критерий отношений вероятностей рано или поздно закончится
- П.2. Верхняя и нижняя границы оперативной характеристики последовательного критерия
- П.2.3. Определение верхней и нижней границ для оперативной характеристики.
- П.2.4. Расчет … для биномиального распределения
- П.2.5. Вычисление … для нормального распределения.
- П.3. Верхняя и нижняя границы для функции среднего числа наблюдений последовательного критерия отношений вероятностей
- П.3.2. Расчет величин … для биномиального и нормального распределений.
- П.4. Вывод точных формул для оперативной характеристики и функции среднего числа наблюдений в случае, когда z может принимать только конечное число значений, кратных постоянному числу
- П. 5. Характеристическая функция и высшие моменты величины n
- П.5.2. Вывод точной формулы для случая, когда z может принимать только конечное число значений, кратных некоторому постоянному числу.
- П.6. Приближенное распределение величины n для случая, когда z распределена по нормальному закону
- П.7. Эффективность последовательного критерия отношений вероятностей
- П.8. Определение оптимальной весовой функции w(O) в некоторых специальных случаях проверки простых гипотез без ограничения возможных конкурирующих значений параметров
- П.8.2. Приложение к проверке средних значений независимых нормально распределенных случайных величин с известными дисперсиями.
- П.9. Определение оптимальных весовых функций … в некоторых специальных случаях проверки сложных гипотез
- П.9.2. Применение к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий).
- ДОПОЛНЕНИЯ. АСИМПТОТИЧЕСКИЕ МИНИМАКСНЫЕ РЕШЕНИЯ ЗАДАЧ ПОСЛЕДОВАТЕЛЬНЫХ ТОЧЕЧНЫХ ОЦЕНОК
- ДИФФЕРЕНЦИРОВАНИЕ ПОД ЗНАКОМ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ В ОСНОВНОМ ТОЖДЕСТВЕ ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА
- НЕКОТОРЫЕ УТОЧНЕНИЯ ГРАНИЦ ДЛЯ СРЕДНЕГО ЧИСЛА НАБЛЮДЕНИЙ В ПОСЛЕДОВАТЕЛЬНОМ КРИТЕРИИ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
- ОПТИМАЛЬНЫЙ ХАРАКТЕР ПОСЛЕДОВАТЕЛЬНОГО КРИТЕРИЯ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
- ОСНОВНЫЕ ИДЕИ ОБЩЕЙ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ