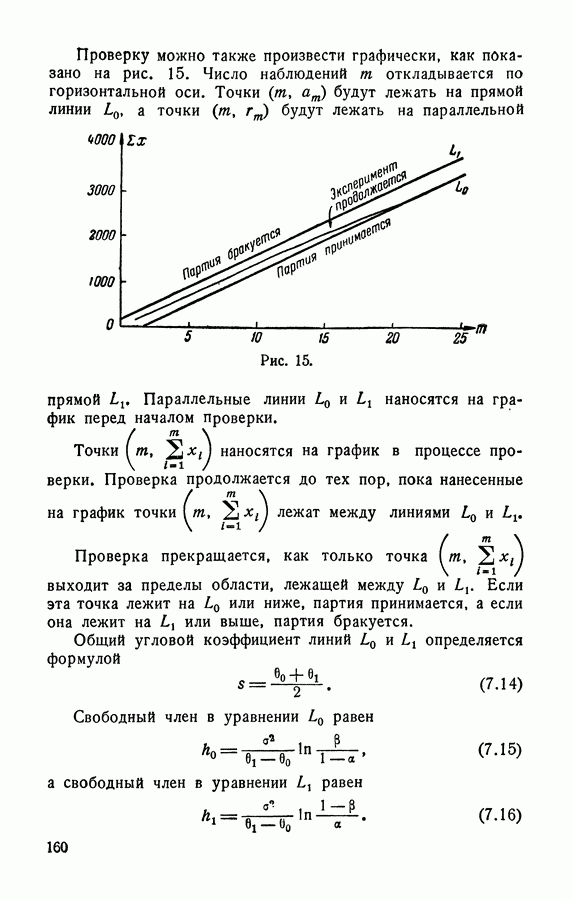
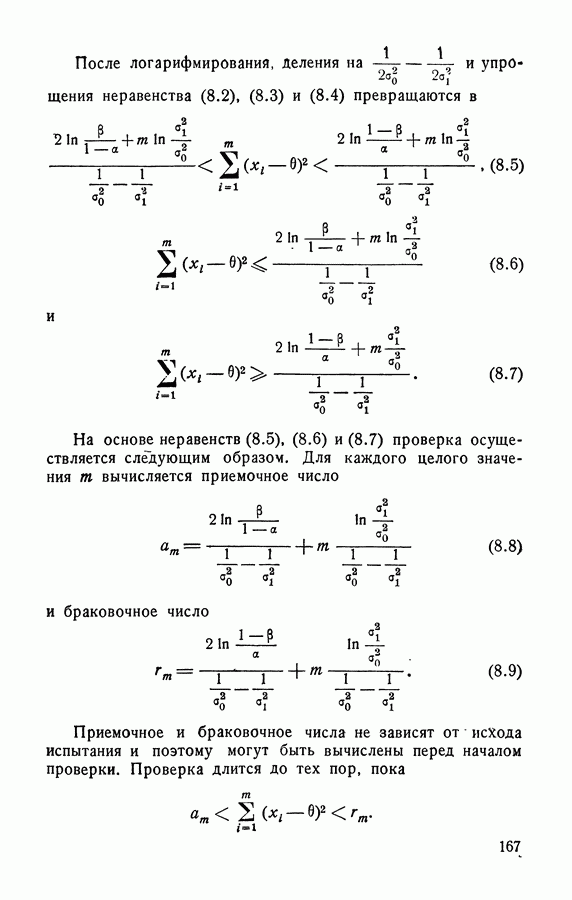
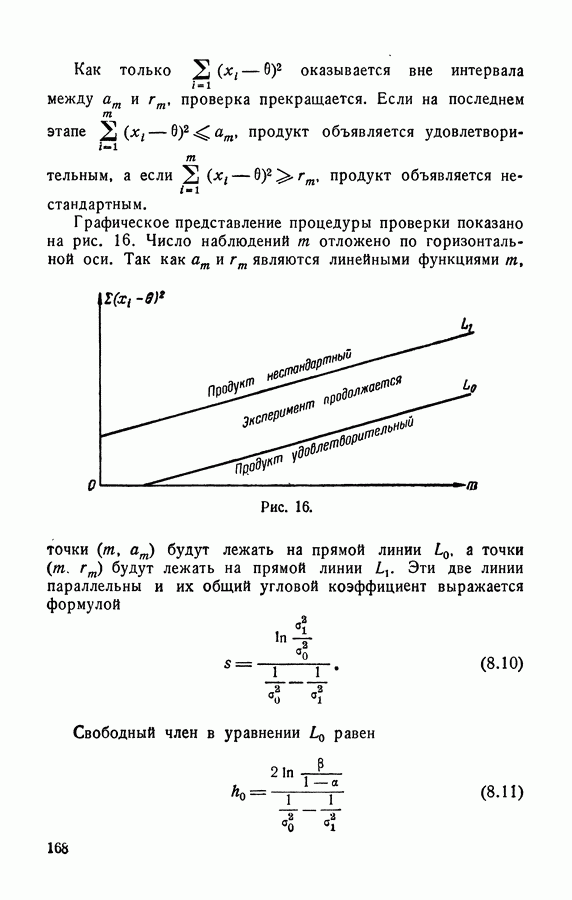
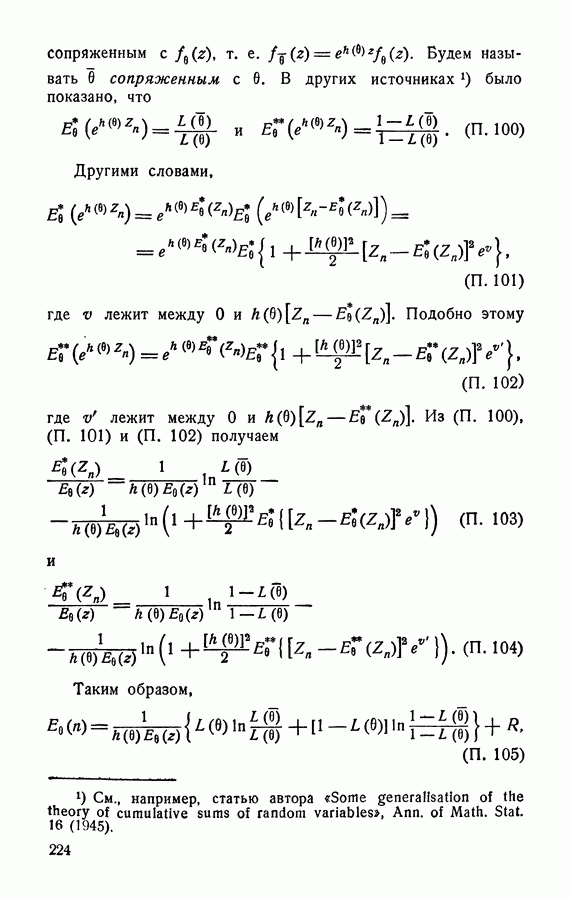| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА 8. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НЕ ПРЕВЫШАЕТ ЗАДАННОГО ЗНАЧЕНИЯ
§ 8.1. Постановка задачи
Пусть  нормально распределенная величина. В этой главе мы займемся проблемой проверки гипотезы о том, что среднее квадратическое отклонение а величины х не превышает заданной величины с. Рассматриваются два случая: с известным и неизвестным средним значением х. Начнем со случая, когда среднее значение х известно. Если среднее значение х неизвестно, необходима, как будет показано, лишь незначительная модернизация методики проверки.
нормально распределенная величина. В этой главе мы займемся проблемой проверки гипотезы о том, что среднее квадратическое отклонение а величины х не превышает заданной величины с. Рассматриваются два случая: с известным и неизвестным средним значением х. Начнем со случая, когда среднее значение х известно. Если среднее значение х неизвестно, необходима, как будет показано, лишь незначительная модернизация методики проверки.
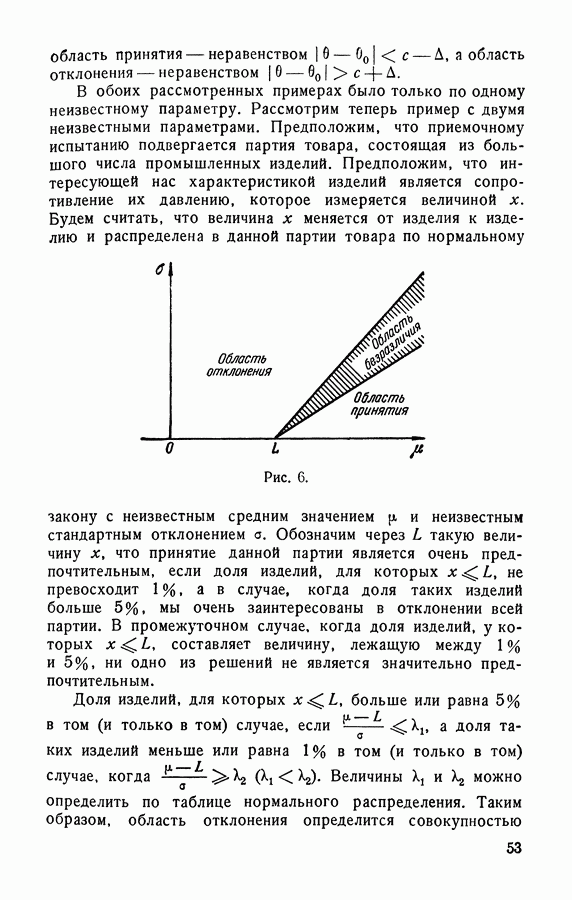
Эта проблема, как и проблема, рассмотренная в главе 7, часто возникает при контроле качества и приемочном контроле. Предположим, что х есть некая измеряемая характеристика качества производственной продукции и что х нормально распределено в совокупности готовых изделий. Предположим, что качество продукции считается тем более высоким, чем меньше среднее квадратическое отклонение а. При этом найдется, вообще говоря, такая величина о, что продукт считается нестандартным, если  и продукт считается удовлетворительным (отвечает спецификации), если а а. Так как а неизвестно, проблема состоит в том, чтобы разработать способ проверки гипотезы
и продукт считается удовлетворительным (отвечает спецификации), если а а. Так как а неизвестно, проблема состоит в том, чтобы разработать способ проверки гипотезы 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- ЧАСТЬ 1. ОБЩАЯ ТЕОРИЯ
- 1.1.1. Понятие случайной величины.
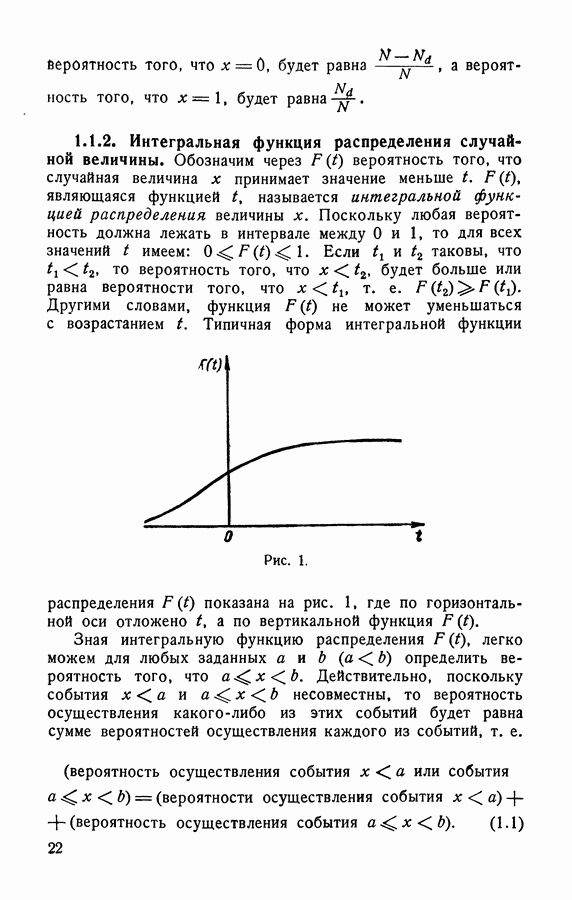
- 1.1.2. Интегральная функция распределения случайной величины.
- 1.1.3. Функция плотности вероятности.
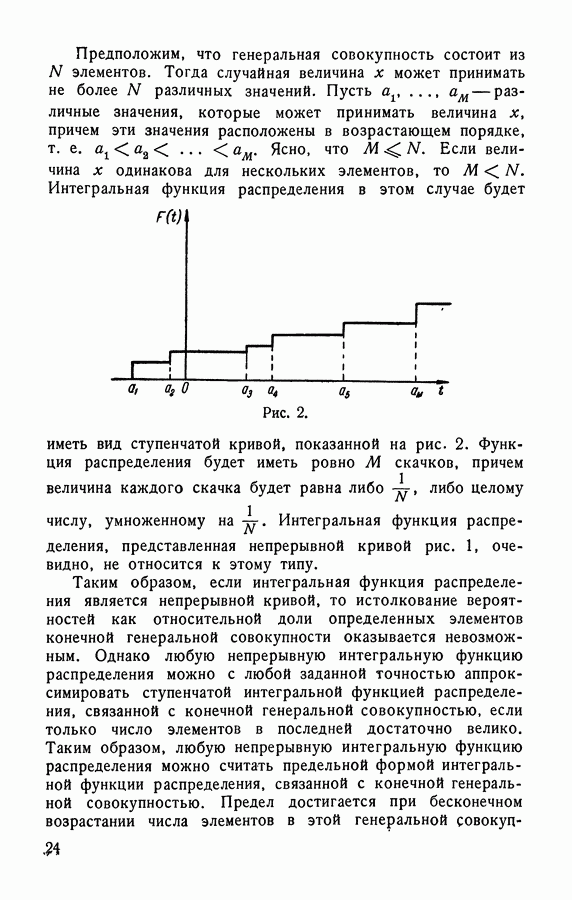
- 1.1.4. Дискретные случайные величины.
- 1.1.5. Математическое ожидание и высшие моменты случайной величины.
- § 1.2. Понятие статистической гипотезы
- 1.2.2. Простые и сложные гипотезы.
- § 1.3. Основные черты существующей методики проверки статистических гипотез
- 1.3.2. Общая методика проверки статистических гипотез.
- 1.3.3. Принципы выбора критической области.
- 1.3.4. Количество наблюдений, необходимых при заданных вероятностях a и b.
- 1.3.5. Проверка гипотезы как выбор между двумя возможными действиями.
- ГЛАВА 2. ПОСЛЕДОВАТЕЛЬНАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ОБЩИЕ ВОПРОСЫ
- § 2.2. Последствия выбора конкретной методики последовательной проверки
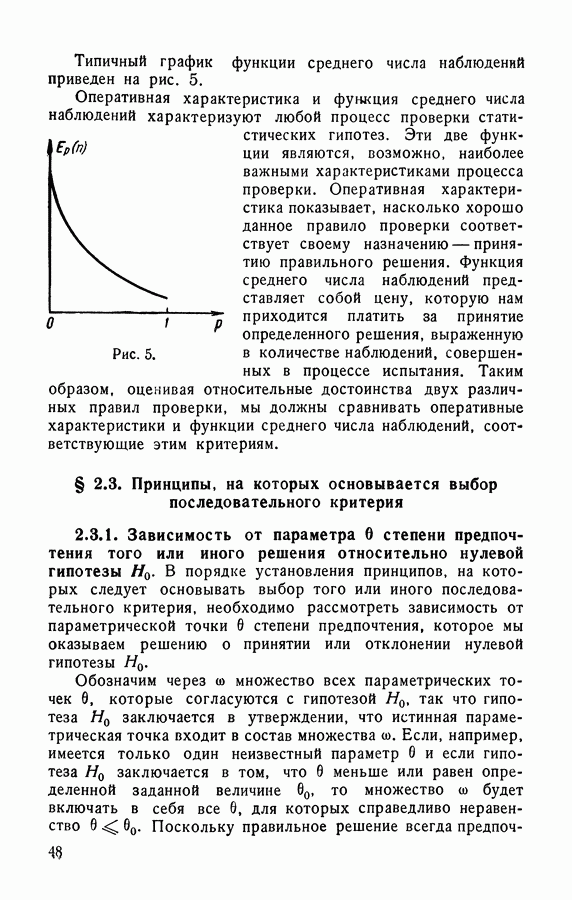
- 2.2.2. Функция среднего числа наблюдений последовательного критерия.
- § 2.3. Принципы, на которых основывается выбор последовательного критерия
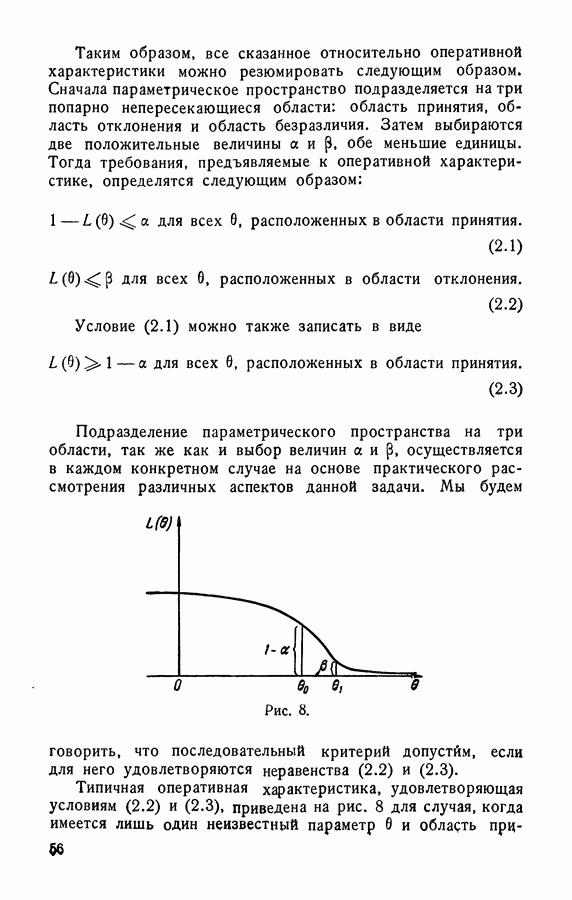
- 2.3.2. Требования, предъявляемые к оперативной характеристике.
- 2.3.3. Функция среднего числа наблюдений как основа для выбора последовательного критерия.
- § 2.4. Проверка простой гипотезы Н0 при единственной конкурирующей гипотезе Н1
- 2.4.2. Эффективность существующей методики проверки гипотез, рассматриваемой как частный случай последовательного критерия.
- ГЛАВА 3. ПОСЛЕДОВАТЕЛЬНЫЙ КРИТЕРИЙ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ ДЛЯ ПРОВЕРКИ ПРОСТОЙ ГИПОТЕЗЫ Н0 ПРОТИВ ЕДИНСТВЕННОЙ КОНКУРИРУЮЩЕЙ ГИПОТЕЗЫ Н1
- § 3.1. Определение последовательного критерия отношений вероятностей
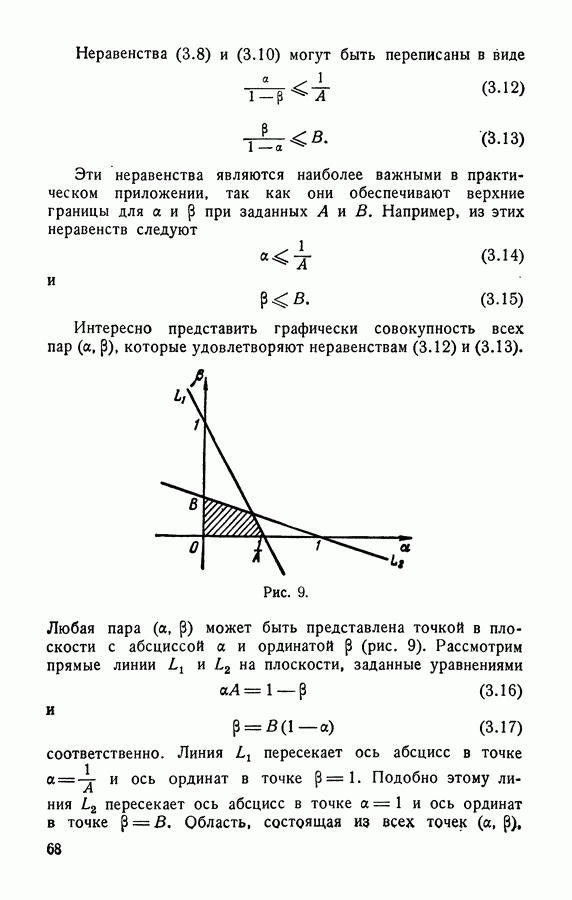
- § 3.2. Основные соотношения между величинами a, b, A и B
- § 3.3. Определение постоянных A и B на практике
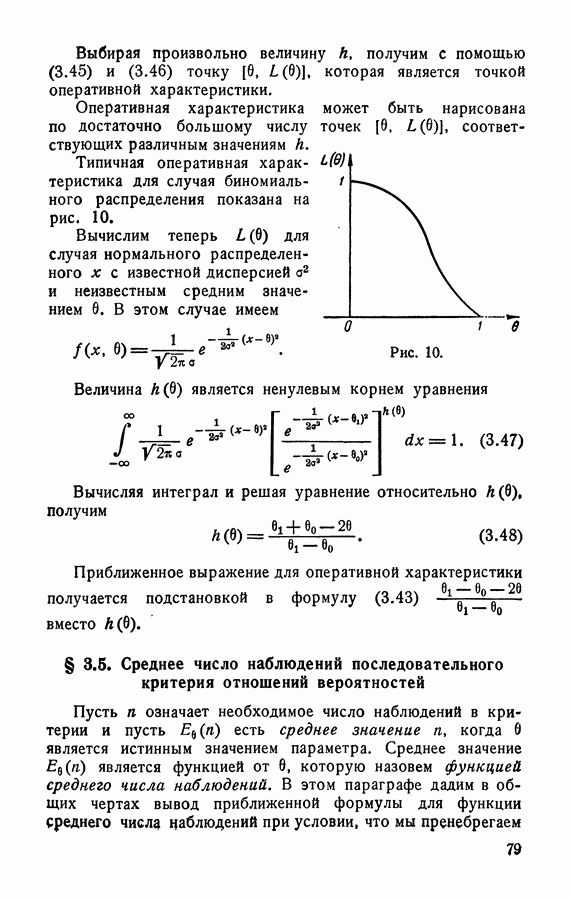
- § 3.4. Оперативная характеристика последовательного критерия отношений вероятностей
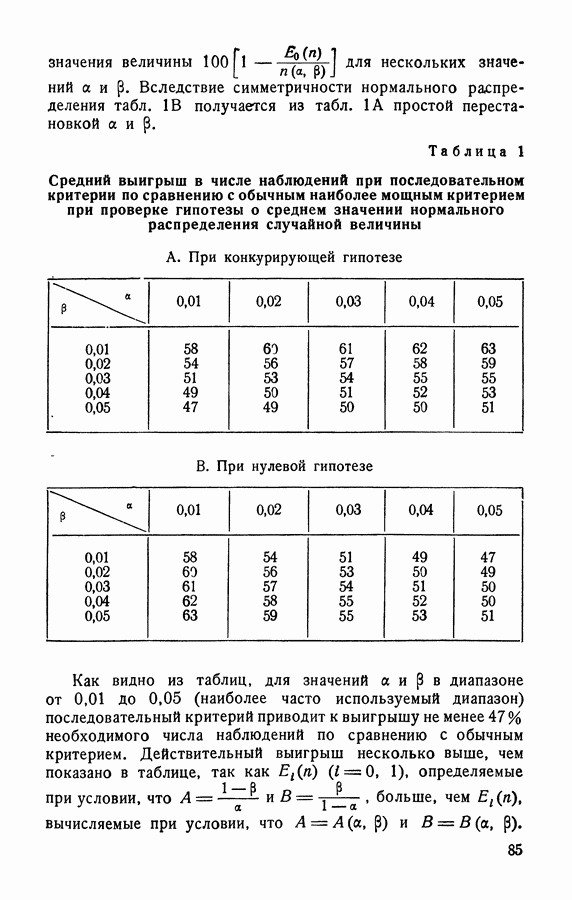
- § 3.5. Среднее число наблюдений последовательного критерия отношений вероятностей
- § 3.6. Выигрыш в числе наблюдений при использовании последовательного критерия отношений вероятностей вместо обычной процедуры проверки
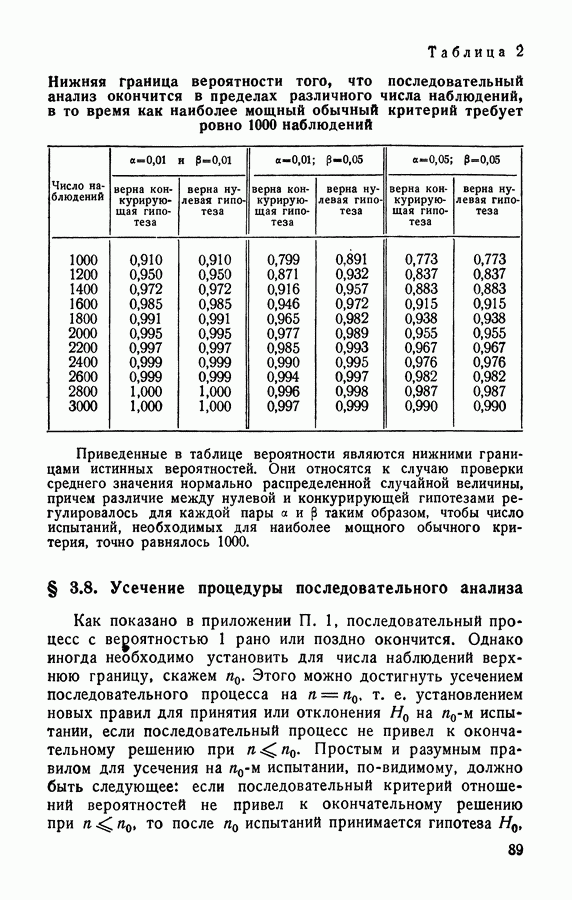
- § 3.7. Нижняя граница вероятности того, что последовательный критерий окончится при числе наблюдений, меньшем или равном заданному числу
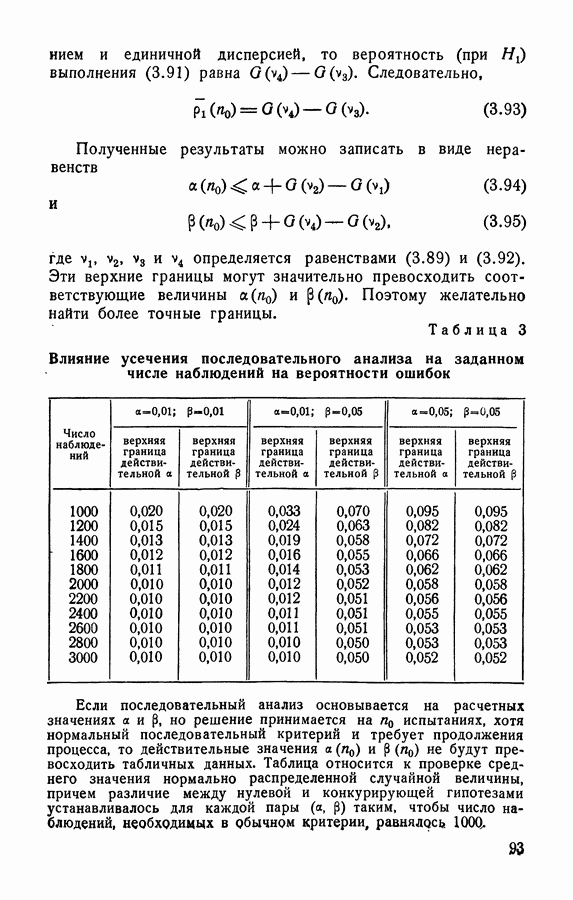
- § 3.8. Усечение процедуры последовательного анализа
- § 3.9. Увеличение среднего числа наблюдений, обусловленное заменой точных значений A(a,b) и B(a,b) на …
- ГЛАВА 4. ОСНОВЫ ТЕОРИИ ПОСЛЕДОВАТЕЛЬНЫХ КРИТЕРИЕВ ДЛЯ ПРОСТЫХ И СЛОЖНЫХ ГИПОТЕЗ ОТНОСИТЕЛЬНО МНОЖЕСТВА КОНКУРИРУЮЩИХ ГИПОТЕЗ
- 4.1.2. Проверка простой гипотезы при односторонних конкурирующих гипотезах.
- 4.1.3. Проверка простой гипотезы в случае, когда на конкурирующие величины неизвестных параметров не накладывается никаких ограничений.
- 4.1.4. Применение общей методики к проверке среднего значения нормального распределения с известной дисперсией.
- § 4.2. Проверка сложных гипотез
- 4.2.2. Описание методики проверки в общем случае.
- 4.2.3. Применение общей методики к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий).
- 4.2.4. Частный класс задач, рассмотренный Гиршиком.
- ЧАСТЬ II. ПРИЛОЖЕНИЕ ОБЩЕЙ ТЕОРИИ К ЧАСТНЫМ СЛУЧАЯМ
- ГЛАВА 5. КРИТЕРИЙ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ (ПРИЕМОЧНАЯ ПРОВЕРКА ПАРТИИ ИЗДЕЛИЙ, В КОТОРОЙ КАЖДОЕ ИЗДЕЛИЕ ОТНЕСЕНО К ОДНОЙ ИЗ ДВУХ КАТЕГОРИЙ)
- § 5.2. Допускаемый риск, связанный с принятием неправильных решений
- § 5.3. Последовательный критерий отношения вероятностей, соответствующий величинам …
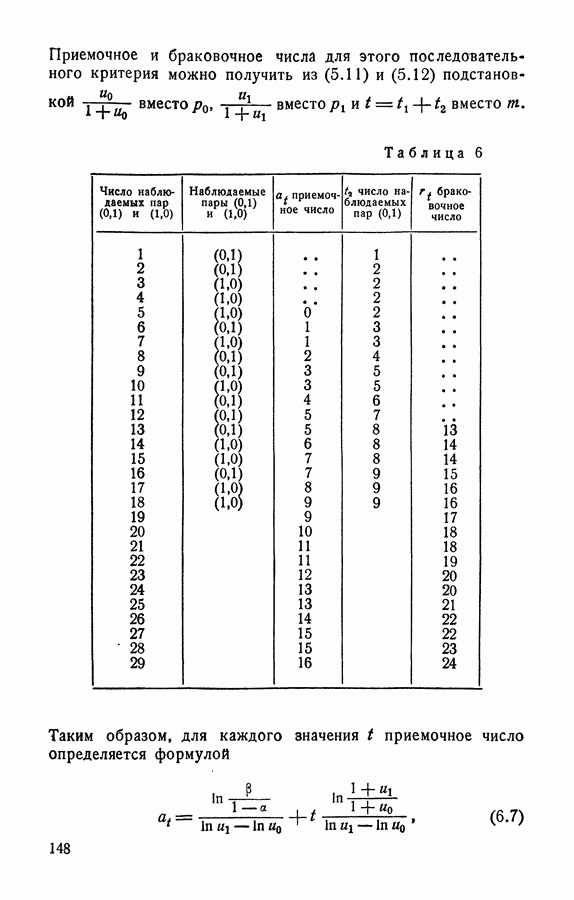
- 5.3.2. Табличный метод проведения контроля.
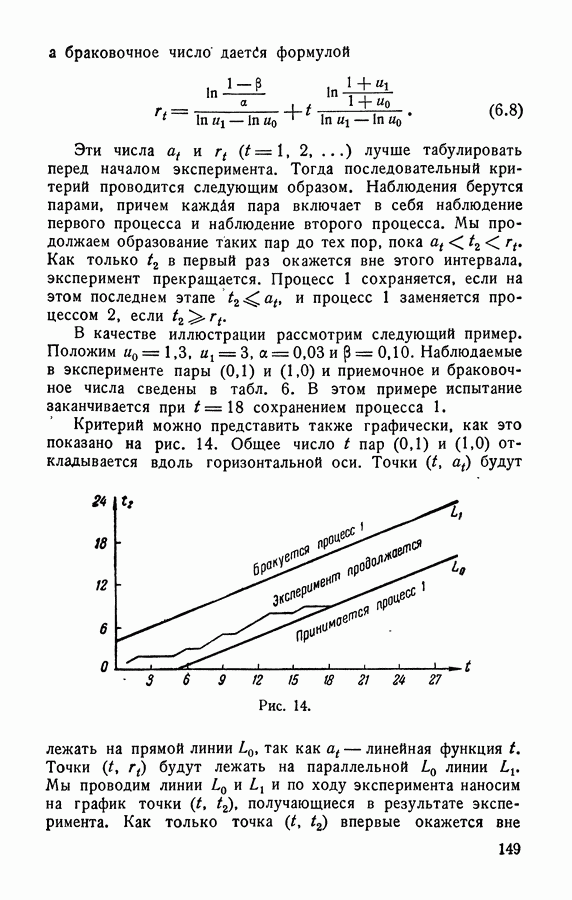
- 5.3.3. Графический метод проведения контроля.
- § 5.4. Оперативная характеристика критерия L(p)
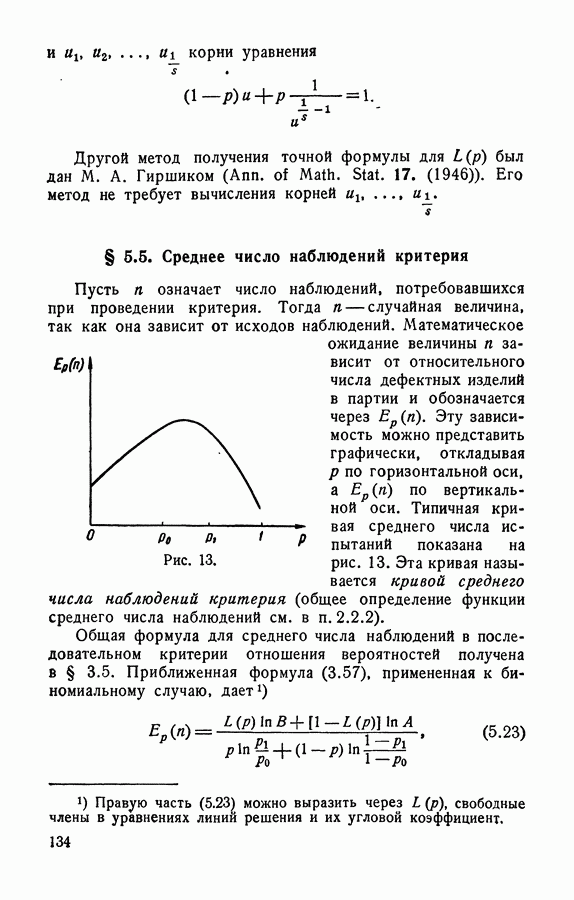
- § 5.5. Среднее число наблюдений критерия
- § 5.6. Группировка наблюдений
- 5.6.2. Влияние группировки на оперативную характеристику и среднее число наблюдений; верхние и нижние границы для них.
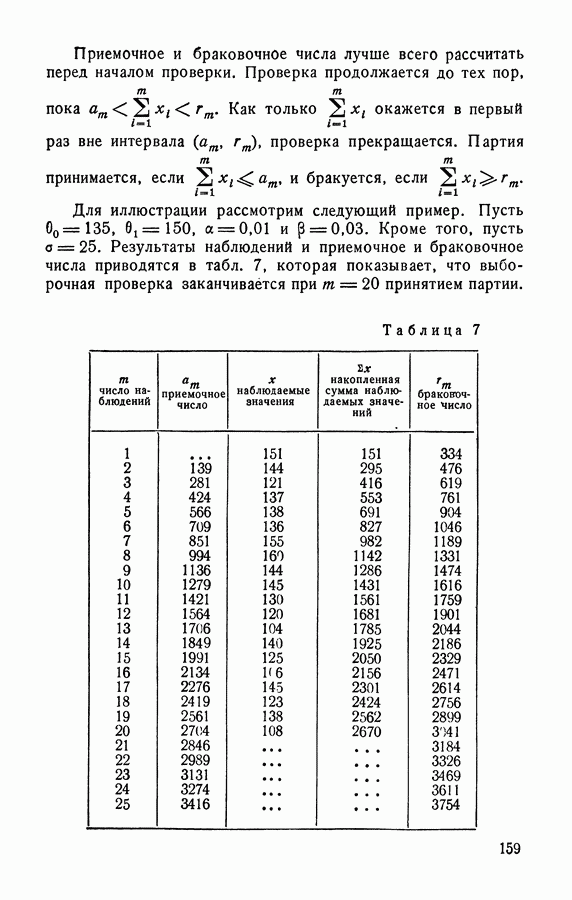
- § 5.7. Усеченный критерий
- ГЛАВА 6. КРИТЕРИЙ ДЛЯ РАЗНОСТИ МЕЖДУ СРЕДНИМИ ЗНАЧЕНИЯМИ ДВУХ БИНОМИАЛЬНЫХ РАСПРЕДЕЛЕНИЙ (ДВОЙНАЯ ДИХОТОМИЯ)
- § 6.4. Последовательный критерий для гипотезы …
- 6.4.1. Допускаемый риск, связанный с принятием неверных решений.
- 6.4.2. Последовательный критерий отношения вероятностей, соответствующий величинам u0, u1, a и b.
- 6.4.3. Кривая оперативной характеристики критерия.
- 6.4.4. Среднее число наблюдений, требуемых в критерии.
- 6.4.6. Наблюдения, осуществляемые группами.
- ГЛАВА 7. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНЫМ СРЕДНИМ КВАДРАТИЧЕСКИМ ОТКЛОНЕНИЕМ НЕ ПРЕВЫШАЕТ ЗАДАННОЙ ВЕЛИЧИНЫ
- § 7.2. Допускаемый риск, связанный с неправильным решением
- § 7.3. Последовательный критерий отношений вероятностей, соответствующий величинам …
- § 7.4. Кривая оперативной характеристики критерия
- § 7.6. Среднее число необходимых наблюдений в критерии
- ГЛАВА 8. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НЕ ПРЕВЫШАЕТ ЗАДАННОГО ЗНАЧЕНИЯ
- § 8.2. Допускаемый риск принятия неверного решения
- § 8.3. Последовательный критерий отношений вероятностей, соответствующий величинам …
- § 8.4. Оперативная характеристика критерия
- § 8.5. Среднее число наблюдений в критерии
- § 8.6. Модификация методики проверки, когда среднее значение генеральной совокупности неизвестно
- ГЛАВА 9. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНОЙ ДИСПЕРСИЕЙ РАВНО ОПРЕДЕЛЕННОЙ ВЕЛИЧИНЕ
- § 9.2. План последовательной проверки, удовлетворяющий заданным требованиям
- ЧАСТЬ III. ПРОБЛЕМА МНОГОЗНАЧНЫХ РЕШЕНИЙ И ОЦЕНКИ
- ГЛАВА 10. ВЫБОР ГИПОТЕЗЫ ИЗ МНОЖЕСТВА ВЗАИМНО ИСКЛЮЧАЮЩИХ ДРУГ ДРУГА ГИПОТЕЗ (МНОГОЗНАЧНОЕ РЕШЕНИЕ)
- § 10.2. Основные черты последовательного критерия для выбора гипотезы из множества взаимно исключающих друг друга гипотез
- § 10.3. Последствия выбора любого частного способа последовательной выборочной проверки
- § 10.4. Принципы выбора плана последовательной выборки
- 10.4.2. Функция риска, связанная с данным способом проверки.
- 10.4.3. Функция риска и среднее число наблюдений как основа для выбора плана последовательной выборки.
- 10.4.4. Использование некоторых простых весовых функций.
- § 10.5. Обсуждение специального класса планов последовательной выборки
- ГЛАВА 11. ПРОБЛЕМА ПОСЛЕДОВАТЕЛЬНОЙ ОЦЕНКИ
- § 11.1. Принципы современной теории оценок интервалами или множествами
- § 11.2. Постановка задачи о последовательной оценке посредством интервалов или множеств
- § 11.3. Специальный класс способов последовательной оценки
- ПРИЛОЖЕНИЯ
- П.1. Доказательство того, что с вероятностью, равной единице, последовательный критерий отношений вероятностей рано или поздно закончится
- П.2. Верхняя и нижняя границы оперативной характеристики последовательного критерия
- П.2.3. Определение верхней и нижней границ для оперативной характеристики.
- П.2.4. Расчет … для биномиального распределения
- П.2.5. Вычисление … для нормального распределения.
- П.3. Верхняя и нижняя границы для функции среднего числа наблюдений последовательного критерия отношений вероятностей
- П.3.2. Расчет величин … для биномиального и нормального распределений.
- П.4. Вывод точных формул для оперативной характеристики и функции среднего числа наблюдений в случае, когда z может принимать только конечное число значений, кратных постоянному числу
- П. 5. Характеристическая функция и высшие моменты величины n
- П.5.2. Вывод точной формулы для случая, когда z может принимать только конечное число значений, кратных некоторому постоянному числу.
- П.6. Приближенное распределение величины n для случая, когда z распределена по нормальному закону
- П.7. Эффективность последовательного критерия отношений вероятностей
- П.8. Определение оптимальной весовой функции w(O) в некоторых специальных случаях проверки простых гипотез без ограничения возможных конкурирующих значений параметров
- П.8.2. Приложение к проверке средних значений независимых нормально распределенных случайных величин с известными дисперсиями.
- П.9. Определение оптимальных весовых функций … в некоторых специальных случаях проверки сложных гипотез
- П.9.2. Применение к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий).
- ДОПОЛНЕНИЯ. АСИМПТОТИЧЕСКИЕ МИНИМАКСНЫЕ РЕШЕНИЯ ЗАДАЧ ПОСЛЕДОВАТЕЛЬНЫХ ТОЧЕЧНЫХ ОЦЕНОК
- ДИФФЕРЕНЦИРОВАНИЕ ПОД ЗНАКОМ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ В ОСНОВНОМ ТОЖДЕСТВЕ ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА
- НЕКОТОРЫЕ УТОЧНЕНИЯ ГРАНИЦ ДЛЯ СРЕДНЕГО ЧИСЛА НАБЛЮДЕНИЙ В ПОСЛЕДОВАТЕЛЬНОМ КРИТЕРИИ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
- ОПТИМАЛЬНЫЙ ХАРАКТЕР ПОСЛЕДОВАТЕЛЬНОГО КРИТЕРИЯ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ
- ОСНОВНЫЕ ИДЕИ ОБЩЕЙ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ